Characterization of Frictional Properties of Single-Layer Molybdenum-Disulfide Film Based on a Coupling of Tip Radius and Tip–Sample Distance by Molecular-Dynamics Simulations
Abstract
:1. Introduction
2. Materials and Methods
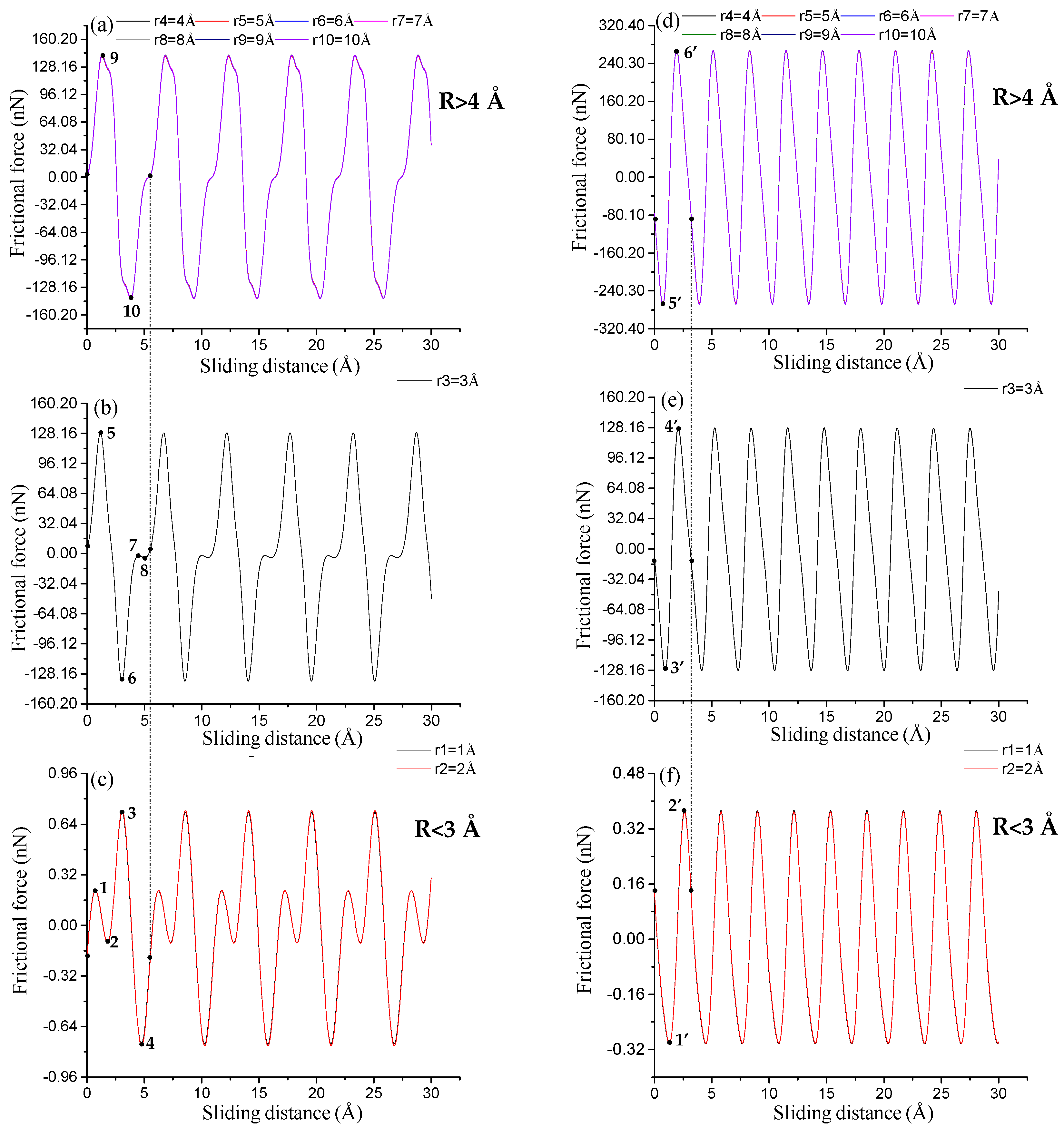
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Uluutku, B.; Baykara, M.Z. Effect of lateral tip stiffness on atomic-resolution force field spectroscopy. J. Vac. Sci. Technol. B 2013, 31, 1801. [Google Scholar] [CrossRef] [Green Version]
- Scherer, V.; Arnold, W.; Bhushan, B. Lateral force microscopy (LFM). Surf. Interface Anal. 2015, 27, 578–587. [Google Scholar] [CrossRef]
- Maragliano, C.; Glia, A.; Stefancich, M.; Chiesa, M. Effective AFM cantilever tip size: Methods for in-situ determination. Meas. Sci. Technol. 2015, 26, 015002. [Google Scholar] [CrossRef]
- Weymouth, A.J.; Hofmann, T.; Giessibl, F.J. Quantifying molecular stiffness and interaction with lateral force microscopy. Science 2014, 343, 1120–1122. [Google Scholar] [CrossRef] [PubMed]
- Uluutku, B.; Baykara, M.Z. Artifacts related to tip asymmetry in high-resolution atomic force microscopy and scanning tunneling microscopy measurements of graphitic surfaces. J. Vac. Sci. Technol. B 2015, 33, 031802. [Google Scholar] [CrossRef] [Green Version]
- Baykara, M.Z.; Dagdeviren, O.E.; Schwendemann, T.C.; Mönig, H.; Altman, E.I.; Schwarz, U.D. Probing three-dimensional surface force fields with atomic resolution: Measurement strategies, limitations, and artifact reduction. Beilstein J. Nanotechnol. 2012, 3, 637–650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kawai, S.; Glatzel, T.; Koch, S.; Baratoff, A.; Meyer, E. Interaction-induced atomic displacements revealed by drift-corrected dynamic force spectroscopy. Phys. Rev. B 2011, 83, 035421. [Google Scholar] [CrossRef]
- Pou, P.; Ghasemi, S.A.; Jelinek, P.; Lenosky, T.; Goedecker, S.; Perez, R. Structure and stability of semiconductor tip apexes for atomic force microscopy. Nanotechnology 2009, 20, 264015. [Google Scholar] [CrossRef] [PubMed]
- Gross, L.; Mohn, F.; Moll, N.; Liljeroth, P.; Meyer, G. Effective AFM cantilever tip size: Methods for in-situ determination. Science 2009, 325, 1110. [Google Scholar] [CrossRef] [PubMed]
- Bamidele, J.; Kinoshita, Y.; Turanský, R.; Lee, S.H.; Naitoh, Y.; Li, Y.J.; Sugawara, Y.; Štich, I.; Kantorovich, L. Chemical tip fingerprinting in scanning probe microscopy of an oxidized Cu(110) surface. Phys. Rev. B 2012, 86, 4093–4096. [Google Scholar] [CrossRef]
- Xue, B.; Yan, Y.; Hu, Z.; Zhao, X. Study on effects of scan parameters on the image quality and tip wear in AFM tapping mode. Scanning 2014, 36, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Akamine, S.; Barrett, R.C.; Quate, C.F. Improved AFM images using micro-cantilevers with sharp tips. Appl. Phys. Lett. 1990, 57, 316–318. [Google Scholar] [CrossRef]
- Komiyama, M.; Ohkubo, S.Y.; Tazawa, K.; Tsujimichi, K.; Hirotani, A.; Kubo, M.; Miyamoto, A. Effects of atomic arrangement at tip apex and tip-sample distance on atomic force microscopy images: A simulation study. Jpn. J. Appl. Phys. 1996, 35, 2318–2325. [Google Scholar] [CrossRef]
- Hölscher, H.; Schwarz, U.D.; Wiesendanger, R. Modelling of the scan process in lateral force microscopy. Surf. Sci. 1997, 375, 395–402. [Google Scholar] [CrossRef]
- Meng, L.; Shi, J.; Liu, L.; Peng, Y.; Ning, X.; Wang, Y. Experimental study and modeling of atomic-scale friction in zigzag and armchair lattice orientations of MoS2. Sci. Technol. Adv. Mater. 2016, 17, 189–199. [Google Scholar]
- Dong, Y.; Vadakkepatt, A.; Martini, A. Analytical models for atomic friction. Tribol. Lett. 2011, 44, 367. [Google Scholar] [CrossRef]
- Molina, F.; Llácer, C.; Vila, A.O.; Puchol, A.; Figueruelo, J. Interaction of ionic compounds with multilamellar liposomes. An electrokinetic model. Colloids Surf. A 1998, 140, 91–101. [Google Scholar] [CrossRef]
- Tichy, G. Interaction potentials in metals. Comput. Mater. Sci. 1994, 2, 375–378. [Google Scholar] [CrossRef]
- Dulieu, O.; Lévy, B.; Magnier, S.; Masnou-Seeuws, F.; Millié, P. Long range potentials for two Na3p atoms including ionic-covalent interaction and fine structure: Application to two-color photoassociation spectroscopy. Phys. Rev. Lett. 1996, 76, 2858. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H.M.; Jung, Y.; Jun, S.C.; Kondaraju, S.; Lee, J.S. Molecular dynamics simulations of nanoscale and sub-nanoscale friction behavior between graphene and a silicon tip: Analysis of tip apex motion. Nanoscale 2015, 7, 6295–6303. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yang, C.; Bai, L.; Li, M.; Li, W. First-principles study on the structural and electronic properties of monolayer MoS2‚ with s-vacancy under uniaxial tensile strain. Nanomaterials 2018, 8, 74. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Xue, F.; Wang, L.; Chen, J.; Luo, J.; Jiang, T.; Zhang, C.; Wang, Z.L. Tribotronic enhanced photoresponsivity of a MoS2 phototransistor. Adv. Sci. 2016, 3, 1500419. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.A.; Kim, S.J.; Song, W.; Chang, S.J.; Park, C.Y.; Myung, S.; Lim, J.; Sun, S.L.; An, K.S. Fabrication of flexible optoelectronic devices based on MoS2/graphene hybrid patterns by a soft lithographic patterning method. Carbon 2017, 116, 167–173. [Google Scholar] [CrossRef]
- Plimpton, S.; Crozier, P.; Thompson, A. Lammps-large-scale atomic/molecular massively parallel simulator. J. Appl. Phys. 2007, 2, 4740–4742. [Google Scholar]
- Wang, W.; Hao, Y.; Yi, C.; Ji, X.; Niu, X. Relaxation properties of graphene nanoribbons at different ambient temperatures: A molecular dynamics. Acta Phys. Sin. 2012, 61, 2021–2036. [Google Scholar]
- Wang, W.; Li, L.; Yang, C.; Soler-Crespo, R.; Meng, Z.; Li, M.L.; Zhang, X.; Keten, S.; Espinosa, H. Plasticity resulted from phase transformation for monolayer molybdenum disulfide film during nanoindentation simulations. Nanotechnology 2017, 28, 164005. [Google Scholar] [CrossRef] [PubMed]
- Xiong, S.; Cao, G. Molecular dynamics simulations of mechanical properties of monolayer MoS2. Nanotechnology 2015, 26, 185705. [Google Scholar] [CrossRef] [PubMed]
- González, C.; Dappe, Y.J.; Biel, B. Reactivity enhancement and fingerprints of point defects on a MoS2 monolayer assessed by ab initio atomic force microscopy. J. Phys. Chem. C 2017, 120, 17115–17126. [Google Scholar] [CrossRef]
- Gyalog, T.; Bammerlin, M.; Lüthi, R.; Meyer, E.; Thomas, H. Mechanism of atomic friction. Europhys. Lett. 2016, 31, 269. [Google Scholar] [CrossRef]
- Yu, Y.Z.; Guo, J.G. Static and dynamic theoretical analyses of a scanning tip on suspended graphene surface. J. Appl. Phys. 2016, 120, 468–475. [Google Scholar] [CrossRef]
- Smolyanitsky, A.; Killgore, J.P. Anomalous friction in suspended graphene. Phys. Rev. B 2012, 86, 1514–1517. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, H.; Li, M.; Gao, C.; Lai, L.; Zhuo, W. Characterization of Frictional Properties of Single-Layer Molybdenum-Disulfide Film Based on a Coupling of Tip Radius and Tip–Sample Distance by Molecular-Dynamics Simulations. Nanomaterials 2018, 8, 387. https://doi.org/10.3390/nano8060387
Pang H, Li M, Gao C, Lai L, Zhuo W. Characterization of Frictional Properties of Single-Layer Molybdenum-Disulfide Film Based on a Coupling of Tip Radius and Tip–Sample Distance by Molecular-Dynamics Simulations. Nanomaterials. 2018; 8(6):387. https://doi.org/10.3390/nano8060387
Chicago/Turabian StylePang, Haosheng, Minglin Li, Chenghui Gao, Lianfeng Lai, and Weirong Zhuo. 2018. "Characterization of Frictional Properties of Single-Layer Molybdenum-Disulfide Film Based on a Coupling of Tip Radius and Tip–Sample Distance by Molecular-Dynamics Simulations" Nanomaterials 8, no. 6: 387. https://doi.org/10.3390/nano8060387
APA StylePang, H., Li, M., Gao, C., Lai, L., & Zhuo, W. (2018). Characterization of Frictional Properties of Single-Layer Molybdenum-Disulfide Film Based on a Coupling of Tip Radius and Tip–Sample Distance by Molecular-Dynamics Simulations. Nanomaterials, 8(6), 387. https://doi.org/10.3390/nano8060387




