A Phase Field Approach to Modeling Heavy Metal Impact in Plasma Spraying
Abstract
:1. Introduction
2. Mathematical Statement
2.1. Governing Equations for Drop Impact Dynamics
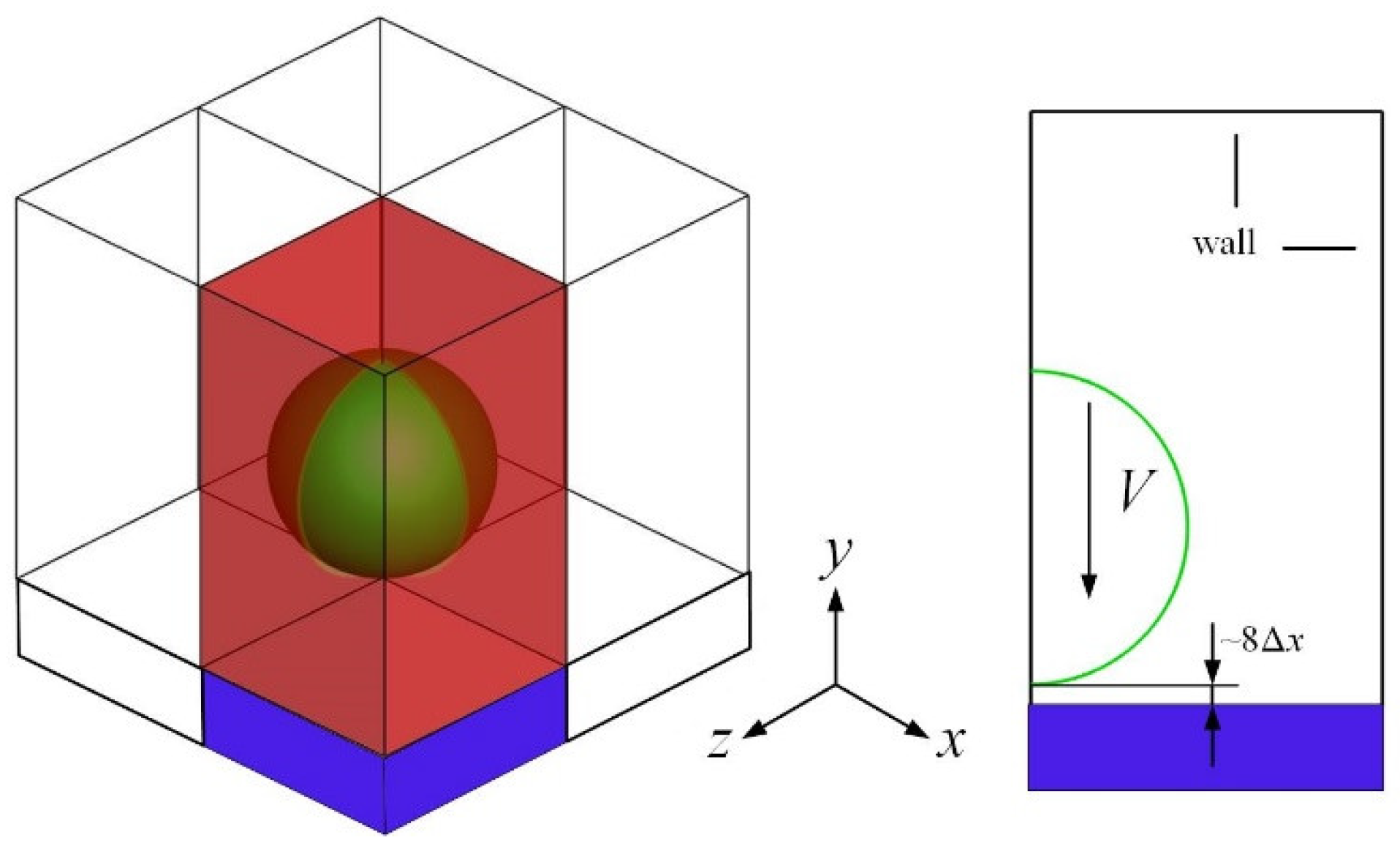
2.2. Boundary and Initial Conditions
2.3. Finite Difference Solution Enhanced with OpenMP
3. Results and Discussion
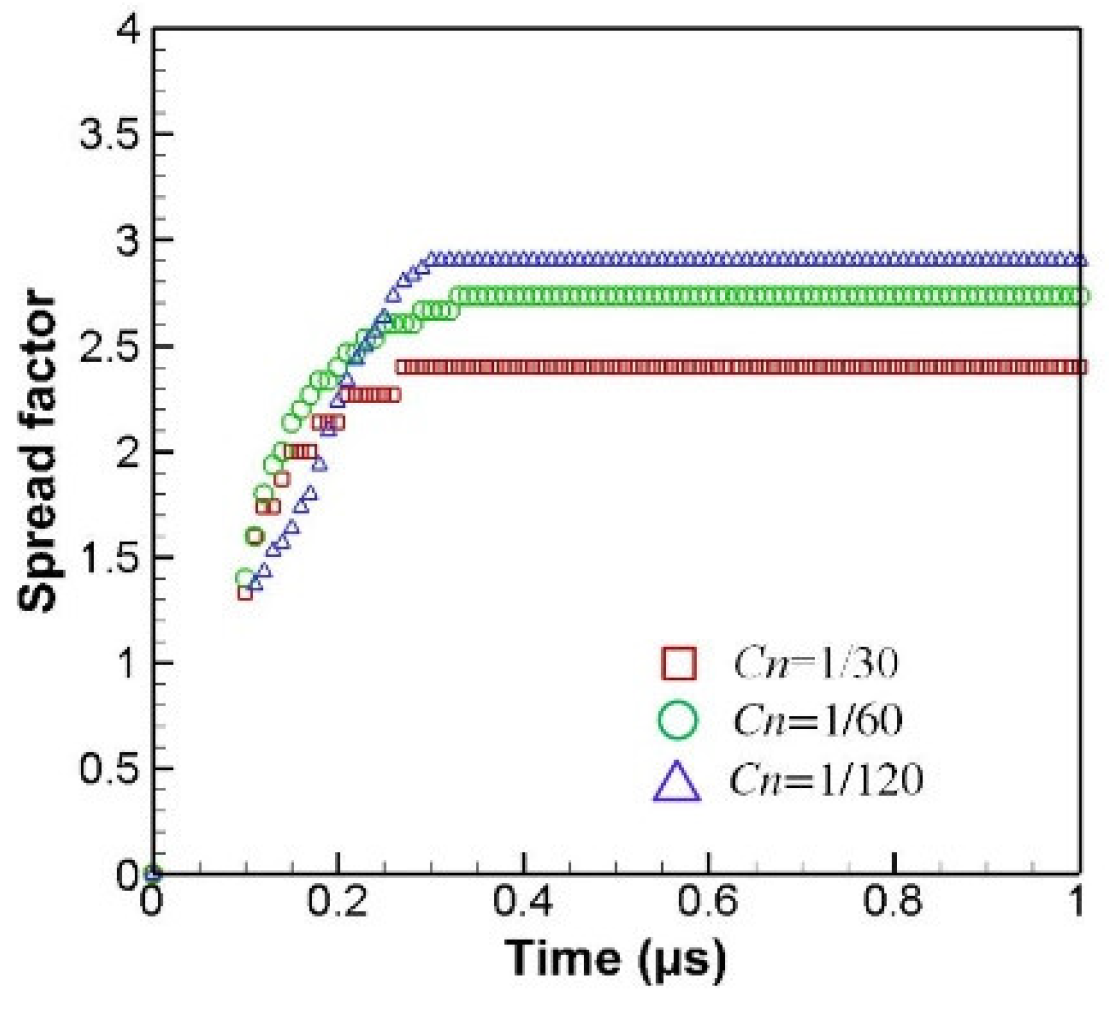
3.1. Mesh Sensitivity Study: Subsonic YSZ Drop Impact
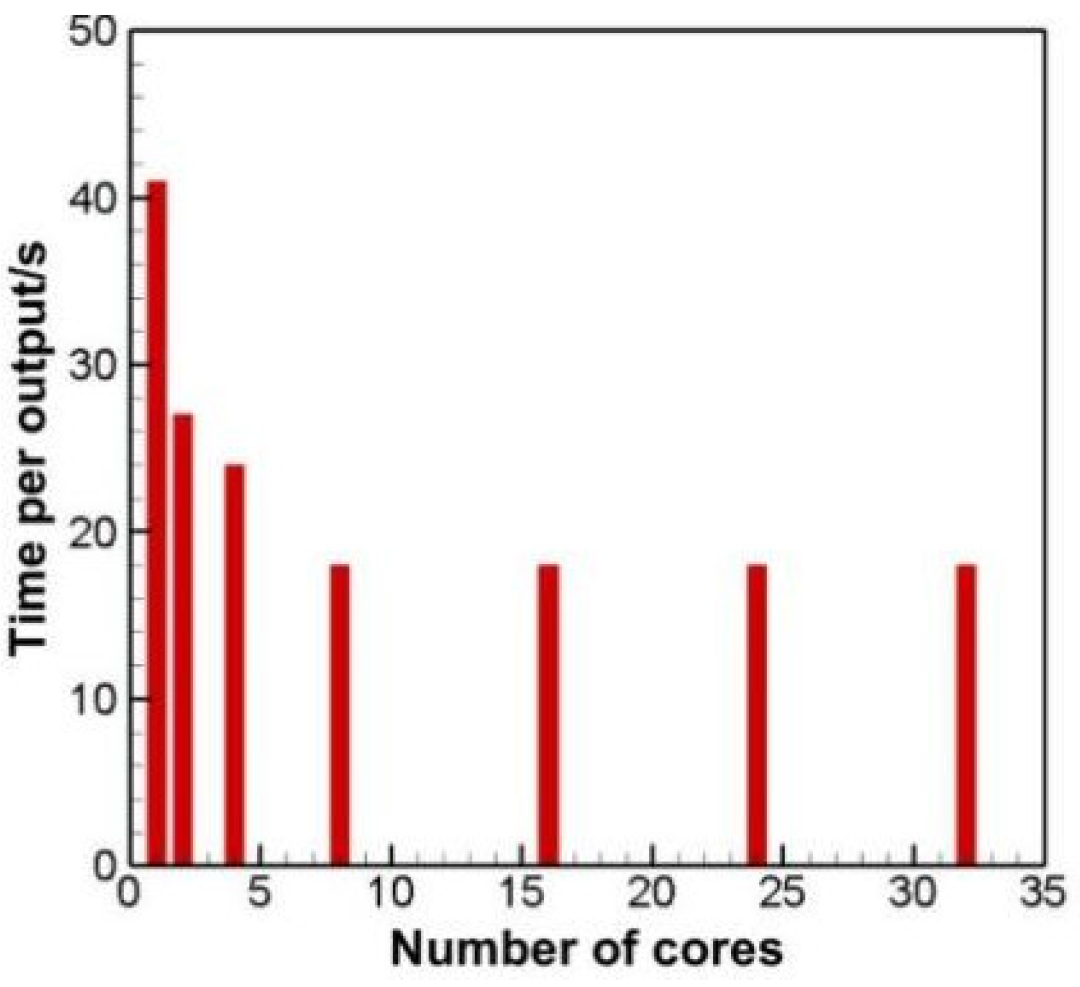
3.2. Efficiency of Parallel Algorithm
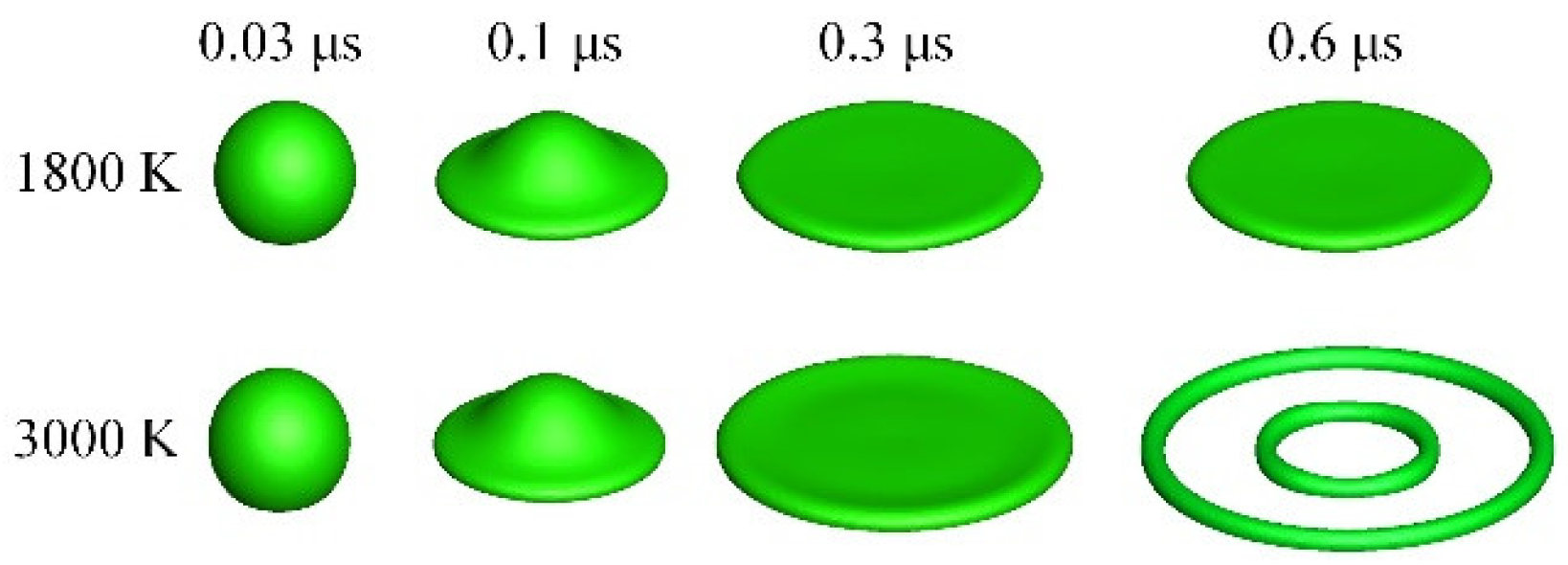
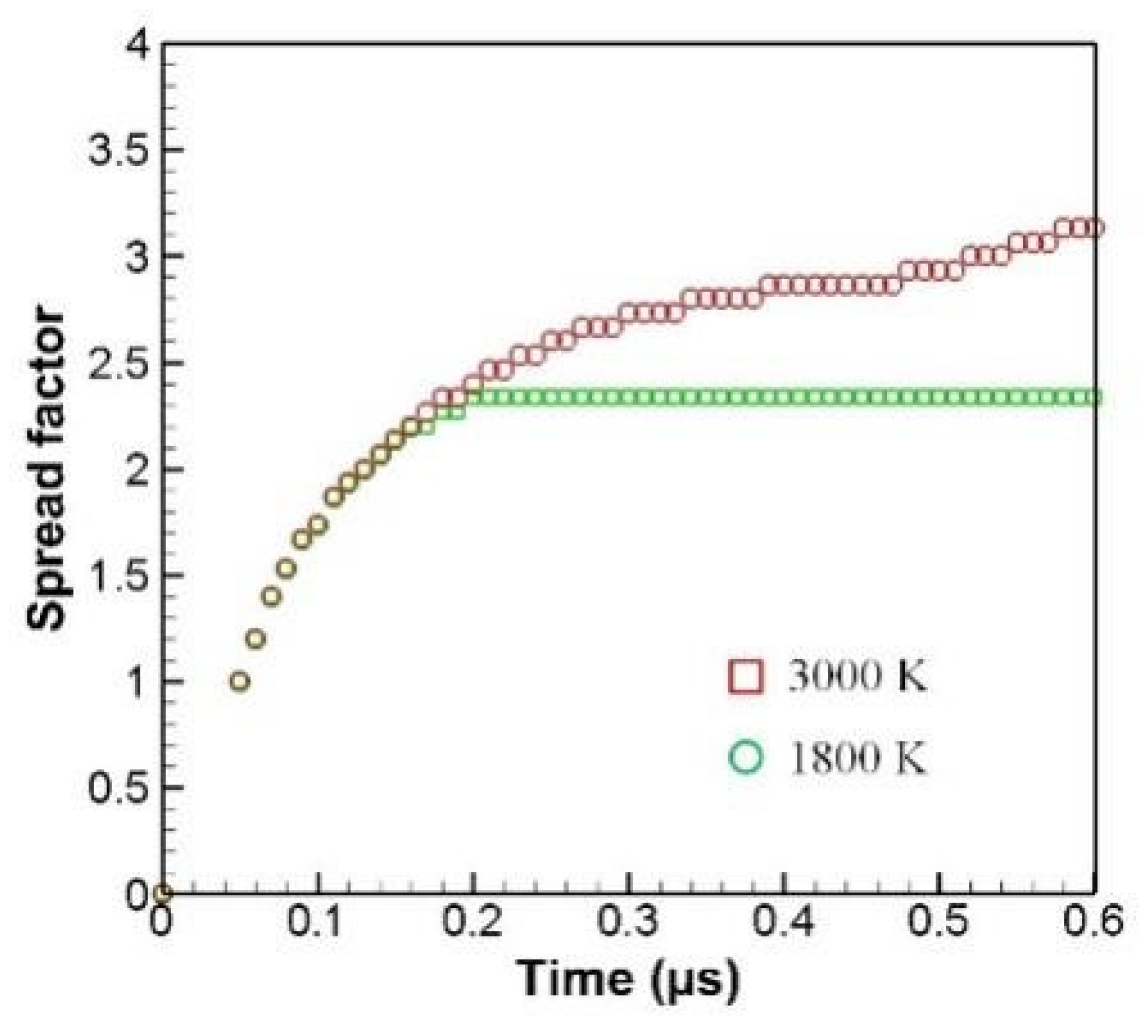
3.3. Solidification Impediment for Drop Spreading
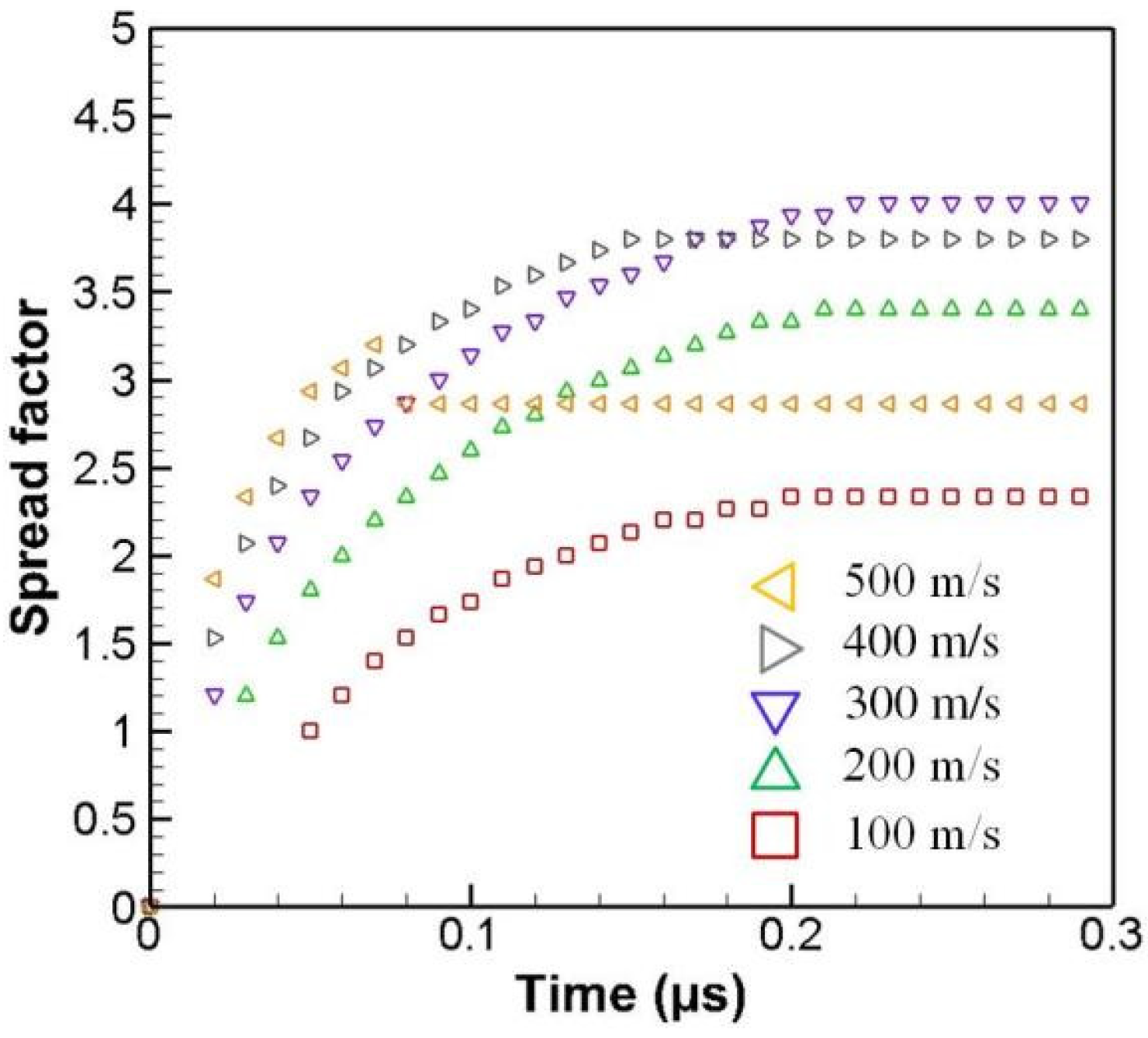
3.4. Effect of Velocity on Droplet Spreading
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J. Phase-Field Models for Multi-Component Fluid Flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J. Comparison study of the conservative Allen-Cahn and the Cahn-Hilliard equations. Math. Comput. Simul. 2016, 119, 35–56. [Google Scholar] [CrossRef]
- Yue, P. Thermodynamically consistent phase-field modelling of contact angle hysteresis. J. Fluid Mech. 2020, 899, A15. [Google Scholar] [CrossRef]
- Yang, C.; Li, S.; Wang, X.; Wang, J.; Huang, H. Phase-field simulation of multi-phase interactions in Fe-C peritectic solidification. Comput. Mater. Sci. 2020, 171, 109220. [Google Scholar] [CrossRef]
- Mirjalili, S.; Ivey, C.B.; Mani, A. A conservative diffuse interface method for two-phase flows with provable boundedness properties. J. Comput. Phys. 2019, 401, 109006. [Google Scholar] [CrossRef]
- Jacqmin, D. Contact-line dynamics of a diffuse fluid interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Imran, M.; Shah, R.; Weera, W. Fractional-View Analysis of Fokker-Planck Equations by ZZ Transform with Mittag-Leffler Kernel. Symmetry 2022, 14, 1513. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto-Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Xiao, J.; Pan, F.; Xia, H.; Zou, S.; Zhang, H.; George, O.A.; Zhou, F.; Huang, Y. Computational Study of Single Droplet Deposition on Randomly Rough Surfaces: Surface Morphological Effect on Droplet Impact Dynamics. Ind. Eng. Chem. Res. 2018, 57, 7664–7675. [Google Scholar] [CrossRef]
- Mukhtar, S.; Shah, R.; Noor, S. The Numerical Investigation of a Fractional-Order Multi-Dimensional Model of Navier-Stokes Equation via Novel Techniques. Symmetry 2022, 14, 1102. [Google Scholar] [CrossRef]
- Jacqmin, D. Calculation of Two-Phase Navier-Stokes Flows Using Phase-Field Modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Ding, H.; Spelt, P.D.; Shu, C. Diffuse interface model for incompressible two-phase flows with large density ratios. J. Comput. Phys. 2007, 226, 2078–2095. [Google Scholar] [CrossRef]
- Shao, J.Y.; Shu, C. A hybrid phase field multiple relaxation time lattice Boltzmann method for the incompressible multiphase flow with large density contrast. Int. J. Numer. Methods Fluids 2015, 77, 526–543. [Google Scholar] [CrossRef]
- Zhan, C.; Chai, Z.; Shi, B. Consistent and conservative phase-field-based lattice Boltzmann method for incompressible two-phase flows. Phys. Rev. E 2022, 106, 025319. [Google Scholar] [CrossRef] [PubMed]
- Amiri, H.A.; Hamouda, A. Evaluation of level set and phase field methods in modeling two phase flow with viscosity contrast through dual-permeability porous medium. Int. J. Multiph. Flow 2013, 52, 22–34. [Google Scholar] [CrossRef]
- Zu, Y.Q.; He, S. Phase-field-based lattice Boltzmann model for incompressible binary fluid systems with density and viscosity contrasts. Phys. Rev. E 2013, 87, 043301. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Feng, J.J. Sharp-interface limit of the Cahn-Hilliard model for moving contact lines. J. Fluid Mech. 2010, 645, 279–294. [Google Scholar] [CrossRef]
- Magaletti, F.; Picano, F.; Chinappi, M.; Marino, L.; Casciola, C.M. The sharp-interface limit of the Cahn-Hilliard/Navier–Stokes model for binary fluids. J. Fluid Mech. 2013, 714, 95–126. [Google Scholar] [CrossRef]
- Gruszczyński, G.; Mitchell, T.; Leonardi, C.; Łaniewski-Wołłk, Ł.; Barber, T. A cascaded phase-field lattice Boltzmann model for the simulation of incompressible, immiscible fluids with high density contrast. Comput. Math. Appl. 2019, 79, 1049–1071. [Google Scholar] [CrossRef]
- Shen, M.; Li, B.Q.; Yang, Q.; Bai, Y.; Wang, Y.; Zhu, S.; Zhao, B.; Li, T.; Hu, Y. A modified phase-field three-dimensional model for droplet impact with solidification. Int. J. Multiph. Flow 2019, 116, 51–66. [Google Scholar] [CrossRef]
- Voller, V.; Swaminathan, C.R. A general source-based method for solidification phase change. Numer. Heat Transfer Part B Fundam. 1991, 19, 175–189. [Google Scholar] [CrossRef]
- Li, C.-J.; Li, J.-L. Transient Contact Pressure During Flattening of Thermal Spray Droplet and Its Effect on Splat Formation. J. Therm. Spray Technol. 2004, 13, 229–238. [Google Scholar] [CrossRef]
- Zhou, C.; Yue, P.; Feng, J.J.; Ollivier-Gooch, C.F.; Hu, H.H. 3D phase-field simulations of interfacial dynamics in Newtonian and viscoelastic fluids. J. Comput. Phys. 2010, 229, 498–511. [Google Scholar] [CrossRef]
- Vardelle, M.; Leger, A.C.; Fauchais, P.; Gobin, D. Influence of particle parameters at impact on splat formation and solidification in plasma spraying processes. J. Therm. Spray Technol. 1995, 4, 50–58. [Google Scholar] [CrossRef]
- Fauchais, P.; Fukumoto, M.; Vardelle, A. Knowledge Concerning Splat Formation: An Invited Review. J. Therm. Spray Technol. 2004, 13, 337–360. [Google Scholar] [CrossRef]
- Jian, Z.; Josserand, C.; Popinet, S.; Ray, P.; Zaleski, S. Two mechanisms of droplet splashing on a solid substrate. J. Fluid Mech. 2017, 835, 1065–1086. [Google Scholar] [CrossRef]
- Zhang, Q.; Qian, T.; Wang, X.-P. Phase field simulation of a droplet impacting a solid surface. Phys. Fluids 2016, 28, 022103. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, P.; Xu, L. Compressible air entrapment in high-speed drop impacts on solid surfaces. J. Fluid Mech. 2013, 716, R9. [Google Scholar] [CrossRef]
- Mandre, S.; Brenner, M.P. The mechanism of a splash on a dry solid surface. J. Fluid Mech. 2011, 690, 148–172. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary effects during droplet impact on a solid surface. Phys. Fluids 1996, 8, 650–659. [Google Scholar] [CrossRef]
- Shen, M.; Li, B.Q.; Bai, Y. Numerical modeling of YSZ droplet impact/spreading with solidification microstructure formation in plasma spraying. Int. J. Heat Mass Transf. 2020, 150, 119267. [Google Scholar] [CrossRef]
- Wang, G.-X.; Goswami, R.; Sampath, S.; Prasad, V. Understanding the Heat Transfer and Solidification of Plasma-Sprayed Yttria-Partially Stabilized Zirconia Coatings. Mater. Manuf. Process. 2004, 19, 259–272. [Google Scholar] [CrossRef]
- An, S.; Zhan, Y.; Yao, J.; Yu, H.; Niasar, V. A greyscale volumetric lattice Boltzmann method for upscaling pore-scale two-phase flow. Adv. Water Resour. 2020, 144, 103711. [Google Scholar] [CrossRef]








| Parameters | Ni | YSZ | Air | Substrate |
|---|---|---|---|---|
| 8900 | 5890 | 1.18 | 8400 | |
| ) | 562 | 713 | 1006 | 575 |
| ) | 71.8 | 2.32 | 0.0263 | 18.8 |
| ) | 6 | 27.8 | 0.0185 | - |
| Surface tension (N/m) | 1.8 | 0.43 | - | - |
| ) | 292 | 707 | - | - |
| Melting point (K) | 1726 | 2923 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, M.; Li, B.Q. A Phase Field Approach to Modeling Heavy Metal Impact in Plasma Spraying. Coatings 2022, 12, 1383. https://doi.org/10.3390/coatings12101383
Shen M, Li BQ. A Phase Field Approach to Modeling Heavy Metal Impact in Plasma Spraying. Coatings. 2022; 12(10):1383. https://doi.org/10.3390/coatings12101383
Chicago/Turabian StyleShen, Mingguang, and Ben Q. Li. 2022. "A Phase Field Approach to Modeling Heavy Metal Impact in Plasma Spraying" Coatings 12, no. 10: 1383. https://doi.org/10.3390/coatings12101383




