An Experimental Study of Surface Icing Characteristics on Blade Airfoil for Offshore Wind Turbines: Effects of Chord Length and Angle of Attack
Abstract
:1. Introduction
2. Experimental Methods
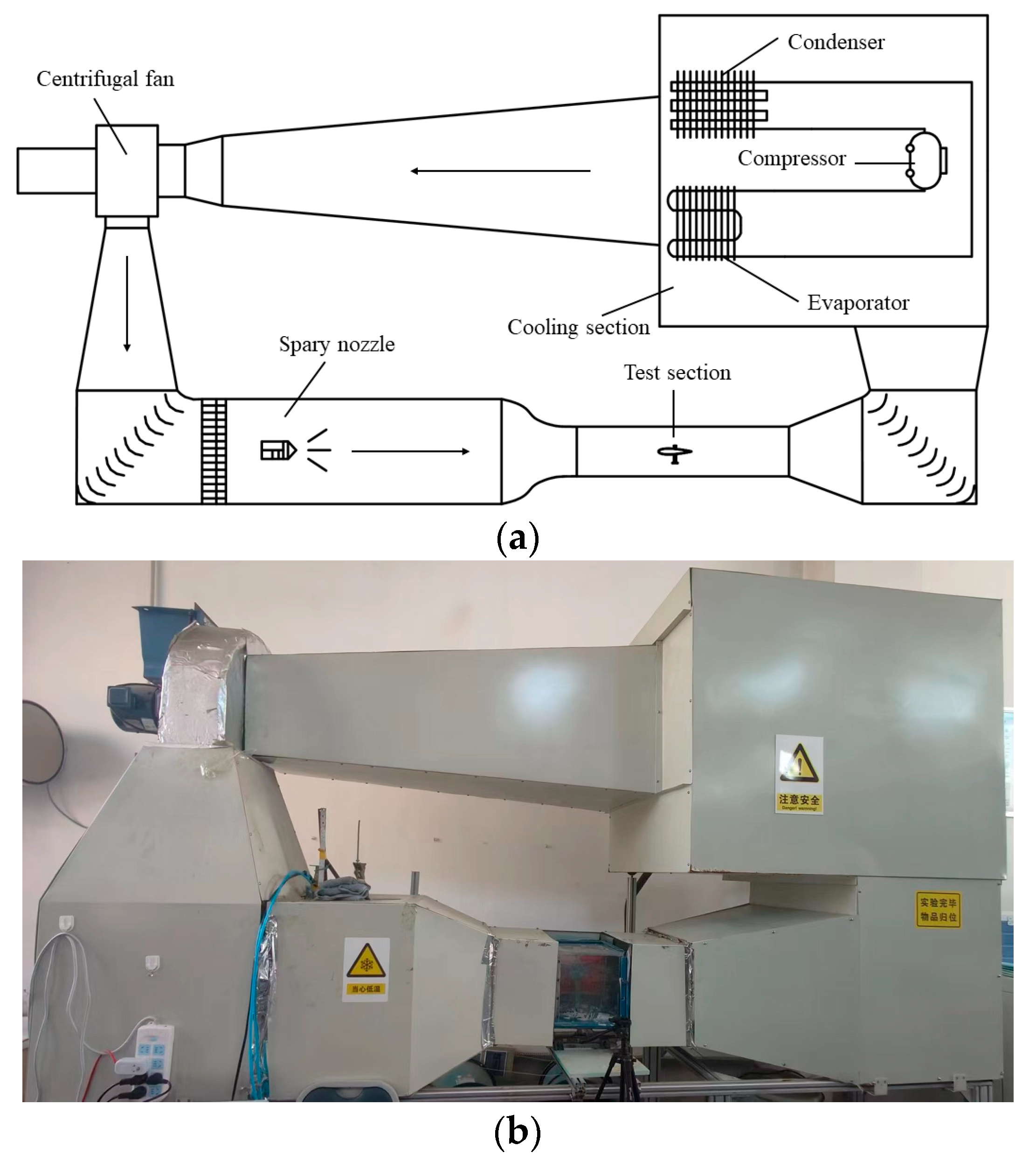
2.1. Experimental Systems
2.2. Experimental Models
2.3. Experimental Schemes
2.3.1. Parameters for Icing Experiment on Blade of Different Chord Lengths
2.3.2. Icing Similarity Experiment Scheme
- Selection of the characteristic length for subscale models:
- 2.
- Selection of test wind speeds for subscale models:
- 3.
- Determine the test temperature T using similar thermodynamic properties:
- 4.
- The test medium volume droplet diameter d was obtained using the modified inertia parameter :
- 5.
- The liquid water content LWC for the subscale modeling test was obtained based on the Weber number of the water film thickness:
- 6.
- Determine the test pressure P based on the dynamic pressure similarity principle:
- 7.
- Determine the test time t based on the similarity of the aggregation factor :where cm is the characteristic length of the subscale model; cf is the characteristic length of the full-size model; k is the scaling factor; vm is the test wind speed of the subscale model; vf is the test wind speed of the full-size model; Tm is the test temperature of the subscale model; Tf is the test temperature of the full-size model; dm is the test MVD of the subscale model; df is the test MVD of the full-size model; (LWC)m is the test LWC for the subscale model; (LWC)f is the test LWC for the full-size model; Pm is the test pressure for the subscale model; Pf is the test pressure for the full-size model; tm is the test time for the subscale model; and tf is the test time for the full-size model.
2.4. Icing Experiment Scheme with Different Chord Lengths
3. Results and Discussion
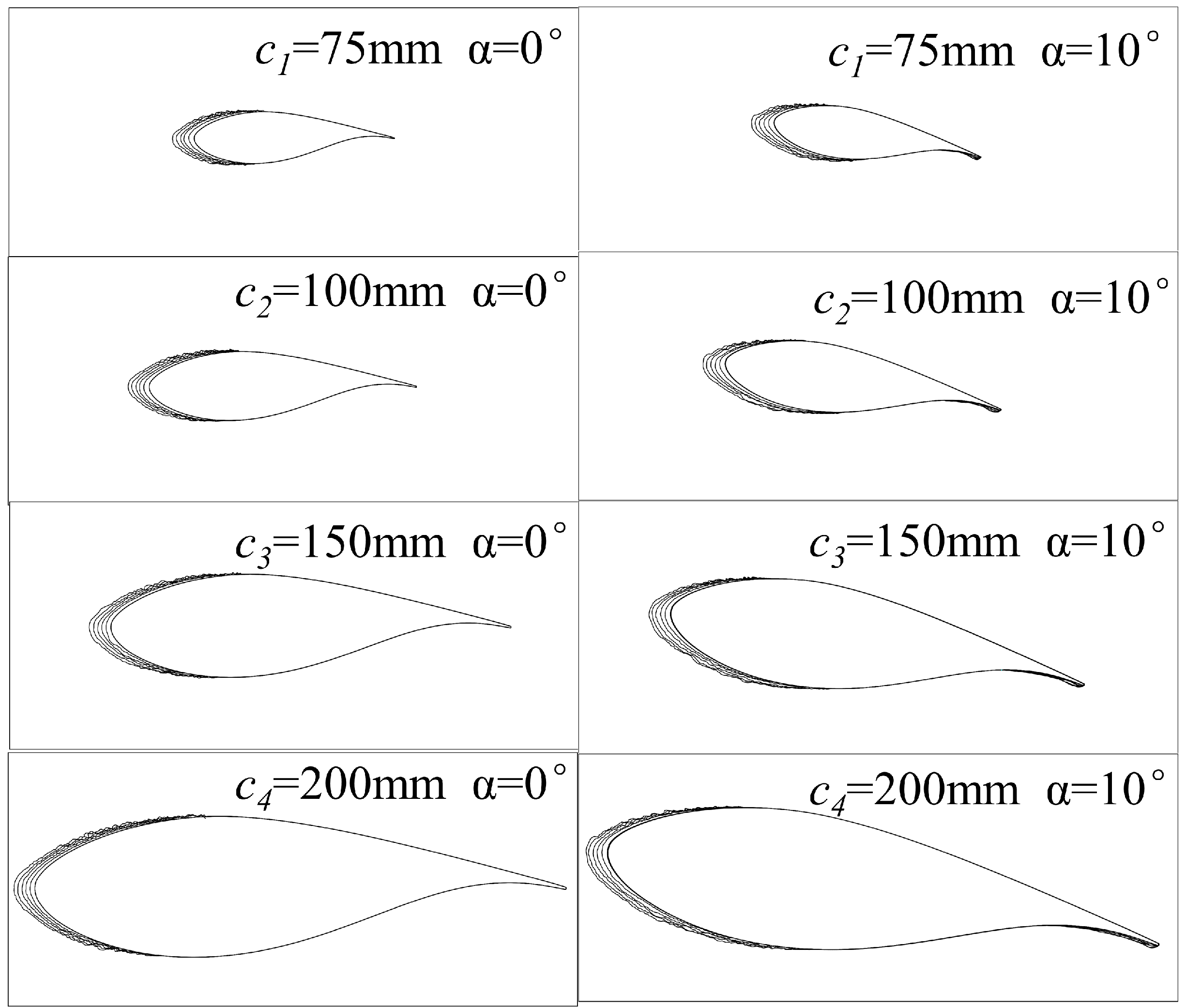
3.1. Icing Distribution
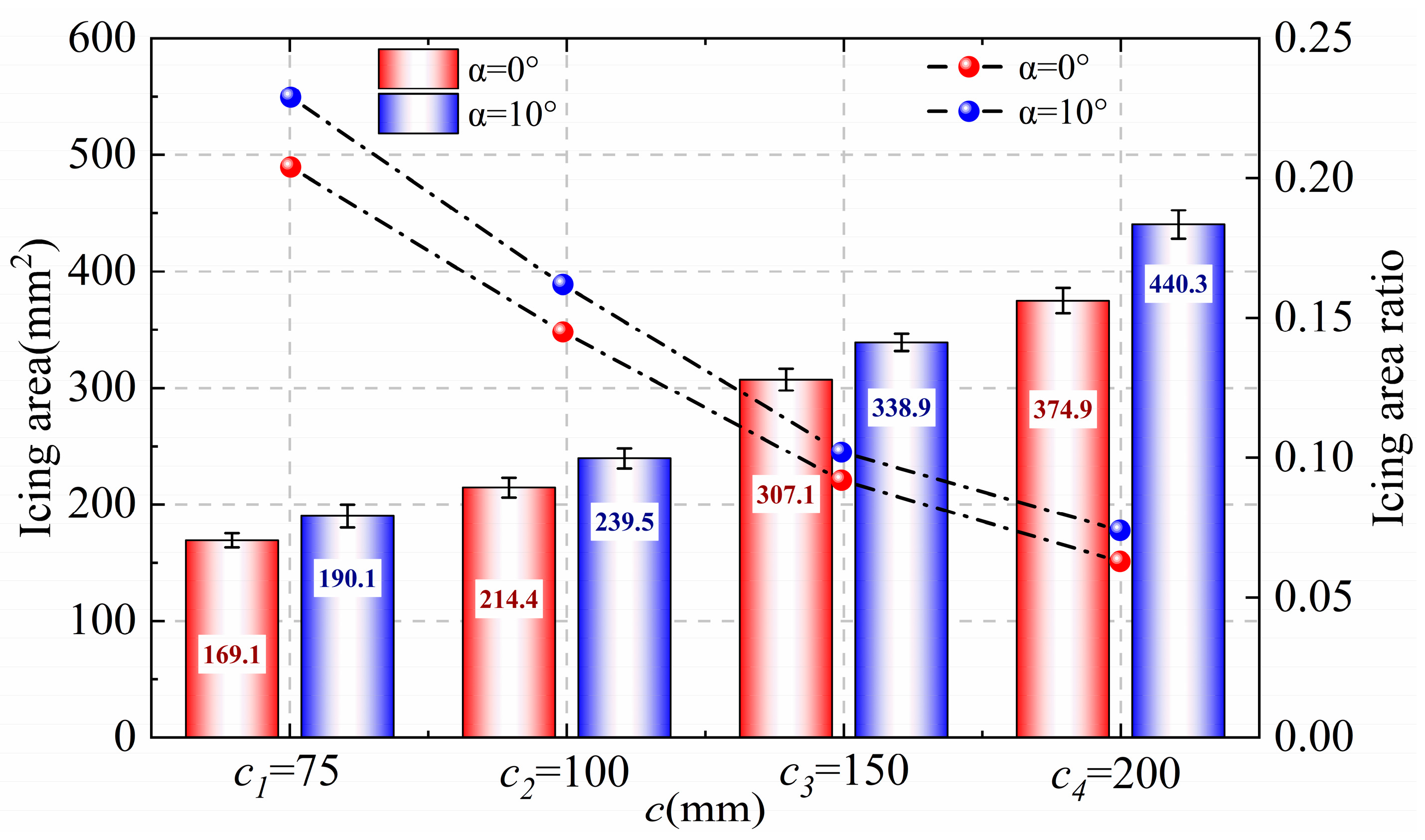
3.2. Icing Area
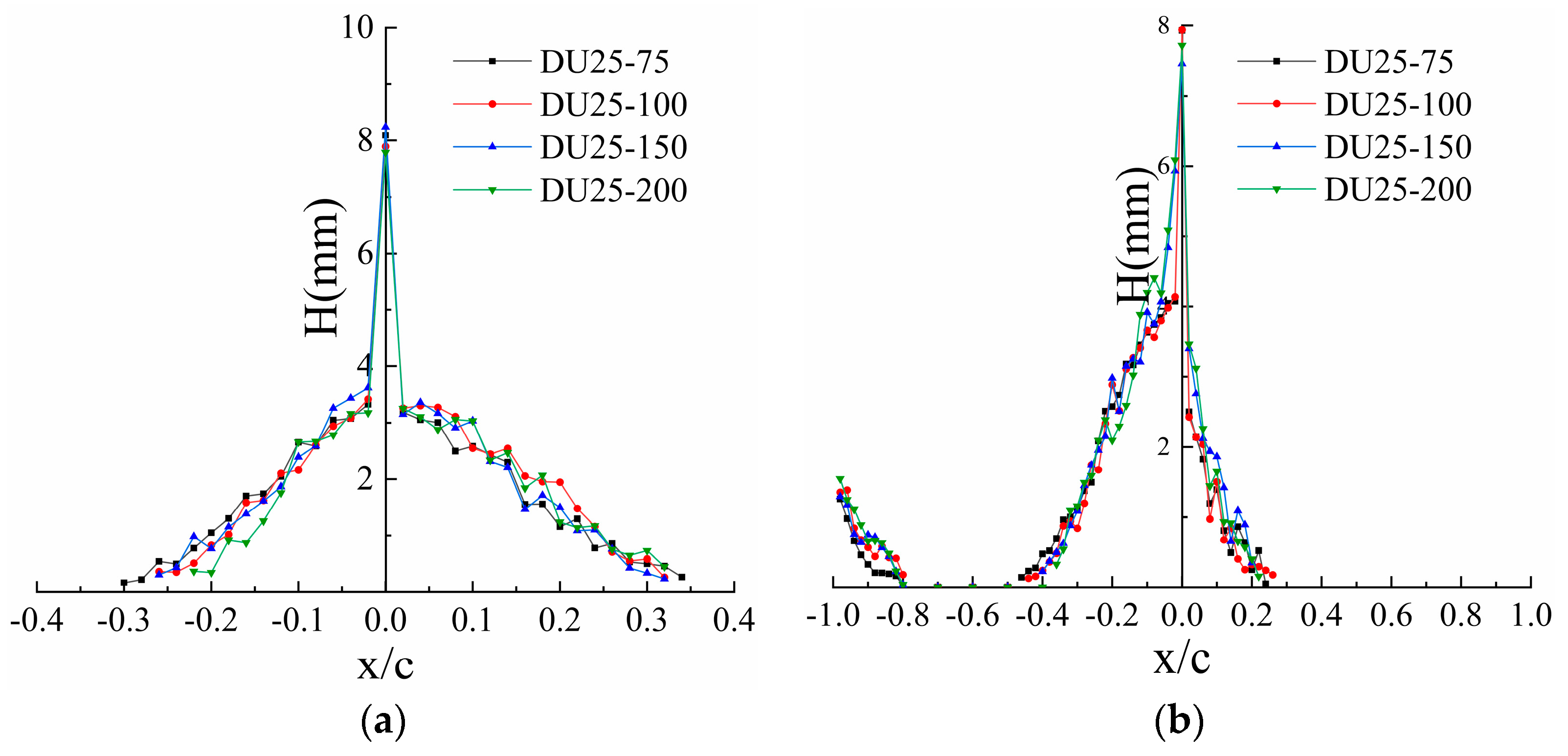
3.3. Average Icing Thickness
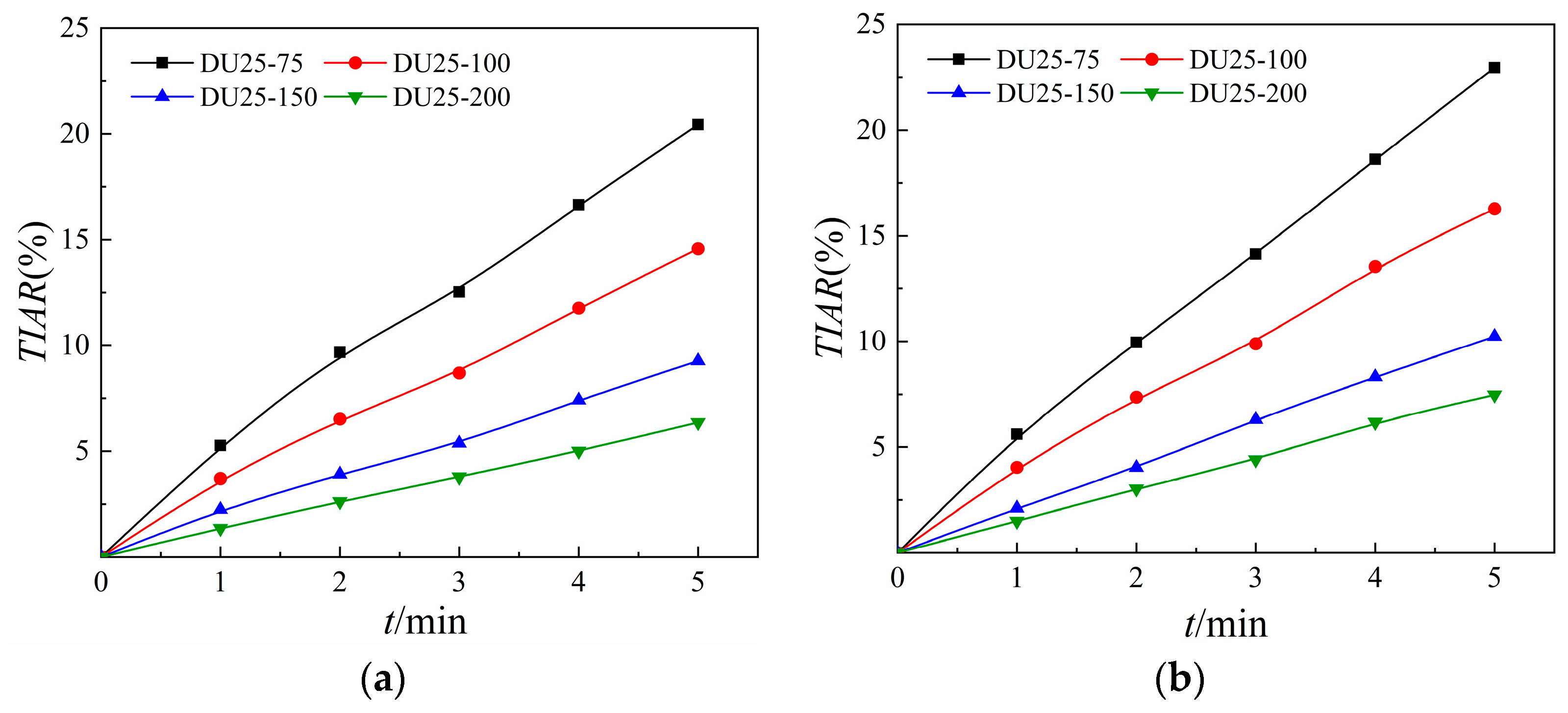
3.4. Icing Rate
3.5. Icing Similarity
4. Conclusions
- (1)
- The relative positions of icing and the average icing thicknesses of the airfoil blades with different chord lengths are basically the same. At α = 0°, the relative position of icing is in the region of −30%~35% of the leading edge of the blade, and at α = 10°, the relative position of icing is in the region of −50%~25% of the leading edge of the blade and −80%~−100% of the trailing edge of the blade.
- (2)
- With an increase in the blade chord length, the growth rate of the net icing area varies from 0.39~0.73 mm2/s to 1.14~1.33 mm2/s at α = 0°, and from 0.57~0.77 mm2/s to 1.27~1.49 mm2/s at α = 10°. In addition, the total icing area rate of the blade decreases with an increase in the chord length, and with the doubling of the chord length, the summarized ice area rate decreases by about a factor of one. the total icing area rate would decrease by about half.
- (3)
- The icing similarity criterion was verified, and the similarity of the icing shapes on the surfaces of the blades at different scales was found to be 84.06%~88.72% under the test conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Sun, Y.; Wu, M. Decision-making methodologies in offshore wind power investments: A review. J. Clean. Prod. 2021, 295, 126459. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Efficiency and effectiveness of global onshore wind energy utilization. Energy Convers. Manag. 2023, 280, 116788. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Y.; Shen, C.; Chen, N. Aerodynamic and structural analysis for blades of a 15MW floating offshore wind turbine. Ocean Eng. 2023, 287, 115785. [Google Scholar] [CrossRef]
- Donadei, V.; Koivuluoto, H.; Sarlin, E. The effect of mechanical and thermal stresses on the performance of lubricated icephobic coatings during cyclic icing/deicing tests. Prog. Org. Coat. 2022, 163, 106614. [Google Scholar] [CrossRef]
- Tao, C.; Tao, T.; He, S.; Bai, X.; Liu, Y. Wind turbine blade icing diagnosis using B-SMOTE-Bi-GRU and RFE combined with icing mechanism. Renew. Energy 2024, 221, 119741. [Google Scholar] [CrossRef]
- Yang, X.; Bai, X.; Cao, H. Influence analysis of rime icing on aerodynamic performance and output power of offshore floating wind turbine. Ocean Eng. 2022, 258, 111725. [Google Scholar] [CrossRef]
- Subeshan, B.; Usta, A.; Asmatulu, R. Deicing and self-cleaning of plasma-treated superhydrophobic coatings on the surface of aluminum alloy sheets. Surf. Interfaces 2020, 18, 100429. [Google Scholar] [CrossRef]
- Chuang, Z.; Li, C.; Liu, S.; Li, X.; Li, Z.; Zhou, L. Numerical analysis of blade icing influence on the dynamic response of an integrated offshore wind turbine. Ocean Eng. 2022, 257, 111593. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, F.; Li, Y.; Sun, Y.; Tagawa, K. A corncob biochar-based superhydrophobic photothermal coating with micro-nano-porous rough-structure for ice-phobic properties. Surf. Coat. Technol. 2023, 457, 129299. [Google Scholar] [CrossRef]
- Dalili, N.; Edrisy, A.; Carriveau, R. A review of surface engineering issues critical to wind turbine performance. Renew. Sustain. Energy Rev. 2019, 13, 428–438. [Google Scholar] [CrossRef]
- Shu, L.; Li, H.; Hu, Q.; Jiang, X.; Qiu, G.; McClure, G.; Yang, H. Study of ice accretion feature and power characteristics of wind turbines at natural icing environment. Cold Reg. Sci. Technol. 2018, 147, 45–54. [Google Scholar] [CrossRef]
- Gao, L.; Hong, J. Wind turbine performance in natural icing environments: A field characterization. Cold Reg. Sci. Technol. 2021, 181, 103193. [Google Scholar] [CrossRef]
- Li, Y.; Yang, S.; Feng, F.; Tagawa, K. A review on numerical simulation based on CFD technology of aerodynamic characteristics of straight-bladed vertical axis wind turbines. Energy Rep. 2023, 9, 4360–4379. [Google Scholar] [CrossRef]
- Tong, G.; Li, Y.; Tagawa, K.; Feng, F. Effects of blade airfoil chord length and rotor diameter on aerodynamic performance of straight-bladed vertical axis wind turbines by numerical simulation. Energy 2023, 265, 126325. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, X.; Hu, C.; Chen, J.; Du, Z. Wind turbines ice distribution and load response under icing conditions. Renew. Energy 2017, 113, 608–619. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Y.; Li, H.; Zhao, W. Numerical Study on Glaze Ice Accretion Characteristics over Time for a NACA 0012 Airfoil. Coatings 2024, 14, 55. [Google Scholar] [CrossRef]
- Gao, L.; Tao, T.; Liu, Y.; Hu, H. A field study of ice accretion and its effects on the power production of utility-scale wind turbines. Renew. Energy 2021, 167, 917–928. [Google Scholar] [CrossRef]
- He, R.; Sun, H.; Gao, X.; Yang, H. Wind tunnel tests for wind turbines: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 166, 112675. [Google Scholar] [CrossRef]
- Hoang, P.H.; Maeda, T.; Kamada, Y. Effect of icing airfoil on aerodynamic performance of horizontal axis wind turbine. J. Energy Resour. Technol. 2022, 144, 011303. [Google Scholar] [CrossRef]
- Sun, H.; Lin, G.; Jin, H.; Bu, X.; Cai, C.; Jia, Q.; Ma, K.; Wen, D. Experimental investigation of surface wettability induced anti-icing characteristics in an ice wind tunnel. Renew. Energy 2021, 179, 1179–1190. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; He, Z. Ice-phobic properties of MoS2-loaded rice straw biogas residue biochar-based photothermal and anti-corrosion coating with low oxygen to carbon ratio. Biochar 2023, 5, 74. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, X. A computational strategy for determining the optimal scaled wind speed in icing wind tunnel experiments. Comput. Fluids 2023, 250, 105734. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Pope, K.; Naterer, G.F. Scaling formulation of multiphase flow and droplet trajectories with rime ice accretion on a rotating wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2023, 232, 105247. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Pope, K.; Naterer, G.F. Extended scaling approach for droplet flow and glaze ice accretion on a rotating wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2023, 233, 105296. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, S.; Yan, B.; Yang, Q.; Zhou, X.; Ishihara, T. Thrust-matched optimization of blades for the reduced-scale wind tunnel tests of wind turbine wakes. J. Wind Eng. Ind. Aerodyn. 2022, 228, 105113. [Google Scholar] [CrossRef]
- Yang, W.; Yu, M.; Yan, B.; Huang, G.; Yang, Q.; Zhang, S.; Deng, X. Wind Tunnel Tests of Wake Characteristics for a Scaled Wind Turbine Model Based on Dynamic Similarity. Energies 2022, 15, 6165. [Google Scholar] [CrossRef]
- Wang, H.; Chen, B. Investigation on aerodynamic noise for leading edge erosion of wind turbine blade. J. Wind Eng. Ind. Aerodyn. 2023, 240, 105484. [Google Scholar] [CrossRef]
- Tabib, M.; Rasheed, A.; Siddiqui, M.S.; Kvamsdal, T. A full-scale 3D Vs. 2.5D Vs. 2D analysis of flow pattern and forces for an industrial-scale 5MW NREL reference wind-turbine. Energy Procedia 2017, 137, 477–486. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Duan, C.; Zheng, J.; Liu, Z.; Ma, G. CFD simulation on wind turbine blades with leading edge erosion. J. Theor. Appl. Mech. 2021, 59, 579–593. [Google Scholar] [CrossRef]









| Test Conditions | Parameters |
|---|---|
| Temperature T/°C | −10 |
| Wind speed v/(m·s−1) | 10 |
| LWC/(g·m−3) | 0.7 |
| MVD/µm | 50 |
| Chord length ci (i = 1, 2, 3, 4)/mm | 75, 100, 150, 200 |
| AOA α/° | 0, 10 |
| Test time t/min | 5 |
| Sampling time interval ∆t/min | 1 |
| Blade airfoil | DU25 |
| Condition | v /m·s−1 | T /°C | MVD /µm | LWC /g·m−3 | Pressure P/Pa | Airfoil | AOA α/° | Chord Length c/mm | Icing Time/min |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | −10 | 50 | 0.7 | 1.01 × 106 | DU25 | 0 | c1, c3 | 2, 4 |
| 2 | 0 | c2, c4 | 2, 4 | ||||||
| 3 | 10 | c1, c3 | 2, 4 | ||||||
| 4 | 10 | c2, c4 | 2, 4 |
| Condition | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| c (mm) | c1–c3 | c2–c4 | c1–c3 | c2–c4 |
| Sim | 84.06% | 84.38% | 86.99% | 88.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, D.; Zhao, P.; Shen, H.; Yang, S.; Chi, H.; Li, Y.; Feng, F. An Experimental Study of Surface Icing Characteristics on Blade Airfoil for Offshore Wind Turbines: Effects of Chord Length and Angle of Attack. Coatings 2024, 14, 623. https://doi.org/10.3390/coatings14050623
Liang D, Zhao P, Shen H, Yang S, Chi H, Li Y, Feng F. An Experimental Study of Surface Icing Characteristics on Blade Airfoil for Offshore Wind Turbines: Effects of Chord Length and Angle of Attack. Coatings. 2024; 14(5):623. https://doi.org/10.3390/coatings14050623
Chicago/Turabian StyleLiang, Dong, Pengyu Zhao, He Shen, Shengbing Yang, Haodong Chi, Yan Li, and Fang Feng. 2024. "An Experimental Study of Surface Icing Characteristics on Blade Airfoil for Offshore Wind Turbines: Effects of Chord Length and Angle of Attack" Coatings 14, no. 5: 623. https://doi.org/10.3390/coatings14050623
APA StyleLiang, D., Zhao, P., Shen, H., Yang, S., Chi, H., Li, Y., & Feng, F. (2024). An Experimental Study of Surface Icing Characteristics on Blade Airfoil for Offshore Wind Turbines: Effects of Chord Length and Angle of Attack. Coatings, 14(5), 623. https://doi.org/10.3390/coatings14050623








