2. The Surface
Different coatings can be applied as liquids, gases or solids and involve the formation of a monolayer or several monolayers covering the original surface. The original surface is usually referred to as the substrate. Combinations of coatings can also be used in order to achieve specific goals. For example, one coating type can be used to improve the attachment of a second coating to a certain substrate. Such initial coatings are performed during a so-called priming procedure, and that coating agent is called a primer. Depending on the properties of a coating, different coatings are used to improve surface properties such as appearance, adhesion, wettability, corrosion resistance, wear resistance, scratch resistance and biological interaction.
The primary goal behind any coating is to change the surface properties of the original substrate. For example, by use of ion-implantation, a surface can be bombarded and saturated with other ions. These ions, as well as the surface stresses they induce when they are implanted, usually increase the surface hardness [
23]. They may also change the way the surface will interact with the environment [
24]. Titanium implants are often plasma coated with hydroxyapatite in an attempt to speed up the healing process at the implant-bone interface [
25]. Depending on the way a coating is performed, different thicknesses of the coating can be formed.
When it comes to different coatings, the key challenge is how well the coating will interact with the substrate and the surrounding environment. The quality of the substrate-coating bond may differ considerable between different coating techniques. Stresses may also be developed between the substrate and the coated layer; stresses that over time may cause failures in either the coated layer or the surface layer of the substrate.
The more one approaches the topic of coating, the more obvious it becomes that the key factors behind a successful coating are how strong the substrate-coating interface is, how well the coating can resist physical stimuli and how well the outer surface of the coating interacts with the surrounding environment. Whether it is an internal surface between a substrate and a coating or an external surface between the coating and the surrounding environment, both these surfaces have their characteristic topography and composition. Surface topography as well as surface composition in turn interact, because as the surface area increases, so does the number of atoms available for reactions.
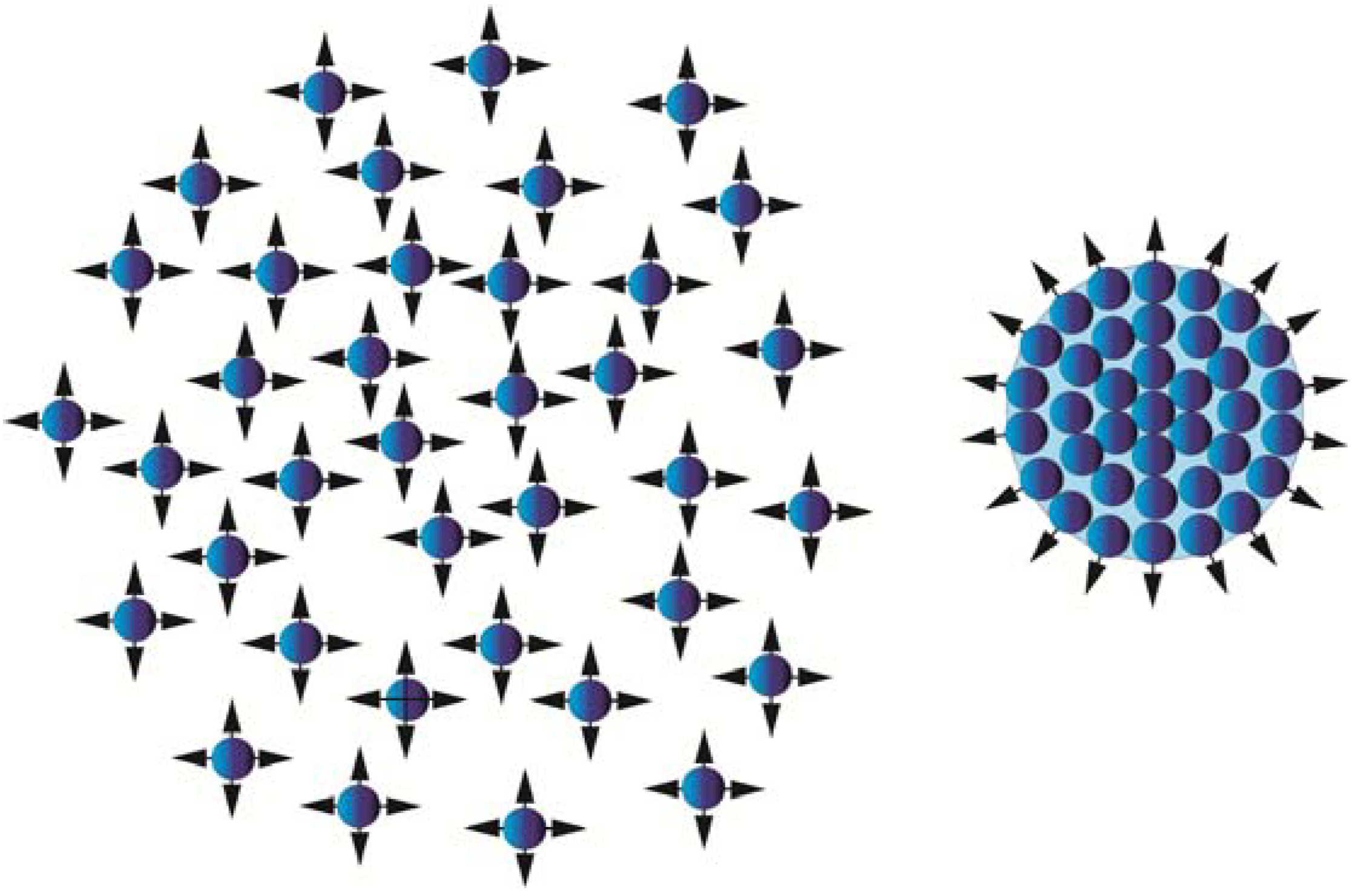
Atoms/molecules isolated in space have unsaturated bonds available for reactions, while if the same atoms/molecules form a cluster, the bonds inside that cluster are balanced by surrounding atoms and molecules, leaving only the surface bonds available for reactions (
Figure 1).
Figure 1.
The isolated atoms/molecules to the left will form a cluster if the kinetic energy of the atoms/molecules decreases below a certain level. During the cluster formation, most of the reactive sites will stick together, leaving only the surface atoms/molecules available for new bond formation.
Figure 1.
The isolated atoms/molecules to the left will form a cluster if the kinetic energy of the atoms/molecules decreases below a certain level. During the cluster formation, most of the reactive sites will stick together, leaving only the surface atoms/molecules available for new bond formation.
The unsaturated bonds available on any exposed surface result in a certain level of surface reactivity, usually referred to as surface energy. Surface energy follows thermodynamic rules, suggesting that nature would like to decrease the energy and increase the entropy. As a consequence, if a liquid with low surface energy is placed on a surface with high energy, the liquid will spread out on the solid surface, and by doing so decrease the surface energy level and increase the entropy of the liquid molecules (
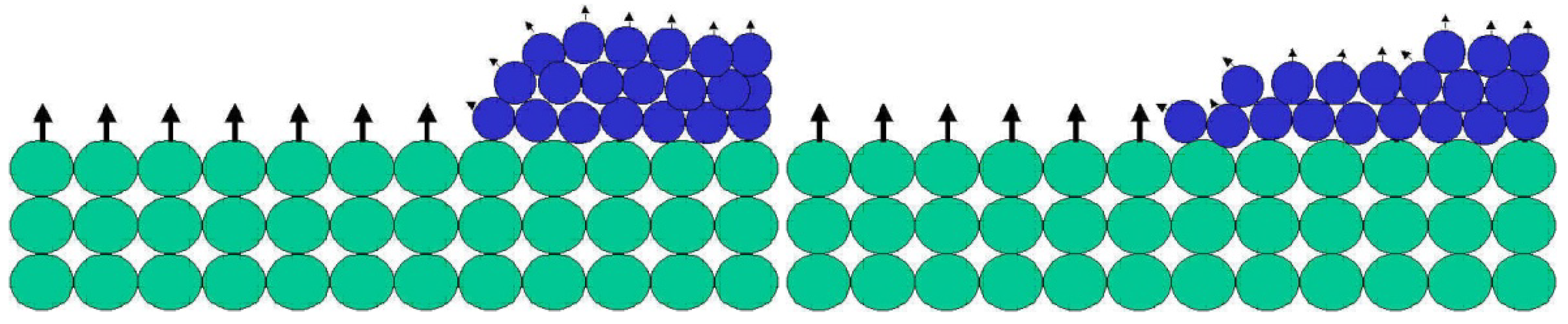
Figure 2). During this process a coating is formed.
Figure 2.
When a liquid with low surface energy (blue spheres) are placed on a solid surface with high surface energy, the blue spheres spread out and cover the green spheres. By doing so, the surface energy of the system decreases while the entropy increases.
Figure 2.
When a liquid with low surface energy (blue spheres) are placed on a solid surface with high surface energy, the blue spheres spread out and cover the green spheres. By doing so, the surface energy of the system decreases while the entropy increases.
What happens in
Figure 2 is that the blue spheres in contact with the green spheres remain bonded to each other, while blue spheres from layers above the bonded blue-green layer are pulled forward in order to establish new bonds with the green spheres. When that occurs, the liquid spreads over the solid surface.
The unit for surface energy is energy/area, often referred to as surface tension (force/length unit). Depending on the size of the surface, different units are used. The interfacial energy and tension values are usually expressed in either cgs (centimeter-gram-second) units or SI (meter-kilogram-second) units as either (erg/cm
2 or dynes/cm) or (mJ/m
2 or mN/m), respectively. By simple unit conversion, it is seen that surface energy and surface tension are equivalent. The values of these parameters range from close to zero to as high as 2000. The lowest values are for liquefied gases. Most organic liquids at and below their atmospheric boiling points range from 20 mN/m to 40 mN/m. The value for water at 20 °C is around 73 mN/m, while the highest values are for molten salts and metals, which are generally several hundred mN/m [
26].
By considering differences in surface energy values, it is possible to draw numerous conclusions regarding the behavior of a coating. For example, what would happen if we could control and change the surface energy of the solid we would plan to coat? Under such circumstances, it would be possible to decrease or increase the spreading of a liquid covering the surface. By increasing the surface energy of the substrate, the surface would become easier to coat. Such an increase in reactivity would also result in faster reactions with other low surface energetic atoms and molecules present in the environment. The reaction with these atoms and molecules would in turn decrease the surface energy below the original surface energy value of the substrate, making it then more difficult to achieve a good coating with the intended coating material. This example shows the importance of a rigid product control when coatings are performed.
An example in dentistry of a case where an environmentally related coating can affect the final clinical outcome is when porcelain-fused-to-metal (PFM) crowns are made. If gold-rich alloys are used for such PFM crowns, it is important to form an oxide film on the gold surface before the porcelain is added. Because of the noble nature of gold, oxide-forming elements such as iron, indium and tin, in concentrations below 1%, are therefore added to these alloys to promote the formation of a thin oxide film on the gold surface. This oxide film is formed by keeping the gold coping in the oven for a certain period of time before porcelain is added. However, when base metals are used as a substrate for gold-rich alloys in PFM crowns, such an extra oxidation should not be performed. The reason is simply that the less noble base metals oxidize much easier and form a significantly thicker oxide film than the one formed on high noble metals for a certain oxidation time. Because of the lower strength of a thicker oxide film, the failure frequency of debonded ceramic layers increased when the first base metal alloys were introduced [
27]. That problem was eliminated by excluding the metal oxidation step for base metals during the formation of such PFM crowns.
When surface energy and surface tension are discussed, particularly in the case of surface tension, it is usually assumed that surface tension is uniform for all surfaces that are isothermal and that they are of the same composition. In general, that assumption is far from true because a solid surface may differ in temperature and composition locally, explaining why a surface may not have the same surface energy level at different locations. As a consequence, the coating film could have preferential spreading directions during coating depending on the heterogeneity of the surface.
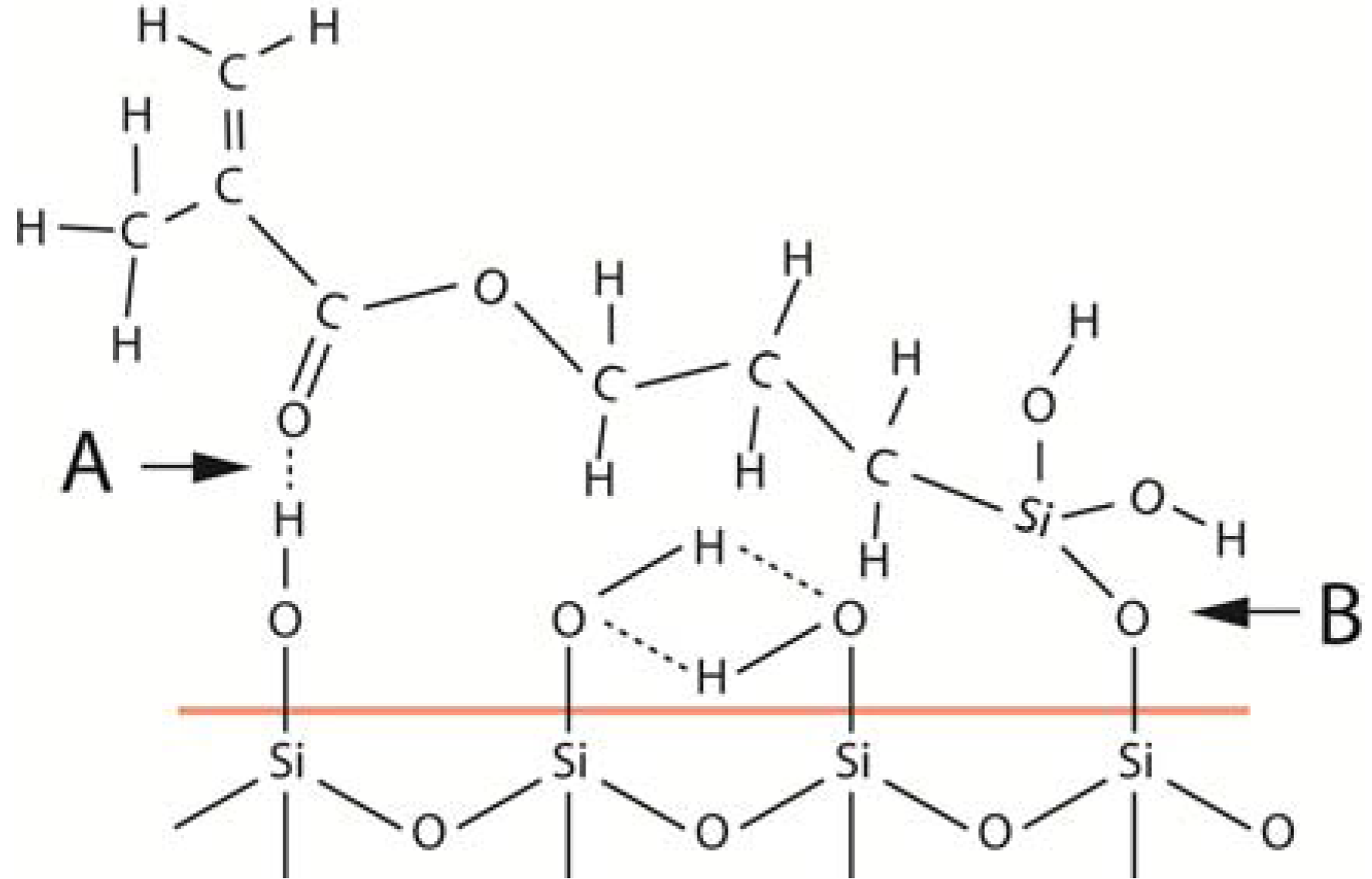
As an example of differences in surface reactivity, consider what happens during the silane treatment of a silica surface [
28]. The initial reactivity between silane and a silica surface can be studied by mixing different concentrations of γ-methacryloxypropyltrimethoxy silane (γ-MPS) with toluene and then mix specific amounts of these silane solutions with fixed amounts of pyrogenic silica. Because of the large surface area of the pyrogenic silica, it is possible to go from an incomplete monolayer coating to multilayer coatings of γ-MPS on the silica surface. The FTIR peaks collected from the different coating amounts can then be recorded to identify any differences in peak locations among the different concentrations. The outcome reveals that the γ-MPS molecules in contact with the silica surface orient themselves parallel to the colloidal silica surface with which the silane molecules form two types of bonds (
Figure 3). One of these bonds is a siloxane bridge formed via a condensation reaction between silanol groups of both the silica surface and the hydrolyzed silane. Water forms during this reaction and soon becomes recaptured by the silanol groups of the silica surface. These water molecules are not available for additional hydrolyzation reactions of the unhydrolyzed silane under the experimental conditions used in this example [
28]. The intensity of the isolated OH-groups on the silica surface decreases because of this reaction. Simultaneous with the condensation reaction, the carbonyl groups of the γ-MPS molecules also form hydrogen bonds. This hydrogen bond formation results in a peak shift of the carbonyl band from 1718–1720 cm
−1 to 1700–1702 cm
−1. This hydrogen bond formation also occurs with the isolated OH-groups. After consumption of the isolated OH-groups, no additional surface reaction occurs because no further OH-groups are available for additional condensation reactions or hydrogen bond formation. By use of available information about the number of OH-groups present on a silica surface [
29], and the amount of γ-MPS that was needed to get a molecular monolayer on the pyrogenic silica [
28], it was possible to show that the bond distance between the Si–OH group and the =CO group of the silane matched the spacing between the nearest isolated OH-groups on the silica surface. This example suggests that the amount of silane needed for filler treatment depends on the number of isolated OH-groups available on the filler surface as well as the size of the silane molecule. The similarity in molecular size of the γ-MPS and the distance between the isolated OH-groups presented on a silica surface may confirm and explain our empirical knowledge that γ-MPS is one of the most efficient silanes when it comes to treating silica surfaces.
Figure 3.
When a silica surface is coated with silane, the first monolayer deposited on the surface orients itself parallel with the silica surface (red line) and forms a covalent bond via a condensation reaction between one silanol group of the silica and one of the silanol groups of the silane (B). In addition, a hydrogen bond forms also between the carbonyl group of the silane and an isolated silanol group of the silica surface (A).
Figure 3.
When a silica surface is coated with silane, the first monolayer deposited on the surface orients itself parallel with the silica surface (red line) and forms a covalent bond via a condensation reaction between one silanol group of the silica and one of the silanol groups of the silane (B). In addition, a hydrogen bond forms also between the carbonyl group of the silane and an isolated silanol group of the silica surface (A).
The above example reveals some important surface related considerations when it comes to coatings [
30,
31]. First, some sites, in the above case the isolated OH-groups on the silica surface, should be able to interact with some groups available in the coating [
31], in this case the silanol groups of the silane molecule. The above example further shows that the spacing of the reactive groups on the substrate surface coincided with the spacing of reactive sites of the silane molecule. If the spacing of the reactive sites on the silica surface does not coincided with that of the reactive silane molecules, only one end of the silane would be able to bond to the silica surface. Second, by orienting the hydrocarbon silane chain surface along the ceramic surface, the surface becomes non-polar. The hydrophobic surface explains why silane coated glass particles do not sink in water despite their higher density (
Figure 4).
Figure 4.
Two jars of water to which equal amounts of silica glass particles (size ~ 1–2 μm) were added. The particles added to the water in the left jar had been pretreated with γ-MPS, while the ones in the right jar had not received any treatment. Despite a particle density of 2.8 g/cm3, the silane treated particles float on the water surface because of their hydrophobic coating, while the untreated particles sedimented into the water. Photo was taken 1 h after particles were added to water.
Figure 4.
Two jars of water to which equal amounts of silica glass particles (size ~ 1–2 μm) were added. The particles added to the water in the left jar had been pretreated with γ-MPS, while the ones in the right jar had not received any treatment. Despite a particle density of 2.8 g/cm3, the silane treated particles float on the water surface because of their hydrophobic coating, while the untreated particles sedimented into the water. Photo was taken 1 h after particles were added to water.
The way the silane reacts with the silica surface in the above example shows the importance of considering local composition and surface energy variations when coatings are considered. For example, from a dental point of view it should be noticed that the surface tension of water increases by the presence of dissolved salts, although these increases are small for low concentrations. The surface tension of water is usually decreased sharply by organic solvents. Both these considerations may vary well affect common dental treatments such as enamel and dentin bonding.
3. The Origin of Surface Tension
Table 1 shows the surface tension of different compounds. By looking at these values and the compounds they represent, a certain pattern emerges. The liquefied gases have the lowest values while the highest surface tension values are among molten salts and metals, which can be related to differences in interatomic and intermolecular bonds among different compounds. The compounds with the lowest surface tension values have pure physical bonds, while as the bond strength increases as we move via hydrogen bonds to primary bonds, so do the surface tension values as well.
Table 1.
Surface tension values of materials in their liquid phase [
26].
Table 1.
Surface tension values of materials in their liquid phase [26].
| Liquid | T (°C) | Surface Tension (mN/m) |
|---|
| Helium | −272 | 0.16 |
| Hydrogen | −254 | 2.4 |
| Oxygen | −183 | 13.2 |
| Silicone (HMDs) | 25 | 15.9 |
| Ethanol | 20 | 22.0 |
| Water | 20 | 72.7 |
| Sodium chloride | 801 | 114 |
| Zinc | 360 | 877 |
| Iron | 1520 | 1700 |
Different theoretical models can be used to describe the bonding behavior [
32]. These models are relatively similar to each other because they all are based on an equilibrium condition between attraction and repulsion [
33]. The weakest bonds are the so-called “van der Waals” forces, which are purely physical bonds without any exchange of electrons between the atoms. Even though there are in principle three types of van der Waals forces, the same physical model can be used to describe them. According to that model, the attraction is proportional to a decrease in potential energy expressed as U(r)
vdW = −B
vdW/r
6, while the repulsion by an increase in potential energy is proportional to U(r)
rep = B
rep/r
12. Based on these relationships, the van der Waals interaction between a pair of these molecules has the form shown in
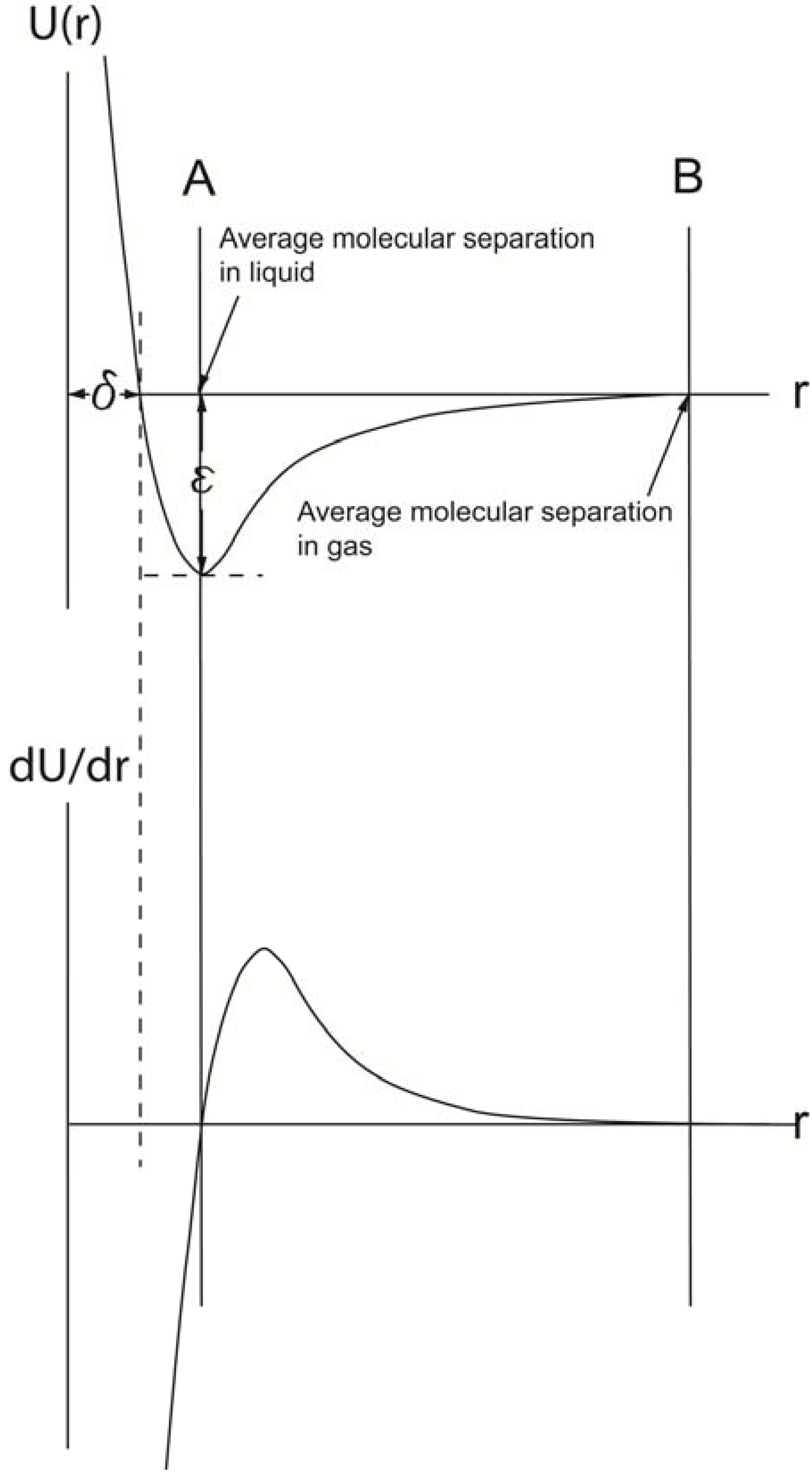
Figure 5.
The interaction only depends on the separation between the centers of the molecules when they are in contact, a distance referred as to δ. At large separations, r > δ, where δ represents the distance when attractive and repulsive potentials are equal, the interaction is attractive, U(r) < 0. For monatomic molecules, this is due to van der Waals attraction, which falls of with separation of r
−6. When r < δ, overlap of the electron orbits of the two molecules gives rise to a repulsion which increases very rapidly as the separation decreases. A common analytical representation of these two effects is represented in Lennard-Jones [
34,
35] formula:
The two parameters σ and ε provide a measure of the size and strength of the interaction between the molecules, and the above formula is applicable for spherical, apolar or weekly polar molecules, where the attractive force of interaction between two molecules is represented by the slope of the potential energy function, expressed as:
The interpretation of the curve suggests that at the average distance of molecular separation in a gas at standard conditions, the intermolecular forces are effectively zero. However, due to thermal motions in the liquid, the average molecular separation does not coincide with an intermolecular force value at zero and has instead a finite positive value and is displaced slightly to the right of line A in
Figure 5.
Figure 5.
The upper curve is derived by combining U(r)vfW and U(r)rep. At a certain distance, δ, these two energy levels balance each other, and an energy curve can be plotted, for which the lowest energy level is equal to ε (Lennard-Jones formula). The derivative of the energy with respect to the distance, r, between the two centers of gravities of the atoms/molecules, when plotted as a function of r, forms the force curve shown in lower graph. A comparison of the two curves reveals that when the force (dU/dr) is zero (lower graph), the U(r) value is the lowest. Thus, at this r value, the average molecular separation has occurred in the liquid (A). When the force curve reaches zero the next time (B), the average molecular separation in its gas phase has been reached.
Figure 5.
The upper curve is derived by combining U(r)vfW and U(r)rep. At a certain distance, δ, these two energy levels balance each other, and an energy curve can be plotted, for which the lowest energy level is equal to ε (Lennard-Jones formula). The derivative of the energy with respect to the distance, r, between the two centers of gravities of the atoms/molecules, when plotted as a function of r, forms the force curve shown in lower graph. A comparison of the two curves reveals that when the force (dU/dr) is zero (lower graph), the U(r) value is the lowest. Thus, at this r value, the average molecular separation has occurred in the liquid (A). When the force curve reaches zero the next time (B), the average molecular separation in its gas phase has been reached.
When it comes to hydrogen bond formation, such bonds require essential direct molecular contact, and thus become more short ranged than attractive van der Waals forces [
36]. An r-dependence curve for such a bond would thus become very steep and have a deep potential minimum. Metallic bonds, ionic bond and covalent bonds are even stronger at close range, and particularly ionic interaction energies are long-ranged varying as 1/r as compared with 1/r
6 for van der Waals energies. By considering these aspects and thereby also the differences in interaction energies between different types of bonds, it becomes clear that stronger molecular energy results in higher surface tension.
Considering the above relationships regarding bond formation, it seems reasonable to assume that the more atoms-molecules that are in close contact with the substrate surface, the more bond sites would establish and the stronger the adhesion would become. For example, two rough solid surfaces in contact with each other would be in intimate contact just at relatively few sites, while a liquid and a gas would be able to approach a contact area up toward 100%. From that point of view, gases and liquids should be able to form more van der Waals bond sites than the rough solids. However, a second important consideration is also the quality of the bonds in the different materials. For example, a gold foil coated with water has a contact area of almost 100%, but these bond sites are transmitted via weak hydrogen bonds. If rather than being coated with water, the gold foil is covered with another gold foil, the total foil-foil contact area is most likely substantially smaller than in the water-foil case. However, because the two gold foils in intimate contact with each other establish metallic bonds at the contact sites, and because the bonds transferring forces between the two foils are stronger than the hydrogen bonds, the foils are more difficult to separate than the foil-water interaction.
4. Forces on Solids in Contact with Liquids
Even though gases, liquids and solids are all used as different coatings in dentistry, the most commonly used precursor is a liquid [
37].
When a liquid such as a sealant is placed on a tooth, its physical interaction with the tooth can vary considerably from case to case making it more difficult to predict the outcome. For example, if a tooth surface is flat, slightly inclined, and a drop of a sealant is placed on it, it may just ball up and roll of leaving the surface as it was before it was exposed to a sealant. However, if the surface has been etched and the sealant is partly stuck to the surface, it may flow down a cusp inclination as a rivulet. Still differently, the sealant may spread out in all directions as a coherent film, sealing in the surface as intended. If the surface is etched and can be described as porous surface, and it is put into contact with the sealant, the sealant may be quickly imbibed into the enamel surface (like water into a sponge) or it may not be. In fact, it may be possible to coat the porous enamel surface with a sealant with no sealant entering the pores at all (e.g., saliva contaminated enamel). All these behaviors are important to consider when it comes to coatings in general, because in order to achieve optimal bonding and maximal seal, a coating has to wet and adapt to the substrate.
4.1. Young’s Equation
When coatings in general are discussed in the dental literature, a corner-stone tends to be to study the ability of a liquid to wet a solid by use Young’s equation (
Figure 6), first published in 1805. What is often neglected is that Young’s equation is a rather crude approach, simply because it was developed before the structure of atoms was known. Because of that, Young’s equation should be regarded as a way to get a general feeling for surface energetic interactions, but far too crude when it comes to explaining surface phenomena on a molecular level [
38]. According to Young’s equation, the contact angle of the liquid, θ, is related to the surface energies,
i.e., the σ’s, of the three interfaces involved, in which the system free energy minimization led to Young’s equation. By using “surface tension” rather than “surface energy” and vectors to describe the magnitude and direction of the interfacial forces represented by the surface tension, the equation becomes
where SG stands for solid-gas interface, SL for solid-liquid interface, and LG for liquid-gas interface. From such a derivation it is noticed that the normal forces on the interline segment require that the upward capillary force of σLGsin θ be balanced by an unsymmetrical stress in the underlying solid. This force is often neglected, but could play a significant role when it comes to the development of stresses in coated objects.
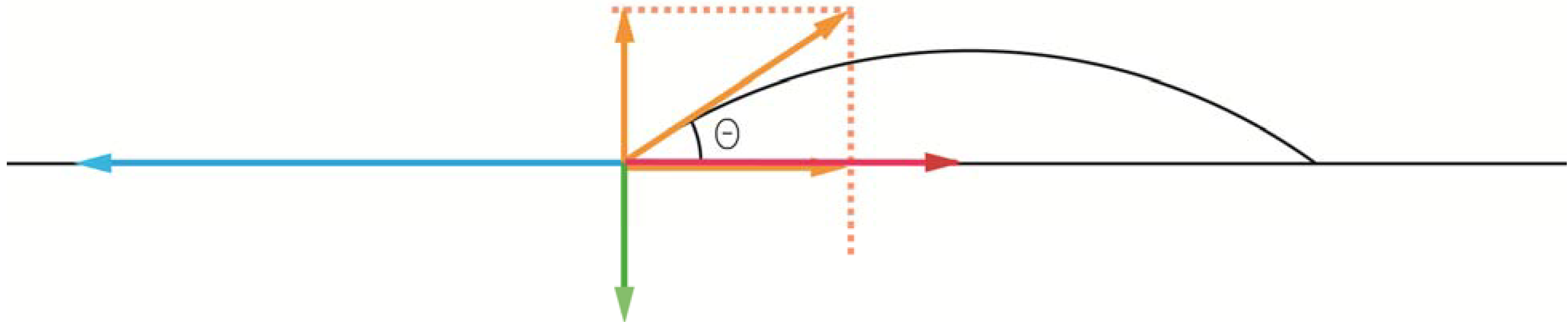
Figure 6.
Force components at a gas-solid-liquid triple point. The blue arrow represents the σSG surface tension, the red arrow the σSL, and the hypotenuse of the yellow arrows the σLG. By knowing the contact angle of the liquid, the σLG vector can be split into a force parallel to the solid surface (σLGcos θ) and one perpendicular to the surface (σLGsin θ). In order to generate a force balance in vertical direction, the green force vector was introduced, for which the magnitude then becomes σLGsin θ. By balancing the horizontal forces, σSG = σSL + σLGcos θ, the expression can be rewritten as cos θ = (σSG – σSL)/ σLG.
Figure 6.
Force components at a gas-solid-liquid triple point. The blue arrow represents the σSG surface tension, the red arrow the σSL, and the hypotenuse of the yellow arrows the σLG. By knowing the contact angle of the liquid, the σLG vector can be split into a force parallel to the solid surface (σLGcos θ) and one perpendicular to the surface (σLGsin θ). In order to generate a force balance in vertical direction, the green force vector was introduced, for which the magnitude then becomes σLGsin θ. By balancing the horizontal forces, σSG = σSL + σLGcos θ, the expression can be rewritten as cos θ = (σSG – σSL)/ σLG.
By looking at Young’s equation, it seems that wettability predictions are relatively easy to perform. However, reality has taught us that contact angle determinations are notoriously irreproducible (
Figure 7), which can be related to two key reasons [
38].
The first reason is that only the uppermost surface layer of the solid is relevant when it comes to determining the contact angle, while in reality, solid surfaces have often contaminations that bear little resemblance to the bulk material beneath. Traces of adsorbing solutes in the fluid phases can play a similar role. The second reason relates to the method used to measure the θ value. If it is measured as the liquid advances over a surface the contact angle is larger than when it is receding. For example, when a drop of liquid is deposited on a solid surface, θ may assume some finite value. Then as more liquid is added, the interline remains fixed (or “pinned”) so that the apparent contact angle increases. Finally, an angle is reached for which the interline “jumps” to a new position. The angle just before the jump occurs is the “static advanced contact angle” and is generally the value reported in the literature. The reverse situation occurs as liquid is withdrawn from that drop, leading to the “static reduced contact angle.” Thus the contact angle values differ for an advancing drop vs. a receding drop. The magnitude of the difference between θA and θR is usually quite large and referred to as contact angle hysteresis. One way to see the differences between θA and θR is to watch a drop of liquid on a sloping plane. As the drop moves down the plane, it develops two contact angles. One in the direction it moves, and one in the opposite direction. Of these two contact angles, the first one, the θA, is larger, while the second one, the θR, is the smaller.
Figure 7.
Surfaces are usually not absolutely flat as assumed by Young’s equation. As a drop of water moves uphill (A), the contact angle at the liquid edge tends to be under-estimated (light blue color) in relationship to a flat horizontal surface (red dotted line). At the tip of the hill (B), the contact angle assumes a value which is equal to an assumed flat surface. As the liquid edge moves downhill (C), the contact angle tends to become over-estimated in relationship to the red horizontal line. The light-blue field represents what would be perceived as contact angles at the different locations under the assumption that the surface is flat.
Figure 7.
Surfaces are usually not absolutely flat as assumed by Young’s equation. As a drop of water moves uphill (A), the contact angle at the liquid edge tends to be under-estimated (light blue color) in relationship to a flat horizontal surface (red dotted line). At the tip of the hill (B), the contact angle assumes a value which is equal to an assumed flat surface. As the liquid edge moves downhill (C), the contact angle tends to become over-estimated in relationship to the red horizontal line. The light-blue field represents what would be perceived as contact angles at the different locations under the assumption that the surface is flat.
Actual dental surfaces are generally both rough and energetically heterogeneous, and the heterogeneity may be both non-uniform and anisotropic (
Figure 8). In the latter case, the contact angle may be different depending on the direction of observation. It seems as though the effect of striae of Retzius and surface perkymata [
39] could be important for enamel wettability, even though it is rarely considered in the dental literature.
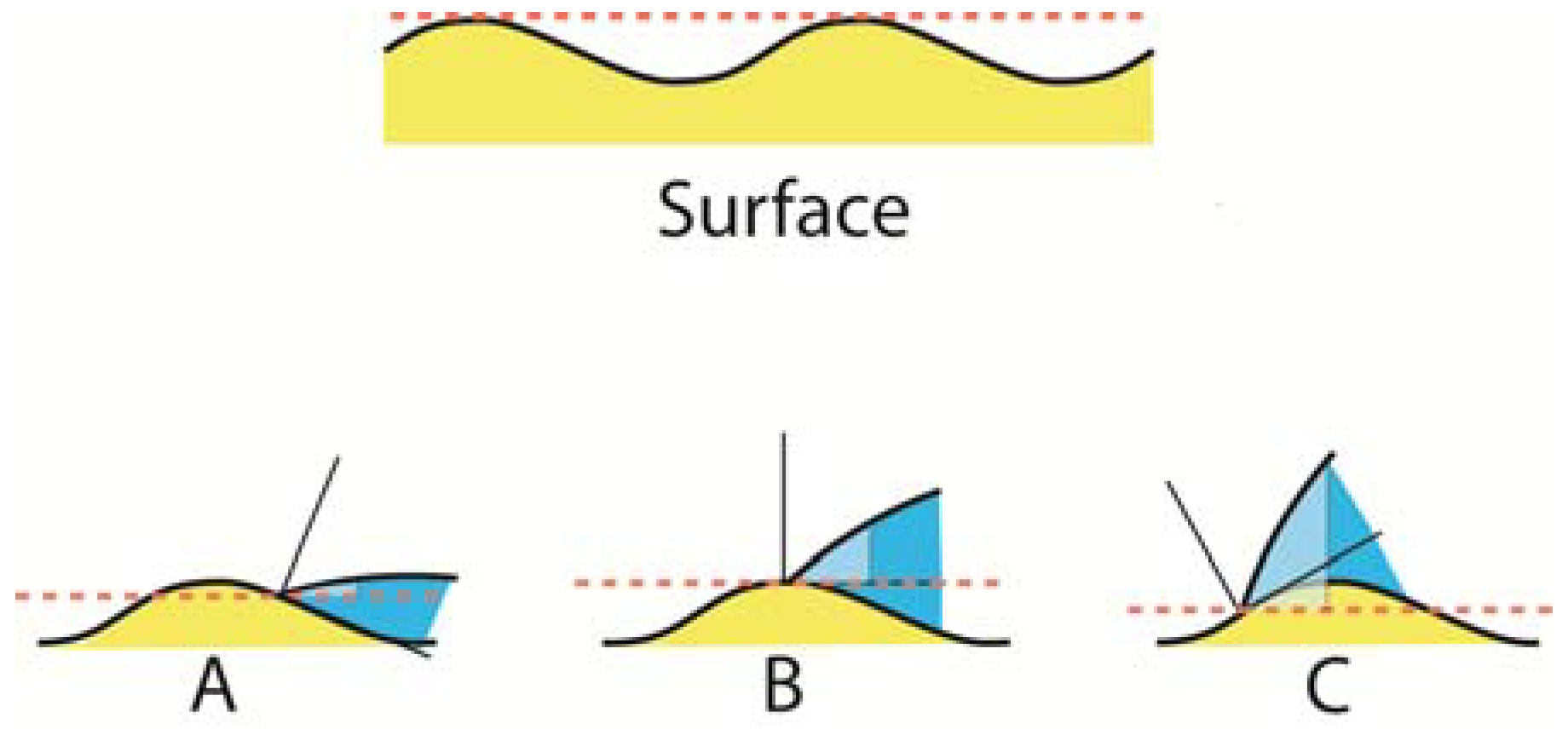
Figure 8 shows a close up picture of a cut enamel surface coated with a self-etching primer. The conclusion we can draw from that picture is that even though the above explanations for contact hysteresis are plausible, they do not provide, in general, for basic predictions of advancing and receding contact angles. As a result of various heterogeneities present on a tooth surface, when a fluid spreads on a surface it occurs through either advanced or receded spread across a solid surface at a finite rate, and it generally does so in a series of jumps referred to as “stick-slip motion.”
The size scale of the surface heterogeneities is important. When these are large (>10 μm) and regular, the hysteresis may take on a predictable character, but if the sizes of the heterogeneities are sufficiently small (<1 μm), other types of analyses must be used. From a dental point of view, this might be important to consider when dentin bonding is discussed and the wetting of the dentin surface located under the exposed collagen is considered. Because the dentin tubuli have diameters ranging from 1.2 μm at the dentin enamel junction to 2.5 μm near the pulp [
39], and the content of the tubules consist of a hydrogel [
39], the dentin structure falls between the above limits. The same should also be true for the enamel rod structure with interrod regions with spacings around 4 μm [
39].
Figure 8.
Enamel trimmed with a sand-paper disk (
right section) and on which a self-etching primer has been placed (
left section). By looking at the advancing edge of the primer, one can see a wavy appearance. That appearance can be explained by considering the behavior shown in
Figure 7 and here occurring along the advancing edge. In this case, different contact angles exist at different locations along the advancing edge of the primer. Also, spreading can occur in both the x- and y-axes on a surface containing scratches and different heterogeneities in surface wetting properties.
Figure 8.
Enamel trimmed with a sand-paper disk (
right section) and on which a self-etching primer has been placed (
left section). By looking at the advancing edge of the primer, one can see a wavy appearance. That appearance can be explained by considering the behavior shown in
Figure 7 and here occurring along the advancing edge. In this case, different contact angles exist at different locations along the advancing edge of the primer. Also, spreading can occur in both the x- and y-axes on a surface containing scratches and different heterogeneities in surface wetting properties.
4.2. Wenzel’s Equation
To come to grip with surface roughness and its impact on wettability, Wenzel [
40] already in 1936 assumed that the true solid surface area could be related to the nominal surface area. He did so by multiplying the nominal surface area with a “rugosity factor”, r. By looking at Young’s equation from a surface energy point of view, he could minimize the total free energy of the system, which led to a modified form of Young’s equation in terms of the observed or apparent contact angle,
viz.The above formula is known as Wenzel’s equation. In order to be valid, the size scale of the roughness must be sufficiently small. The liquid mass (drop) must also be large relative to the size-scale of the roughness. Wenzel’s equation reveals that one can increase the wettability of a solid by a wettable liquid (θ0 < 90), or decrease the wettability of a solid by liquid that does not wet it. Since r > 1 for a roughened surface, if cos θ is positive (θ0 < 90), the cos θapp will be larger, viz.
If the liquid is non-wetting, cos θ is negative, and cos θapp will become more negative if the surface is roughened. The ability to change wetting characteristics by roughening is important in a number of applications. In particular, if θapp can be made to go to 0°, wetting out will occur. The rugosity factor required for this to occur is r = cos−1 θ, and since r-values up to 2.0 can readily be achieved, this is often possible.
4.3. Cassie and Baxter’s Equation
Cassie and Baxter [
41] have developed a similar approach for chemically heterogeneous surfaces. In the case of a surface with two types of heterogenicities, for which the intrinsic contact angles are θ
1 and θ
2 respectively, minimization of the free energy leads to the Cassie-Baxter equation written as
The two terms, Φ1 and Φ2, represent the area fractions for the two types of surface. The formula can readily be extended to the case of many different types of patches. One important case is that in which pores in the surface lead to vapor gaps across which the liquid does not contact the solid. The effective contact angle over such gaps is 180°, and if the area fraction of them is Φ2, the Cassie-Baxter equation becomes
Structures of this type are the ones that produce “ultra-hydrophobic” surfaces, which are defined as θ > 130°. Many plant leaves, most notably those of the lotus flower, have ultra-hydrophobic surfaces owing to a very fine surface structure coated with hydrophobic wax crystals of about 1 nm diameter. Beads of water roll off the surface, collecting dirt particles as they go, so the lotus leaves are self-cleaning in a process known as the “lotus effect.” This approach has been mimicked by researchers who have developed sprays that can make wood, paper, masonry, leather, etc., water repellant. Maybe future nanotechnology advances in dentistry could lead to such coatings that could be placed on tooth surfaces and thus minimize plaque adhesion.
From the Cassie-Baxter equation, assume that an etched and rough tooth surface is coated with a resin. The small pores on the surface may be prefilled by capillary condensation of the wetting liquid, and the nominal area fraction of the filled pores may be taken as Φ2. Over this area, the contact angle is 0°, causing the Cassie-Baxter equation to take the form
which usually results in wetting out, i.e., θ→0°.
Depending on circumstances, one may want to alter the wetting characteristics of a solid material. All of these approaches can be understood in terms of Young’s equation
For good wetting, cos θ should be as high as possible (θ→0°), and for poor wetting or non-wetting, it should be as small (or as large negative value) (θ→180°) as possible.
5. Adhesion and Adhesion Mechanisms
Based on the surface properties discussed so far, one can say that adhesion is an extension of surface wettability and that it refers to solid surfaces sticking together by molecular attraction across their common interface or a bridging solid or liquid. Because of the surface roughness and the presence of contaminants of most solids there is usually little direct molecular contact between real solid surfaces. Therefore there are relatively few points of true contact between the solids where molecular interactions can occur. The size of the contact surface will depend on the softness of the materials and the compressive force applied, but in general, sufficient intimacy can be achieved only if one of the materials, the adhesive, is in liquid form. In other words, adhesion is often initiated through a liquid-solid interaction [
42]. In the case of adhesion, the solid surface to which the adhesive is applied is termed the adherend (previously referred to as the substrate in connection to surface properties). In the ideal case, the liquid adhesive completely contacts the solid over all its area, and by doing so the adhesive displaces any physiosorbed contamination from the surface. One can further idealize the assumption by assuming that as the liquid solidifies (cures) and remain in contact with the surface.
Wetting and spreading of the adhesive play a key role in the phenomenon of adhesion, but there is much more to it than that [
42]. Today it is believed that there are four principal mechanisms of adhesion [
26] (
Figure 10). The first is contact adhesion, in which molecular interaction (physical, acid-base or covalent) occurs across a more or less smooth, defined interface. This type of adhesion can be related to the van der Waals interaction discussed earlier, and how the principles behind Lennard-Jones formula can be extended to other bond types. It is to this physical/chemical mechanism that most of what follows applies. The second adhesion mechanism is diffusion induced interface adhesion, generally applicable to the bonding between polymeric adhesives and adherends. Again, the surface first interacts as under the first type of adhesion. Then, if there is adequate mutual solubility and adequate contact time between the adhesive and the surface, the mobile adhesive molecules (not locked into a tightly cross-linked or crystallized structure) can diffuse into the solid surface, leading to the formation of an interphase of some thickness. The third adhesion mechanism is mechanical interlocking. In this case, the liquid adhesive penetrates the cavities of a rough or porous adherend, and upon solidification the adhesive forms effective “hooks” holding the phases together. The final adhesion mechanism proposed is that of electrostatic interaction across the interface. The contribution of this mechanism is generally thought to be small. In many situations, two or more of the above mechanisms are important. It appears likely that while wetting behavior may directly relate to contact adhesion (first type), that behavior must also play some role in the remaining mechanisms, because if good physical intimacy between the phases is not achieved, it will be difficult for the remaining three mechanisms to be effective.
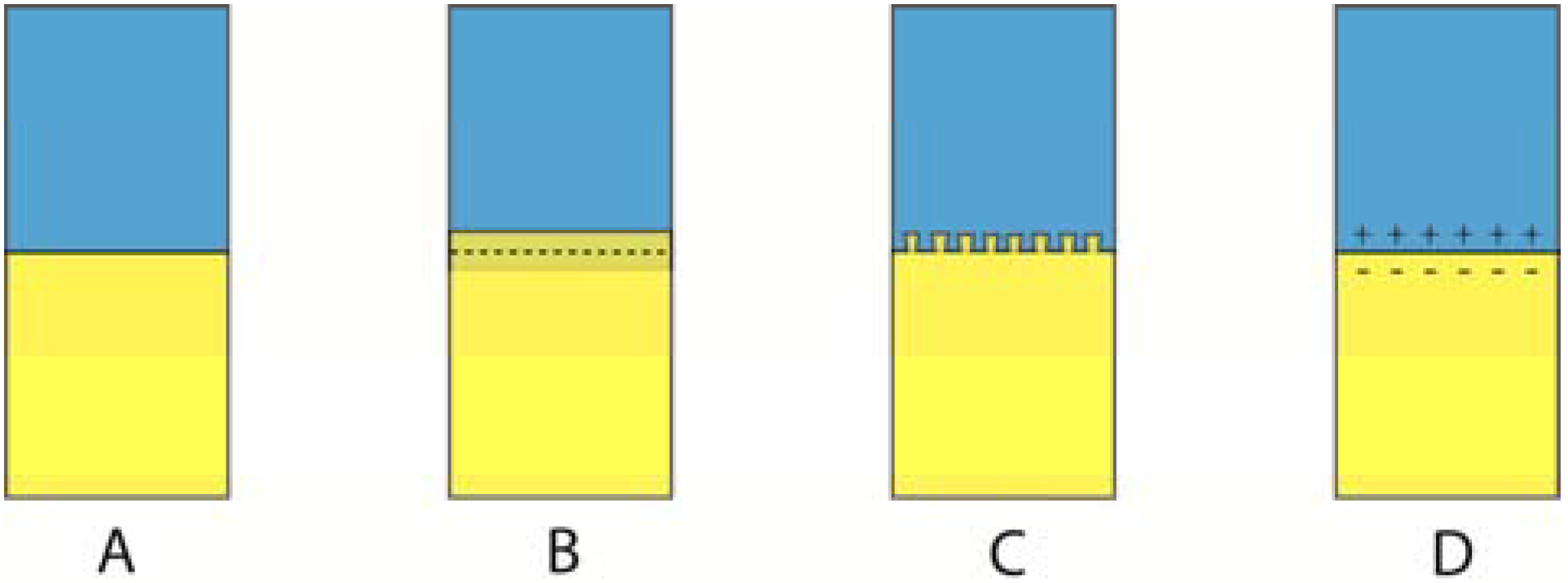
Figure 10.
Of these four adhesion mechanisms, (A) represents contact adhesion, in which molecules interact (physical, acid-base or covalent), (B) diffusion induced interface adhesion, (C) mechanical interlocking, and (D) electrostatic interaction across the interface. Adhesion in general tend to use a combination of these four mechanisms.
Figure 10.
Of these four adhesion mechanisms, (A) represents contact adhesion, in which molecules interact (physical, acid-base or covalent), (B) diffusion induced interface adhesion, (C) mechanical interlocking, and (D) electrostatic interaction across the interface. Adhesion in general tend to use a combination of these four mechanisms.
Even though the practical consequences of adhesion, and the general approaches usually used to describe it are macroscopic, its origin is molecular interaction. At the molecular level, adhesion behavior often appears counter-intuitive, as pointed out by Kendall [
43], who suggests three “Laws of Molecular Adhesion” as follows:
1. All atoms and molecules adhere with considerable force. If two solid bodies approach to nanometer separations across a vacuum, they will jump into contact.
2. The effect of contaminant “wetting” molecules is to reduce adhesion, or even to make the bodies repel each other. It would thus appear that “adhesives” reduce molecular adhesion.
3. Molecular adhesion forces are of such short range that various factors, such as roughness, Brownian motion, cracking, plastic deformation, etc., can have large effects on macroscopic adhesion while molecular adhesion remains the same.
The first two of these “laws” can readily be understood by considering the section about van der Waals forces discussed earlier. According to Lennard-Jones formula, attractive forces increase as molecules approach each other. When molecules first come very close to each other, their electron clouds start interacting preventing further attraction. At that point the molecules assume an equilibrium where attractive and repulsive forces balance each other. The second law can be understood by considering the effect of a thin film of low surface energy covering a surface. For example, when the first space craft landed on the Moon it was noticed that dust particles bonded to the window surfaces, something that did not occur on Earth. The reason for that difference can be explained by considering the effect atmospheric atoms have on glass surfaces on Earth, while there is no such atmosphere on the Moon containing such molecules [
43]. The third law of molecular adhesion addresses how roughness and surface contaminations of actual macroscopic surfaces prevent intimacy of contact, which is vital due to the short range of the adhesive forces. If the system is subjected to stress (say shear stress), micro-cracks will develop at the points of molecular contact. The Brownian motion or diffusion of molecules or nano-sized portions of the material at the crack tip will continually probe the crack configuration. The existence of stresses biases the system against re-healing when microscopic motion is in the direction of the advancing of the crack.
Many attempts have been made to quantify the strength or the durability of the bond between two solids by use of different mechanical tests. Such adhesive strength values are of interest for actual application, but are difficult to pin down, depending always on the method used for its measurement and the condition of that measurement (e.g., peel test, lap test or pull out test) [
42]. It is essential to keep in mind that adhesion involves many things in addition to the chemistry and the physics of the interface (or often an “interphase” of finite thickness in which the adhesive and the adherend have inter-diffused). These include roughness and mechanical interlocking, electrostatic effects, and the mechanics of the bulk phases near the boundary (e.g., the existence and level of residual stresses), and the rheology of the disjoining event (plastic vs. brittle failure).
Minimizing the contact angle between adhesive and adherend is important for reasons other than maximizing the work of adhesion [
44]. Often the first step in the formation of a bond between two solid surfaces by means of an adhesive is the establishment of a liquid bridge. The strength of this “capillary adhesion” is directly proportional to cos θ. When the liquid bridge is cured to a solid, the mechanical properties of the bonding are also dependent on the contact angle. The magnitude of the stress concentration factor (local stress/applied stress) in a stressed lap joint increases quite sharply with contact angle beyond about 30 degrees [
26]. Furthermore, the locus of stress concentration moves out to the edge of the adhesive layer when the contact angle increases. Such stress concentrations are not unlike those that exist at the site of vapor inclusions or voids between adhesive and rough porous surfaces, as shown in
Figure 11.
Figure 11.
The adhesive placed on the substrate surface in this drawing does not wet the substrate surface. The reason could be unfavorable differences in surface tension properties of the adhesive and the substrate, or the presence of contaminants. The defects introduced will act as stress concentrators and increase the risk for catastrophic failure of the adhesive-substrate connection.
Figure 11.
The adhesive placed on the substrate surface in this drawing does not wet the substrate surface. The reason could be unfavorable differences in surface tension properties of the adhesive and the substrate, or the presence of contaminants. The defects introduced will act as stress concentrators and increase the risk for catastrophic failure of the adhesive-substrate connection.
The presence of a row of such voids can lead to a zippering type of failure. Voids are also a serious problem in the formation of composite materials as shown in
Figure 12. The presence of such voids is minimized when the contact angle is minimized and the best condition is of course θ = 0°.
It is clear in Wenzel’s formula that roughness of the adherend may be either favorable or unfavorable to good practical adhesion, depending on wettability. If wetting is complete, roughness will lead to greater molecular contact area, and possibly to mechanical interlocking. On the other hand, if wetting is incomplete, roughness may produce air pockets or voids leading to reduced molecular contact area and to sites for high local stress concentrations. Given the central importance of wetting to the establishment of effective bonds, many of the practical strategies discussed above for optimizing wetting are also appropriate for maximizing adhesion.
Figure 12.
When filler particles are mixed with a resin matrix, there is always a risk that pour filler-resin wetting, impurities and air incorporation can result in numerous defects in the mixed composite. In addition to causing a decrease in strength and wear properties, such defects will also impact the aesthetic properties of the restoration by increasing the staining ability and changing the optical properties of the composite.
Figure 12.
When filler particles are mixed with a resin matrix, there is always a risk that pour filler-resin wetting, impurities and air incorporation can result in numerous defects in the mixed composite. In addition to causing a decrease in strength and wear properties, such defects will also impact the aesthetic properties of the restoration by increasing the staining ability and changing the optical properties of the composite.
An important consideration is also in which order different materials are placed. Take, for example, epoxy and polyethylene resins used as adhesives on cured epoxy or polyethylene resin surfaces [
45]. In those cases, the adhesion is poor when liquid (uncured) epoxy resin is deposited as an adhesive on the polyethylene substrate. On the other hand, if the epoxy is first cured, and then molten polyethylene is applied to it as the adhesive, the adhesion is excellent. Since the same interface was presumably created in both cases, one would assume that the work of adhesion would be the same, but the results are dramatically different. The difference is that the polyethylene solid has rather low surface energy and is not wet by the epoxy liquid (θ > 0°), while the low surface tension of molten polyethylene spontaneously spreads over the cured epoxy adherend (θ = 0°). It was argued that in the absence of spontaneous spreading, forced spreading was required to apply the adhesive, resulting in incomplete contact (micro air pockets) between the adhesive (epoxy) and the adherend (polyethylene), leading to poor adhesion.
Another approach to form a coating adhering to a surface is to use acid-base effects [
46,
47]. The theory behind such a bond formation is that surface energies consist of contributions due to dispersion forces plus polar effects,
i.e., σ = σ
d + σ
p, and that the latter may act across the interface with the same geometric mean mixing rule as is valid for dispersion forces [
48,
49,
50]. In addition to simple dispersion interactions, there may be those due to metallic bonding or to specific chemical interactions. Virtually all of the latter may be lumped into “acid-base” interactions, when they are considered in the most general “Lewis” sense. A Lewis acid-base interaction occurs whenever an electron pair from one of the participants is shared and may vary from an ionic interaction in one extreme to a covalent bond in the other.
It might be interesting to notice that already in 1967 at the General Motors Symposium on Interfaces, acid-base interaction was suggest as being key for successful car painting [
51], which was achieved when one surface (e.g., the metal surface of the car) acted as a base, while the paint acted as an acid. The key, however, was to find the right balance between these two interactions. A too weak interaction resulted in paint that pealed of, while a too strong acid resulted in a paint that pealed of with a dissolved layer of metal.
The acid-base theory of adhesion has met with qualitative success. For example, when a basic polymer film, poly(methyl methacrylate), PMMA, was cast against a basic soda glass substrate, poor adhesion was obtained, but when the acidic polymer, post-chlorinated poly(vinyl chloride), CPVC, was cast against the basic substrate, adhesion was very strong [
26]. In dentistry, the acid-base bonding approach is used when cements such as polycarboxylate and glass ionomers are used. In these cases, the acidic polyalkeonic acids donate protons to the hydroxyapatite surface, where the protons react with the hydroxyl groups and form water. As a result of this reaction, the polyalkeonic acid becomes negatively charged and lines up parallel to the positively charge apatite surface. This behavior may very well explain why clinical studies suggest that the best retention rate of bonded Class V restorations are achieved with glass ionomers, a finding that might be related to the multiple charge sizes along a single polyalkeonic acid molecule.