Modeling and Analysis of a Low-Voltage DC Distribution System
Abstract
:1. Introduction
2. Modeling of Components in LVDC Distribution System

2.1. Power Electronic Device Modeling
2.1.1. AC/DC Converter

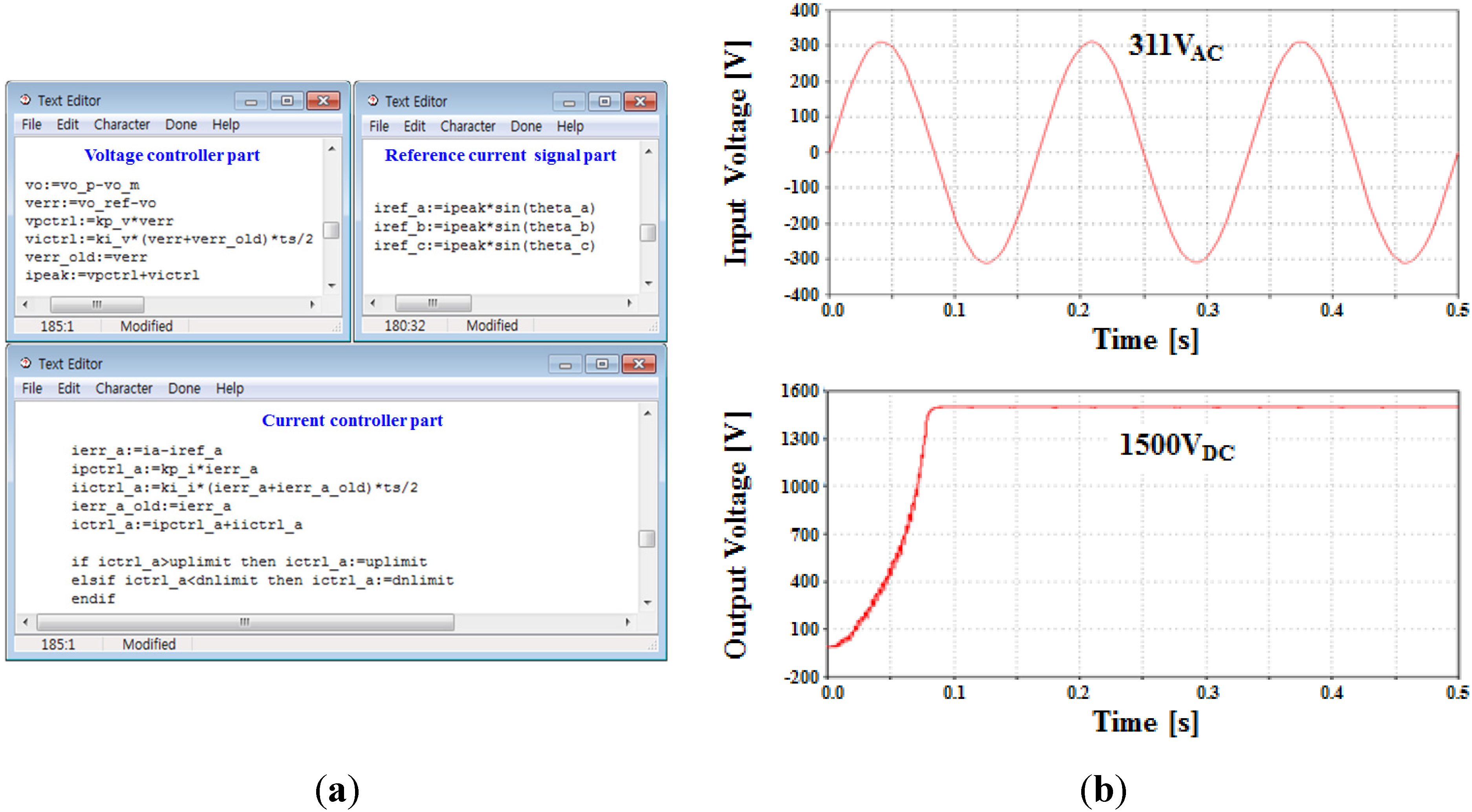
2.1.2. DC/DC Converter


2.1.3. DC/AC Inverter


2.2. Distribution Line Modeling
2.2.1. Overhead Distribution Line

| Dimension (mm2) | Outer Diameter (mm) | Total Cable Diameter(mm) | Conductor Resistance (Ω/km) |
|---|---|---|---|
| 100 | 13.0 | 16.0 | 0.185 |

2.2.2. Underground Cable

| Dimension (mm2) | Core diameter (mm) | Sheath layer(mm) | Conductor resistance (Ω/km) |
|---|---|---|---|
| 240 | 18.3 | 2.6 | 0.0754 |

2.3. Load Modeling

| Parameter | Value | |
|---|---|---|
| DC Input Voltage | 380 VDC | |
| DC/AC Inverter | Output voltage | 220 VAC,RMS, 60 Hz |
| Amplitude modulation index (ma) | 0.84 | |
| Frequency modulation index (mf) | 200 | |
| Switching Frequency | 12 kHz | |
| Efficiency of DC/DC Converter | 95% | |
| Voltage of Equivalent Resistance | 12 VDC | |
| Load | Component | Factor | Value |
|---|---|---|---|
| AC Load | Diode Rectifier | Input Voltage | 220 V |
| Input Current | 0.0953 A | ||
| Input Power | 20.97 W | ||
| Efficiency | 75.08% | ||
| DC/DC Buck converter | Input Voltage | 178.91 V | |
| Input Current | 0.088 A | ||
| Input Power | 15.744 W | ||
| Efficiency | 91.46% | ||
| Total efficiency | 68.67% | ||
| DC Load | DC/DC Buck converter | Input Voltage | 380 V |
| Input Current | 0.045 A | ||
| Input Power | 15.465 W | ||
| Efficiency | 90.44% | ||
2.4. PV Generation System and ESS System Modeling
2.4.1. PV Generation System

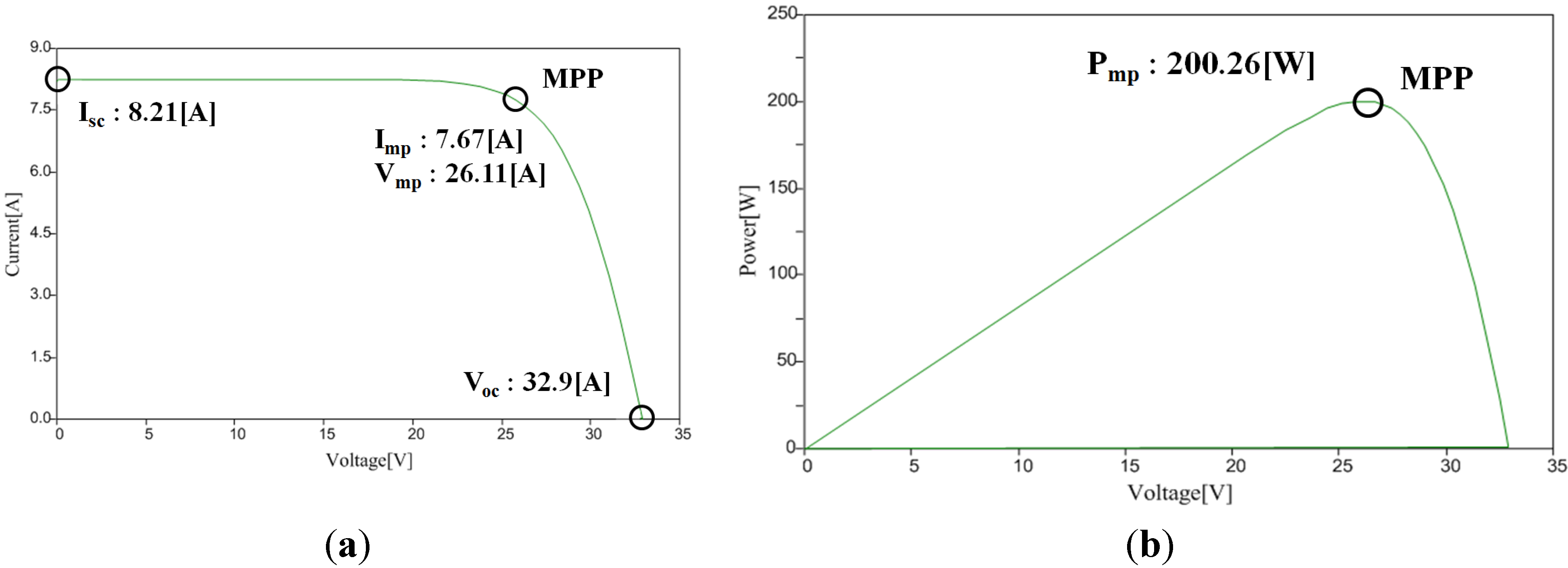
| Output | ISC (A) | VOC (V) | Imp (A) | Vmp (V) | Pmp (W) |
|---|---|---|---|---|---|
| Data sheet | 8.21 | 32.9 | 7.61 | 26.30 | 200.143 |
| Model output | 8.21 | 32.9 | 7.67 | 26.11 | 200.260 |
| Error [%] | 0 | 0 | 0.78 | 0.72 | 0.06 |

2.4.2. ESS System
| ESS Energy (kWh) | ESS Power (kW) | Input and Output Voltage (V) | Input and Output Current (A) |
|---|---|---|---|
| 100 | 20 | 500 | 40 |
| 200 | 40 | 500 | 80 |
| 250 | 50 | 500 | 100 |
| 500 | 100 | 500 | 200 |
| 1000 | 200 | 500 | 400 |
- - ① :
- Measurement of voltage and current/ Calculation of demand power
- - ② :
- Control of ESS input and output
- - ③ :
- Control of ESS operation algorithm
- - ④ :
- Control of ESS connection or ESS disconnection to main DC system
- - ⑤ :
- Calculation of Li-ion battery output voltage


3. Analysis of Characteristics in Steady-State in an LVDC Distribution System
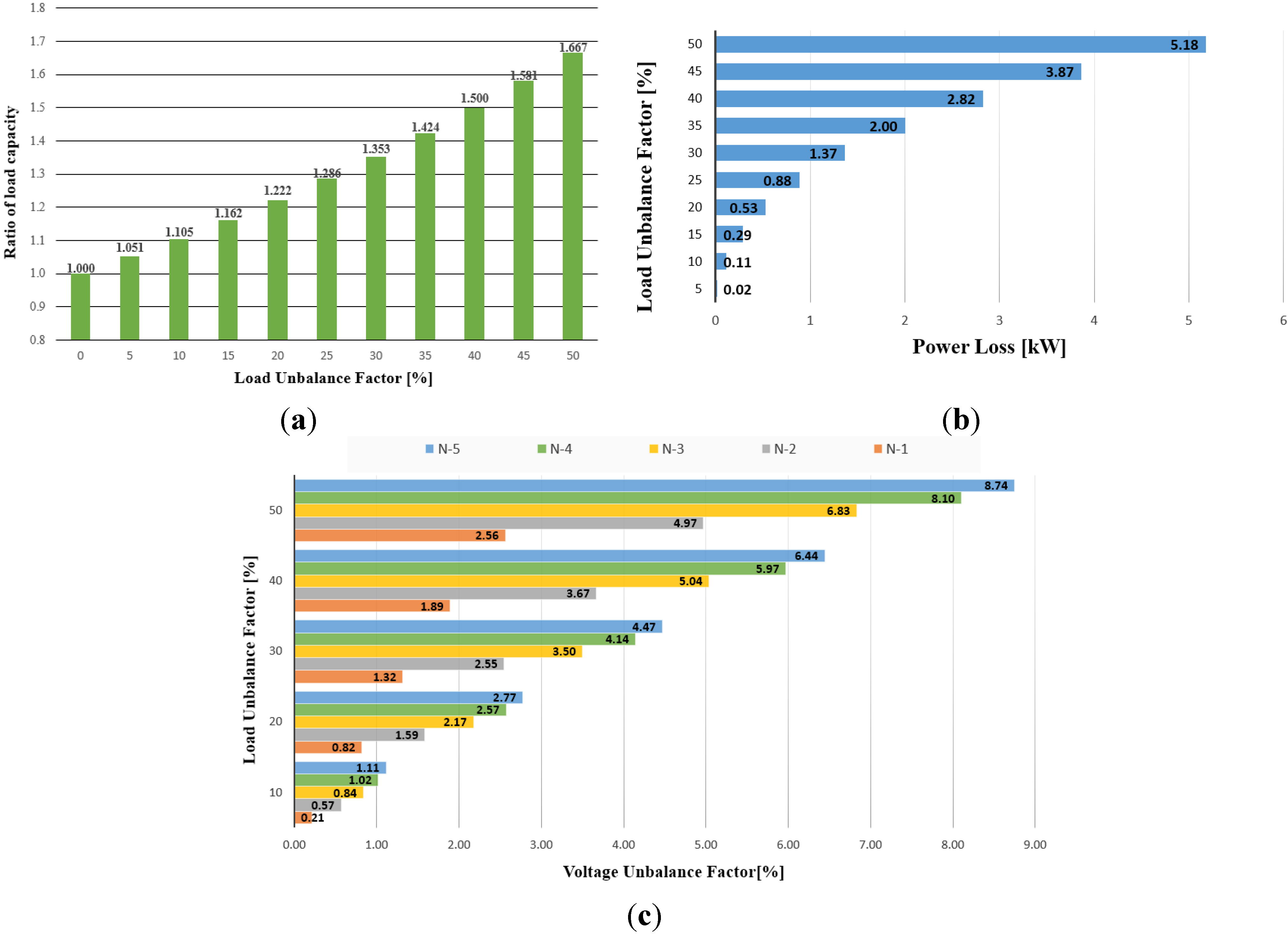
3.1. Analysis of Voltage and Load Unbalance in an LVDC Distribution System

3.2. Analysis of Reverse Power Flow by Interconnection of a PV System with an LVDC Distribution System

| Penetration Level | PV System | Main System | ||||
|---|---|---|---|---|---|---|
| IPV (A) | IA (A) | IB (A) | IC (A) | ID (A) | IE (A) | |
| 10% | 5.3469 | 13.252 | 13.938 | 8.7412 | 5.5306 | 2.7067 |
| 20% | 10.718 | 9.097 | 13.807 | 8.1953 | 5.362 | 3.0286 |
| 30% | 16.147 | 5.2707 | 13.845 | 8.4679 | 5.5082 | 2.872 |
| 40% | 21.545 | 2.0244 | 13.932 | 8.3401 | 5.7503 | 2.7137 |
| 50% | 27 | −1.8334 | 13.676 | 7.873 | 5.3046 | 3.01 |
| Penetration Level | PV System | Main System | ||||
|---|---|---|---|---|---|---|
| IPV (A) | IA (A) | IB (A) | IC (A) | ID (A) | IE (A) | |
| 10% | 5.3469 | 13.122 | 10.455 | 4.8462 | 1.6026 | −0.75044 |
| 20% | 10.718 | 9.1231 | 6.4522 | 0.8022 | −1.7459 | −4.7446 |
| 30% | 16.147 | 5.4109 | 2.6408 | −3.0168 | −5.3671 | −7.9439 |
| 40% | 21.545 | 1.934 | −1.092 | −6.0445 | −9.824 | −11.584 |
| 50% | 27 | −1.9489 | −5.253 | −10.492 | −12.997 | −16.12 |
4. Analysis of Characteristics in the Transient State in an LVDC Distribution System
4.1. Analysis of a Series Arc Fault in an LVDC Distribution System

| Case No. | Fault Type | First Event | Second Event |
|---|---|---|---|
| Case 3 | Fixed gap distance fault | Fault | - |
| Case 4 | Constant gap speed fault | Fault | - |
| Case 5 | Fixed gap distance fault | Load injection | Fault |
| Case 6 | Constant gap speed fault | Load injection | Fault |
4.2. Analysis of a Line Fault in an LVDC Distribution System
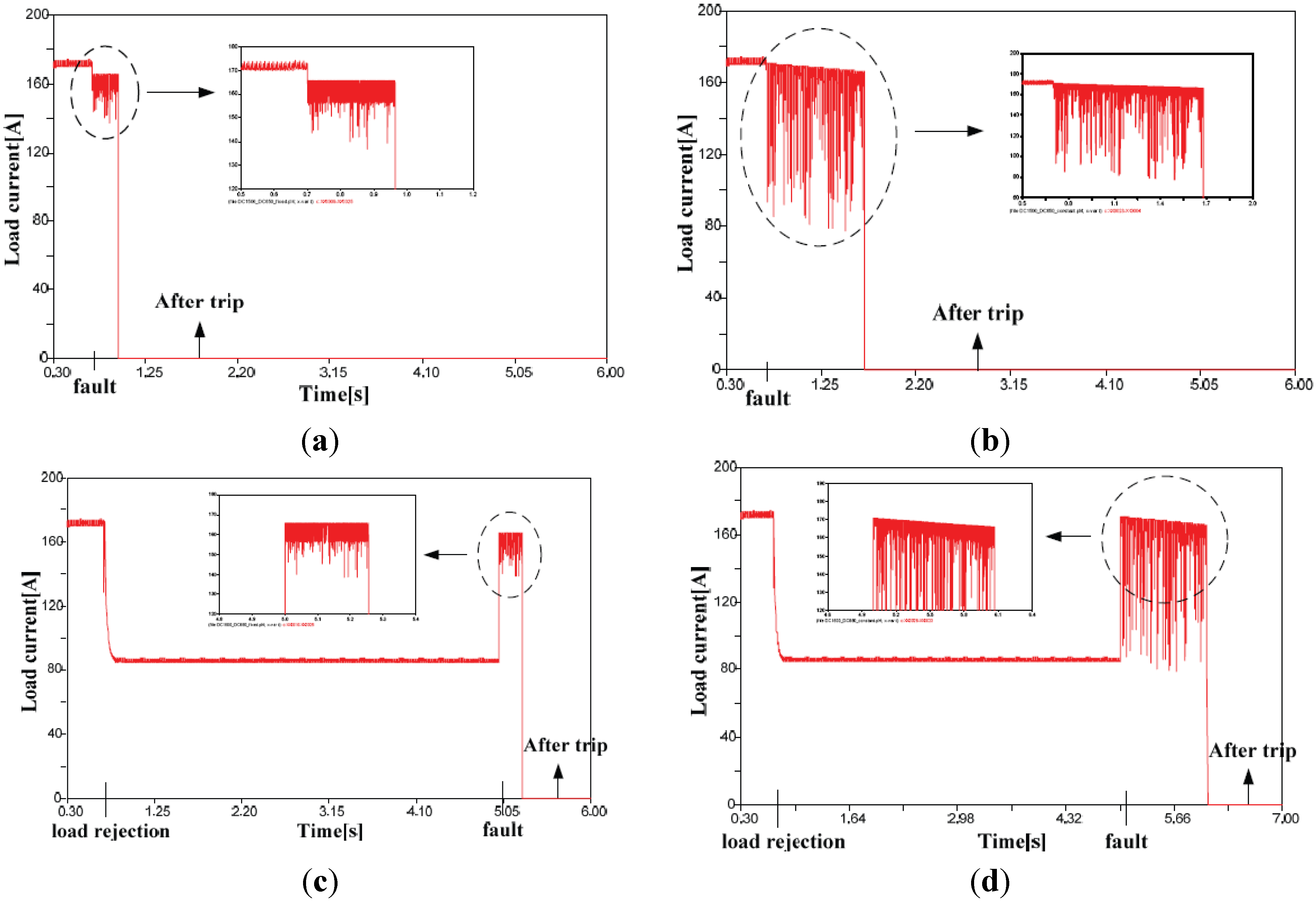


5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brenna, M.; Lazaroiu, G.C.; Tironi, E. High Power Quality and DG Integrated Low Voltage DC Distribution System. In Proceedings of the IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006.
- Alessandro, A.; Morris, B.; Giuseppe, S.; Enrico, T.; Giovanni, U. LV DC Distribution Network with Distributed Energy Resources: Analysis of Possible Structures. In Proceedings of the International Conference on Electricity Distribution CIRED, Turin, Italy, 6–9 June 2005.
- Agustoni, A.; Borioli, E.; Brenna, M.; Simioli, G.; Tironi, E.; Ubezio, G. LVDC Distribution Network with Distributed Energy Resources: Analysis of Possible Structures. In Proceedings of the International Conference on Electricity Distribution CIRED, Turin, Italy, 6–9 June 2005.
- Byeon, G.; Yoon, H.L.T.; Jang, G.; Chae, W.; Kim, J. A research on the characteristics of fault current of DC distribution system and AC distribution system. In Proceedings of the IEEE International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May 2011–3 June 2011.
- Kaipia, T.; Salonen, P.; Lassila, J.; Partanen, J. Possibilities of the low voltage DC distribution systems. In Proceedings of the Nordic Distribution and Asset Management Conference (NORDAC 2006), Stockholm, Sweden, 21–22 August 2006.
- Salonen, P.; Kaipia, T.; Nuutinen, P.; Peltoniemi, P.; Partanen, J. An LVDC distribution system concept. In Proceedings of the Nordic Workshop on Power and Industrial Electronics, Espoo, Finland, 9–11 June 2008.
- Nilsson, D.; Sannino, A. Efficiency analysis of low and medium voltage DC distribution systems. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004.
- Sannino, A.; Postiglione, G.; Bollen, M. Feasibility of a DC network for commercial facilities. IEEE Trans. Ind. Appl. 2003, 39, 1499–1507. [Google Scholar] [CrossRef]
- Salonen, P.; Kaipia, T.; Nuutinen, P.; Peltoniemi, P.; Partanen, J. Fault Analysis of LVDC Distribution System. In Proceedings of the International World Energy System Conference, Lasi, Romania, 30 June–2 July 2008.
- Brenna, M.; Tironi, E.; Ubezio, G. Proposal of a local DC distribution network with distributed energy resources. In Proceedings of the IEEE International Conference on Harmonics and Quality of Power, New York, NY, USA, 12–15 September 2004.
- Nilsson, D. DC Distribution Systems. Ph.D. Thesis, Chalmers University of Technology, Gotenborg, Sweden, 2005. [Google Scholar]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: a survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Dixon, J.W.; Ooi, D.T. Indirect Current Control of a Unity Power Factor Sinusoidal Current Boost Type Three-phase Rectifier. IEEE Trans. Ind. Electron. 1998, 35, 508–515. [Google Scholar] [CrossRef]
- Noh, E.C.; Jung, G.B.; Choi, N.S. Power Conversion System, Power Electronics, 3rd ed.; Munundang: Seoul, Korea, 2011; pp. 311–413. [Google Scholar]
- Betten, J.; Kollman, R. Interleaving DC-DC Converters Boost Efficiency and Voltage; Texas Instruments: Attleboro, MA, USA, 2005. [Google Scholar]
- Jeong, H.J. Control of 3 Phase Interleaved Bidirectional DC/DC Converter for EV. Master’s Thesis, Sungkyunkwan University, Suwon, Korea, February 2011. [Google Scholar]
- Andrzej, M. Trzynadlowski, Introduction to Modern Power Electronics; WILEY: Hoboken, NJ, USA, 2010. [Google Scholar]
- Finnish Standards Association SFS 4879-0.6/1 kV power cables. XLPE-insulated Al-cables. Construction and testing; SESKO Standardization: Helsinki, Finland.
- Finnish Standards Association SFS 4880-0.6/1 kV power cables. PVC-insulated PVC-sheathed cables. Construction and testing; SESKO Standardization: Helsinki, Finland.
- Kim, E.S. Present Situation and Prospect of DC Distribution Technology. In Journal of the Electrical World/Monthly Magazine; Seoul, Korea, April 2010; pp. 61–65. [Google Scholar]
- Salomonsson, D; Sannino, A. Low-Voltage DC Distribution System for Commercial Power Systems with Sensitive Electronic Loads. IEEE Trans. Power Deliv. 2007, 22, 1620–1627. [Google Scholar]
- Seo, G.; Baek, J.; Choi, K.; Bae, H.; Cho, B. Modeling and analysis of DC distribution systems. In Proceedings of the IEEE 8th International Conference on Power Electronics and ECCE Asia (ICPE & ECCE), Jeju, Korea, 30 May 2011–3 June 2011.
- Rauschenbach, H.S. Solar Cell Array Design Handbook; Van Nostrand Reinhold: New York, NY, USA, 1980. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Electric Power Research Institute (EPRI). Price Elasticity of Demand for Electricity: A Primer and Synthesis; Technical Report; EPRI: Palo Alto, CA, USA, January 2008. [Google Scholar]
- Kim, J.H.; Lee, S.J.; Kim, E.S.; Kim, S.K.; Kim, C.H.; Prikler, L. Modeling of Battery for EV using EMTP/ATPDraw. J. Electr. Eng. Technol. 2014, 9, 98–105. [Google Scholar] [CrossRef]
- Hatta, H.; Asari, M.; Kobayashi, H. Study of Energy Management for Decreasing Reverse Power Flow from Photovoltaic Power Systems. In Proceedings of the IEEE PES/IAS Conference on Sustainable Alternative Energy (SAE), Valencia, Spain, 28–30 September 2009.
- Potter, T.E.; Lavado, M. Arc Fault Circuit Interruption Requirements for Aircraft Applications; Texas Instruments: Attleboro, MA, USA, 2005. [Google Scholar]
- Schoepf, T.J.; Naidu, M.; Gopalakrishnan, S. Mitigation and analysis of arc faults in automotive DC networks. IEEE Trans. Compon. Packag. Technol. 2005, 28, 319–326. [Google Scholar] [CrossRef]
- Uriarte, F.M.; Gattozzi, A.L.; Herbst, J.D.; Estes, H.B.; Hotz, T.J.; Kwasinsky, A.; Hebner, R.E. DC Arc Model for Series Faults in Low Voltage Microgrids. IEEE Trans. Smart Grid 2012, 3, 2063–2070. [Google Scholar] [CrossRef]
- Oh, Y.S.; Han, J.; Gwon, G.H.; Kim, D.W.; Kim, C.H. Development of Fault Detector for Series Arc Fault in Low Voltage DC Distribution System using Wavelet Singular Value Decomposition and State Diagram. J. Electr. Eng. Technol. 2015, 10, 766–776. [Google Scholar] [CrossRef]
- Park, J.D.; Candelaria, J. Fault detection and isolation in low voltage DC-bus microgrid system. IEEE Trans. Power Deliv. 2013, 28, 779–787. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Oh, Y.-S.; Gwon, G.-H.; Kim, D.-U.; Noh, C.-H.; Jung, T.-H.; Lee, S.-J.; Kim, C.-H. Modeling and Analysis of a Low-Voltage DC Distribution System. Resources 2015, 4, 713-735. https://doi.org/10.3390/resources4030713
Han J, Oh Y-S, Gwon G-H, Kim D-U, Noh C-H, Jung T-H, Lee S-J, Kim C-H. Modeling and Analysis of a Low-Voltage DC Distribution System. Resources. 2015; 4(3):713-735. https://doi.org/10.3390/resources4030713
Chicago/Turabian StyleHan, Joon, Yun-Sik Oh, Gi-Hyeon Gwon, Doo-Ung Kim, Chul-Ho Noh, Tack-Hyun Jung, Soon-Jeong Lee, and Chul-Hwan Kim. 2015. "Modeling and Analysis of a Low-Voltage DC Distribution System" Resources 4, no. 3: 713-735. https://doi.org/10.3390/resources4030713
APA StyleHan, J., Oh, Y. -S., Gwon, G. -H., Kim, D. -U., Noh, C. -H., Jung, T. -H., Lee, S. -J., & Kim, C. -H. (2015). Modeling and Analysis of a Low-Voltage DC Distribution System. Resources, 4(3), 713-735. https://doi.org/10.3390/resources4030713





