Global Scattering Center Representation of Target Wide-Angle Single Reflection/Diffraction Mechanisms Based on the Multiple Manifold Concept
Abstract
:1. Introduction
2. Principle
2.1. Relationship between SC Locations and Radar View Based on GO/GTD
2.2. Relationship between SC Locations and Radar View Based on PO/PTD
2.3. 6D Feature Space Combining SC Locations with Radar View and Its Multimanifold Data Structure
3. Algorithm
3.1. Multimanifold Clustering
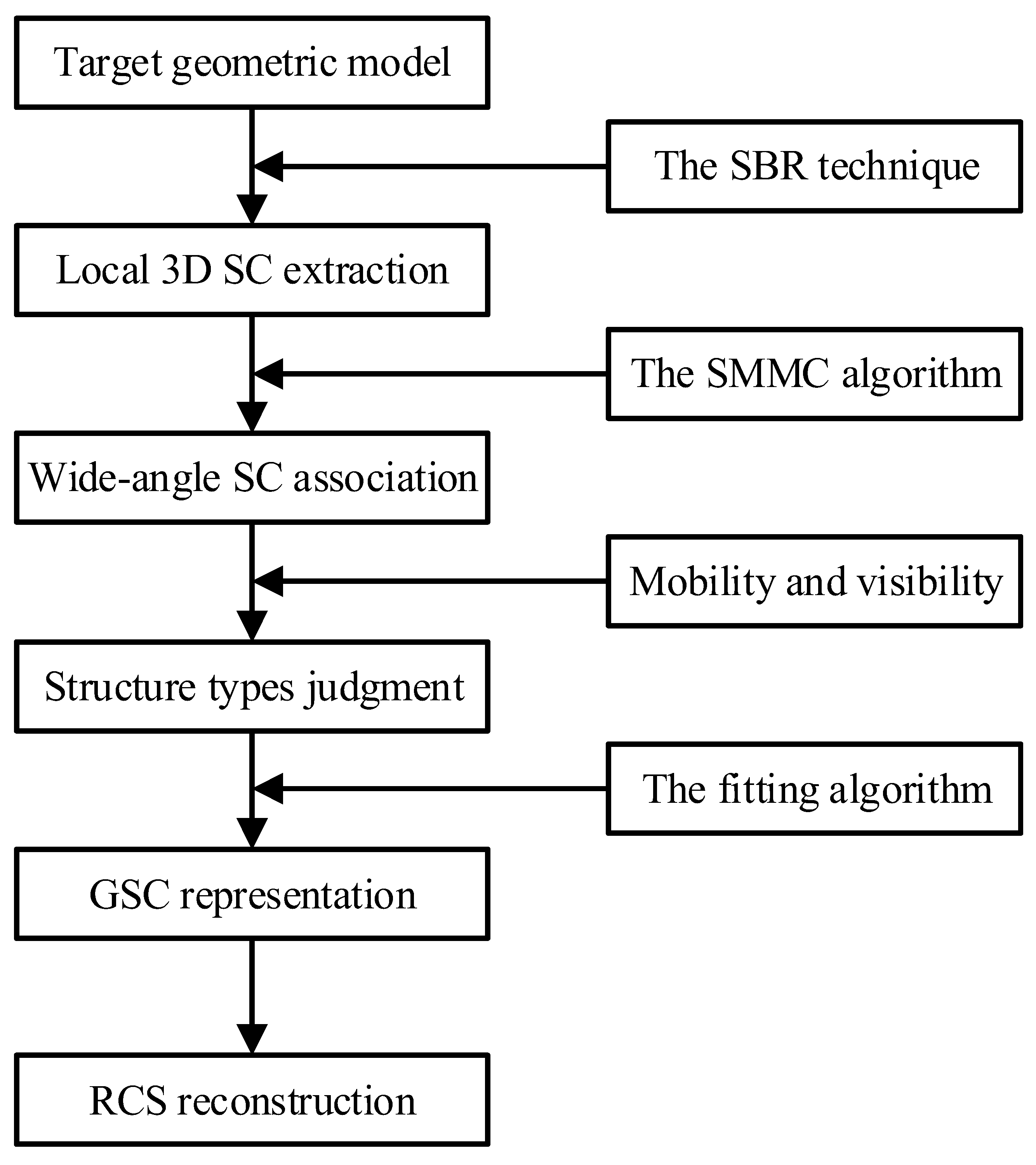
3.2. Data Processing Flow
3.2.1. Local 3D SC Extraction
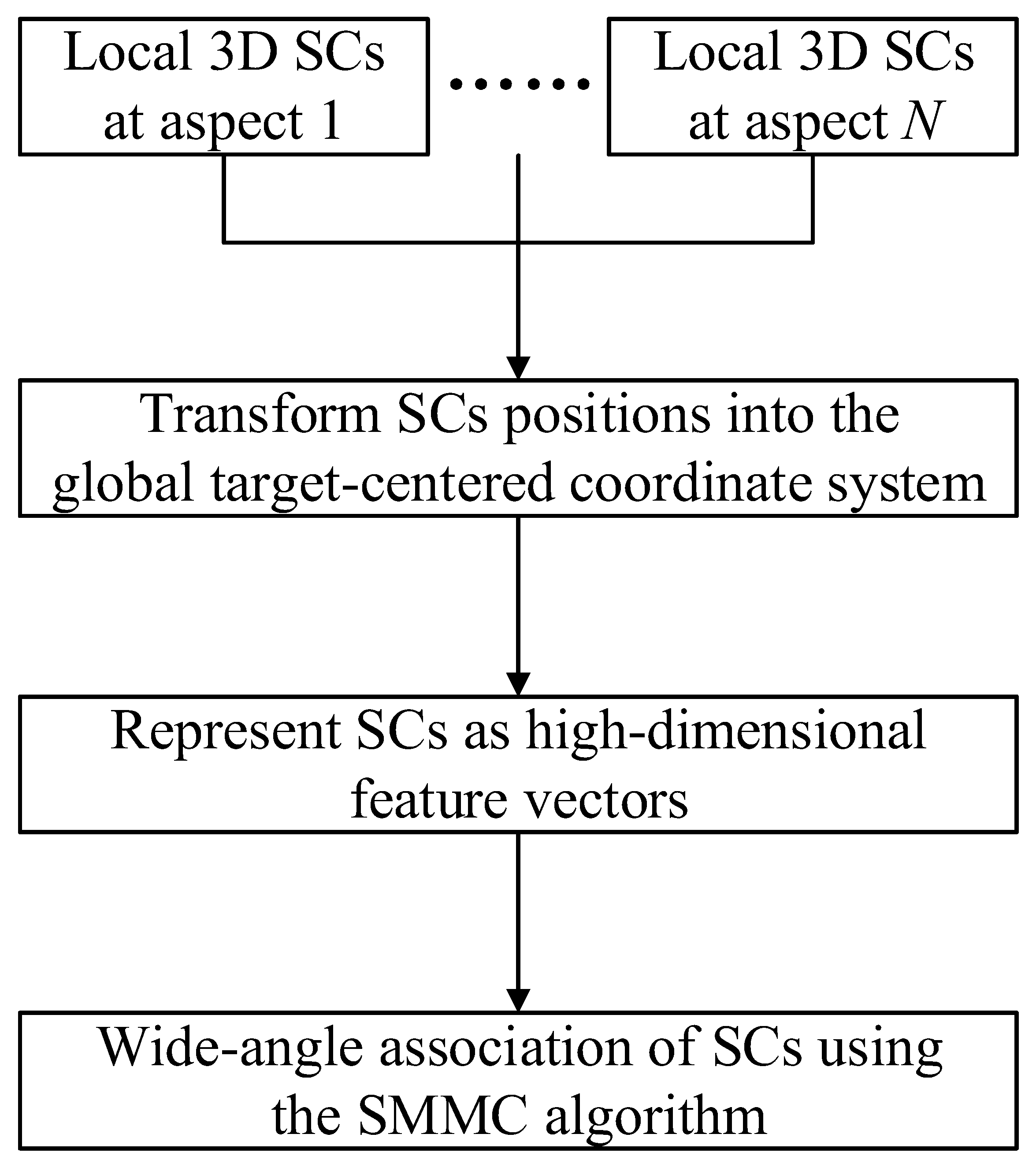
3.2.2. Wide-Angle Association of 3D SCs
3.2.3. Type Judgment of Scattering Structures
3.2.4. GSC Representation
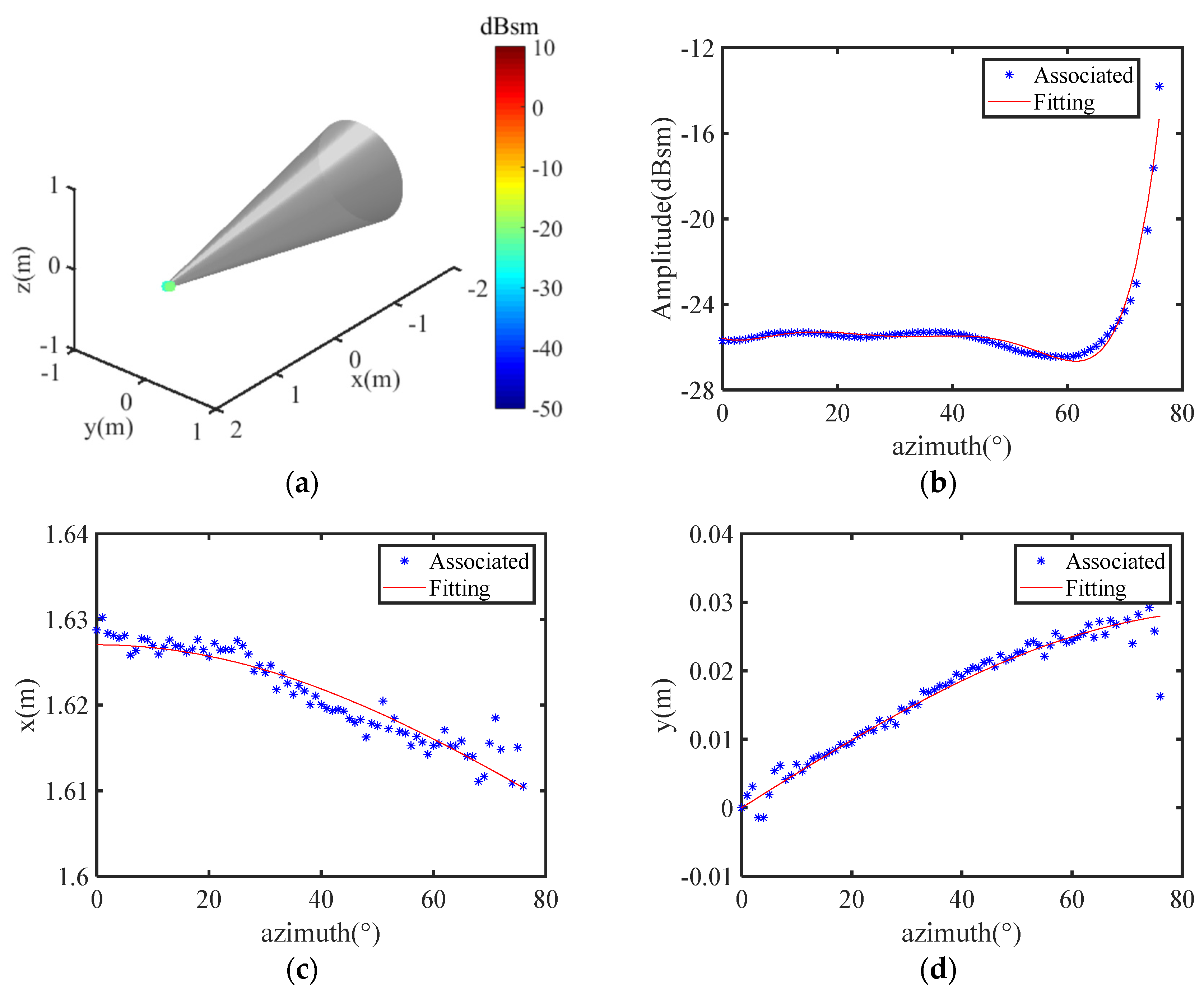
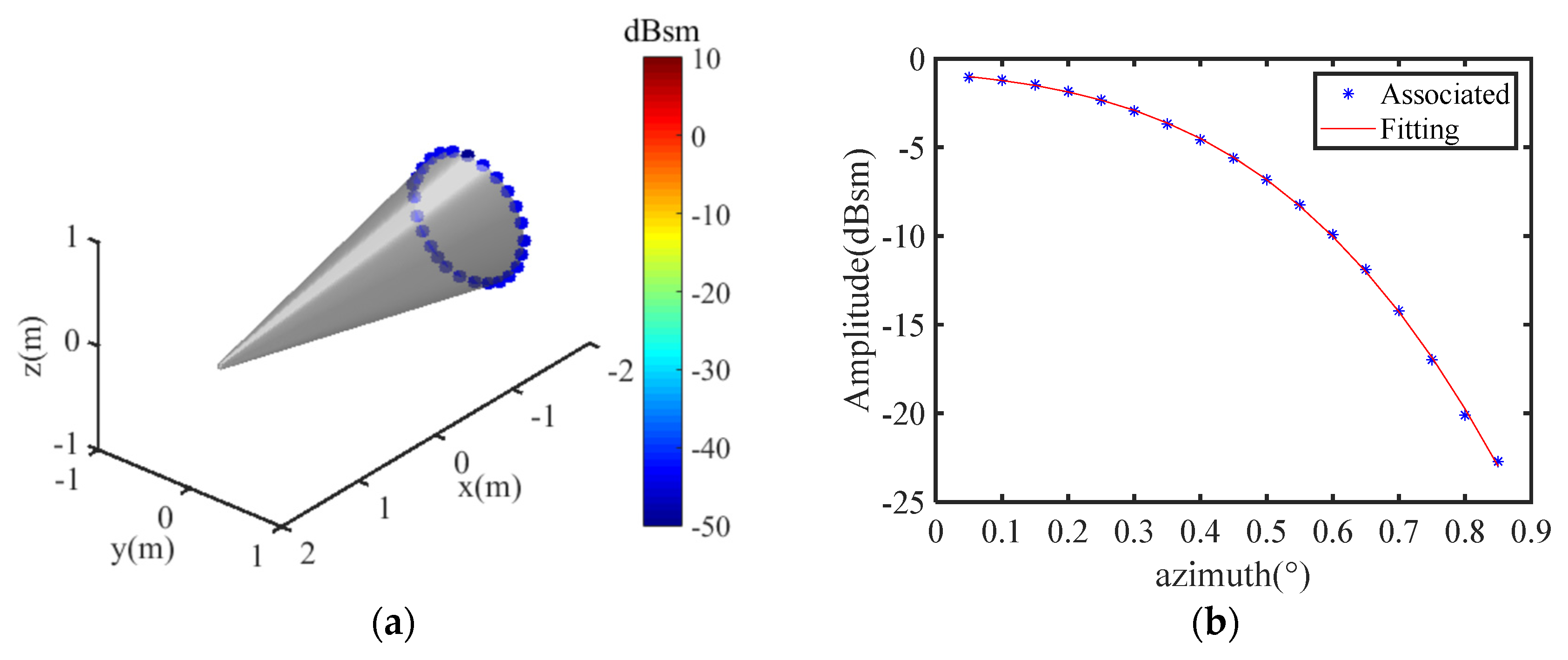
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Keller, J.B. Geometrical theory of diffraction. J. Opt. Soc. Am. 1962, 52, 116–130. [Google Scholar] [CrossRef] [PubMed]
- Hua, Y.; Sarkar, T.K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 814–824. [Google Scholar] [CrossRef] [Green Version]
- Hurst, M.P.; Mittra, R. Scattering center analysis via Prony’s method. IEEE Trans. Antennas Propag. 1987, 35, 986–988. [Google Scholar] [CrossRef]
- Potter, L.C.; Chiang, D.M.; Carriere, R.; Gerry, M.J. A GTD-based parametric model for radar scattering. IEEE Trans. Antennas Propag. 1995, 443, 1058–1067. [Google Scholar] [CrossRef]
- Gerry, M.J.; Potter, L.C.; Gupta, I.J.; Merwe, A.V.D. A parametric model for synthetic aperture radar measurements. IEEE Trans. Antennas Propagat. 1999, 47, 1179–1188. [Google Scholar] [CrossRef]
- Zheng, S.Y.; Zhang, X.K.; Zong, B.F.; Xu, J.H. Parameter estimation of the 2D-GTD model and RCS reconstruction based on an improved 2D-ESPRIT algorithm. Int. RF Microw. Comput. Aided Eng. 2020, 30, e22230. [Google Scholar] [CrossRef]
- Zheng, S.Y.; Zhang, X.K.; Zhao, W.C.; Zhou, J.X.; Zong, B.F.; Xu, J.H. Parameter estimation of GTD model and RCS extrapolation based on a modified 3D-ESPRIT algorithm. J. Syst. Eng. Electron. 2020, 31, 1206–1215. [Google Scholar]
- Li, S.S.; Wang, X.K.; Fu, Z.Q.; Zhang, J.T. Extraction of scattering center parameter and RCS reconstruction based on the improved TLS-ESPRIT algorithm of Hankel matrix. Syst. Eng. Electron. 2021, 43, 62–73. [Google Scholar]
- Ghasemi, M.; Sheikhi, A. Joint scattering center enumeration and parameter estimation in GTD model. IEEE Trans. Antennas Propag. 2020, 68, 4786–4798. [Google Scholar] [CrossRef]
- Jing, M.Q.; Zhang, G. Attributed scattering center extraction with genetic algorithm. IEEE Trans. Antennas Propag. 2021, 69, 2810–2819. [Google Scholar] [CrossRef]
- Bhalla, R.; Ling, H. Three-dimensional scattering center extraction using the shooting and bouncing ray technique. IEEE Trans. Antennas Propag. 1996, 44, 1445–1453. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, L.; Lu, J.W.; Xing, X.Y.; Li, S.; Yin, H.C. Frequency-dependent factor expression of GTD scattering center model for arbitrary multiple scattering mechanism. J. Radars 2021, 10, 370–381. [Google Scholar]
- Lu, J.W.; Yan, H.; Zhang, L.; Yin, H.C. 3D-GTD model construction method using the shooting and bouncing ray technique. Syst. Eng. Electron. 2021, 43, 2028–2036. [Google Scholar]
- Bhalla, R.; Moore, J.; Ling, H. A global scattering center representation of complex targets using the shooting and bouncing ray technique. IEEE Trans. Antennas Propag. 1997, 45, 1850–1856. [Google Scholar] [CrossRef]
- Zhou, J.X.; Zhao, H.Z.; Shi, Z.G.; Fu, Q. Global scattering center model extraction of radar targets based on wideband measurements. IEEE Trans. Antennas Propag. 2008, 56, 2051–2060. [Google Scholar] [CrossRef]
- Zhou, J.X.; Shi, Z.G.; Fu, Q. Three-dimensional scattering center extraction based on wide aperture data at a single elevation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1638–1655. [Google Scholar] [CrossRef]
- Hu, J.M.; Wei, W.; Zhai, Q.L.; Ou, J.P.; Zhan, R.H.; Zhang, J. Global scattering center extraction for radar targets using a modified RANSAC method. IEEE Trans. Antennas Propag. 2016, 64, 3573–3586. [Google Scholar] [CrossRef]
- Guo, K.Y.; Li, Q.F.; Sheng, X.Q.; Gashinova, M. Sliding scattering center model for extended streamlined targets. Prog. Electromagn. Res. 2013, 139, 499–516. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y. High Frequency Electromagnetic Scattering Prediction and Scattering Feature Extraction. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2005. [Google Scholar]
- Raynal, A.M. Feature-Based Exploitation of Multidimensional Radar Signatures. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2008. [Google Scholar]
- Zhou, Z.F. Parametric Scattering Center Model Reconstruction of Canonical Bodies and Its Applications. Master’s Thesis, The Second Academy of CASIC, Beijing, China, 2016. [Google Scholar]
- Yan, H. Parametric Representation and Modeling of Electromagnetic Scattering from Objects. Ph.D. Thesis, Communication University of China, Beijing, China, 2020. [Google Scholar]
- Lee, S.W. Electromagnetic reflection from a conducting surface: Geometrical optics solution. IEEE Trans. Antennas Propag. 1975, 23, 184–191. [Google Scholar]
- Perez, J.; Catedra, M.F. Application of physical optics to the RCS computation of bodies modeled with NURBS surfaces. IEEE Trans. Antennas Propag. 1994, 42, 1404–1411. [Google Scholar] [CrossRef] [Green Version]
- Michaeli, A. Equivalent edge currents for arbitrary aspects of observation. IEEE Trans. Antennas Propag. 1984, 32, 252–258. [Google Scholar] [CrossRef]
- Jackson, J.A.; Rigling, B.D.; Moses, R.L. Canonical scattering feature models for 3D and bistatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 525–541. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Y.; Wu, Y. Spectral clustering on multiple manifolds. IEEE Trans. Neural Netw. 2011, 22, 1149–1161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tipping, M.E.; Bishop, C.M. Mixtures of probabilistic principal component analyzers. Neural Comput. 1999, 11, 443–482. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K. Data clustering: 50 years beyond k-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Ling, H.; Chou, R.C.; Lee, S.W. Shooting and bouncing rays: Calculating the RCS of an arbitrarily shaped cavity. IEEE Trans. Antennas Propag. 1989, 37, 194–205. [Google Scholar] [CrossRef]
- Bhalla, R.; Ling, H. A fast algorithm for signature prediction and image formation using the shooting and bouncing ray technique. IEEE Trans. Antennas Propag. 1995, 43, 727–731. [Google Scholar] [CrossRef]
- Tsao, J.; Steinberg, B.D. Reduction of sidelobe and speckle artifacts in microwave imaging: The CLEAN technique. IEEE Trans. Antennas Propag. 1988, 36, 543–556. [Google Scholar] [CrossRef]
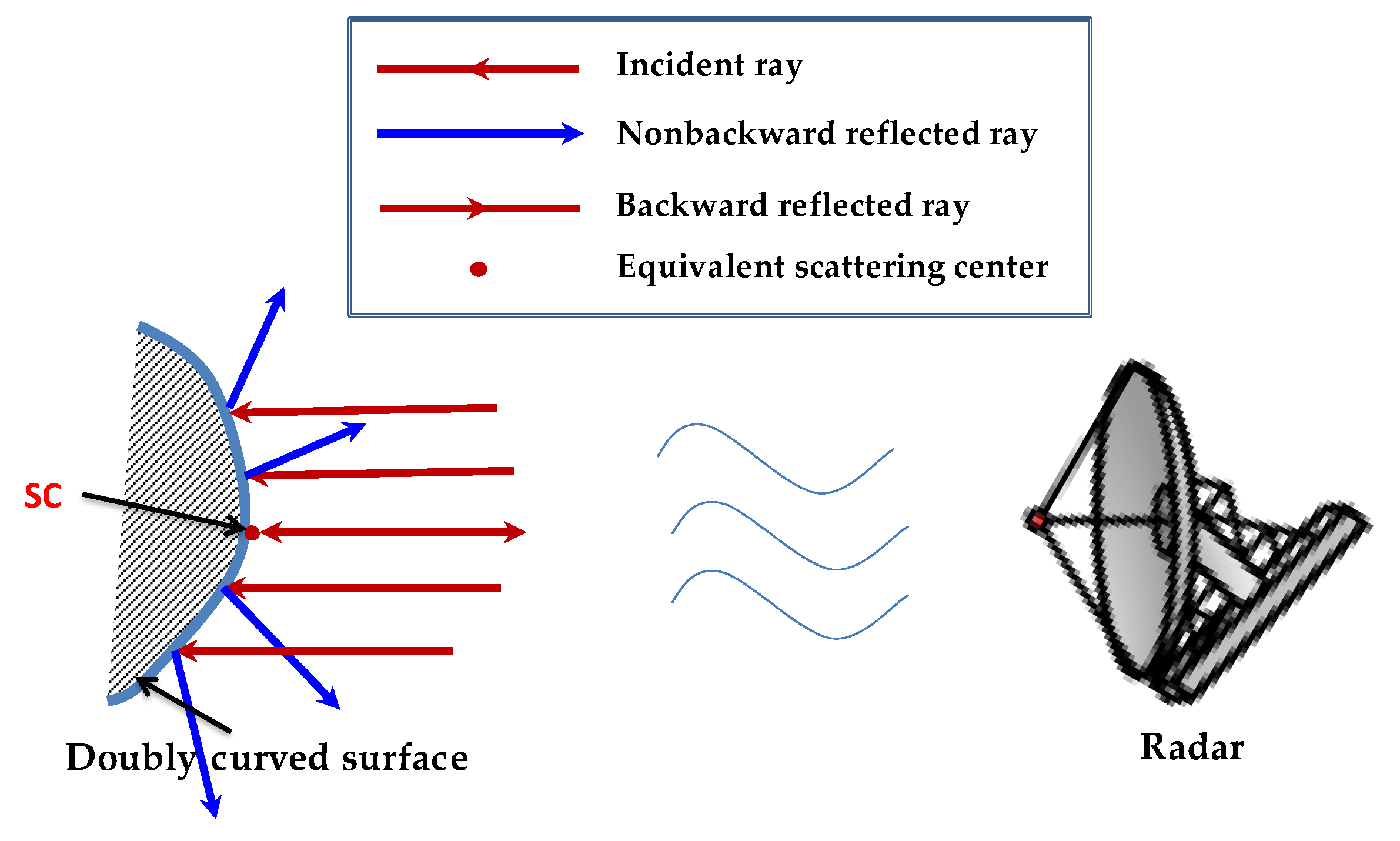
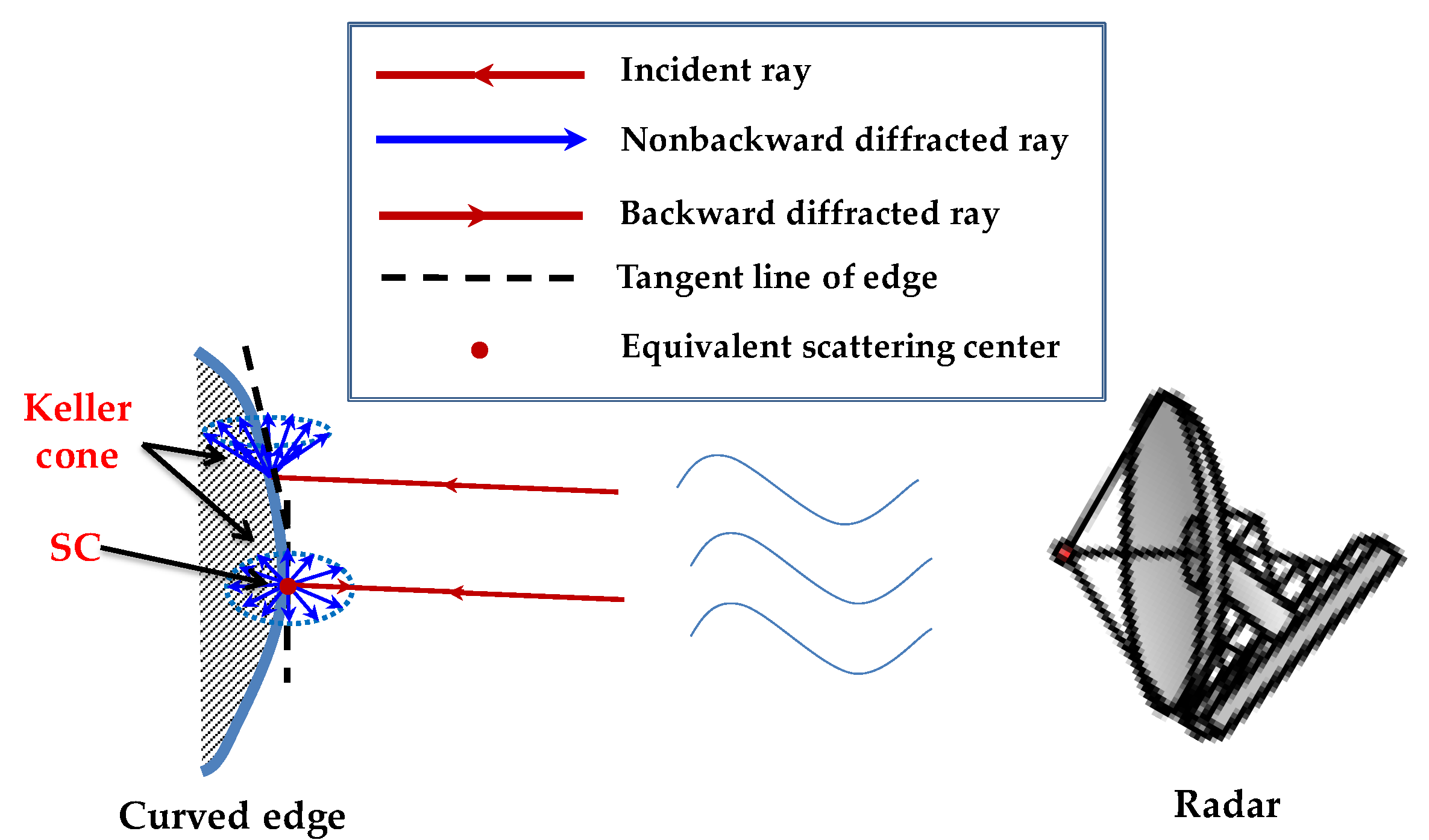

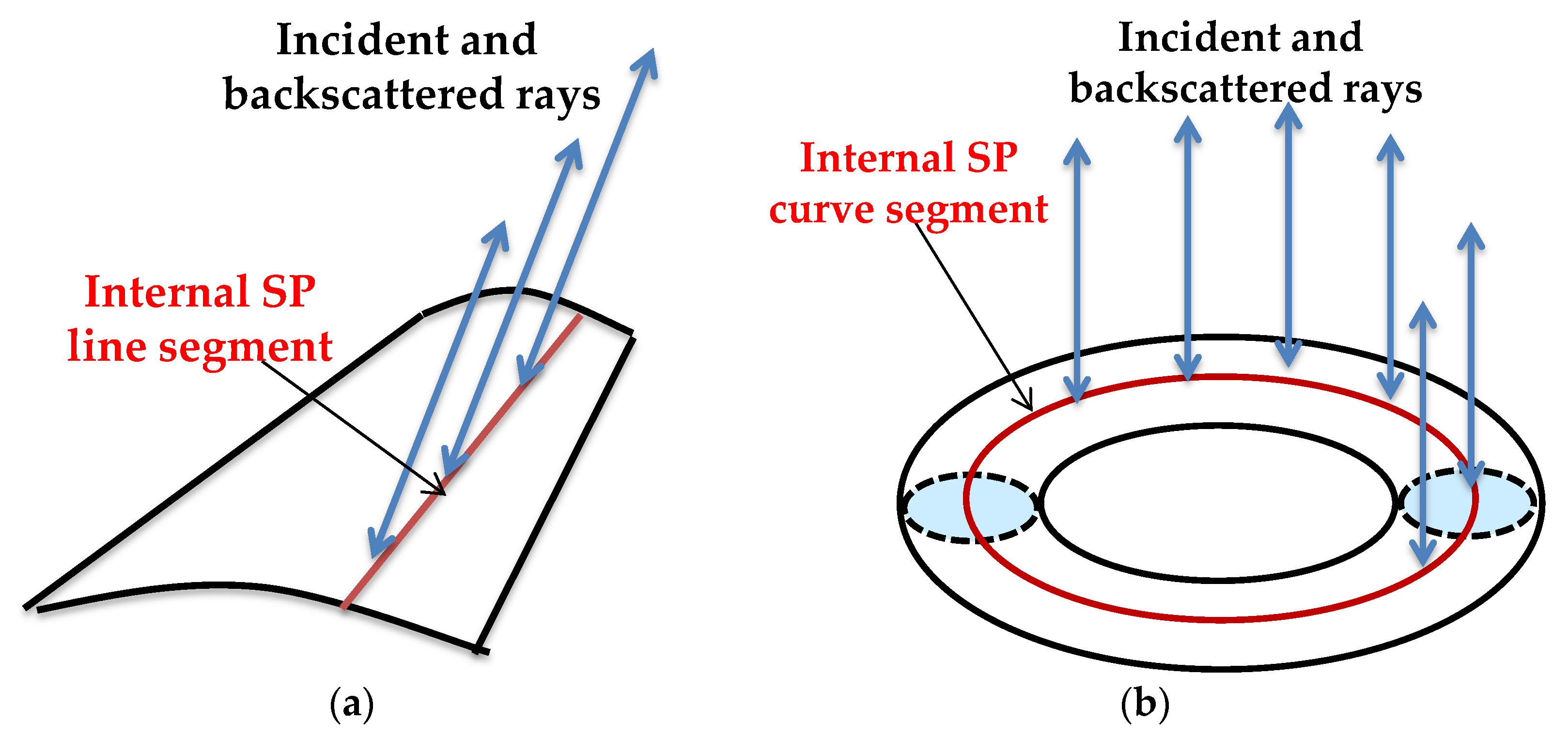

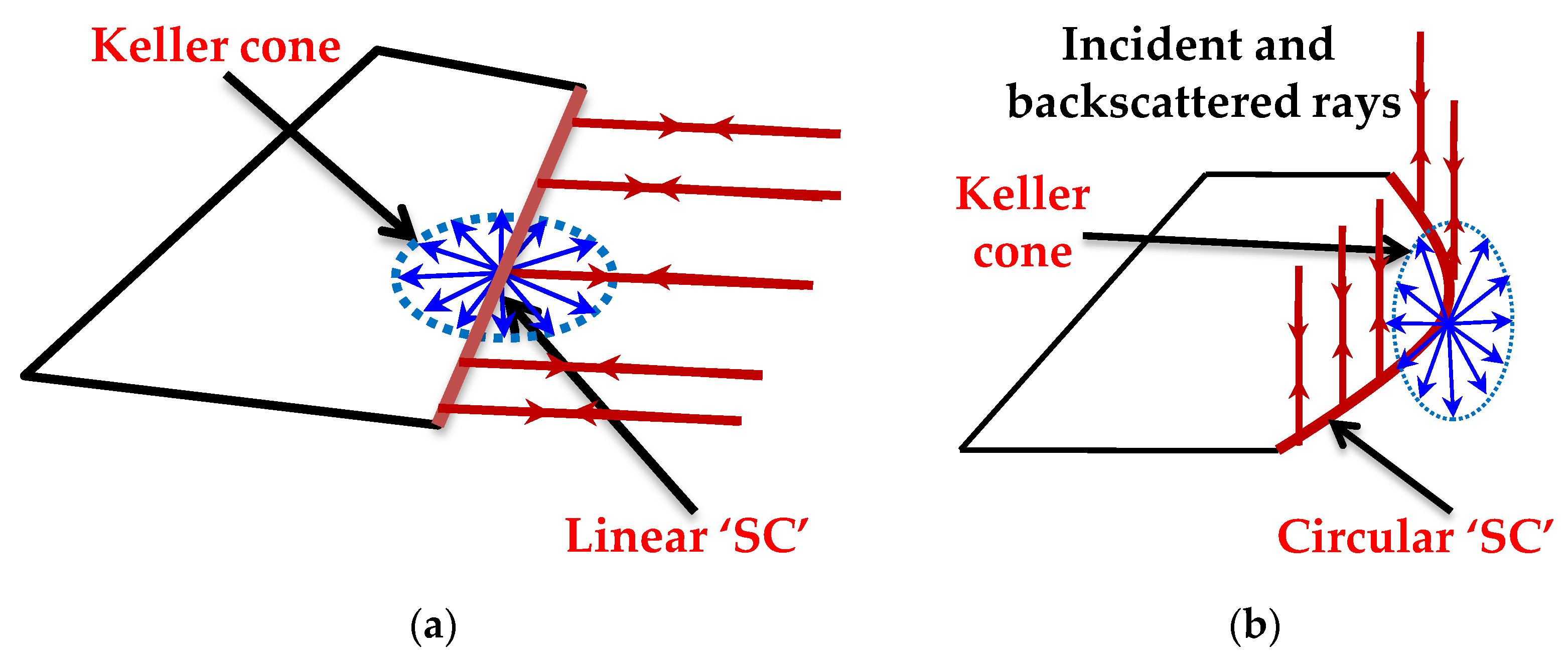


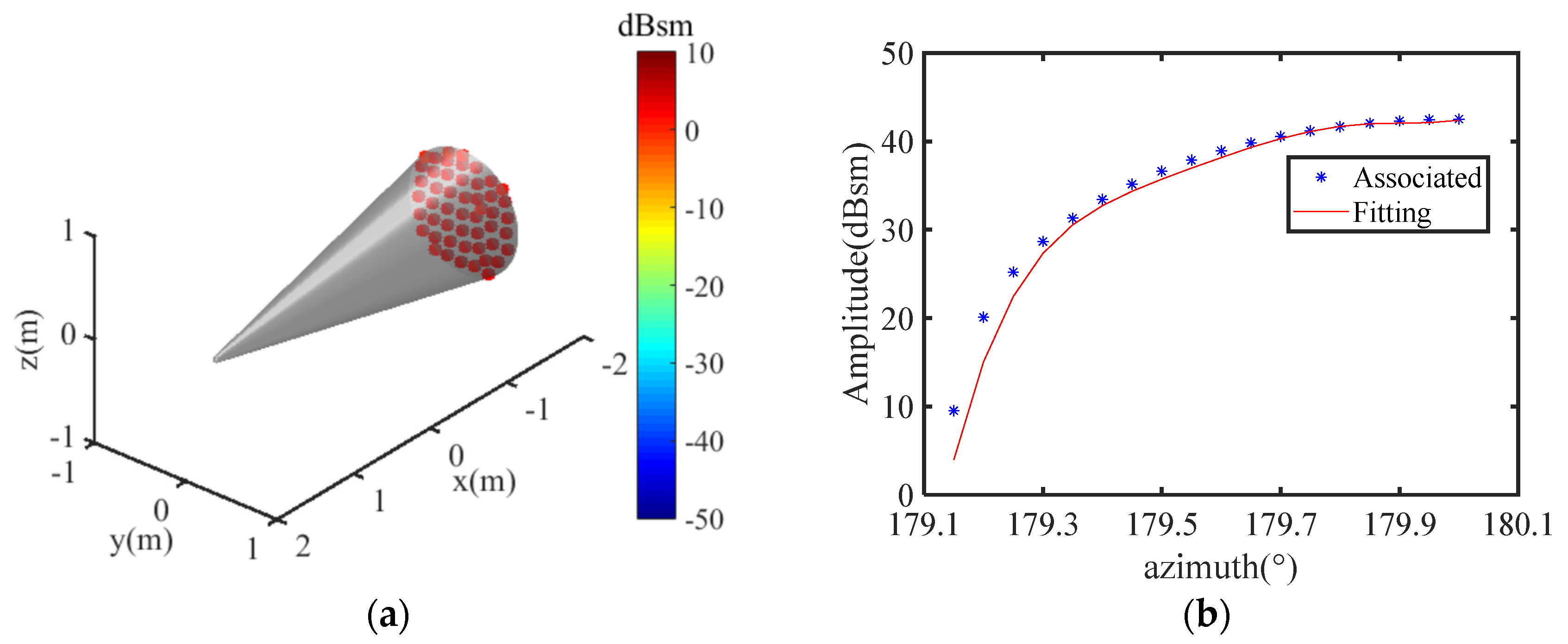
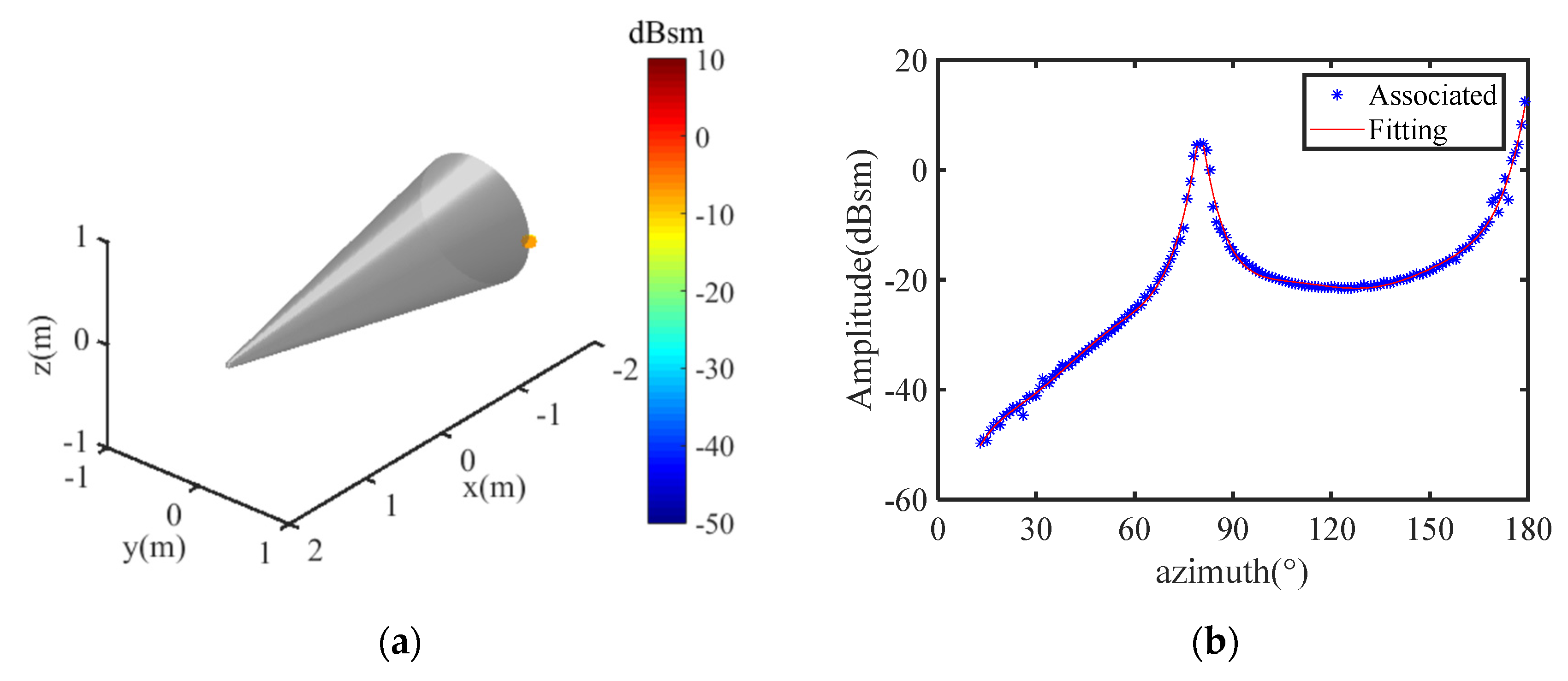


| Scattering Structures | GSC Types * | ||||
|---|---|---|---|---|---|
| Doubly curved surface | SS | 0 | 0 | 2 | 2 |
| Singly curved surface | SD | 1 | 0 | 2 | 1 |
| Torus surface | DD | 2 | 0 | 2 | 0 |
| Plate | DD | 2 | 0 | 2 | 0 |
| Curved edge (nonaxially incident) | FS | 0 | 1 | 1 | 2 |
| Circular edge (axially incident) | DD | 2 | 0 | 2 | 0 |
| Straight edge | FD | 1 | 1 | 1 | 1 |
| Tip/corner | FF | 0 | 2 | 0 | 2 |
| Canonical Structure | Scattering Type | |||
|---|---|---|---|---|
| spherical head | 0.07 | 0.09 | 44.20 | Sliding |
| conical surface | 0.95 | 0.40 | 0.33 | Distributed |
| circular edge | 0 | 0.65 | 0.55 | Distributed |
| bottom surface | 0 | 0.54 | 0.47 | Distributed |
| right-curved edge | 0.0018 | 0.0019 | 91.71 | Fixed |
| left-curved edge | 0.0033 | 0.0032 | 33.70 | Fixed |
| Canonical Structures | Angle | Amplitude | Location |
|---|---|---|---|
| spherical head | 2 | 7 | 4 |
| conical surface | 2 | 3 | 3 |
| circular edge | 2 | 4 | 3 |
| bottom surface | 2 | 6 | 3 |
| right-curved edge | 4 | 13 | 3 |
| left-curved edge | 2 | 5 | 3 |
| Simulation | Local SC Model | GSC Model | |
|---|---|---|---|
| Parameters Number | 10,803 | 23,466 | 71 |
| Compression Rate/% | / | 217.22 | 0.66 |
| RMSE/dB | / | 1.18 | 1.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Zhang, Y.; Yan, H.; Zhang, L.; Yin, H. Global Scattering Center Representation of Target Wide-Angle Single Reflection/Diffraction Mechanisms Based on the Multiple Manifold Concept. Electronics 2022, 11, 4209. https://doi.org/10.3390/electronics11244209
Lu J, Zhang Y, Yan H, Zhang L, Yin H. Global Scattering Center Representation of Target Wide-Angle Single Reflection/Diffraction Mechanisms Based on the Multiple Manifold Concept. Electronics. 2022; 11(24):4209. https://doi.org/10.3390/electronics11244209
Chicago/Turabian StyleLu, Jinwen, Yanjin Zhang, Hua Yan, Lei Zhang, and Hongcheng Yin. 2022. "Global Scattering Center Representation of Target Wide-Angle Single Reflection/Diffraction Mechanisms Based on the Multiple Manifold Concept" Electronics 11, no. 24: 4209. https://doi.org/10.3390/electronics11244209





