Analysis of Series-Parallel (SP) Compensation Topologies for Constant Voltage/Constant Current Output in Capacitive Power Transfer System
Abstract
:1. Introduction
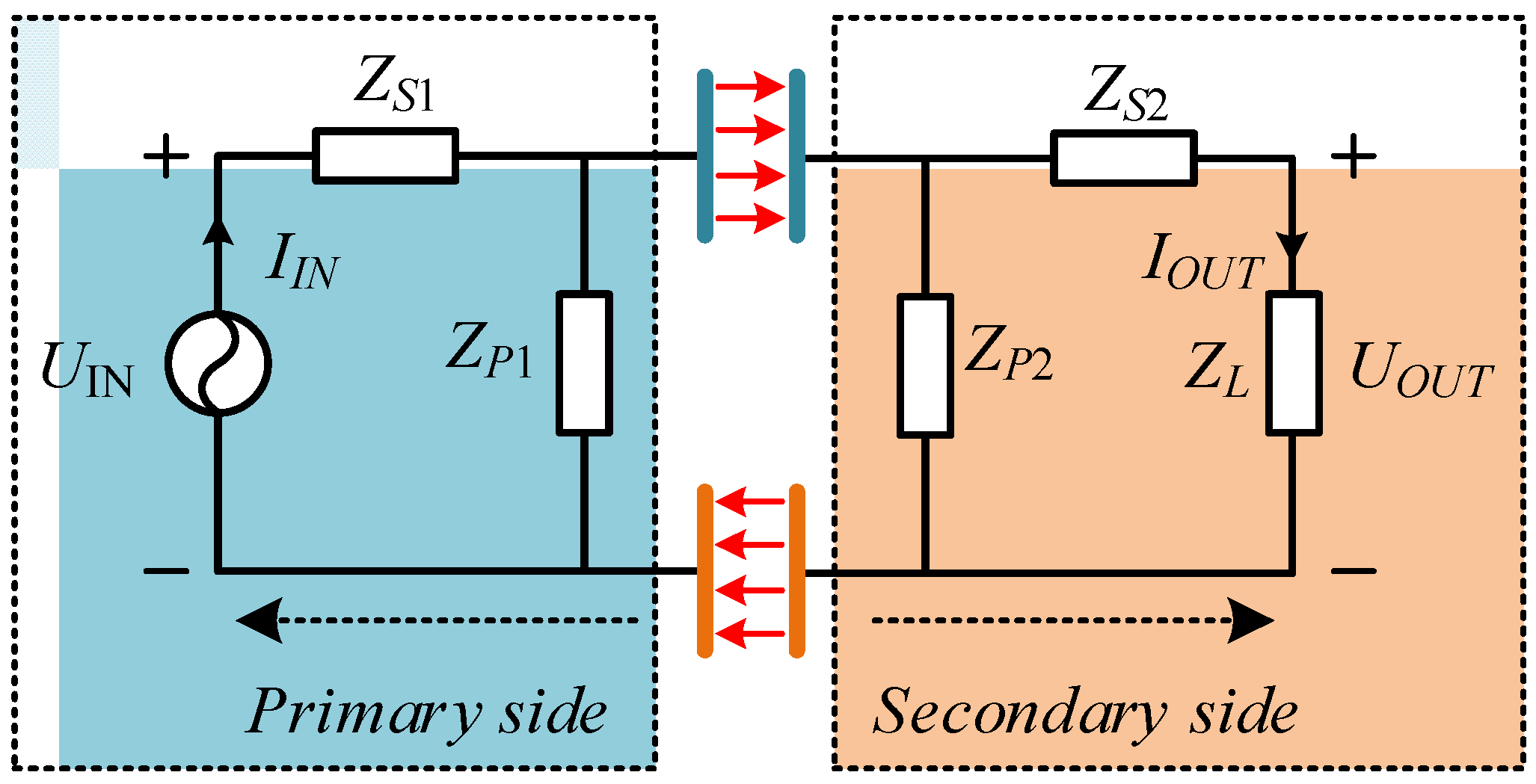
2. Modeling of SP—Based CPT Topology
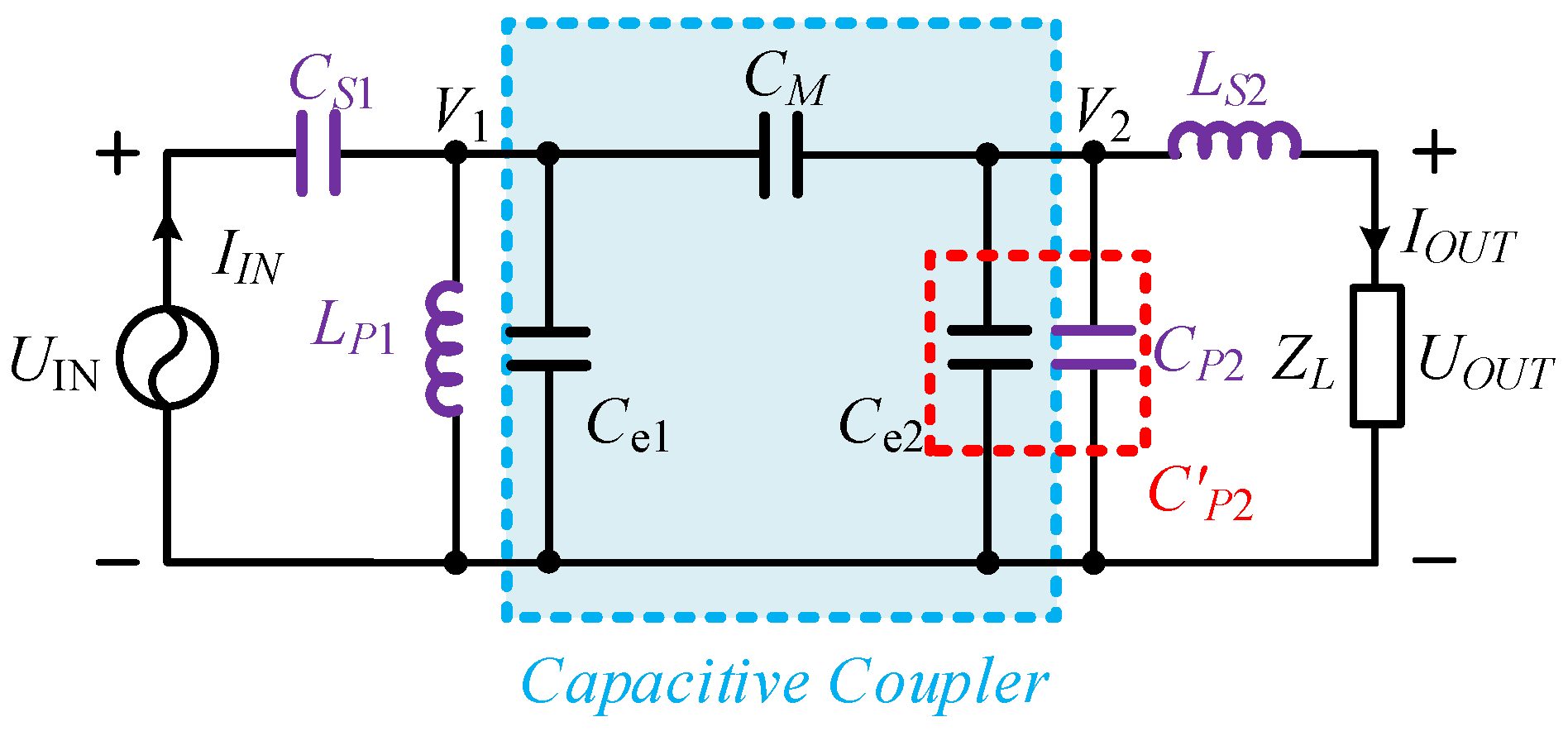
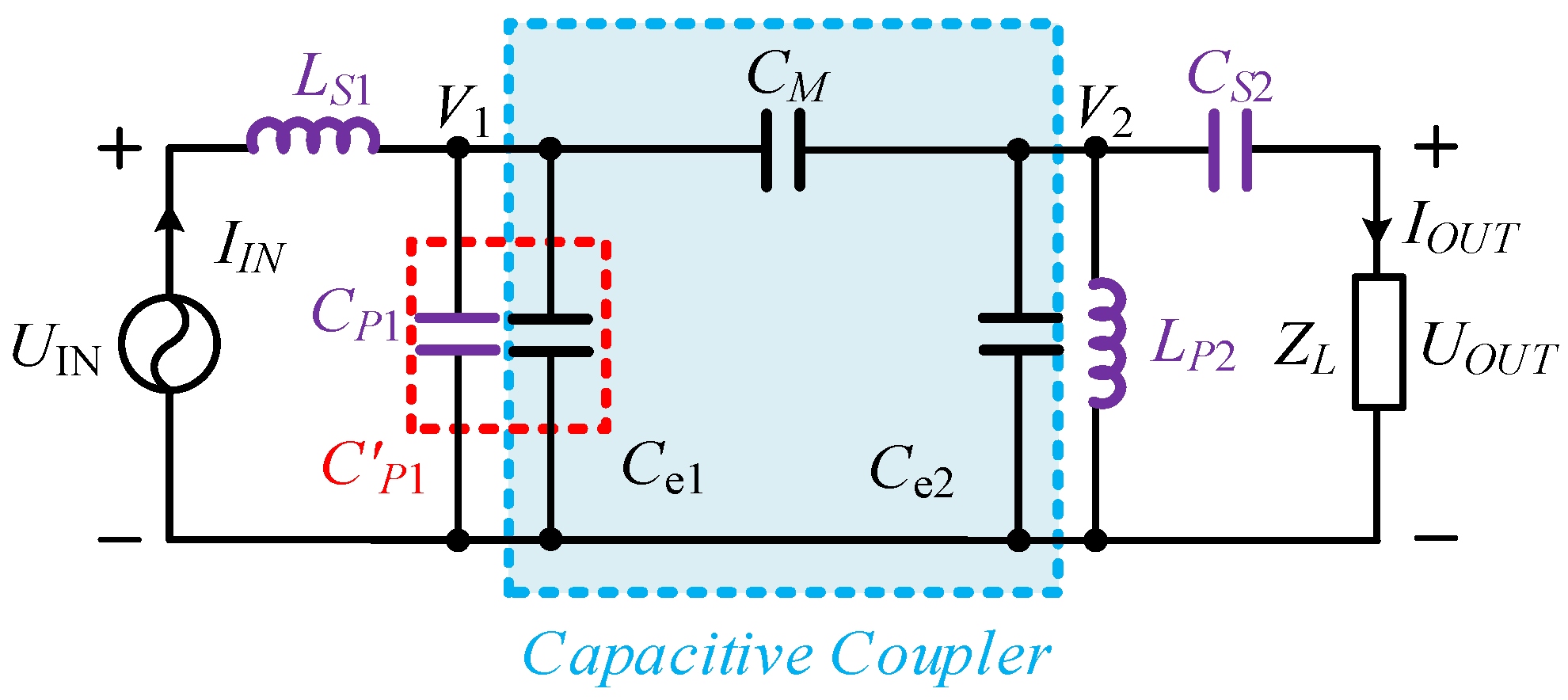
2.1. The Capacitive Coupler Structure
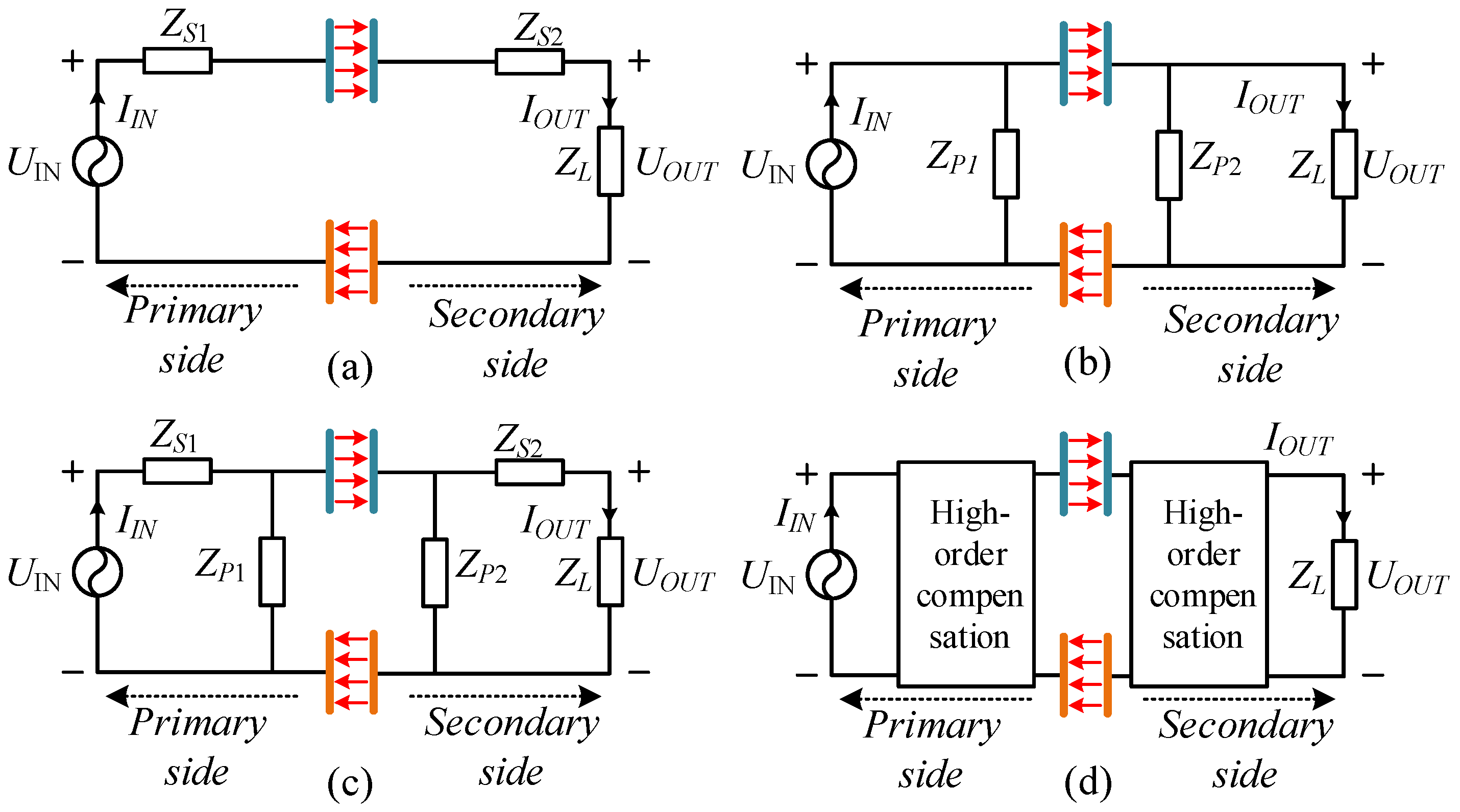
2.2. The SP Compensation Topologies
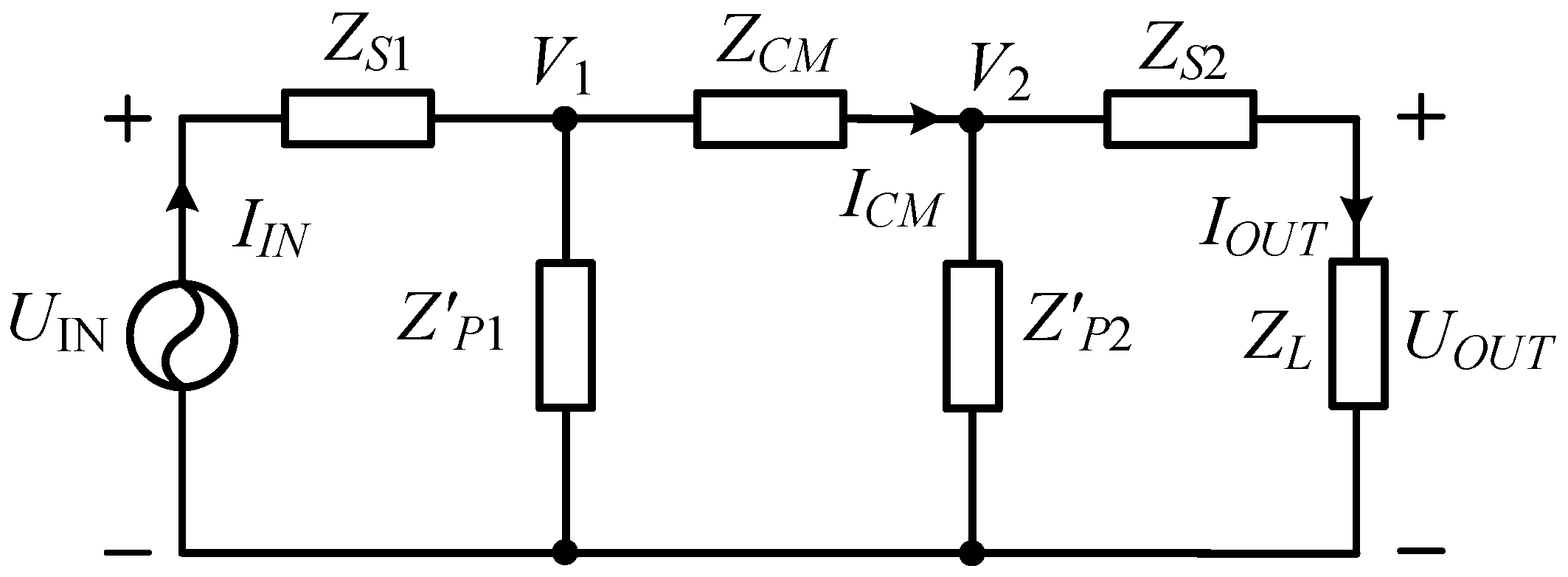
3. Circuit Analysis of Specific SP Topology
3.1. Double-Sided LC Compensation Topology
3.2. Double-Sided CL Compensation Topology
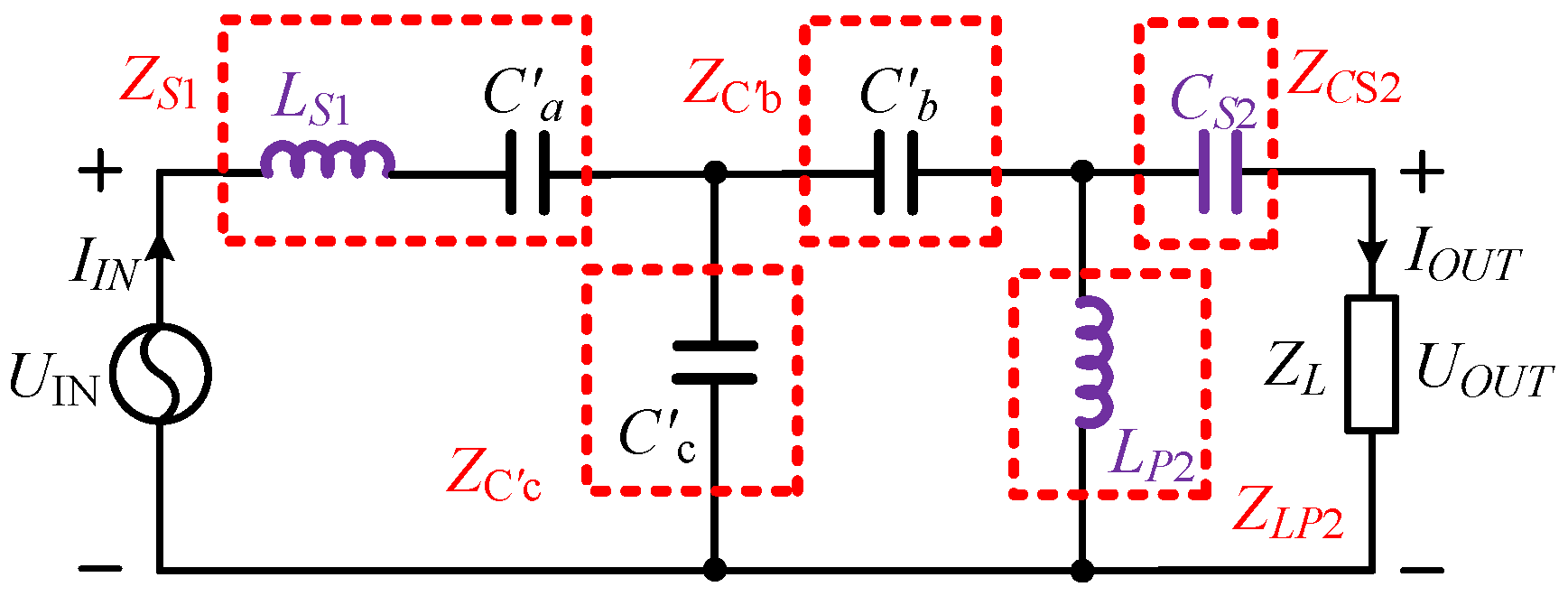
3.3. CL−LC Compensation Topology
3.4. LC−CL Compensation Topology
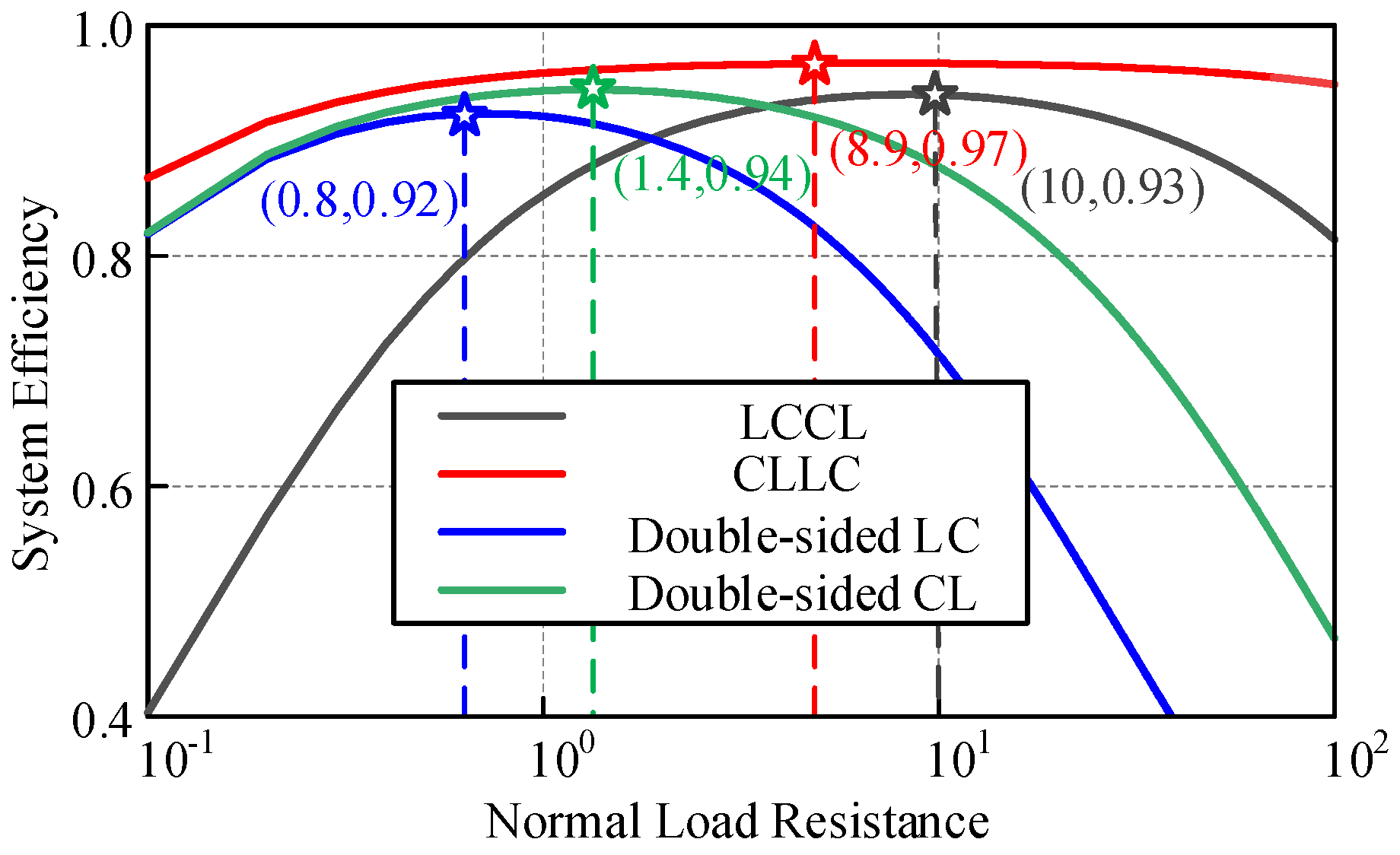
4. Efficiency Analysis of SP-Based CPT Topology
5. Experimental Verification
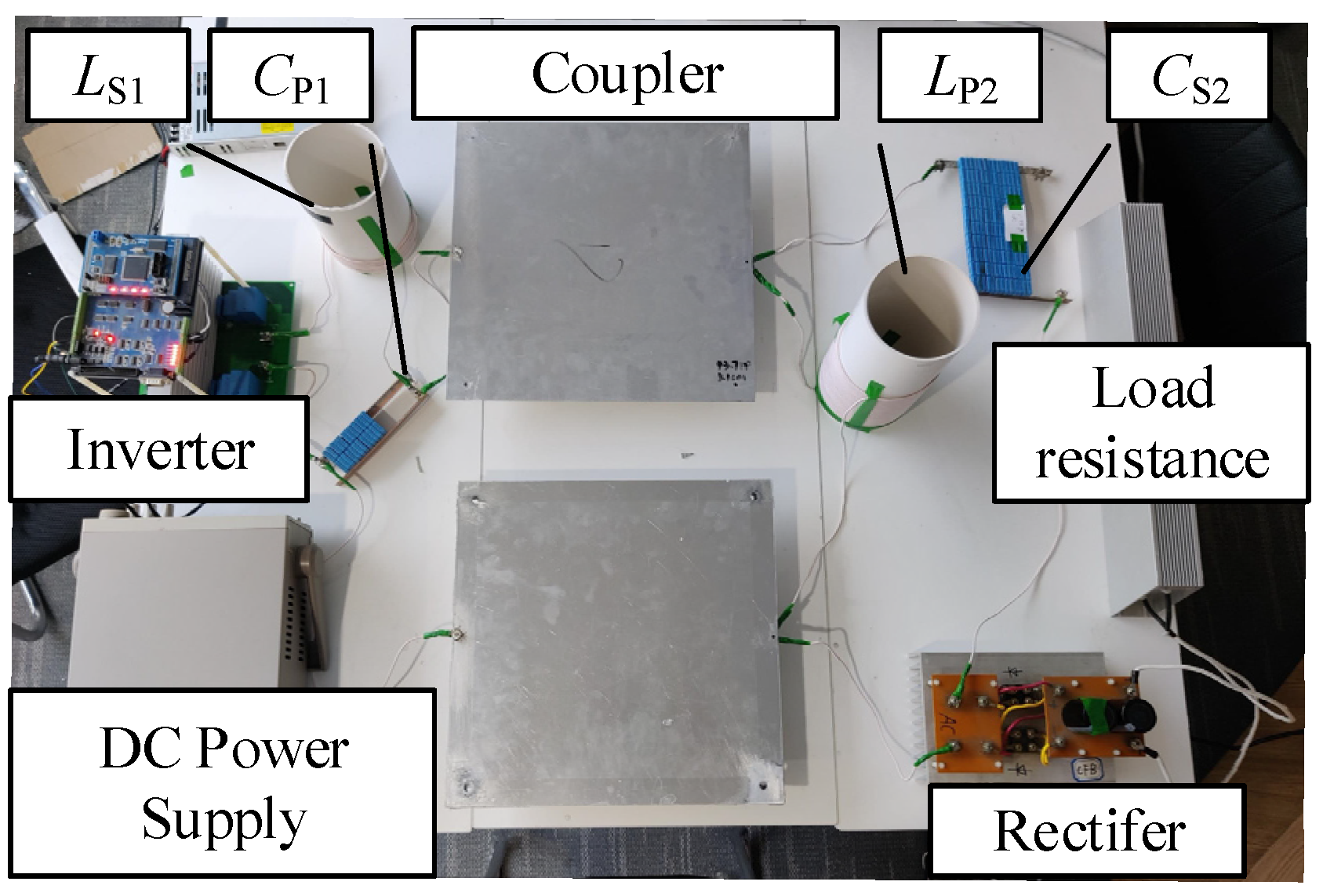
5.1. Experimental Prototype
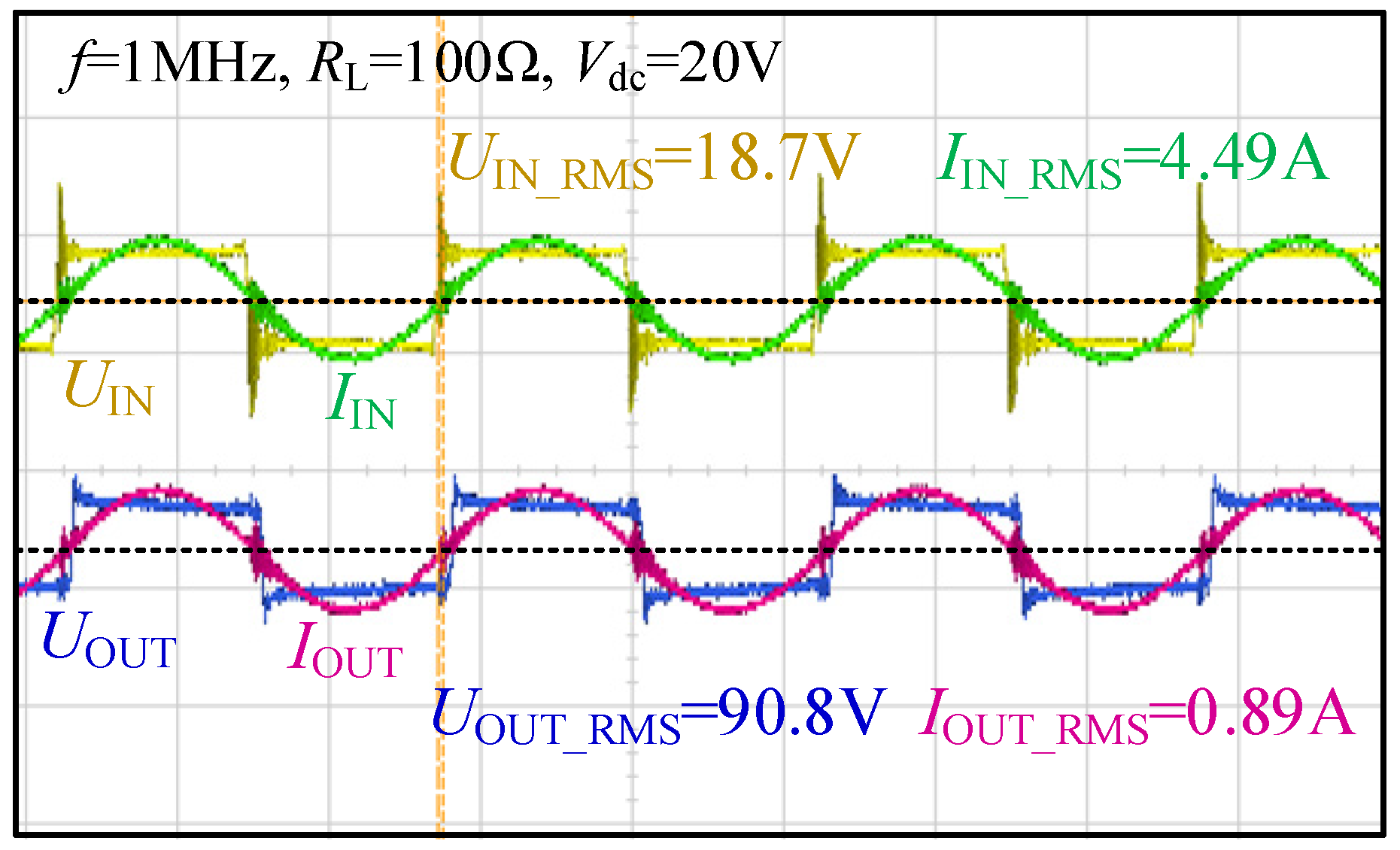
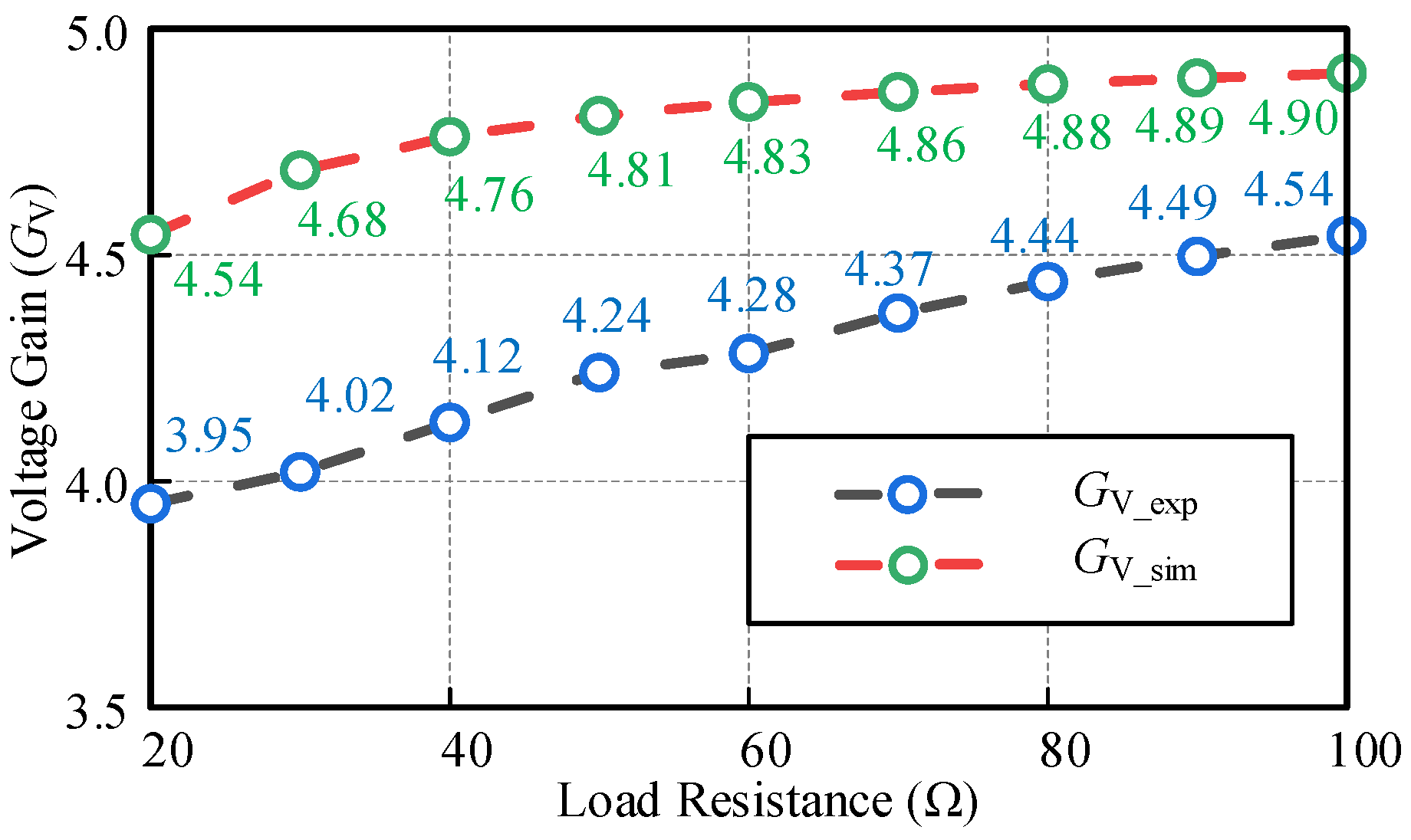
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Pang, H.; Georgiadis, A.; Cecati, C. Wireless Power Transfer—An Overview. IEEE Trans. Ind. Electron. 2019, 66, 1044–1058. [Google Scholar] [CrossRef]
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrif. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Luo, B.; Hu, A.P.; Munir, H.; Zhu, Q.; Mai, R.; He, Z. Compensation Network Design of CPT Systems for Achieving Maximum Power Transfer Under Coupling Voltage Constraints. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 138–148. [Google Scholar] [CrossRef]
- Luo, B.; Long, T.; Guo, L.; Dai, R.; Mai, R.; He, Z. Analysis and Design of Inductive and Capacitive Hybrid Wireless Power Transfer System for Railway Application. IEEE Trans. Ind. Appl. 2020, 56, 3034–3042. [Google Scholar] [CrossRef]
- Dai, J.; Ludois, D.C. A Survey of Wireless Power Transfer and a Critical Comparison of Inductive and Capacitive Coupling for Small Gap Applications. IEEE Trans. Power Electron. 2015, 30, 6017–6029. [Google Scholar] [CrossRef]
- Jeong, N.S.; Carobolante, F. Wireless Charging of a Metal-Body Device. IEEE Trans. Microw. Theory Tech. 2017, 65, 1077–1086. [Google Scholar] [CrossRef]
- Chen, Q.; Wong, S.C.; Tse, C.K.; Ruan, X. Analysis, Design, and Control of a Transcutaneous Power Regulator for Artificial Hearts. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 23–31. [Google Scholar] [CrossRef]
- Hui, S.Y. Planar Wireless Charging Technology for Portable Electronic Products and Qi. Proc. IEEE 2013, 101, 1290–1301. [Google Scholar] [CrossRef] [Green Version]
- Luo, B.; Long, T.; Mai, R.; Dai, R.; He, Z.; Li, W. Analysis and design of hybrid inductive and capacitive wireless power transfer for high-power applications. IET Power Electron. 2018, 11, 2263–2270. [Google Scholar] [CrossRef]
- Nagendra, G.R.; Chen, L.; Covic, G.A.; Boys, J.T. Detection of EVs on IPT Highways. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 584–597. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Modern Trends in Inductive Power Transfer for Transportation Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Moon, H.; Kim, S.; Park, H.H.; Ahn, S. Design of a Resonant Reactive Shield With Double Coils and a Phase Shifter for Wireless Charging of Electric Vehicles. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Xu, J.; Zeng, Y.; Zhang, R. UAV-Enabled Wireless Power Transfer: Trajectory Design and Energy Optimization. IEEE Trans. Wirel. Commun. 2018, 17, 5092–5106. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Chen, Y.; Yang, S.-H. UAV-Enabled Wireless Power Transfer With Base Station Charging and UAV Power Consumption. IEEE Trans. Veh. Technol. 2020, 69, 12883–12896. [Google Scholar] [CrossRef]
- Thrimawithana, D.J.; Madawala, U.K. A Generalized Steady-State Model for Bidirectional IPT Systems. IEEE Trans. Power Electron. 2013, 28, 4681–4689. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Cho, K.; Lee, H.; Seo, C.; Ahn, S.; Kim, J.; Kim, D.-H.; Cho, Y.; Kim, H.; et al. Low Leakage Electromagnetic Field Level and High Efficiency Using a Novel Hybrid Loop-Array Design for Wireless High Power Transfer System. IEEE Trans. Ind. Electron. 2019, 66, 4356–4367. [Google Scholar] [CrossRef]
- Mohammad, M.; Wodajo, E.T.; Choi, S.; Elbuluk, M.E. Modeling and Design of Passive Shield to Limit EMF Emission and to Minimize Shield Loss in Unipolar Wireless Charging System for EV. IEEE Trans. Power Electron. 2019, 34, 12235–12245. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Mi, C. A Review on the Recent Development of Capacitive Wireless Power Transfer Technology. Energies 2017, 10, 1752. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Lu, F.; Hofmann, H.; Liu, W.; Mi, C.C. Six-Plate Capacitive Coupler to Reduce Electric Field Emission in Large Air-Gap Capacitive Power Transfer. IEEE Trans. Power Electron. 2018, 33, 665–675. [Google Scholar] [CrossRef]
- Zhu, Q.; Zou, L.J.; Su, M.; Hu, A.P. Four-Plate Capacitive Power Transfer System with Different Grounding Connections. Int. J. Electr. Power Energy Syst. 2020, 115, 105494. [Google Scholar] [CrossRef]
- Wang, S.; Liang, J.; Fu, M. Analysis and Design of Capacitive Power Transfer Systems Based on Induced Voltage Source Model. IEEE Trans. Power Electron. 2020, 35, 10532–10541. [Google Scholar] [CrossRef]
- Theodoridis, M.P. Effective Capacitive Power Transfer. IEEE Trans. Power Electron. 2012, 27, 4906–4913. [Google Scholar] [CrossRef]
- Liang, H.W.R.; Lee, C.-K.; Hui, S.Y.R. Design, Analysis, and Experimental Verification of a Ball-Joint Structure With Constant Coupling for Capacitive Wireless Power Transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3582–3591. [Google Scholar] [CrossRef]
- Karagozler, M.E.; Goldstein, S.C.; Ricketts, D.S. Analysis and Modeling of Capacitive Power Transfer in Microsystems. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 1557–1566. [Google Scholar] [CrossRef] [Green Version]
- Jegadeesan, R.; Guo, Y.X.; Je, M. Electric Near-Field Coupling for Wireless Power Transfer in Biomedical Applications. In Proceedings of the 2013 IEEE MTT—S International Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications (IMWS-BIO), Singapore, 11–13 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–3. [Google Scholar]
- Shmilovitz, D.; Ozeri, S.; Ehsani, M.M. A Resonant LED Driver with Capacitive Power Transfer. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1384–1387. [Google Scholar]
- Lu, F.; Zhang, H.; Mi, C. A Two-Plate Capacitive Wireless Power Transfer System for Electric Vehicle Charging Applications. IEEE Trans. Power Electron. 2018, 33, 964–969. [Google Scholar] [CrossRef]
- Zou, L.J.; Liu, Y.; Su, Y.-G.; Hu, A.P. Study of Power Flow Mechanism of Capacitive Power Transfer System Based on Poynting Vector Analysis. Int. J. Electr. Power Energy Syst. 2022, 134, 107374. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C. A Double-sided LCLC Compensated Capacitive Power Transfer System for Electric Vehicle Charging. IEEE Trans. Power Electron. 2015, 30, 6011–6014. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, F.; Hofmann, H.; Liu, W.; Mi, C. A 4-Plate Compact Capacitive Coupler Design and LCL-Compensated Topology for Capacitive Power Transfer in Electric Vehicle Charging Applications. IEEE Trans. Power Electron. 2016, 31, 8541–8551. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z.; Zhao, H.; Zhu, L.; Shuai, C.; Chen, Z. Wireless Power Transfer by Electric Field Resonance and Its Application in Dynamic Charging. IEEE Trans. Ind. Electron. 2016, 63, 6602–6612. [Google Scholar] [CrossRef]
- Liu, W.; Luo, B.; Xu, Y.; Pan, S.; Zhou, W.; Jiang, C.; Mai, R. A Multi-Load Capacitive Power Transfer System With Load-Independent Characteristic for Reefer Container Application. IEEE Trans. Power Electron. 2022, 37, 6194–6205. [Google Scholar] [CrossRef]
- Luo, B.; Mai, R.; Guo, L.; Wu, D.; He, Z. LC–CLC Compensation Topology for Capacitive Power Transfer System to Improve Misalignment Performance. IET Power Electron. 2019, 12, 2626–2633. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C. A CLLC-Compensated High Power and Large Air-Gap Capacitive Power Transfer System for Electric Vehicle Charging Applications. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1721–1725. [Google Scholar]
- Sinha, S.; Kumar, A.; Regensburger, B.; Afridi, K.K. Design of High-Efficiency Matching Networks for Capacitive Wireless Power Transfer Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 104–127. [Google Scholar] [CrossRef]
- Su, Y.-G.; Xie, S.-Y.; Hu, A.P.; Tang, C.-S.; Zhou, W.; Huang, L. Capacitive Power Transfer System With a Mixed-Resonant Topology for Constant-Current Multiple-Pickup Applications. IEEE Trans. Power Electron. 2017, 32, 8778–8786. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C.C. A Double-sided LC-Compensation Circuit for Loosely Coupled Capacitive Power Transfer. IEEE Trans. Power Electron. 2018, 33, 1633–1643. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Gao, F.; Wang, S.; Deng, J. A Family of Compensation Topologies for Capacitive Power Transfer Converters for Wireless Electric Vehicle Charger. Appl. Energy 2020, 260, 114156. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Lu, F. Review, Analysis, and Design of Four Basic CPT Topologies and the Application of High-order Compensation Networks. IEEE Trans. Power Electron. 2022, 37, 6181–6193. [Google Scholar] [CrossRef]
- Lillholm, M.B.; Dou, Y.; Chen, X.; Zhang, Z. Analysis and Design of 10-MHz Capacitive Power Transfer With Multiple Independent Outputs for Low-Power Portable Devices. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 149–159. [Google Scholar] [CrossRef]
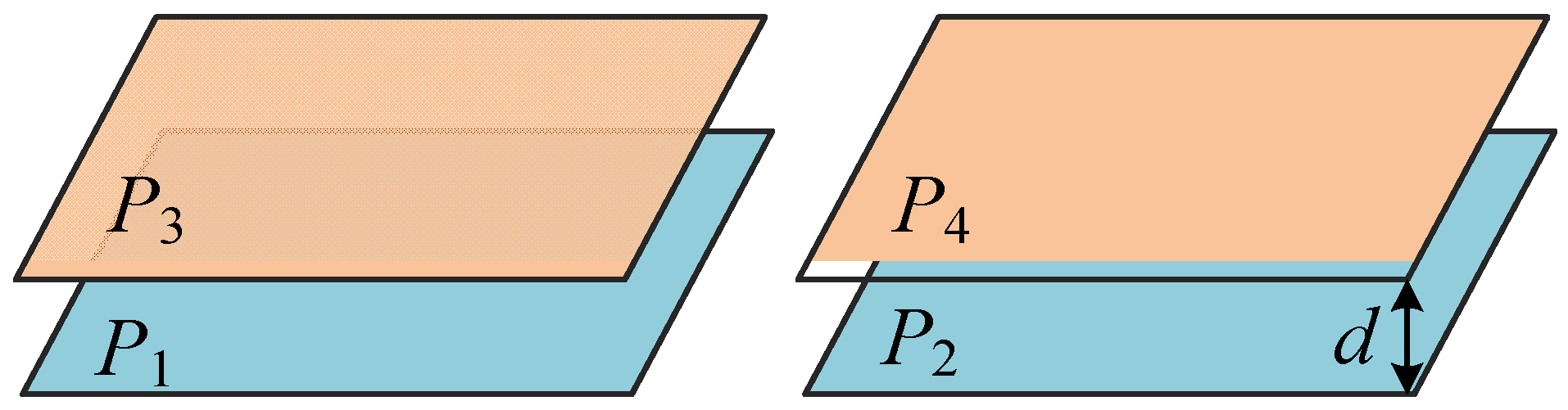







Constant Voltage Input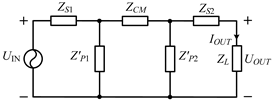 | Constant Current Input | ||
|---|---|---|---|
| CC Output | Condition | ||
| Output Gain | |||
| Input Impedance | |||
| CV Output | Condition | ||
| Output Gain | |||
| Input Impedance | |||
| Compensation Topologies | CC Output | |
|---|---|---|
| Conditions | Output Current | |
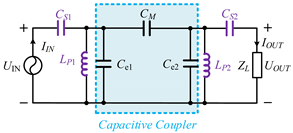
 Double-sided LC compensation topology | Where | |
| ZPA can be achieved with the condition: | ||
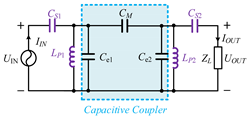 Double-sided CL compensation topology | ZPA can be achieved with the condition: | Where |
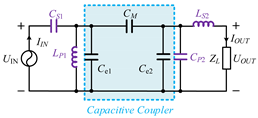 CL−LC compensation topology | Where and C′P2 = CP2 + Ce2 | |
| ZPA can be achieved with the condition: | ||
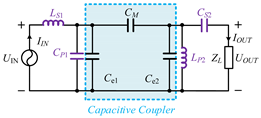 LC−CL compensation topology | Where and C′P1 = CP1 + Ce1 | |
| ZPA can be achieved with the condition: | ||
| Compensation Topologies | CV Output | |
|---|---|---|
| Conditions | Voltage Gain | |
 Double-sided LC compensation topology | Where C′P1 = CP1 + Ce1, C′P2 = CP2 + Ce2 | |
| ZPA cannot be achieved | ||
 Double-sided CL compensation topology | Where | |
| ZPA cannot be achieved | ||
 CL−LC compensation topology | Where and C′P2 = CP2 + Ce2 | |
| ZPA can be achieved | ||
 LC−CL compensation topology | Where and C′P2 = CP2 + Ce2 | |
| ZPA can be achieved with the condition: | ||
| Capacitor | Inductor | |||
|---|---|---|---|---|
| Circuit model |  | 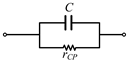 | 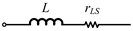 | 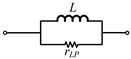 |
| Parasitic resistance | rCS = 1/(ωC · QC) | rCP = QC/(ωC) | rLS = (ωL)/QL | rLP = ωL · QL |
| Symbol | Value |
|---|---|
| Udc/V | 20 |
| RL/Ω | 100 |
| f/MHz | 1 |
| CM/pF | 114.8 |
| CP1/nF | 1 |
| CS2/pF | 202.1 |
| LS1/μH | 25.28 |
| LP2/μH | 125.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Tang, C.; Cheng, H.; Wang, Z.; Luo, B.; Jiang, J. Analysis of Series-Parallel (SP) Compensation Topologies for Constant Voltage/Constant Current Output in Capacitive Power Transfer System. Electronics 2023, 12, 245. https://doi.org/10.3390/electronics12010245
Li S, Tang C, Cheng H, Wang Z, Luo B, Jiang J. Analysis of Series-Parallel (SP) Compensation Topologies for Constant Voltage/Constant Current Output in Capacitive Power Transfer System. Electronics. 2023; 12(1):245. https://doi.org/10.3390/electronics12010245
Chicago/Turabian StyleLi, Shiqi, Chunlin Tang, Hao Cheng, Zhulin Wang, Bo Luo, and Jing Jiang. 2023. "Analysis of Series-Parallel (SP) Compensation Topologies for Constant Voltage/Constant Current Output in Capacitive Power Transfer System" Electronics 12, no. 1: 245. https://doi.org/10.3390/electronics12010245





