Design of UWB Filtering Impedance Transformers and Power Dividers Using Stepped-Impedance Resonators
Abstract
:1. Introduction
2. Structure, Design Method, and Results of UWB Filtering Impedance Transformer
2.1. Design Concept and Theory
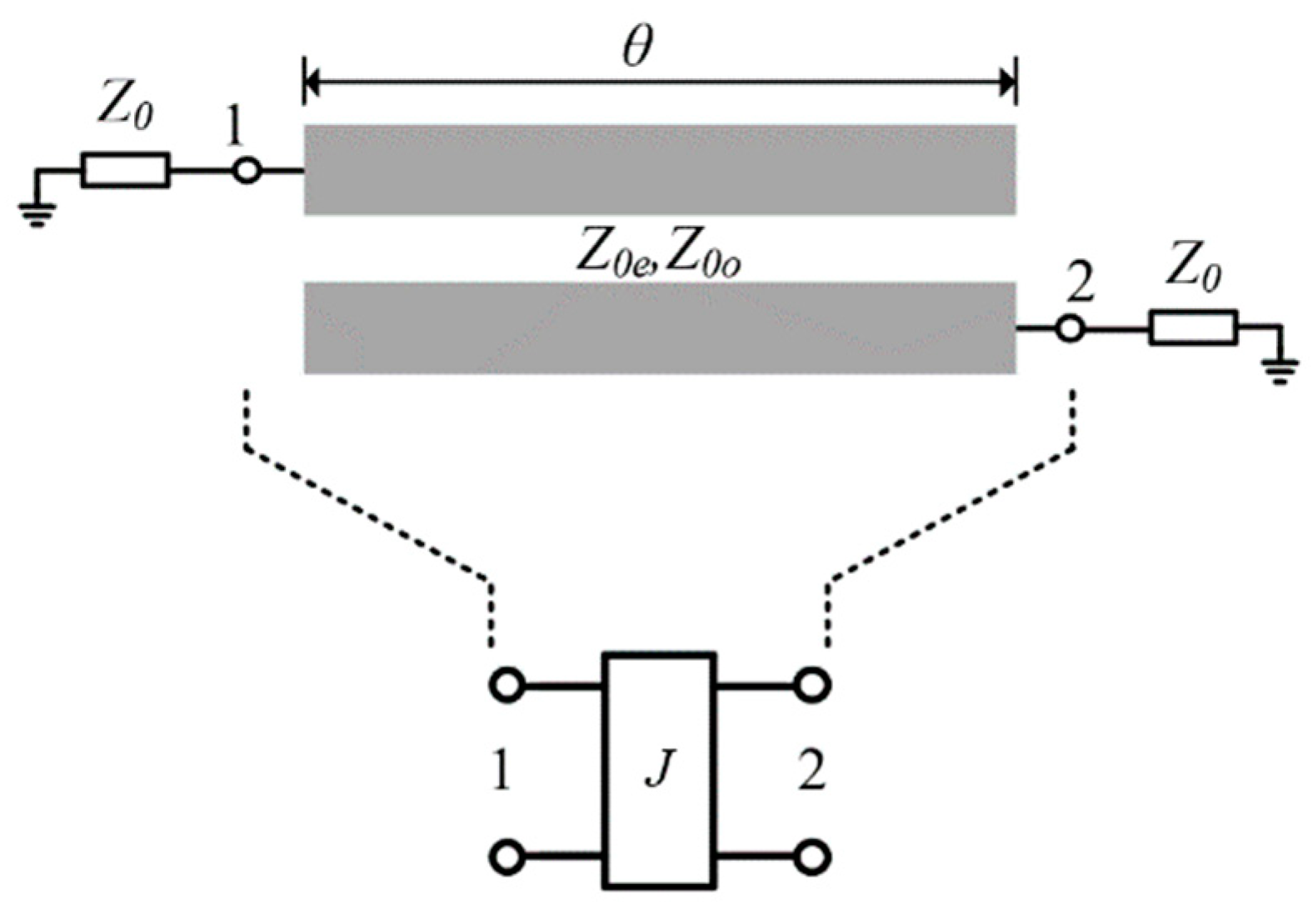
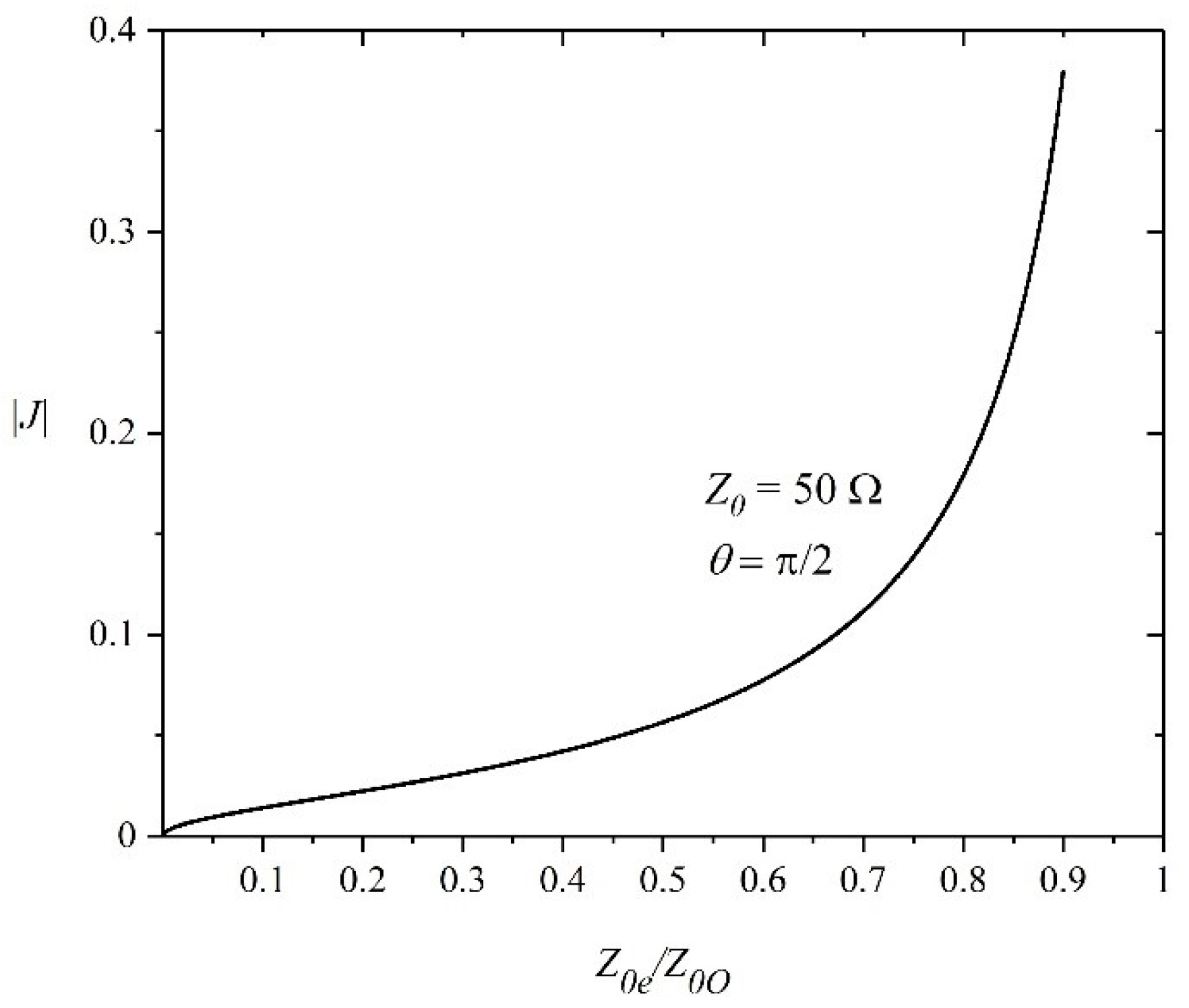
2.1.1. Theory of Parallel-Coupled Lines
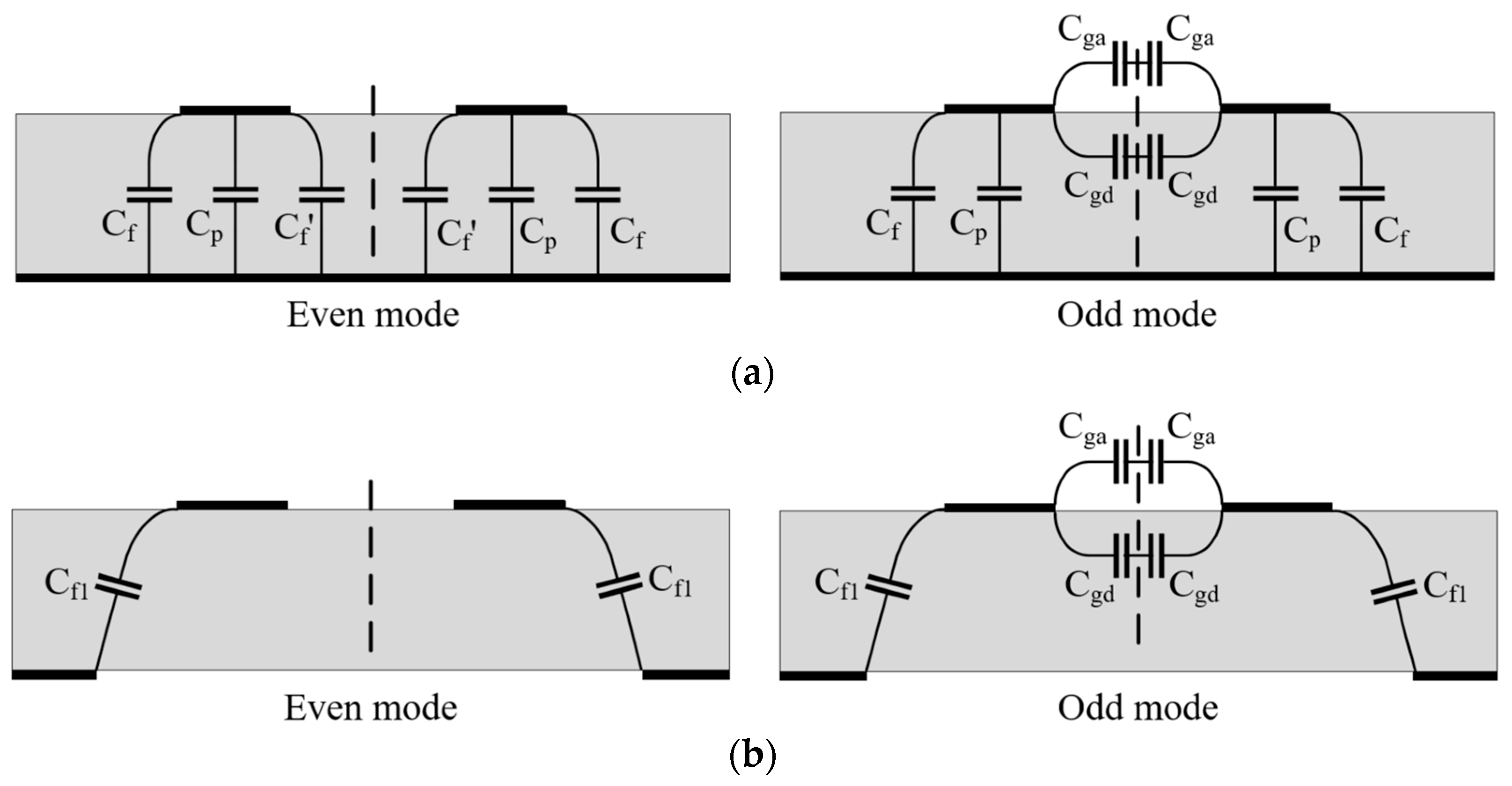
2.1.2. Theory of Defected Ground Structure
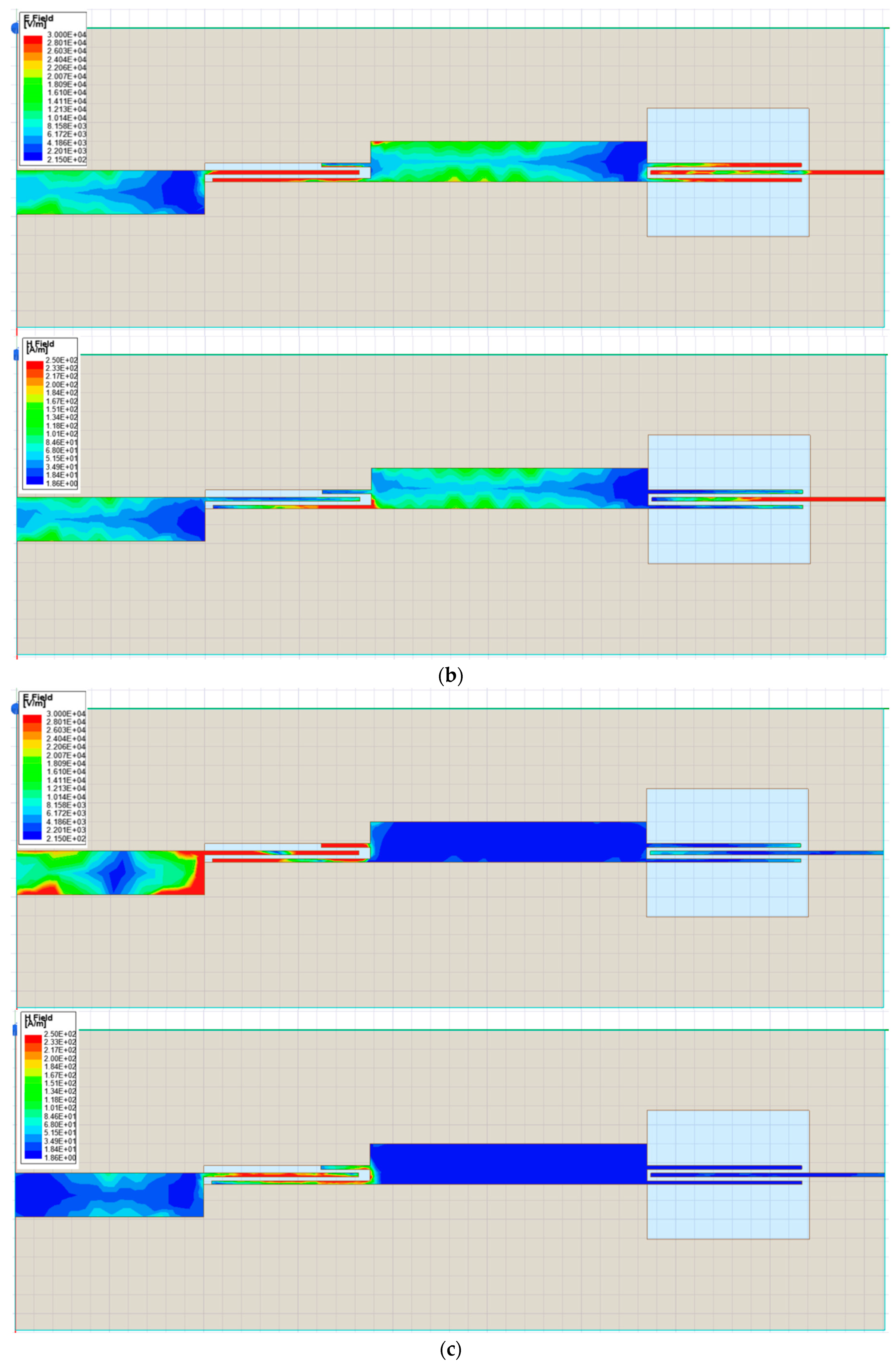
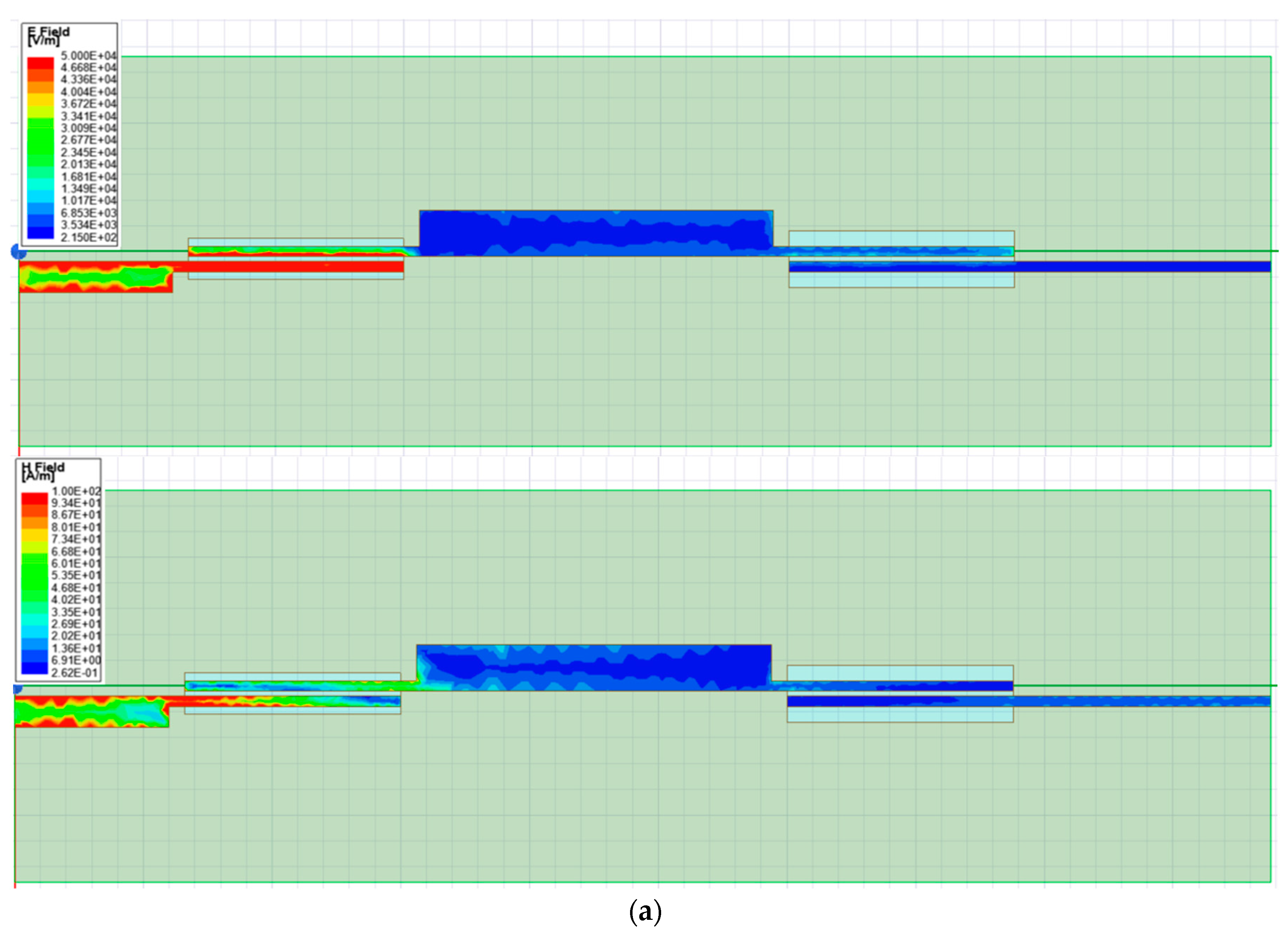
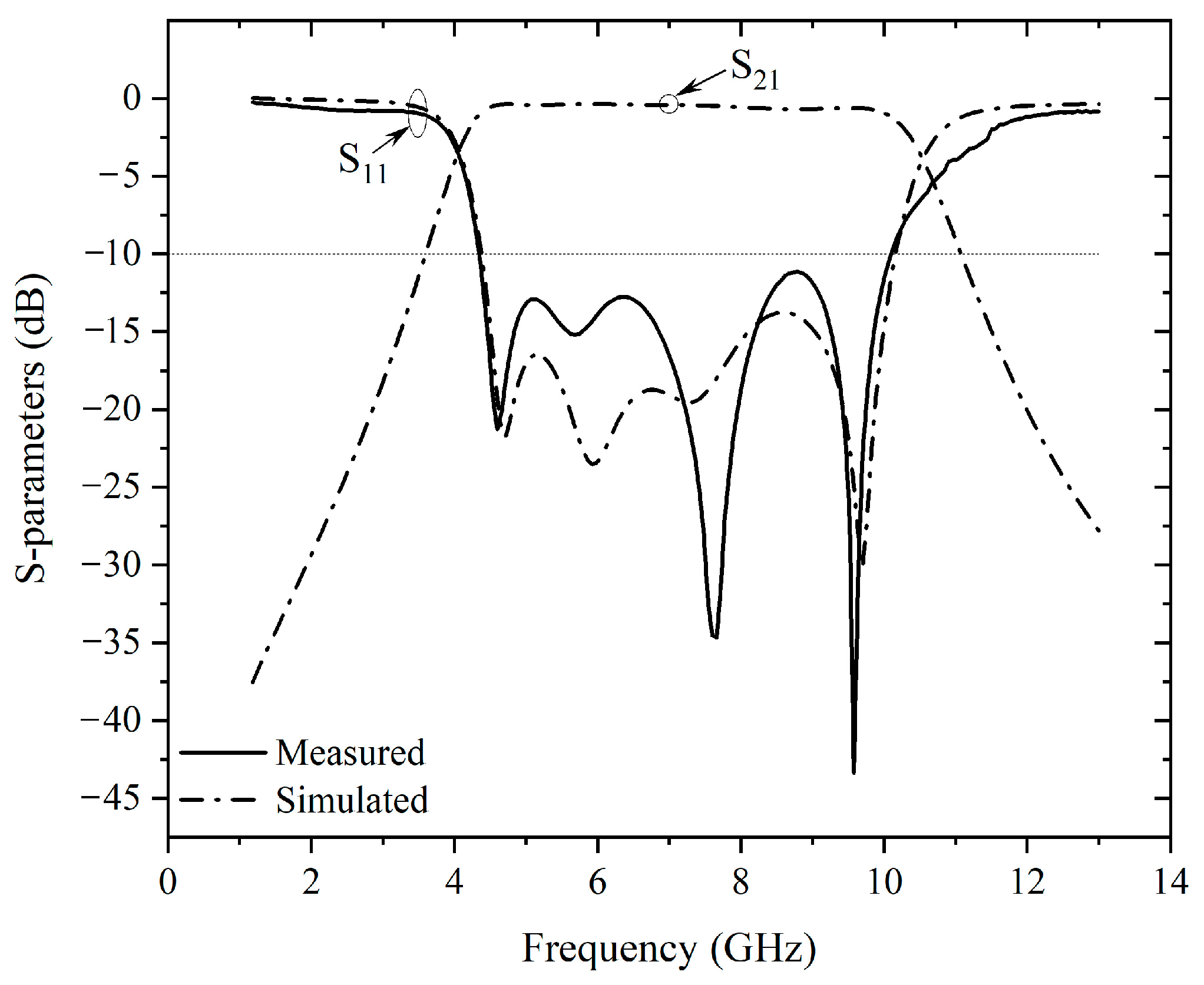
2.2. UWB Filtering Transformer from 50 Ω to 100 Ω
2.3. UWB Filtering Transformer from 50 Ω to 25 Ω
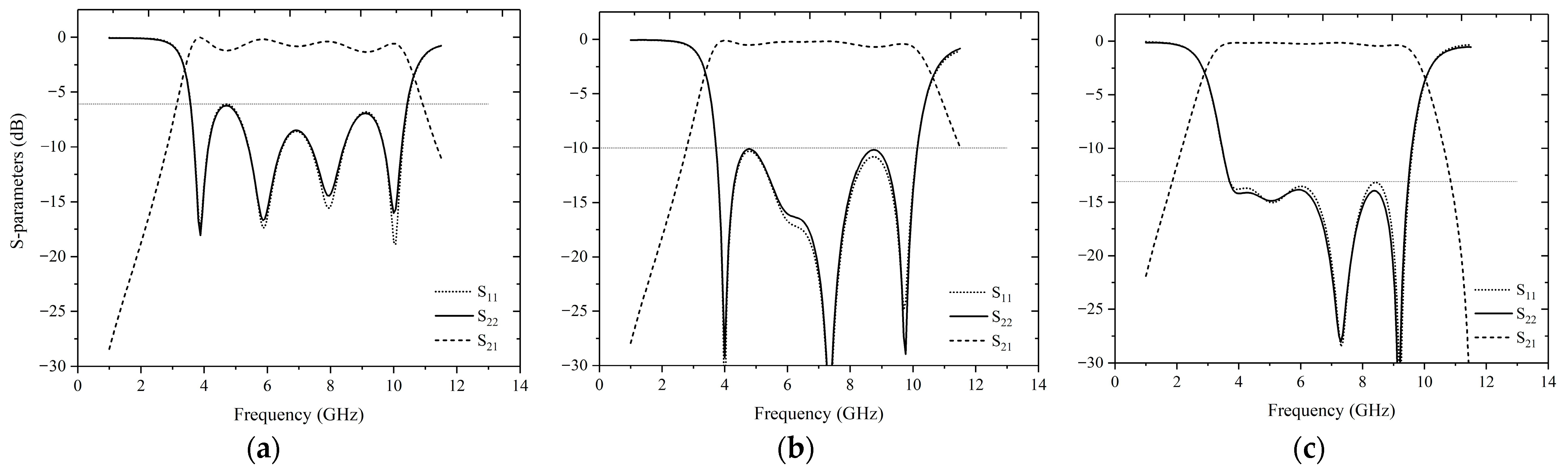
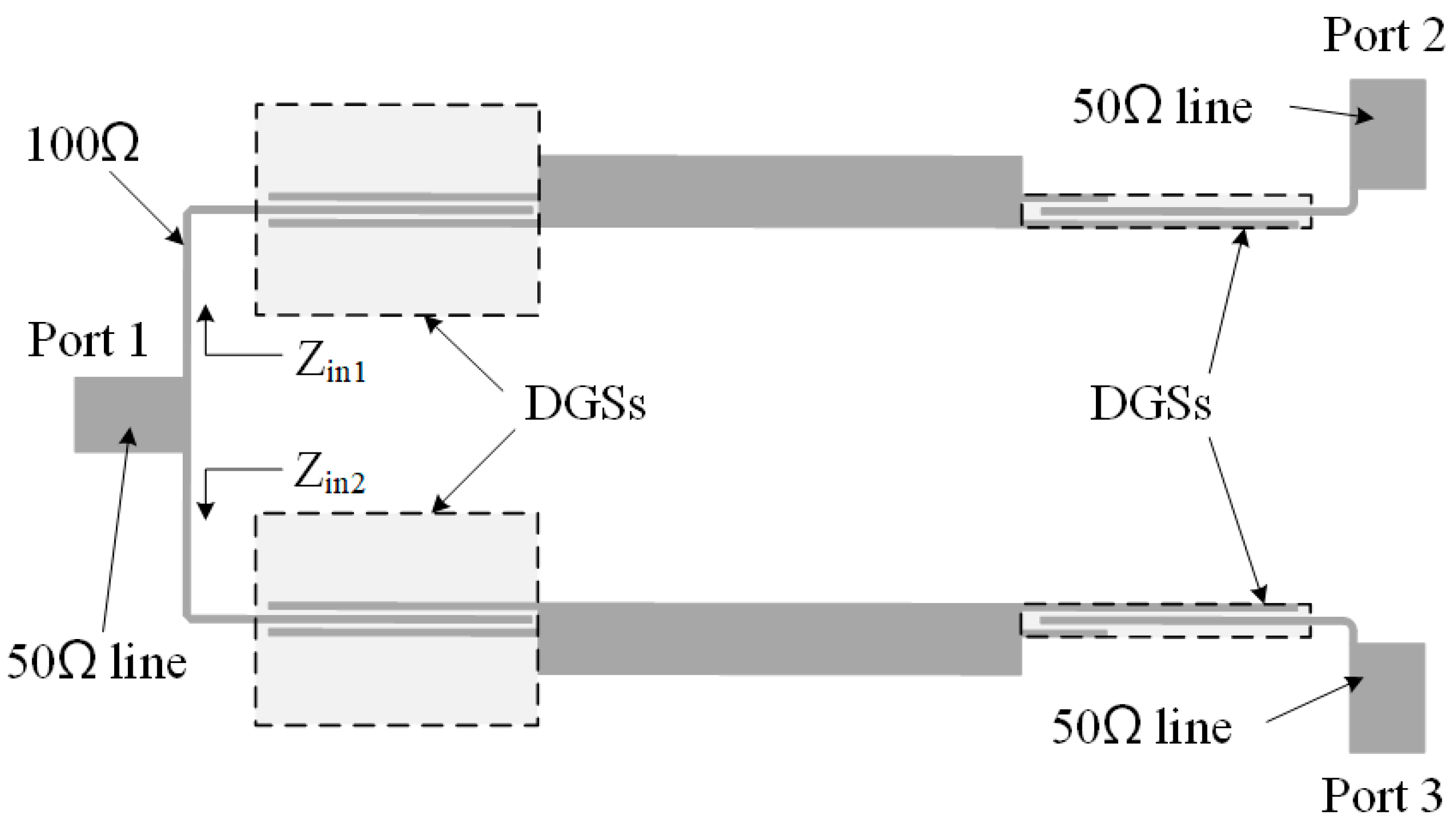
3. Structures and Results of UWB Filtering Power Dividers
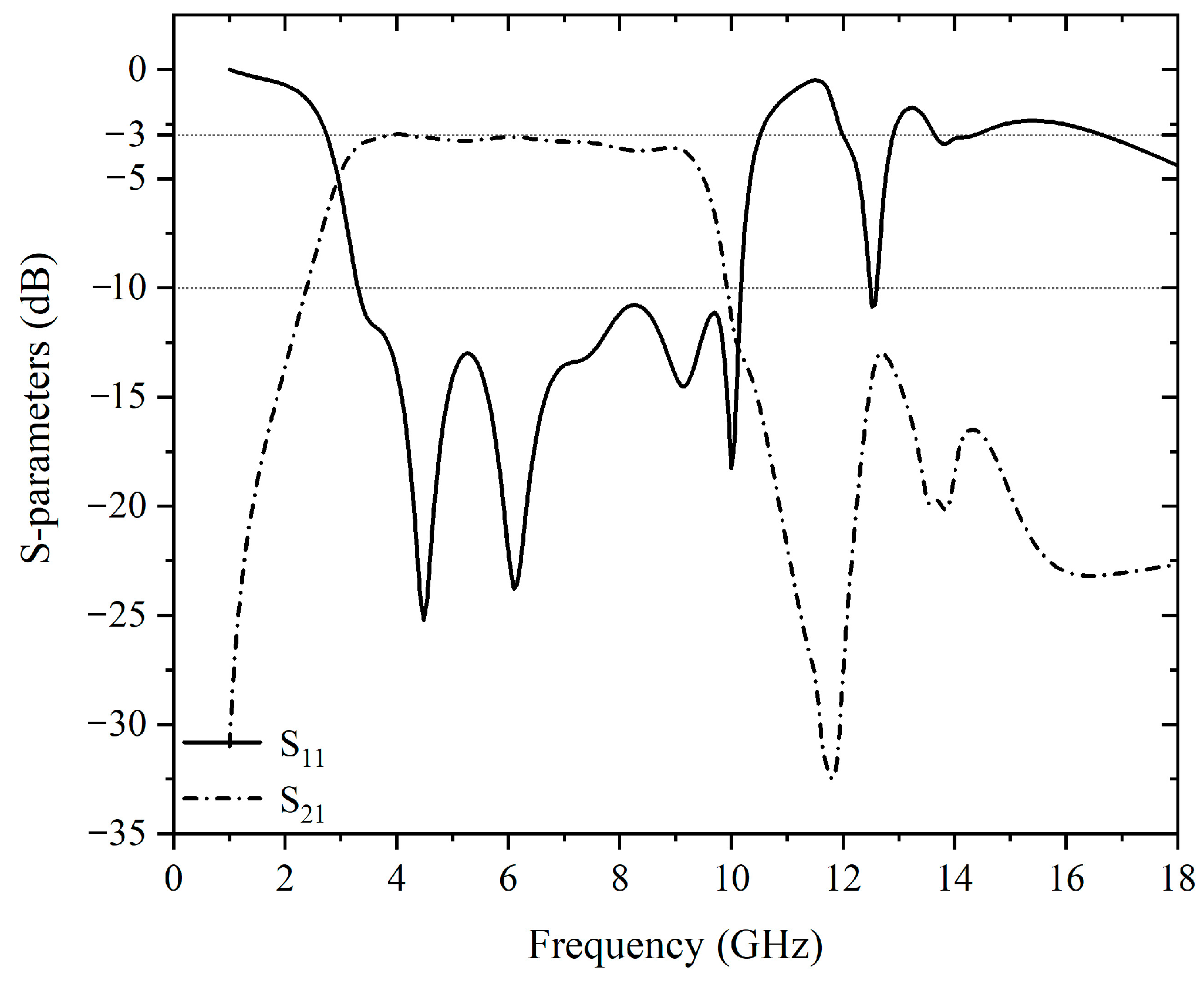
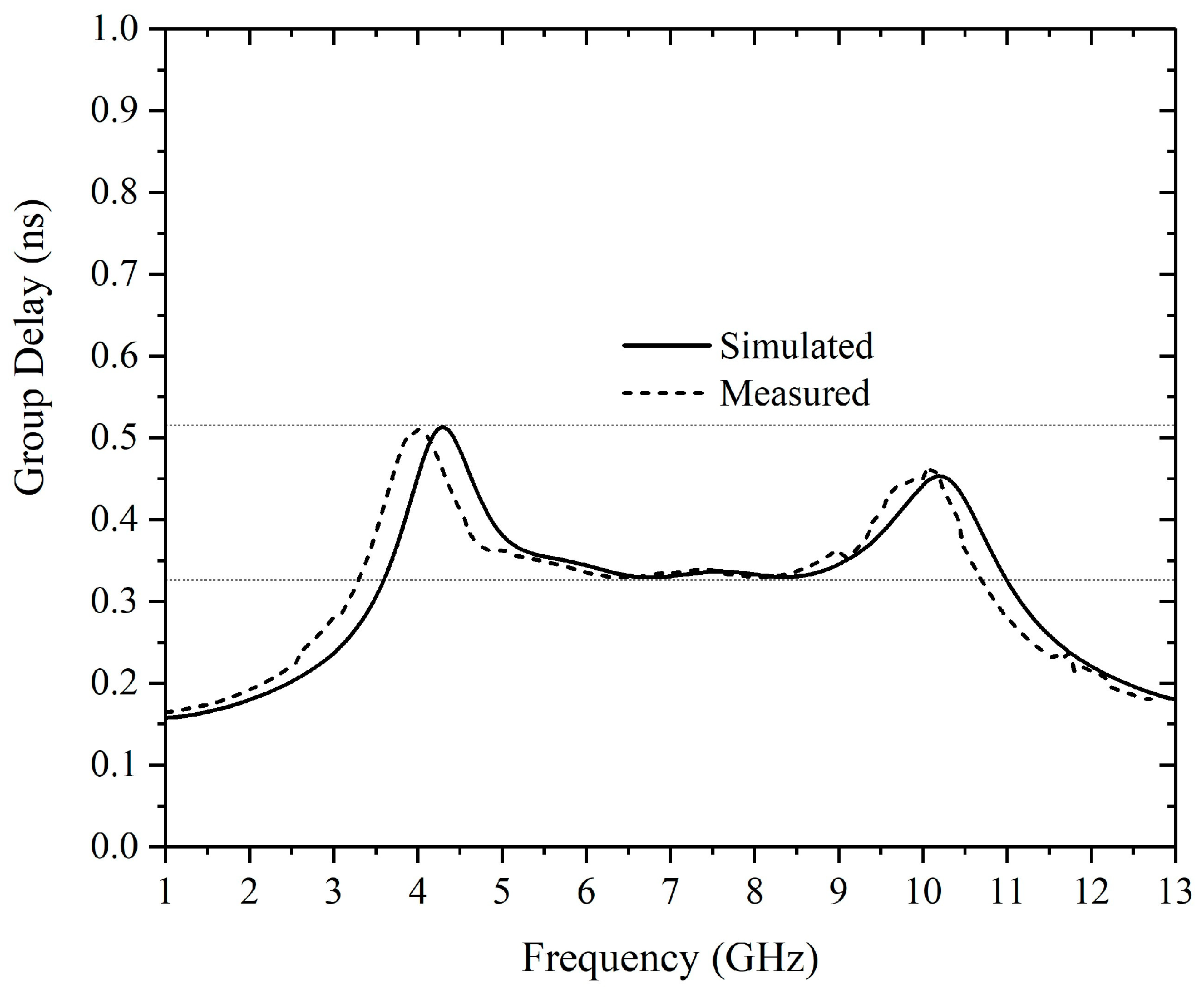
3.1. UWB Filtering Power Divider Based on Impedance Transformers from 50 Ω to 100 Ω
3.2. UWB Filtering Power Divider Based on Impedance Transformers from 50 Ω to 25 Ω
3.3. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, Z.; Chen, Y.; Meng, H. A W-Band Two-Dimensional Monopulse Sparse Array Antenna. IEEE Trans. Antennas Propag. 2022, 70, 9260–9269. [Google Scholar] [CrossRef]
- Lakrit, S.; Medkour, H.; Das, S.; Madhav, B.T.P.; Ali, W.A.E.; Dwivedi, R.P. Design and analysis of integrated Wilkinson power divider-fed conformal high-gain UWB array antenna with band rejection characteristics for WLAN applications. J. Circuits Syst. Comput. 2021, 30, 2150133. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, L.; Zaman, A.U.; Yang, J. Ultra-wideband millimeter-wave planar array antenna with an upside-down structure of printed ridge gap waveguide for stable performance and high antenna efficiency. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1721–1725. [Google Scholar] [CrossRef]
- Ghimire, J.; Choi, D.-Y. Ultra-Wide Band Double-Slot Podal and Antipodal Vivaldi Antennas Feed by Compact Out-Of-Phase Power Divider Slot for Fluid Properties Determination. Sensors 2022, 22, 4543. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Yun, J.; Giannini, F.; Ng, H.J.; Kissinger, D.; Colantonio, P. 168–195 GHz power amplifier with output power larger than 18 dBm in BiCMOS technology. IEEE Access 2020, 8, 79299–79309. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bialkowski, M.E.; Abbosh, A.M. Design of a compact UWB out-of-phase power divider. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 289–291. [Google Scholar] [CrossRef]
- Abbosh, A.; Bialkowski, M.E.; Mazierska, J. An UWB planar out-of-phase power divider employing microstrip-slot and parallel stripline-microstrip transitions. In Proceedings of the 2006 Asia-Pacific Microwave Conference, Yokohama, Japan, 12–15 December 2006; pp. 905–908. [Google Scholar]
- Zhou, B.; Wang, H.; Sheng, W. A novel UWB Wilkinson power divider. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 4–6 December 2010; pp. 1763–1765. [Google Scholar]
- Liu, W.-Q.; Wei, F.; Pang, C.-H.; Shi, X.-W. Design of a compact ultra-wideband power divider. In Proceedings of the 2012 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shenzhen, China, 5–8 May 2012; pp. 1–3. [Google Scholar]
- Wei, F.; Chen, L.; Shi, X.-W.; Wu, Q.-Y.; Huang, Q.-L. Design of compact UWB power divider with one narrow notch-band. J. Electromagn. Waves Appl. 2010, 24, 2343–2352. [Google Scholar] [CrossRef]
- Makimoto, M.; Yamashita, S. Compact bandpass filters using stepped impedance resonators. Proc. IEEE 1979, 67, 16–19. [Google Scholar] [CrossRef]
- Makimoto, M.; Yamashita, S. Bandpass filters using parallel coupled stripline stepped impedance resonators. IEEE Trans. Microw. Theory Tech. 1980, 28, 1413–1417. [Google Scholar] [CrossRef]
- Zhu, L.; Bu, H.; Wu, K. Aperture compensation technique for innovative design of ultra-broadband microstrip bandpass filter. In Proceedings of the 2000 IEEE MTT-S International Microwave Symposium Digest (Cat. No. 00CH37017), Boston, MA, USA, 11–16 June 2000; pp. 315–318. [Google Scholar]
- Zhu, L.; Menzel, W.; Wu, K.; Boegelsack, F. Theoretical characterization and experimental verification of a novel compact broadband microstrip bandpass filter. In Proceedings of the 2001 Asia-Pacific Microwave Conference (Cat. No. 01TH8577), Taipei, Taiwan, 3–6 December 2001; pp. 625–628. [Google Scholar]
- Menzel, W.; Zhu, L.; Wu, K.; Bogelsack, F. On the design of novel compact broad-band planar filters. IEEE Trans. Microw. Theory Tech. 2003, 51, 364–370. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, S.; Menzel, W. Ultra-wideband (UWB) bandpass filters using multiple-mode resonator. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 796–798. [Google Scholar]
- Sun, S.; Zhu, L. Capacitive-ended interdigital coupled lines for UWB bandpass filters with improved out-of-band performances. IEEE Microw. Wirel. Compon. Lett. 2006, 16, 440–442. [Google Scholar] [CrossRef]
- Wei, F.; Yang, Z.-J.; Qin, P.-Y.; Guo, Y.J.; Li, B.; Shi, X.-W. A balanced-to-balanced in-phase filtering power divider with high selectivity and isolation. IEEE Trans. Microw. Theory Tech. 2018, 67, 683–694. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L.; Liang, C.; Majid, I. Compact planar tunable filter with constant absolute bandwidth and wide-frequency tuning range using DGS coupling structure. IEEE Access 2021, 9, 157259–157266. [Google Scholar] [CrossRef]
- Kuo, J.-T.; Shih, E. Microstrip stepped impedance resonator bandpass filter with an extended optimal rejection bandwidth. IEEE Trans. Microw. Theory Tech. 2003, 51, 1554–1559. [Google Scholar]



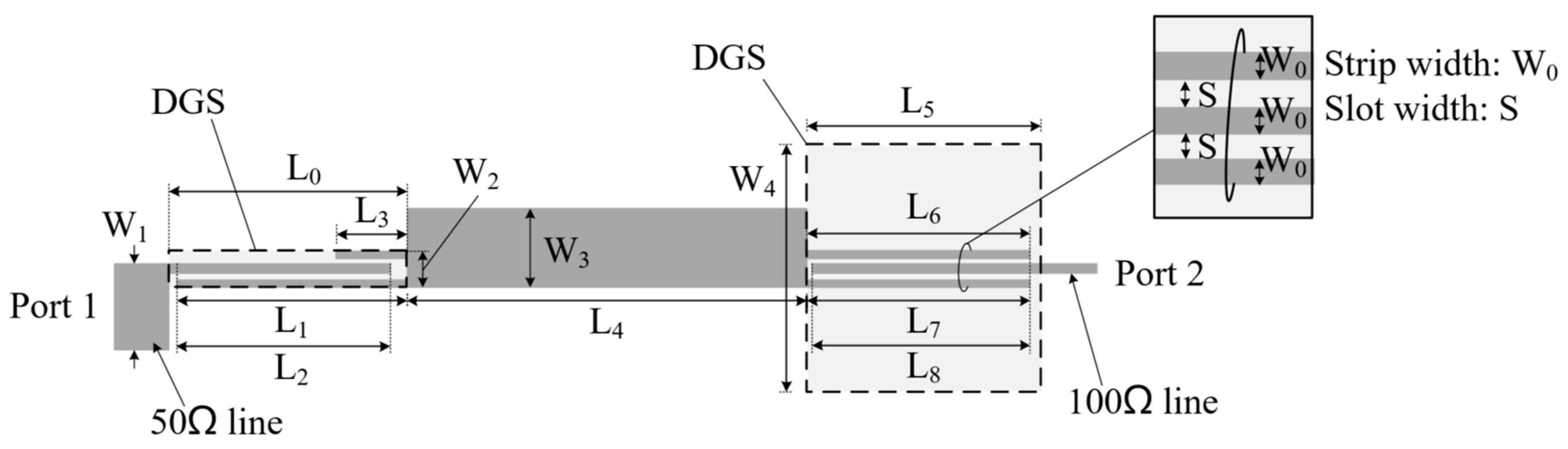















| L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 |
| 4.4 | 4.2 | 3.9 | 1.3 | 7.34 | 4.3 | 4.1 | 4.1 | 4 |
| W0 | W1 | W2 | W3 | W4 | S | unit: mm | ||
| 0.1 | 1.16 | 0.5 | 1.08 | 3.4 | 0.1 | |||
| L0 | L1 | L2 | L3 | L4 | S | |||
| 4.4 | 4.7 | 6.9 | 4.2 | 4.5 | 0.1 | |||
| W0 | W1 | W2 | W3 | W4 | W5 | unit: mm | ||
| 0.2 | 0.2 | 1.1 | 0.9 | 0.8 | 0.6 | |||
| Ref. | Passband (GHz) | RL (dB) | IL (dB) | Sizes (mm × mm) | Filtering |
|---|---|---|---|---|---|
| [8] | 3.1–10.6 | 10 | 3.5 | 30 × 40 (2.3λ × 3λ) | N/A |
| [9] | 3.1–10.6 | 10 | 3.5 | 16 × 18 (1.2λ × 1.3λ) | N/A |
| [10] | 3.1–10.6 | 10 | 4–5 | 20 × 43 (1.5λ × 3.2λ) | N/A |
| [11] | 2.8–10.6 | 10 | 3.5 | 23 × 27 (1.7λ × 2λ) | N/A |
| This Work | 4–10 | >11 | 3.6–4.5 | 17 × 28 (1.2λ × 2.1λ) | UWB filtering |
| 4–10.6 | >12 | 3.5–4.4 | 6.6 × 23.6 (0.5λ × 1.74λ) | UWB filtering |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Liu, Y.; Liang, C.; Majid, I. Design of UWB Filtering Impedance Transformers and Power Dividers Using Stepped-Impedance Resonators. Electronics 2023, 12, 2800. https://doi.org/10.3390/electronics12132800
Cao Z, Liu Y, Liang C, Majid I. Design of UWB Filtering Impedance Transformers and Power Dividers Using Stepped-Impedance Resonators. Electronics. 2023; 12(13):2800. https://doi.org/10.3390/electronics12132800
Chicago/Turabian StyleCao, Ziheng, Yun Liu, Chen Liang, and Irfan Majid. 2023. "Design of UWB Filtering Impedance Transformers and Power Dividers Using Stepped-Impedance Resonators" Electronics 12, no. 13: 2800. https://doi.org/10.3390/electronics12132800





