Development of a Compliant Lower-Limb Rehabilitation Robot Using Underactuated Mechanism
Abstract
:1. Introduction
2. Proposed Robot Design
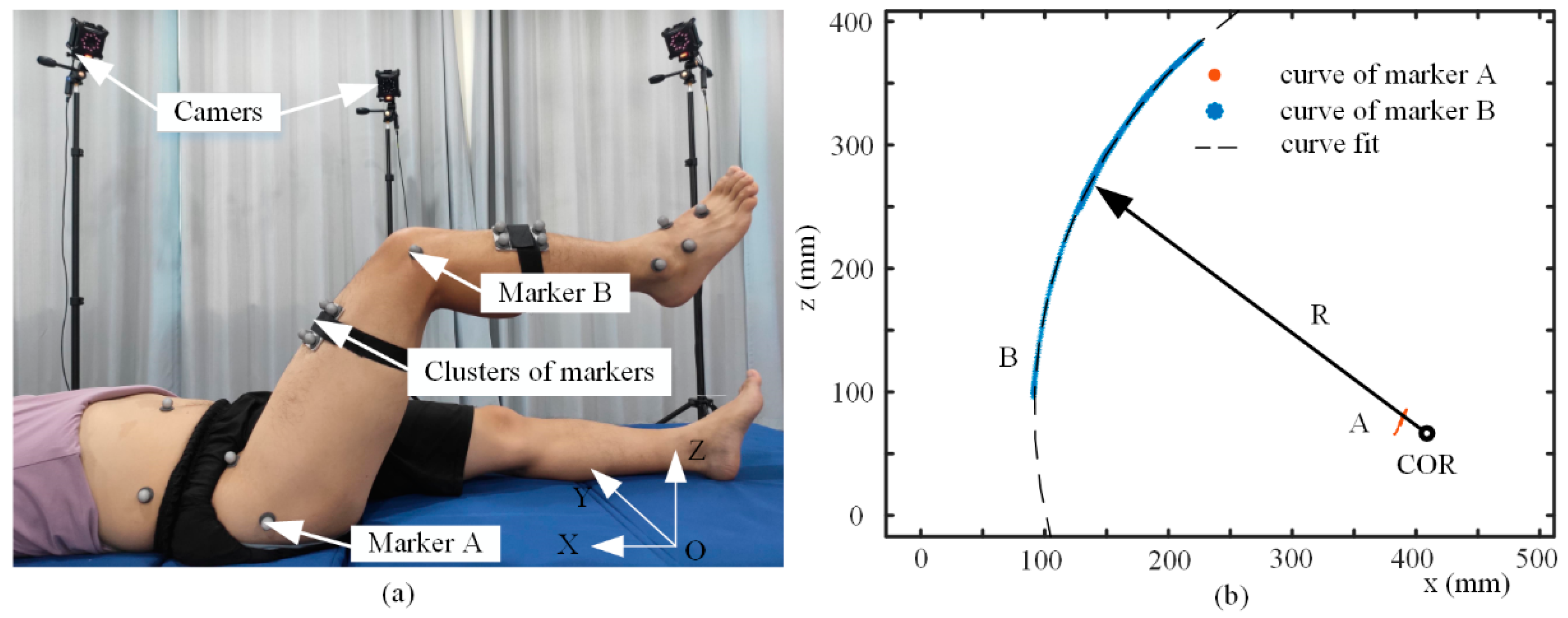
2.1. Recording of the Human Hip Trajectory
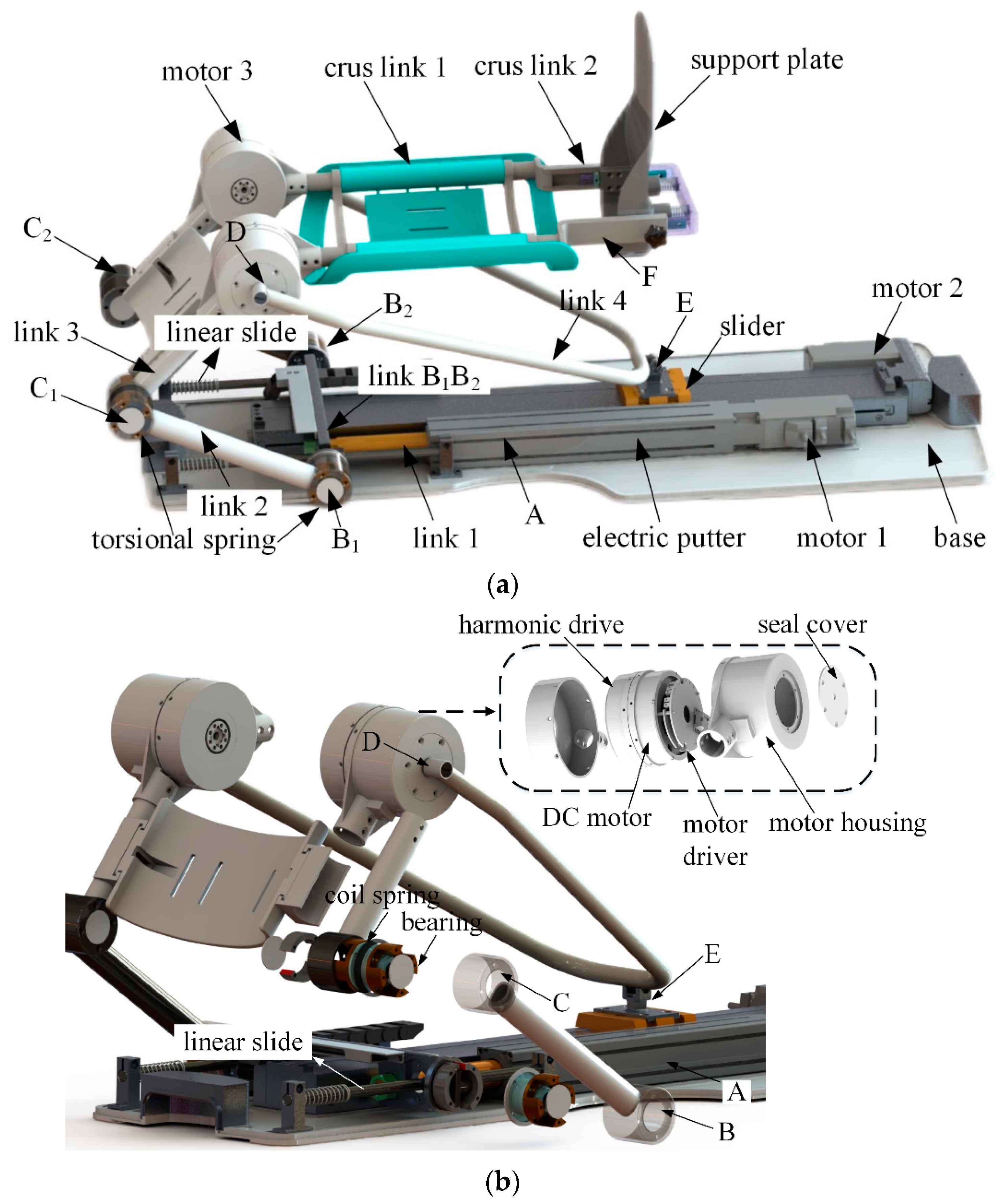
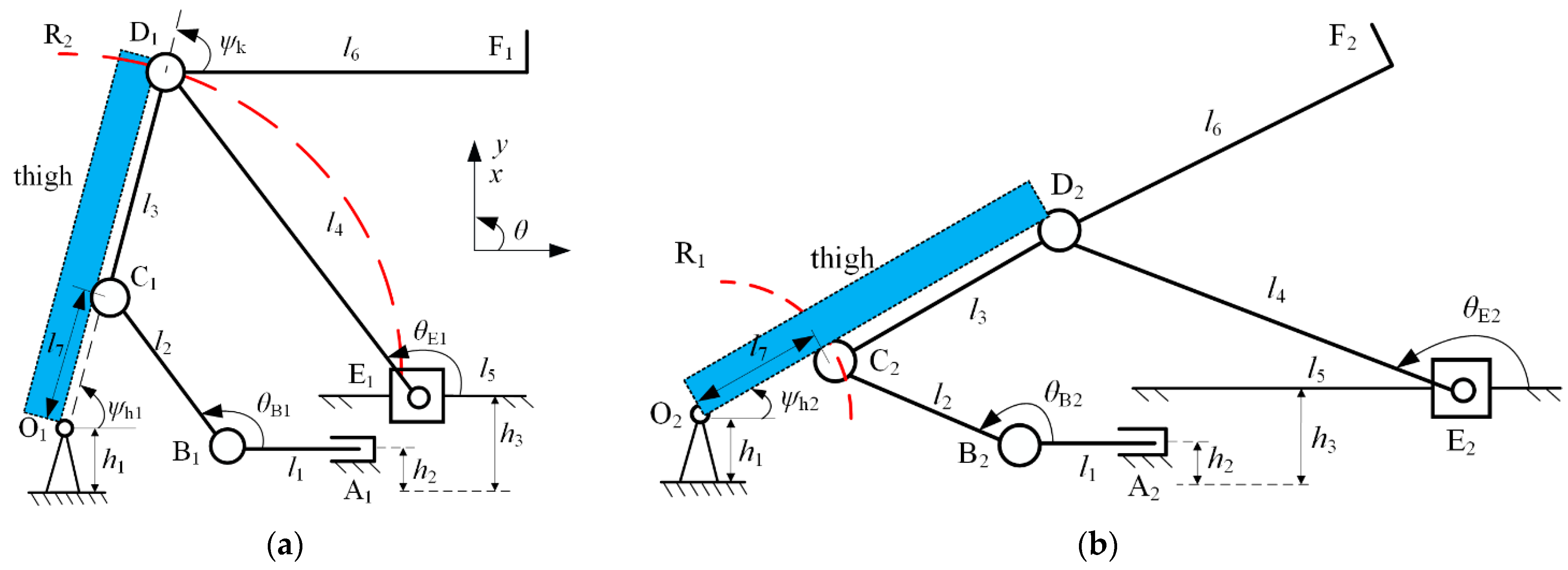
2.2. Underactuated Mechanism Design
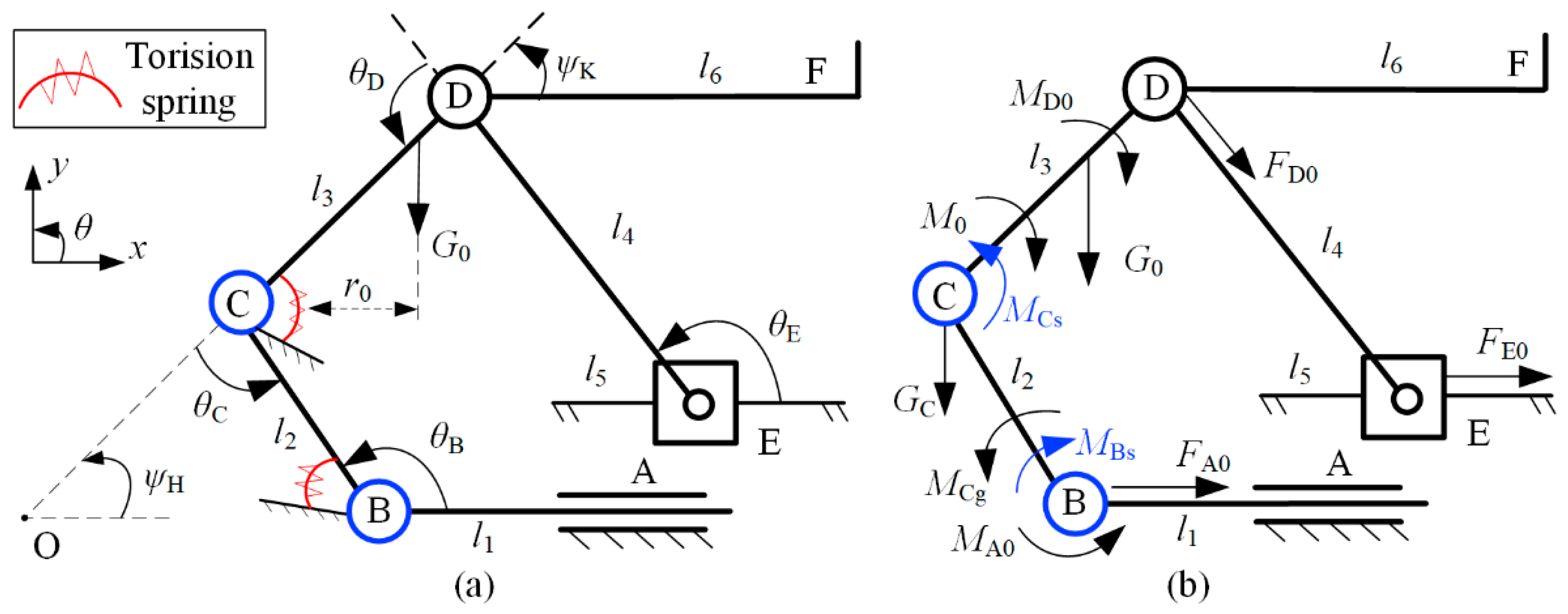
2.3. Motion Principle of the Underactuated Mechanism Design
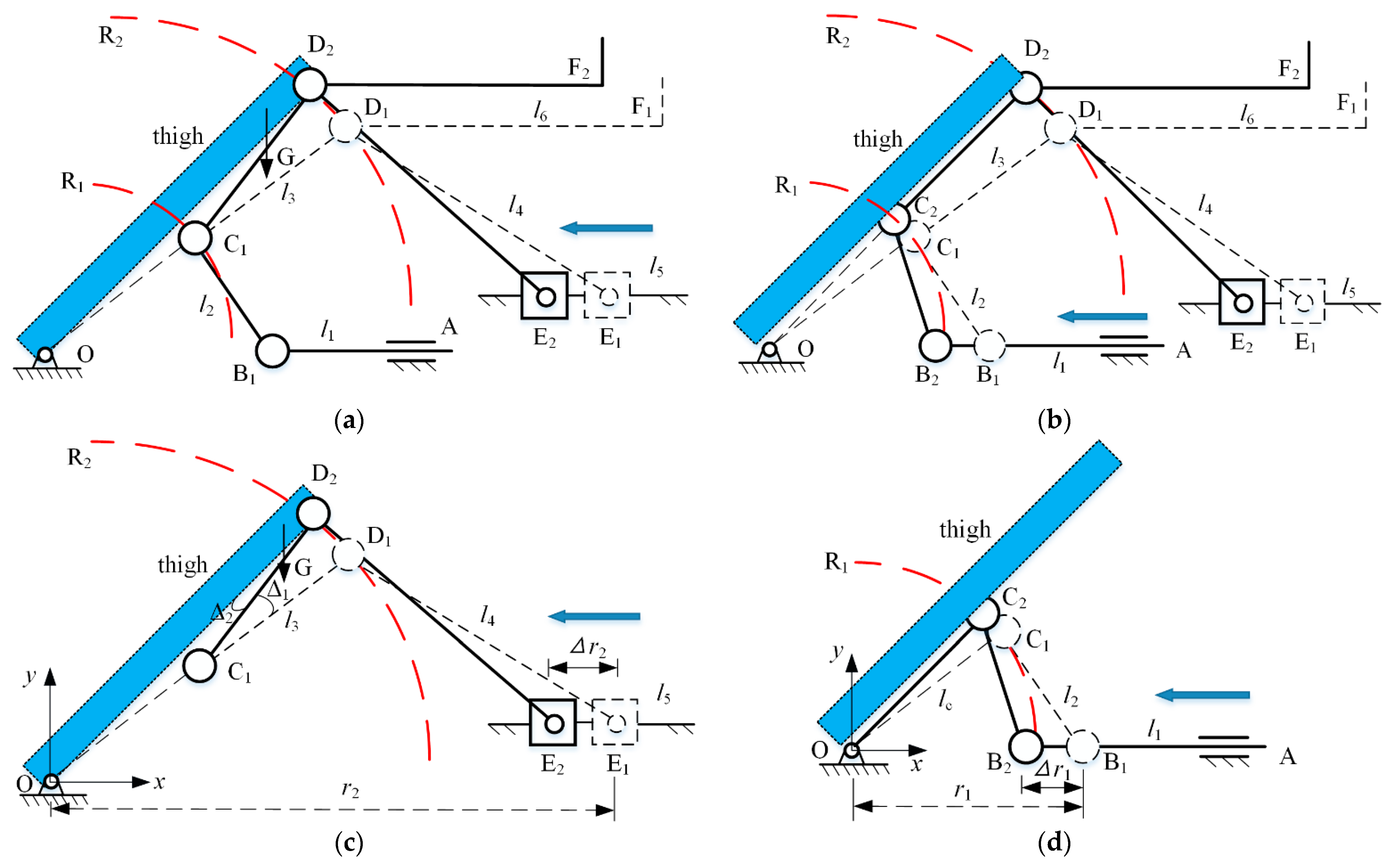
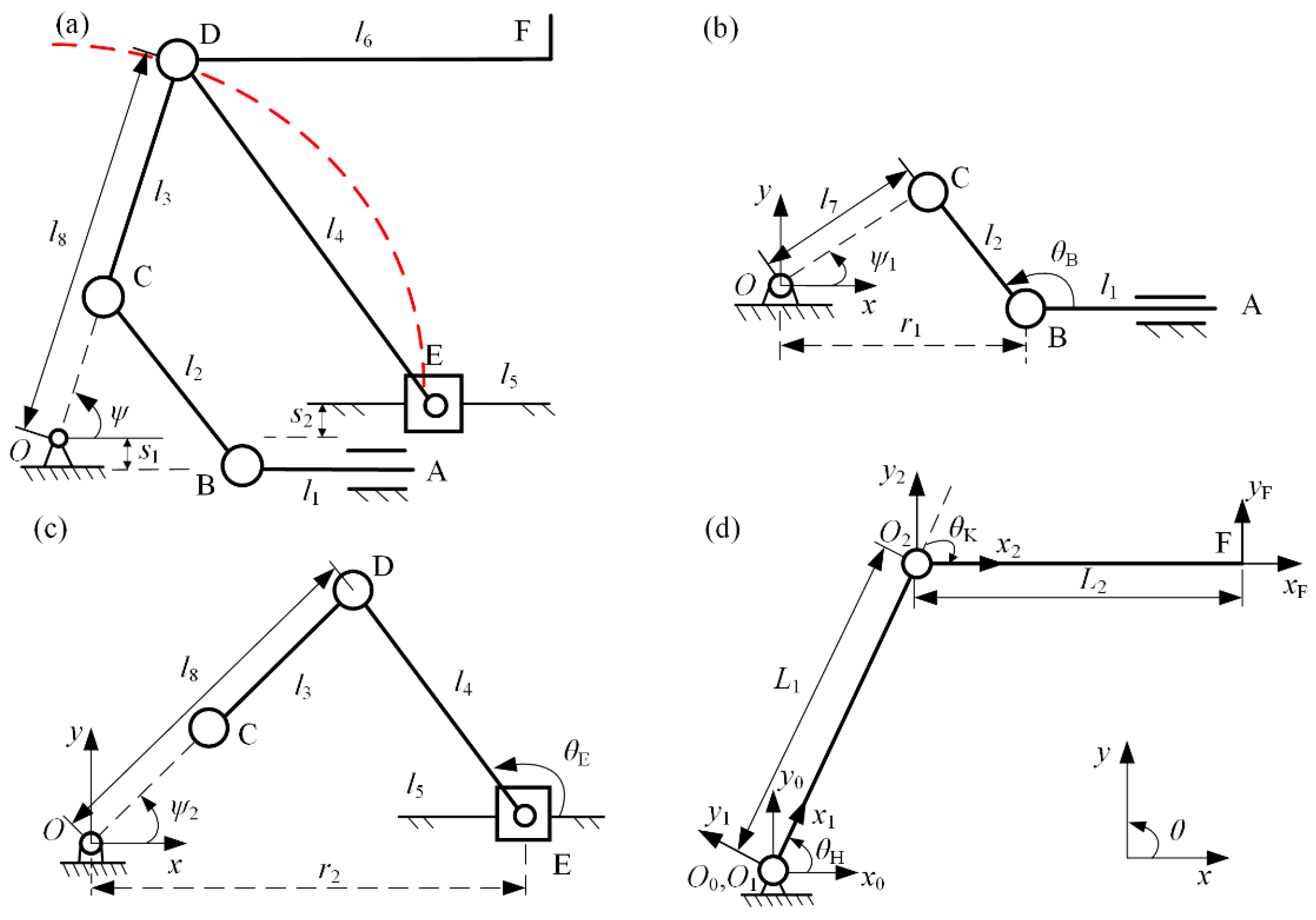
2.4. Optimization of the Underactuated Mechanism
- (1)
- maximum number of generations: 200;
- (2)
- population: 50;
- (3)
- minimum of the inertia weight (wmin): 0.4;
- (4)
- c1 and c2: 2.
2.5. Knee and Ankle Joint Mechanisms
3. Kinematic Analysis
4. Experimental Protocol and Evaluation
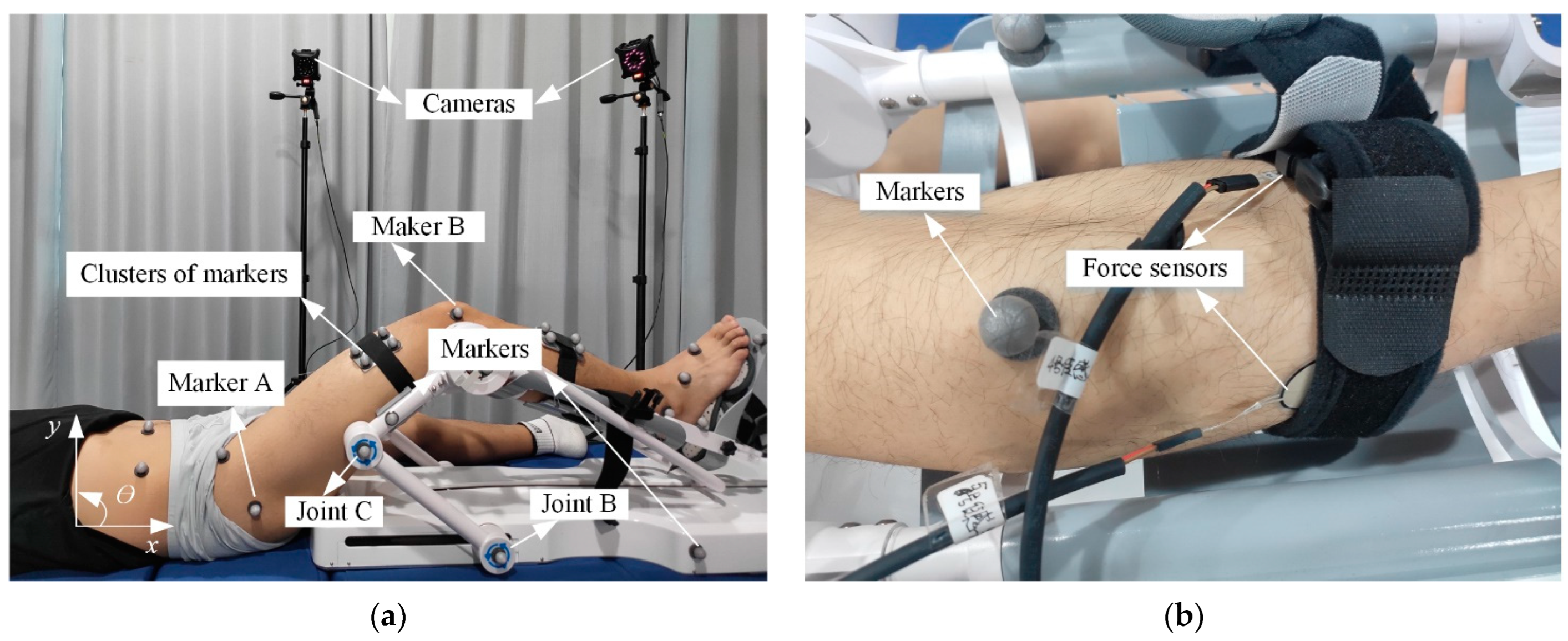
4.1. Experimental Protocol
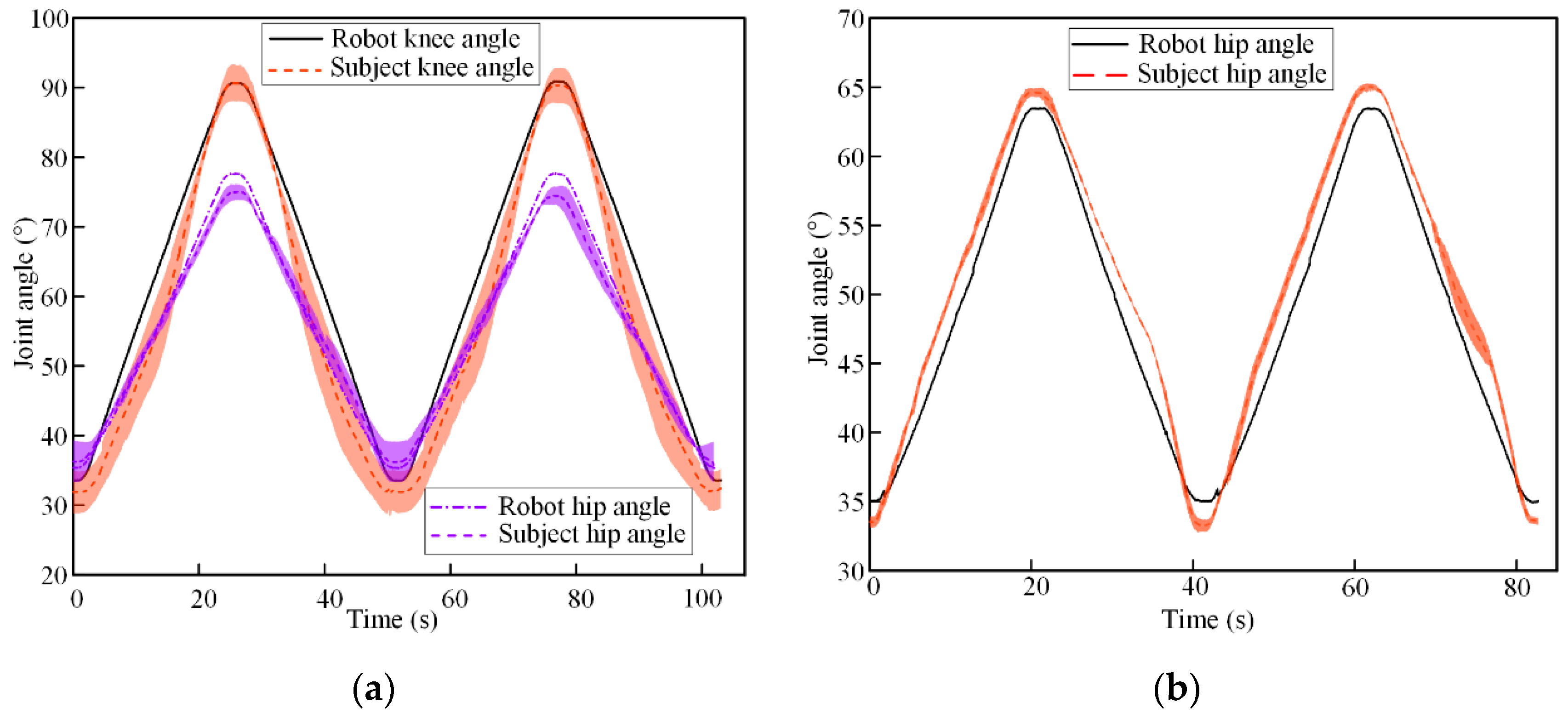
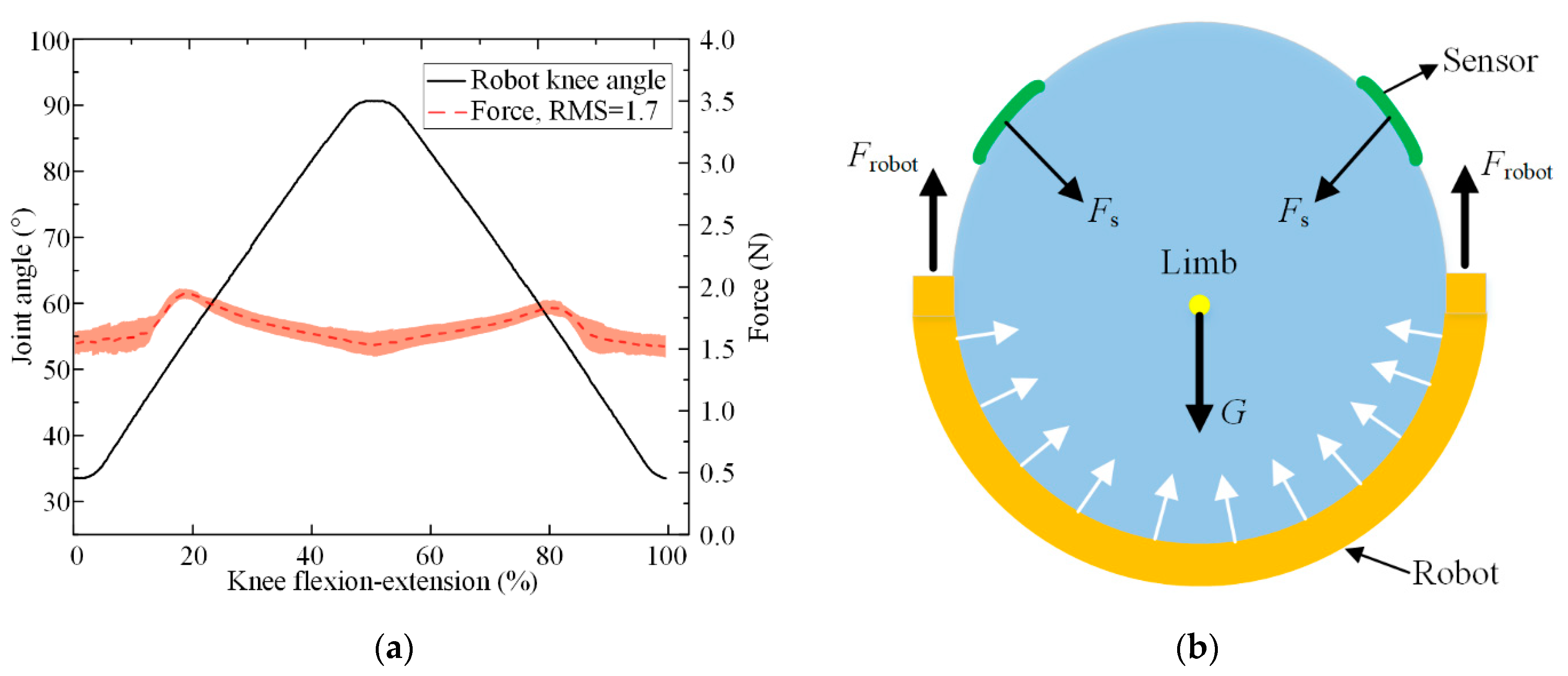
4.2. Kinematics and Interaction Force
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, L.; Wang, A.; Zhong, J. Inverse Dynamics Modeling and Analysis of Healthy Human Data for Lower Limb Rehabilitation Robots. Electronics 2022, 11, 3848. [Google Scholar] [CrossRef]
- Preston, J.S.; KBateman, D.; Tria, A.J., Jr. Constraint in Revision Total Knee Arthroplasty. Mastering Orthop. Tech. Revis. Knee Arthop. 2019, 1, 1–7. [Google Scholar]
- Sarajchi, M.; Al-Hares, M.K.; Sirlantzis, K. Wearable Lower-Limb Exoskeleton for Children with Cerebral Palsy: A Systematic Review of Mechanical Design, Actuation Type, Control Strategy, and Clinical Evaluation. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2695–2720. [Google Scholar] [CrossRef] [PubMed]
- Sarajchi, M.; Sirlantzis, K. Design and Control of a Single-Leg Exoskeleton with Gravity Compensation for Children with Unilateral Cerebral Palsy. Sensors 2023, 23, 6103. [Google Scholar] [CrossRef] [PubMed]
- Susanto, S.; Simorangkir, I.T.; Analia, R.; Pamungkas, D.S.; Soebhakti, H.; Sani, A.; Caesarendra, W. Real-Time Identification of Knee Joint Walking Gait as Preliminary Signal for Developing Lower Limb Exoskeleton. Electronics 2021, 10, 2117. [Google Scholar] [CrossRef]
- Dupont, P.E.; Nelson, B.J.; Goldfarb, M.; Hannaford, B.; Menciassi, A.; O’Malley, M.K.; Simaan, N.; Valdastri, P.; Yang, G.-Z. A decade retrospective of medical robotics research from 2010 to 2020. Sci. Robot. 2021, 6, eabi8017. [Google Scholar] [CrossRef]
- Calabrò, R.S.; Billeri, L.; Andronaco, V.A.; Accorinti, M.; Milardi, D.; Cannavò, A.; Aliberti, E.; Militi, A.; Bramanti, P.; Naro, A. Walking on the Moon: A randomized clinical trial on the role of lower body positive pressure treadmill training in post-stroke gait impairment. J. Adv. Res. 2020, 21, 15–24. [Google Scholar] [CrossRef]
- Wang, D.; Lee, K.-M.; Ji, J. A passive gait-based weight-support lower extremity exoskeleton with compliant joints. IEEE Trans. Robot. 2016, 32, 933–942. [Google Scholar] [CrossRef]
- Duschau-Wicke, A.; Von Zitzewitz, J.; Caprez, A.; Lunenburger, L.; Riener, R. Path control: A method for patient-cooperative robot-aided gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 18, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Qiu, S.; Pei, Z.; Wang, C.; Tang, Z. Systematic Review on Wearable Lower Extremity Robotic Exoskeletons for Assisted Locomotion. J. Bionic Eng. 2023, 20, 436–469. [Google Scholar] [CrossRef]
- Li, W.; Liu, K.; Li, C.; Sun, Z.; Liu, S.; Gu, J. Development and Evaluation of a Wearable Lower Limb Rehabilitation Robot. J. Bionic Eng. 2022, 19, 688–699. [Google Scholar] [CrossRef]
- Wang, W.; Hou, Z.-G.; Tong, L.; Zhang, F.; Chen, Y.; Tan, M. A novel leg orthosis for lower limb rehabilitation robots of the sitting/lying type. Mech. Mach. Theory 2014, 74, 337–353. [Google Scholar] [CrossRef]
- Komada, S.; Hashimoto, Y.; Okuyama, N.; Hisada, T.; Hirai, J. Development of a biofeedback therapeutic-exercise-supporting manipulator. IEEE Trans. Ind. Electron. 2009, 56, 3914–3920. [Google Scholar] [CrossRef]
- van Kammen, K.; Boonstra, A.M.; van der Woude, L.H.; Visscher, C.; Reinders-Messelink, H.A.; den Otter, R. Lokomat guided gait in hemiparetic stroke patients: The effects of training parameters on muscle activity and temporal symmetry. Disabil. Rehabil. 2020, 42, 2977–2985. [Google Scholar] [CrossRef] [Green Version]
- Jezernik, S.; Colombo, G.; Keller, T.; Frueh, H.; Morari, M. Robotic orthosis lokomat: A rehabilitation and research tool. Neuromodul. Technol. Neural Interface 2003, 6, 108–115. [Google Scholar] [CrossRef]
- Vaida, C.; Birlescu, I.; Pisla, A.; Ulinici, I.-M.; Tarnita, D.; Carbone, G.; Pisla, D. Systematic design of a parallel robotic system for lower limb rehabilitation. IEEE Access 2020, 8, 34522–34537. [Google Scholar] [CrossRef]
- Husty, M.; Birlescu, I.; Tucan, P.; Vaida, C.; Pisla, D. An algebraic parameterization approach for parallel robots analysis. Mech. Mach. Theory 2019, 140, 245–257. [Google Scholar] [CrossRef]
- Wang, H.; Lin, M.; Jin, Z.; Yan, H.; Liu, G.; Liu, S.; Hu, X. A 4-DOF Workspace Lower Limb Rehabilitation Robot: Mechanism Design, Human Joint Analysis and Trajectory Planning. Appl. Sci. 2020, 10, 4542. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, H.; Guo, J.; Yu, F.; Yao, Y. Estimation of Tibiofemoral Joint Contact Forces Using Foot Loads during Continuous Passive Motions. Sensors 2022, 22, 4947. [Google Scholar] [CrossRef]
- Mohan, S.; Mohanta, J.; Kurtenbach, S.; Paris, J.; Corves, B.; Huesing, M. Design, development and control of a 2PRP-2PPR planar parallel manipulator for lower limb rehabilitation therapies. Mech. Mach. Theory 2017, 112, 272–294. [Google Scholar] [CrossRef]
- Barbosa, A.M.; Carvalho, J.C.M.; Gonçalves, R.S. Cable-driven lower limb rehabilitation robot. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 1–11. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kim, K.; Park, W.M.; Yoon, K.H. Reduction of knee range of motion during continuous passive motion due to misaligned hip joint centre. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 801–806. [Google Scholar] [CrossRef] [PubMed]
- Bible, J.E.; Simpson, A.K.; Biswas, D.; Pelker, R.R.; Grauer, J.N. Actual knee motion during continuous passive motion protocols is less than expected. Clin. Orthop. Relat. Res.® 2009, 467, 2656–2661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarkisian, S.V.; Ishmael, M.K.; Lenzi, T. Self-aligning mechanism improves comfort and performance with a powered knee exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 629–640. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Villamañan, M.d.C.; Gonzalez-Vargas, J.; Torricelli, D.; Moreno, J.C.; Pons, J.L. Compliant lower limb exoskeletons: A comprehensive review on mechanical design principles. J. Neuroeng. Rehabil. 2019, 16, 55. [Google Scholar] [CrossRef]
- Stienen, A.H.A.; Hekman, E.E.G.; Helm, F.C.T.V.D.; Kooij, H.V.D. Self-Aligning Exoskeleton Axes Through Decoupling of Joint Rotations and Translations. IEEE Trans. Robot. 2009, 25, 628–633. [Google Scholar] [CrossRef]
- Bessler-Etten, J.; Schaake, L.; Prange-Lasonder, G.B.; Buurke, J.H. Assessing effects of exoskeleton misalignment on knee joint load during swing using an instrumented leg simulator. J. Neuroeng. Rehabil. 2022, 19, 13. [Google Scholar] [CrossRef]
- Zanotto, D.; Akiyama, Y.; Stegall, P.; Agrawal, S.K. Knee joint misalignment in exoskeletons for the lower extremities: Effects on user’s gait. IEEE Trans. Robot. 2015, 31, 978–987. [Google Scholar]
- Guzmán, C.H.; Blanco, A.; Brizuela, J.A.; Gómez, F.A. Robust control of a hip–joint rehabilitation robot. Biomed. Signal Process. Control 2017, 35, 100–109. [Google Scholar] [CrossRef]
- Rupp, R.; Schließmann, D.; Plewa, H.; Schuld, C.; Gerner, H.J.; Weidner, N.; Hofer, E.P.; Knestel, M. Safety and efficacy of at-home robotic locomotion therapy in individuals with chronic incomplete spinal cord injury: A prospective, pre-post intervention, proof-of-concept study. PLoS ONE 2015, 10, e0119167. [Google Scholar]
- Kuroda, Y.; Young, M.; Shoman, H.; Punnoose, A.; Norrish, A.R.; Khanduja, V. Advanced rehabilitation technology in orthopaedics—A narrative review. Int. Orthop. 2021, 45, 1933–1940. [Google Scholar] [CrossRef]
- Baiden, D.; Wilkening, A.; Ivlev, O. Safety and handling concept for assistive robotic devices with pneumatic rotary soft-actuators. In Proceedings of the 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, Hungary, 3–7 July 2011; pp. 754–759. [Google Scholar]
- Deaconescu, T.; Deaconescu, A. Pneumatic muscle actuated isokinetic equipment for the rehabilitation of patients with disabilities of the bearing joints. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 18–20 March 2009. [Google Scholar]
- Wang, Y.; Wang, K.; Zhang, Z.; Mo, Z. Control strategy and experimental research of a cable-driven lower limb rehabilitation robot. IEEE Access 2021, 235, 2468–2481. [Google Scholar]
- Rupp, R.; Plewa, H.; Hofer, E.P.; Knestel, M. MotionTherapy@Home—A robotic device for automated locomotion therapy at home. In Proceedings of the 2009 IEEE International Conference on Rehabilitation Robotics, Kyoto, Japan, 23–26 June 2009. [Google Scholar]
- Lee, K.; Wang, Y.; Zheng, C. TWISTER Hand: Underactuated Robotic Gripper Inspired by Origami Twisted Tower. IEEE Trans. Robot. 2020, 36, 488–500. [Google Scholar]
- Khullar, G.; Schmitz, A.; Hsu, C.; Sathe, P.; Funabashi, S.; Sugano, S. A Multi-Fingered Robot Hand with Remote Center of Motion Mechanisms for Covering Joints with Soft Skin. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; pp. 564–570. [Google Scholar]
- Smits, J.; Reynaerts, D.; Vander Poorten, E. Synthesis and methodology for optimal design of a parallel remote center of motion mechanism: Application to robotic eye surgery. Mech. Mach. Theory 2020, 151, 103896. [Google Scholar]
- Chen, G.; Wang, J.; Wang, H. A New Type of Planar Two Degree-of-Freedom Remote Center-of-Motion Mechanism Inspired by the Peaucellier–Lipkin Straight-Line Linkage. J. Mech. Des. 2018, 141, 015001. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evolut. Comput. 2021, 63, 100868. [Google Scholar]
- Langley, B.; Jones, A.; Board, T.; Greig, M. Modified conventional gait model vs. Six degrees of freedom model: A comparison of lower limb kinematics and associated error. Gait Posture 2021, 89, 1–6. [Google Scholar]
- Näf, M.B.; Junius, K.; Rossini, M.; Rodriguez-Guerrero, C.; Vanderborght, B.; Lefeber, D. Misalignment compensation for full human-exoskeleton kinematic compatibility: State of the art and evaluation. Appl. Mech. Rev. 2018, 70, 050802. [Google Scholar]
- China Standards GB/T 10000-1988; Human Dimensions of Chinese Adults. Administration of Technology Supervision, People’s Republic of China: Beijing, China, 1988; Volume GB 10000-88. (In Simplified Chinese).
- Feng, Y.; Tsai, T.-Y.; Li, J.-S.; Rubash, H.E.; Li, G.; Freiberg, A. In-vivo analysis of flexion axes of the knee: Femoral condylar motion during dynamic knee flexion. Clin. Biomech. 2016, 32, 102–107. [Google Scholar]
- Jarrassé, N.; Morel, G. Connecting a Human Limb to an Exoskeleton. IEEE Trans. Robot. 2012, 28, 697–709. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Xu, L.; Li, Y.; Cheng, G.; Shi, J.; Liu, J.; Chen, S. A multi-channel reinforcement learning framework for robotic mirror therapy. IEEE Robot. Autom. Lett. 2020, 5, 5385–5392. [Google Scholar] [CrossRef]



| Hip | Knee | Ankle | |
|---|---|---|---|
| Minimal angle (°) | 0 | 0 | −25 |
| Maximal angle (°) | 80 | 120 | 10 |
| Device | Size (L × W × H m3) | Weight (kg) | Complaint Type | Active DOF |
|---|---|---|---|---|
| Underactuated LLRR | 0.91 × 0.3 × 0.26 | 11.8 | Elastic strap and passive DOF | 3 |
| CLLRTR [34] | 2.3 × 1.2 × 0.8 | >50 | - | 3 |
| Lokomat [9] | 2.6 × 1.2 × 2.2 | >80 | Elastic strap | 4 |
| Hip Bot [29] | 2.0 × 1.0 × 0.7 | >50 | - | 5 |
| Motion Therapy [35] | 1.9 × 1.0 × 1.4 | 55 | Pneumatic muscles | 3 |
| iLeg [12] | 1.8 × 0.8 × 1.5 | >50 | Elastic strap | 3 |
| i | αi−1 | ai−1 | di | θi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | θH |
| 2 | 0 | L1 | 0 | θK |
| Point F | 0 | L2 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Guo, J.; Yao, Y.; Yin, H. Development of a Compliant Lower-Limb Rehabilitation Robot Using Underactuated Mechanism. Electronics 2023, 12, 3436. https://doi.org/10.3390/electronics12163436
Yang Y, Guo J, Yao Y, Yin H. Development of a Compliant Lower-Limb Rehabilitation Robot Using Underactuated Mechanism. Electronics. 2023; 12(16):3436. https://doi.org/10.3390/electronics12163436
Chicago/Turabian StyleYang, Yunlong, Junlong Guo, Yufeng Yao, and Hesheng Yin. 2023. "Development of a Compliant Lower-Limb Rehabilitation Robot Using Underactuated Mechanism" Electronics 12, no. 16: 3436. https://doi.org/10.3390/electronics12163436





