A Multiobjective Array Beamforming Method for Arrays of Flexible Shape
Abstract
1. Introduction
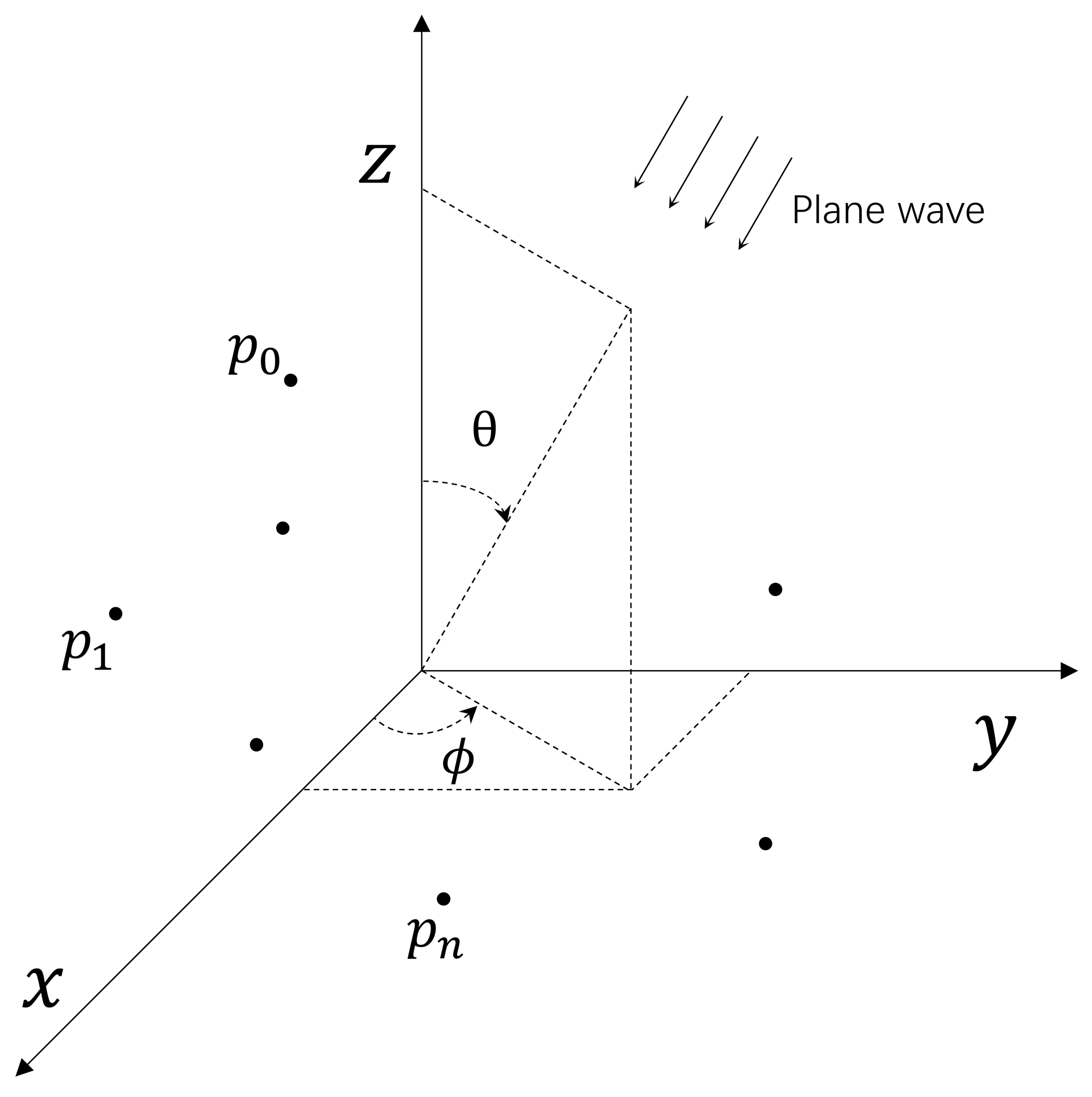
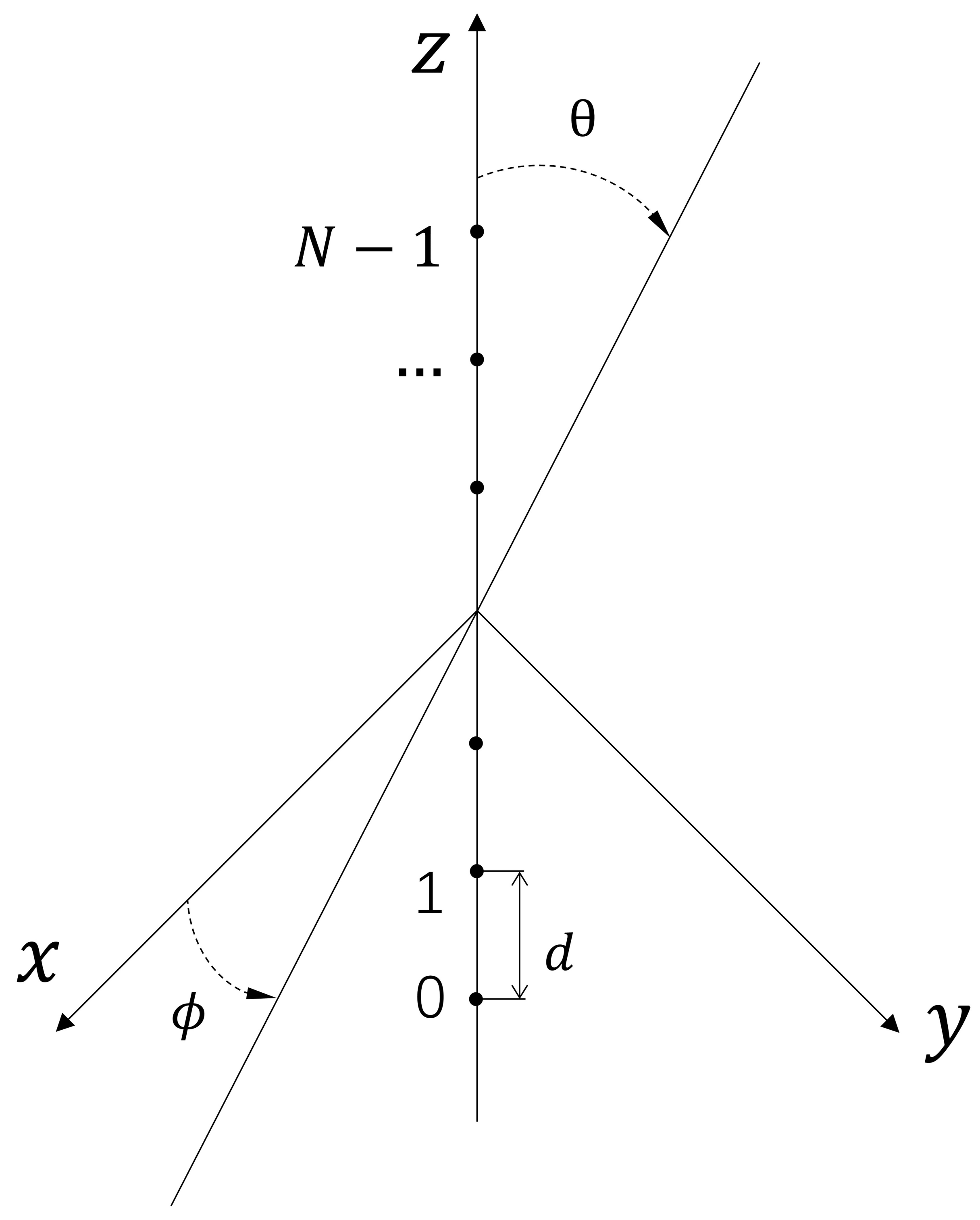
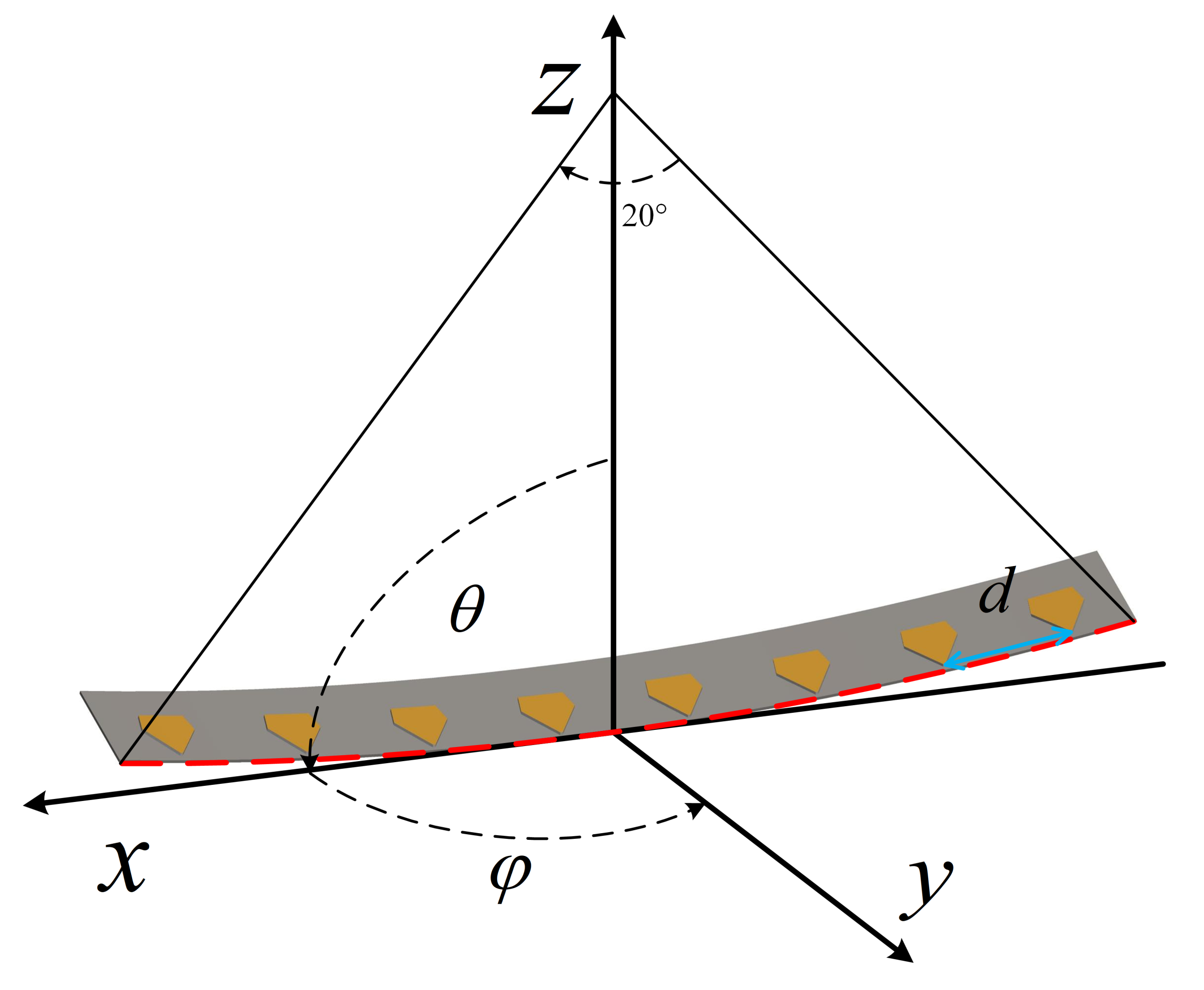
2. Array Beamforming
3. Beamforming Algorithms
3.1. Problem Description
3.2. Classical PSO
3.2.1. Particle Swarm Optimization
3.2.2. Parameters in PSO
- Inertia weight, w, which is linearly decreasing with the iteration number, is defined as,where is the maximum inertia weight and is the minimum, typically and ; t is current iteration number; denotes the maximum number of iterations designated in the algorithm.
- Two random parameters, and are uniformly distributed values in the interval .
- Swarm size, is also named population size or the number of particles, which is usually set between 70 and 100 to be safe. For higher-dimensional problems, PSO often demonstrates a better performance with a larger swarm size [36].
3.2.3. Position and Velocity Initialization
3.2.4. Position and Velocity Bounds
3.3. Modified PSO Algorithm
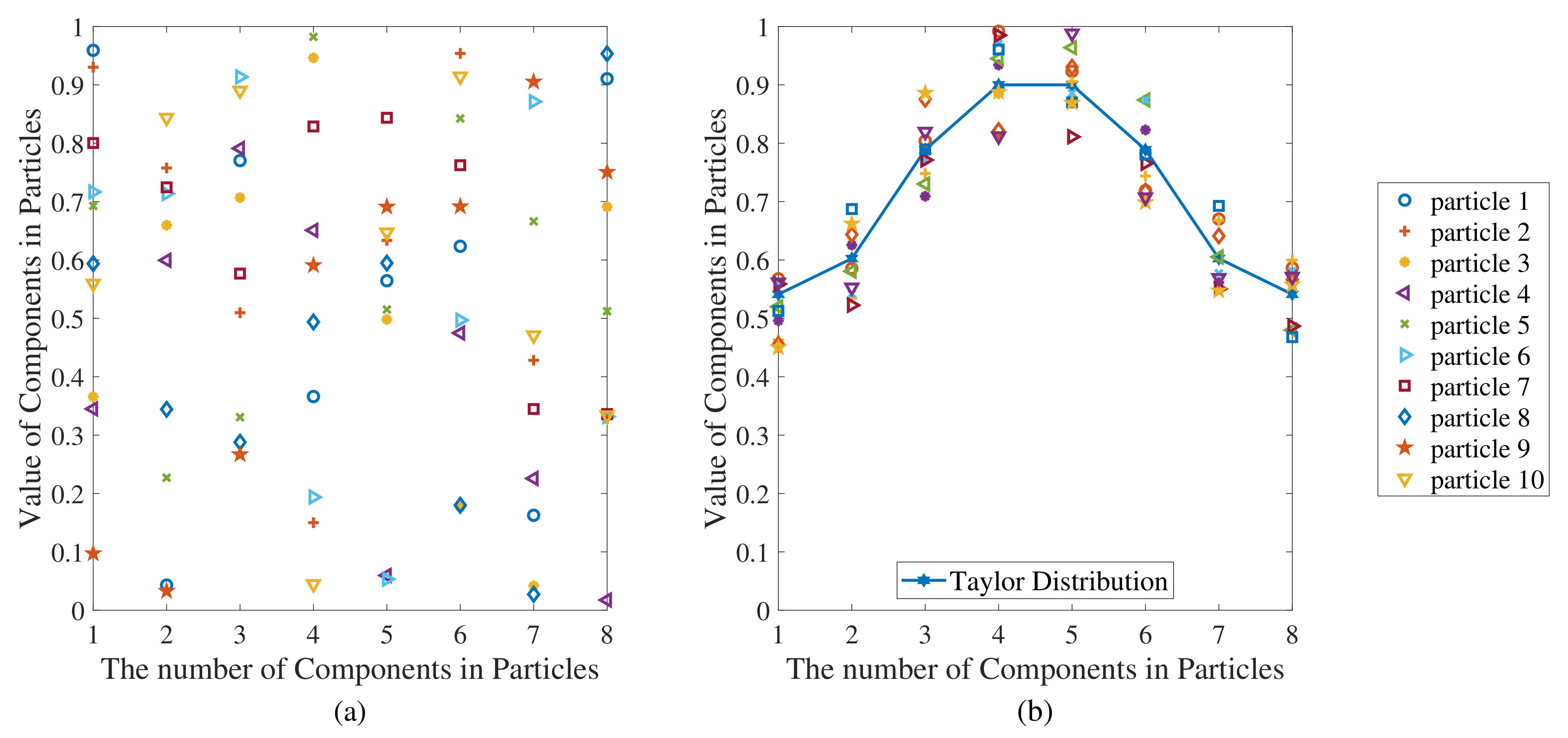
3.3.1. Establishing Initialization Strategy
- First, work out the weights following a Taylor distribution, the entries required comprise the total number of array elements and the desired peak sidelobe level;
- Obtain the initial particle positions by adding the Taylor weights with random values, and the calculation is described in detail in the following section;
- Assemble the particle swarm using the initial particle positions, ready to carry out the optimizing iterations.
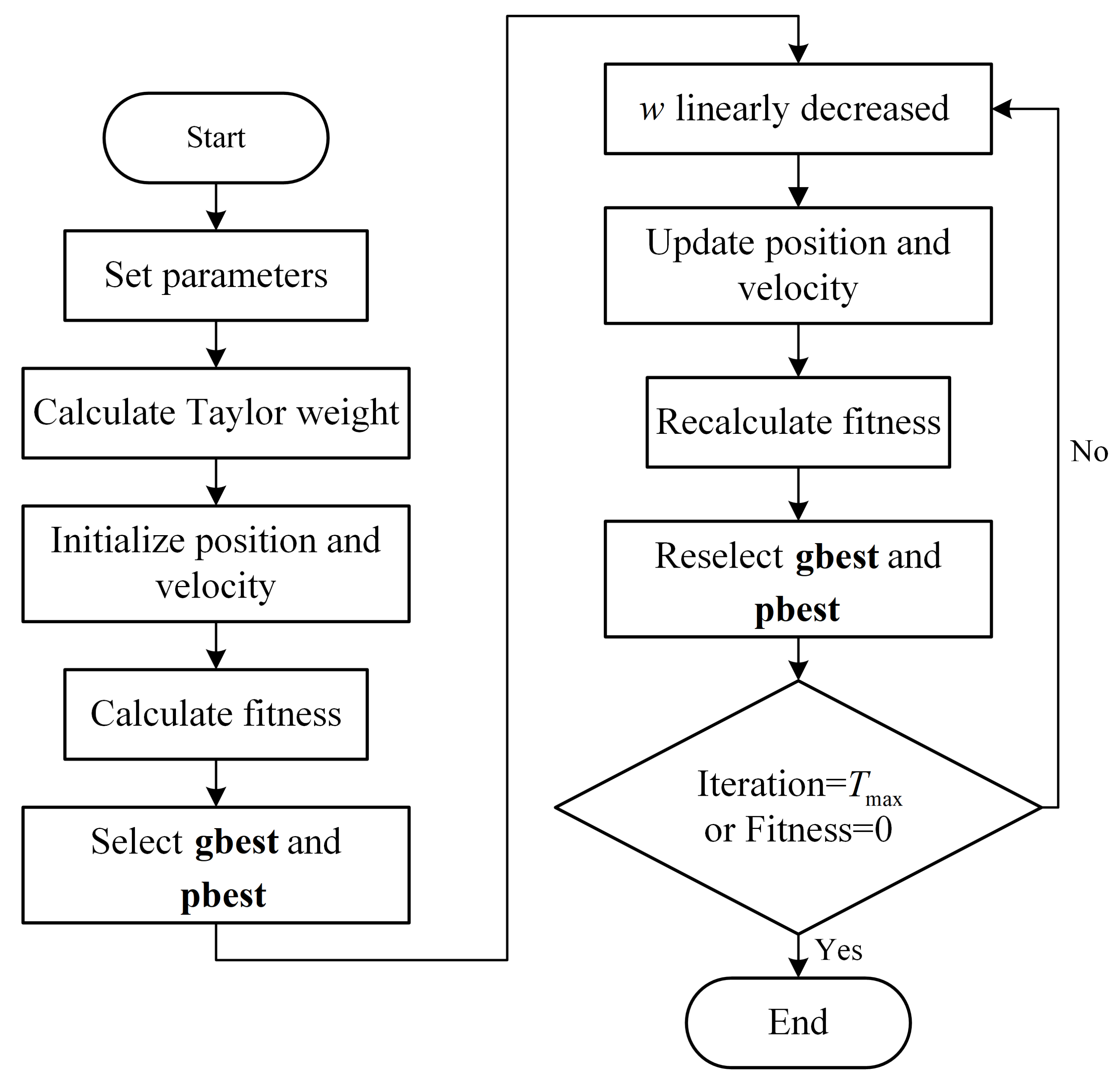
3.3.2. Procedure for the Modified PSO
| Algorithm 1: Modified PSO |
Input: array elements N, , , fitness function , position upper bound , position lower bound , Output: Optimized
|
3.4. Fitness Function Definition
4. Numerical Analysis
4.1. One Main Lobe
4.1.1. Single Null
4.1.2. Multiple Nulls
4.1.3. Broad Nulls
4.2. Multiple Beams
4.2.1. Two Main Lobes
4.2.2. Thirteen Main Lobes
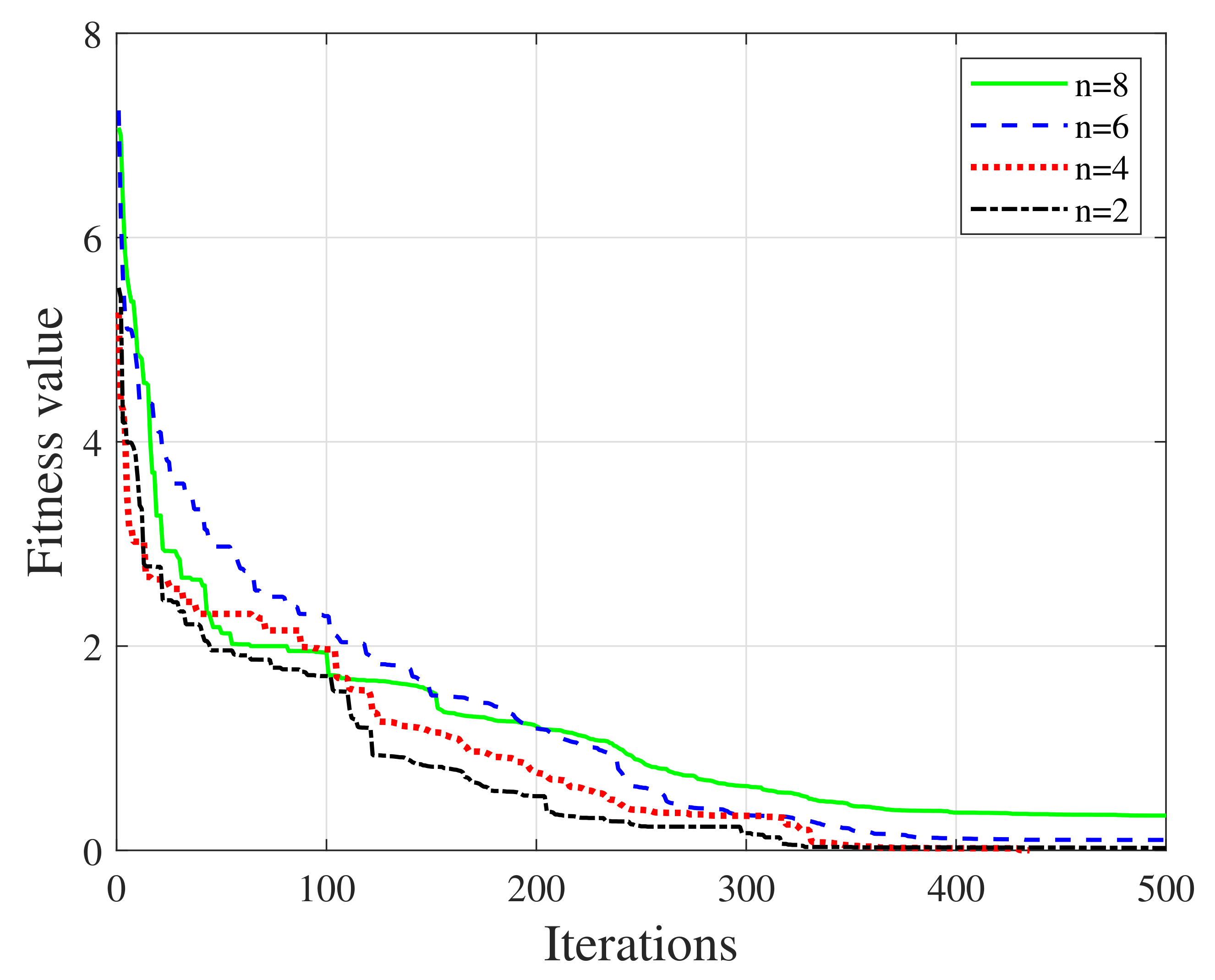
4.3. Modified PSO versus Classic PSO
4.4. Beamwidth
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, S.; Fang, Z.; Sun, G.; Liu, Y.; Qu, G.; Zhang, Y. Sidelobe Reductions of Antenna Arrays via an Improved Chicken Swarm Optimization Approach. IEEE Access 2020, 8, 37664–37683. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Mailloux, R.J.; Massa, A. Unconventional Phased Array Architectures and Design Methodologies—A Review. Proc. IEEE 2016, 104, 544–560. [Google Scholar] [CrossRef]
- Hong, W.; Jiang, Z.; Yu, C.; Zhou, J.; Chen, P.; Yu, Z.; Zhang, H.; Yang, B.; Pang, X.; Jiang, M.; et al. Multibeam Antenna Technologies for 5G Wireless Communications. IEEE Trans. Antennas Propag. 2017, 65, 6231–6249. [Google Scholar] [CrossRef]
- Ahmed, I.; Khammari, H.; Shahid, A.; Musa, A.; Kim, K.S.; De Poorter, E.; Moerman, I. A Survey on Hybrid Beamforming Techniques in 5G: Architecture and System Model Perspectives. IEEE Commun. Surv. Tutor. 2018, 20, 3060–3097. [Google Scholar] [CrossRef]
- Temiz, M.; Alsusa, E.; Baidas, M.W. Optimized Precoders for Massive MIMO OFDM Dual Radar-Communication Systems. IEEE Trans. Commun. 2021, 69, 4781–4794. [Google Scholar] [CrossRef]
- Han, S.; I, C.l.; Xu, Z.; Rowell, C. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G. IEEE Commun. Mag. 2015, 53, 186–194. [Google Scholar] [CrossRef]
- Molisch, A.F.; Ratnam, V.V.; Han, S.; Li, Z.; Nguyen, S.L.H.; Li, L.; Haneda, K. Hybrid Beamforming for Massive MIMO: A Survey. IEEE Commun. Mag. 2017, 55, 134–141. [Google Scholar] [CrossRef]
- Temiz, M.; Alsusa, E.; Danoon, L.; Zhang, Y. On the Impact of Antenna Array Geometry on Indoor Wideband Massive MIMO Networks. IEEE Trans. Antennas Propag. 2021, 69, 406–416. [Google Scholar] [CrossRef]
- Sohrabi, F.; Yu, W. Hybrid Digital and Analog Beamforming Design for Large-Scale Antenna Arrays. IEEE J. Sel. Top. Sign. Proces. 2016, 10, 501–513. [Google Scholar] [CrossRef]
- Temiz, M.; Alsusa, E.; Baidas, M.W. A Dual-Function Massive MIMO Uplink OFDM Communication and Radar Architecture. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 750–762. [Google Scholar] [CrossRef]
- Owoola, E.O.; Xia, K.; Wang, T.; Umar, A.; Akindele, R.G. Pattern Synthesis of Uniform and Sparse Linear Antenna Array Using Mayfly Algorithm. IEEE Access 2021, 9, 77954–77975. [Google Scholar] [CrossRef]
- Haupt, R. Phase-only adaptive nulling with a genetic algorithm. IEEE Trans. Antennas Propag. 1997, 45, 1009–1015. [Google Scholar] [CrossRef]
- Keizer, W.P.M.N. Amplitude-Only Low Sidelobe Synthesis for Large Thinned Circular Array Antennas. IEEE Trans. Antennas Propag. 2012, 60, 1157–1161. [Google Scholar] [CrossRef]
- Aslan, Y.; Puskely, J.; Roederer, A.; Yarovoy, A. Phase-Only Control of Peak Sidelobe Level and Pattern Nulls Using Iterative Phase Perturbations. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2081–2085. [Google Scholar] [CrossRef]
- Mahto, S.K.; Choubey, A. A Novel Hybrid IWO/WDO Algorithm for Interference Minimization of Uniformly Excited Linear Sparse Array by Position-Only Control. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 250–254. [Google Scholar] [CrossRef]
- Guney, K.; Onay, M. Amplitude-only pattern nulling of linear antenna arrays with the use of bees algorithm. Prog. Electromagn. Res.-Pier 2007, 70, 21–36. [Google Scholar] [CrossRef]
- Ni, G.; Song, Y.; Chen, J.; He, C.; Jin, R. Single-Channel LCMV-Based Adaptive Beamforming With Time-Modulated Array. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1881–1885. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Zardi, F.; Nayeri, P.; Rocca, P.; Haupt, R. Artificial intelligence for adaptive and reconfigurable antenna arrays: A review. IEEE Antennas Propag. Mag. 2020, 63, 28–38. [Google Scholar] [CrossRef]
- Chen, K.; He, Z.; Han, C. A modified real GA for the sparse linear array synthesis with multiple constraints. IEEE Trans. Antennas Propag. 2006, 54, 2169–2173. [Google Scholar] [CrossRef]
- Jin, N.; Rahmat-Samii, Y. Advances in particle swarm optimization for antenna designs: Real-number, binary, single-objective and multiobjective implementations. IEEE Trans. Antennas Propag. 2007, 55, 556–567. [Google Scholar] [CrossRef]
- Khodier, M.M.; Christodoulou, C.G. Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization. IEEE Trans. Antennas Propag. 2005, 53, 2674–2679. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chatterjee, S.; Poddar, D.R. Synthesis of linear array using Taylor distribution and Particle Swarm Optimisation. Int. J. Electron. 2015, 102, 514–528. [Google Scholar] [CrossRef]
- Rajo-Iglesias, E.; Quevedo-Teruel, O. Linear array synthesis using an ant-colony-optimization-based algorithm. IEEE Antennas Propag. Mag. 2007, 49, 70–79. [Google Scholar] [CrossRef]
- Saxena, P.; Kothari, A. Optimal pattern synthesis of linear antenna array using grey wolf optimization algorithm. Int. J. Antennas Propag. 2016, 2016, 1205970. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, X.; Ligthart, L.P.; Peng, S.; Xie, M. Synthesis of broadside linear aperiodic arrays with sidelobe suppression and null steering using whale optimization algorithm. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 347–350. [Google Scholar] [CrossRef]
- Hassan, R.; Cohanim, B.; De Weck, O.; Venter, G. A comparison of particle swarm optimization and the genetic algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; p. 1897. [Google Scholar]
- Ludwig Barbosa, V.; Schlosser, E.; Machado, R.; Heckler, M.V.T. Beamforming of a linear array applying pso algorithm with restrictive approach. J. Commun. Inf. Syst. 2016, 31, 118–126. [Google Scholar]
- Chang, J.C. A robust adaptive array beamformer using particle swarm optimization for space–time code division multiple access systems. Inf. Sci. 2014, 278, 174–186. [Google Scholar] [CrossRef]
- Azhiri, F.A.; Tazehkand, B.M.; Abdolee, R. PSO-based optimal beamforming in MmWave-NOMA systems with sparse antenna array. Soft Comput. 2022, 26, 10513–10526. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings: IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Eberhart; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Republic of Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Population size in particle swarm optimization. Swarm Evol. Comput. 2020, 58, 100718. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Engelbrecht, A. Particle swarm optimization: Velocity initialization. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Eberhart, R.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 84–88. [Google Scholar] [CrossRef]
- Cazzaniga, P.; Nobile, M.S.; Besozzi, D. Prediction of high-throughput protein-protein interactions based on protein sequence information. In Proceedings of the 2015 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Niagara Falls, ON, Canada, 12–15 August 2015. [Google Scholar]
- Taylor, T.T. Design of line-source antennas for narrow beamwidth and low side lobes. IRE Trans. Antennas Propag. 1955, 3, 16–28. [Google Scholar] [CrossRef]
- Goudos, S.K.; Moysiadou, V.; Samaras, T.; Siakavara, K.; Sahalos, J.N. Application of a Comprehensive Learning Particle Swarm Optimizer to Unequally Spaced Linear Array Synthesis With Sidelobe Level Suppression and Null Control. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 125–129. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.; Chen, Z.; Liang, S.; Wang, A.; Zhang, Y. Radiation Beam Pattern Synthesis of Concentric Circular Antenna Arrays Using Hybrid Approach Based on Cuckoo Search. IEEE Trans. Antennas Propag. 2018, 66, 4563–4576. [Google Scholar] [CrossRef]

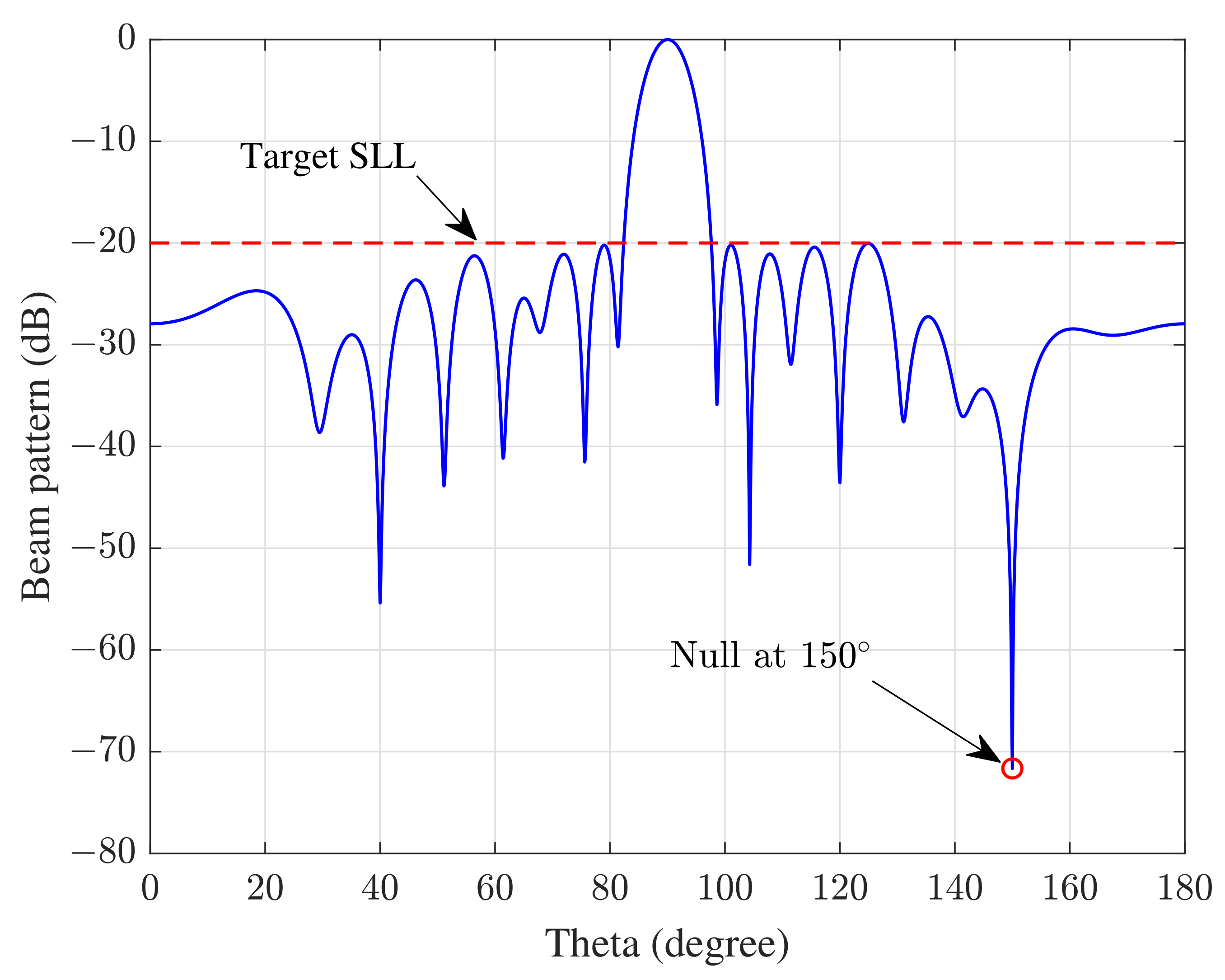
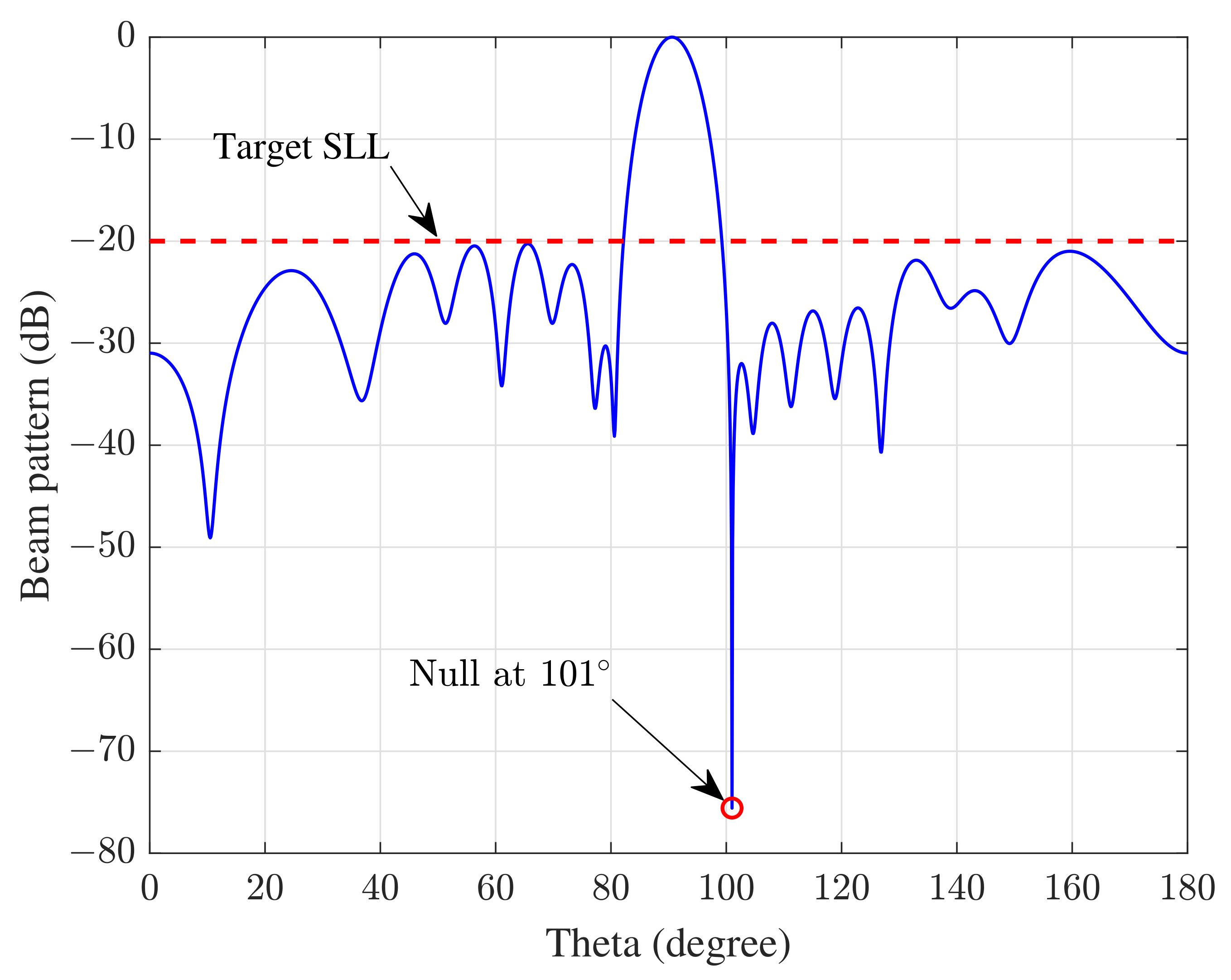
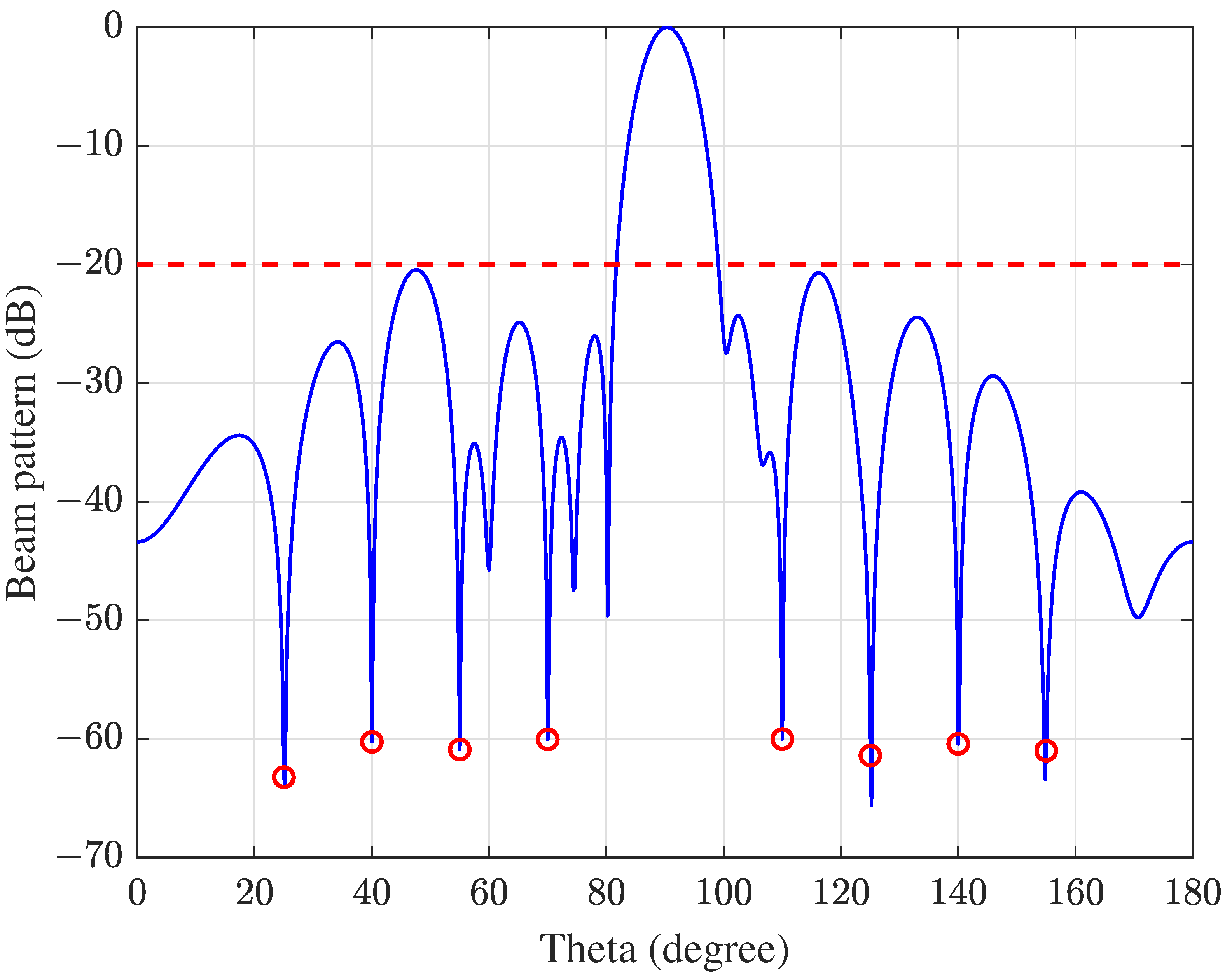
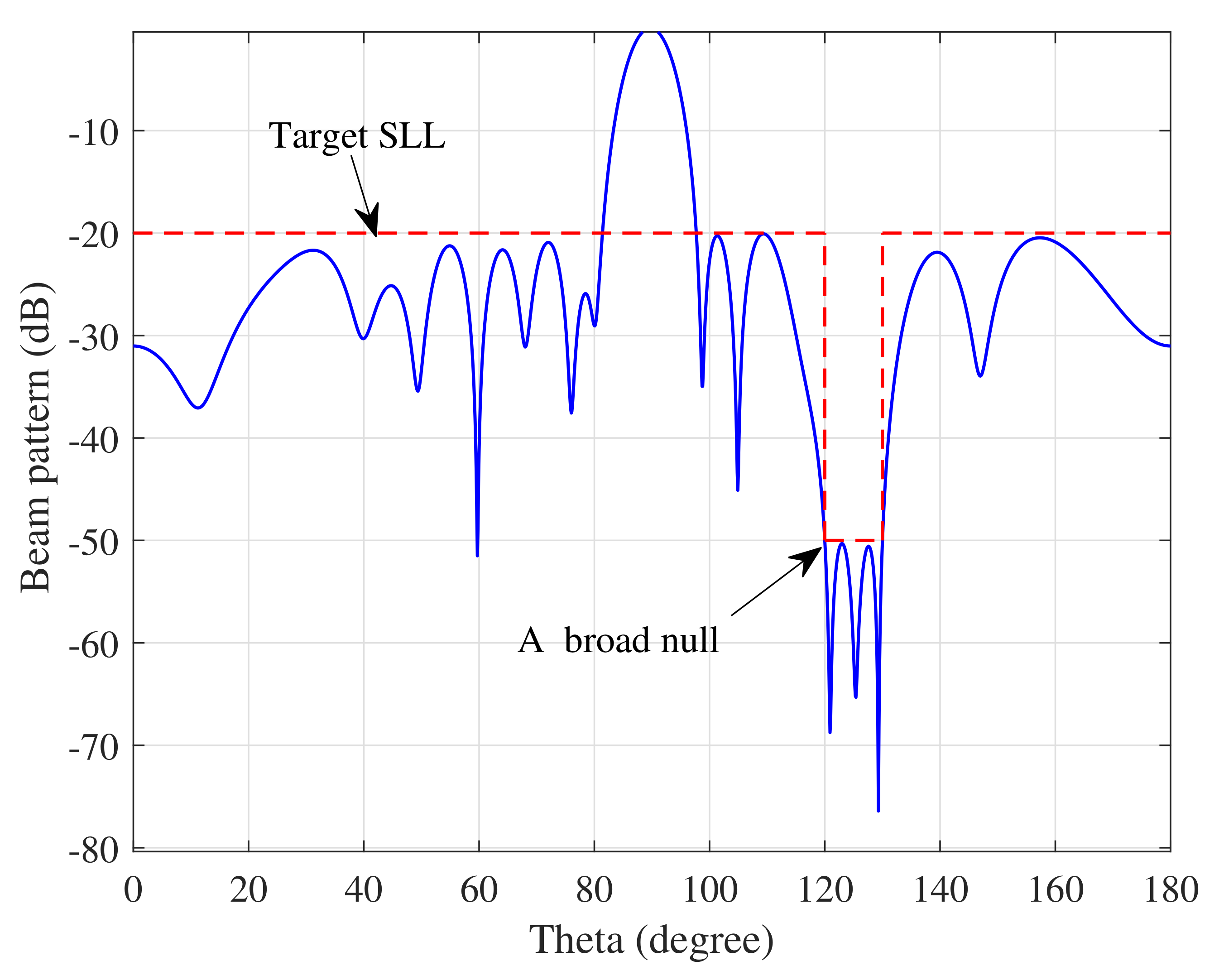
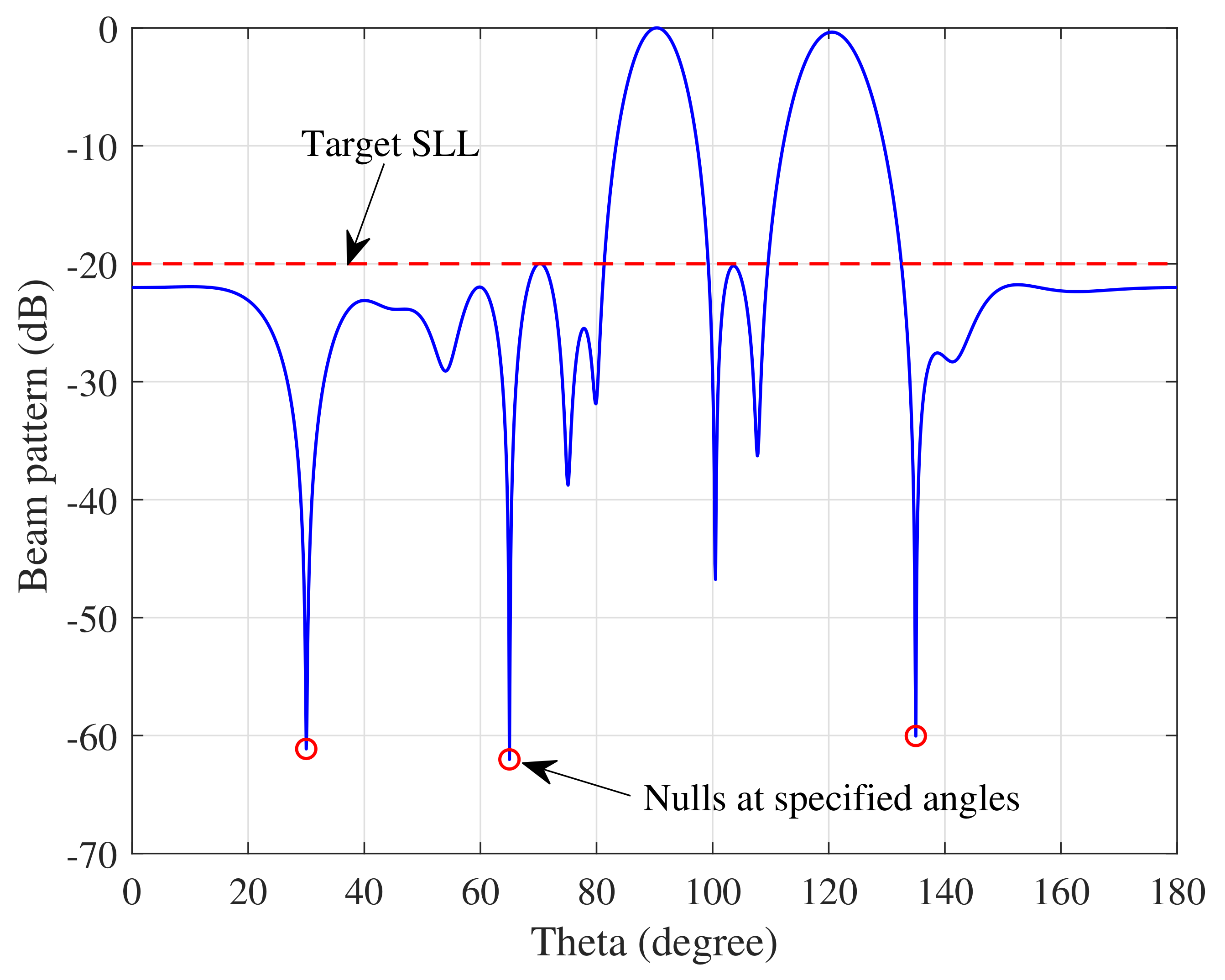
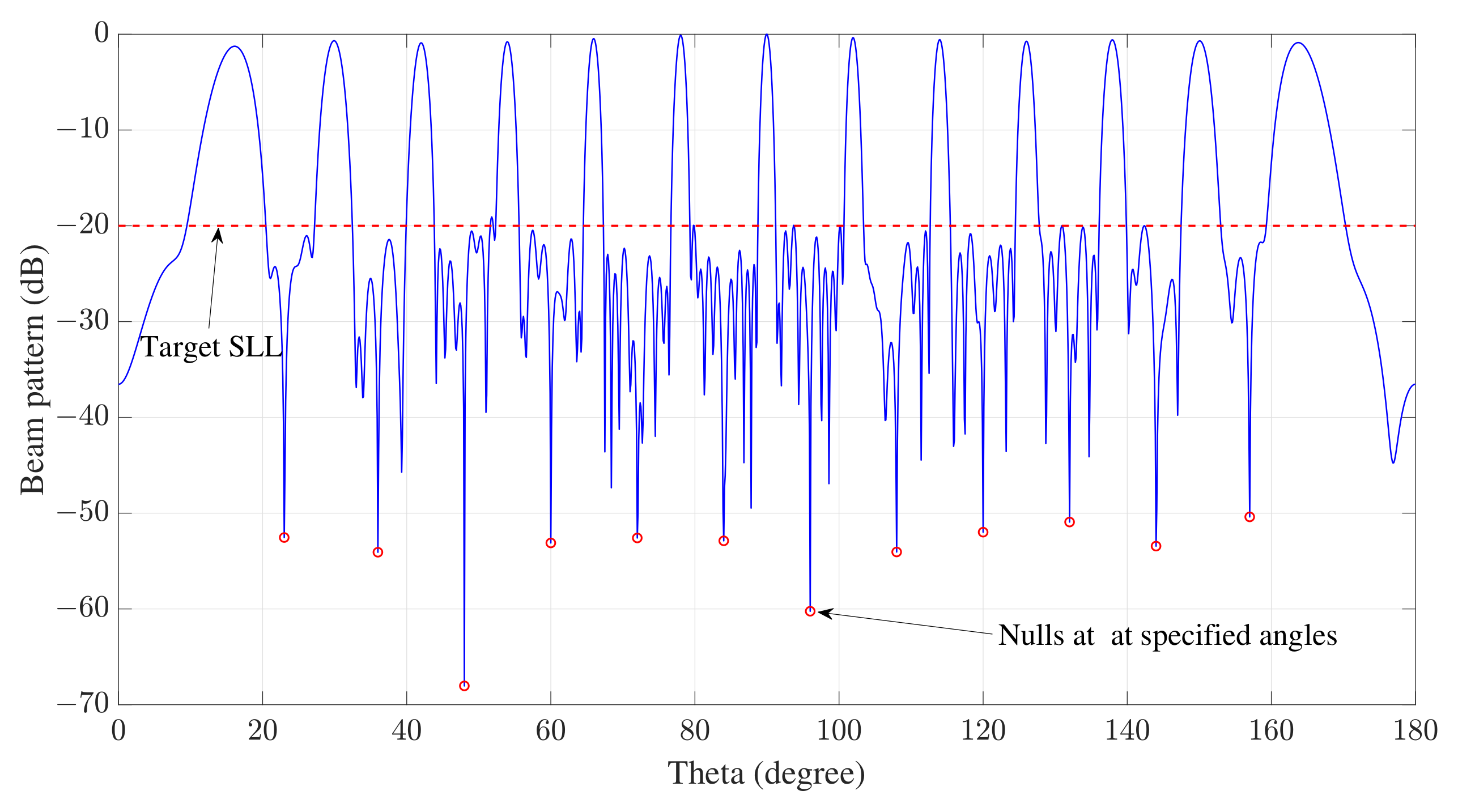


| Scenario | Array Elements | Null Number or Type | Main Lobe Number | DNDL | DSLL |
|---|---|---|---|---|---|
| 1 | 16 | 1 | 1 | −70 dB | −20 dB |
| 2 | 16 | 8 | 1 | −60 dB | −20 dB |
| 3 | 16 | range | 1 | −50 dB | −20 dB |
| 4 | 16 | 3 | 2 | −60 dB | −20 dB |
| 5 | 100 | 12 | 13 | −50 dB | −20 dB |
| Angle (Degree) | Depth (dB) | Angle (Degree) | Depth (dB) |
|---|---|---|---|
| 25 | −63.24 | 110 | −60.03 |
| 40 | −60.26 | 125 | −61.42 |
| 55 | −60.91 | 140 | −60.43 |
| 70 | −60.05 | 155 | −61.01 |
| Angle (Degree) | Depth (dB) | Angle (Degree) | Depth (dB) | Angle (Degree) | Depth (dB) |
|---|---|---|---|---|---|
| 23 | −50.09 | 72 | −50.49 | 120 | −50.35 |
| 36 | −49.98 | 84 | −50.04 | 132 | −50.94 |
| 48 | −58.07 | 96 | −53.02 | 144 | −50.00 |
| 60 | −55.53 | 108 | −52.61 | 157 | −49.99 |
| Scenario | Average Fitness Value | Average Execution Time (s) | |||
|---|---|---|---|---|---|
| Classic PSO | Modified PSO | Classic PSO | Modified PSO | ||
| 1 | 100 | 2.089 | 0 | 67.97 | 3.97 |
| 2 | 200 | 2.729 | 0.093 | 129.83 | 85.28 |
| 3 | 100 | 3.239 | 0.027 | 64.97 | 39.12 |
| 4 | 100 | 2.009 | 0.016 | 46.82 | 33.89 |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Modified PSO | Classic PSO | Modified PSO | Classic PSO | Modified PSO | Classic PSO | Modified PSO | Classic PSO | |
| E1 | 0.64 + j0.60 | 0.57 + j0.68 | 0.26 + j0.37 | 0.16 + j0.01 | 0.29 + j0.42 | 0.35 + j0.35 | 0.26 + j0.15 | 0.39 + j0.98 |
| E2 | 0.41 + j0.23 | 0.35 + j0.59 | 0.31 + j0.26 | 0.25 + j0.19 | 0.43 + j0.01 | 0.27 + j0.45 | 0.12 + j0.32 | 0.63 + j0.51 |
| E3 | 0.61 + j0.36 | 0.48 + j0.39 | 0.38 + j0.31 | 0.43 + j0.47 | 0.43 + j0.46 | 0.76 + j0.36 | 0.11 + j0.12 | 0.32 + j0.96 |
| E4 | 0.69 + j0.58 | 0.61 + j0.49 | 0.59 + j0.63 | 0.53 + j0.49 | 0.45 + j0.54 | 0.27 + j0.51 | 0.35 + j0.49 | 0.79 + j0.96 |
| E5 | 0.61 + j0.59 | 0.59 + j0.63 | 0.63 + j0.62 | 0.38 + j0.51 | 0.80 + j0.77 | 0.75 + j0.58 | 0.48 + j0.70 | 0.92 + j0.79 |
| E6 | 0.79 + j0.73 | 0.36 + j0.92 | 0.78 + j0.77 | 0.66 + j0.74 | 0.91 + j0.84 | 0.84 + j0.70 | 0.82 + j0.80 | 1.00 + j0.77 |
| E7 | 0.79 + j0.82 | 0.54 + j0.64 | 0.83 + j0.88 | 0.80 + j0.79 | 0.87 + j0.72 | 0.78 + j0.72 | 0.90 + j0.66 | 1.00 + j0.51 |
| E8 | 0.74 + j0.87 | 0.45 + j0.63 | 0.70 + j0.73 | 0.60 + j0.68 | 0.96 + j0.86 | 0.72 + j0.72 | 0.75 + j0.87 | 0.74 + j1.00 |
| E9 | 0.77 + j0.84 | 0.68 + j0.89 | 0.71 + j0.75 | 0.53 + j0.65 | 0.86 + j0.81 | 0.61 + j0.87 | 0.84 + j0.89 | 0.90 + j0.83 |
| E10 | 0.84 + j0.80 | 0.75 + j0.63 | 0.84 + j0.89 | 0.67 + j0.64 | 0.86 + j0.80 | 0.72 + j0.55 | 0.76 + j0.74 | 0.79 + j0.00 |
| E11 | 0.76 + j0.73 | 0.37 + j0.86 | 0.77 + j0.75 | 0.73 + j0.67 | 0.84 + j0.87 | 0.62 + j0.46 | 0.45 + j0.86 | 0.80 + j0.91 |
| E12 | 0.69 + j0.71 | 0.67 + j0.73 | 0.60 + j0.59 | 0.72 + j0.68 | 0.71 + j0.73 | 0.58 + j0.52 | 0.65 + j0.68 | 0.77 + j1.00 |
| E13 | 0.55 + j0.47 | 0.49 + j0.36 | 0.59 + j0.69 | 0.58 + j0.48 | 0.43 + j0.72 | 0.68 + j0.43 | 0.71 + j0.37 | 0.58 + j0.29 |
| E14 | 0.57 + j0.43 | 0.39 + j0.56 | 0.40 + j0.42 | 0.33 + j0.29 | 0.49 + j0.63 | 0.36 + j0.41 | 0.58 + j0.01 | 0.75 + j0.00 |
| E15 | 0.39 + j0.40 | 0.12 + j0.27 | 0.30 + j0.33 | 0.41 + j0.37 | 0.04 + j0.49 | 0.48 + j0.41 | 0.26 + j0.37 | 0.51 + j0.76 |
| E16 | 0.87 + j0.63 | 0.56 + j0.54 | 0.24 + j0.34 | 0.40 + j0.18 | 0.35 + j0.35 | 0.21 + j0.00 | 0.21 + j0.21 | 0.31 + j0.05 |
| Element Number | FNBW (Degree) | HPBW (Degree) | Target SLL (dB) | Target Null Angle (Degree) | Obtained SLL (dB) | Obtained NDL (dB) |
|---|---|---|---|---|---|---|
| 16 | 15.1 | 6.4 | −15 | 135 | −15.02 | −64.25 |
| 16 | 15.8 | 6.6 | −15 | 85 | −15.21 | −68.45 |
| 16 | 15.5 | 6.8 | −15 | 20 | −15.67 | −67.02 |
| 16 | 18.1 | 7.2 | −20 | 135 | −20.03 | −68.66 |
| 16 | 17.3 | 7.1 | −20 | 85 | −20.07 | −72.50 |
| 16 | 17.5 | 7.1 | −20 | 20 | −21.00 | −65.05 |
| 16 | 19.9 | 7.7 | −25 | 135 | −25.19 | −64.25 |
| 16 | 19.6 | 7.6 | −25 | 85 | −25.02 | −62.37 |
| 16 | 20.2 | 7.7 | −25 | 20 | −25.21 | −60.01 |
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | ||
|---|---|---|---|---|---|---|---|---|---|
| Analytic | Amplitude | 0.76 | 0.85 | 1.11 | 1.27 | 1.27 | 1.11 | 0.85 | 0.76 |
| Determination | Phase (rad) | 8.94 | 6.46 | 3.89 | 1.25 | −1.47 | −4.26 | −7.12 | −10.03 |
| Modified PSO | Amplitude | 0.63 | 0.69 | 0.75 | 0.75 | 0.68 | 0.60 | 0.42 | 0.42 |
| Phase (rad) | 8.98 | 6.46 | 4.02 | 1.34 | −1.36 | −3.81 | −6.80 | −9.87 |
| Ref. | Algorithm | Design | Function | Performance |
|---|---|---|---|---|
| [25] | GWO | Uniform linear array. | Optimal antenna positions and amplitudes for achieving minimum SLL along with null placement and suppression of the first side lobe. | Lower SLL was obtained; however, GWO is more computationally time-consuming than PSO. |
| [26] | WOA | Linear aperiodic array. | WOA was applied to the synthesis of uniformly excited broadside linear aperiodic arrays with sidelobe suppression and null steering under constraints on beamwidth requirements. | The average fitness result of WOA is slightly higher than that of CLPSO [42]. WOA has fewer iterations than CLPASO [42] and higher iterations than IWO-WDO [15]. |
| [11] | Mayfly Algorithm (MA) | Uniform and sparse linear array. | MA was applied for sidelobe suppression and null placement in the following two ways: by optimizing amplitudes while maintaining uniform spacing and by optimizing the antenna positions while assuming a uniform amplitude excitation. | MA is able to obtain a considerable improvement in peak SLL suppression and null control. However, MA requires a longer computation time and more parameters than PSO. |
| [15] | Hybrid invasive weed optimization and wind-driven optimization (IWO/WDO) | Linear sparse array. | The proposed algorithm is implemented to synthesize the uniformly excited linear sparse array pattern having an SLL and null control with a constraint on beamwidth by optimizing the element position only. | The Hybrid algorithm has improved performance in terms of null control, beamwidth control, and the rate of convergence. The proposed algorithm requires fewer iterations for convergence compared to PSO. |
| [43] | Cuckoo Search (CS) | Large scale concentric circular antenna array (CCAA). | A hybrid approach to suppress the SLL of large-scale CCAA is proposed, which includes an improved discrete cuckoo search algorithm (IDCSA) for thinning the CCAA and a cuckoo search-invasive weed algorithm (CSIWA) for further optimizing the thinned CCAA. | The proposed IDCSA and CSIWA can obtain a lower maximum SLL but do not have advantages in terms of processing time. |
| This work | Modified PSO | Uniform linear array. | A modified PSO algorithm is proposed for optimizing multiple objectives in radiation pattern, including SLL, null, and main lobe direction, by optimizing the excitation phase and amplitude of the elements. | The proposed algorithm has shown good performance compared to classical PSO in multiple design scenarios, and its effectiveness was verified with a curved array. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, C.; Zhang, Y.; Temiz, M.; El-Makadema, A. A Multiobjective Array Beamforming Method for Arrays of Flexible Shape. Electronics 2024, 13, 752. https://doi.org/10.3390/electronics13040752
Meng C, Zhang Y, Temiz M, El-Makadema A. A Multiobjective Array Beamforming Method for Arrays of Flexible Shape. Electronics. 2024; 13(4):752. https://doi.org/10.3390/electronics13040752
Chicago/Turabian StyleMeng, Chenfeng, Yongwei Zhang, Murat Temiz, and Ahmed El-Makadema. 2024. "A Multiobjective Array Beamforming Method for Arrays of Flexible Shape" Electronics 13, no. 4: 752. https://doi.org/10.3390/electronics13040752
APA StyleMeng, C., Zhang, Y., Temiz, M., & El-Makadema, A. (2024). A Multiobjective Array Beamforming Method for Arrays of Flexible Shape. Electronics, 13(4), 752. https://doi.org/10.3390/electronics13040752







