Effect of Edge Roughness on Static Characteristics of Graphene Nanoribbon Field Effect Transistor

Abstract

In this paper, we present a physics-based analytical model of GNR FET, which allows for the evaluation of GNR FET performance including the effects of line-edge roughness as its practical specific non-ideality. The line-edge roughness is modeled in edge-enhanced band-to-band-tunneling and localization regimes, and then verified for various roughness amplitudes. Corresponding to these two regimes, the off-current is initially increased, then decreased; while, on the other hand, the on-current is continuously decreased by increasing the roughness amplitude.

1. Introduction

The exponential trend in scaling MOSFET has satisfied Moore’s law for decades, leading to denser chips with more functionality, a lower price per chip, faster switching and lower power consumption. However, the International Technology Roadmap for Semiconductors (ITRS) [1] has predicted the demise of silicon-CMOS technology due to the fundamental limits of CMOS FETs, and has put forward alternate channel materials to silicon such as carbon nanotubes and newly discovered graphene [2]. Graphene is one atomic layer of carbon sheet in a honeycomb lattice, which can outperform state-of-the-art silicon in many applications [2,3] due to its excellent electronic properties. The carrier transport in graphene is similar to the transport of massless particles since 2D electron gas in graphene [4] provides both high carrier velocity and high carrier concentration, resulting in large carrier mobility and, consequently, faster switching capability [5]. Despite the fascinating properties of graphene, it is a semimetal with an overlapping zero bandgap and is not satisfactory for digital applications [6]. The quantum confinement of graphene sheet in the form of one-dimensional (1D) strips with a very narrow width known as graphene nanoribbon (GNR) provides the energy gap of several hundred meV required for FET operations in digital applications [7,8]. As the fabrication technology of GNR FETs in this structure is still in an early stage, performance evaluation of futuristic graphene-based circuits requires a SPICE-compatible model. The state-of-the-art patterning technique is far from achieving atomic-scale precision, and GNRs with perfect smooth edges cannot be fabricated; such that, line-edge roughness may play an important role in the production of narrow GNRs for channel material of GNR FETs. The edge roughness enhances the edge scattering and generates edge states in the bandgap, which can significantly enhance the leakage current and reduce the drive current. Thus, modeling edge roughness is very useful to examine the effect of process variation on circuit performance of GNR FET. The dispersion of the electrical characteristics due to random edge defects in realistic nanoribbons can be precisely evaluated by statistical analysis at the device-level, based on the atomistic quantum transport simulations of large ensembles of randomly-generated GNRs [9]. However, the device-level analysis requires extensive computational time; therefore, the same statistical approach cannot be used for circuit-level simulations.

The ideal smooth-edge GNR FETs give an estimation of the upper bound performance, however, the line-edge roughness needs to be considered for practical GNR FETs which deteriorate their performance. A semi-analytical model for GNR FET with perfectly smooth edges was developed in [10], which involved numerical integrations; thereby, it cannot be used for circuit simulation. In [11], a circuit model was implemented based on lookup table techniques to use the results of device-level quantum transport simulations for circuit simulations. However, with a single change in a design parameter, the intensive device-level simulations need to be repeated to rebuild the model accordingly, which makes it inappropriate for evaluating the optimized design parameters of GNR FET circuits. A SPICE-compatible model of GNR FET including the edge roughness is presented in [12]. In this model, the effect of rough edges on the increasing leakage current of GNR (N,0) is considered by effective bandgap due to the bandgap of GNR (N-1,0), while the real GNRs with rough edges are composed of all neighboring GNRs. Also, the effect of rough edges on decreasing on-current was modeled by a fitting equation regardless of the physical scattering mechanisms in a GNR channel. In addition, this model cannot capture the effect of large line-edge roughness on localization of carriers, which tends to reduce both off- and on-currents of GNR FETs. It has been shown both experimentally [13] and theoretically [14] that strong localization can appear in single layer GNRs for high line-edge roughness.

In this work, we develop a physics-based analytical model for circuit simulation of GNR FETs. The band-to-band-tunneling (BTBT) from drain to channel regions can be important for small bandgap GNRs, which has been modeled by a current source in parallel with another current source for the thermionic current. The line-edge roughness in GNRs is modeled using an exponential autocorrelation function. The model incorporates the effect of edge states on the initial increase of BTBT and high edge scattering of carriers in a localization regime. The device-level simulation is performed to evaluate the static performance of GNR FETs in edge-enhanced BTBT and localization regimes. The results of our analytical model are verified by numerical results from accurate quantum transport simulations based on non-equilibrium Green function (NEGF) formalism. The organization of this paper is as follows: In Section 2, we describe the structure of GNR FETs in all-graphene architecture; Section 3 presents the model equations and equivalent circuit model of GNR FET for the circuit simulation in SPICE. Model validation is described in Section 4 and Section 5; finally, the last section draws summarizing conclusions.

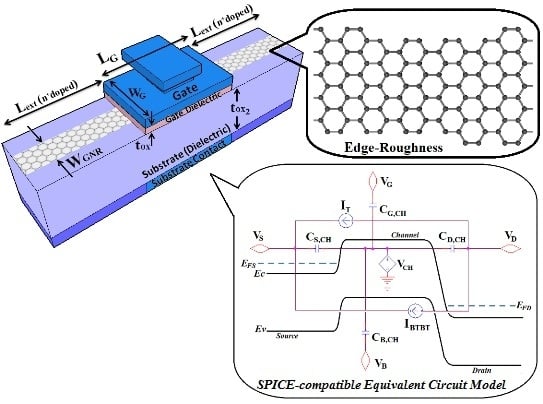
2. GNR FET Structure

Figure 1 shows the 3D view of a GNR FET, where the ribbon of the armchair chirality GNR is the channel material in a MOSFET-like structure. This structure is expected to demonstrate a higher I_ON/I_OFF ratio, outperforming the GNR FET with Schottky barriers in logic applications [15]. The intrinsic GNR channel (L_CH) has the same length underneath as the gate contact (L_G), while its width (W_G) is extended equally from each side of the GNR channel. The width of the intrinsic GNR is $W_{GNR}=(N+1)\sqrt{3}{a}_{cc}/2$, where $a_{cc}$ is the carbon-carbon bonding length and N is the number of dimer lines for the armchair GNR (N,0). The symmetric regions of the GNR channel between the gate and contacts with the length of $L_{RES}$ are doped with the n-type dopants concentration of $f_{dop}$ per carbon atom as the source and drain reservoirs. The metallic source and drain electrodes are omitted in the model as the two doped regions of GNRs can be directly connected to the GNR interconnect in all-graphene architecture [16], avoiding the series resistance of metal-to-graphene contacts. Aluminum nitride (AlN) insulator layers with a relative dielectric permittivity of $\mathsf{\kappa }=9$ are assumed. The large-scale and cost-effective production of thin AlN dielectric layers with good reproducibility and uniformity [17,18] can result in small equivalent oxide thickness (EOT) while reducing phonon scattering in epitaxial graphene, enabling near ballistic carrier transport in a short channel GNR FET [19].

3. GNR FET Model

Figure 2a shows the energy band diagram and the corresponding components in the equivalent circuit model of the GNR FET. The model contains four capacitors, C_G,CH, C_S,CH, C_B,CH, C_D,CH, to account for the electrostatic coupling of the channel to the potentials at gate, source, substrate and drain electrodes, respectively. Two current sources model the thermal current flowing through the channel and band-to-band-tunneling (BTBT) current from drain to channel regions. These current sources account for the DC behavior while a voltage-controlled voltage source (V_CH) in the model accounts for the charging and discharging the GNR channel, thereby the transient AC behavior of GNR FETs.

3.1. Computing GNR Subbands

The minimum energy ($E_b$) and effective mass ($m_b^{*}$) of subbands for different armchair GNRs need to be obtained for transport equations. Tight-binding (TB) calculation can be employed based on the nearest neighbor orthogonal p_z orbitals as basis functions equal to the number of atoms in a desired unit cell in the transverse direction [20]. The nearest neighbor hopping energy for the atoms not located at the edge is t = −2.7 eV, while it is assumed $1.12t$ for the pairs of carbon atoms along the edges of the GNR, to take into account the edge bond relaxation due to the lattice termination and occupation of hydrogen atoms at the edges [21]. Further detail about the TB calculation and the effective mass extraction using non-parabolic effective mass model can be followed in [22].

The bandgap is increased by decreasing the GNR width due to the quantum confinement of carriers in one dimension while it increases the effective mass due to the degradation of the band linearity near the Dirac point. For narrow armchair GNRs, removing or adding one edge atom along the nanoribbon can significantly change the bandgap energy and effective mass of armchair GNRs. Two thirds of armchair GNRs, GNR (3p+1,0) and GNR (3p,0) have proper bandgaps, large enough for replacing silicon as a channel material. The third subclass, GNR (3p+2,0), has a very small bandgap. Although, the bandgap of GNR (3p+1,0) is slightly larger than GNR (3p,0), both GNR families follow the same trends of decreasing bandgaps by increasing the GNR widths. Thus, we have omitted one semiconducting family in our studies to prevent the confusion resulted from chirality dependence of bandgap. Also, we have omitted the incorporation of upper subbands in the model as the first three subbands can accurately describe the carrier transport of GNR FETs, considering the bias voltages and the position of minimum conduction subbands in energy.

3.2. Finding Channel Surface Potential

The key parameter for evaluating GNR FET current is to find the variation of channel surface potential (${\mathsf{\Psi }}_{ch}$) in response to the variation of gate and source/drain voltages. For a channel material with infinite density of states (DOS), the channel potential can be obtained by geometrical transient capacitance network, such that the channel potential is dominantly controlled by the voltage bias at electrodes, especially gate voltage for long channel devices. For a semiconducting channel with a finite DOS, the channel surface potential changes with the gate bias at a rate $\Delta {\mathsf{\Psi }}_{ch}/\Delta V_G<1$. This promotes the device operation close to quantum capacitance limit (QCL) [23]. GNR has very small DOS due to the atomically thin channel in vertical direction and quantum mechanical confinement in the transverse direction. Thus, evaluating the channel surface potential is very important, which can be modeled using the charge conservation equations by series implementation of two voltage-controlled current sources in SPICE simulation as shown in Figure 2b [24]. This forces the two currents to be equal in magnitude. In other words, the charge induced by the capacitances networks connected to the contacts (Q_CAP) has to be equal to the charge capacity of the GNR channel limited by its DOS. This implementation results in the automatic calculation of the channel voltage (V_CH) and the corresponding channel surface potential (${\mathsf{\Psi }}_{ch}$).

3.2.1. Computing Channel Charge

In n-type GNR FETs, the hole concentration in the channel is suppressed due to the n-doped drain and source reservoirs, thereby, the electron density of b^th subband in GNR channel ($n_b$) can be obtained considering DOS of GNR ($D_b(E)$) from the carrier density relationship as follows [10]:

$$n_b={\displaystyle \underset{0}{\overset{\infty }{\int }}f(E)D_b(E)dE}$$

(1)

$$D_b(E)=\frac{2(E_b+E)}{\mathsf{\pi }\hslash }\sqrt{\frac{m_b^{*}}{E_{b}E(E+2E_b)}}$$

(2)

where $\hslash$ is the reduced Planck constant and $f(E)$ is the Fermi-Dirac distribution function. In order to solve the integral in Equation (1) and obtain an analytical equation, the Fermi-Dirac distribution function can be approximated by Boltzmann distribution $f(E)=\exp ((E_F-E)/kT)$ when the Fermi level is more than 3 kT away from the subband energy [10]. As the bandgap of GNRs can be very small, the assumption is inaccurate in many bias conditions of the GNR FETs. In order to accurately evaluate the electron density in GNRs, $f(E)$ needs to be approximated depending on the relative location of Fermi levels at the terminals to conduction band energy ($E_{FC}^b=E_{F,i}-E_C^b$). Equation (3) provides a smooth transition between two approximations: (1) exponential carrier concentration ($n_b^{\exp }$) when the Fermi level is near the conduction band (high DOS, $E_{FC}\cong 0$); and (2) step carrier concentration ($n_b^{step}$) when the Fermi level is 3 kT away from the subband energy ($E_{FC}>3\text{KT}$) [12].

$$n_b(E_{FC})=w\times n_b^{\exp }(E_{FC}^b)+(1-w)\times n_b^{step}(E_{FC}^b)$$

(3)

$$n_b^{\exp }(E_{FC})=\frac{\sqrt{m_b^{*}{\mathsf{\alpha }}^3}\left(1+2E_b/\mathsf{\alpha }\right)}{2\mathsf{\pi }\hslash E_b}\exp (E_{FC}/\mathsf{\alpha })$$

(4)

$$n_b^{step}(E_{FC})=(2\sqrt{m_b^{*}}/\mathsf{\pi }\hslash )\times \sqrt{\max ((E_{FC}(E_{FC}+2E_b)/E_b),0)}$$

(5)

where $w=1/[1+\exp (3(E_{FC}-\text{kT})/\text{kT})]$ is the relative weight of the two approximations and $\mathsf{\alpha }=3\text{kT}/\ln \left[f(E_{FC})\times (1+\exp ((3\text{kT}-E_{FC})/\text{kT}))\right]$. Thus, the total electron density in the GNR channel can be obtained by summation over the carrier density of subbands as follows:

$$Q_{GNR}^n=-\frac{q{L}_{CH}}{2}{\displaystyle \sum _b[n_b(E-(E_{FS}-E_C^b))+n_b(E-(E_{FD}-E_C^b)))]}$$

(6)

where q is an electron charge; $E_C^b=E_b-{\mathsf{\Psi }}_{ch}$ is the conduction band energy; $E_{FS}=E_F-q{V}_S$ and $E_{FD}=E_F-q{V}_D$ are the Fermi levels corresponding to the voltages at source and drain electrodes, respectively. The equilibrium Fermi level of doped reservoirs ($E_F$) sets both $E_{FS}$ and $E_{FD}$ above the conduction band of source and drain regions. We only consider n-type GNR FET throughout this paper, though similar analysis can be applied to p-type GNR FET. In the same scenario, the energy difference between the valence band and the Fermi-level at the terminals, $E_{VF}^b=E_V^b-E_{F,i}$ and the polarity of the terminal voltage needs only to be changed due to the symmetry of the conduction and valence subbands in GNRs.

3.2.2. Computing Transient Capacitance Charge

The induced charge by capacitance network can be calculated as follows [25]:

$$Q_{CAP}^n={\displaystyle \sum _{i=G,B}{C}_{i,CH}\times (V_i-V_{FB,i}-q{\mathsf{\Psi }}_{ch})}$$

(7)

where V_FB is the flat-band voltage due to the work function difference between metal and graphene. The geometrical capacitances, $C_{G,CH}$ and $C_{B,CH}$ model the electrostatic coupling between the GNR channel and two electrodes of the gate and the substrate. As the gate width is larger than the GNR width and the oxide thickness, these capacitances can be modeled by the analytical equation of micro-strip lines as follows [26]:

$$C_{i,CH}=\mathsf{\beta }{L}_G\frac{5.55\times {10}^{-11}{\mathsf{\epsilon }}_r}{\ln [5.98t_{ox}/(0.8W_{GNR}+t_{GNR})]}$$

(8)

where $t_{GNR}\cong 0$ is the GNR thickness, $t_{ox}$ is the dielectric thickness, and $\mathsf{\beta }={(1+1.5t_{ox}/W_G)}^{-1}$ is a correction term for a case when the gate width is not much larger than the oxide thickness [27].

3.3. Current Modeling

Given the surface potential (${\mathsf{\Psi }}_{ch}$), both the DC and AC behaviors of GNR FETs can be incorporated in the current calculation. Figure 3a shows the energy position resolved local density of states (LDOS) of a typical GNR FET, which is numerically simulated by NEGF formalism [22]. The bandgap with quite low local density of states, potential barrier of the channel together with the source and drain regions, can be easily identified. The quantum interference pattern due to incident and reflected electron waves in the generated quantum well in the valence band of the channel is also apparent. As can be seen from the LDOS of GNR FET, the carrier transport can be associated with three mechanisms: (1) thermionic current (I_T) for electrons with energies above the channel potential barrier; (2) direct source-to-drain tunneling current through channel potential barrier and (3) band-to-band tunneling, (I_BTBT) between hole states in the source and electron states in the drain. While the study on the direct source-to-drain tunneling [28] shows that its contribution in leakage current can be dominant well below 10 nm channel length, the band-to-band tunneling can be comparable to thermionic current at subthreshold regions of GNR FETs, depending on the bias condition and the bandgap of GNR channel. We will show that incorporating the two mechanisms of the thermionic current and the band-to-band tunneling current using two current sources in the equivalent model of GNR FET can result in sufficiently accurate I-V characteristics of GNR FET for the channel length larger than 10 nm.

3.3.1. Computing Thermionic Current

The thermionic current can be computed using the Landauer-Buttiker formalism [29], in which the probability of the electrons being injected onto the conduction band from the source side is subtracted from the probability of the electrons being injected onto the conduction band from the drain side as follows:

$$I_T=\frac{2q}{h}{\displaystyle \sum _b{\displaystyle \underset{0}{\overset{\infty }{\int }}T(E)[f(E-(E_{FS}-E_C^b))-f(E-(E_{FD}-E_C^b))]dE}}$$

(9)

where $h$ is Planck constant. The integral in the above expression can be evaluated analytically considering the Fermi-Dirac integral of order 0, which results in the current at the ballistic limits as follows:

$$I_T=\frac{2q}{h}{k}_{B}T{\displaystyle \sum _b[\ln (1+\exp ((E_{FS}-E_C^b)/kT))-\ln (1+\exp ((E_{FD}-E_C^b)/kT))]}$$

(10)

3.3.2. Evaluating Band-to-Band-Tunneling Current and Charge

While the thermionic current strongly dominates the carriers transport at very high drain voltages, the band-to-band-tunneling (BTBT) can be comparable to the thermionic current in subthreshold region (small V_GS) and sufficiently high V_DS as shown in Figure 3b. As the wider GNRs can have very small bandgaps and high effective masses, the BTBT can significantly increase leakage current of GNR FETs. Band-to-band-tunneling occurs when the confined states in the valence band of the channel align with the occupied states in the drain. This can happen when the conduction band at the drain side is below the valance band at channel side ($V_{CH,D}>2E_b$) and empty states were sufficiently available at the drain side for the electrons that tunnel from the channel region. Assuming ballistic transport for the tunneling process, the BTBT current can be approximated by the maximum possible tunneling current integrating from the conduction band at the drain side up to the valance band at the source side times the BTBT tunneling probability as follows [24]:

$$I_{BTBT}=\frac{2q}{h}{k}_{B}T{\displaystyle \sum _b[T_{BTBT}\ln (\frac{1+\exp ((q{V}_{CH,D}-E_b-E_F)/k_{B}T)}{1+\exp ((E_b-E_F)/k_{B}T)})}\times \frac{\max (q{V}_{CH,D}-2E_b,0)}{q{V}_{CH,D}-2E_b}]$$

(11)

where $E_F$ is the Fermi level of the doped regions at the drain side of GNR FET. $T_{BTBT}$ is the Wentzel–Kramers–Brillouin-like transmission coefficient that can be calculated following the work of Kane [30] as follows:

$$T_{BTBT}\approx \frac{{\mathsf{\pi }}^2}{9}\exp (-\frac{\mathsf{\pi }{m}_b^{*}{}^{(1/2)}{({\mathsf{\eta }}_{b}2E_b)}^{3/2}}{2^{3/2}q\hslash F})$$

(12)

In Equation (12), $F=(V_{CH,D}+(E_F-{\mathsf{\Psi }}_{ch})/q)/l_{relax}$ is the electrical field triggering the tunneling process through the junction at the drain side of the GNR channel when the potential across the drain-channel junction is $V_{CH,D}$. ${\mathsf{\eta }}_b$ models the bandgap narrowing effect under a high electrical field [31], which is set to 0.5 corresponding to that of carbon nanotube in [24]. Basically, a graphene nanoribbon channel is an unfolded lattice structure of carbon nanotube with the same one-dimensional channel. As such, it is an appropriate assumption that both have the same bandgap narrowing effects under a high electrical field. $l_{relax}$ is the relaxation length of potential drop, which has been extracted with the procedure explained in Section 3.5.

Although the thermionic emission of holes into the channel is negligible for n-type GNR FET, the band-to-band-tunneling significantly increases the accumulation of holes in the channel, especially at a high V_DS. As such, both the charges of the GNR channel (Equation (6)) and the charge induced by the capacitance network (Equation (7)) need to be corrected corresponding to the tunneling coefficient ($Tr$) as follows:

$$Q_{GNR}^{}=Q_{GNR}^n+Tr.p_b(E_V^b-E_{FD})$$

(13)

$$Q_{CAP}^{}=Q_{CAP}^n+Tr.\mathsf{\beta }.C_{i,CH}\times ((E_V^b-E_{FD})/q)$$

(14)

$$Tr=1-[1+\exp (\frac{q{V}_{CH,D}-{\mathsf{\eta }}_b{E}_b-E_F}{\mathsf{\delta }})]{}^{-1}$$

(15)

where $E_V^b=-E_b-{\mathsf{\Psi }}_{ch}$ is the valence band energy and $\mathsf{\beta }=l_{relax}/L_{CH}$. $\mathsf{\delta }$ is a fitting parameter, which controls how fast $Tr$ increases by increasing the band bending between the channel and drain, corresponding to the value of $V_{CH,D}$. The transient capacitance network in Figure 2b can be computed by introducing the intrinsic capacitors as the derivatives of the channel charge with respect to drain and source voltages, $C_{S,CH}=\partial Q_{GNR}/\partial V_S$ and $C_{D,CH}=\partial Q_{GNR}/\partial V_D$, which can be implemented in SPICE by voltage-controlled capacitors.

3.4. Non-Ballistic Transport

The experimental results show that the carrier mobility in graphene can be as high as 200,000 cm²/Vs [32]. However, different scattering mechanisms due to the intrinsic acoustic phonons (AP) and optical phonons (OP) of graphene [33], the interaction of carriers with optical phonons of the substrate [34] and the line-edge roughness (LER) in narrow GNRs [35] can limit its mobility to orders of magnitude lower values. While the transmission coefficient of the carriers can be assumed to be at unity for developing the compact model based on ballistic assumptions [25], these scattering mechanisms must be incorporated in the model as they have been shown to play an important role in the performance of GNR FETs [36]. The transmission of carriers is decreased by scattering in the channel, which can cause a carrier to return to the source region under a low drain bias. The back-scattering of carriers to the source continues under a high drain bias within an approximate critical length of $l=(\hslash {\mathsf{\omega }}_{op}/q{V}_D)L_{CH}$ near the source end of the channel while the scattered carriers in the channel will be absorbed by the drain beyond this critical distance without having a direct effect on the source-drain current [36]. In the absence of scattering mechanisms, the carrier transport is in the ballistic regime and the conductance is independent of the device length. However, carrier scattering in the channel results in the diffusive transport of carriers, thereby making the conductance inversely proportional to the channel length. The channel transmission coefficient provides a simple way to describe the device in the presence of scattering mechanisms [37] as follows:

$$T=\{\begin{array}{ll}{\mathsf{\lambda }}^{eff}/({\mathsf{\lambda }}^{eff}+L_{CH})& ifq{V}_D<\hslash {\mathsf{\omega }}_{op}\\ \frac{{\mathsf{\lambda }}^{eff}}{({\mathsf{\lambda }}^{eff}+(\hslash {\mathsf{\omega }}_{op}/q{V}_D)L_{CH})}& ifq{V}_D>\hslash {\mathsf{\omega }}_{op}\end{array}$$

(16)

where $L_{CH}$($=L_G$) is the channel length and $\hslash {\mathsf{\omega }}_{op}\cong 0.18\text{\hspace{0.17em}eV}$ [38] is the OP energy and ${\mathsf{\lambda }}^{eff}$ is the effective mean free path (MFP) of GNR, which can be obtained using Mattheissen’s rule as follows [39],

$$\frac{1}{{\mathsf{\lambda }}^{eff}}=\frac{1}{{\mathsf{\lambda }}^{sub}}+\frac{1}{{\mathsf{\lambda }}^{ac}}+\frac{1}{{\mathsf{\lambda }}^{LER}}$$

(17)

where ${\mathsf{\lambda }}^{sub}$ is the substrate-limited MFP which is reported close to $100\text{\hspace{0.17em}nm}$ and $300\text{\hspace{0.17em}nm}$ for the GNR on top of SiO₂ and h-BN dielectrics [39], respectively. ${\mathsf{\lambda }}^{ac}$ is the acoustic phonons-limited MFP [34] as follows:

$${\mathsf{\lambda }}_{ap}=\frac{h^2{\mathsf{\rho }}_s{v}_s^2{v}_f^2{W}_{GNR}}{{\mathsf{\pi }}^2{D}_A^2{k}_{B}T}$$

(18)

where $v_s=2.1\times {10}^4\mathrm{m}/\mathrm{s}$ is the sound velocity in graphene, $D_A^{}=17\pm 1\text{\hspace{0.17em}eV}$ is the acoustic deformation potential, and ${\mathsf{\rho }}_s=6.5\times {10}^{-7}{\text{kg}/\mathrm{m}}^2$ is the 2D mass density of graphene. ${\mathsf{\lambda }}^{LER}$ is the line-edge roughness (LER) scattering-limited MFP which can be as small as a few tens of nanometers [40], which can exhibit the dominant scattering mechanism in narrow GNRs as it has been predicted in both experimental data [35] and theoretical studies [41,42]. The edge disorder has been analytically modeled by Anderson distribution in [43] assuming that atoms at the edges are randomly removed with uniform probability, such that the correlation between edge disorders has been neglected. As line-edge roughness is a statistical phenomenon, a more realistic model needs an autocorrelation function as have been already used for modeling Si/SiO₂ interface roughness [44] and the line-edge roughness in GNRs [45,46]. In this paper, we consider an exponential spatial autocorrelation function as follows:

$$R(x)=\Delta W^2\exp (-\frac{\left|x\right|}{\Delta L})$$

(19)

where $\Delta W$ is the root mean square of the width fluctuation amplitude or roughness amplitude and $\Delta L$ is the roughness correlation. Increasing $\Delta W$ or decreasing $\Delta L$ initially makes the carrier transport more diffusive. The line-edge roughness causes fluctuations in the edge potential and bandgap modulation due to the localized edge states as shown in Figure 4a. The decrease in the conductivity of narrow GNRs as a result of line-edge roughness can be incorporated by introducing the effective bandgap in the transport calculation corresponding to the LER scattering-limited MFP as follows [46]:

$$\frac{1}{{\mathsf{\lambda }}^{LER}}={\displaystyle \sum _b\frac{1}{{\mathsf{\lambda }}_b^{LER}}}={\displaystyle \sum _b\frac{1}{A\{(E-E_{}^b)+B{(E-E_{}^b)}^2\}}}$$

(20)

$$\Delta E_g=2{(\frac{2k_{B}T{L}_{CH}}{AB})}^{1/3}$$

(21)

$$A={(\frac{W_{GNR}}{\Delta W})}^2\frac{{\hslash }^2}{8m_b^{*}\Delta L{E}_b^2},B=\frac{8m_b^{*}\Delta L^2}{{\hslash }^2}$$

(22)

Using Equation (21), the effective subband energy of GNR (N,0), $E_{b,eff}^N$ can be modeled as follows:

$$E_{b,eff}^N=E_b^N+\mathsf{\gamma }(\Delta E_g/2)(E_b^N/E_1^N)$$

(23)

where $\mathsf{\gamma }$ is a fitting parameter, which weights the increase in the subbands energy corresponding to the calculated effective bandgap due to LER scattering mechanism. While the increase in subbands’ energy of GNRs in Equation (23) can model the decrease in carrier transport, the line-edge roughness can also contribute to the formation of some localized states in the band gap, which enhances the band-to-band-tunneling of carriers, leading to the initial increase in off-current of GNR FETs at small roughness amplitudes [47]. As GNR channel has a large number of carbon rings and is long enough to provide sufficient averaging, the increase in BTBT current of GNR (N,0) due to the variation in its width can be analytically modeled by summation over the BTBT of its neighbor GNRs (conceptual example of N = 9, 10 and 11 is shown in Figure 4b) as follows:

$$I_{BTBT,rough}^N=I_{BTBT}^N+{\mathsf{\alpha }}_r\frac{{\displaystyle \sum _{i=1}^m[(I_{BTBT}^{N-i}+I_{BTBT}^{N+i}){(\frac{\Delta W}{W_{GNR}}-\frac{i}{N-1})}^{-1}]}}{{\displaystyle \sum _{i=1}^m{[\frac{\Delta W}{W_{GNR}}-\frac{i}{N-1}]}^{-1}}}\exp (-{((\frac{\Delta W}{W_{GNR}}-\frac{\Delta W_c}{W_{GNR}})/{\mathsf{\beta }}_r)}^2+\frac{N}{2})$$

(24)

where ${\mathsf{\alpha }}_r$ and ${\mathsf{\beta }}_r$ are fitting parameters, which model the dominant effects between carriers localization and carriers tunneling corresponding to the amount of roughness amplitude. Equation (24) models the increase in BTBT due to the edge states in the bandgap by summing and normalizing the neighboring GNRs. The integer m has the value of the ratio $\Delta W/\sqrt{3}{a}_{cc}$. ΔW_c = 0.04 is the critical width fluctuation amplitude. The BTBT through edge states in the bandgap leads to the increase in net transport of carriers from source to drain; consequently, the increase in the conduction of GNR FET for ΔW_c > ΔW. By increasing the roughness amplitude larger than ΔW_c, however, the tunneling of carriers occurs mostly between the localized states without a net transport of carriers from source to drain regions. The exponential decrease in device conductivity in the localization regime has been modeled with both the increase in the subband energies in Equation (23) and in the exponential term in Equation (24).

3.5. Extracting Fitting Parameters

The fitting parameters in our developed GNR FET model have been extracted by matching its transfer characteristics with numerical data in regards to the following procedure:

(1)

Obtain the numerical data from NEGF simulation for bias conditions and the device geometries related to BTBT phenomena.

(2)

Obtain the analytical results using the developed model for the same bias conditions and device geometries for a given fitting parameter.

(3)

Change a fitting parameter according to its broad range to determine the best value in which the root mean square error (RMSE) between the numerical and analytical data is minimized.

The above procedure is relatively quick since numerical data, which can be computationally intensive, needs to be calculated only once for a device setting. Then, the analytical model provides prompt results that need to be repeated to search for the best value of the fitting parameters. In addition, all the fitting parameters in this work are used for modeling BTBT from drain to channel with only dominant effects on the total current of FET structure for narrow-bandgap GNRs and under bias conditions of high V_DS and low V_GS (see Figure 3b). As such, the fitting procedure can be limited to those bias conditions (subthreshold region) and wider GNR channels, which corresponds to higher RMSE between numerical and analytical results.

The dependence of fitting parameters on the GNR width can be eliminated by including another fitting dimension for semiconducting GNR chiralities such as GNR(N,0) shown in Figure 5. The figure shows an example of a two-dimensional fitting procedure, in which all the analytical results versus gate voltage and GNR widths are repeated for different values of a fitting parameter, e.g., $\mathsf{\delta }$, approaching the best fit with smallest average RMSE in two dimensions.

The fitting procedure is repeated until the RMSE reaches ±10% and ±20% of the numerical data for fitting parameters related to ideal GNRs and non-ideal GNRs, respectively. The maximum error values are our assigned acceptable errors for obtaining general fitting parameters independent of device dimensions, which correspond to the GNR FETs with 16 nm channel length of GNR(24,0) at V_DS = 0.8 V and V_GS = 0.05 (significant BTBT phenomena). Two fitting parameters, l_relax and δ in Equation (15) are associated with ballistic transport in ideal GNRs while γ, ${\mathsf{\alpha }}_r$ and ${\mathsf{\beta }}_r$ in Equations (23) and (24) are related to the non-ballistic transport modeling of carriers in rough-edge GNRs.

Table 1. Obtained values of fitting parameters, the searching ranges and step, along with the corresponding errors.

Fitting Parameter	Obtained Value	Searching Range	Searching Step	% RMSE
lrelax	40 nm	10 nm–100 nm	5 nm	<10%
δ	0.05	0.01–0.1	0.025
γ	2.9	0–3	0.5, then 0.1	<20%
${\mathsf{\alpha }}_r$	6 × 10-6	From 0	Different (Nonlinear)
${\mathsf{\beta }}_r$	0.0145	From 0	0.01, 0.001 and 0.0001

shows the searching ranges and obtained values of fitting parameters, as well as the maximum errors with regard to the numerical data. For example, by altering l_relax in a range from 10 nm to 100 nm, the analytical results match the numerical data in the subthreshold region within the acceptable RMSE at l_relax = 40 nm. A similar method was used to obtain l_relax of Stanford CNT FET model [24]. As the fitting parameters in our GNR FET model only need to be obtained just once and their values are valid for all the device geometries and line-edge roughness in this study, as indicated in

Table 2. Scope of the device dimension and line-edge roughness in GNR FET Model.

Device Dimension	GNR Channel Length ($L_{CH}$)	$10\text{\hspace{0.17em}nm\hspace{0.17em}\hspace{0.17em}}-45\text{\hspace{0.17em}nm}$
	GNR Channel Width (WGNR, GNR(N,0))	$~0.87\text{\hspace{0.17em}nm\hspace{0.17em}}(N=6)-~3.18\text{\hspace{0.17em}nm\hspace{0.17em}}(N=25)$
	Oxide Thickness ($t_{OX}$)	$0.5\text{\hspace{0.17em}nm\hspace{0.17em}\hspace{0.17em}}-2.0\text{\hspace{0.17em}nm}$
Line-edge Roughness	Roughness Amplitude ($\Delta W$)	$0.0-0.2$
	Roughness Correlation ($\Delta L$)	$3\text{\hspace{0.17em}nm\hspace{0.17em}\hspace{0.17em}}-10\text{\hspace{0.17em}nm}$

.

4. Model Validation

The dimension and bias conditions of most experimental works are much larger than the target ranges of GNR FET for emerging technology. For example, the GNR width (W_GNR) and gate voltage, (V_G) are mostly studied in the range of 10–150 nm and 10–50 V, respectively [48,49,50]. Therefore, we have validated the accuracy of our developed analytical model against the device-level atomistic numerical simulation based on NEGF formalism as described for ideal GNR FET in [22] and for GNR FET with line-edge roughness in [46]. Figure 6a,b shows the I_DS–V_GS characteristic of GNR FETs with three different GNR indices of N = 6, 12 and 18 for drain voltages of 0.1 V and 0.5 V, respectively. It is shown that our analytical model agrees well with numerical simulations. The device dimensions in the simulation are, L_G = 16 nm, W_G = 2 nm and $t_{ox}=1\text{\hspace{0.17em}nm}$. For the comparison with device-level simulation, the Fermi level due to the work function difference between metallic gate and graphene is set to E_F = 0, while its nominal value is kept equal to E_F = 0.4 eV for the other simulations. It can be observed that increasing GNR width or drain voltage leads to the increase in off-current as both can provide more subbands to incorporate in BTBT of carriers from drain to channel. Figure 6c shows the I_DS–V_DS characteristics of GNR FET at different gate voltages, demonstrating that the results of the analytical model in this work are in correlation with those of numerical simulations.

Figure 6d shows the effect of line-edge roughness on the off-state and on-state currents of GNR FET with the channel of GNR (15,0). It can be seen that the analytical model agrees very well with the numerical simulations, which can be obtained at the expense of long computational time by statistical averaging many GNR samples with the same roughness parameters [14]. Furthermore, the GNR FET with perfectly smooth edges can have more than three orders of magnitude difference between on- and off-currents. The off-current increases by increasing the roughness amplitude, as the formation of some localized states in the band gap significantly increases the band-to-band-tunneling (BTBT) of carriers. Conversely, the on-current decreases by increasing the roughness amplitude due to the increase in carrier scattering associated with line-edge roughness (LER). By increasing the line-edge roughness, the carrier transport becomes more diffusive and the trend continues up to the critical roughness amplitude (ΔW_c). For LER amplitude larger than ΔW_c, the BTBT of carriers through localized edge states is dominated by the localization of carriers in those states; while, the back-scattering of carriers occur due to the localized potential barriers of edge disorders. The critical roughness amplitude corresponds with the maximum off-current and the minimum value of I_ON/I_OFF ratio. By increasing the roughness amplitude, the off-current is decreased as the carriers transport takes place by tunneling between localized edge states, leading to the reduction in the effective net transport of carriers from drain to channel. It is worth mentioning that the uniform edge roughness has been assumed in some works [51,52] by defining roughness percentage, p, which neglects the correlation between edge disorders. This assumption underestimates the effect of line-edge roughness; thereby, only the initial increase in off-current due to BTBT phenomena has been exhibited while larger line-edge roughness reduces off-current similar to on-state current.

Figure 7 shows the I_DS–V_GS characteristic of three GNR FETs with the channels of GNR (9,0), GNR (15,0) and GNR (24,0) at V_DS = 0.25 V for various LER amplitudes and constant roughness correlation of ΔL = 10 nm. It can be seen that the narrower ribbon, i.e., GNR (9,0), has lower off-current than GNR (15,0) and GNR (24,0) for all LER amplitudes. At V_DS = 0.25 V, the BTBT of GNR FET with larger bandgap, i.e., GNR (9,0), is very small, thus the edge states introduced in the bandgap by increasing LER amplitude cannot lead to a significant increase in off-state current (V_GS = 0). This increasing LER amplitude only increases the scattering of carriers, consequently, reducing the currents. For GNR(24,0), however, the bandgap is small and the BTBT can be significant at V_DS = 0.25 V, thus the off-current initially increases by increasing the roughness amplitude up to the critical roughness amplitude (∆W_c = 0.04), then decreases at larger roughness amplitude due to the back-scattering of carriers from localized edge states. However, the edge roughness continuously increases the scattering of thermionic carriers at on-state; thereby the reduction of on-current is continuous, correspondingly. Both increasing off-current and decreasing on-current can deteriorate the device performance at a critical roughness amplitude. For large LER amplitude, however, the main source of performance degradation is the significant decrease in on-current of GNR FET. The same effect of roughness amplitude can be observed in narrower GNRs (larger bandgaps) and at higher V_DS.

Figure 8 shows the off-current, on-current and I_ON/I_OFF ratio as a function of GNR width (Semiconducting GNR index N = 3p, where p is an integer). It can be seen that both on- and off-currents of ideal GNR FETs increases by widening GNR width, as larger numbers of subbands can contribute to carrier transport by decreasing bandgap at a given supply voltage. The I_ON/I_OFF ratio is increased by decreasing the GNR width, as the leakage current associated with BTBT phenomena is significantly decreased by increasing the bandgap. At the scaled supply voltage (V_DD = 0.5 V), GNR(6,0) with larger bandgap is not fully at the on-state resulting in smaller I_ON /I_OFF ratio. GNR FETs demonstrate larger off-current at the critical LER amplitude of ∆W/W_GNR = 0.04 due to the maximum number of BTBT from drain to channel occurring through the generated edge states in the bandgap. While I_OFF is larger and I_ON is smaller than ideal narrow GNR FETs due to the decrease in carrier scattering at on-state, which leads to significant deterioration of the I_ON/I_OFF ratio for ∆W/W_GNR = 0.04. Larger line-edge roughness amplitudes, e.g., ∆W/W_GNR = 0.1, can set the carrier transport in localization regime such that both off- and on- currents are reduced resulting from the decrease in the MFP of edge scattering and the increase in the back-scattering of carriers occurred by a larger number of localized edge states.

5. Validation of Single-Particle Calculations

It has been shown both experimentally [13,53] and theoretically [14] that strong localization can appear in a single-layer GNR for large line-edge roughness, known as Anderson-type localization [54]. Edge-disorder increases the number of localized carriers and their corresponding density of states at the edges, which blocks the conductive paths of carrier transport through the graphene nanoribbon. This can potentially increase the importance of electron–electron interaction for carrier transport, such that the validity of single-particle calculations for this problem needs to be justified. The effects of electron–electron interactions on carrier transport need to be investigated using numerical simulations, then the corresponding results can be incorporated in the analytical calculations. Many samples need to be created with given roughness parameters and each has to be simulated by a self-consistent iteration algorithm between the carrier transport problem using the non-equilibrium Green’s function formalism and the electrostatic problem using the Poisson equation. Incorporating the electron–electron interaction in the problem will add another iteration algorithm between the Green’s function and the electron-electron self-energy [55]. From the obtained numerical data and using equation: $<T(E)>=M(E)/(1+L_{CH}/\mathsf{\lambda }(E))$, where $M(E)$ is the number of active conduction channels and $<T(E)>$ is the average transmission probability, the mean free path of the carriers can be extracted to investigate the role of line-edge roughness scattering and the electron–electron interaction in the transport problem [55].

Figure 9 shows the mean free paths associated with line-edge roughness and the electron–electron interaction. In the simulation, the edge roughness is set to be highly correlated, ΔL = 3 nm, which reduces the mean free path below the nanometer range and the electron–electron scattering rate is assumed 50 ps for a momentum conserving interaction [56]. It can be seen that the analytical results of Equation (20) for line-edge roughness are in agreement with the numerical simulations and are in correspondence with Fermi’s golden rule (${\mathsf{\lambda }}^{LER}\propto 1/\Delta W^2$) [45]. By incorporating the electron–electron interaction, there is a deviation in total mean free path of carriers at small roughness amplitudes. The total MFP is dominated by the effects of the electron–electron interaction at small roughness while the line-edge roughness scattering is the dominant scattering mechanism at larger roughness amplitudes. Electron–electron interactions are known to have significant effects on the carrier transport in materials with one-dimensional (1D) confinement, e.g., GNR interconnects. As the GNRs in this application need to be long, the 1D problem is very strong and carrier transport is deep in the localization regime [57]. The carriers transport can only take place by tunneling between localized edge states [58] which results in significant reduction of transmission probability [54]. However, the GNR length as a channel material is 16 nm in our simulation, which is a typical channel length for emerging transistors and the GNR width is ~1.6 nm; thus, the strength of 1D problem corresponding to the ratio of the GNR channel length to GNR width (W/L ≈ 1/10) is not large enough to make electron–electron interaction a considerable portion for most roughness amplitudes. However, the soundness of single-particle calculations with regard to width-to-length ratio of GNR is still controversial in the literature, such that charge localization due to strong edge roughness has been reported in some works [59,60] as a responsible mechanism for Coulomb blockade and the formation of bottlenecks for carrier transport in GNR channels. Further research is required to understand the exact mechanism for charge localization along the edge. Particularly, the manner in which the edge disorder changes the potential landscape in a graphene nanoribbon so that electrons prefer to be located along the edge rather than transported in the bulk needs to be investigated.

6. Conclusions

We present a physics-based analytical model compatible with SPICE for the circuit simulation of GNR FETs. The carrier charge and current have been analytically calculated and compared with the numerical data obtained by NEGF formalism. We presented the device-level performance of non-ideal GNR FETs in edge-enhanced band-to-band-tunneling and localization regimes for various roughness amplitudes. Corresponding to these two regimes, I_OFF is initially increased, then decreased; while, on the other hand, I_ON is continuously decreased by increasing roughness amplitude. The band-to-band-tunneling and the corresponding increase in off-current can be reduced by accurately choosing the supply voltage for a given GNR width. The line-edge roughness increases the threshold voltage and limits the advantage of bandgap engineering of GNR FETs for scaling down the supply voltages. Our results show that the line-edge roughness in the GNR channels associated with the lack of atomic-scale precision in current patterning technique significantly degrades the performance of GNR FETs.