Novel Neural Control of Single-Phase Grid-Tied Multilevel Inverters for Better Harmonics Reduction
Abstract
:1. Introduction
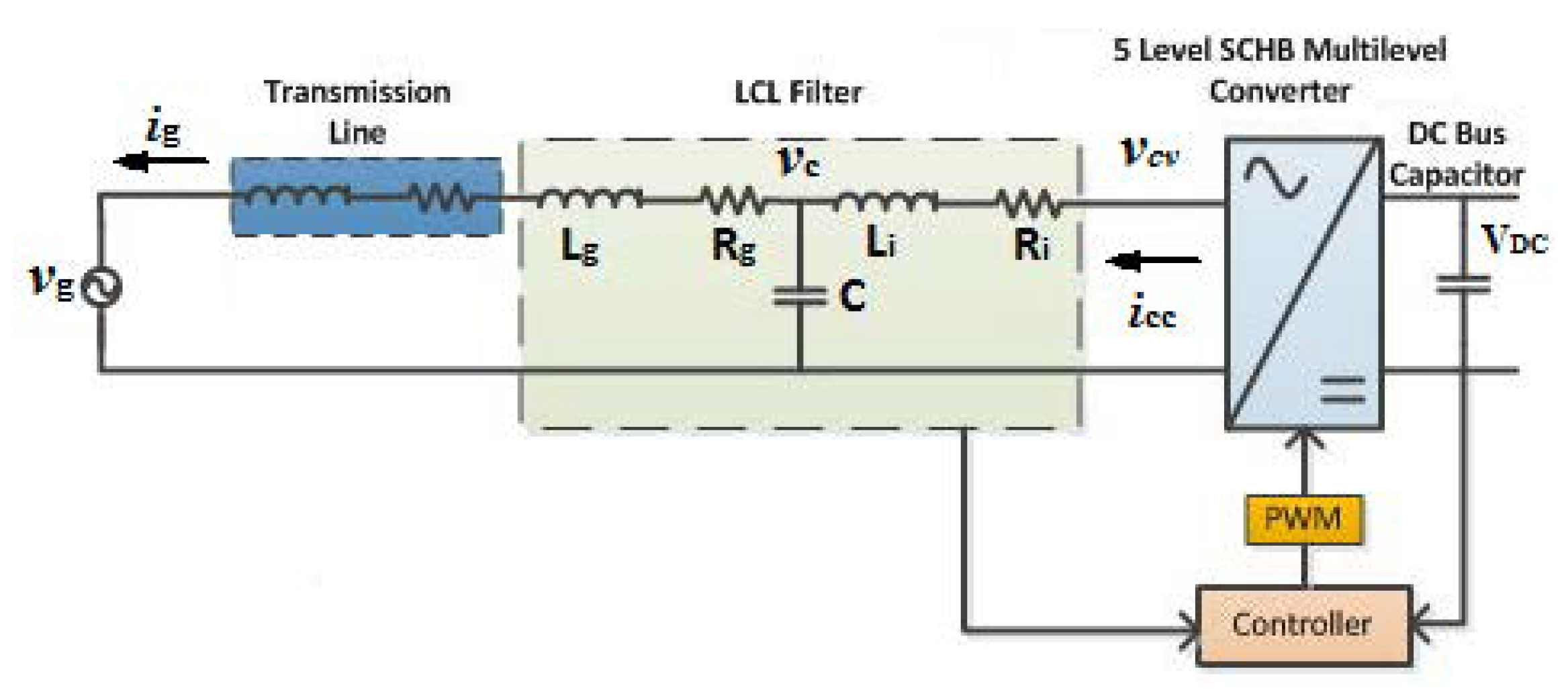
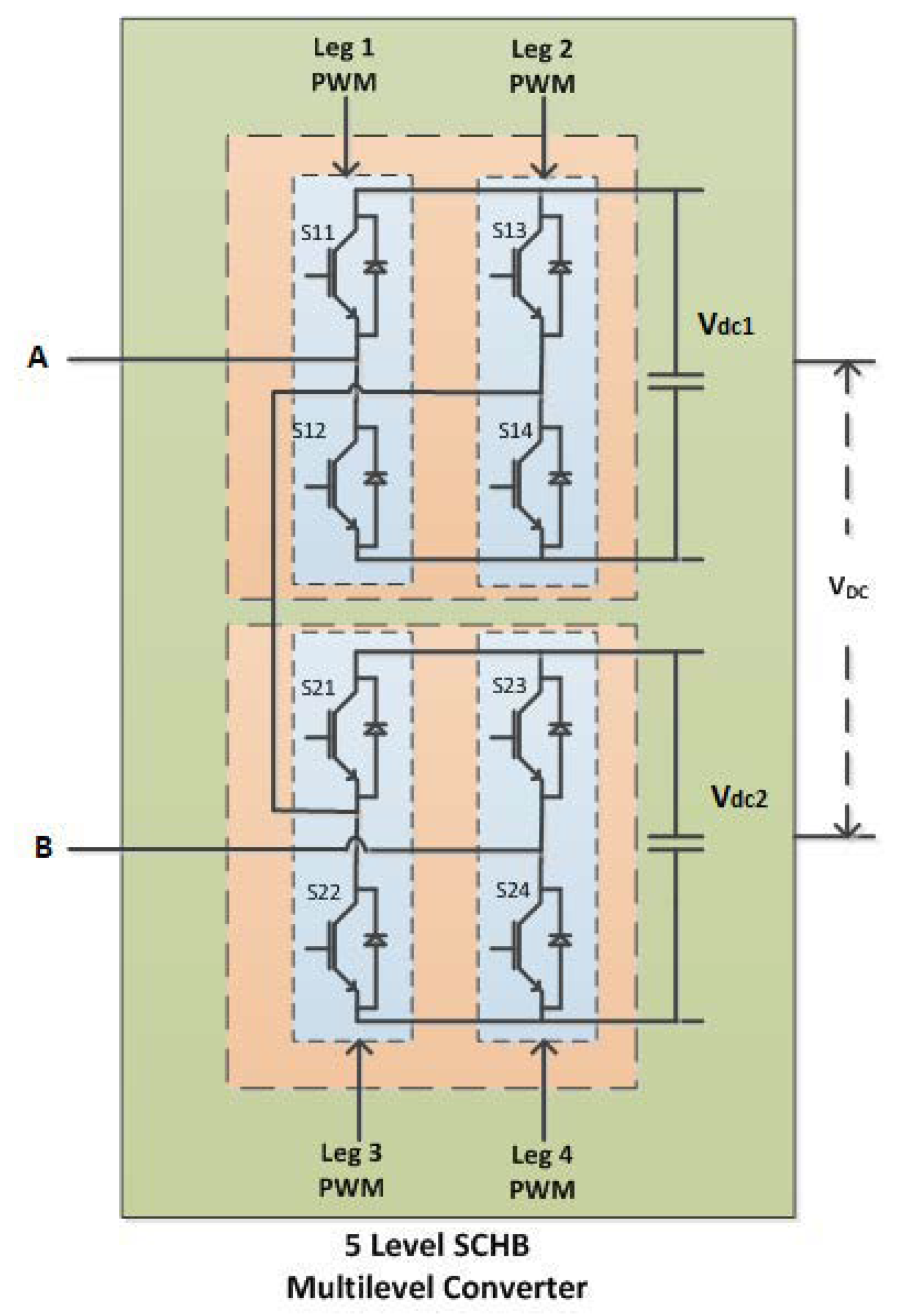
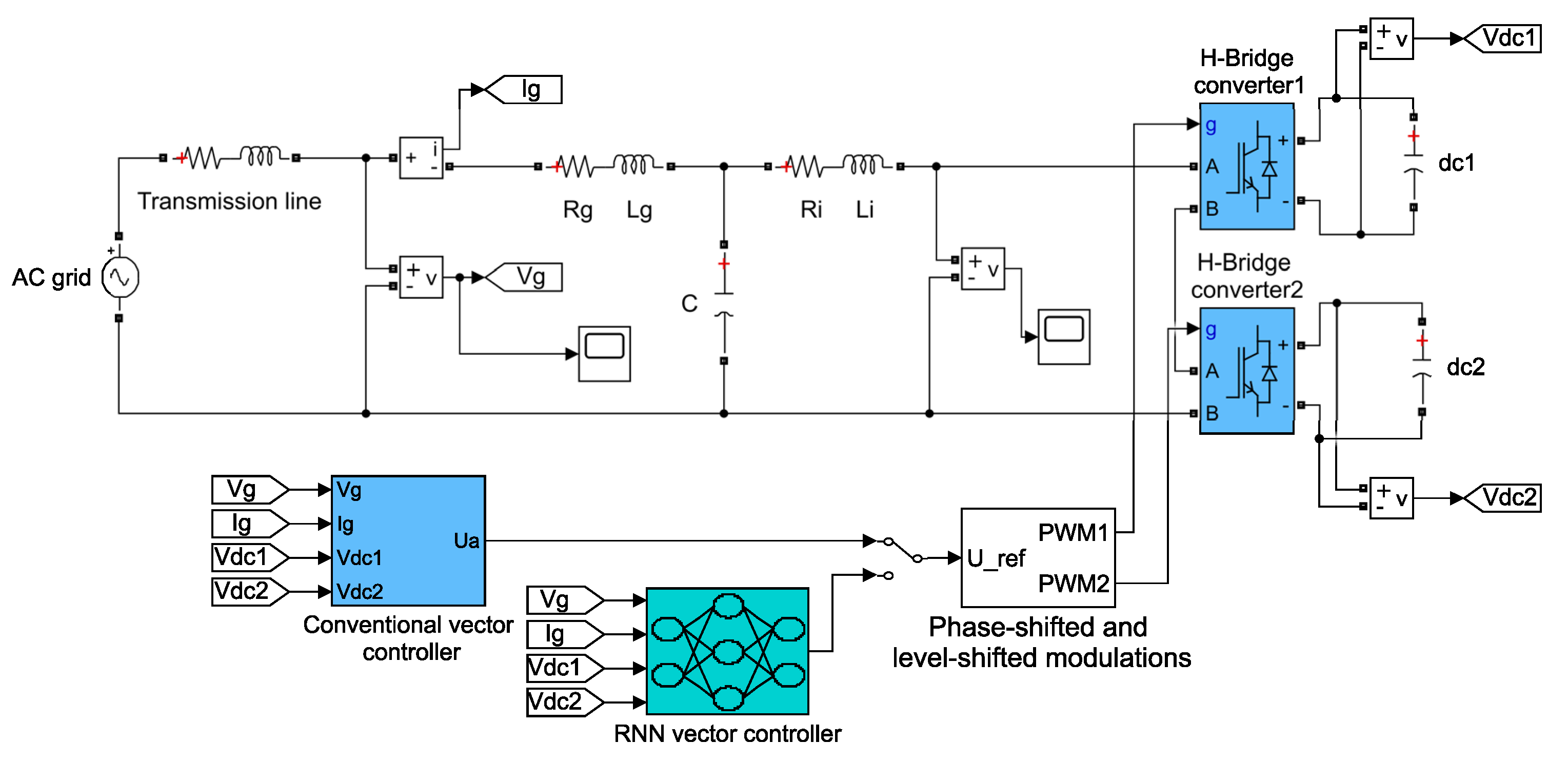
2. Single-Phase Grid-Tied Multilevel Inverters
Grid-Tied Multilevel Inverter
3. Control Strategy and Modulation Technique
3.1. Imaginary Circuit
3.2. Mathematical Model
3.3. PI-Based Vector Control
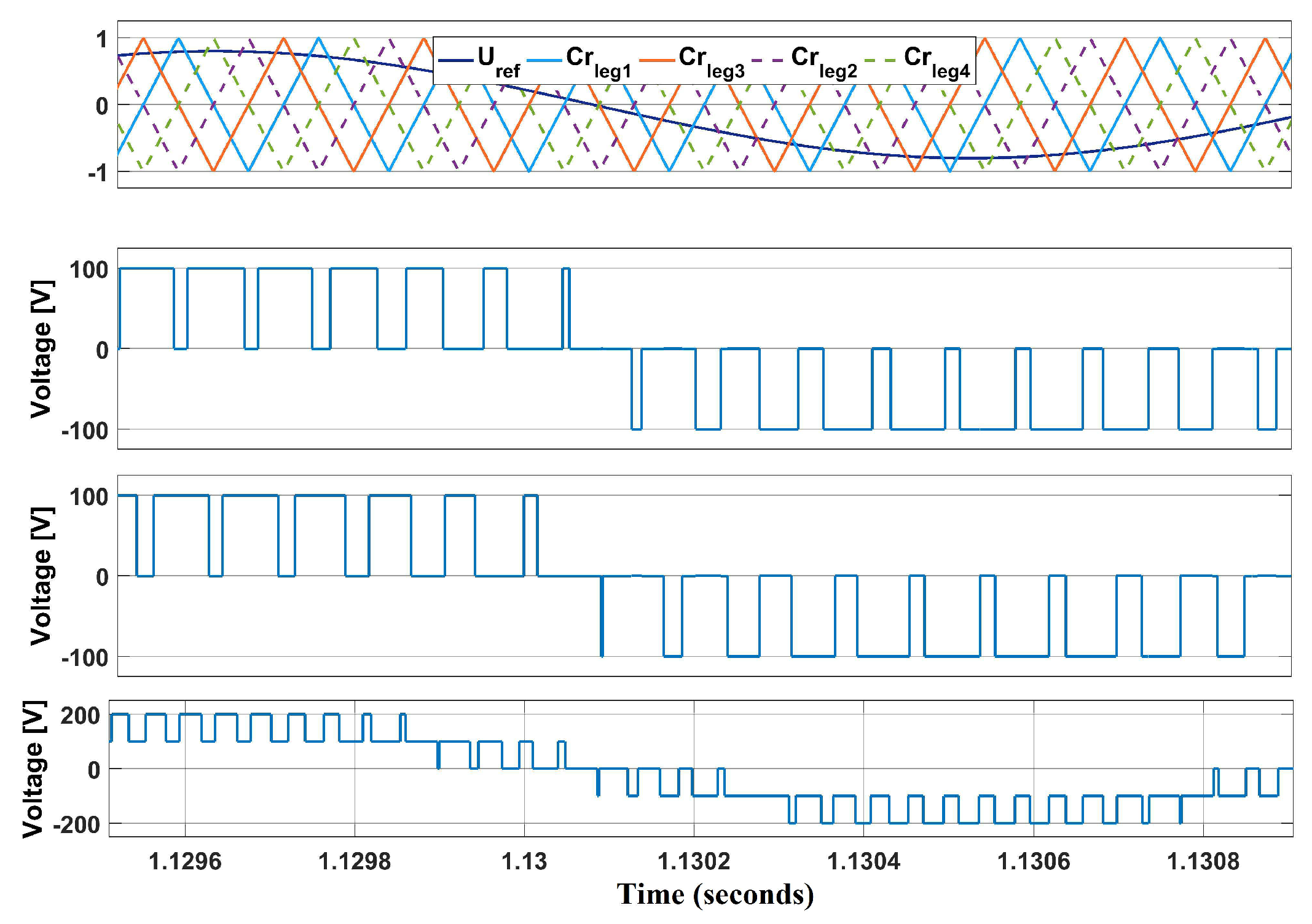
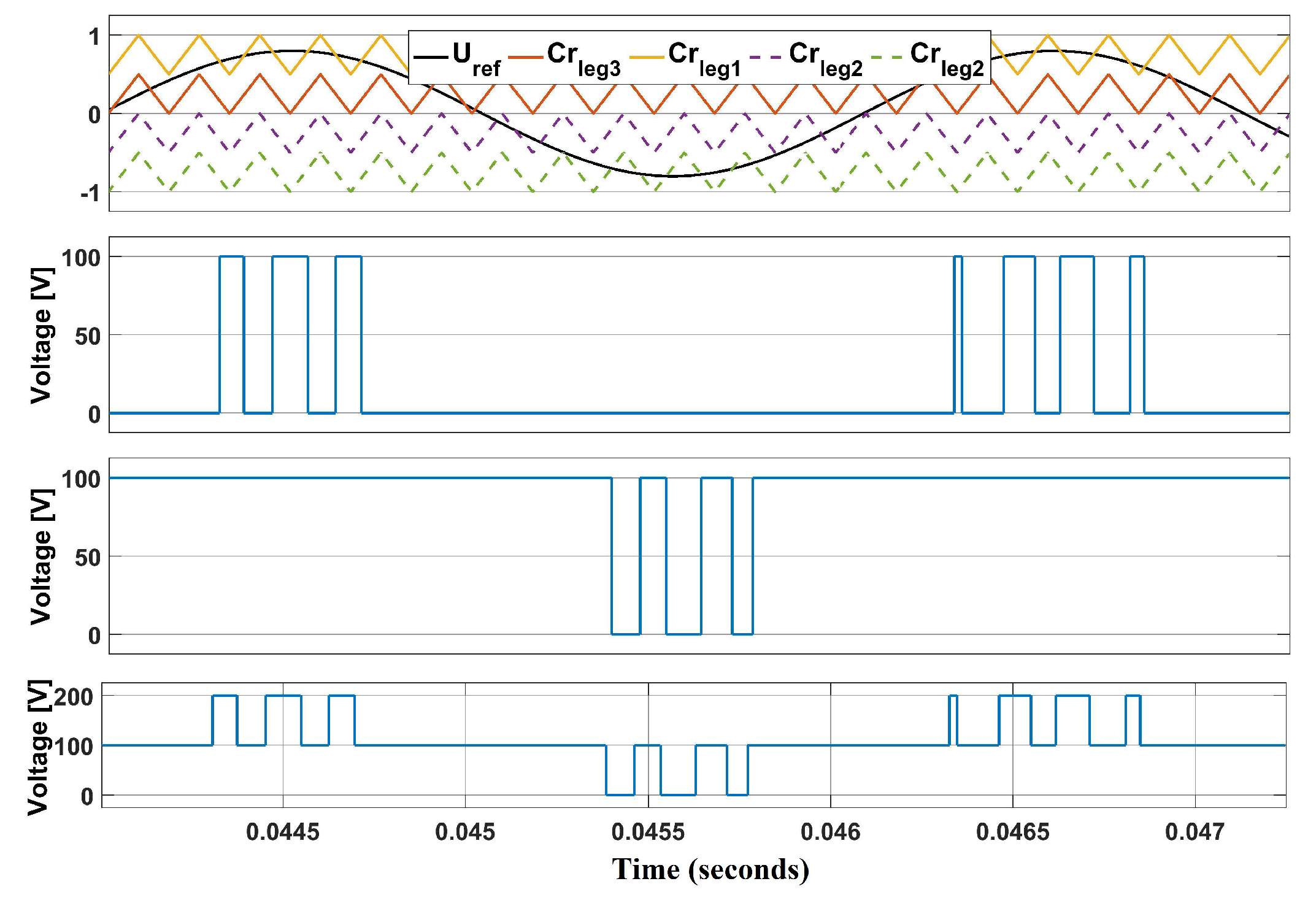
3.4. Modulation Technique
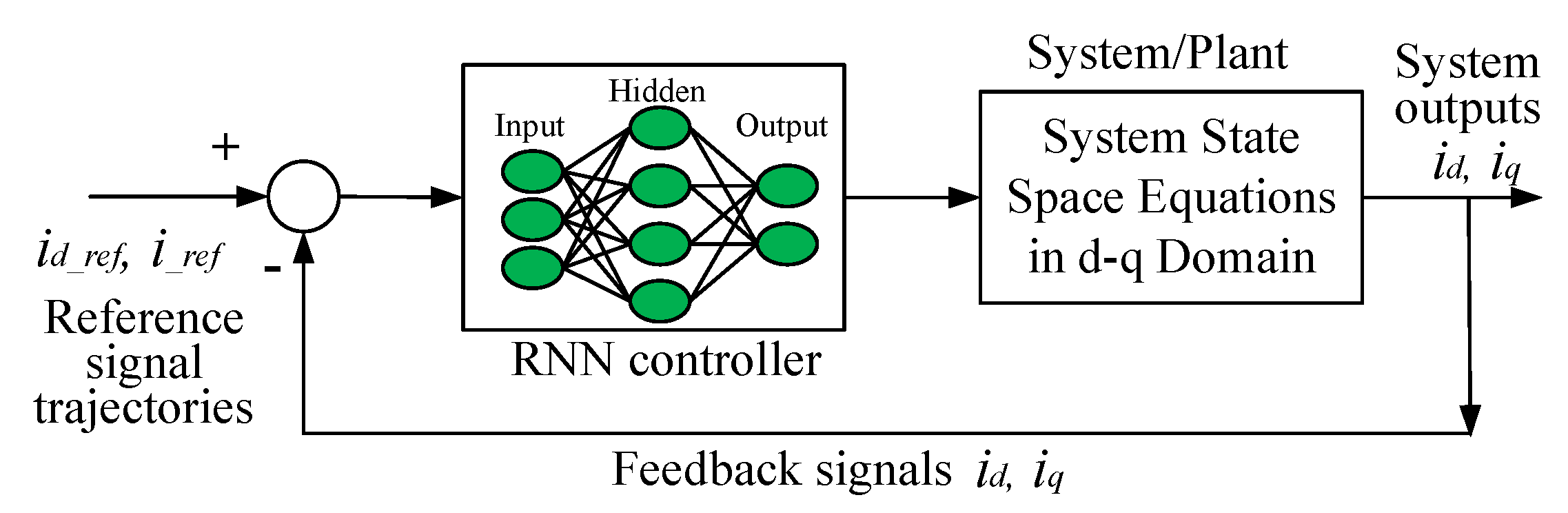
4. Novel Neural Control Technique
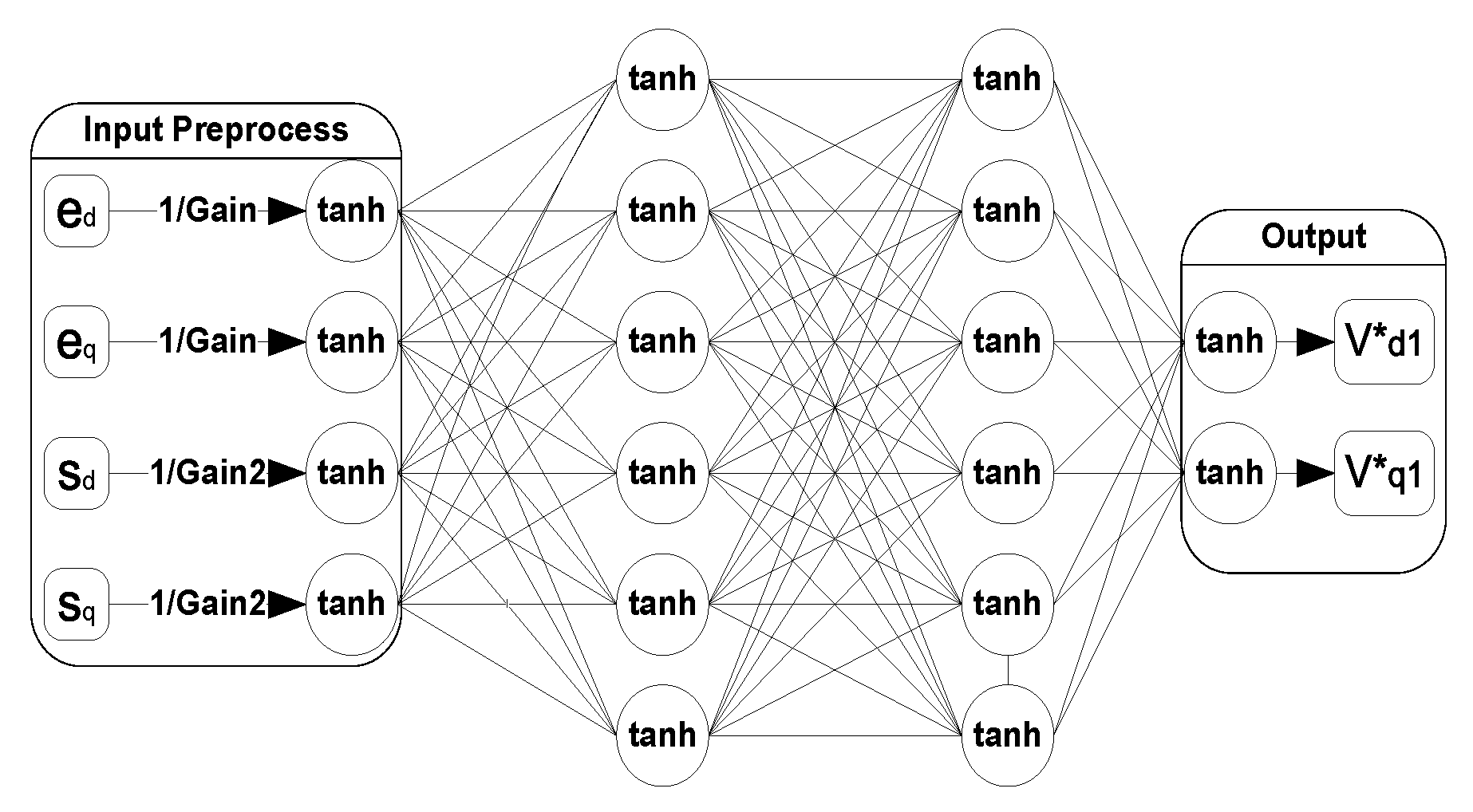
4.1. Current-Loop Neural Network Controller
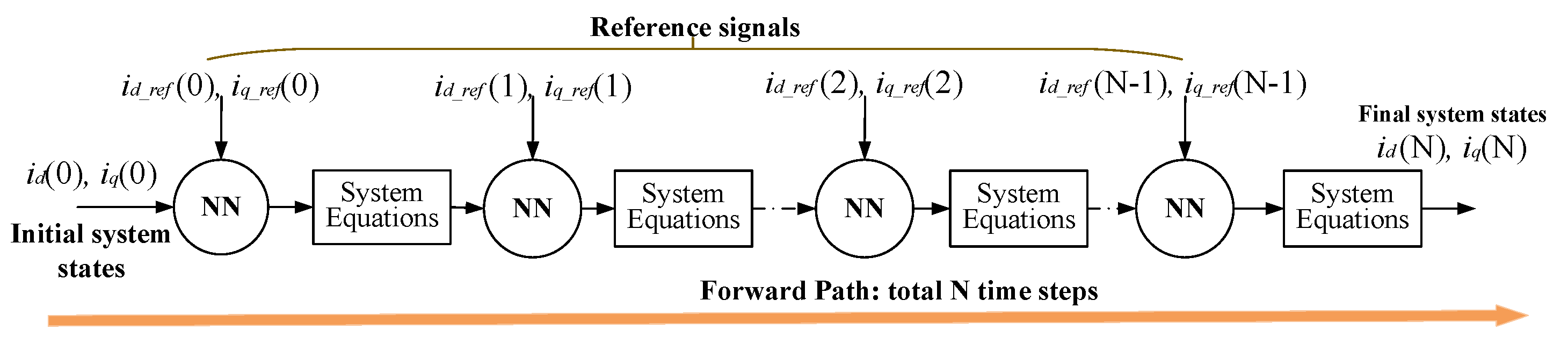
4.2. Training Neural Network Controller
5. Simulation Results
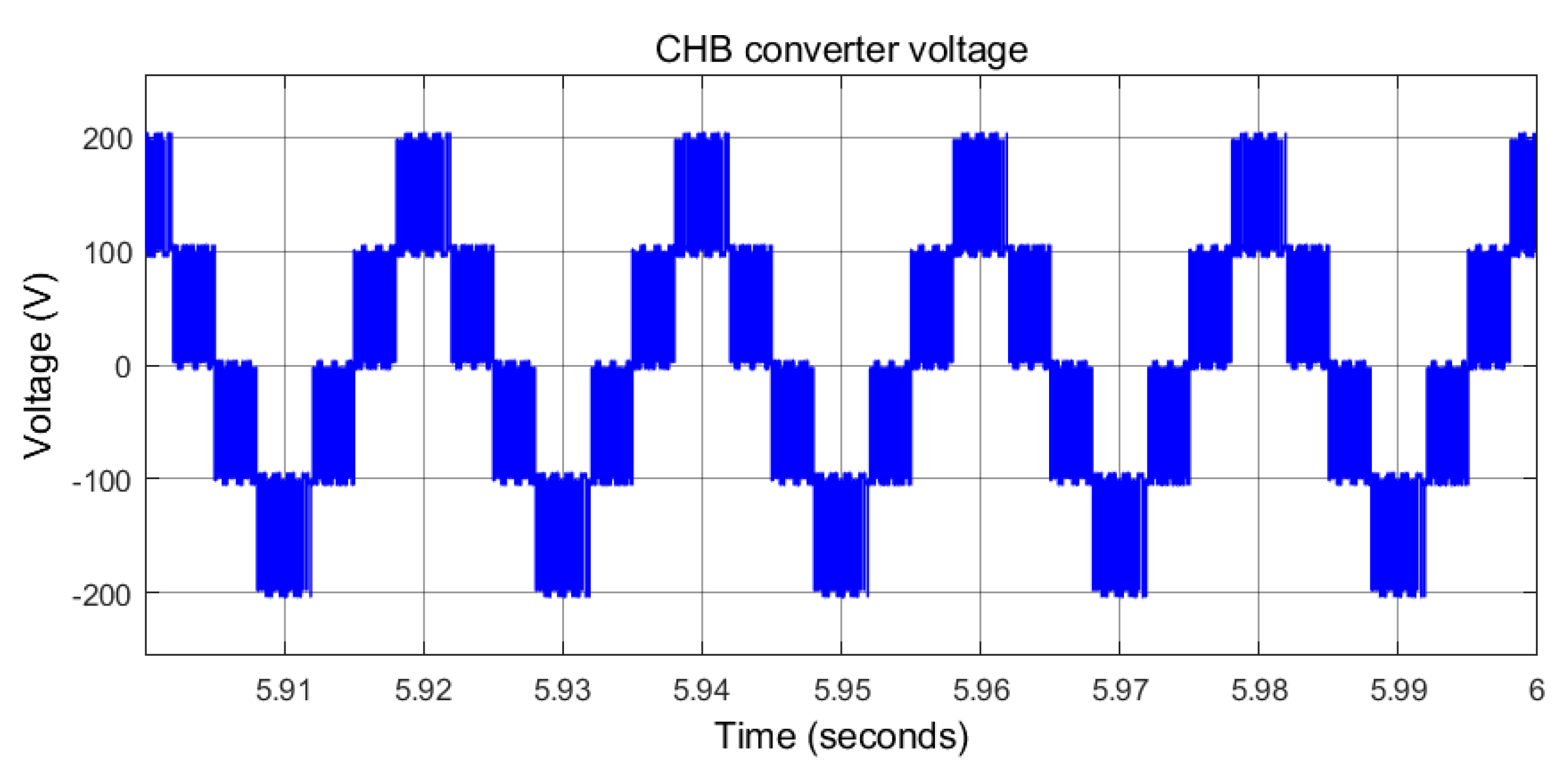
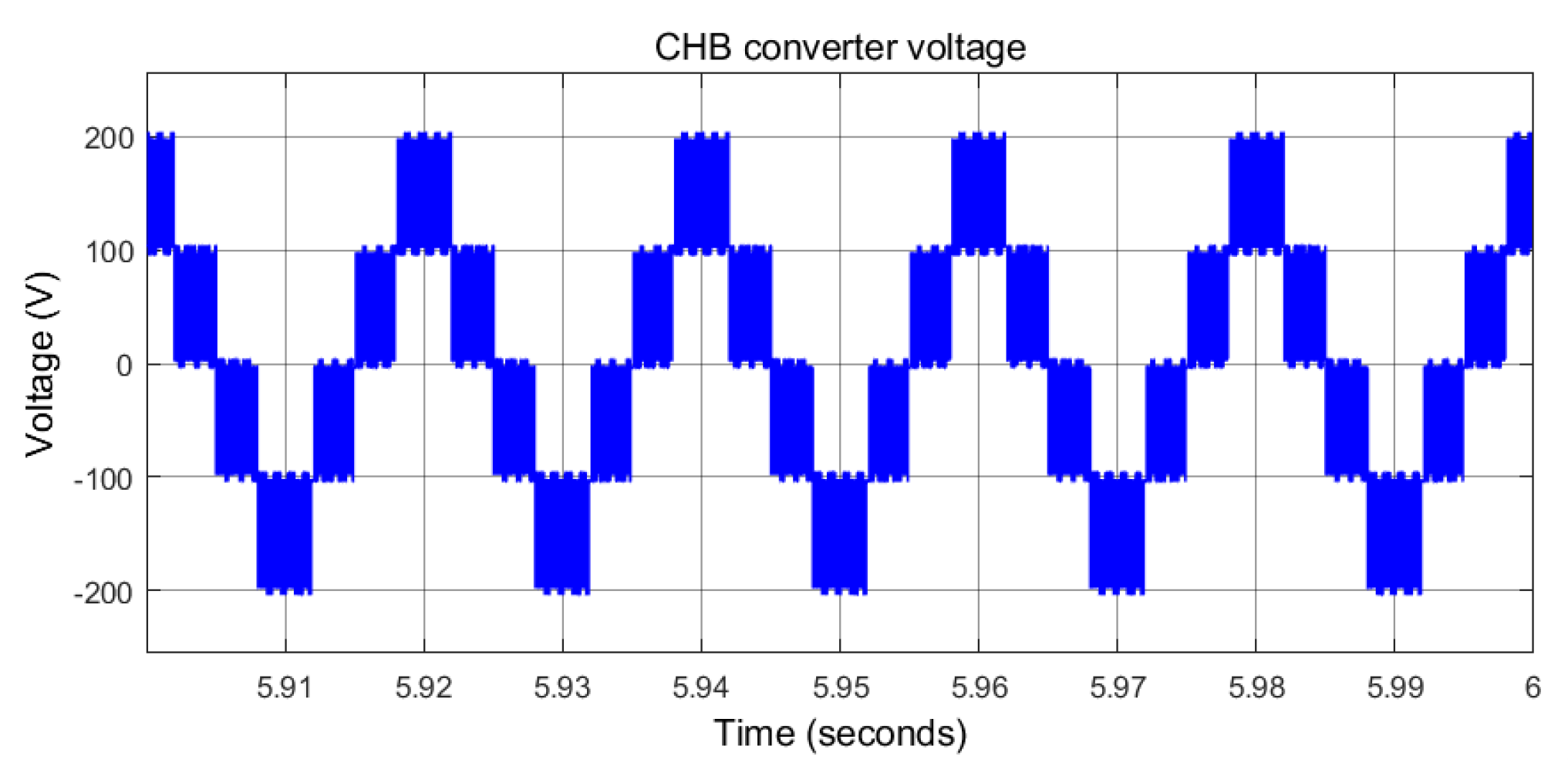
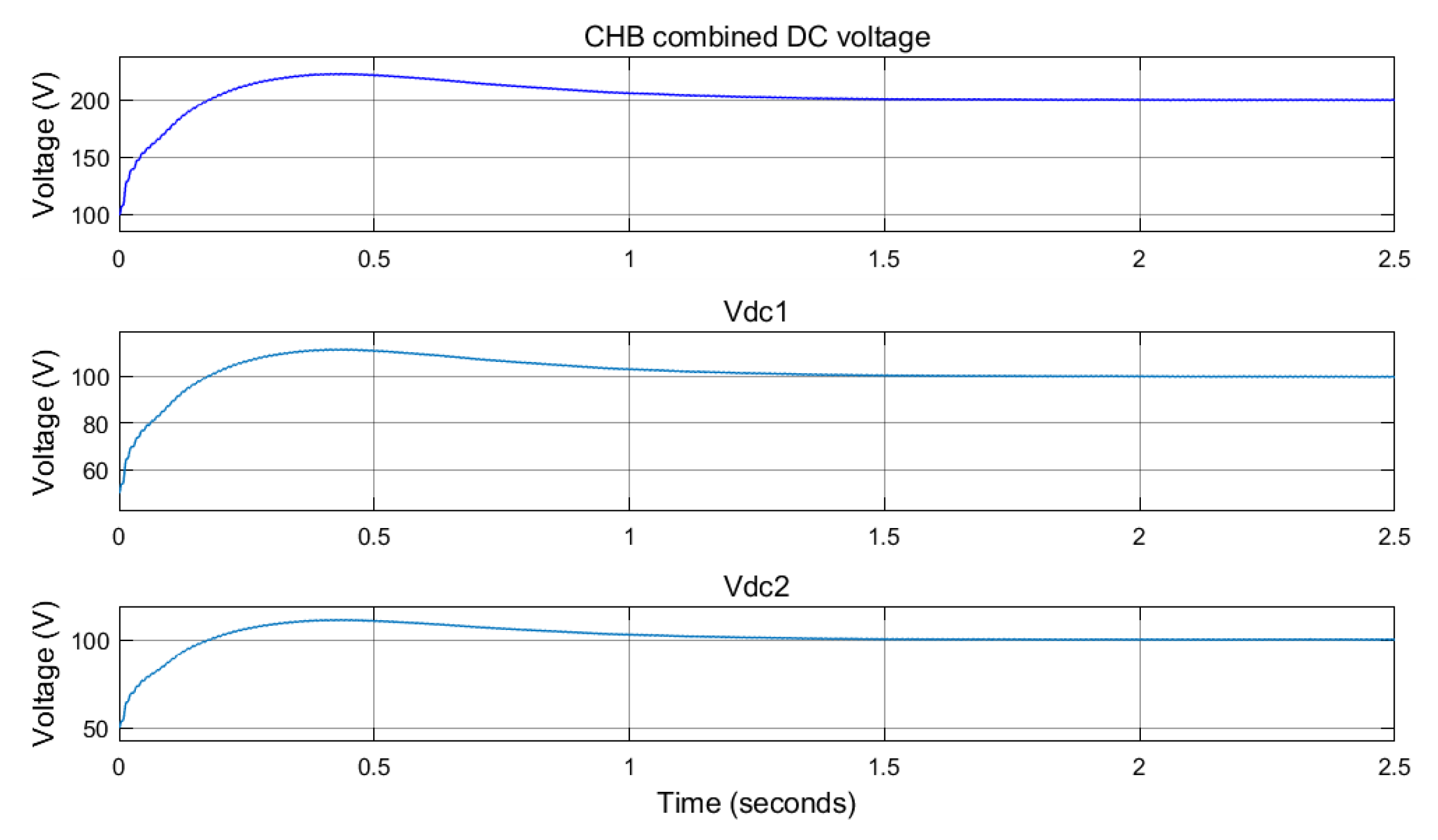
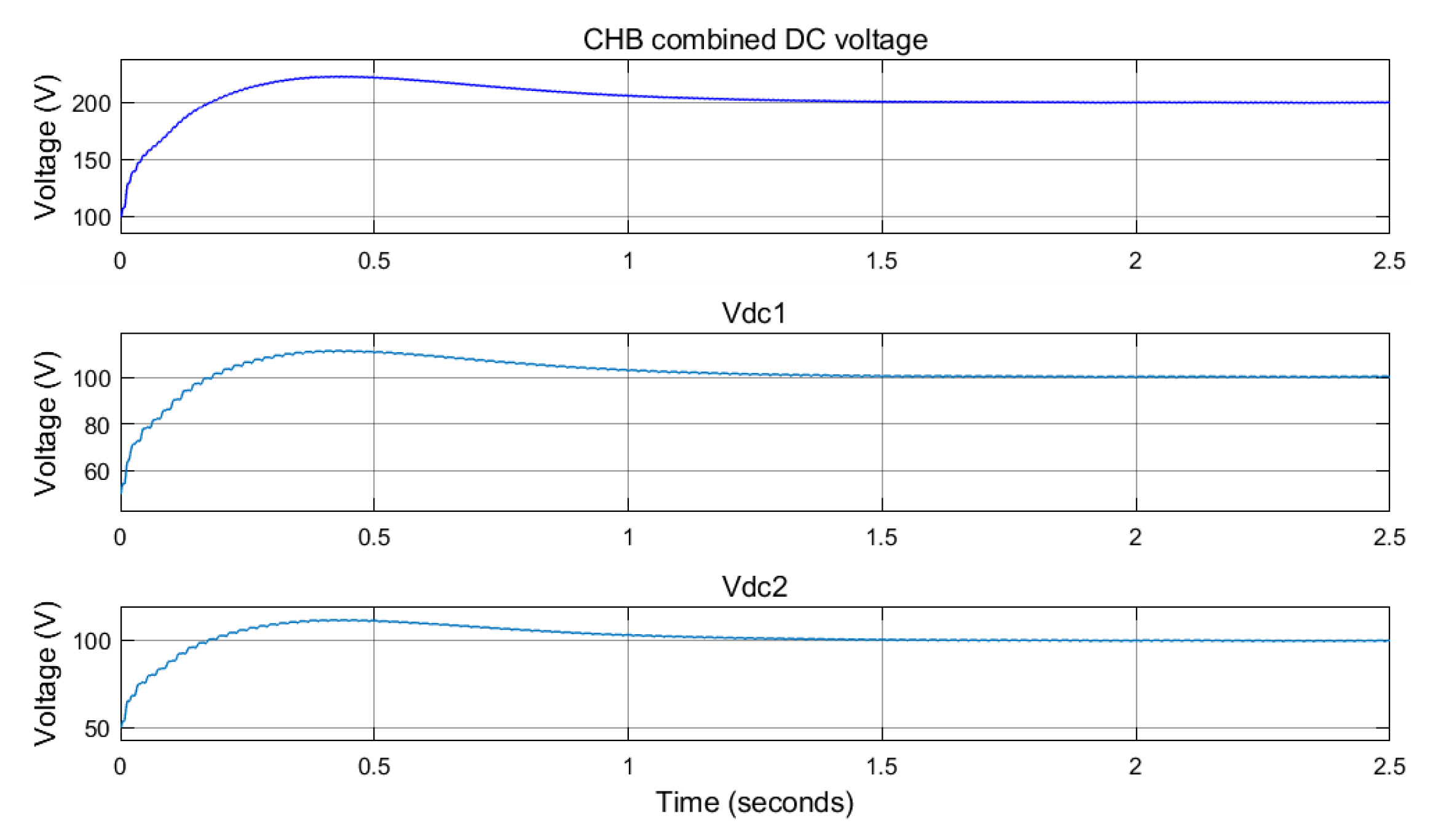
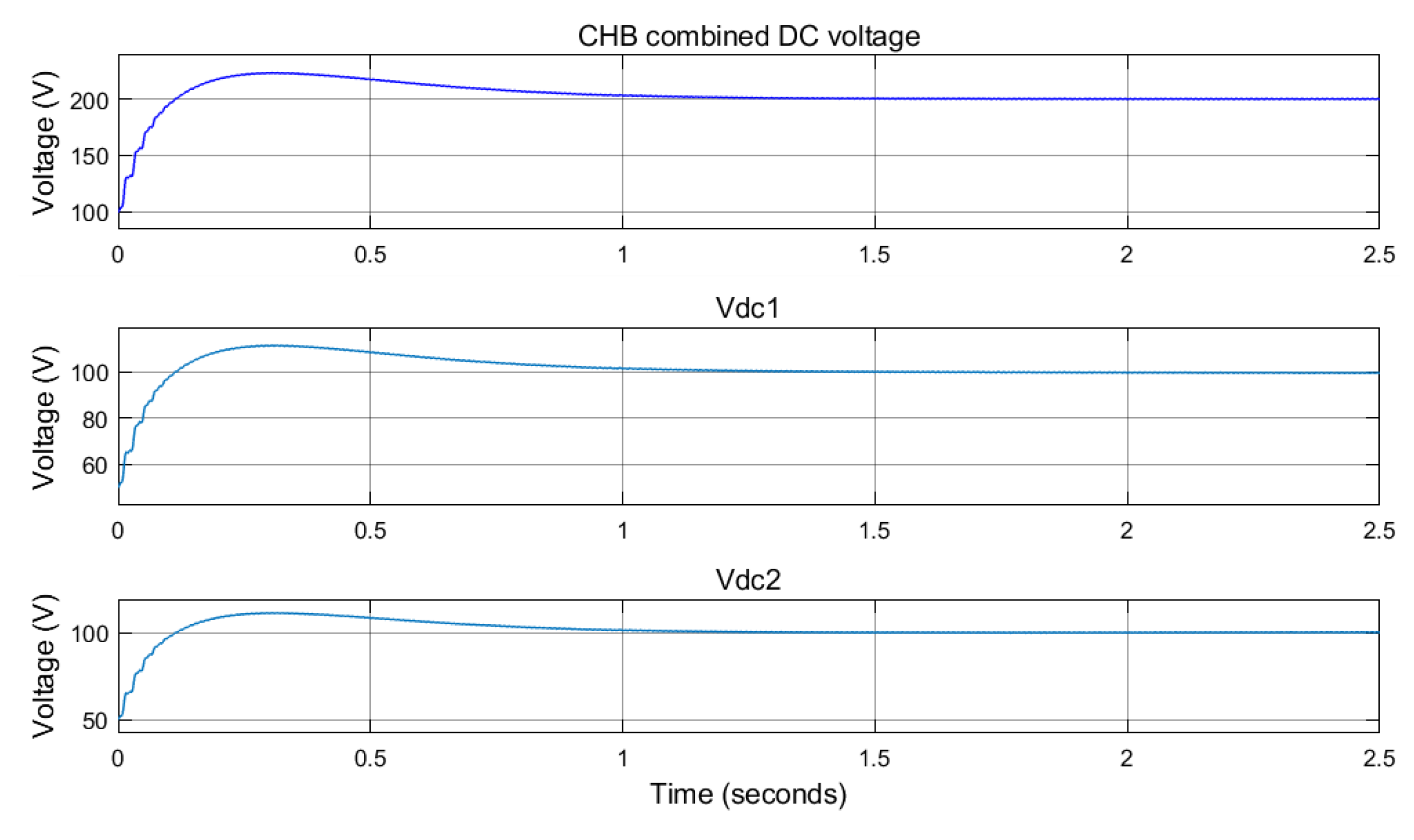
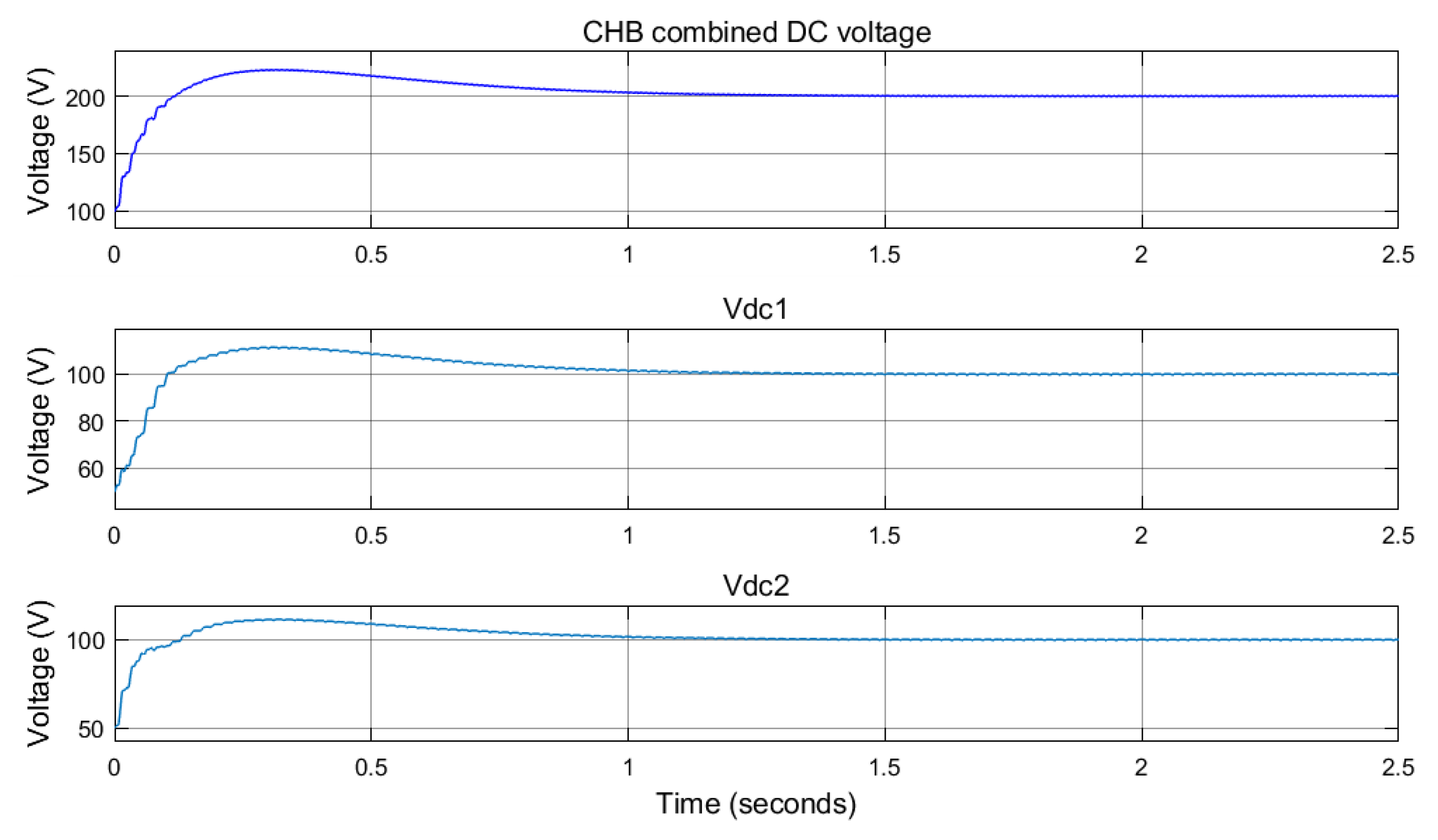
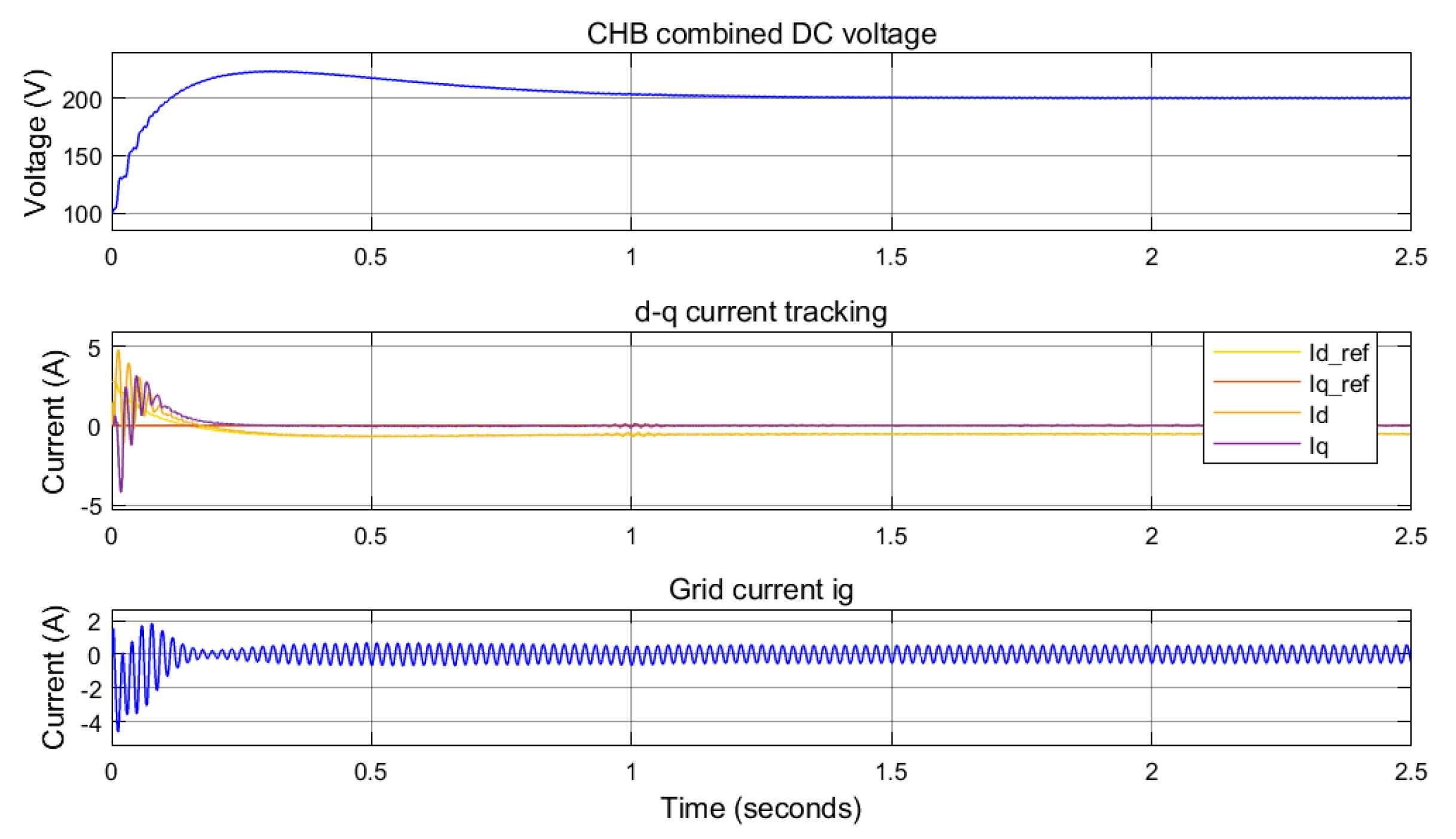
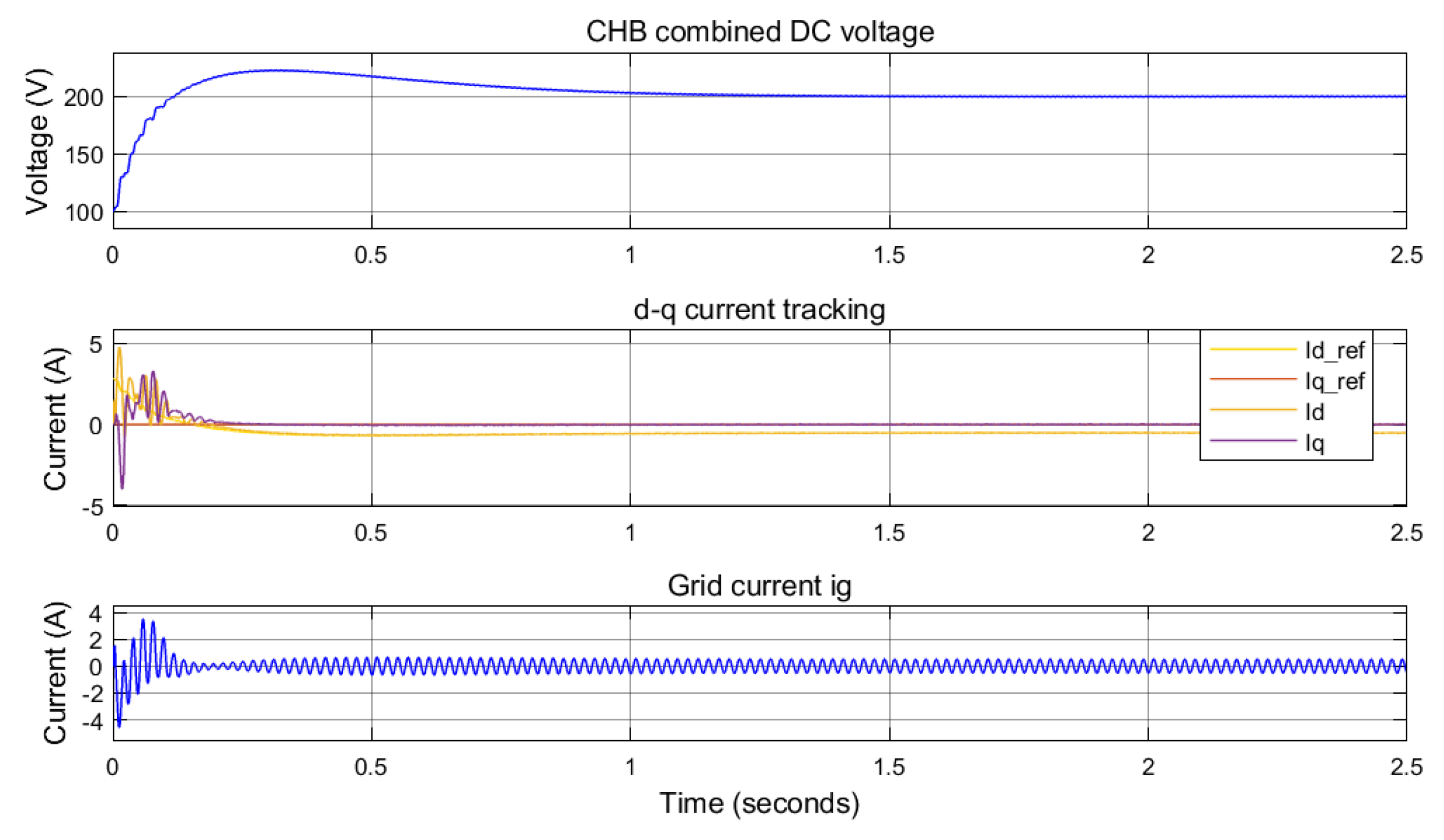
5.1. Five-Level CHB DC Voltage
5.2. Voltage Tracking
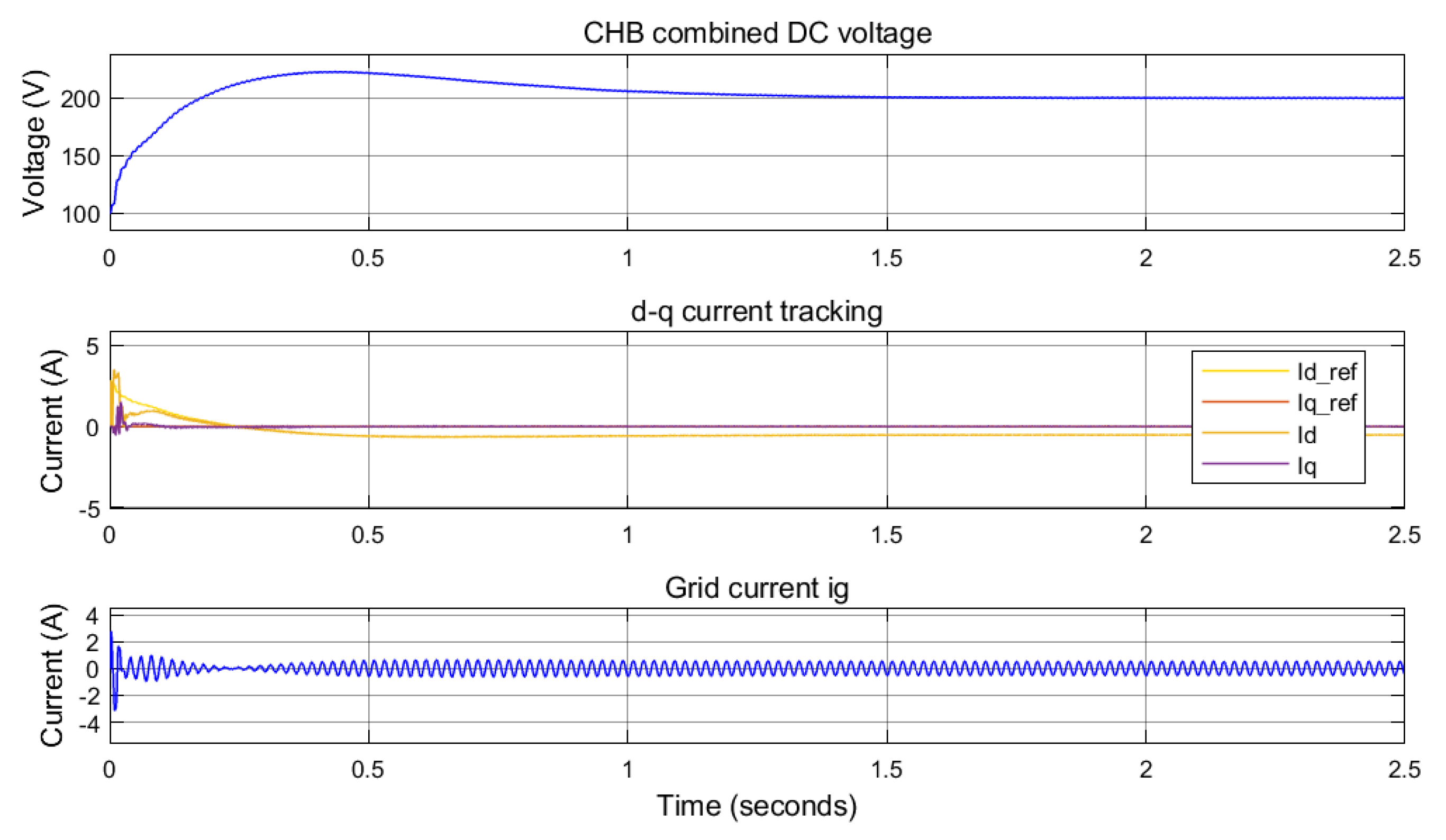
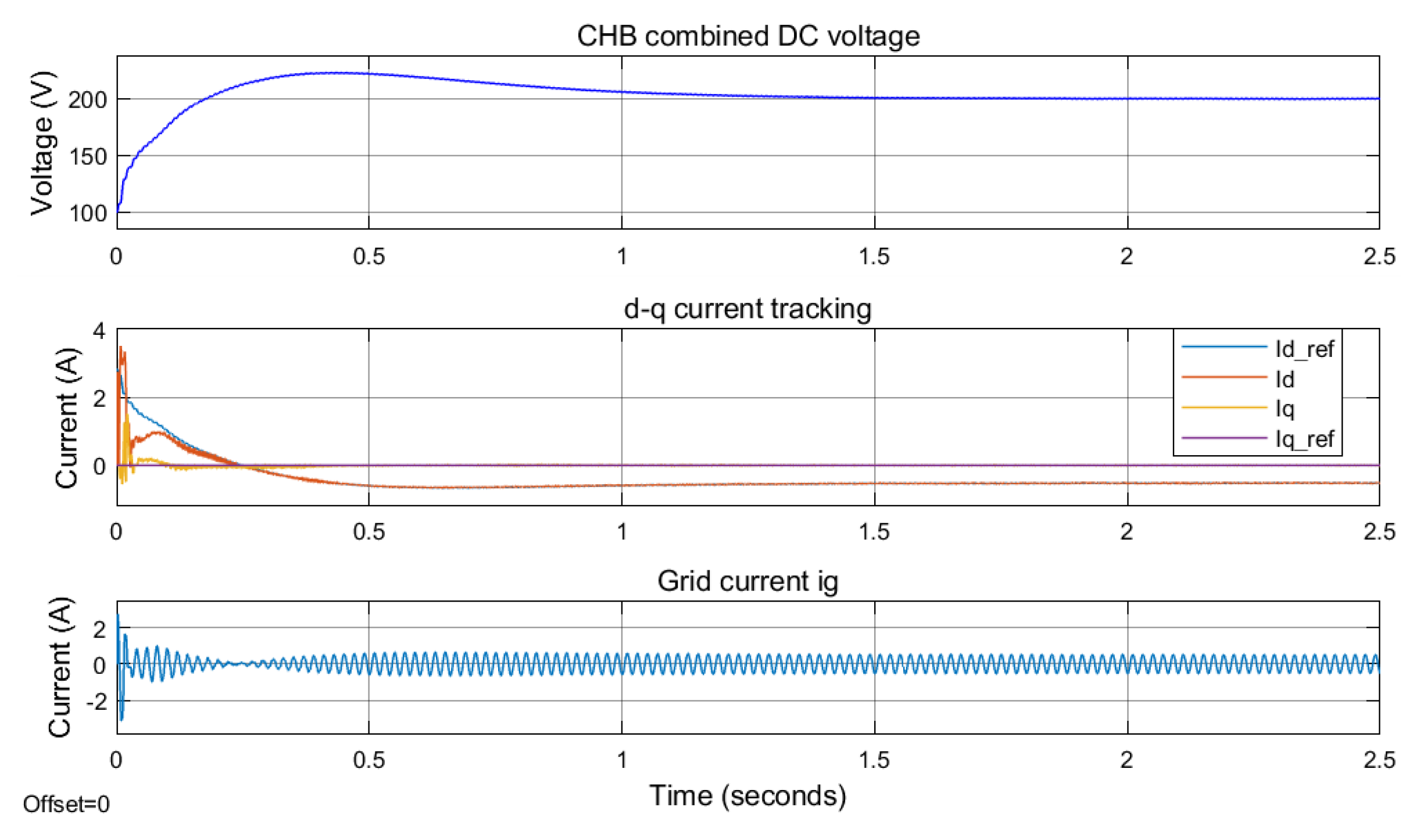
5.3. Current Tracking in the d-q Domain
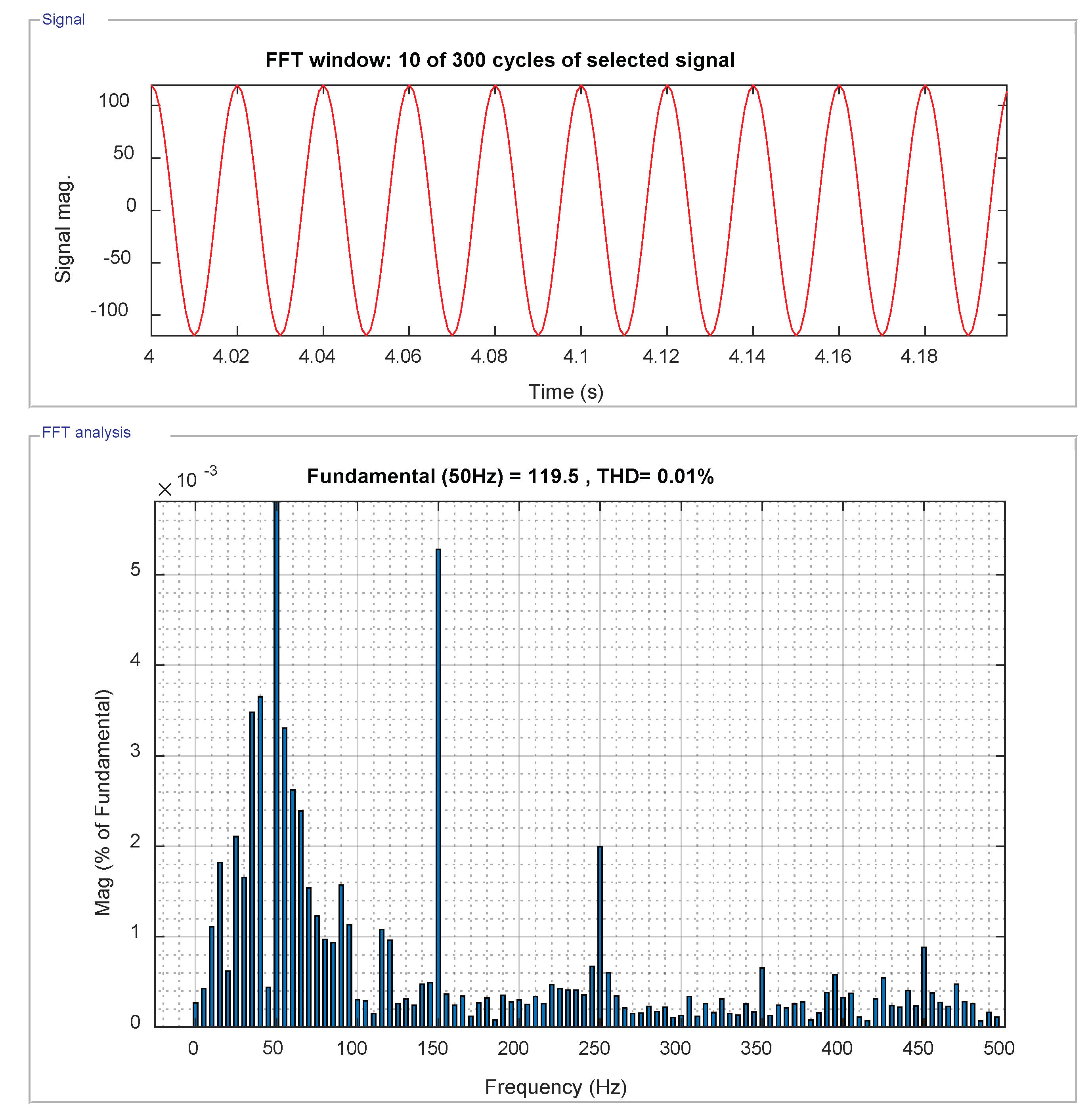
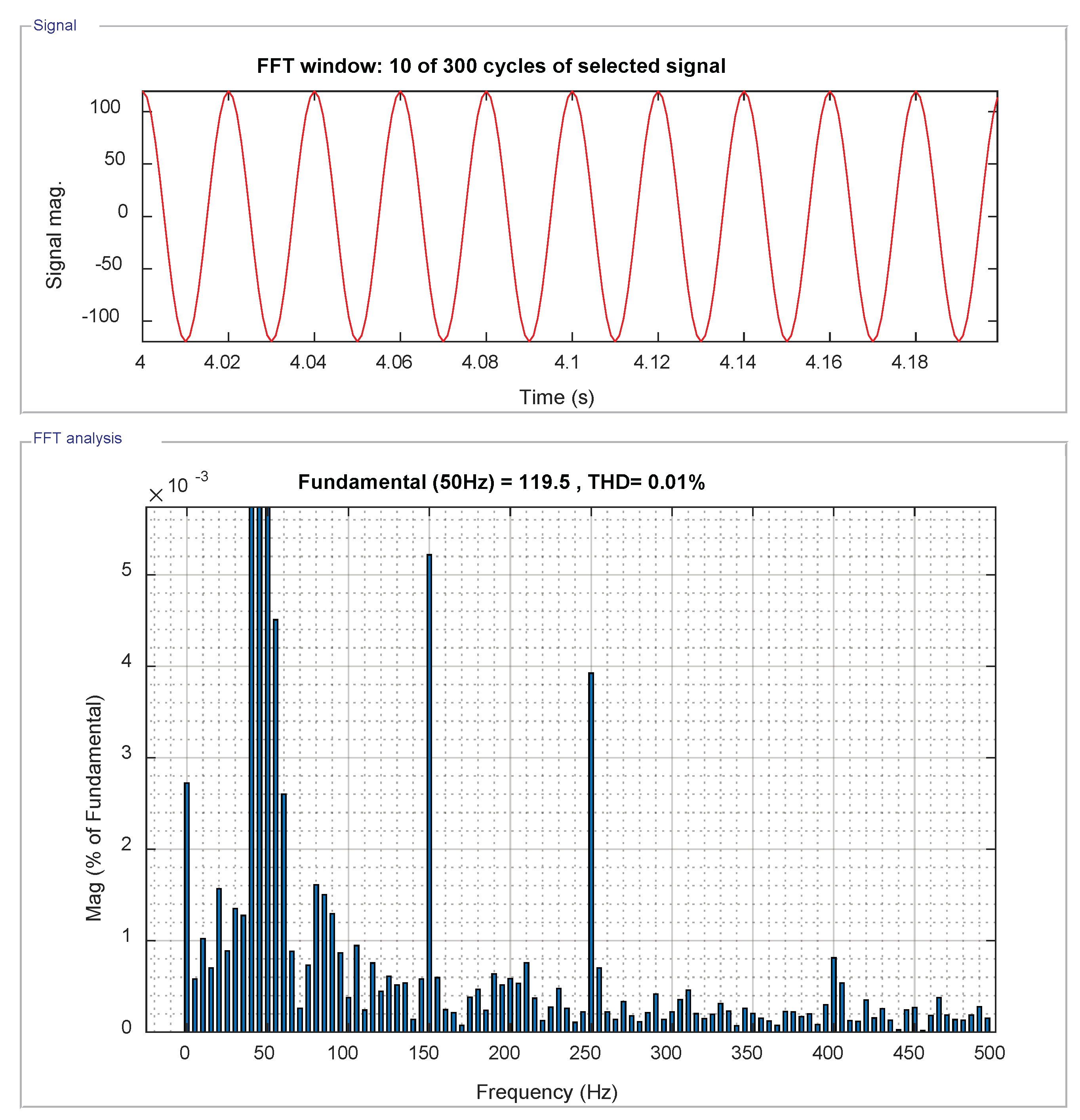
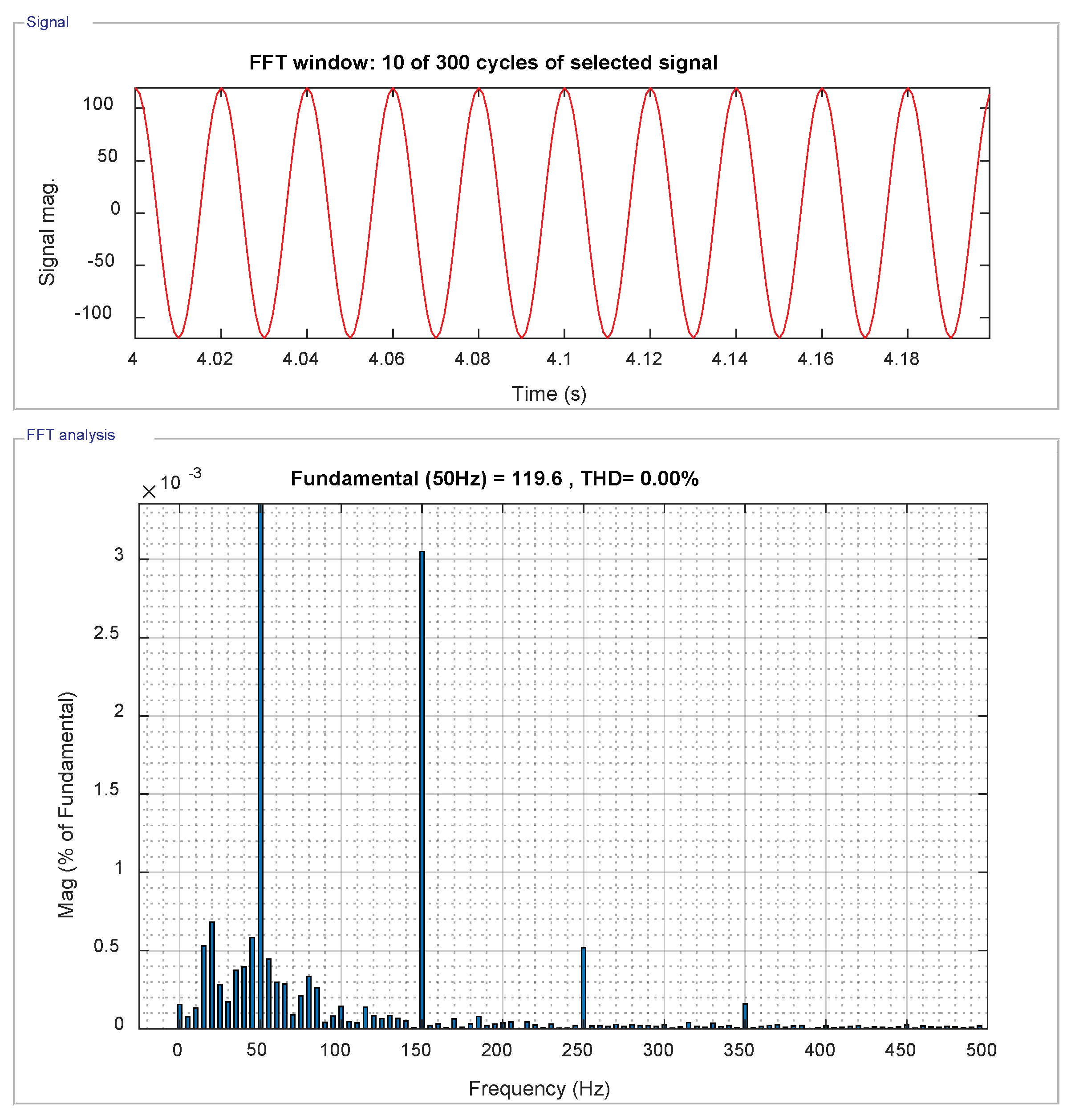
5.4. Total Harmonic Distortion of the Inverter Voltage ()
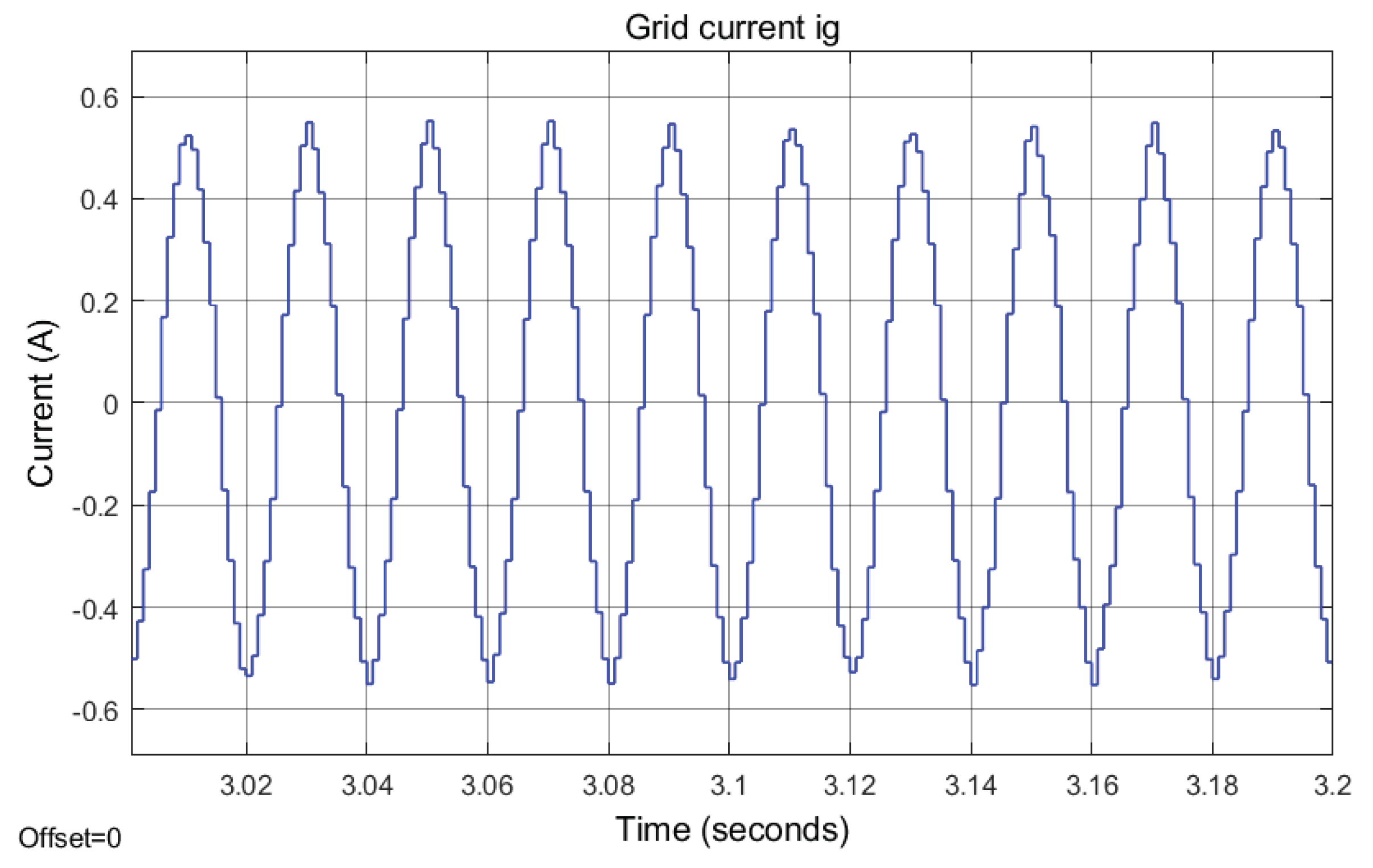
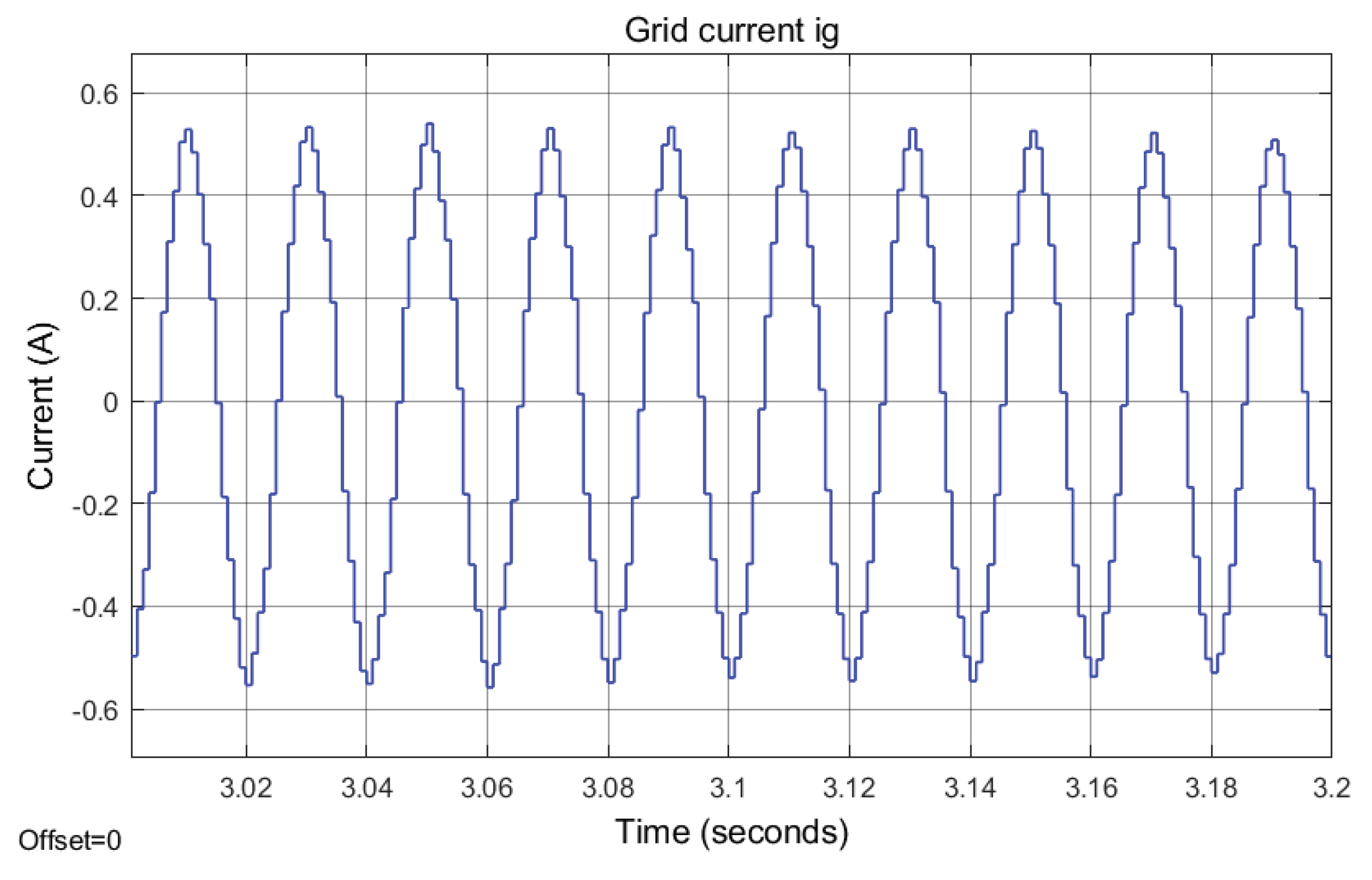
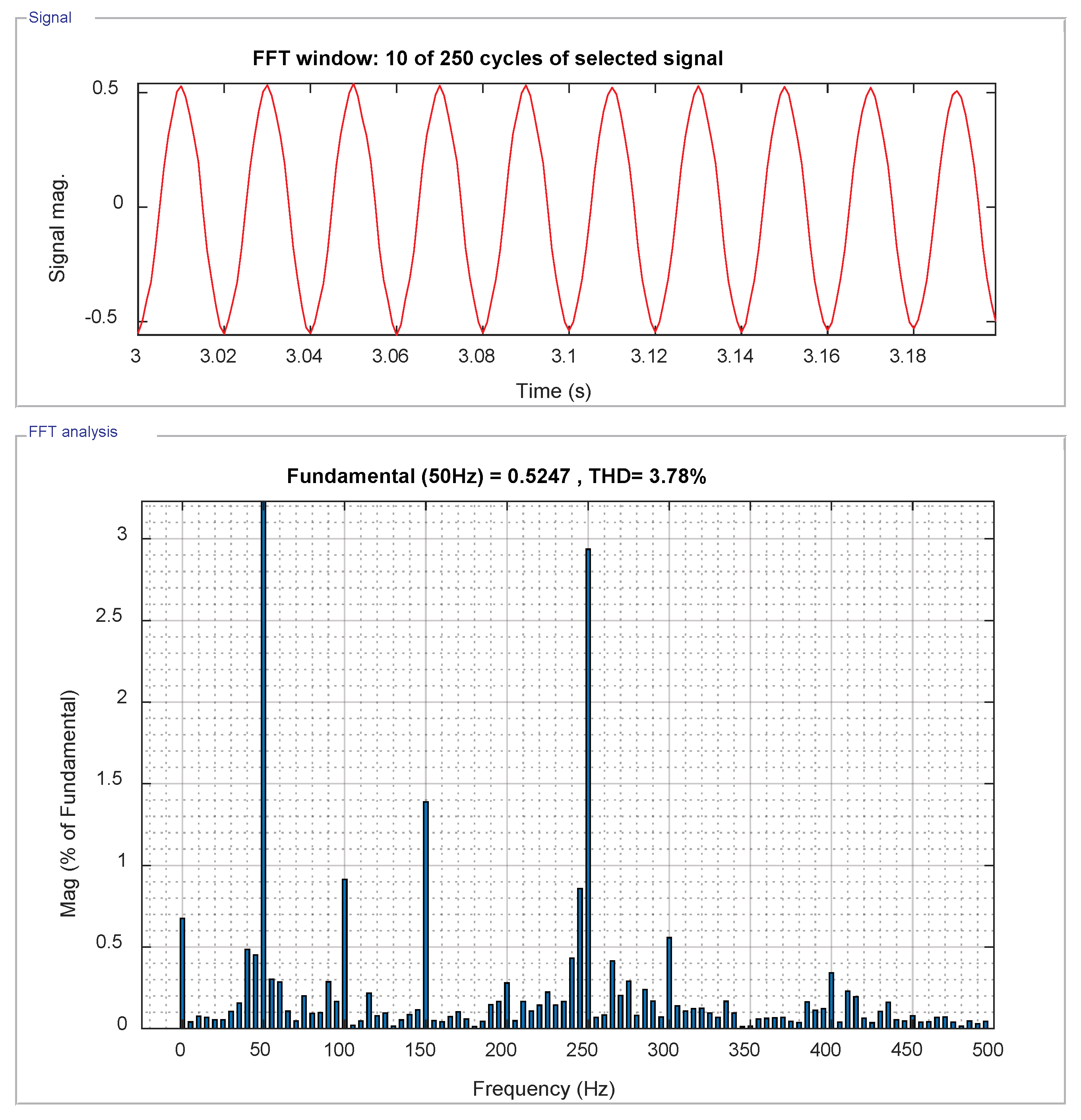
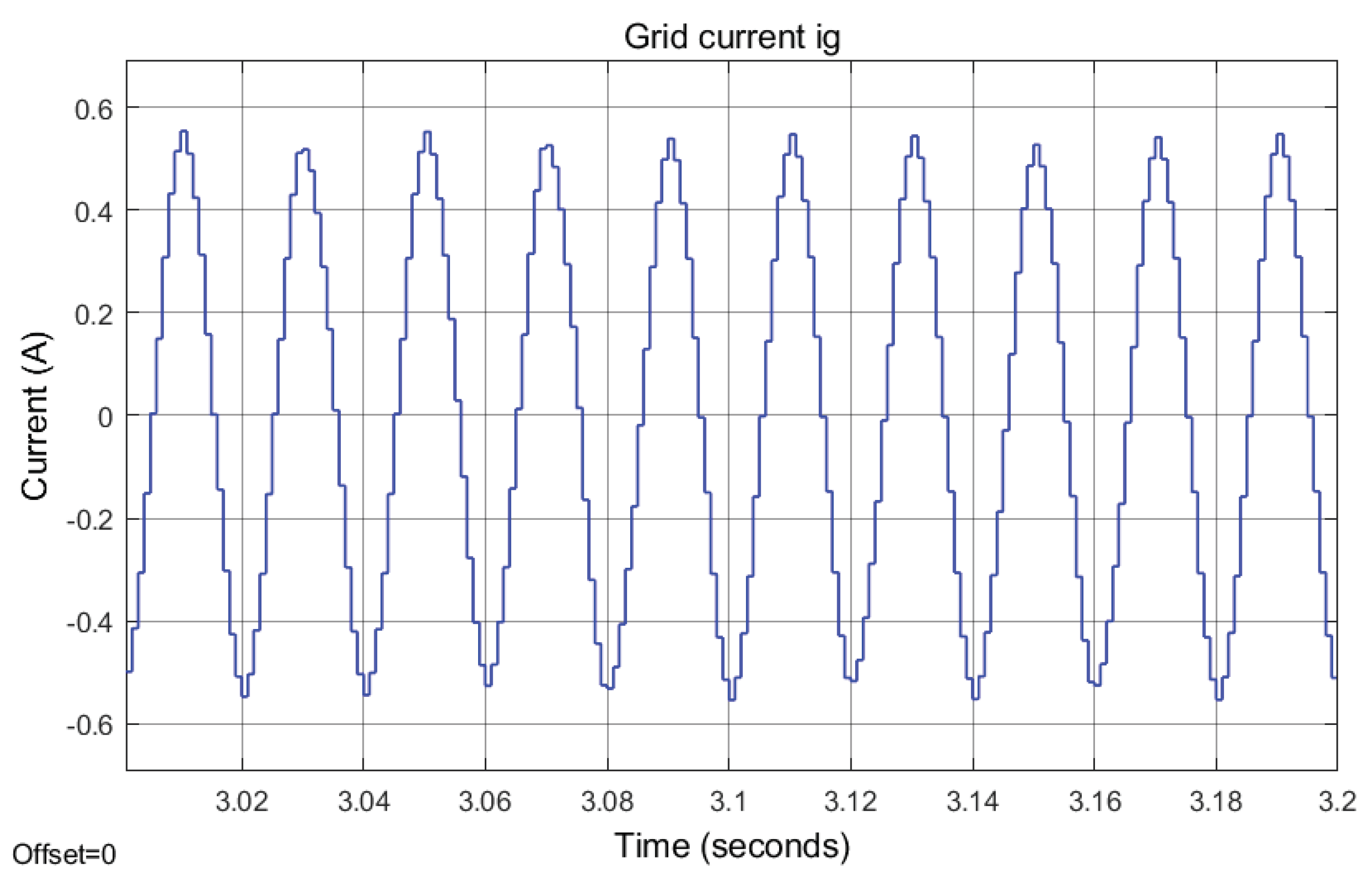
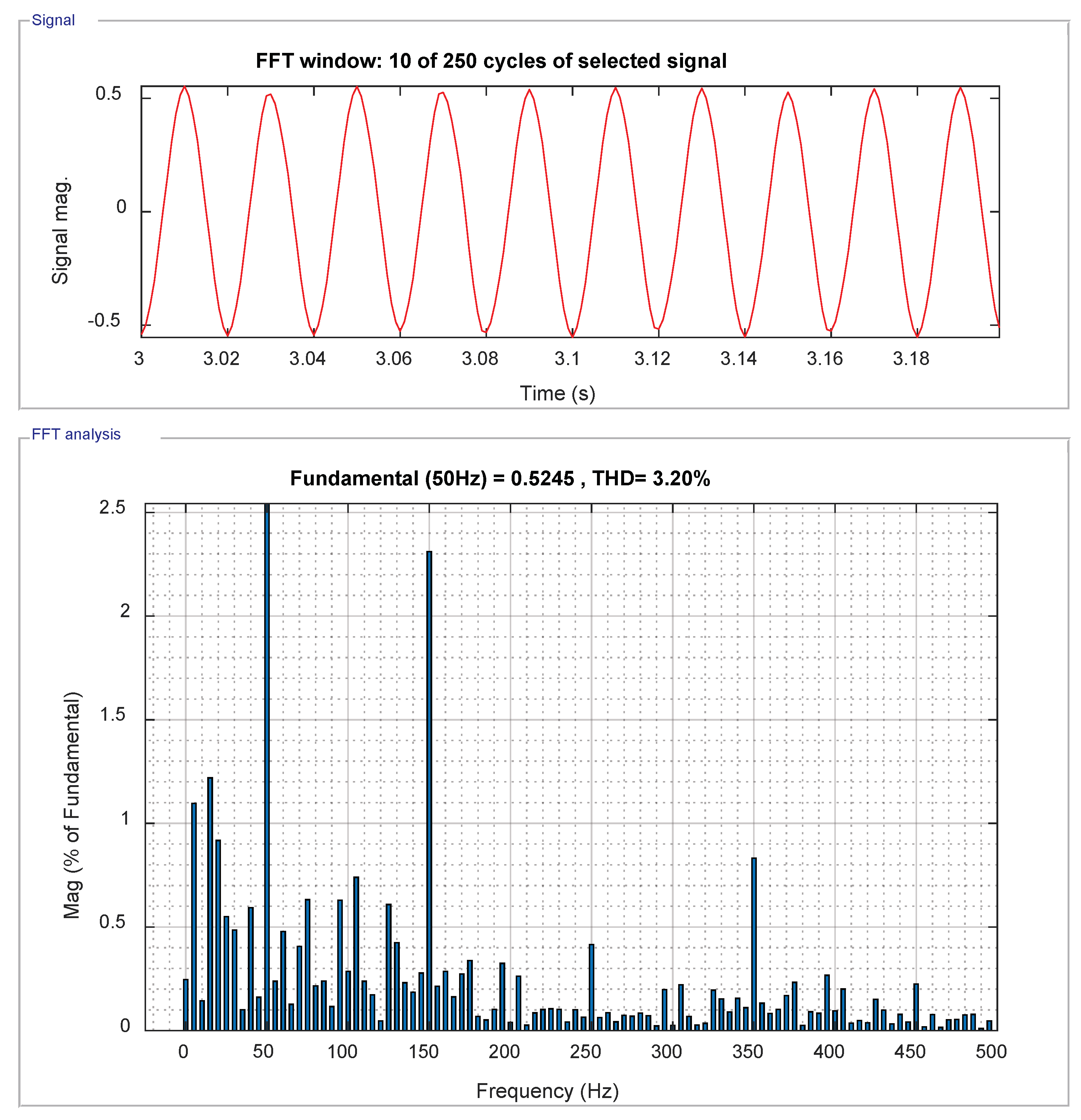
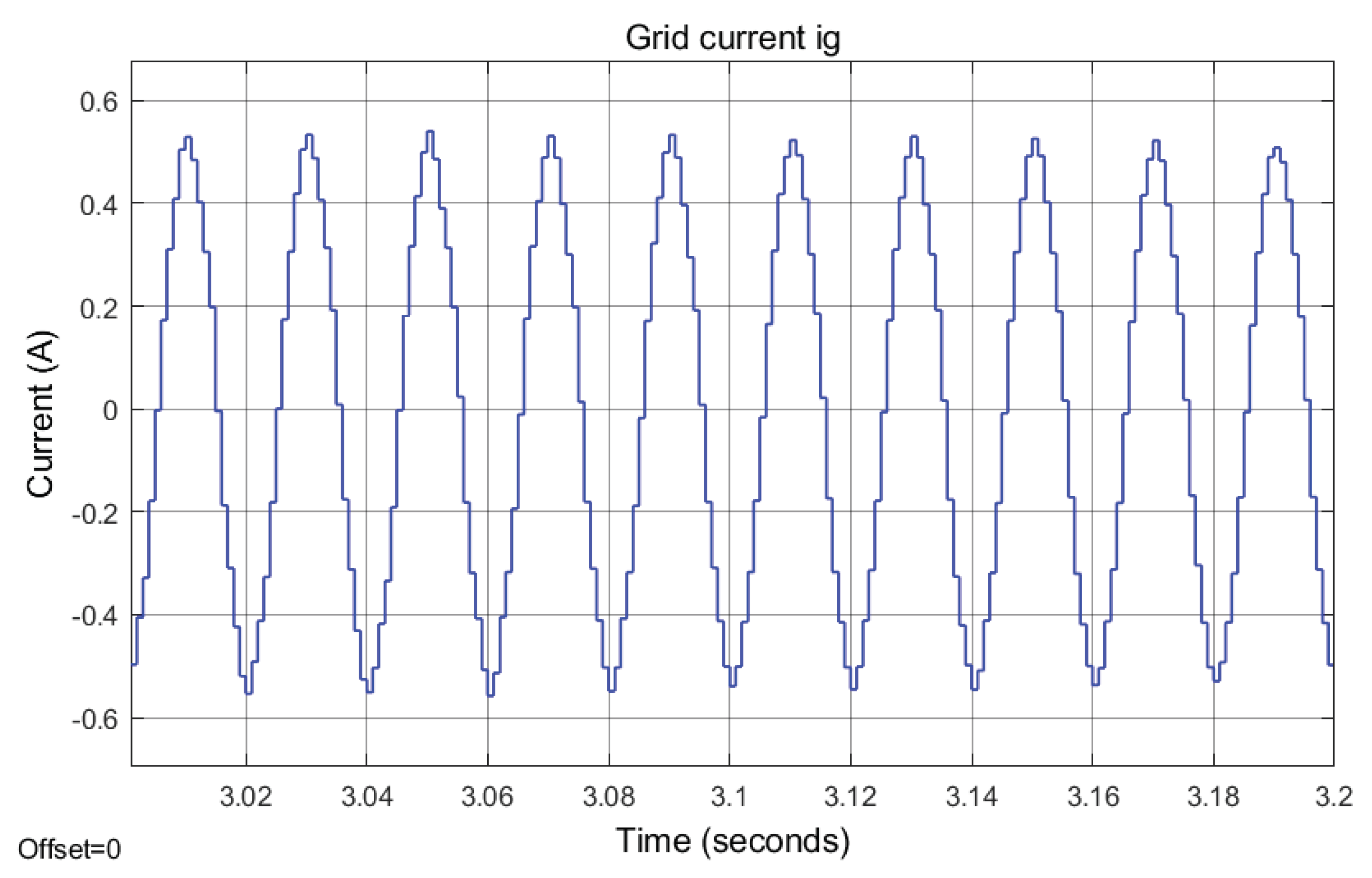
5.5. Total Harmonic Distortion of Grid Current
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CHB | Cascaded H-Bridge |
| DP | Dynamic Programming |
| FATT | Forward Accumulation Through Time |
| GCC | Grid-Connected Converter |
| LM | Levenberg-Marquardt |
| NN | Neural Network |
| PI | Proportional Integral |
| PWM | Pulse Width Modulation |
| RNN | Recurrent Neural Network |
| THD | Total Harmonic Distortion |
References
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Xue, Y.; Chang, L.; Kjær, S.B.; Bordonau, J.; Shimizu, T. Topologies of single-phase inverters for small distributed power generators: An overview. IEEE Trans. Power Electron. 2004, 19, 1305–1314. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, Z.; Wang, F. Overview of high voltage SiC power semiconductor devices: Development and application. CES Trans. Electr. Mach. Syst. 2017, 1, 254–264. [Google Scholar]
- Patil, S.S.; Patil, U.V. Solar photovoltaic power conversion using modular multilevel converter. Int. J. Ind. Electron. Electr. Eng. 2016, 4, 117–122. [Google Scholar]
- Calais, M.; G.Agelidis, V.; Meinhardt, M. Multilevel converters for single-phase grid connected photovoltaic systems: An overview. Solar Energy 1999, 66, 325–335. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.S.; Essakiappan, S.; Enjeti, P.N.; Balog, R.S.; Ahmed, S. A new multilevel converter for Megawatt scale solar photovoltaic utility integration. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1431–1438. [Google Scholar]
- Lai, J.; Peng, F. Multilevel converters—A new breed of power converters. IEEE Trans. Ind. Appl. 1996, 32, 2348–2356. [Google Scholar]
- Krug, D.; Bernet, S.; Fazel, S.S.; Jalili, K.; Malinowski, M. Comparison of 2.3-kV medium-voltage multilevel converters for industrial medium-voltage drives. IEEE Trans. Ind. Electron. 2007, 54, 2979–2992. [Google Scholar] [CrossRef]
- Essakiappan, S.; Krishnamoorthy, H.S.; Enjeti, P.N.; Balong, R.S.; Ahmed, S. Multilevel medium frequency link inverter for utility-scale photovoltaic integration. IEEE Trans. Power Electron. 2015, 30, 3674–3684. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Balakrishnan, S.N.; Biega, V. Adaptive-critic-based neural networks for aircraft optimal control. J. Guid. Control Dyn. 1996, 19, 893–898. [Google Scholar] [CrossRef]
- Prokhorov, D.V.; Wunsch, D.C. Adaptive critic designs. IEEE Trans. Neural Netw. 1997, 8, 997–1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, F.; Zhang, H.; Liu, D. Adaptive dynamic programming: An introduction. IEEE Comput. Intell. Mag. 2009, 4, 39–47. [Google Scholar] [CrossRef]
- Li, S.; Fairbank, M.; Wunsch, D.C.; Alonso, E. Vector Control of a Grid-Connected Rectifier/Inverter Using an Artificial Neural Network. In Proceedings of the IEEE World Congress on Computational Intelligence, Brisbane, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar]
- Li, S.; Fairbank, M.; Johnson, C.; Wunsch, D.C.; Alonso, E.; Proaño, J.L. Artificial neural networks for control of a grid-connected rectifier/inverter under disturbance, dynamic and power converter switching conditions. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 738–750. [Google Scholar] [PubMed]
- Fu, X.; Li, S.; Jaithwa, I. Implement Optimal Vector Control for LCL-Filter-Based Grid-Connected Converters by Using Recurrent Neural Networks. IEEE Trans. Ind. Electron. 2015, 62, 4443–4454. [Google Scholar] [CrossRef]
- Fu, X.; Li, S. Control of single-phase grid-connected converters with LCL filters using recurrent neural network and conventional control methods. IEEE Trans. Power Electron. 2016, 31, 5354–5364. [Google Scholar] [CrossRef]
- Zhang, R.; Cardinal, M.; Szczesny, P.; Dame, M. A grid simulator with control of single-phase power converters in D-Q rotating frame. In Proceedings of the IEEE Power Electronics Specialists Conference, Cairns, Australia, 23–27 June 2002; pp. 1431–1436. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Blasko, V.; Kaura, V. A novel control to actively damp resonance in input LC filter of a three-phase voltage source converter. IEEE Trans. Ind. Appl. 1997, 33, 542–550. [Google Scholar] [CrossRef]
- Peña-Alzola, R.; Liserre, M.; Blaabjerg, F.; Sebastián, R.; Dannehl, J.; Fuchs, F.W. Analysis of the passive damping losses in LCL-filter-based grid converters. IEEE Trans. Power Electron. 2013, 28, 2642–2646. [Google Scholar] [CrossRef]
- Dannehl, J.; Liserre, M.; Fuchs, F.W. Filter-based active damping of voltage source converters with LCL filter. IEEE Trans. Ind. Electron. 2011, 58, 3623–3633. [Google Scholar] [CrossRef]
- Jalili, K.; Bernet, S. Design of LCL filters of active-front-end two level voltage-source converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Hong, Y.K.; Xu, L. Direct-current vector control of three-phase grid-connected rectifier-inverter. Electr. Power Syst. Res. 2011, 81, 357–366. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodrigues, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 1932–4529. [Google Scholar] [CrossRef]
- Caciotta, M.; Giarnetti, S.; Leccese, F.; Orioni, B.; Oreggia, M.; Pucci, C.; Rametta, S. Flavors mapping by Kohonen network classification of panel tests of extra virgin olive oil. Meas. J. Int. Meas. Confed. 2016, 78, 366–372. [Google Scholar] [CrossRef]
- Caciotta, M.; Giarnetti, S.; Leccese, F. Hybrid Neural Network System for Electric Load Forecasting of Telecomunication Station. In Proceedings of the 19th XIX IMEKO World Congress Fundamental and Applied Metrology, Lisbon, Portugal, 6–11 September 2009; pp. 657–661. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 2002. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design, 3rd ed.; John Wiley and Sons: Chichester, West Sussex, UK, 2002. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Li, S.; Fairbank, M.; Wunsch, D.C.; Alonso, E. Training recurrent neural networks with the Levenberg-Marquardt algorithm for optimal control of a grid-connected converter. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1900–1912. [Google Scholar] [CrossRef] [PubMed]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. J. Appl. Math. 1994, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley and Sons: Chichester, West Sussex, UK, 2011. [Google Scholar]
- Castilla, M.; Miret, J.; Matas, J.; de Vicuña, L.G.; Guerrero, J.M. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 4492–4501. [Google Scholar]
- Castilla, M.; Miret, J.; Matas, J.; de Vicuña, L.G.; Guerrero, J.M. Control design guidelines for single-phase grid-connected photovoltaic inverters with damped resonant harmonic compensators. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501. [Google Scholar] [CrossRef]







| Symbol | Quantity | Value | Units |
|---|---|---|---|
| nominal grid voltage (rms) | 120 | V | |
| f | nominal grid frequency | 50 | Hz |
| DC-link voltage | 200 | V | |
| & | LCL filter inductor | 25 | mH |
| & | LCL filter resistor | 0.25 | |
| C | LCL filter parallel capacitor | 2.2 | F |
| & | DC capacitors | 1630 | F |
| the PWM switching frequency | 6000 | Hz | |
| the sampling time | 1 | ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Li, S.; Hadi, A.A.; Challoo, R. Novel Neural Control of Single-Phase Grid-Tied Multilevel Inverters for Better Harmonics Reduction. Electronics 2018, 7, 111. https://doi.org/10.3390/electronics7070111
Fu X, Li S, Hadi AA, Challoo R. Novel Neural Control of Single-Phase Grid-Tied Multilevel Inverters for Better Harmonics Reduction. Electronics. 2018; 7(7):111. https://doi.org/10.3390/electronics7070111
Chicago/Turabian StyleFu, Xingang, Shuhui Li, Abdullah Al Hadi, and Rajab Challoo. 2018. "Novel Neural Control of Single-Phase Grid-Tied Multilevel Inverters for Better Harmonics Reduction" Electronics 7, no. 7: 111. https://doi.org/10.3390/electronics7070111
APA StyleFu, X., Li, S., Hadi, A. A., & Challoo, R. (2018). Novel Neural Control of Single-Phase Grid-Tied Multilevel Inverters for Better Harmonics Reduction. Electronics, 7(7), 111. https://doi.org/10.3390/electronics7070111






