A Dynamic Bayesian Network for Vehicle Maneuver Prediction in Highway Driving Scenarios: Framework and Verification
Abstract
:1. Introduction
Contribution
2. State of the Art
3. System Architecture
4. Dynamic Bayesian Network for Maneuver Prediction
4.1. Network Structure
- -
- LLE/RLE: the existence of a left or right lane next to the occupied lane of the PV.
- -
- LCU: the lane curvature of the road. LCU can decide whether a lane change is probabilistically acceptable. For instance, a lane change is not common in roads with large curvatures.
- -
- LBRV/LARV: the state of an adjacent vehicle before/after the PV in the attention area of the left lane. The state contains the existence, the relative velocity to the PV.
- -
- RBRV/RARV: the state of an adjacent vehicle before/after the PV in the attention area of the right lane.
- -
- FVRV: the state of a leading vehicle of the PV in the attention area of the same lane.
- -
- VC: the classification of the vehicle, which includes a motorcycle, a truck, and an automobile. VC is placed in the causal evidence layer as it is a factor that is evaluated for lane change and will not be changed during the driving.
- -
- TI/BI: the state of turn indicators or brake indicators of the PV, which contains two states: on and off.
- -
- LO: the direction of lateral velocity, which contains two states: left and right.
- -
- YA: the yaw rate to the road tangent.
- -
- BO: the boundary distance to neighboring lane lines.
4.2. Parameter Estimation and Probabilistic Inference
5. Feature Extraction
| Algorithm 1: Extraction algorithm for road-structure features: LLE and RLE |
| Require: (the center point of the PV), (the set of lane lines) Ensure: states of LLE and RLE 1: for all l in do 2: 3: 4: if then 5: 6: else 7: 8: end if 9: end for 10: 11: |
6. Experiments and Results
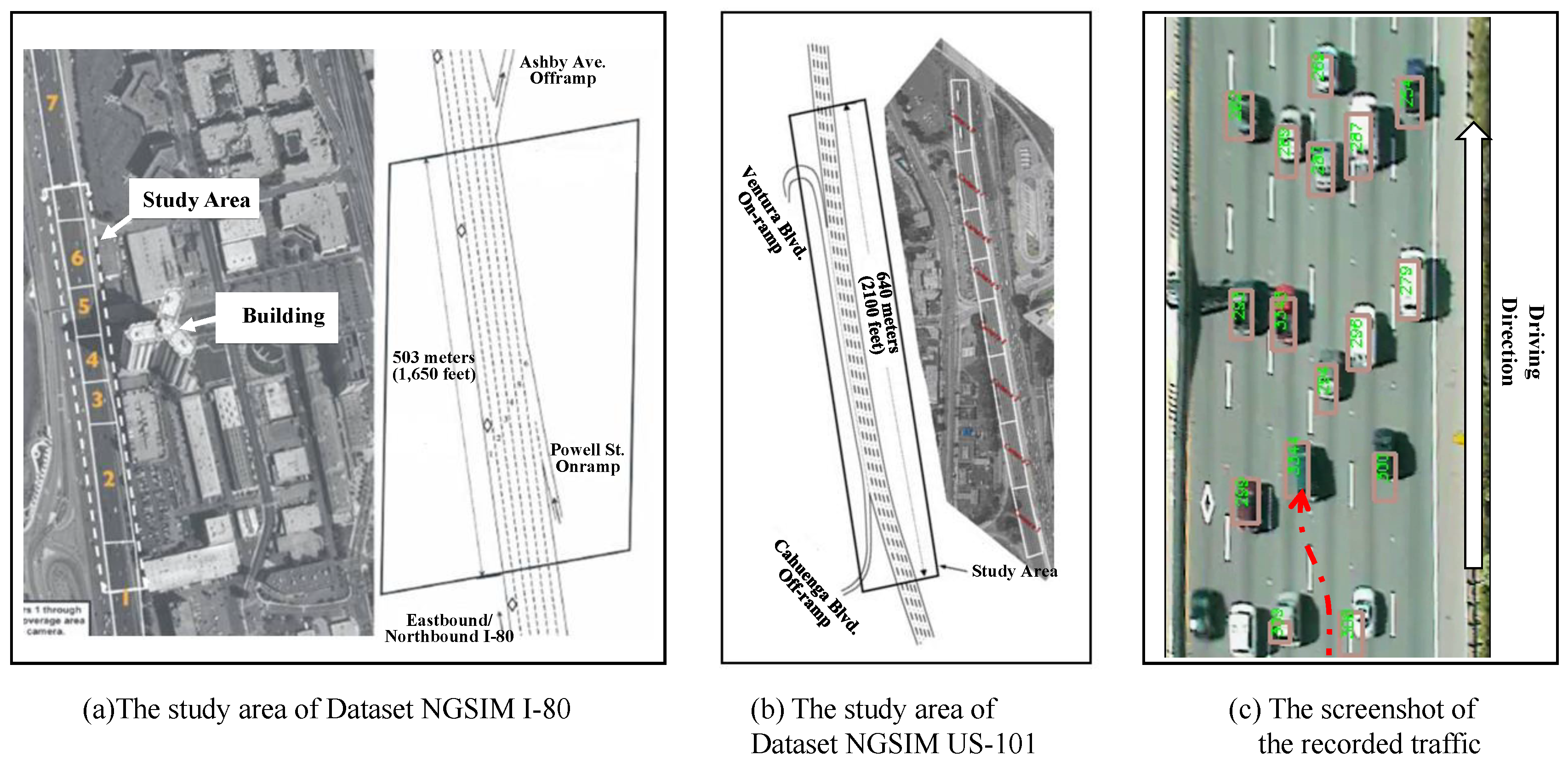
6.1. Datasets
6.2. Selection for Discretized Parameters
6.3. Performance Metrics and Filtering Window
- (1)
- Precision (PRE) is the fraction of correct classification of corresponding lane change out of all events predicted to be positive, i.e.,where means true positive and means false positive.
- (2)
- Recall, also named true positive rate (TPR), is the fraction of correct classification of corresponding lane change out of all true events, i.e.,where means false negative.
- (3)
- F1 Score is the harmonic mean of the two metrics (precision and recall), i.e.,
- (4)
- Accuracy (ACC) is the fraction of correctly classified maneuvers out of all predicted maneuvers, i.e.,where means true negative.
6.4. Comparison with Other Approaches
6.5. Limitation of the Results
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jalal, A.; Sarif, N.; Kim, J.T.; Kim, T.S. Human activity recognition via recognized body parts of human depth silhouettes for residents monitoring services at smart home. Indoor Built Environ. 2013, 22, 271–279. [Google Scholar] [CrossRef]
- Jalal, A.; Rasheed, Y.A. Collaboration achievement along with performance maintenance in video streaming. In Proceedings of the IEEE Conference on Interactive Computer Aided Learning, Villach, Austria, 16–19 October 2007; Volume 2628, p. 18. [Google Scholar]
- Jalal, A.; Kim, J.T.; Kim, T.S. Human activity recognition using the labeled depth body parts information of depth silhouettes. In Proceedings of the 6th International Symposium on Sustainable Healthy Buildings, Seoul, Korea, 10 February 2012; Volume 27. [Google Scholar]
- Jalal, A.; Kim, J.T.; Kim, T.S. Development of a life logging system via depth imaging-based human activity recognition for smart homes. In Proceedings of the 6th International Symposium on Sustainable Healthy Buildings, Seoul, Korea, 10 February 2012; Volume 19. [Google Scholar]
- Jalal, A.; Kim, Y.; Kim, D. Ridge body parts features for human pose estimation and recognition from RGB-D video data. In Proceedings of the International Conference on Computing, Communication and Networking Technologies (ICCCNT), Hefei, China, 11–13 July 2014; pp. 1–6. [Google Scholar]
- Kamal, S.; Jalal, A.; Kim, D. Depth images-based human detection, tracking and activity recognition using spatiotemporal features and modified HMM. J. Electr. Eng. Technol. 2016, 11, 1921–1926. [Google Scholar] [CrossRef]
- Liebner, M.; Ruhhammer, C.; Klanner, F.; Stiller, C. Generic driver intent inference based on parametric models. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, The Hague, The Netherlands, 6–9 October 2013; Volume 5, pp. 268–275. [Google Scholar]
- Xie, G.; Zhang, X.; Gao, H.; Qian, L.; Wang, J.; Ozguner, U. Situational Assessments Based on Uncertainty-Risk Awareness in Complex Traffic Scenarios. Sustainability 2017, 9, 1582. [Google Scholar] [CrossRef]
- Lefèvre, S.; Vasquez, D.; Laugier, C. A survey on motion prediction and risk assessment for intelligent vehicles. ROBOMECH J. 2014, 1, 1. [Google Scholar] [CrossRef]
- Jalal, A.; Kim, S. Global security using human face understanding under vision ubiquitous architecture system. World Acad. Sci. Eng. Technol. 2006, 13, 7–11. [Google Scholar]
- Farooq, A.; Jalal, A.; Kamal, S. Dense RGB-D map-based human tracking and activity recognition using skin joints features and self-organizing map. KSII Trans. Internet Inf. Syst. 2015, 9, 1856–1869. [Google Scholar]
- Kamal, S.; Jalal, A. A hybrid feature extraction approach for human detection, tracking and activity recognition using depth sensors. Arab. J. Sci. Eng. 2016, 41, 1043–1051. [Google Scholar] [CrossRef]
- Xu, W.; Pan, J.; Wei, J.; Dolan, J.M. Motion Planning under Uncertainty for On-Road Autonomous Driving. In Proceedings of the 2014 IEEE International Conference on Robotics & Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2507–2512. [Google Scholar]
- Althoff, M.; Mergel, A. Comparison of Markov chain abstraction and Monte Carlo simulation for the safety assessment of autonomous cars. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1237–1247. [Google Scholar] [CrossRef]
- Liebner, M.; Baumann, M.; Klanner, F.; Stiller, C. Driver intent inference at urban intersections using the intelligent driver model. IEEE Intell. Veh. Symp. Proc. 2012, 1162–1167. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, C.; Lin, Y.; Guillemard, F.; Geronimi, S.; Aioun, F. On-Road Vehicle Trajectory Collection and Scene-Based Lane Change Analysis: Part II. IEEE Trans. Intell. Transp. Syst. 2017, 18, 206–220. [Google Scholar] [CrossRef]
- Althoff, M.; Magdici, S. Set-Based Prediction of Traffic Participants on Arbitrary Road Networks. IEEE Trans. Intell. Veh. 2016, 1, 187–202. [Google Scholar] [CrossRef]
- Koschi, M.; Althoff, M. SPOT: A tool for set-based prediction of traffic participants. IEEE Intell. Veh. Symp. Proc. 2017, 1686–1693. [Google Scholar] [CrossRef] [Green Version]
- Schlechtriemen, J.; Wedel, A.; Hillenbrand, J.; Breuel, G.; Kuhnert, K.D. A Lane Change Detection Approach using Feature Ranking with Maximized Predictive Power. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium (IV), Dearborn, MI, USA, 8–11 June 2014; pp. 108–114. [Google Scholar] [CrossRef]
- Geng, X.; Liang, H.; Yu, B.; Zhao, P.; He, L.; Huang, R. A Scenario-Adaptive Driving Behavior Prediction Approach to Urban Autonomous Driving. Appl. Sci. 2017, 7, 426. [Google Scholar] [CrossRef]
- Hu, M.; Liao, Y.; Wang, W.; Li, G.; Cheng, B.; Chen, F. Decision tree-based maneuver prediction for driver rear-end risk-avoidance behaviors in cut-in scenarios. J. Adv. Transp. 2017, 2017. [Google Scholar] [CrossRef]
- Jo, K.; Lee, M.; Member, S.; Kim, J. Tracking and Behavior Reasoning of Moving Vehicles Based on Roadway Geometry Constraints. IEEE Trans. Intell. Transp. Syst. 2017, 18, 460–476. [Google Scholar] [CrossRef]
- Xie, G.; Gao, H.; Qian, L.; Huang, B.; Li, K.; Wang, J. Vehicle Trajectory Prediction by Integrating Physics- and Maneuver-based Approaches Using Interactive Multiple Models. IEEE Trans. Ind. Electron. 2017, 65, 5999–6008. [Google Scholar] [CrossRef]
- Huang, R.; Liang, H.; Zhao, P.; Yu, B.; Geng, X. Intent-Estimation- and Motion-Model-Based Collision Avoidance Method for Autonomous Vehicles in Urban Environments. Appl. Sci. 2017, 7, 457. [Google Scholar] [CrossRef]
- Xie, G.; Gao, H.; Huang, B.; Qian, L.; Wang, J. A Driving Behavior Awareness Model based on a Dynamic Bayesian Network and Distributed Genetic Algorithm. Int. J. Comput. Intell. Syst. 2018, 11, 469–482. [Google Scholar] [CrossRef]
- Jalal, A.; Kim, Y.H.; Kim, Y.J.; Kamal, S.; Kim, D. Robust human activity recognition from depth video using spatiotemporal multi-fused features. Pattern Recognit. 2017, 61, 295–308. [Google Scholar] [CrossRef]
- Lee, D.; Kwon, Y.P.; Mcmains, S.; Hedrick, J.K. Convolution neural network-based lane change intention prediction of surrounding vehicles for ACC. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Phillips, D.J.; Wheeler, T.A.; Kochenderfer, M.J. Generalizable intention prediction of human drivers at intersections. IEEE Intell. Veh. Symp. Proc. 2017, 1665–1670. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef] [PubMed]
- Altché, F.; de La Fortelle, A. An LSTM Network for Highway Trajectory Prediction. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Yokohama, Japan, 16–19 October 2017. [Google Scholar] [CrossRef]
- Deo, N.; Rangesh, A.; Trivedi, M.M. How would surround vehicles move? A unified uramework for maneuver classification and motion prediction. IEEE Trans. Intell. Veh. 2018, 3, 129–140. [Google Scholar] [CrossRef]
- Kasper, D.; Weidl, G.; Dang, T.; Breuel, G.; Tamke, A.; Rosenstiel, W. Object-oriented Bayesian networks for detection of lane change maneuvers. Intell. Transp. Syst. Mag. 2012, 4, 673–678. [Google Scholar] [CrossRef]
- Gindele, T.; Brechtel, S.; Dillmann, R. Learning driver behavior models from traffic observations for decision making and planning. IEEE Intell. Transp. Syst. Mag. 2015, 7, 69–79. [Google Scholar] [CrossRef]
- Schreier, M.; Willert, V.; Adamy, J. An Integrated Approach to Maneuver-Based Trajectory Prediction and Criticality Assessment in Arbitrary Road Environments. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2751–2766. [Google Scholar] [CrossRef]
- Bahram, M.; Hubmann, C.; Lawitzky, A.; Aeberhard, M.; Wollherr, D. A Combined Model- and Learning-Based Framework for Interaction-Aware Maneuver Prediction. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1538–1550. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Jiang, B.; Zhu, Q. A maneuver-prediction method based on dynamic bayesian network in highway scenarios. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 3392–3397. [Google Scholar]
- Agamennoni, G.; Nieto, J.I.; Nebot, E.M. Estimation of multivehicle dynamics by considering contextual information. IEEE Trans. Robot. 2012, 28, 855–870. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N.; Bach, F. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Koiter, J.R. Visualizing Inference in Bayesian Networks. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 16 June 2006. [Google Scholar]
- Deo, N.; Trivedi, M.M. Convolutional Social Pooling for Vehicle Trajectory Prediction. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar] [CrossRef]
- Scheel, O.; Schwarz, L.; Navab, N.; Tombari, F. Situation Assessment for Planning Lane Changes: Combining Recurrent Models and Prediction. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–26 May 2018; p. 7. [Google Scholar]
- U.S. Department of Transportation. NGSIM—Next Generation Simulation. 2007. Available online: https://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm (accessed on 22 December 2018).
- Zhang, Y.; Lin, Q.; Wang, J.; Verwer, S.; Dolan, J.M. Lane-change Intention Estimation for Car-following Control in Autonomous Driving. IEEE Trans. Intell. Veh. 2018, 3, 276–286. [Google Scholar] [CrossRef]
- Lee, D.; Hansen, A.; Karl Hedrick, J. Probabilistic inference of traffic participants lane change intention for enhancing adaptive cruise control. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 855–860. [Google Scholar] [CrossRef]
- Nilsson, J.; Fredriksson, J.; Coelingh, E. Rule-Based Highway Maneuver Intention Recognition. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Las Palmas, Spain, 15–18 September 2015; pp. 950–955. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the Fifteenth Annual Conference of the International Speech Communication Association, Singapore, 14–18 September 2014. [Google Scholar]







| Applied Features | Approaches | |
|---|---|---|
| Unique | Physics related | motion model [13,14], intelligent driver model [15], prototype trajectory set [16] |
| Road structure-related | set-based prediction [17,18] | |
| Multiple | Without traffic interaction (combined the physics and road structure) | naive Bayesian approach [19], rule-based approach [20], decision tree-based approach [21], interacting multiple model filter [22,23], hidden Markov model [24,25,26] |
| With traffic interaction | convolutional neural network [27], long short-term memory network [28,29,30], interactive hidden Markov model [31], Bayesian network and its variations [32,33,34,35,36] | |
| I-80 | Threshold for BO (Unit:m) | US-101 | Threshold for BO (Unit:m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.5 | 0.7 | 0.9 | 1.1 | 0.3 | 0.5 | 0.7 | 0.9 | 1.1 | ||
| (I) | 0.508 | 0.554 | 0.501 | 0.437 | 0.350 | (IV) | 0.330 | 0.512 | 0.552 | 0.503 | 0.426 |
| (II) | 0.495 | 0.509 | 0.371 | 0.294 | 0.294 | (V) | 0.289 | 0.463 | 0.537 | 0.512 | 0.450 |
| (III) | 0.468 | 0.497 | 0.441 | 0.373 | 0.291 | (VI) | 0.316 | 0.491 | 0.575 | 0.539 | 0.467 |
| I-80 | Threshold for YA (Unit:degree) | US-101 | Threshold for YA (Unit:degree) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1 | 1.5 | 2 | 2.5 | 0.5 | 1 | 1.5 | 2 | 2.5 | ||
| (I) | 0.674 | 0.704 | 0.699 | 0.675 | 0.637 | (IV) | 0.485 | 0.467 | 0.403 | 0.335 | 0.269 |
| (II) | 0.637 | 0.616 | 0.599 | 0.586 | 0.539 | (V) | 0.616 | 0.628 | 0.595 | 0.543 | 0.480 |
| (III) | 0.657 | 0.661 | 0.649 | 0.633 | 0.613 | (VI) | 0.681 | 0.675 | 0.653 | 0.607 | 0.539 |
| I-80 | Threshold for Distance (Unit:m) | US-101 | Threshold for Distance (Unit:m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 60 | 80 | 100 | 120 | 120 | 140 | 160 | 180 | 200 | ||
| (I) | 0.0112 | 0.0116 | 0.0117 | 0.0117 | 0.0117 | (IV) | 0.0091 | 0.0092 | 0.0091 | 0.0091 | 0.0092 |
| (II) | 0.0111 | 0.0114 | 0.0114 | 0.0115 | 0.0114 | (V) | 0.0084 | 0.0084 | 0.0084 | 0.0084 | 0.0084 |
| (III) | 0.0116 | 0.0119 | 0.0119 | 0.0121 | 0.0121 | (VI) | 0.0061 | 0.0061 | 0.0062 | 0.0062 | 0.0062 |
| I-80 | Threshold for Distance (Unit:m) | US-101 | Threshold for Distance (Unit:m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 12 | 14 | 16 | 18 | 10 | 12 | 14 | 16 | 18 | ||
| (I) | 0.0170 | 0.0161 | 0.0153 | 0.0145 | 0.0140 | (IV) | 0.0130 | 0.0127 | 0.0123 | 0.0119 | 0.0118 |
| (II) | 0.0153 | 0.0143 | 0.0135 | 0.0130 | 0.0127 | (V) | 0.0102 | 0.0099 | 0.0096 | 0.0093 | 0.0092 |
| (III) | 0.0149 | 0.0138 | 0.0131 | 0.0127 | 0.0124 | (VI) | 0.0079 | 0.0077 | 0.0074 | 0.0071 | 0.0070 |
| Parameter | Dataset I-80 | Dataset US-101 |
|---|---|---|
| boundary distance threshold to the neighbor lane lines (m) | 0.5 | 0.7 |
| yaw rate threshold to the road tangent (deg) | 0.5 (II) 1 (I), (III) | 0.5 (IV, VI) 1 (V) |
| the distance threshold of attention areas in neighboring lanes (m) | 100 | 200 |
| the distance threshold of front attention area (m) | 10 | 10 |
| Method | Our Approach | MPC-Based [43] | BN Based [34] | RNN Based [41] | HMM Based [44] | Rule Based [45] | ||
|---|---|---|---|---|---|---|---|---|
| Dataset | I-80 | US-101 | I-80 | US-101 | Both | Both | Self-collected | I-80 Only |
| precision | 0.73 | 0.68 | 0.91 | 0.89 | 0.53 | [-] | [-] | [-] |
| recall | 0.99 | 0.89 | 0.70 | 0.74 | 0.72 | [-] | [-] | [-] |
| F1 | 0.83 | 0.76 | 0.78 | 0.81 | 0.61 | [-] | [-] | [-] |
| Accuracy | 0.72 | 0.63 | 0.81 | 0.82 | 0.57 | 0.83–0.89 | 0.91 | 0.39 |
| Prediction time | 2.39 | 5.11 | 4.39 | 4.73 | 1.03 | [-] | 1.5 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Dai, B.; Li, X.; Xu, X.; Liu, D. A Dynamic Bayesian Network for Vehicle Maneuver Prediction in Highway Driving Scenarios: Framework and Verification. Electronics 2019, 8, 40. https://doi.org/10.3390/electronics8010040
Li J, Dai B, Li X, Xu X, Liu D. A Dynamic Bayesian Network for Vehicle Maneuver Prediction in Highway Driving Scenarios: Framework and Verification. Electronics. 2019; 8(1):40. https://doi.org/10.3390/electronics8010040
Chicago/Turabian StyleLi, Junxiang, Bin Dai, Xiaohui Li, Xin Xu, and Daxue Liu. 2019. "A Dynamic Bayesian Network for Vehicle Maneuver Prediction in Highway Driving Scenarios: Framework and Verification" Electronics 8, no. 1: 40. https://doi.org/10.3390/electronics8010040
APA StyleLi, J., Dai, B., Li, X., Xu, X., & Liu, D. (2019). A Dynamic Bayesian Network for Vehicle Maneuver Prediction in Highway Driving Scenarios: Framework and Verification. Electronics, 8(1), 40. https://doi.org/10.3390/electronics8010040





