Fast Imaging of Short Perfectly Conducting Cracks in Limited-Aperture Inverse Scattering Problem
Abstract
:1. Introduction
2. Direct Scattering Problem and Far-Field Pattern
3. Single-Frequency Subspace Migration in Limited-Aperture Problem: Introduction, Analysis, and Numerical Simulations
3.1. Introduction to Imaging Function of Subspace Migration
| Algorithm 1 Procedure of imaging via subspace migration at given wavenumber k. | |
| 1: procedure Subspace migration(k) | |
| 2: Initialize | |
| 3: for to M do | |
| 4: for to N do | |
| 5: collect far-field data | ▹ see (3) |
| 6: end for | |
| 7: end for | |
| 8: perform SVD of | ▹ see (5) |
| 9: select and | ▹ see (6) |
| 10: for do | |
| 11: evaluate and | ▹ see (7) |
| 12: initialize | |
| 13: for to S do | |
| 14: | |
| 15: end for | |
| 16: | |
| 17: end for | |
| 18: plot | |
| 19: end procedure | |
3.2. Analysis of Imaging Function
- 1.
- As and for all , we can examine that when for all s. This means that the terms and does not contribute to the imaging of cracks. Furthermore, due to the oscillating properties of Bessel functions, some artifacts will be appear in the map of .
- 2.
- The imaging performance of is significantly depending on the range of incident and observation directions. For a detail, if the range of incident or observations is narrow, i.e., if the value of either or is small, it will be very hard to recognize the location of because the term , which contributes to the imaging of cracks, is dominate by either or . Otherwise, if the range of both incident and observation directions is wide, it will be possible to obtain good results.
- 3.
- Based on the above observation, eliminating the terms and will be a method of improvement of imaging performance. Notice that since the secrackhing point is arbitrary, it is impossible to make . This means that one must find a condition to satisfyandOne possible selection is , i.e., full-aperture configuration. Another possible option is and . Unfortunately, this selection is ideal because we have no a priori information of the location of cracks. Nevertheless, this selection indicates us that if the range of both incident and observation directions is wider than π, it will be possible to obtain good result via the map of .
- 4.
- As the following asymptotic property holds for sufficiently large kit is possible to eliminate and by applying . However, this is an ideal condition.
- 5.
- In the limited-view problem, i.e., if for with then since , can be expressed asThis is the same result derived in the work by the authors of [17].
- 6.
- In the full-aperture problem, i.e., if then since , can be expressed asThis is the same result derived in [4].
4. Simulation Results
4.1. Imaging of Well-Separated Small Cracks
4.2. Imaging of Closely Located Small Cracks: Resolution Limit
4.3. Further Results: Imaging of Cracks with Neumann Boundary Condition
5. Conclusions
Funding
Conflicts of Interest
References
- Ammari, H.; Garnier, J.; Kang, H.; Park, W.K.; Sølna, K. Imaging schemes for perfectly conducting cracks. SIAM J. Appl. Math. 2011, 71, 68–91. [Google Scholar] [CrossRef]
- Ammari, H.; Garnier, J.; Kang, H.; Lim, M.; Sølna, K. Multistatic imaging of extended targets. SIAM J. Imag. Sci. 2012, 5, 564–600. [Google Scholar] [CrossRef]
- Borcea, L.; Papanicolaou, G.; Vasquez, F.G. Edge illumination and imaging of extended reflectors. SIAM J. Imag. Sci. 2008, 1, 75–114. [Google Scholar] [CrossRef]
- Park, W.K. Multi-frequency subspace migration for imaging of perfectly conducting, arc-like cracks in full- and limited-view inverse scattering problems. J. Comput. Phys. 2015, 283, 52–80. [Google Scholar] [CrossRef] [Green Version]
- Park, W.K. Real-time microwave imaging of unknown anomalies via scattering matrix. Mech. Syst. Signal Proc. 2019, 118, 658–674. [Google Scholar] [CrossRef]
- Acharya, R.; Wasserman, R.; Stevens, J.; Hinojosa, C. Biomedical imaging modalities: A tutorial. Comput. Med. Imaging Graph. 1995, 19, 3–25. [Google Scholar] [CrossRef]
- Kim, C.K.; Lee, J.S.; Chae, J.S.; Park, S.O. A modified stripmap SAR processing for vector velocity compensation using the cross-correlation estimation method. J. Electromagn. Eng. Sci. 2019, 19, 159–165. [Google Scholar] [CrossRef]
- Soldovieri, F.; Solimene, R. Ground penetrating radar subsurface imaging of buried objects. In Radar Technology; Kouemou, G., Ed.; IntechOpen: London, UK, 2010; Chapter 6; pp. 105–126. [Google Scholar]
- Cox, B.T.; Arridge, S.; Beard, P.C. Photoacoustic tomography with a limited-aperture planar sensor and a reverberant cavity. Inverse Probl. 2007, 23, S95–S112. [Google Scholar] [CrossRef]
- Delbary, F.; Erhard, K.; Kress, R.; Potthast, R.; Schulz, J. Inverse electromagnetic scattering in a two-layered medium with an application to mine detection. Inverse Probl. 2008, 24, 015002. [Google Scholar] [CrossRef]
- Mager, R.; Bleistein, N. An examination of the limited aperture problem of physical optics inverse scattering. IEEE Trans. Antennas Propag. 1978, 26, 695–699. [Google Scholar] [CrossRef]
- Taillet, E.; Lataste, J.F.; Rivard, P.; Denis, A. Non-destructive evaluation of cracks in massive concrete using normal dc resistivity logging. NDT E Int. 2014, 63, 11–20. [Google Scholar] [CrossRef]
- Ammari, H.; Kang, H.; Lee, H.; Park, W.K. Asymptotic imaging of perfectly conducting cracks. SIAM J. Sci. Comput. 2010, 32, 894–922. [Google Scholar] [CrossRef]
- Chen, X. Computational Methods for Electromagnetic Inverse Scattering; Wiley-IEEE: Hoboken, NJ, USA, 2018. [Google Scholar]
- Kress, R. Inverse scattering from an open arc. Math. Meth. Appl. Sci. 1995, 18, 267–293. [Google Scholar] [CrossRef]
- Ahn, C.Y.; Jeon, K.; Park, W.K. Analysis of MUSIC-type imaging functional for single, thin electromagnetic inhomogeneity in limited-view inverse scattering problem. J. Comput. Phys. 2015, 291, 198–217. [Google Scholar] [CrossRef]
- Kwon, Y.M.; Park, W.K. Analysis of subspace migration in limited-view inverse scattering problems. Appl. Math. Lett. 2013, 26, 1107–1113. [Google Scholar] [CrossRef]
- Nazarchuk, Z.T. Singular Integral Equations in Diffraction Theory; Mathematics and Applications Series; Karpenko Physicomechanical Institute, Ukrainian Academy of Sciences: Lviv, Ukraine, 1994. [Google Scholar]
- Ammari, H. An Introduction to Mathematics of Emerging Biomedical Imaging; Mathematics and Applications Series; Springer: Berlin, Germany, 2008; Volume 62. [Google Scholar]
- Hou, S.; Sølna, K.; Zhao, H. A direct imaging algorithm for extended targets. Inverse Problems 2006, 22, 1151–1178. [Google Scholar] [CrossRef]
- Park, W.K. Asymptotic properties of MUSIC-type imaging in two-dimensional inverse scattering from thin electromagnetic inclusions. SIAM J. Appl. Math. 2015, 75, 209–228. [Google Scholar] [CrossRef]
- Park, W.K. A novel study on subspace migration for imaging of a sound-hard arc. Comput. Math. Appl. 2017, 74, 3000–3007. [Google Scholar] [CrossRef]
- Park, W.K.; Lesselier, D. Electromagnetic MUSIC-type imaging of perfectly conducting, arc-like cracks at single frequency. J. Comput. Phys. 2009, 228, 8093–8111. [Google Scholar] [CrossRef]
- Park, W.K.; Lesselier, D. MUSIC-type imaging of a thin penetrable inclusion from its far-field multistatic response matrix. Inverse Probl. 2009, 25, 075002. [Google Scholar] [CrossRef]
- Hou, S.; Sølna, K.; Zhao, H. A direct imaging method using far-field data. Inverse Probl. 2007, 23, 1533–1546. [Google Scholar] [CrossRef] [Green Version]
- Ammari, H.; Iakovleva, E.; Lesselier, D. A MUSIC algorithm for locating small inclusions buried in a half-space from the scattering amplitude at a fixed frequency. Multiscale Model. Sim. 2005, 3, 597–628. [Google Scholar] [CrossRef]
- Ammari, H.; Kang, H. Reconstruction of Small Inhomogeneities from Boundary Measurements; Lecture Notes in Mathematics; Springer-Verlag: Berlin, Germany, 2004; Volume 1846. [Google Scholar]
- Marengo, E.A.; Gruber, F.K.; Simonetti, F. Time-reversal MUSIC imaging of extended targets. IEEE Trans. Image Process. 2007, 16, 1967–1984. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Chen, X. MUSIC imaging and electromagnetic inverse scattering of multiple-scattering small anisotropic spheres. IEEE Trans. Antennas Propag. 2007, 55, 3542–3549. [Google Scholar] [CrossRef]

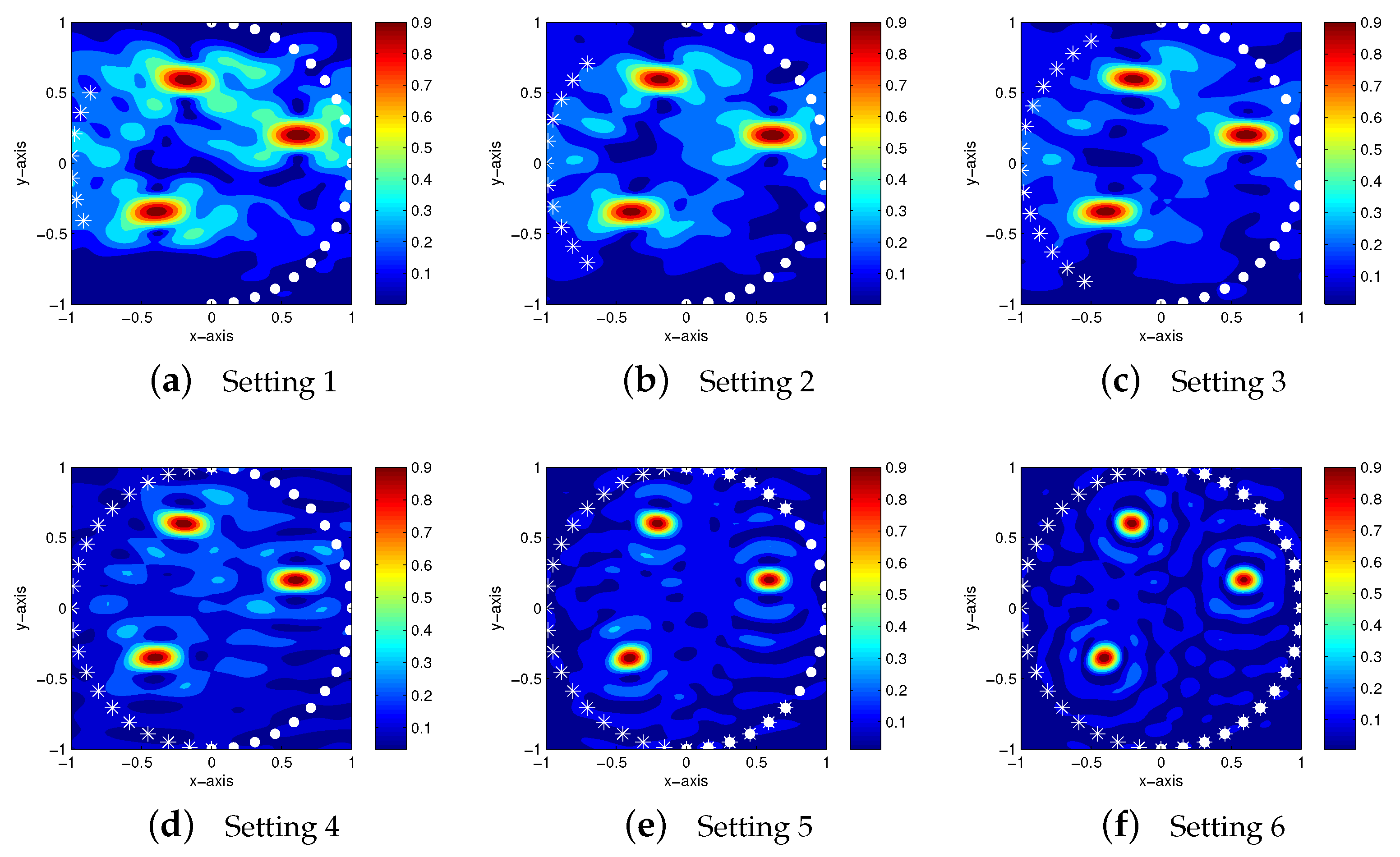
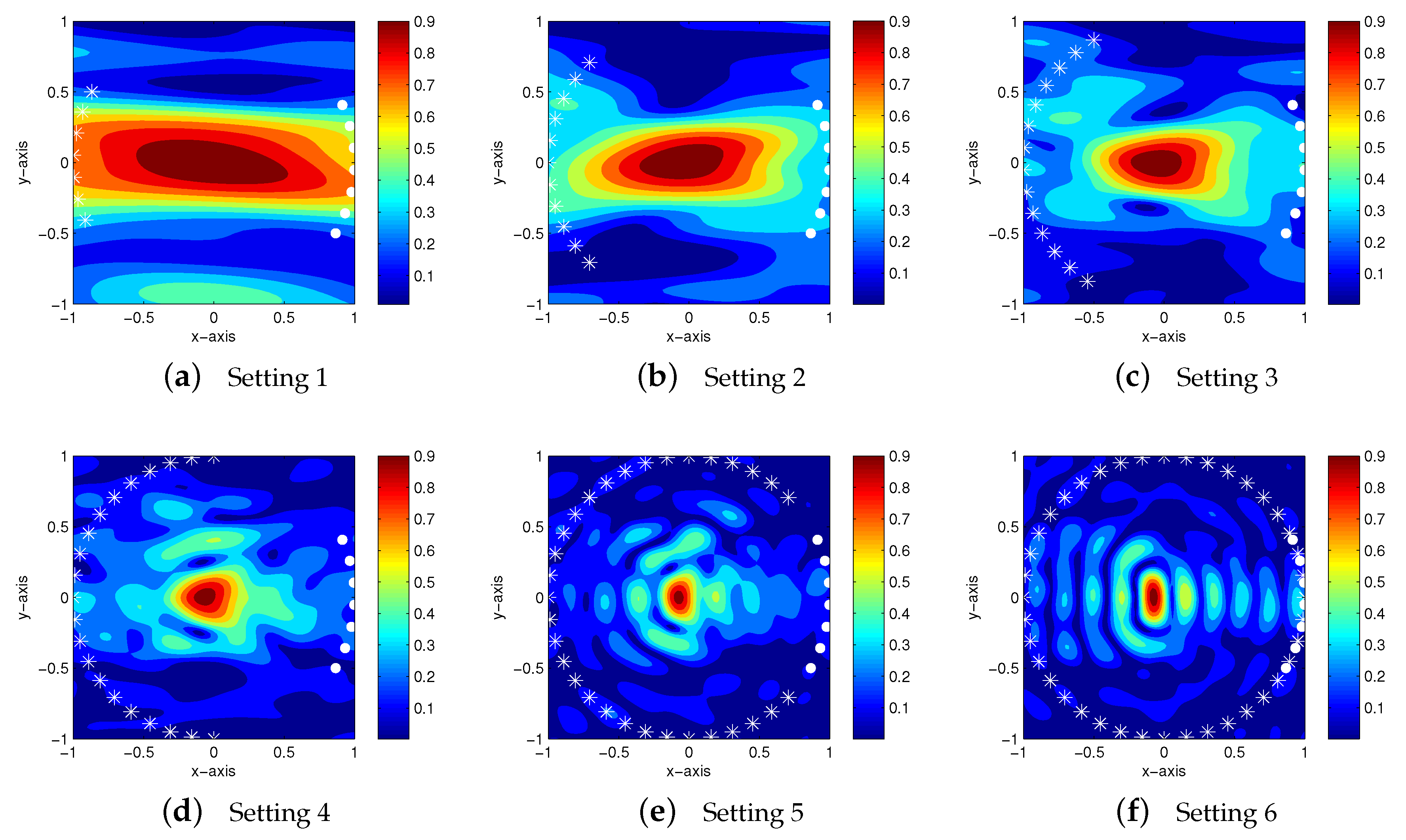
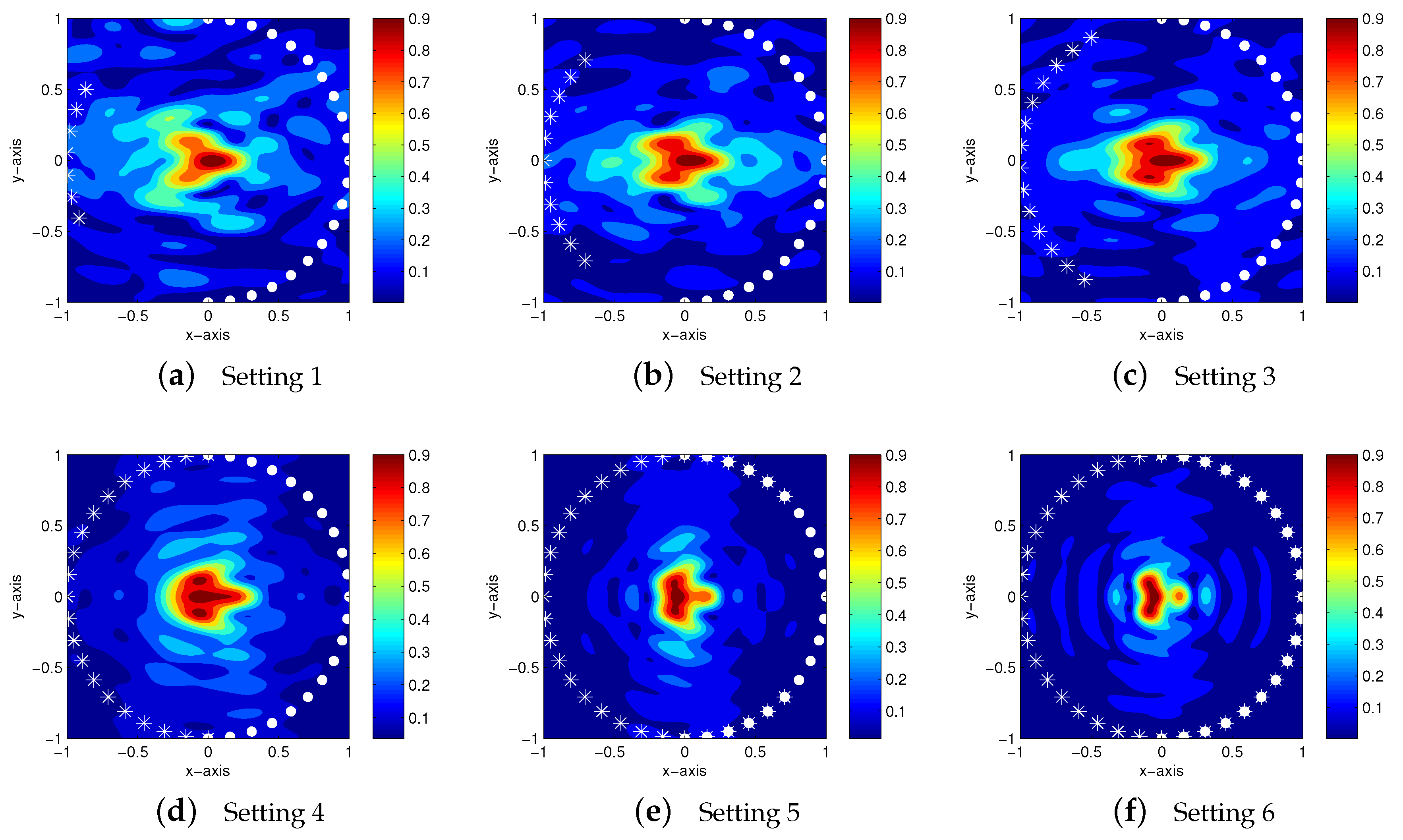
| Setting 1 | Setting 2 | Setting 3 | Setting 4 | Setting 5 | Setting 6 | |
|---|---|---|---|---|---|---|
| 0 | ||||||
| M | 7 | 11 | 14 | 21 | 31 | 41 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, W.-K. Fast Imaging of Short Perfectly Conducting Cracks in Limited-Aperture Inverse Scattering Problem. Electronics 2019, 8, 1050. https://doi.org/10.3390/electronics8091050
Park W-K. Fast Imaging of Short Perfectly Conducting Cracks in Limited-Aperture Inverse Scattering Problem. Electronics. 2019; 8(9):1050. https://doi.org/10.3390/electronics8091050
Chicago/Turabian StylePark, Won-Kwang. 2019. "Fast Imaging of Short Perfectly Conducting Cracks in Limited-Aperture Inverse Scattering Problem" Electronics 8, no. 9: 1050. https://doi.org/10.3390/electronics8091050





