Measuring the Lense–Thirring Orbital Precession and the Neutron Star Moment of Inertia with Pulsars
Abstract
:1. Introduction
1.1. The Equation of State of Dense Matter
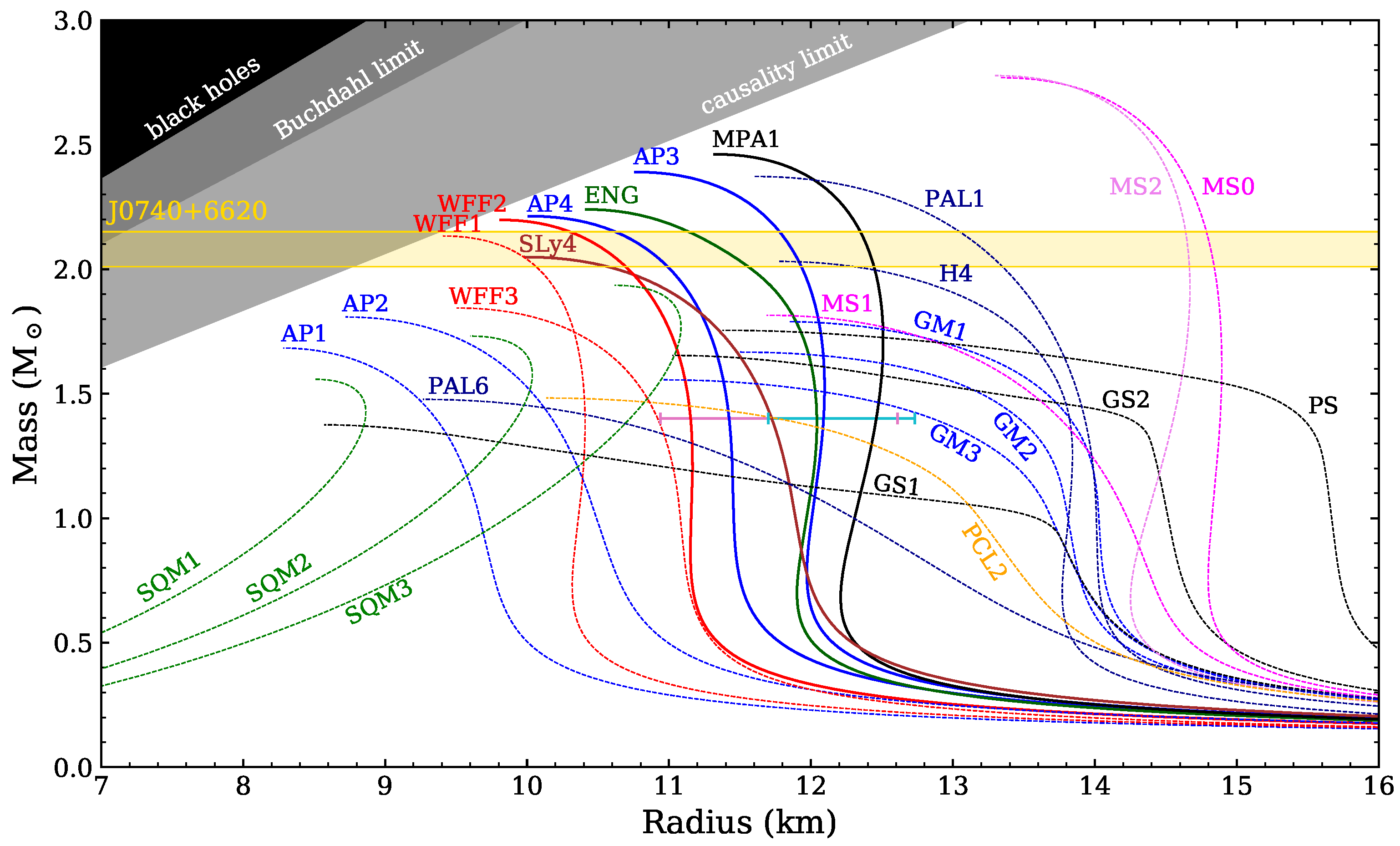
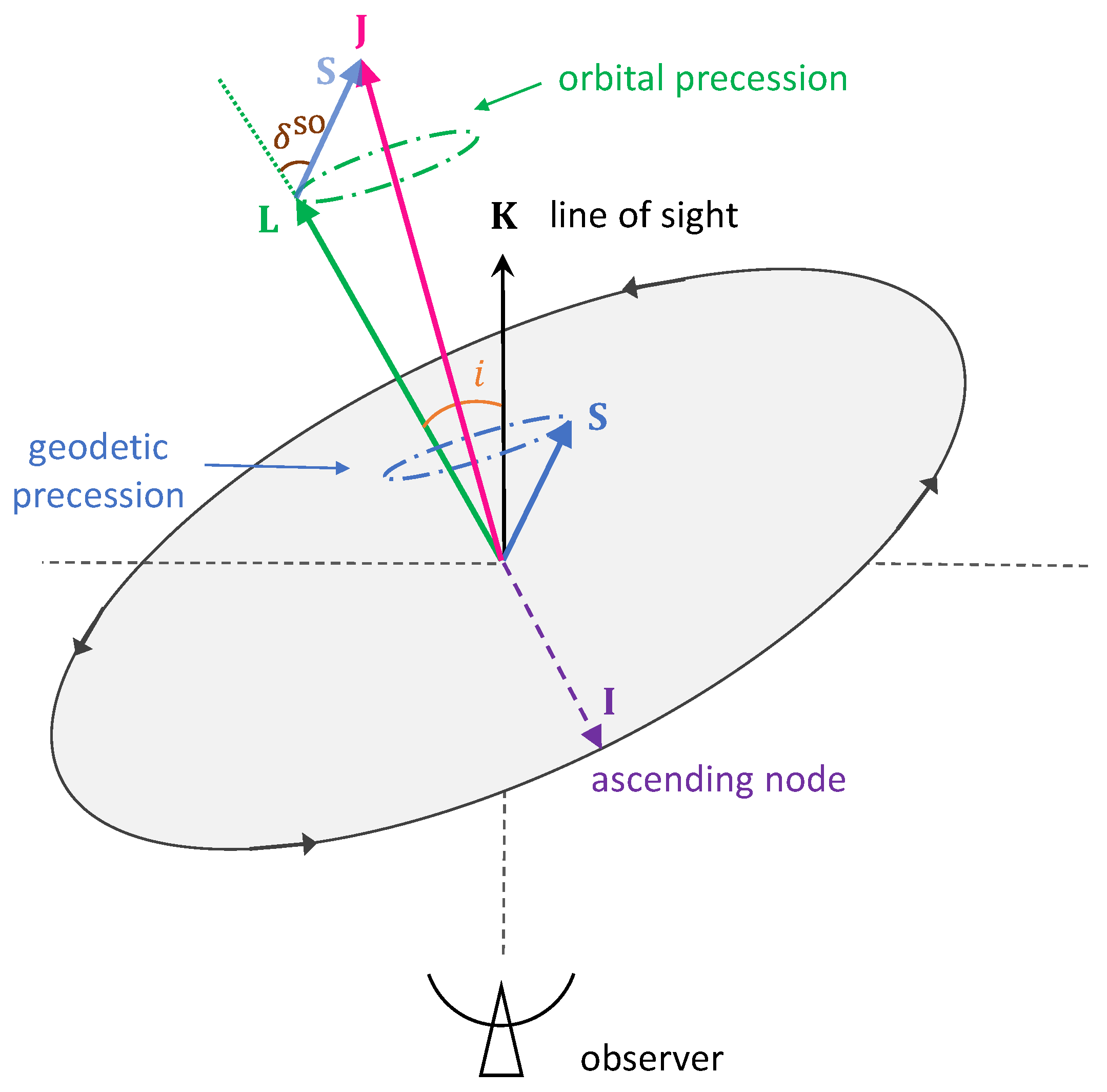
1.2. Spin–Orbit Coupling and Geodetic Precession
2. The Lense–Thirring Precession
2.1. Spin–Orbit Coupling in Periastron Advance
2.2. Spin–Orbit Coupling in Orbital Inclination
3. Evolution of Binary Pulsars
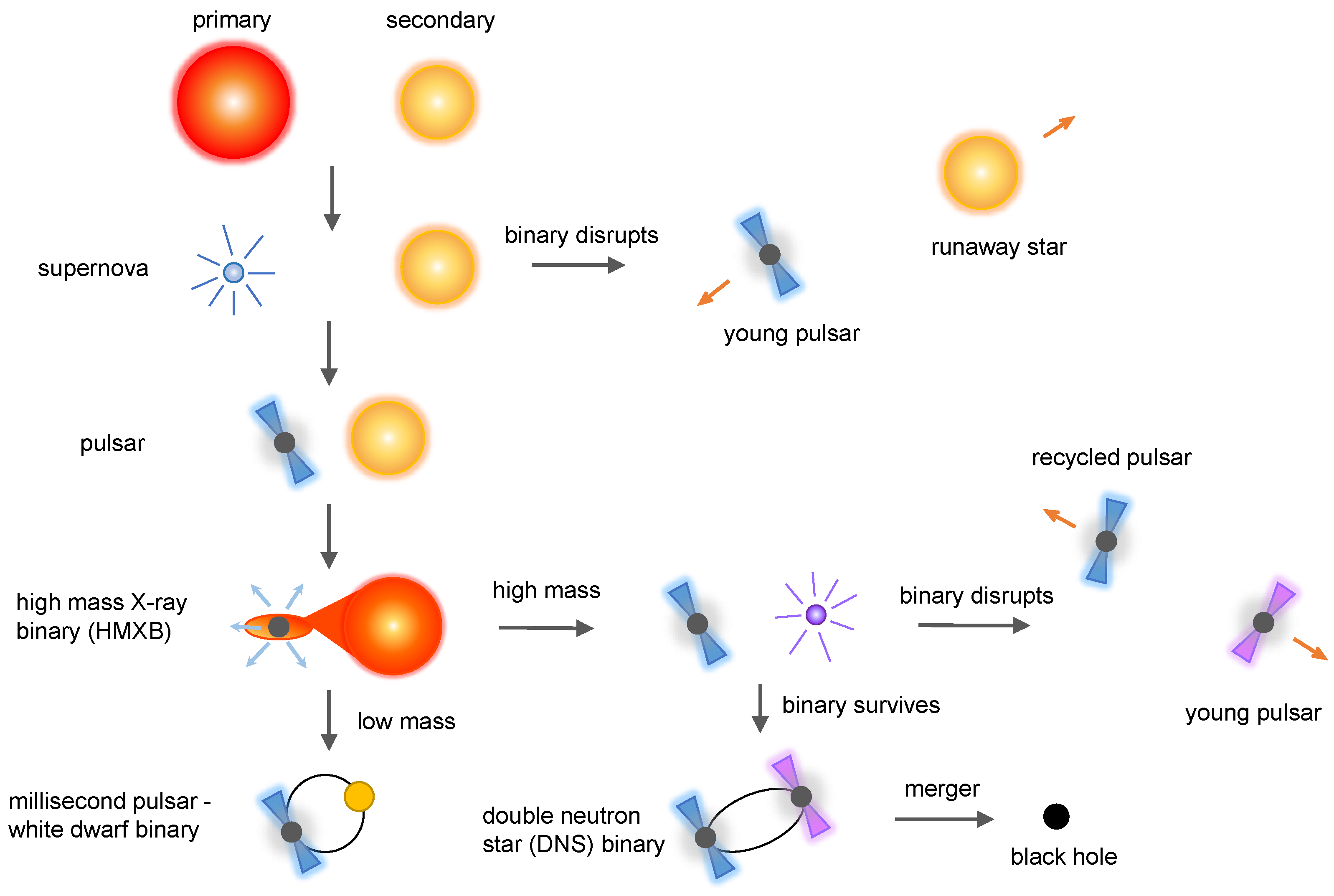
3.1. Types of Binary Pulsars
- If it is massive enough, it will also go through an SN explosion; the system then either disrupts (a likely occurrence) or forms an eccentric DNS system, which will consist of a recycled pulsar and a short-lived “normal” pulsar. The high risk of disruption makes these systems relatively rare (<1%). These systems are necessarily eccentric because of the mass loss and the kick associated with the SN (the average kick for young isolated radio pulsars is 400–500 [68,69]; this is likely to be slightly less in binary systems). Because of this kick, the orbital plane after the SN might become very different from what it was before the explosion, causing a misalignment between the spin of the recycled pulsar and the orbital angular momentum. The most compact of these systems will coalesce in a Hubble time, forming a light black hole (BH) (for an extensive discussion on these systems, see [70]).
- If the secondary is light, then it will slowly evolve into a WD star. In this case, the system will retain a low orbital eccentricity and the alignment between the spin and orbital angular momentum.
3.2. Suitability for Measurements of LT Precession
4. Measuring the LT Precession via Pulsar Timing
4.1. Lense–Thirring Precession in
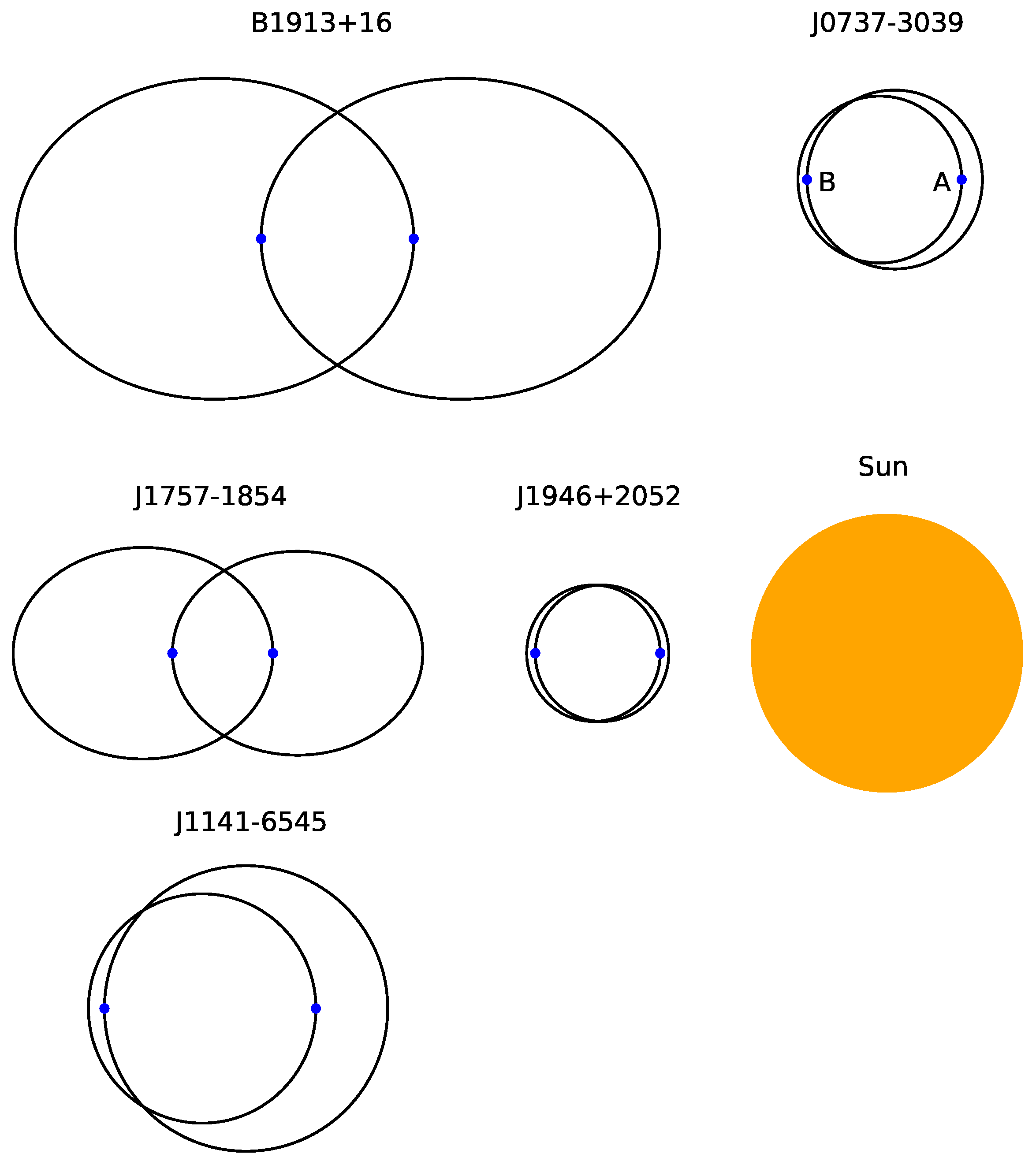
4.1.1. PSR J1141−6545, a Young Pulsar with a Massive White Dwarf Companion
4.1.2. PSR J1757−1854, the Most Accelerated Binary Pulsar
4.2. Lense–Thirring Precession in
4.2.1. PSR J0737−3039A/B, the Unique Double-Pulsar System
4.2.2. Measure the Neutron Star Moment of Inertia with , and
4.2.3. PSR J1946+2052, the Most Compact Double-Neutron Star System
5. PSR J0514−4002E, a Massive Binary with a Companion in the Mass Gap
6. Future Discoveries
7. Summary and Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BH | black hole |
| DNS | double-neutron star |
| EoS | equation of state |
| GR | General Relativity |
| GW | gravitational wave |
| LT | Lense–Thirring |
| MoI | moment of inertia |
| NS | neutron star |
| PSR | pulsar |
| SBH | stellar-mass black hole |
| SN | supernova |
| UFF | universality of free fall |
| WD | white dwarf |
References
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M. Neutron Star Mass and Radius Measurements. Universe 2019, 5, 159. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625–632. [Google Scholar] [CrossRef]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef] [PubMed]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Am. Astron. Soc. 2021, 915, L12. [Google Scholar] [CrossRef]
- Koehn, H.; Rose, H.; Pang, P.T.H.; Somasundaram, R.; Reed, B.T.; Tews, I.; Abac, A.; Komoltsev, O.; Kunert, N.; Kurkela, A.; et al. An overview of existing and new nuclear and astrophysical constraints on the equation of state of neutron-rich dense matter. arXiv 2024, arXiv:2402.04172. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952−0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Linares, M.; Shahbaz, T.; Casares, J. Peering into the Dark Side: Magnesium Lines Establish a Massive Neutron Star in PSR J2215+5135. Astrophys. J. 2018, 859, 54. [Google Scholar] [CrossRef]
- van Kerkwijk, M.H.; Breton, R.P.; Kulkarni, S.R. Evidence for a massive neutron star from a radial-velocity study of the companion to the black-widow pulsar PSR B1957+20. Astrophys. J. 2011, 728, 95. [Google Scholar] [CrossRef]
- Clark, C.J.; Kerr, M.; Barr, E.D.; Bhattacharyya, B.; Breton, R.P.; Bruel, P.; Camilo, F.; Chen, W.; Cognard, I.; Cromartie, H.T.; et al. Neutron star mass estimates from gamma-ray eclipses in spider millisecond pulsar binaries. Nat. Astron. 2023, 7, 451–462. [Google Scholar] [CrossRef] [PubMed]
- Ascenzi, S.; Graber, V.; Rea, N. Neutron-star Measurements in the Multi-messenger Era. arXiv 2024, arXiv:2401.14930. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Adkins, P.W.; Albert, C.L.; Anders, J.F.; Aylward, A.T.; Baker, C.L.; Balsamo, E.R.; Bamford, W.A.; Benegalrao, S.S.; et al. The Neutron star Interior Composition Explorer (NICER): Design and development. In Proceedings of the Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, Edinburgh, UK, 1–26 June 2016; den Herder, J.W.A., Takahashi, T., Bautz, M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA; Volume 9905, p. 99051H. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Vinciguerra, S.; Salmi, T.; Watts, A.L.; Choudhury, D.; Riley, T.E.; Ray, P.S.; Bogdanov, S.; Kini, Y.; Guillot, S.; Chakrabarty, D.; et al. An Updated Mass-Radius Analysis of the 2017–2018 NICER Data Set of PSR J0030+0451. Astrophys. J. Lett. 2024, 961, 62. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Damour, T.; Schäfer, G. Higher-order relativistic periastron advances and binary pulsars. Nuovo C B Ser. 1988, 101B, 127–176. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q relations in neutron stars and their applications to astrophysics, gravitational waves, and fundamental physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Schutz, B.F. Constraining the Equation of State with Moment of Inertia Measurements. Astrophys. J. 2005, 629, 979–984. [Google Scholar] [CrossRef]
- Barker, B.M.; O’Connell, R.F. Relativistic effects in the binary pulsar PSR 1913+16. Astrophys. J. 1975, 199, L25. [Google Scholar] [CrossRef]
- Damour, T.; Ruffini, R. Sur certaines vérifications nouvelles de la Relativité Générale rendues possibles par la découverte d’un pulsar membre d’un système binaire. C.R. Acad. Sc. Paris 1974, 279, 971–973. [Google Scholar]
- Barker, B.M.; O’Connell, R.F. Gravitational two-body problem with arbitrary masses, spins, and quadrupole moments. Phys. Rev. D 1975, 12, 329–335. [Google Scholar] [CrossRef]
- Prša, A.; Harmanec, P.; Torres, G.; Mamajek, E.; Asplund, M.; Capitaine, N.; Christensen-Dalsgaard, J.; Depagne, É.; Haberreiter, M.; Hekker, S.; et al. Nominal Values for Selected Solar and Planetary Quantities: IAU 2015 Resolution B3. Am. Astron. Soc. 2016, 152, 41. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N. General relativistic celestial mechanics of binary systems. II. The post-newtonian timing formula. Ann. De L’institut Henri Poincare (A) Phys. Theor. 1986, 44, 263–292. [Google Scholar]
- Esposito, L.W.; Harrison, E.R. Properties of the Hulse-Taylor binary pulsar system. Astrophys. J. 1975, 196, L1. [Google Scholar] [CrossRef]
- Kramer, M. Determination of the Geometry of the PSR B1913+16 System by Geodetic Precession. Astrophys. J. 1998, 509, 856–860. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Taylor, J.H. General Relativistic Geodetic Spin Precession in Binary Pulsar B1913+16: Mapping the Emission Beam in Two Dimensions. Astrophys. J. 2002, 576, 942–949. [Google Scholar] [CrossRef]
- Stairs, I.H.; Thorsett, S.E.; Arzoumanian, Z. Measurement of Gravitational Spin-Orbit Coupling in a Binary-Pulsar System. Phys. Rev. Lett. 2004, 93, 141101. [Google Scholar] [CrossRef]
- Ridolfi, A. Long-Term Timing of Pulsars in Globular Clusters. Ph.D. Thesis, Rheinische Friedrich Wilhelms University of Bonn, Bonn, Germany, 2017. [Google Scholar]
- Cameron, A.D.; Bailes, M.; Champion, D.J.; Freire, P.C.C.; Kramer, M.; McLaughlin, M.A.; Ng, C.; Possenti, A.; Ridolfi, A.; Tauris, T.M.; et al. New constraints on the kinematic, relativistic, and evolutionary properties of the PSR J1757−1854 double neutron star system. Mon. Not. R. Astron. Soc. 2023, 523, 5064–5085. [Google Scholar] [CrossRef]
- Meng, L.; Zhu, W.; Kramer, M.; Miao, X.; Desvignes, G.; Shao, L.; Hu, H.; Freire, P.C.C.; Zhang, Y.; Xue, M.; et al. The Relativistic Spin Precession in the Compact Double Neutron Star System PSR J1946+2052. Available online: https://arxiv.org/abs/2403.17828 (accessed on 21 February 2024).
- Kramer, M. Relativistic Spin-Precession in Binary Pulsars. In Proceedings of the Twelfth Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories, Paris, France, 12–18 July 2009; Damour, T., Jantzen, R., Ruffini, R., Eds.; World Scientific Publishing Co Pte Ltd.: Singapore, 2012; pp. 241–260. [Google Scholar] [CrossRef]
- Kramer, M. New results from testing relativistic gravity with radio pulsars. In Proceedings of the Sixteenth Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, Online, 5–10 July 2021; Ruffino, R., Vereshchagin, G., Eds.; World Scientific Publishing Co Pte Ltd.: Singapore, 2023; pp. 3–21. [Google Scholar] [CrossRef]
- Burgay, M.; Possenti, A.; Manchester, R.N.; Kramer, M.; McLaughlin, M.A.; Lorimer, D.R.; Stairs, I.H.; Joshi, B.C.; Lyne, A.G.; Camilo, F.; et al. Long-Term Variations in the Pulse Emission from PSR J0737−3039B. Astrophys. J. 2005, 624, L113–L116. [Google Scholar] [CrossRef]
- Hotan, A.W.; Bailes, M.; Ord, S.M. Geodetic Precession in PSR J1141−6545. Astrophys. J. 2005, 624, 906–913. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Stairs, I.H.; Freire, P.C.; Cordes, J.M.; Camilo, F.; Faulkner, A.J.; Lyne, A.G.; Nice, D.J.; Ransom, S.M.; Arzoumanian, Z.; et al. Arecibo Pulsar Survey Using ALFA. II. The Young, Highly Relativistic Binary Pulsar J1906+0746. Astrophys. J. 2006, 640, 428. [Google Scholar] [CrossRef]
- Desvignes, G.; Kramer, M.; Lee, K.; van Leeuwen, J.; Stairs, I.; Jessner, A.; Cognard, I.; Kasian, L.; Lyne, A.; Stappers, B.W. Radio emission from a pulsar’s magnetic pole revealed by general relativity. Science 2019, 365, 1013–1017. [Google Scholar] [CrossRef]
- Breton, R.P.; Kaspi, V.M.; Kramer, M.; McLaughlin, M.A.; Lyutikov, M.; Ransom, S.M.; Stairs, I.H.; Ferdman, R.D.; Camilo, F.; Possenti, A. Relativistic Spin Precession in the Double Pulsar. Science 2008, 321, 104. [Google Scholar] [CrossRef] [PubMed]
- Lower, M.E.; Kramer, M.; Shannon, R.M.; Breton, R.P.; Wex, N.; Johnston, S.; Bailes, M.; Buchner, S.; Hu, H.; Venkatraman Krishnan, V.; et al. A MeerKAT view of the Double Pulsar eclipses. Geodetic precession of pulsar B and system geometry. Astron. Astrophys. 2024, 682, A26. [Google Scholar] [CrossRef]
- Pfister, H. On the history of the so-called Lense–Thirring effect. Gen. Relativ. Gravit. 2007, 39, 1735–1748. [Google Scholar] [CrossRef]
- Klein, M.J.; Kox, A.J.; Renn, J.; Schulmann, R. (Eds.) The Collected Papers of Albert Einstein; Princeton University Press: Princeton, NJ, USA, 1995; Volume 4. [Google Scholar]
- Einstein, A.; Grossmann, M. Entwurf Einer Verallgemeinerten Relativitätstheorie und Einer Theorie der Gravitation; Teubner: Leipzig, Germany, 1913. [Google Scholar]
- Thirring, H. Über die Wirkung rotierender ferner Massen in der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 33. [Google Scholar]
- Lense, J.; Thirring, H. Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 156. [Google Scholar]
- Mashhoon, B.; Hehl, F.W.; Theiss, D.S. On the gravitational effects of rotating masses: The Thirring-Lense papers. Gen. Relativ. Gravit. 1984, 16, 711–750. [Google Scholar] [CrossRef]
- van Patten, R.A.; Everitt, C.W.F. Possible experiment with two counter-orbiting drag-free satellites to obtain a new test of Einstein’s general theory of relativity and improved measurements in geodesy. Phys. Rev. Lett. 1976, 36, 629–632. [Google Scholar] [CrossRef]
- van Patten, R.A.; Everitt, C.W.F. A Possible Experiment with Two Counter-Orbiting Drag-Free Satellites to Obtain a New Test of Einstein’s General Theory of Relativity and Improved Measurements in Geodesy. Celestial Mech. 1976, 13, 429–447. [Google Scholar] [CrossRef]
- Ciufolini, I. Measurement of the Lense–Thirring drag on high-altitude, laser-ranged artificial satellites. Phys. Rev. Lett. 1986, 56, 278–281. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Pavlis, E.; Ries, J.; Koenig, R.; Matzner, R.; Sindoni, G. The LARES Space Experiment: LARES Orbit, Error Analysis and Satellite Structure. In General Relativity and John Archibald Wheeler; Ciufolini, I., Matzner, R.A.A., Eds.; Astrophysics and Space Science Library: Austin, TX, USA, 2010; Volume 367, p. 467. [Google Scholar] [CrossRef]
- Ciufolini, I.; Pavlis, E.C. A confirmation of the general relativistic prediction of the Lense–Thirring effect. Nature 2004, 431, 958–960. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sindoni, G.; Ries, J.; Matzner, R.; Koenig, R.; Paris, C.; Gurzadyan, V.; Penrose, R. An improved test of the general relativistic effect of frame-dragging using the LARES and LAGEOS satellites. Eur. Phys. J. C 2019, 79, 872. [Google Scholar] [CrossRef]
- Schiff, L.I. Possible New Experimental Test of General Relativity Theory. Phys. Rev. Lett. 1960, 4, 215–217. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2004; Volume 4. [Google Scholar]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astrophys. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Tauris, T.M.; van den Heuvel, E.P.J. Physics of Binary Star Evolution: From Stars to X-ray Binaries and Gravitational Wave Sources; Princeton University Press: Princeton, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef] [PubMed]
- Lorimer, D.R. Binary and Millisecond Pulsars at the New Millennium. Living Rev. Relativ. 2001, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.M.; Johnston, S.; Manchester, R.N. The kinematics and orbital dynamics of the PSR B1259-63/LS 2883 system from 23 yr of pulsar timing. Mon. Not. R. Astron. Soc. 2014, 437, 3255–3264. [Google Scholar] [CrossRef]
- Kaspi, V.M.; Bailes, M.; Manchester, R.N.; Stappers, B.W.; Bell, J.F. Evidence from a precessing pulsar orbit for a neutron-star birth kick. Nature 1996, 381, 584–586. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Faulkner, A.J.; Lyne, A.G.; Manchester, R.N.; Kramer, M.; McLaughlin, M.A.; Hobbs, G.; Possenti, A.; Stairs, I.H.; Camilo, F.; et al. The Parkes Multibeam Pulsar Survey—VI. Discovery and timing of 142 pulsars and a Galactic population analysis. Mon. Not. R. Astron. Soc. 2006, 372, 777–800. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Ng, C.Y.; Lyne, A.G.; Stappers, B.W.; Coe, M.J.; Halpern, J.P.; Johnson, T.J.; Steele, I.A. Multiwavelength monitoring and X-ray brightening of Be X-ray binary PSR J2032+4127/MT91 213 on its approach to periastron. Mon. Not. R. Astron. Soc. 2017, 464, 1211–1219. [Google Scholar] [CrossRef]
- Lyne, A.G.; Lorimer, D.R. High birth velocities of radio pulsars. Nature 1994, 369, 127–129. [Google Scholar] [CrossRef]
- Hobbs, G.; Lorimer, D.R.; Lyne, A.G.; Kramer, M. A statistical study of 233 pulsar proper motions. Mon. Not. R. Astron. Soc. 2005, 360, 974–992. [Google Scholar] [CrossRef]
- Tauris, T.M.; Kramer, M.; Freire, P.C.C.; Wex, N.; Janka, H.T.; Langer, N.; Podsiadlowski, P.; Bozzo, E.; Chaty, S.; Kruckow, M.U.; et al. Formation of Double Neutron Star Systems. Astrophys. J. 2017, 846, 170. [Google Scholar] [CrossRef]
- Prince, T.A.; Anderson, S.B.; Kulkarni, S.R.; Wolszczan, A. Timing Observations of the 8 Hour Binary Pulsar 2127+11C in the Globular Cluster M15. Astrophys. J. Lett. 1991, 374, L41. [Google Scholar] [CrossRef]
- Freire, P.C.; Gupta, Y.; Ransom, S.M.; Ishwara-Chandra, C.H. Giant Metrewave Radio Telescope Discovery of a Millisecond Pulsar in a Very Eccentric Binary System. Astrophys. J. 2004, 606, L53–L56. [Google Scholar] [CrossRef]
- Wex, N.; Johnston, S.; Manchester, R.N.; Lyne, A.G.; Stappers, B.W.; Bailes, M. Timing models for the long orbital period binary pulsar PSR B1259−63. Mon. Not. R. Astron. Soc. 1998, 298, 997–1004. [Google Scholar] [CrossRef]
- Lai, D.; Bildsten, L.; Kaspi, V.M. Spin-Orbit Interactions in Neutron Star/Main-Sequence Binaries and Implications for Pulsar Timing. Astrophys. J. 1995, 452, 819. [Google Scholar] [CrossRef]
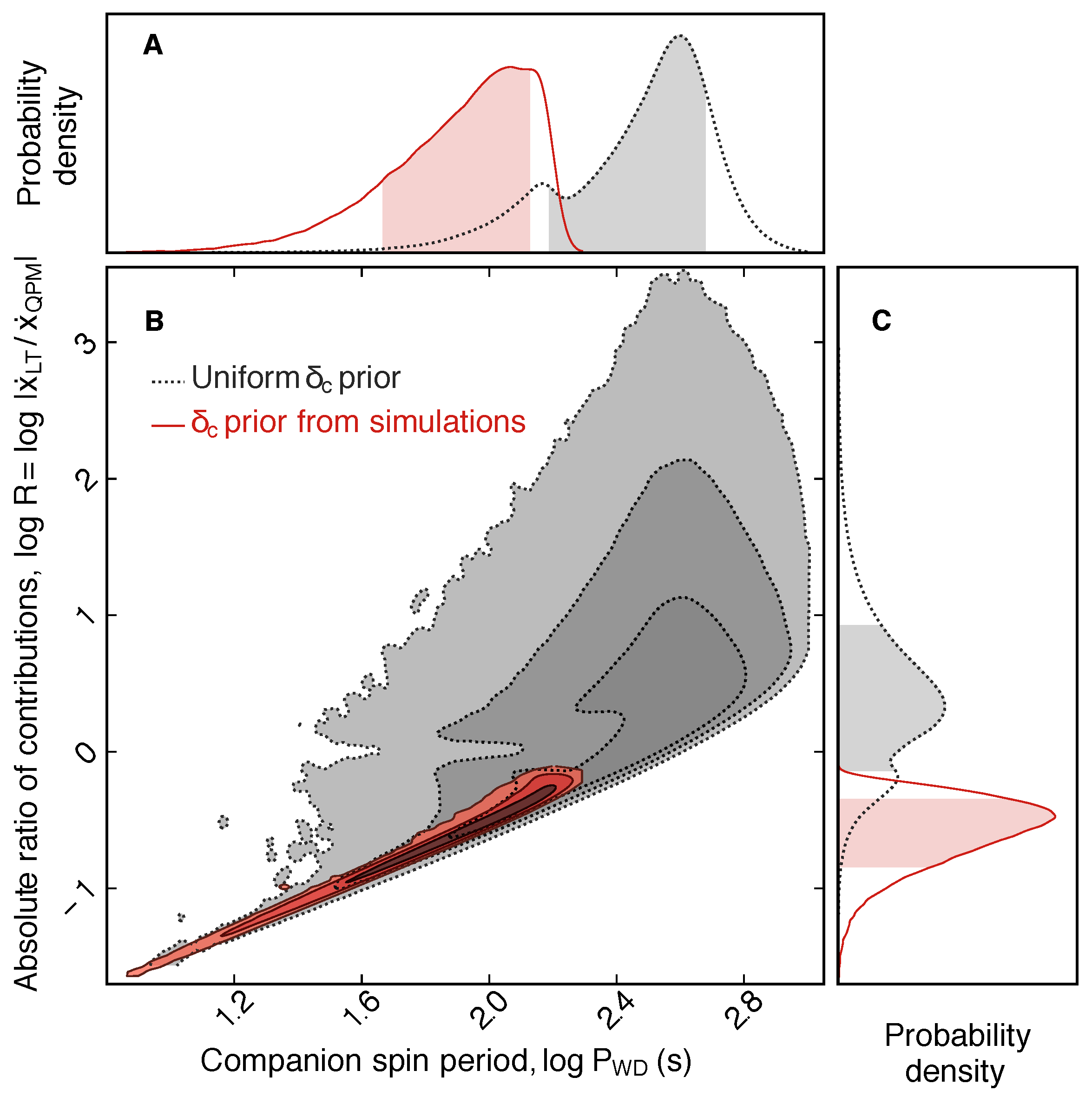
- Venkatraman Krishnan, V.; Bailes, M.; van Straten, W.; Wex, N.; Freire, P.C.C.; Keane, E.F.; Tauris, T.M.; Rosado, P.A.; Bhat, N.D.R.; Flynn, C.; et al. Lense–Thirring frame dragging induced by a fast-rotating white dwarf in a binary pulsar system. Science 2020, 367, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double-Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Huang, Y. Relativistic Measurements from Timing the Binary Pulsar PSR B1913+16. Astrophys. J. 2016, 829, 55. [Google Scholar] [CrossRef]
- Hu, H.; Kramer, M.; Champion, D.J.; Wex, N.; Parthasarathy, A.; Pennucci, T.T.; Porayko, N.K.; van Straten, W.; Venkatraman Krishnan, V.; Burgay, M.; et al. Gravitational signal propagation in the Double Pulsar studied with the MeerKAT telescope. Astron. Astrophys. 2022, 667, A149. [Google Scholar] [CrossRef]
- Stovall, K.; Freire, P.C.C.; Chatterjee, S.; Demorest, P.B.; Lorimer, D.R.; McLaughlin, M.A.; Pol, N.; van Leeuwen, J.; Wharton, R.S.; Allen, B.; et al. PALFA Discovery of a Highly Relativistic Double Neutron Star Binary. Astrophys. J. Lett. 2018, 854, L22. [Google Scholar] [CrossRef]
- Antoniadis, J.; Bassa, C.G.; Wex, N.; Kramer, M.; Napiwotzki, R. A white dwarf companion to the relativistic pulsar PSR J1141-6545. Mon. Not. R. Astron. Soc. 2011, 412, 580–584. [Google Scholar] [CrossRef]
- Tauris, T.M.; Sennels, T. Formation of the binary pulsars PSR B2303+46 and PSR J1141-6545. Young neutron stars with old white dwarf companions. Astron. Astrophys. 2000, 355, 236–244. [Google Scholar] [CrossRef]
- Cameron, A.D.; Champion, D.J.; Kramer, M.; Bailes, M.; Barr, E.D.; Bassa, C.G.; Bhandari, S.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; et al. The High Time Resolution Universe Pulsar Survey—XIII. PSR J1757−1854, the most accelerated binary pulsar. Mon. Not. R. Astron. Soc. 2018, 475, L57–L61. [Google Scholar] [CrossRef]
- Kramer, M.; Wex, N. TOPICAL REVIEW: The Double Pulsar system: A unique laboratory for gravity. Class. Quantum Gravity 2009, 26, 073001. [Google Scholar] [CrossRef]
- Hu, H.; Kramer, M.; Wex, N.; Champion, D.J.; Kehl, M.S. Constraining the dense matter equation-of-state with radio pulsars. Mon. Not. R. Astron. Soc. 2020, 497, 3118–3130. [Google Scholar] [CrossRef]
- Barr, E.D.; Dutta, A.; Freire, P.C.C.; Cadelano, M.; Gautam, T.; Kramer, M.; Pallanca, C.; Ransom, S.M.; Ridolfi, A.; Stappers, B.W.; et al. A pulsar in a binary with a compact object in the mass gap between neutron stars and black holes. Science 2024, 383, 275–279. [Google Scholar] [CrossRef] [PubMed]
- Perera, B.B.P.; McLaughlin, M.A.; Kramer, M.; Stairs, I.H.; Ferdman, R.D.; Freire, P.C.C.; Possenti, A.; Breton, R.P.; Manchester, R.N.; Burgay, M.; et al. The Evolution of PSR J0737−3039B and a Model for Relativistic Spin Precession. Astrophys. J. 2010, 721, 1193–1205. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Manchester, R.N.; Kramer, M.; Possenti, A.; Lyne, A.G.; Burgay, M.; Stairs, I.H.; Hotan, A.W.; McLaughlin, M.A.; Lorimer, D.R.; Hobbs, G.B.; et al. The Mean Pulse Profile of PSR J0737−3039A. Astrophys. J. 2005, 621, L49. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Manchester, R.N.; Lyne, A.G.; Breton, R.P.; McLaughlin, M.A.; Possenti, A.; Burgay, M. The Double Pulsar: Evolutionary constraints from the system geometry. In Proceedings of the 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, Montreal, QC, Canada, 12–17 August 2007; American Institute of Physics Conference Series. Bassa, C., Wang, Z., Cumming, A., Kaspi, V.M., Eds.; American Institute of Physics: College Park, MD, USA, 2008; Volume 983, pp. 474–478. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Breton, R.P.; McLaughlin, M.A.; Freire, P.C.C.; Possenti, A.; Stappers, B.W.; Kaspi, V.M.; Manchester, R.N.; et al. The Double Pulsar: Evidence for Neutron Star Formation without an Iron Core-collapse Supernova. Astrophys. J. 2013, 767, 85. [Google Scholar] [CrossRef]
- Willems, B.; Kaplan, J.; Fragos, T.; Kalogera, V.; Belczynski, K. Formation and progenitor of PSR J0737−039: New constraints on the supernova explosion forming pulsar B. Phys. Rev. D 2006, 74, 043003. [Google Scholar] [CrossRef]
- Stairs, I.H.; Thorsett, S.E.; Dewey, R.J.; Kramer, M.; McPhee, C.A. The formation of the Double Pulsar PSR J0737−3039A/B. Mon. Not. R. Astron. Soc. Lett. 2006, 373, L50–L54. [Google Scholar] [CrossRef]
- Pol, N.; McLaughlin, M.; Kramer, M.; Stairs, I.; Perera, B.B.P.; Possenti, A. A Direct Measurement of Sense of Rotation of PSR J0737−3039A. Astrophys. J. 2018, 853, 73. [Google Scholar] [CrossRef]
- Iorio, L. Prospects for measuring the moment of inertia of pulsar J0737-3039A. New Astron. 2009, 14, 40–43. [Google Scholar] [CrossRef]
- Kehl, M.S.; Wex, N.; Kramer, M.; Liu, K. Future measurements of the Lense–Thirring effect in the Double Pulsar. In Proceedings of the 14th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, Rome, Italy, 12–18 July 2015; Bianchi, M., Jantzen, R., Ruffini, R., Eds.; World Scientific Publishing Co Pte Ltd.: Singapore, 2017; Volume 2, pp. 1860–1865. [Google Scholar] [CrossRef]
- Nice, D.J.; Taylor, J.H. PSR J2019+2425 and PSR J2322+2057 and the Proper Motions of Millisecond Pulsars. Astrophys. J. 1995, 441, 429. [Google Scholar] [CrossRef]
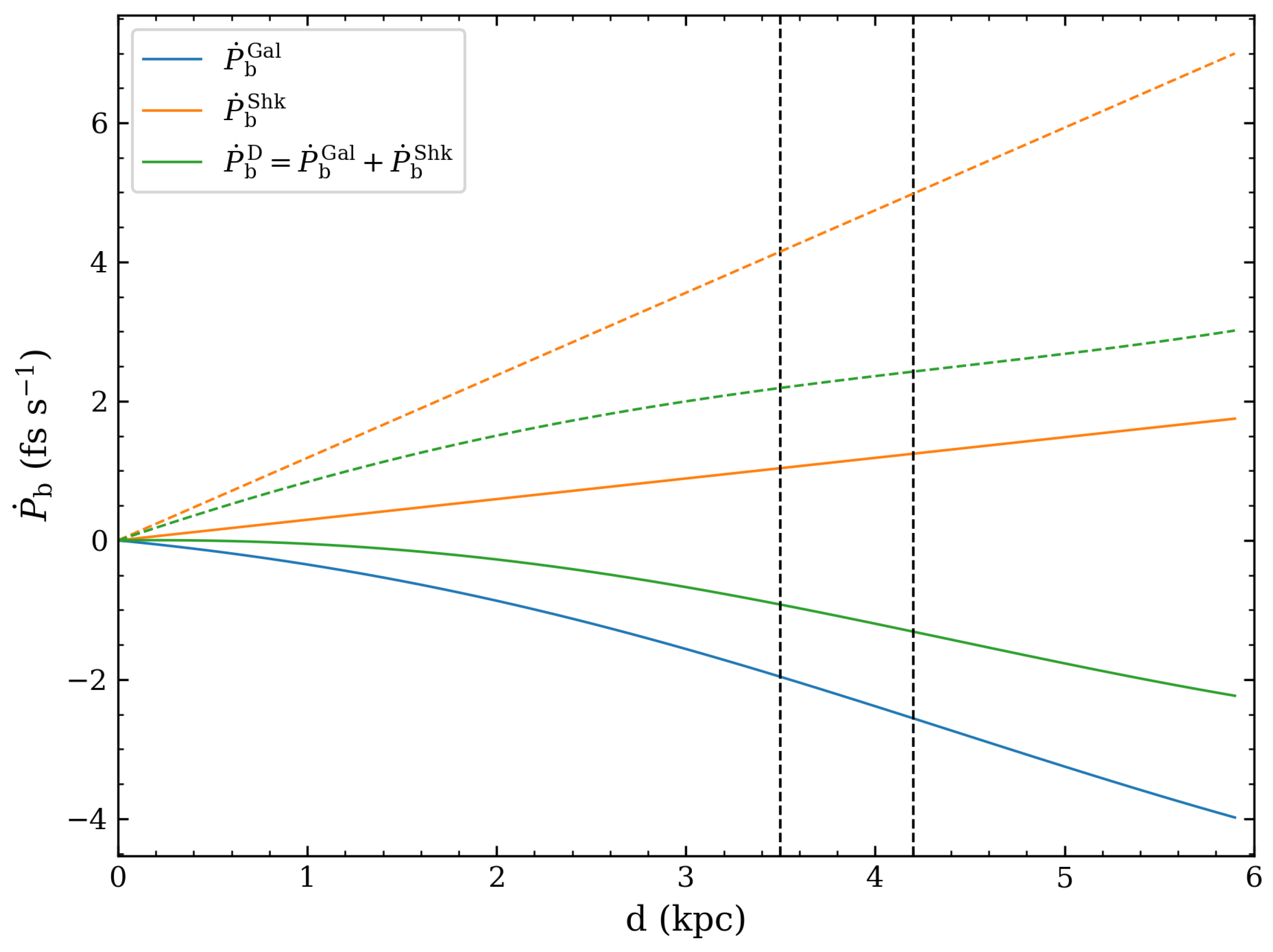
- Shklovskii, I.S. Possible Causes of the Secular Increase in Pulsar Periods. Sov. Astron. 1970, 13, 562. [Google Scholar]
- Peters, P.C.; Mathews, J. Gravitational Radiation from Point Masses in a Keplerian Orbit. Phys. Rev. 1963, 131, 435–440. [Google Scholar] [CrossRef]
- Wagoner, R.V. Test for the existence of gravitational radiation. Astrophys. J. 1975, 196, L63–L65. [Google Scholar] [CrossRef]
- Morrison, I.A.; Baumgarte, T.W.; Shapiro, S.L.; Pand haripande, V.R. The Moment of Inertia of the Binary Pulsar J0737-3039A: Constraining the Nuclear Equation of State. Astrophys. J. 2004, 617, L135–L138. [Google Scholar] [CrossRef]
- Cordes, J.M.; Lazio, T.J.W. NE2001.I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations. arXiv 2002, arXiv:astro-ph/0207156. [Google Scholar] [CrossRef]
- Yao, J.M.; Manchester, R.N.; Wang, N. A New Electron-density Model for Estimation of Pulsar and FRB Distances. Astrophys. J. 2017, 835, 29. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Freire, P.C.C.; Perera, B.B.P.; Pol, N.; Camilo, F.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Hessels, J.W.T.; Kaspi, V.M.; et al. Asymmetric mass ratios for bright double neutron-star mergers. Nature 2020, 583, 211–214. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Chen, Z.C.; Liu, L. Is PSR J0514−4002E in a PBH-NS binary? arXiv 2024, arXiv:2401.12889. [Google Scholar] [CrossRef]
- Liu, K.; Eatough, R.P.; Wex, N.; Kramer, M. Pulsar-black hole binaries: Prospects for new gravity tests with future radio telescopes. Mon. Not. R. Astron. Soc. 2014, 445, 3115–3132. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farèse, G. Nonperturbative strong-field effects in tensor-scalar theories of gravitation. Phys. Rev. Lett. 1993, 70, 2220–2223. [Google Scholar] [CrossRef]
- Batrakov, A.; Hu, H.; Wex, N.; Freire, P.C.C.; Venkatraman Krishnan, V.; Kramer, M.; Guo, Y.J.; Guillemot, L.; McKee, J.W.; Cognard, I.; et al. A new pulsar timing model for scalar-tensor gravity with applications to PSR J2222−0137 and pulsar-black hole binaries. Astron. Astrophys. 2023. [Google Scholar] [CrossRef]
- Pan, Z.; Lu, J.G.; Jiang, P.; Han, J.L.; Chen, H.L.; Han, Z.W.; Liu, K.; Qian, L.; Xu, R.X.; Zhang, B.; et al. A binary pulsar in a 53-minute orbit. Nature 2023, 620, 961–964. [Google Scholar] [CrossRef] [PubMed]
- Lau, M.Y.M.; Mandel, I.; Vigna-Gómez, A.; Neijssel, C.J.; Stevenson, S.; Sesana, A. Detecting double neutron stars with LISA. Mon. Not. R. Astron. Soc. 2020, 492, 3061–3072. [Google Scholar] [CrossRef]
- Kyutoku, K.; Nishino, Y.; Seto, N. How to detect the shortest period binary pulsars in the era of LISA. Mon. Not. R. Astron. Soc. 2019, 483, 2615–2620. [Google Scholar] [CrossRef]
- Thrane, E.; Osłowski, S.; Lasky, P.D. Ultrarelativistic astrophysics using multimessenger observations of double neutron stars with LISA and the SKA. Mon. Not. R. Astron. Soc. 2020, 493, 5408–5412. [Google Scholar] [CrossRef]
- Miao, X.; Xu, H.; Shao, L.; Liu, C.; Ma, B.Q. Stringent Tests of Gravity with Highly Relativistic Binary Pulsars in the Era of LISA and SKA. Astrophys. J. 2021, 921, 114. [Google Scholar] [CrossRef]
- Nordtvedt, K. Equivalence Principle for Massive Bodies. II. Theory. Phys. Rev. 1968, 169, 1017–1025. [Google Scholar] [CrossRef]
- Eardley, D.M. Observable effects of a scalar gravitational field in a binary pulsar. Astrophys. J. 1975, 196, L59–L62. [Google Scholar] [CrossRef]
- Nordtvedt, K. Equivalence Principle for Massive Bodies. I. Phenomenology. Phys. Rev. 1968, 169, 1014–1016. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Wex, N.; Esposito-Farèse, G.; Verbiest, J.P.W.; Bailes, M.; Jacoby, B.A.; Kramer, M.; Stairs, I.H.; Antoniadis, J.; Janssen, G.H. The relativistic pulsar-white dwarf binary PSR J1738+0333—II. The most stringent test of scalar-tensor gravity. Mon. Not. R. Astron. Soc. 2012, 423, 3328–3343. [Google Scholar] [CrossRef]
- Guo, Y.J.; Freire, P.C.C.; Guillemot, L.; Kramer, M.; Zhu, W.W.; Wex, N.; McKee, J.W.; Deller, A.; Ding, H.; Kaplan, D.L.; et al. PSR J2222−0137. I. Improved physical parameters for the system. Astron. Astrophys. 2021, 654, A16. [Google Scholar] [CrossRef]
- Archibald, A.M.; Gusinskaia, N.V.; Hessels, J.W.T.; Deller, A.T.; Kaplan, D.L.; Lorimer, D.R.; Lynch, R.S.; Ransom, S.M.; Stairs, I.H. Universality of free fall from the orbital motion of a pulsar in a stellar triple system. Nature 2018, 559, 73–76. [Google Scholar] [CrossRef]
- Voisin, G.; Cognard, I.; Freire, P.C.C.; Wex, N.; Guillemot, L.; Desvignes, G.; Kramer, M.; Theureau, G. An improved test of the strong equivalence principle with the pulsar in a triple star system. Astron. Astrophys. 2020, 638, A24. [Google Scholar] [CrossRef]
- TRAPUM. Available online: http://www.trapum.org/discoveries/ (accessed on 21 February 2024).
- FAST GC Pulsar Discoveries. Available online: https://fast.bao.ac.cn/cms/article/65/ (accessed on 21 February 2024).
- FAST-CRAFTS Pulsars. Available online: http://groups.bao.ac.cn/ism/CRAFTS/202203/t20220310_683697.html (accessed on 21 February 2024).
- The FAST Galactic Plane Pulsar Snapshot Survey. Available online: http://zmtt.bao.ac.cn/GPPS/GPPSnewPSR.html (accessed on 21 February 2024).
- SKAMPI Takes Off: The SKA-MPIfR Telescope in South Africa is Ready for Science Operations. Available online: https://www.mpifr-bonn.mpg.de/pressreleases/2024/3?c=9060 (accessed on 25 January 2024).
- MeerKAT+: The MeerKAT Extension. The Handover of the First Dish of the MeerKAT Extension Signals an Important Milestone for the SKA-MID Construction. Available online: https://www.mpifr-bonn.mpg.de/pressreleases/2024/5?c=9060 (accessed on 21 February 2024).



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Freire, P.C.C. Measuring the Lense–Thirring Orbital Precession and the Neutron Star Moment of Inertia with Pulsars. Universe 2024, 10, 160. https://doi.org/10.3390/universe10040160
Hu H, Freire PCC. Measuring the Lense–Thirring Orbital Precession and the Neutron Star Moment of Inertia with Pulsars. Universe. 2024; 10(4):160. https://doi.org/10.3390/universe10040160
Chicago/Turabian StyleHu, Huanchen, and Paulo C. C. Freire. 2024. "Measuring the Lense–Thirring Orbital Precession and the Neutron Star Moment of Inertia with Pulsars" Universe 10, no. 4: 160. https://doi.org/10.3390/universe10040160





