Investigating the Influence of Different DEMs on GIS-Based Cost Distance Modeling for Site Catchment Analysis of Prehistoric Sites in Andalusia

Abstract

The overall objective of this work is to apply GIS-based cost distance modeling (CDM) to site catchment modeling and analysis of prehistoric (Solutrean) sites in Andalusia. The implementation of a GIS-method for slope-based CDM was explained in detail, so that it can be replicated easily in future studies. Additional cost components, vegetation and stream networks, were included in the method. The presented CDM approach uses slope rasters as input data, which were derived from digital elevation models (DEMs). Various DEMs that differ in cell size, accuracy and other characteristics can be applied to this method. Thus, a major goal of this work is to investigate the influence different publicly available DEMs (SRTM, ASTER GDEM, EU-DEM, official 5-m/10-m cell size DEMs) have on the results of GIS-based CDM. While the investigation was conducted on sites from different chronocultural periods, a case study was performed on Solutrean sites in order to test the CDM approach by producing actual results and then comparing and interpreting them from an archaeological perspective. The results of the DEM evaluation with resampled horizontal resolutions show a clear influence of the DEM cell size on the modeled catchment area sizes. The investigation also indicates that this influence can be superimposed by other factors, such as noise and residuals of filtered anthropogenic features, when using DEMs of different origins.

1. Introduction

The interaction of prehistoric hunter-gatherer societies with their environment is a key research area in archeology. In this context, the spatial behavior of such societies is very difficult to investigate. Site catchment analysis (SCA) is a classic method to gain knowledge about relationships between the inhabitants of archaeological sites and their environment [1]. The key idea of SCA is to determine the area around a site that was used to gather resources in order to investigate the mobility of and any potential economic resources available to the prehistoric inhabitants [1,2]. In modern archaeological and geographical sciences, the analysis of spatial interactions is usually conducted using GIS software, combined with modeling approaches [3,4,5]. The umbrella term for the modeling approach applied to enable GIS-based site catchment modeling is cost distance or least-cost modeling, which is realized with walking speed models in this study.

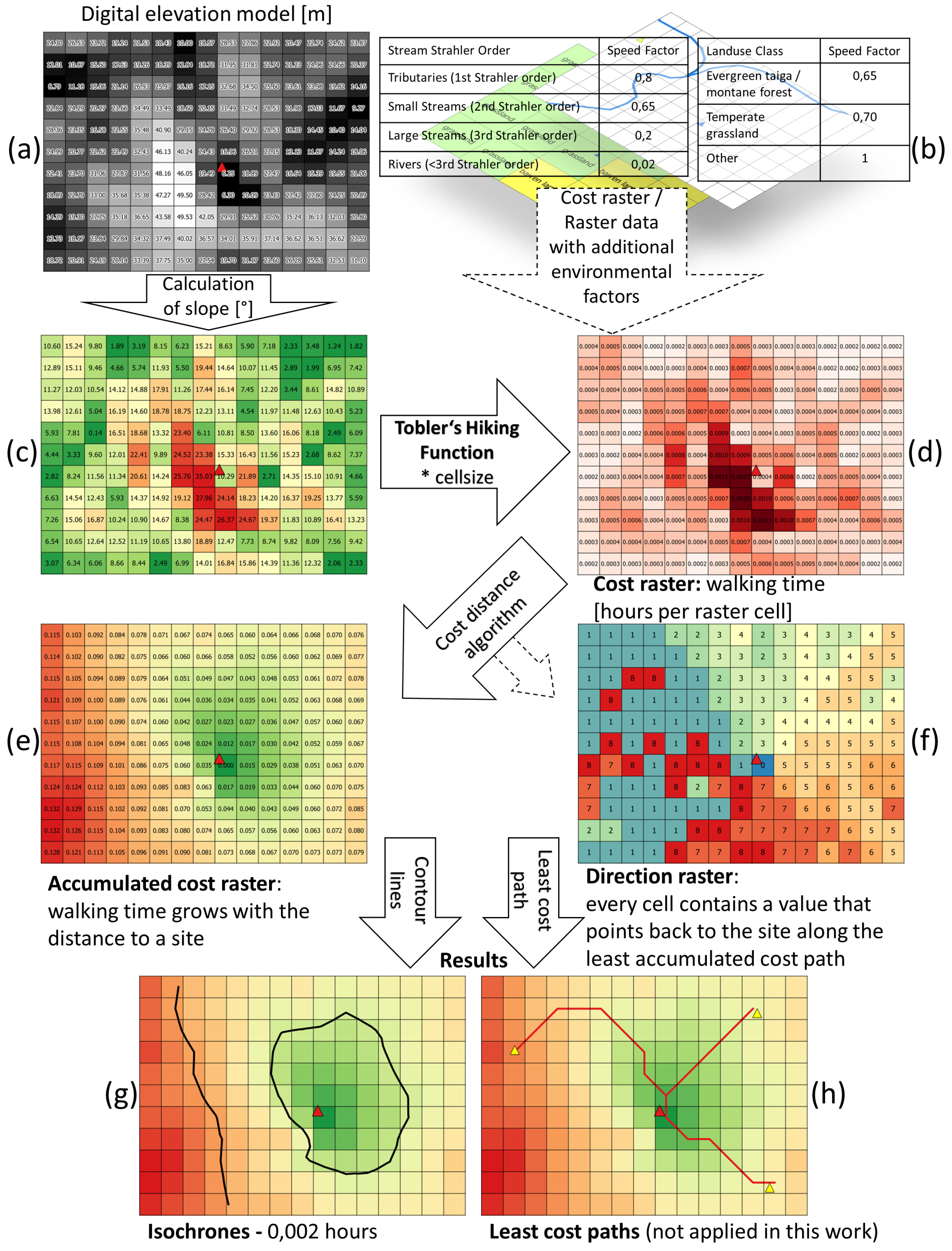
A cost distance model describes the relationship between travel distances and their associated costs, which are generic and can be of different types. In this study, slope-based walking-speed is applied as the cost value, calculated with a hiking function to derive the walking time over distance. The most important parameters that define the output of cost distance models are the modeling algorithms, the applied walking-speed model, the input data and their processing.

Important input data for GIS-based cost distance modeling are environmental datasets, such as digital elevation models (DEMs), and other data of landscape elements, such as vegetation or stream networks. Good examples for GIS-based SCA are given by Uthmeier et al. [6], Marín-Arroyo [7], Jobe and White [8], Surface-Evans [9], Gravel-Miguel [10] or Henry et al. [11]. From these studies, it is obvious that elevation data are of key importance for modeling site catchment areas of prehistoric inhabitants.

In a GIS software environment, elevation data are usually represented as a DEM, which is a digital representation of the Earth’s surface [12]. The elevation data utilized in this study are raster-based, where each raster cell stores a height value. A wide variety of such DEMs exist, and each has different characteristics due to data acquisition and processing techniques, which result in different spatial resolutions and accuracies of the elevation values [13,14]. The data used in this study are typically post-processed to remove buildings and, in some cases, vegetation. This representation of the bare ground surface is also often referred to as a digital terrain model (DTM) [15]. The CDM approach applied in this study uses slope rasters derived from such DEMs, on which the cell size of a raster DEM has a significant influence [16].

Insufficient evaluation of the input data causes major restrictions in the adequate implementation of walking speed modeling, an issue often neglected in former archaeological CDM studies. Therefore, apart from the presentation and discussion of the CDM approach with additional cost components, the major objective for this study is to investigate the influence that different DEM datasets have on the site catchment modeling results discussed above. For this investigation, three main objectives have to be considered: (i) examination of studies and reports that evaluate the quality of publicly-available DEM datasets (ASTER GDEM [17], SRTM [18,19,20], EU-DEM [21], official DEMs from the Spanish National Geographic Institute and the Regional Government of Andalusia [22,23]); (ii) evaluation of elevation profiles, error rasters and slope values derived from the DEMs; (iii) evaluation of the influence of the different DEMs and environmental datasets on the site catchment models.

2. On Site Catchment Analysis, Cost Distance Modeling and Slope Estimation

The term site catchment analysis originates from an archaeological context and was proposed by Vita-Finzi and Higgs [1] in 1970. They describe a method to investigate and understand the relationship between human settlements and their local environments. A site’s catchment is defined as the area that is regularly exploited by its inhabitants, comparable to the classical meaning of a river catchment or a watershed in hydrology, where the term was borrowed from [24]. As a site catchment is not known at the beginning of a study, different methods were designed to determine it. Assuming that inhabitants of a site covered the distances to exploit the resources of an area by walking, the size of the area can be defined by the time it takes to cover them. Therefore, the early approaches were quite simple and based on drawing circles of 5 km or 10 km in radius around a site (“fixed-distance radii”, 20 km in this work). This was followed by a more elaborated practice of interpolating the distances of actual walked transects (for instance: north-south and east-west) in the given area, to incorporate the effect that the actual topography has on the walking time [24,25,26].

With GIS software becoming more popular and advanced, it was obvious to develop a modeling approach that allows the consideration of topographic data to try to overcome these limitations. Hunt [27] summarized the benefits of the application of GIS software in catchment analysis, while Wheatley and Gillings [4] present plenty of GIS-based methods that can be applied to several archaeological approaches. One of them is site catchment analysis, and the fundamental approach that allows us to model site catchments is cost distance modeling. The cost distance models are used to derive isochrones (lines of equal time) or raster surfaces that represent a hypothetical site catchment as applied before by Tripcevich [28] and Marín-Arroyo [7].

The application of cost distance analysis in Prehistory is based on the necessity for hunter-gatherers to alter their behavior and routes in order to optimize their energy expenditure (least cost assumption) [9,29]. The results of the cost distance analysis of an archaeological site can be compared with the archaeological data from which information about the mobility and behavior of hunter-gatherers can be inferred [30,31]. For this case study, we use lithic raw materials, but there are also other elements that can help archaeologists to interpret the mobility of human groups, such as exotic raw materials (obsidian, amber, etc.) or mobile art.

Originally unrelated to these archaeological questions, William Naismith proposed a rule in 1892 that related human walking speed to the slope of the terrain [32], which was refined later by Aitken [33] and Langmuir [34]. This formula is implemented in a cost distance tool in GRASS GIS [35], but this work applies a different formula that was established later. In 1993, the geographer Waldo Tobler proposed the Tobler hiking function [36] to estimate slope-derived walking speeds that has been applied in this study, as well.

Jobe and White [8] built a cost distance model for human accessibility that is based on energetic expenditure while hiking through a given terrain. It incorporates different landscape features, such as vegetation, trails, streams and slope. They concluded that slope, followed by vegetation, is the dominant contributor to the mean accessibility of the model. Ullah [26] used the r.walk module of GRASS GIS to conduct the slope-dependent cost distance analyses, but additional costs were not taken into account. Howey [37] selected vegetation cover, waterways and slope (as a relative cost value) as criteria critical to prehistoric movement. She also suggested that although many studies acknowledged the importance of incorporating multiple criteria in cost surface models, they usually only included slope as a variable. Surface-Evans [9] incorporated slope (as a relative cost value and with Tobler’s hiking function) and rivers, both as obstacle and transportation routes in her movement models.

Verhagen [38] identified cost surfaces, least cost paths (LCP) and network analysis as useful tools to identify places that are more connected or isolated, in order to draw conclusions about the suitability of a landscape for settlement or other activities. Surface-Evans [9] attested that least cost analysis (which includes cost distance analysis) has potential in modeling idealized expectations for regional patterns of land use, for example to test behavioral hypotheses. Ullah [26] suggested that SCA should be viewed as a type of experimental archeology, since SCA does not produce “the site’s catchment”, but rather returns a range of site catchment scenarios that are plausible for the available data that were used in the case.

In the approach presented in this study, the slope, which is derived from the DEM, is the most important input variable. Apart from varying slope estimations based on the applied algorithm, as shown by Jones [39], Warren et al. [40] and Herzog and Posluschny [41], the DEM cell size is an important factor. Hasan et al. [42] investigated the relationship between DEM resolution and slope, drainage area and topographic wetness index variation. They concluded that the estimates of slope differ significantly with the resolution of the DEM for the investigated peat land area in northern Sweden. The works of Zhang and Montgomery [43], Sørensen and Seibert [44], Vaze et al. [45], Kantner [46] and Grohmann [47] show that the overall slope values increase with the horizontal resolution (reduced cell size) in their respective study areas. This has important implications for the modeling results produced in this work.

3. Data

In the following paragraph, the various DEMs, including important information about their accuracy and further characteristics, the biome dataset and the research area, including the Palaeolithic sites used for the evaluation and cost distance modeling, are introduced.

3.1. DEMs

Digital elevation models can be generated with different data acquisition methods and remote sensing approaches. Popular examples are the almost globally-available synthetic aperture radar-based SRTM DEM and the ASTER GDEM products, which are based on stereo-optical imagery. In recent times, LiDAR (Light detection and ranging) has played an increasingly important role for the collection of global elevation data [48]. Due to the different data acquisition and post-processing methods, the DEMs differ in horizontal and vertical resolution and accuracy. If necessary, the raster data were re-projected to ETRS89 / ETRS-TM30 (European Terrestrial Reference System 1989, Universal Transverse Mercator Zone 30), EPSG:3042 (European Petroleum Survey Group) in the interest of providing a comparable basis and a consistent processing extent. For evaluation purposes, a list with uniform information about the horizontal resolution, vertical accuracy and data sources was compiled in

Table 1. Basic information about the applied DEMs [21,22,23,51,52,53,54,55,56].

	ASTER GDEM V2	CGIAR SRTM-3 V4/JPL SRTM-1 V3	EU-DEM	10-m DEM	5-m DEM
Data Source	ASTER	Space shuttle radar	SRTM and ASTER	Photogrammetric	Photogrammetric, LiDAR
Creation and distribution	METI/NASA	NASA/USGS	European Environment Agency	Regional Government of Andalusia	Centro Nacional de Información Geográfica
Release year	2011	2003	2013	2005	-
Data acquisition	2000 ongoing	11 days in 2000	2000, same as ASTER/SRTM	2001/2002	2009–2012
Resolution	1 arc second	3/1 arc seconds	1 arc second	-	-
Projected resolution	28.29 m	84.79 m/28.28 m	25 m	10 m	5 m
Absolute vertical accuracy (standard deviation)	7–14 m [51]	10 m [51]	2.85 m [52]	-	-
Absolute vertical accuracy (linear error at 90% or 95% confidence)	17.01 m (LE95) [53]	7.86 m (LE95) [53], <9 m (LE90) [54], ≤16 (LE90) [55,56]	5.69 m (LE95) [52]	-	2–4 m(LE90) Photogrammetric [23], -
RMSE	8.68 m, <12 m [53]	4.01 m, <12 m [53]	2.9 m [52]	-	1–2 m Photogrammetric, 0.5–1 m LiDAR [23]

. When clipping of the landmass was necessary (SRTM-1, 5-m, 10-m DEM) it was clipped with the Corine land cover coastline from the European Environment Agency [49]. The ETOPO1 (1 arc-minute global relief model) data [50] was used as the base map for bodies of water in the resulting maps.

Different versions of the SRTM [57,58,59,60] DEM are available in three-arc second and one-arc second resolution. For this work, the three-arc second resolution hole-filled CGIAR-CSI (Consultative Group on International Agricultural Research, Consortium for Spatial Information) SRTM V4.1 (SRTM-3) DEM data from Jarvis et al. [18] were used. In September 2014, the publication of the one-arc second SRTM (SRTM-1) [19,20] elevation data was started, which meant that we could incorporate it in our work.

The ASTER GDEM V2 [17] is generated from data collected by the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), a spaceborne Earth-observing optical instrument. Version 2 of the published dataset underwent quality improvements [51], such as enhanced ground resolution, filled voids, correction of anomalies and flat lake surfaces.

The EU-DEM is based on SRTM and ASTER GDEM data, combined by a weighted averaging approach [61]. The dataset is a realization of the Copernicus program and is available in a horizontal resolution of one-arc second or 25 meters [21].

The 10-m horizontal resolution DEM is the product of a collaboration of the Regional Ministries of Public Works and Transport, Environment and Agriculture and Fisheries of the Regional Government of Andalusia. The DEM was generated from photogrammetric flight data and was released by the Junta de Andalucia [22].

The DEM with 5-m horizontal resolution is a product of the Centro Nacional de Información Geográfica (National Center for Geoinformation) of Spain. The data can be obtained in tiles that are either generated from photogrammetric or LiDAR flights from the Plan Nacional de Ortofotografía Aérea (National Aerial Orthophotography Plan, PNOA), depending on the area. The geodetic reference system is ETRS89 with the corresponding UTM Zone 29 or 30 for the Iberian Peninsula [23]. Apart from the high resolution, this DEM is also the overall most accurate one of the DEMs used in this work.

Since the DEM is the most important input data for this CDM approach, the characteristic differences of the free access DEMs based on SRTM and ASTER data are investigated to assess and compare their characteristics. Hayakawa et al. [62] compared the ASTER GDEM and the SRTM-3 DEM and concluded, that, in the investigated area, the terrain representation of the ASTER GDEM is superior to that of the SRTM-3 DEM for most landscape elements and that the SRTM-3 DEM exhibits higher noise levels. Mukherjee et al. [14] and Li et al. [63] assessed that the vertical accuracy of the ASTER GDEM V2 is higher than that of the SRTM-3 DEM in their study area. However, in spite of the higher horizontal resolution of the ASTER GDEM V2, other studies from Athmania and Achour [55], Suwandana et al. [64], Rexer and Hirt [65], Pulighe [66] attest that the SRTM v4.1 (SRTM-3) data have a higher or similar [67] vertical accuracy as the ASTER GDEM V2 [55,64,65,66]. The work of Tachikawa et al. [53] shows for the U.S. that the absolute vertical accuracy of the one-arc second SRTM DEM is higher than that of the ASTER GDEM V2 (see also Table 1). Noise errors (local variability) are also a characteristic of both DEMs, while the ASTER GDEM V2 exhibits more high frequency noise than V1 overall and as the (although limited) SRTM-1 DEM examples [53]. While vegetation and tree canopy are present in both DEMs [68,69], it is stated that GDEM2 has higher elevations than SRTM in many forested areas [53,69] and that higher slopes and elevation are correlated with errors in SRTM DEMs [70,71] and ASTER GDEM V2, but less strong [14] or not apparent in the case of elevation [53]. Further, SRTM DEMs tend to overestimate valley-floor elevation and underestimate ridge elevation [62,72]. In addition, Gesch [13] and Tachikawa et al. [53] assess that the true horizontal resolution of both DEMs is less than the one-arc second cell size implies. The EU-DEM was evaluated in the EU-DEM Statistical Validation Report [52]. The report concludes that the EU-DEM dataset has a fundamental vertical accuracy of 2.9 meters. However, since it is a hybrid DEM based on SRTM-3 and ASTER GDEM V1 data [61], it is questionable if the one-arc second cell size reflects the effective horizontal resolution of the dataset.

3.2. Stage3 Biome3.5

The Stage3 Biome3.5 simulation dataset [73] is part of the Penn State University’s Stage3 Paleoclimatic Simulations. The available data originates from the Phase 4 runs from 1999–2000. The Biome3.5 data of the 21 ka (Last Glacial Maximum, LGM) simulation run seen in Figure 1 were used, since biomes can be translated into the vegetation classes that White and Barber [74], Frakes et al. [75] and Theobald et al. [76] used in their least cost models and, thus, be incorporated into the model. This has to be considered as an experimental proof of concept. Unfortunately, the dataset does not contain data in the coastal areas of the study area. Due to the lack of high resolution alternatives, the data are used nonetheless to test the approach. For future work, the PMIP3/CMIP5 (Paleoclimate Modelling Intercomparison Project Phase III/Coupled Model Intercomparison Project Phase 5) model simulations look very promising, but the horizontal resolution of the data is even lower. The point data were processed to Thiessen polygons, reprojected to ETRS89/ETRS-TM30 (EPSG:3042) and used as described in Section 4.4.

3.3. Palaeolithic Sites

Eight sites, seen in Figure 1, were utilized to conduct the DEM evaluation (Section 5.1), but only five of those, Ardales, Bajondillo, Nerja, La Pileta and Zafarraya, can be attributed to the chronocultural period of the Solutrean, as shown in

Table 2. Solutrean dating from Bajondillo and Nerja. Bj: Bajondillo NV: Nerja Vestíbulo area, TL: Thermoluminescence dating, AMS C14: Accelerator mass spectrometry radiocarbon dating, C14: Radiocarbon dating.

Site	Area	Level	Technocomplex Subphase	Method	Dating	Material	References
Bajondillo		Bj/7	upper evolved	TL	17582 ± 1521	carbonate	[77]
Bajondillo		Bj/8	upper evolved	TL	18701 ± 2154	carbonate	[77]
Bajondillo		Bj/9	upper	TL	16438 ± 1497	flint	[77]
Bajondillo		Bj/9a		AMS C14	19990 ± 480	bone	[77,78]
Nerja	Galerías altas	rock art		AMS C14	19900 ± 210	charcoal	[79,80,81]
Nerja	Vestíbulo	NV VIII (=9a)		?	21140 ± 190	charcoal	[78,79,82]
Nerja	Vestíbulo	8i	evolved	C14	15990 ± 260	charcoal	[79,80,83,84]
Nerja	Vestíbulo	NV 8k-l	evolved	C14	18420 ± 530	charcoal	[77,79,83,85]
Nerja	Vestíbulo	NV 8/s (fireplace)	evolved	C14	17940 ± 200	charcoal	[83]

. Therefore, the cost distance modeling, including the stream network, vegetation and the archaeological discussion, is performed only for these sites.

Table 3. Description of the Solutrean levels in the sample of sites. AD: Ardales, Bj: Bajondillo.

Site	Solutrean Levels	References
Ardales	AD 2.6	[86]
Bajondillo	Bj/6, Bj/7, Bj/8, Bj/9	[87,88]
Nerja	Vestíbulo area: NV/IX-VIII-VII NV/9-8-7. Mina area: 80A/8-7	[89]
La Pileta	Level D (also contains the Magdalenian)	[90]
Zafarraya	Reworked part of the upper stratigraphic complex	[91]

lists the Solutrean levels of the selected sites and shows that a good stratigraphical record is available only for the sites Nerja and Bajondillo. The lack of a clear stratigraphical sequence is a problem for the analysis of other aspects of the archaeological record, such as lithic and faunal assemblages, whose results are essential for the interpretation of the mobility of hunter-gatherer groups. This makes a comparison of the cost distance models and the archaeological data difficult for the remaining sites.

4. Methods and Implementation

In this section, the approach to evaluate the influence of different DEMs on the modeling results is shown. Subsequently, the fundamental steps of the CDM approach that results in site catchment models (represented by isochrones) are presented, and the implementation is explained in detail. The applied GIS and additional software are ArcGIS [92] for the CDM and mapping, QGIS [93], SAGA GIS [94] and GDAL [95] for various tasks, like the generation of elevation profiles or processing of raster data. The statistical analysis was performed with Microsoft Excel. The area of investigation is in UTM Zone 30 coordinates (SW/NE): 264704E, 4029686N/504163E, 4216227N.

4.1. DEM Evaluation

First, in order to evaluate the DEMs used in this work, studies and data specifications concerning the quality and other considerations associated with cost distance modeling are investigated (see Section 3.1). The further DEM evaluation is done in two steps:

• Selected sample areas are evaluated using elevation profiles and a comparison of hillshades of the DEMs. An error estimation is performed for the area of interest by generating error rasters and calculating the RMSE and correlation of the elevation and slope.
• A descriptive statistical analysis of the modeled site catchment areas in relation to the horizontal resolutions of the various DEMs.

(1) Three elevation profiles were determined (flat and hilly terrain, a populated area near the coast and a primarily mountainous area) in the area of investigation These were used in the ProfileTool [96] plugin for QGIS in order to obtain the elevation values and to produce elevation profiles with Excel for the six available DEMs. The hillshade analysis was generated with ArcGIS. The DEMs were all re-projected with GDAL (resampling method: bilinear) to ETRS89 / ETRS-TM30 (EPSG:3042) before the analysis. These profiles and the hillshades reveal differences in the DEMs directly and help to understand what causes deviations in the results of our cost distance results. As the 5-m DEM has the highest overall accuracy, error rasters of the remaining DEMs were calculated by subtracting the 5-m DEM. The error rasters were used to calculate the RMSE between the ASTER GDEM V2, SRTM-1 and -3 DEMs, 10-m DEM and the 5-m DEM. Further, the correlation coefficients between the elevation and slope rasters were calculated with SAGA GIS [94].

(2) In order to gain further insight into the influence of different DEMs on the results and their suitability for SCA and to perform a descriptive statistical analysis, a list of the area sizes of 4-hsite catchments is compiled. To achieve this, the 5-m DEM (this is considered as the DEM with the highest absolute and relative vertical and horizontal accuracy) is resampled to the horizontal resolution of the other DEMs (10 m, 25 m, 28.29 m, 28.28 m, 84.79 m) and further intermediate cell sizes (20 m, 30 m, 50 m, 160 m) to serve as a reference and to investigate the effect of the cell size. Further, the 10-m DEM and EU-DEM were resampled to 30 m to compare the effects at a cell size similar to the ASTER and SRTM DEMs. These resampled versions of the 5-m DEM and the other DEMs are used to perform the procedure shown in Figure 2. Using the results of the modeling process, the correlation of the resulting 4-h site catchment area sizes, with the changes in cell size and the mean slope and the correlation of the mean slope with the cell size, is investigated, by calculating the coefficient of determination (R${}^2$).

4.2. Cost Distance Modeling

As introduced in Section 2, GIS-based site catchment modeling in archeology is based fundamentally on cost distance modeling. The concept of CDM is that a given cost value grows with the distance from a source point. In raster-based CDM, this means that cost values in a cost raster (or cost surface) have to be accumulated with the distance from a source point with a cost distance raster (Figure 2e) as a result. This is a function many GIS software packages provide (GRASS: r.cost; SAGA: Accumulated Cost): in this case, the cost distance tool from ArcMap’s Spatial Analyst tool set is used.

The applied process presented in Figure 2 was adapted from Wheatley and Gillings [4], Tripcevich [28] and Marín-Arroyo [7]. The incorporation of topographic variables, in addition to the DEM, was adapted from Jobe and White [8], Frakes et al. [75], Theobald et al. [76]; White and Barber [74]. Some of the steps and the input data can be modified to simulate different scenarios or for the purposes of the evaluation presented in this work. Another important factor is the function that is used to calculate walking speeds from the slope values. In this work, Tobler’s hiking function (see Equation (1)) is applied and slightly changed to calculate walking time per meter, because it is popular in raster-based CDM or least cost analysis [9,41,97] and also well suited for implementation in ArcGIS for this application. Tobler’s hiking function calculates walking speed based on slope inclination. For example, the calculated walking speed on a 0${}^{\circ }$ slope is about 5.037 km/h. It should be noted that this modeling approach, applying the cost distance tool, only considers positive slope values, which corresponds to uphill walking. Furthermore, it does not factor in the case of walking in parallel to a (steep) slope (which would result in a slope of 0${}^{\circ }$ in the walking direction). These issues are discussed in detail in Section 6.

$$\frac{h}{m}=0.000166666\ast \left(exp(3.5\ast \left(abs(tan\left(rad\left(slope\right)\right)+0.05)\right))\right)$$

(1)

Tobler’s hiking function is changed to calculate hours per meter [28,36], and the slope is in degrees.

The following paragraph introduces the incorporation of additional landscape elements that affect the speed of human walking in order to test the performance of the modeling approach. Based on the permeability values developed by Frakes et al. [75], Theobald et al. [76] compiled a list with various permeability values (speed coefficients) for different water-bodies (see

Table 4. Speed coefficients for different water bodies [76].

Stream Order	Speed Coefficient
Tributaries (1st Strahler order)	0.80
Small streams (2nd Strahler order)	0.65
Large streams (3rd Strahler order)	0.20
Rivers (>3rd Strahler order)	0.02

) and vegetation classes (see

Table 5. Speed coefficients for different biomes (abundant in the area of interest) from the climate and vegetation simulation database of the Stage Three Project [73]. Speed coefficients are derived from the works of White and Barber [74], Frakes et al. [75], Theobald et al. [76].

Biome Class Number	Class Name	Speed Coefficient
10	Evergreen taiga/montane forest	0.65
16	Temperate grassland	0.70
other	-	1

).

To include these into the analysis, a stream network based on the DEM is modeled with the appropriate GIS tools, to be able to classify the streams following Strahler’s stream order [98]. The stream order numbers of the resulting raster are then reclassified to the corresponding speed coefficients. The original Tobler cost raster is then divided by the raster dataset containing the speed coefficients, and this result is used to execute the cost distance calculations for the sites.

To incorporate vegetation into the cost distance calculations, it is possible to work with any raster that contains vegetation or equivalent data. Similar to the aforementioned stream network raster data, the vegetation raster can be reclassified to speed coefficients that represent a speed change induced by a plant cover. The proposed speed coefficients from White and Barber [74], Frakes et al. [75], Theobald et al. [76] were transferred to the Biome3.5 21k plant cover paleodataset (see Section 3.2) from the Stage Three Project.

4.3. Slope

The slope rasters are calculated with ArcGIS’ slope tool. The slope function in ArcGIS calculates the maximum rate of change for any given cell in the raster compared to all of its neighboring cells [46,99]. It uses Horn’s method [100] to calculate the rate of change for the x and y directions, which are then used to determine the slope value of the central cell of this 3 × 3 grid.

4.4. Implementation of the Cost Distance Model

The process is implemented with ArcMap’s Modelbuilder as a custom tool, which allows the application of the modeling process to multiple archaeological sites. The tool uses a DEM and point data (archaeological sites) as input. The user can adjust selected parameters, such as the interval of the isochrones around the sites, the processing extent and the target folder for the resulting data. The results are accumulated cost rasters, isochrones in the desired interval and least cost paths (not applied in this work) from every point to every other point in the input dataset. The tool generates the results in the following steps, which can be reproduced manually, as well:

• Calculation of the cost raster

  (a)

  Generation of a slope raster (Figure 2a–c) from the DEM.

  (b)

  The raster calculator to divide the slope raster by 57.29577951 to get the radians, since tan() from ArcMap interprets values as radians.

  (c)

  The raster calculator to calculate the final cost raster (Figure 2d) with Equation (1).

• The cost raster and the point data (sites) are used as input data for the cost distance tool from the spatial analyst tool set (in ArcMap, the results are automatically multiplied with the pixel size of the raster). This is done for every point available in the point dataset (Figure 2e,f) to calculate the cost distance and the cost direction raster.
• If a cost distance and cost direction raster are finished for a site:

  (a)

  The countour tool is used to generate the isochrones for the site with the requested interval.

  (b)

  For every site, a file with the associated isochrones (Figure 2g) and LCPs (Figure 2h; LCPs are optional and not applied in this work) is saved.

To be able to classify the stream network with the Strahler order, the stream network is modeled with a hydrology tool set. Here, the hydrology tool set of ArcMap’s spatial analyst extension was used to apply the following procedure:

• Fill the DEM (5-m DEM: z-limit: 2).
• Flow direction.
• Flow accumulation.
• Use Con or setnull with the Flow accumulation raster to filter for a specific threshold value (set null Value < 1000).

After these steps, the resulting raster has to be reclassified to mirror the speed coefficients shown in Table 4. The Tobler cost raster is divided by the speed factor raster afterwards, and the result is used with the cost distance functionality of the GIS software.

• Reclassify the stream network with the stream order tool (Strahler order).
• Reclassify Strahler order to speed coefficients. (afterwards: copy raster 32 bit float).
• Divide the Tobler cost raster by the speed factor raster with the raster calculator.

The influence of vegetation is incorporated in the same way. The Stage3 biome 21k dataset [73] is reclassified to the speed coefficients shown in Table 5 and used to divide the cost raster by the speed factors derived from the dataset.

• Reclassify the vegetation raster with the reclassify tool to speed coefficients (afterwards: copy raster 32 bit float).
• Divide the Tobler cost raster by the speed factor raster with the raster calculator.

5. Results

The results of this work are separated into three parts. First, the results of the evaluation of the DEMs are explained. Subsequently, the results of the descriptive statistical evaluation of the influence of different DEMs and their cell size on the modeled catchments are presented. After that, the modeled site catchments (isochrones) are shown in a sample of five Solutrean sites.

5.1. Evaluation of the DEMs Used for CDM

For the evaluation of the DEMs with emphasis on their influence on cost distance analysis, three elevation profiles located in sample areas representing characteristic morphometric categories in the study area (Figure 3) were examined (see Figure 4 and Figure 5a–c). It is noticeable that the elevation data in the DEMs show some strong variations on a local and regional scale. It is suggested that this is caused by the data acquisition method and the applied post-processing methods. Overall, the quality and accuracy of the 5-m DEM, the ASTER GDEM V2 or SRTM-3/-1 and the EU-DEM are well known by the published specifications (see Table 1). This current work aims to allow a more informed decision about which DEM to choose for prehistoric site catchment analysis, especially in our area of investigation.

Figure 4a shows the elevation plots of a mostly flat area, which then transitions into a hill. The first impression is that the ASTER GDEM V2 data exhibit more noise than the other datasets, especially in the flat areas. Compared to the 5-m cell size DEM, which is considered as the most accurate reference (see Table 1), both the SRTM datasets and the EU-DEM deviate from these profiles. Regarding Figure 4b, it is clear that the ASTER GDEM V2 data differentiate themselves from the other DEMs, by containing ridges that are not present in the other DEMs. The plots in Figure 4c appear more homogeneous again, with a few deviations. While the curve of the SRTM-1 DEM dataset is very similar to the 10-m and the 5-m ones, the SRTM-3 DEM, while it is also distinctly smoother; ASTER GDEM V2 and EU-DEM show occasional extreme deviations of 20 or 50 meters especially in valley and mountain ridge areas. Examining the hillshades (Figure 5a–c), many of the observations are supported. The 5-m and 10-m DEMs show very little noise and the most detail, with residuals of many anthropogenic objects (mostly streets, bridges) present in the data. These residuals also change the slope values and, thus, the modeling results. ASTER GDEM V2 appears to contain more noise compared to the other DEMs, followed by the SRTM-1 DEM. An important measure of the ASTER DEM quality is the stacking number, which describes the number of stacked ASTER DEM scenes used to compute the elevation values. The RMSE should decrease with increasing stack number, while the error reduces significantly between one and 10 scenes, with only little improvement after about 15 scenes [55]. In the study area, the positive ASTER GDEM V2 stacking number range is 1–37 with the majority at 12, which does not point to notable problems in this area, although the stacking number differs for the different sites with a stripe of higher numbers (>22) around the site of Ardales. The EU-DEM hillshade exhibits less noise than both ASTER GDEM V2 and SRTM-1 DEM, but in some areas, the data look almost smoothed compared to their source DEMs (SRTM-3 DEM and ASTER GDEM V2).

When comparing the RMSE differences (see

Table 6. Correlations of the elevation and slope value rasters between the 5-m reference DEM and the other DEMs. RMSE of the elevation relative to the 5-m reference DEM.

	R${}^{\mathbf{2}}$ of Elevation Values	R${}^{\mathbf{2}}$ of Slope Values	RMSE of Elevation Values
	5-m DEM	5-m DEM	5-m DEM
5-m DEM	1	1	-
10-m DEM	0.99	0.88	3.46 m
EU-DEM	0.99	0.64	7.39 m
ASTER GDEM V2	0.99	0.64	8.61 m
SRTM-1 DEM	0.99	0.76	4.12 m
SRTM-3 DEM	0.99	0.65	4.74 m

) between the DEMs relative to the 5-m DEM, the results are mostly in line with the published information, apart from the EU-DEM, which performs worse. For the 10-m DEM, it is the only measure of accuracy available, but higher accuracy was expected. Table 6 also shows that, although the correlation between the elevation values of the DEMs is very strong, the correlations between the slope values of the 5-m DEM and the other DEMs are substantially weaker. Further, a similar succession of quality is found here, while the 10-m DEM performs best, followed by the SRTM DEMs and, after that, ASTER GDEM V2 and EU-DEM.

5.2. Statistical Evaluation of the DEM Influence on the Modeling Results

Concerning the results of the statistical evaluation, it has to be noted that the sites of Bajondillo and Nerja are situated near the coast, so the modeled site catchments are noticeably smaller. As the coastline was in a different position and exhibited a different sea level during the Last Glacial Maximum, the actual site catchments were presumably larger during that period [101]. Lacking an appropriate high resolution DEM for the bathymetry, it is not possible to take this into account.

The results for the resampled 5-m DEM (

Table 7. Statistical evaluation of the correlations between area size, DEM resolution, mean slope. * = sites are located near the coast and excluded from the calculation of the mean area size.

	Correlation of Resulting Area Sizes With Different DEM Properties
	R Resolution	R${}^{\mathbf{2}}$	t	p-Value	R Mean Slope	R${}^{\mathbf{2}}$	t	p-Value
Ardales	0.75	0.56	2.26	0.04	−0.99	0.99	17.83	0.00
Bajondillo *	0.51	0.26	1.18	0.15	−0.56	0.31	1.34	0.13
Carihuela	0.67	0.45	1.80	0.07	−0.90	0.81	4.09	0.01
La Graja	0.76	0.57	2.32	0.04	−1.00	1.00	36.02	0.00
Hora	0.64	0.40	1.65	0.09	−0.85	0.72	3.20	0.02
Nerja*	0.78	0.61	2.52	0.03	−0.98	0.97	10.61	0.00
La Pileta	0.50	0.25	1.15	0.16	−0.66	0.44	1.78	0.07
Zafarraya	0.53	0.28	1.24	0.14	−0.45	0.20	1.01	0.18
Mean area size	0.74	0.55	2.21	0.05	−0.95	0.90	6.10	0.00
Mean area size *	0.74	0.55	2.21	0.05	−0.95	0.91	6.31	0.00
	Correlation of Resulting Area Sizes with Different Properties of the Resampled 5-m DEM
	R resolution	R${}^{\mathbf{2}}$	t	p-Value	R Mean Slope	R${}^{\mathbf{2}}$	t	p-Value
Ardales	0.99	0.98	19.11	0.00	−0.97	0.93	9.89	0.00
Bajondillo *	0.98	0.96	12.44	0.00	−0.96	0.92	8.72	0.00
Carihuela	0.99	0.98	19.60	0.00	−0.96	0.92	8.97	0.00
La Graja	0.99	0.99	24.52	0.00	−0.99	0.98	17.53	0.00
Hora	0.99	0.97	15.71	0.00	−0.95	0.91	8.33	0.00
Nerja*	0.92	0.84	6.05	0.00	−0.85	0.73	4.35	0.00
La Pileta	0.81	0.66	3.71	0.00	−0.70	0.49	2.59	0.02
Zafarraya	0.97	0.94	10.65	0.00	−0.99	0.97	15.42	0.00
Mean area size	0.99	0.98	17.24	0.00	−0.96	0.92	9.09	0.00
Mean area size *	0.99	0.98	20.18	0.00	−0.97	0.93	9.91	0.00

and

Table A1. Slope characteristics and resulting area sizes of 4-h site catchments calculated with the presented method. The method was applied to 8 prehistoric sites with the various DEMs and with resampled versions of the 5-m DEM as input data (lower section of the table). * = sites are located near the coast, and the associated area sizes are excluded in the calculation of the mean area size.

	Resulting Area Sizes of the Various DEMs (km${}^{\mathbf{2}}$)
DEM	5-m	10-m		EU-DEM	SRTM-1	ASTER GDEM V2					SRTM-3
Resolution (m)	5	10		25	28.28	28.29					84.79
Mean Slope (${}^{\circ }$)	12.04	11.87		8.77	9.85	10.73					8.02
Ardales	344,561	335,969		488,042	431,991	395,879					493,715
Bajondillo *	315,214	309,272		336,508	305,741	287,460					340,091
Carihuela	538,442	533,430		614,617	572,557	522,906					617,532
La Graja	374,378	378,025		468,276	428,986	411,154					471,881
Hora	577,138	572,990		653,720	606,154	551,300					655,960
Nerja *	142,350	134,932		179,859	160,526	152,706					185,474
La Pileta	301,762	278,461		323,990	310,947	266,354					326,114
Zafarraya	266,113	267,405		411,185	185,361	388,410					413,100
Mean area size	357,495	351,310		434,525	375,283	372,021					437,983
Mean area size *	400,399	394,380		493,305	422,666	422,667					496,384
	Resulting Area Sizes of the Resampled 5-m, 10-m and EU-DEM DEMs (km${}^{\mathbf{2}}$)
Origin DEM	5 m	5-m	5-m	5-m	5-m	5-m	5-m	10-m	EU-DEM	5-m	5-m	5-m
Resolution (m)	5	10	20	25	28.28	28.29	30	30	30	50	84.79	160
Mean Slope (${}^{\circ }$)	12.04	11.23	11.28	10.47	10.31	10.31	10.77	10.68	8.67	9.12	8.26	7.14
Ardales	344,561	335,793	348,835	345,829	349,439	349,820	353,478	359,056	488,759	385,228	437,472	519,731
Bajondillo *	315,214	313,525	312,986	313,352	314,700	314,923	315,265	315,566	337,361	326,895	336,827	355,072
Carihuela	538,442	534,628	540,589	538,999	541,205	541,294	542,003	548,372	615,530	561,033	588,904	641,562
La Graja	374,378	373,560	385,878	385,245	389,627	389,612	392,504	399,894	470,270	413,793	444,762	492,288
Hora	577,138	572,652	576,584	573,972	578,266	576,471	578,251	585,160	654,758	596,253	627,885	677,888
Nerja *	142,350	133,528	127,203	125,341	126,184	126,582	126,257	132,322	179,348	138,613	162,058	192,230
La Pileta	301,762	280,778	274,544	270,388	279,357	271,997	276,072	283,915	330,925	274,810	296,630	343,654
Zafarraya	266,113	266,011	298,620	291,001	299,749	289,190	293,906	306,922	417,143	339,653	353,686	410,982
Mean area size	357,495	351,309	358,155	355,516	359,816	357,486	359,717	366,401	436,761	379,534	406,028	454,176
Mean area size *	400,399	393,904	404,175	400,905	406,274	403,064	406,036	413,886	496,231	428,461	458,223	514,351

in the Appendix A) show moderate (La Pileta and Nerja) to very strong positive correlations between the horizontal resolution and the (mean) area sizes of the modeled 4-hcatchments ($R^2$ = 0.98, t = 18.25, p = 0.00). Thus, the area size grows with the cell size of the raster. Overall, there is a moderate (La Pileta, Nerja) to strong negative correlation between the mean slope and the area size ($R^2$ = 0.87, t = 6.76, p = 0.00), while the mean slope decreases with the horizontal resolution ($R^2$ = 0.87, t = 6.93, p = 0.00). Regarding the results of the various DEMs (see Table 7), the main difference to the 5-m DEM resamples are the weaker correlations (moderate to strong) between the catchment area size and the horizontal DEM resolution ($R^2$ = 0.53, t = 2.14, p = 0.05), while the correlation between the mean area size and the mean slope is still strong ($R^2$ = 0.94, t = 7.68, p = 0.00). The slope also decreases, although not as highly correlated, with the horizontal resolution ($R^2$ = 0.68, t = 6.93, p = 0.00), with the exception of the EU-DEM, which is linked to a much lower mean slope than that of ASTER GDEM V2 or the SRTM-1 DEM.

When comparing the relative differences of resulting area sizes in

Table 8. Resulting relative area sizes of 4-h site catchments calculated with the presented method. The results of the 5-m DEM are the reference with a size index of 1. The method was applied to 8 prehistoric sites with the various DEMs and with resampled versions of the 5-m DEM and 30-m resamples of the EU-DEM and the 10-m DEM as input data, to allow comparison at similar horizontal resolution. * = sites are located near the coast and excluded from the calculation of the mean area size.

	Resulting Relative Area Sizes Based on the Various DEMs
DEM	5-m	10-m		EU-DEM	SRTM-1	ASTER GDEM V2					SRTM-3
Resolution (m)	5	10		25	28.28	28.29					84.79
Mean Slope (${}^{\circ }$)	12.04	11.87		8.77	9.85	10.73					8.02
Ardales	1.00	0.98		1.42	1.25	1.15					1.43
Bajondillo *	1.00	0.98		1.07	0.97	0.91					1.08
Carihuela	1.00	0.99		1.14	1.06	0.97					1.15
La Graja	1.00	1.01		1.25	1.15	1.10					1.26
Hora	1.00	0.99		1.13	1.05	0.96					1.14
Nerja *	1.00	0.95		1.26	1.13	1.07					1.30
La Pileta	1.00	0.92		1.07	1.03	0.88					1.08
Zafarraya	1.00	1.00		1.55	0.70	1.46					1.55
Mean area size	1.00	0.98		1.22	1.05	1.04					1.23
Mean area size *	1.00	0.98		1.23	1.06	1.06					1.24
	Resulting Relative Area Sizes Based on the Resampled 5-m, 10-m and EU-DEM DEMs
Origin DEM	5-m	5-m	5-m	5-m	5-m	5-m	5-m	10-m	EU-DEM	5-m	5-m	5-m
Resolution (m)	5	10	20	25	28.28	28.29	30	30	30	50	84.79	160
Mean Slope (${}^{\circ }$)	12.04	11.23	11.28	10.47	10.31	10.31	10.77	10.68	8.67	9.12	8.26	7.14
Ardales	1.00	0.97	1.01	1.00	1.01	1.02	1.03	1.04	1.42	1.12	1.27	1.51
Bajondillo *	1.00	0.99	0.99	0.99	1.00	1.00	1.00	1.00	1.07	1.04	1.07	1.13
Carihuela	1.00	0.99	1.00	1.00	1.01	1.01	1.01	1.02	1.14	1.04	1.09	1.19
La Graja	1.00	1.00	1.03	1.03	1.04	1.04	1.05	1.07	1.26	1.11	1.19	1.31
Hora	1.00	0.99	1.00	0.99	1.00	1.00	1.00	1.01	1.13	1.03	1.09	1.17
Nerja *	1.00	0.94	0.89	0.88	0.89	0.89	0.89	0.93	1.26	0.97	1.14	1.35
La Pileta	1.00	0.93	0.91	0.90	0.93	0.90	0.91	0.94	1.10	0.91	0.98	1.14
Zafarraya	1.00	1.00	1.12	1.09	1.13	1.09	1.10	1.15	1.57	1.28	1.33	1.54
Mean area size	1.00	0.98	1.00	0.99	1.01	1.00	1.01	1.02	1.22	1.06	1.14	1.27
Mean area size *	1.00	0.98	1.01	1.00	1.01	1.01	1.01	1.03	1.24	1.07	1.14	1.28

, it is obvious that the differences that occur when the different DEM products are used outweigh the differences occurring when the resampled 5-m DEM is used. This is supported by the results produced with DEMs and DEM resamples in a similar horizontal resolution. While the mean area sizes change by a factor of 1.00/1.01* when the 5 m is resampled to 30 m, 28.28 m or 28.29 m, the mean differences caused by the EU-DEM (1.22/1.23*), SRTM-1 (1.05, 1.06*) and ASTER GDEM V2 (1.04, 1.06*) are higher. The differences increase more when the results of single sites are compared. They are consistently greater between the tested DEM products (e.g., Zafarraya: EU-DEM: 1.55, SRTM-1: 0.70, ASTER GDEM V2: 1.46; 5-m to 25 m: 1.09, 5-m to ASTER GDEM V2: 1.13, 5-m to SRTM-3: 1.09) than between the resampled 5-m DEM tests.

5.3. Isochrones Representing the Site Catchment

Figure 6 shows the results (isochrones for the site of Ardales) of the six different DEMs that were used to perform the cost distance calculations with Tobler’s hiking function described earlier. The results of the investigation of the DEMs in Section 5.1 can be observed with the help of the isochrones, as well. Apart from the overall area size, the shape of the isochrones is important. The resulting isochrones react to topographic features like flat areas and hilly terrain with growing or shrinking distances to the starting point (the cave of Ardales, in this case). The resulting EU-DEM and SRTM-3 isochrones are very similar, although the horizontal resolution of the EU-DEM is much higher. Furthermore, the influence of hilly terrain is much weaker than on all of the other DEMs, while it is the strongest on the 5-m and 10-m DEMs.

Figure 7 and Figure 8 show the resulting isochrones for the Solutrean sites of the area. The maps contain the results based on Tobler’s hiking function, the 5-m and SRTM-1 DEMs for comparison, which were selected using the quality assessments in Section 3.1 and Section 5.1. The results incorporate the stream network and the Stage3 Biome3.5 21k data, as well as a combination of both. The maps also include a 20-km radius around the sites, to provide a reference to the classic site catchment analysis approach. Differences in the results caused by the source DEM exist as expected and are evaluated in Section 3.1 and Section 5.1; stronger differences are caused by the position of a site and the surrounding topography, respectively (also, see Table A1 for the 4-h site catchment area sizes). The incorporation of the stream network has a visible, but small negative effect on the size of the catchment area in the case of the 5-m DEM. The strongest change occurs after the incorporation of the Stage3 Biome3.5 21k dataset, with significantly smaller area sizes and distances between the isochrones. Notable examples are the sites of Bajondillo and Nerja. Both sites are (currently) in a coastal area, but the modeled 4- or 8-h catchment size of Nerja is much smaller than around Bajondillo, due to the surrounding terrain with steep slopes (elevation ranges from around 50 m–1800 m at the peak north of the cave). The area north of Bajondillo is much flatter. The very small differences between the two models at these sites are explained by the fact that the Stage3 Biome3.5 21k dataset contains no data in this area, so that no additional movement costs occur. The sites of Ardales, Pileta and Zafarraya are situated in a rather hilly terrain, while the terrain around Pileta and Zafarraya is more varied (or extreme) than around Ardales. The 4- and 8-h catchment sizes of the three sites are comparable, but they again differ in shape, caused by the surrounding mountain ranges. If the vegetation is taken into account (see Figure 7 and Figure 8), the catchment areas would be considerably smaller (in this case, the amount is determined by the speed factors from Table 5).

6. Discussion

In the context of GIS-based SCA in archeology, a slope-based cost distance modeling (CDM) approach is presented, and the influence of different DEMs on the results of CDM approach is investigated.

In this study, the walking speed model (also: hiking- or cost function) is the basis for the CDM. Although it is used frequently, the applied hiking function from Waldo Tobler is not free from issues. Herzog [102] argues that Tobler refers to data published by Imhof [103], but that his estimation does not fit Imhof’s data very well. Kondo and Seino [104] tried to evaluate and improve the formula on the basis of an ancient route in Japan and a GPS-aided walking experiment. They assessed that their measured walking speeds largely fit the Tobler curve in the slope range from −0.20–0.20 (−18${}^{\circ }$–18${}^{\circ }$), but that their measurements deviate below and above those slope values. They attempted to adjust the function to their measurements, but the problem in their study was that it was based on a sample size of only two persons. Consequently, their adjusted function has to be evaluated before its application. Hence, in the future, it would be very interesting and surely useful to derive a slope-based cost function that includes a measure of time, from GPS measurements, by a larger group of test subjects.

Further, it is important to take into account that the calculation of slope alone can differ among several geographical information system applications. As described in Section 4.3, the slope function in ArcGIS uses Horn’s method [16,39,99,100] to determine the slope values of the raster cells in the DEM. This is similar in GRASS GIS. SAGA GIS, on the other hand, offers additional different slope algorithms. It is important to consider this, as the application of different slope algorithms can cause different modeling results by producing different slope values [40,41]. Horn’s method performed well in a comparative study by Jones [39]. In this study, only ArcGIS’s slope tool was applied, so that the results are comparable. Another problem with the method is that only positive (uphill) slope values are considered. The slightly faster downhill walking, included in Tobler’s hiking function, was not taken into account, so the modeling is isotropic. The same is true for potential walking paths along an elevation contour line, where the cost is also direction dependent [97] because the applied cost spreading algorithm of the cost distance tool does not support anisotropy. ArcGIS’s path distance tool supports anisotropic cost modeling via a vertical factor table, but it was not applied here. We would argue that the importance of anisotropy is negligible for site catchment modeling, which is the main point of this work, as a presumed outbound trip and the way back would compensate substantially for the difference of up- or down-hill hiking. While this study investigates a specific question with respect to an already established method, the implementation of a different walking or cost spreading model, possibly using another data model, could address these restrictions in future research. When considering the cost distance tools, it is possible to transfer the method to other GIS software, such as GRASS GIS or SAGA, which provide respective cost spreading algorithms. GRASS’s cost distance tools allow more movement directions for the value accumulation (see Figure 2), 17 vs. 9 in a 3 × 3 grid (Knight’s move), which could lead to slightly more accurate modeling results. The latter was not in the focus of this study and is mentioned only for consideration in future work. The above-mentioned differences are more important to consider in least cost path modeling than in CDM. Furthermore, the presented evaluation results concerning the influence of different DEMs and their resolution are valid, regardless of whether the applied cost distance algorithm supports isotropy or not.

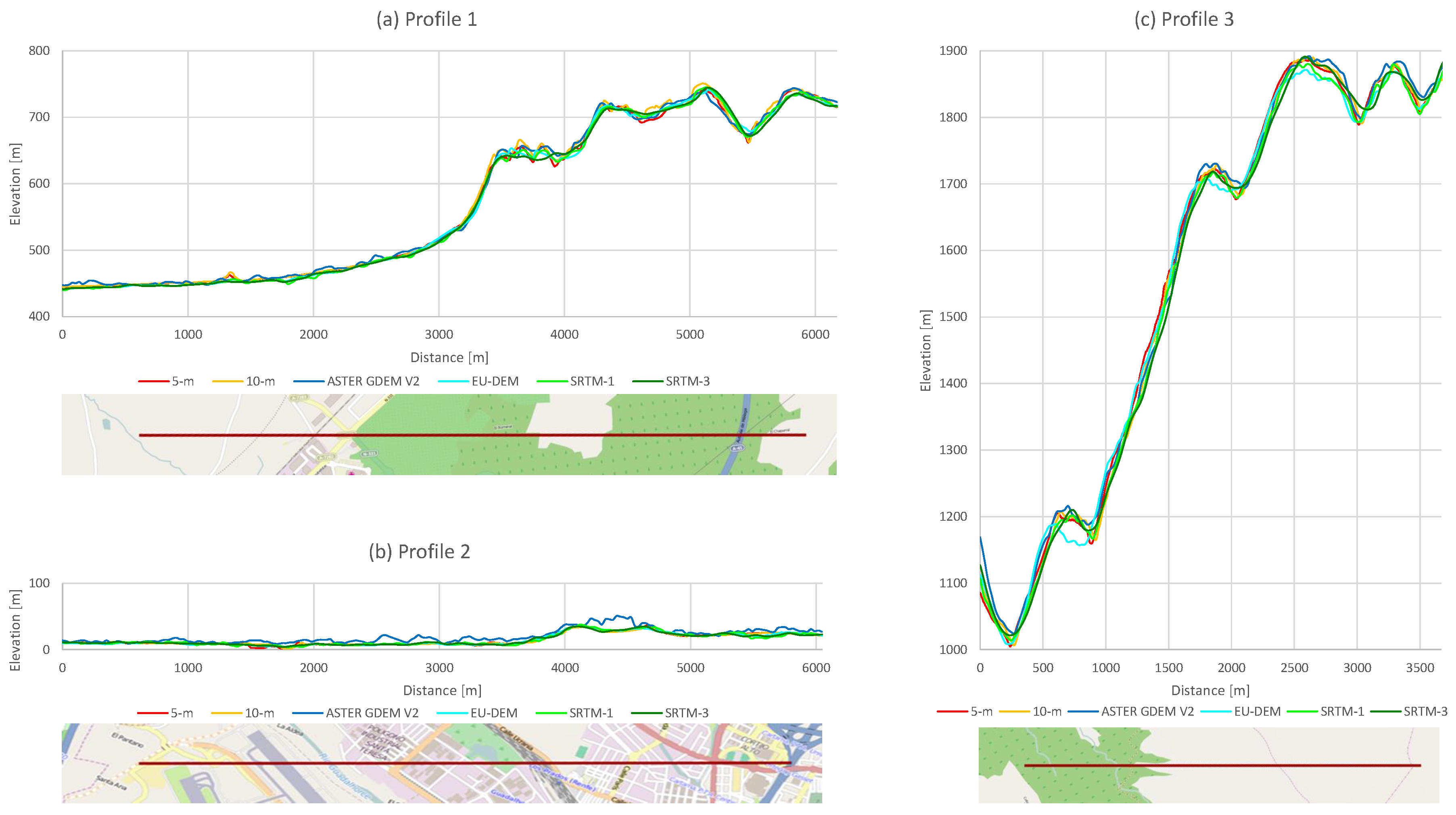
The initial evaluation of the DEM quality components (Section 3.1) and their specific characteristics (Section 5.1) shows that the DEMs exhibit substantial differences. Apart from the absolute vertical accuracy, noise and other error characteristics of the elevation data, the most noticeable difference is the raster cell size, which is in the range of 5 m to about 90 m. The results of the evaluation show that the choice of the DEM is quite important for various reasons. The studies on the relationship of slope to DEM cell size, covered in Section 2, reveal that increasing cell size leads to decreased slope values. For slope-based cost distance modeling, this indicates that the calculated movement speeds through the raster cells should increase. This is confirmed by the results of the statistical DEM evaluation, where one source DEM was resampled to a range of cell sizes to perform the site catchment modeling (see Table 7, Table 8 and Table A1 in the Appendix A). The modeled area sizes of the catchments correlate with the horizontal resolution and the mean slope of the applied DEM. However, the published accuracy information (Table 1), the qualitative and quantitative observations made in Section 5.1, the correlations of the slope rasters (Table 6) and the statistical evaluation (Section 5.2) indicate that the horizontal resolution is not the only important factor. Notable examples are the comparable results of EU-DEM and SRTM-3 (mean area size; mean slope of EU-DEM: 434,525 km${}^2$; 8.77${}^{\circ }$/SRTM-3: 437,923 km${}^2$; 8.02${}^{\circ }$), although the EU-DEM raster data have a much smaller cell size. Further, SRTM-1 leads to slightly larger catchment areas than ASTER GDEM V2 (mean area size; mean slope of SRTM-1: 375,283 km${}^2$; 9.85${}^{\circ }$/ASTER GDEM V2: 372,021 km${}^2$; 10.73${}^{\circ }$), with remarkable negative or positive differences depending on the site location (see Table 8 and Table A1), which is not apparent in the results based on the resampled data. As their cell size difference is minimal, these variations must be attributed to other differences in the DEM characteristics, such as lower absolute vertical accuracy (see Table 1), varying amounts of noise or other errors caused by vegetation and tree canopy, slope or elevation of the landscape (see Section 3.1) and the specific characteristics of the data acquisition method, respectively, as well as residuals of removed anthropogenic objects present in the data (see Section 3.1 and Figure 4 and Figure 5a–c). These differences are reflected in different slope values, which are observable in the correlation of the slope rasters relative to the 5-m reference DEM (Table 6).

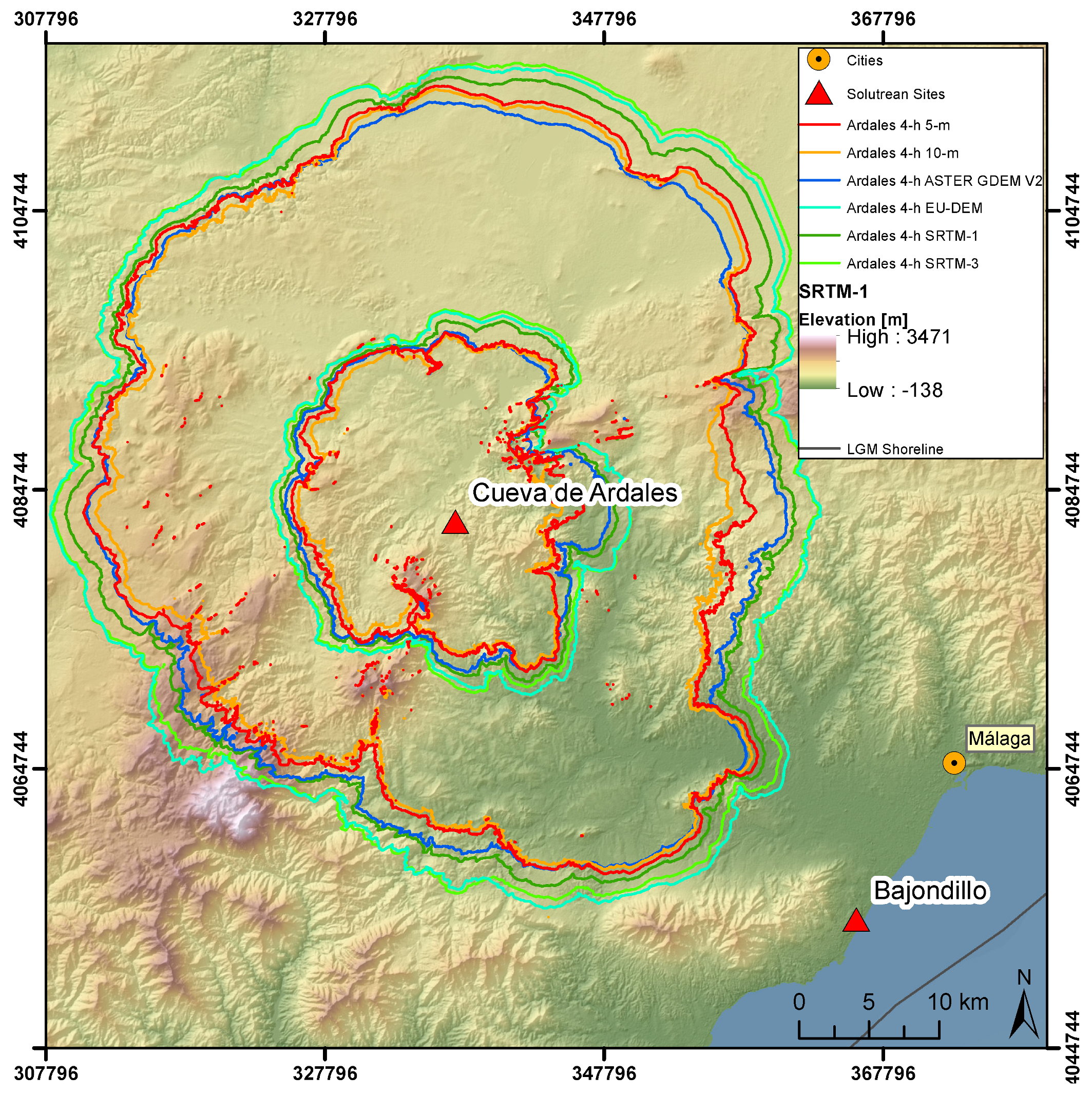
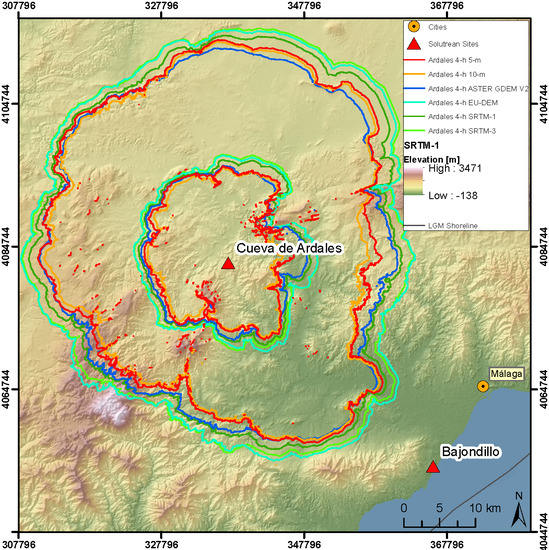
Archaeological CDM aims to provide a better estimation of a site’s catchment than a simple radius, which was the traditional approach in site catchment studies [9,24]. Since the DEM is the most crucial input data, the first thought might be that the higher horizontal resolution and vertical accuracy leads to better results. As seen in the evaluation results and the modeled site catchments (see Figure 6), the main difference produced by higher resolution DEMs is a change in size of the modeled site catchments. This change is, in theory, systematic and, thus, predictable. Smaller differences are noticeable regarding the overall shape of the catchment. In detail, the isochrones are more jagged because the influence of small-scale landscape features is stronger than in the lower resolution DEMs, which also leads to comparably slower accumulated walking speeds in hilly terrain (see Figure 6). It is likely that the higher resolution DEMs enable more realistic results, when considering the observation that average slope values decrease with lower cell size. The applied high resolution DEMs include one specific problem. Whereas vegetation and buildings are filtered out of the data, the 5-m and 10-m DEMs still contain many residuals of anthropogenic features in the landscape, such as bridges, trenches or channels, which definitely were not part of the topography at the time frames under investigation. In this regard, the SRTM DEMs and ASTER GDEM V2 perform better in our sample areas. Clear advantages of the 5-m DEM are the high vertical and horizontal accuracy and fewer noise artifacts, which should lead to more consistent modeling results, as the height error in ASTER GDEM V2 or the SRTM DEMs also varies with location (see Section 3.1). An example of where the use of high resolution DEMs should be more appropriate is a site within a narrow canyon. Here, a DEM at a horizontal resolution of 30 m is simply not able to reproduce such small-scale details. This is especially relevant if the effective horizontal resolution is even lower than the cell size of the data, as was assessed for ASTER GDEM V2 and SRTM-1 (see Section 3.1).

The incorporation of additional topography and vegetation costs into the CDM was implemented. The approach of generating a raster with speed coefficients that are derived from a classified stream network or vegetation (in our case, biomes) raster works, but the current implementation has the potential for improvement for various reasons. Apart from the missing data in the coastal area, at about 60 km × 60 km, the spatial resolution of the Stage3 Biome3.5 21k data is rather low. The Stage3 Biome3.5 21k raster data have a more global effect on the size of the site catchments and do not change their shape, except when the catchment traverses a border between two different biome classes. Vegetation data like these could prove useful as a kind of off-path factor as described by Tobler [36]. However, the validity or benefit of an off-path factor is open for discussion, as well. It is very likely that the inhabitants of a site used established paths for resource procurement or transportation of food or resources between sites, because of the tendency to conserve energy. In this case, an off-path factor would make less sense. As there is no alternative high resolution vegetation data for the time period in question known to the authors, this is a clear task for future work. Ecological niche modeling approaches or further efforts in paleovegetation modeling could fill the gap by providing high resolution land cover data. The coefficients for both vegetation and stream networks are based on expert knowledge [75,76] or actual energy cost measurements conducted by [8,74,105]. These were mapped from the vegetation or land cover classes to the available biome classes, which works well, but the coefficients might be considered for re-evaluation in future work. Furthermore, the incorporation of stream networks itself is not optimal at this point; a key problem is that the stream width is directly connected to the horizontal resolution of the DEM. The cost coefficients take this into account to a certain extent, but the effect on the results is very small. This is a complex problem investigated by Dean et al. [106], and the modeling approach could be much improved in this area. Further, it has to be mentioned that no other water bodies were included in the analyses, which leads to another fundamental issue. The applied data (apart from the Stage3 Biome3.5 21k dataset) are recent and cannot take into account the possible changes in geomorphology or hydrology since the Last Glacial Maximum. Incorporation of lakes into the analysis would involve filtering out anthropogenic reservoirs. Furthermore, lakes and reservoirs are normally part of the surface reproduced in the DEMs, so that the bottom of a lake is not available in the data. The same applies to the bathymetry on the coastal areas, where the sea level has changed since the LGM. Despite the above-mentioned issues, we could show that it is possible to include such data into the current modeling approach. Therefore, if the paleo-modeling community provides improved high resolution environmental data, direct improvement of the modeling results would be expected.

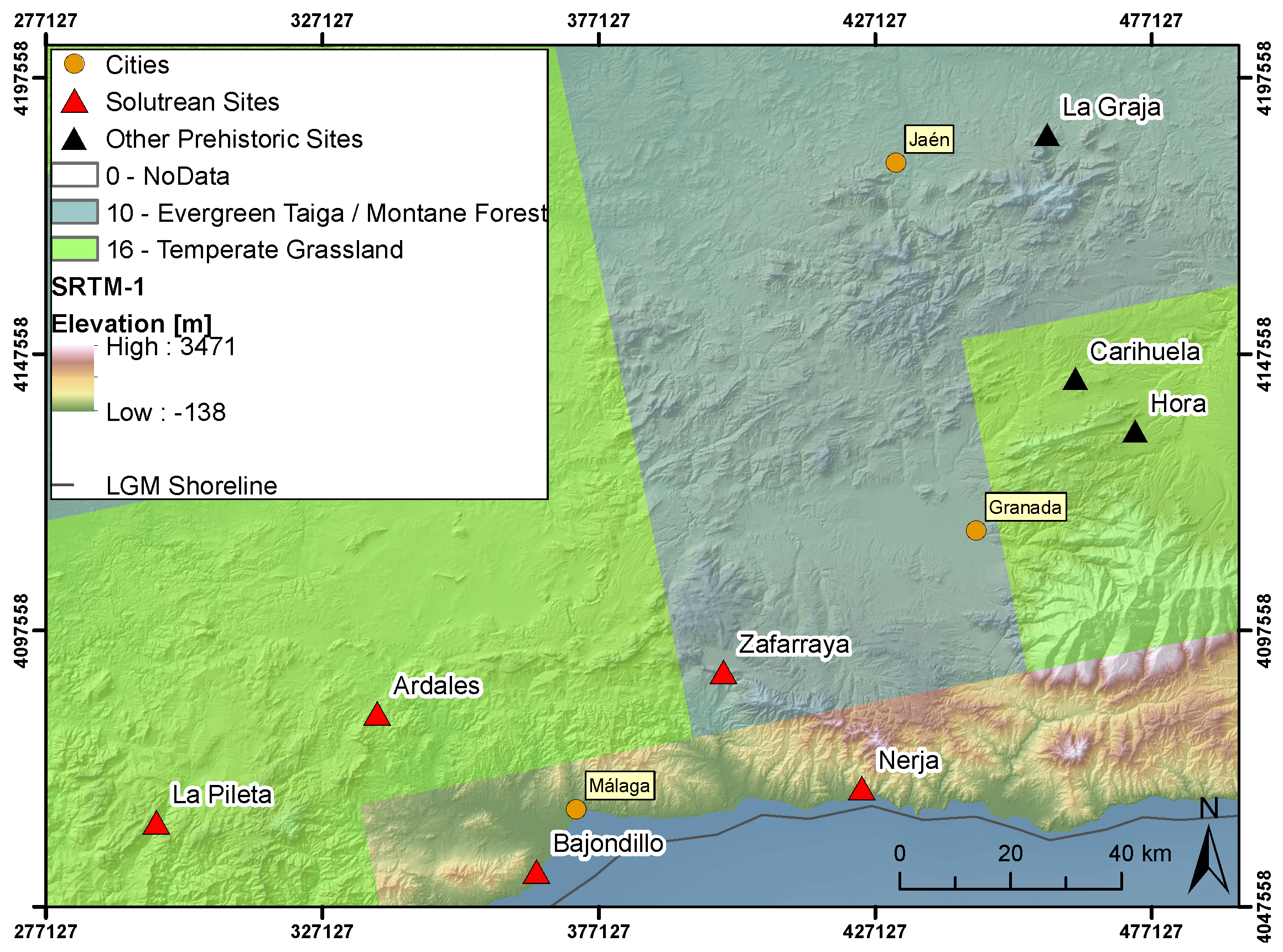
This section aims to discuss the results that were worked out in this study from an archaeological point of view. In order to be suitable for a study of this type, the sample of archaeological sites must have the same chronological framework (Table 2). Solutrean sites have a similar chronology, enhancing the possibilities of a good analysis and comparison of the sites. In Section 3.3, it was explained that, of the five Solutrean sites in our sample, only the sites Nerja and Bajondillo are suitable for an archaeological analysis, because only these exhibit a good stratigraphical record. Further, it should be taken into account that, concerning the catchment modeling of the sample of sites, the Stage3 Biome 21k dataset does not contain data in the areas of Nerja and Bajondillo. Therefore, the additional cost of vegetation is not considered in either site, which currently exhibit a similar environment. Bajondillo is located 200 m and Nerja less than 1 km from the coast line, but during the time period of our analysis (LGM), the coast was about 5–8 km distant from the sites. Raw material data are available for both sites, although in the case of Nerja, the data are partially problematic, as the analysis of the raw materials also includes Gravettian levels, the sources of which are not very well identified. In the case of Bajondillo, as we do not have archaeological information about the faunal remains, this part of the record has to be discarded, as well. The rest of the sites are problematic for an archaeological analysis, as well, as the levels are reworked or the archaeological record is limited to surface evidence.

In any future investigation, the following conditions should be applicable for any site sample: The sample sites need to be contemporaneous, with good chronological data and a good stratigraphical context. Sites should also contain good raw material data (lithic remains and sources of raw material) and, if possible, good faunal data in order to be able to deduce the economic behavior and mobility of hunter-gatherer groups.

7. Conclusions

In the context of archaeological site catchment analysis, the focus of this work lies on the evaluation of the influence that different DEMs exert on the site catchment modeling results for prehistoric sites. It was demonstrated that the size of the modeled slope-derived site catchments correlates negatively with the resolution of the input DEM. Further, the quality and characteristics of a DEM, such as accuracy, noise and the reproduction of residuals of anthropogenic landscape features, are important factors for archaeological cost distance modeling, as well. The choice of the DEM is shown to be of paramount importance to the research, as the DEMs investigated in this work showed much variation in these characteristics. The 5-m and the 10-m DEM, while delivering the highest accuracy, contain the largest amount of such residuals. The inclusion of these contemporary residuals must be considered in this context, as the modeling results should reflect only prehistoric conditions. Nevertheless, the higher resolution is clearly valuable if a site is situated in a steep canyon, for example, which simply cannot be reproduced at a 30-m cell size, and the architectural features are not an issue in areas that are still unaffected by anthropogenic constructions. Further, the high accuracy should lead to more consistent and predictable results. Until 2015, the (presumed) advantage of the ASTER GDEM V2 was the higher horizontal resolution compared to the SRTM-3 DEM. As the SRTM-1 DEM was made available over the course of 2015 and the dataset is of higher accuracy and contains fewer artifacts in our research area, the SRTM-1 DEM is also very well suited for this purpose; especially if no official DEM with higher resolution and accuracy is available for the area of interest. The EU-DEM however, does not offer any advantages compared to the other DEMs.

Overall, the GIS-based cost distance modeling approach, which was presented in detail, works well, and these results are expected to provide a better approximation of the actual conditions than a simple radius would do. Besides issues with the applied paleoenvironmental data (and their conversion into cost coefficients, which have to be evaluated in future work to ensure comparable results in order to diminish the limitations of this part of the method), it was shown that it is possible to include additional factors, like vegetation and river networks, into the modeling approach.

If, as discussed at the end of the last section, the conditions concerning the archaeological data apply, the cost distance model that derives slope-based site catchments enables useful qualitative and quantitative assertions for archaeological sites regarding their environment and their interconnection. With the presented CDM approach, it is possible to classify and characterize archaeological sites using the topographic features, landforms and faunal species found in the modeled catchment areas.