Mapping Comparison and Meteorological Correlation Analysis of the Air Quality Index in Mid-Eastern China
Abstract
:1. Introduction
2. Materials
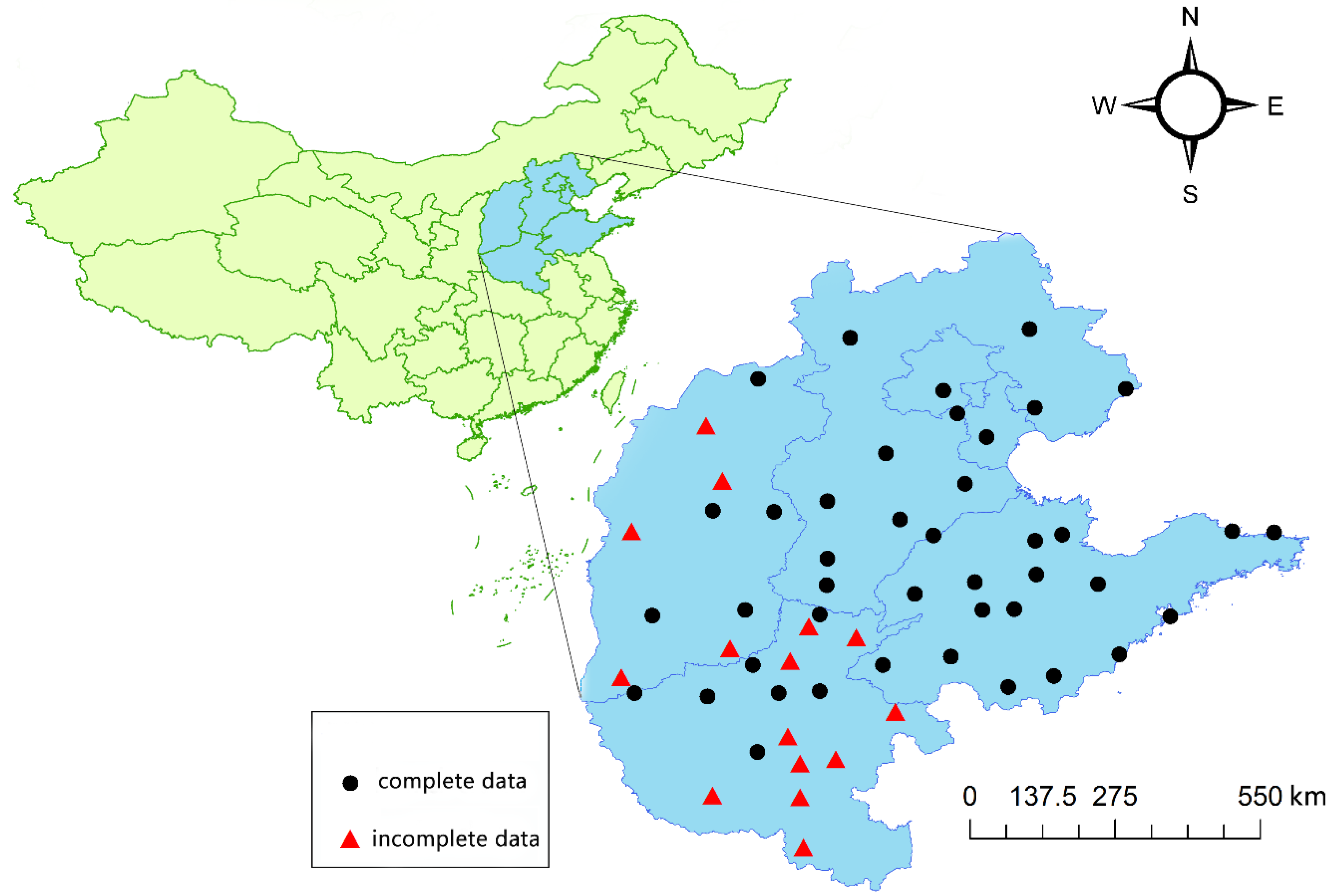
2.1. Study Area
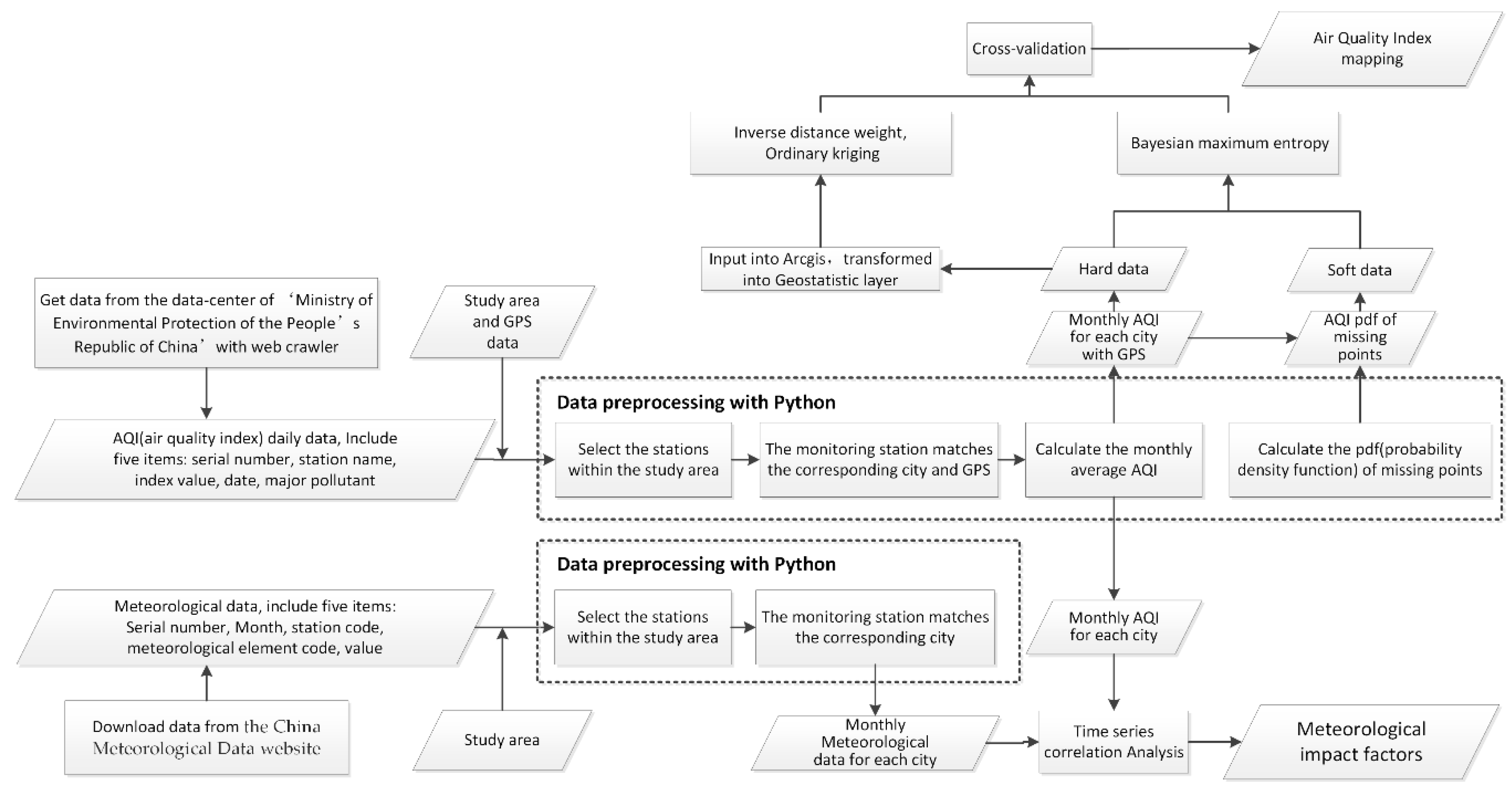
2.2. Data
3. Methods
3.1. Spatial Interpolation
3.2. Spatial Autocorrelation
3.3. Cross-Validation
3.4. Interpolation Accuracy Evaluation
3.5. Temporal Correlation
4. Analysis of Temporal and Spatial Characteristics
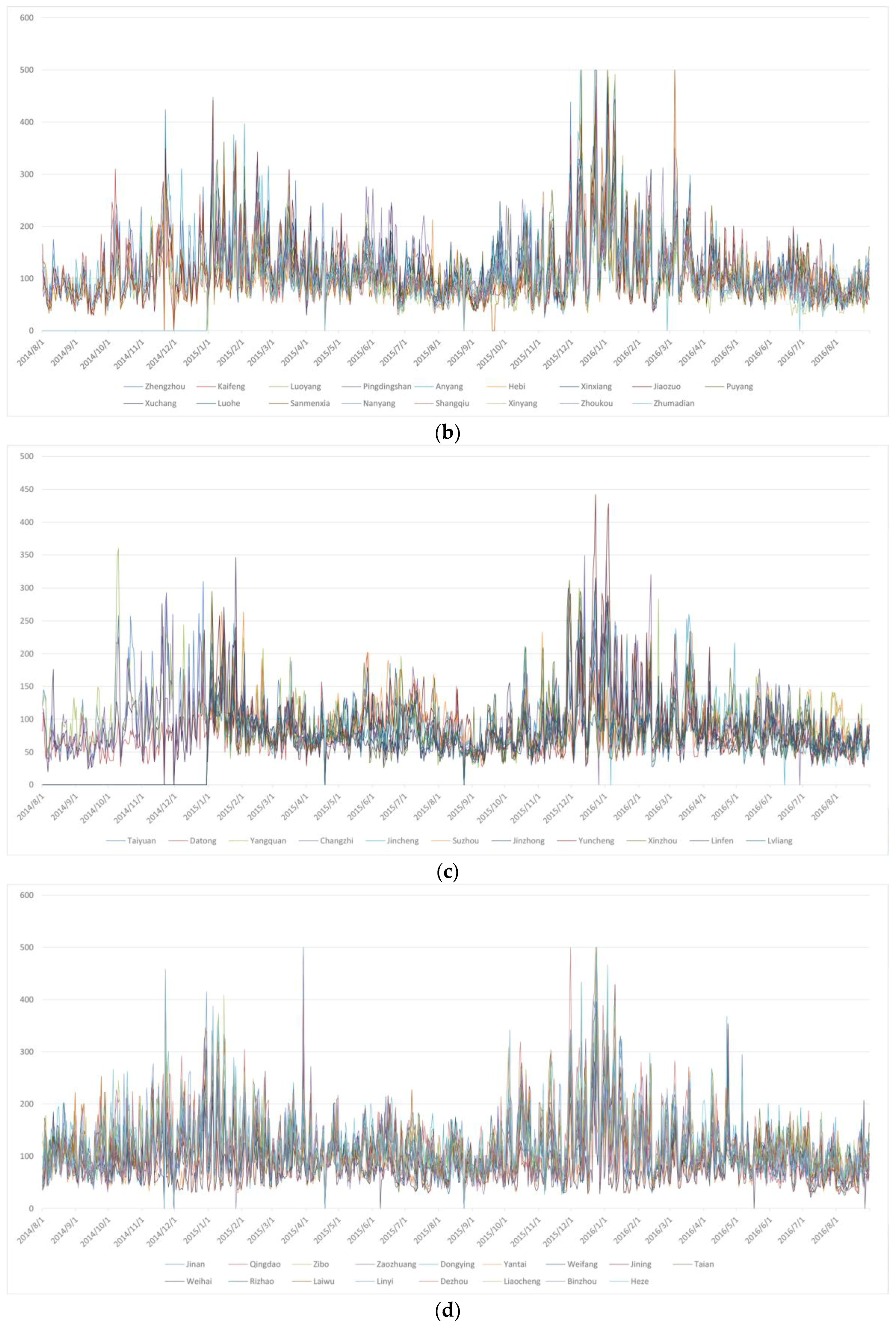
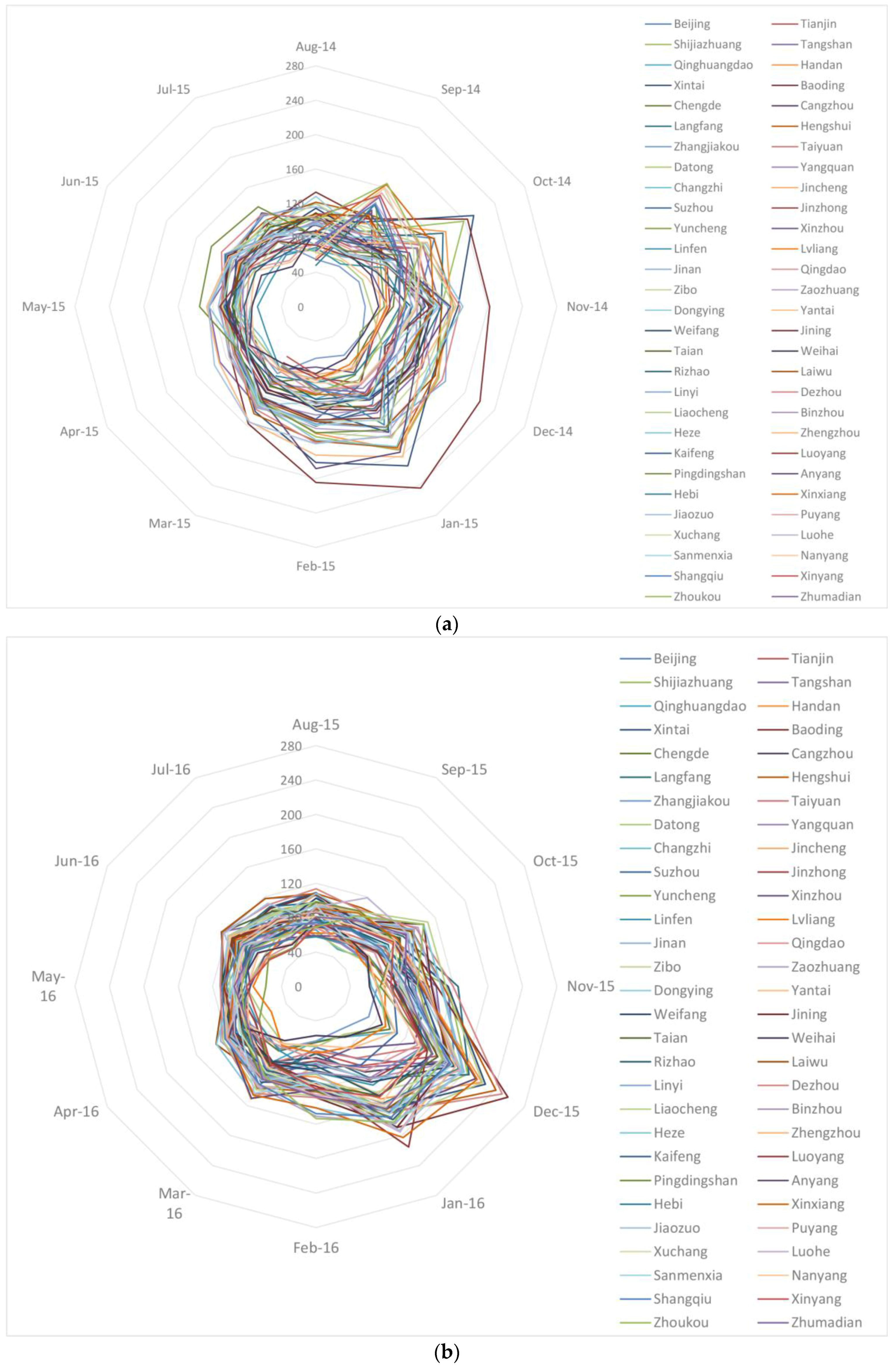
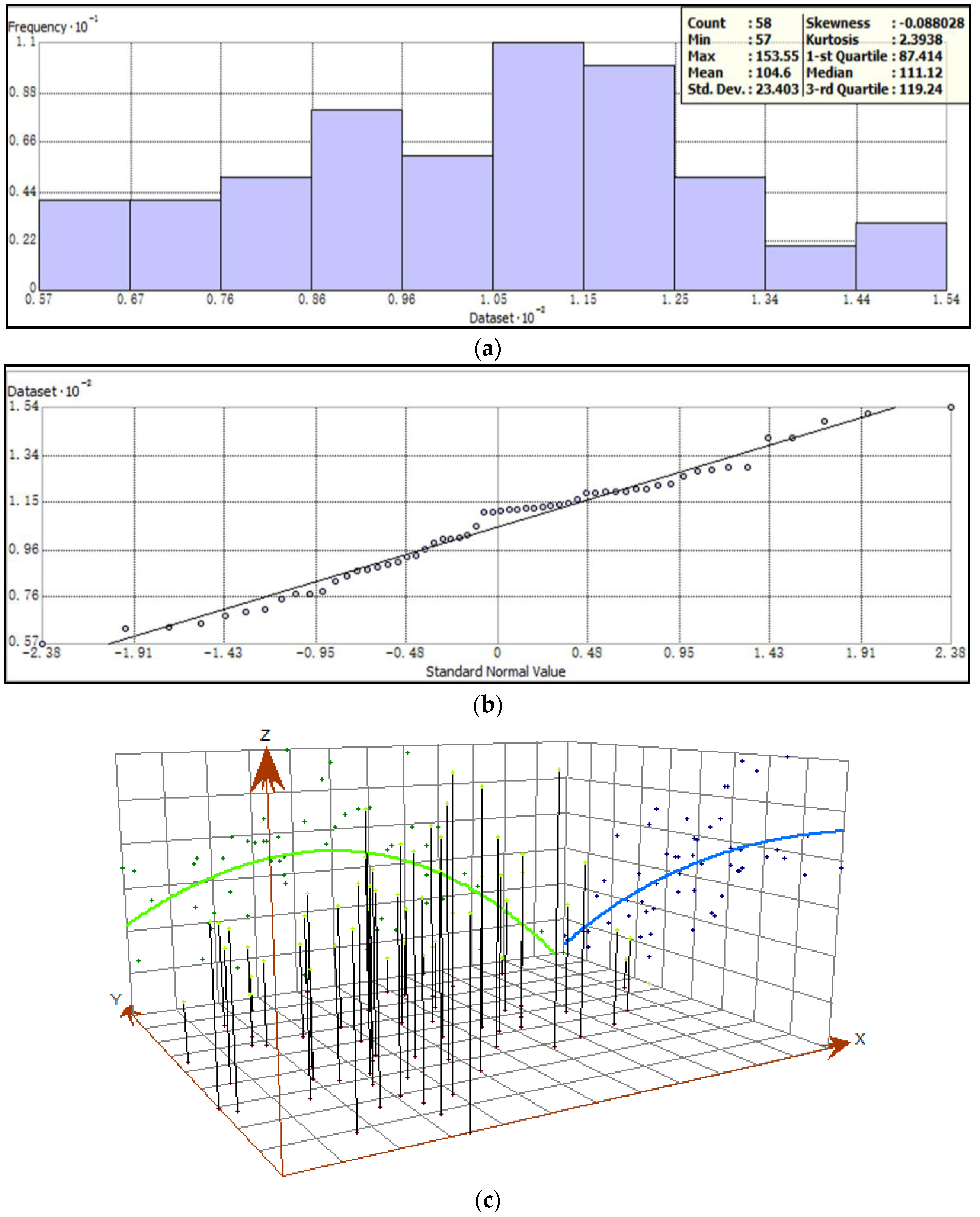
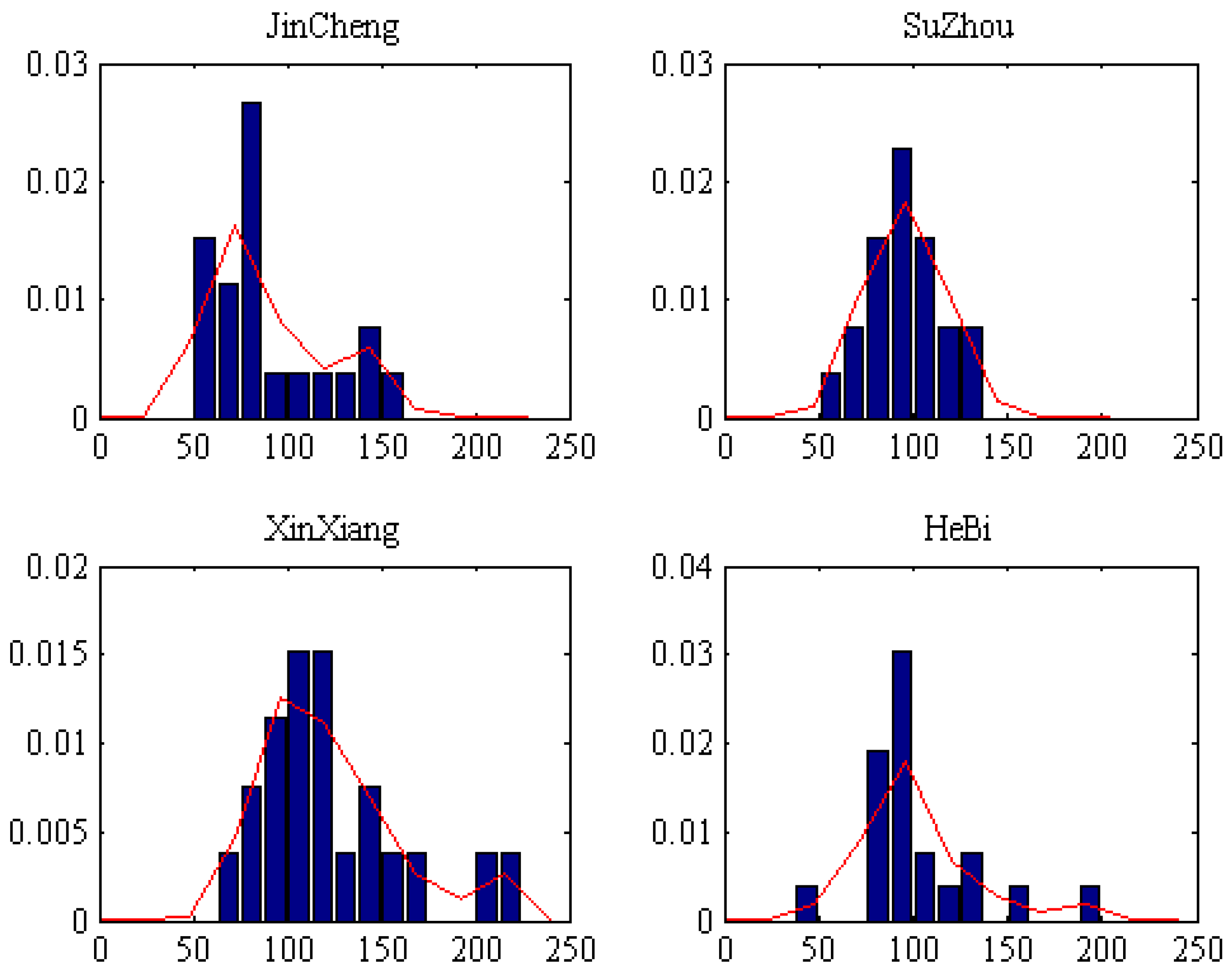
4.1. Temporal Characteristics
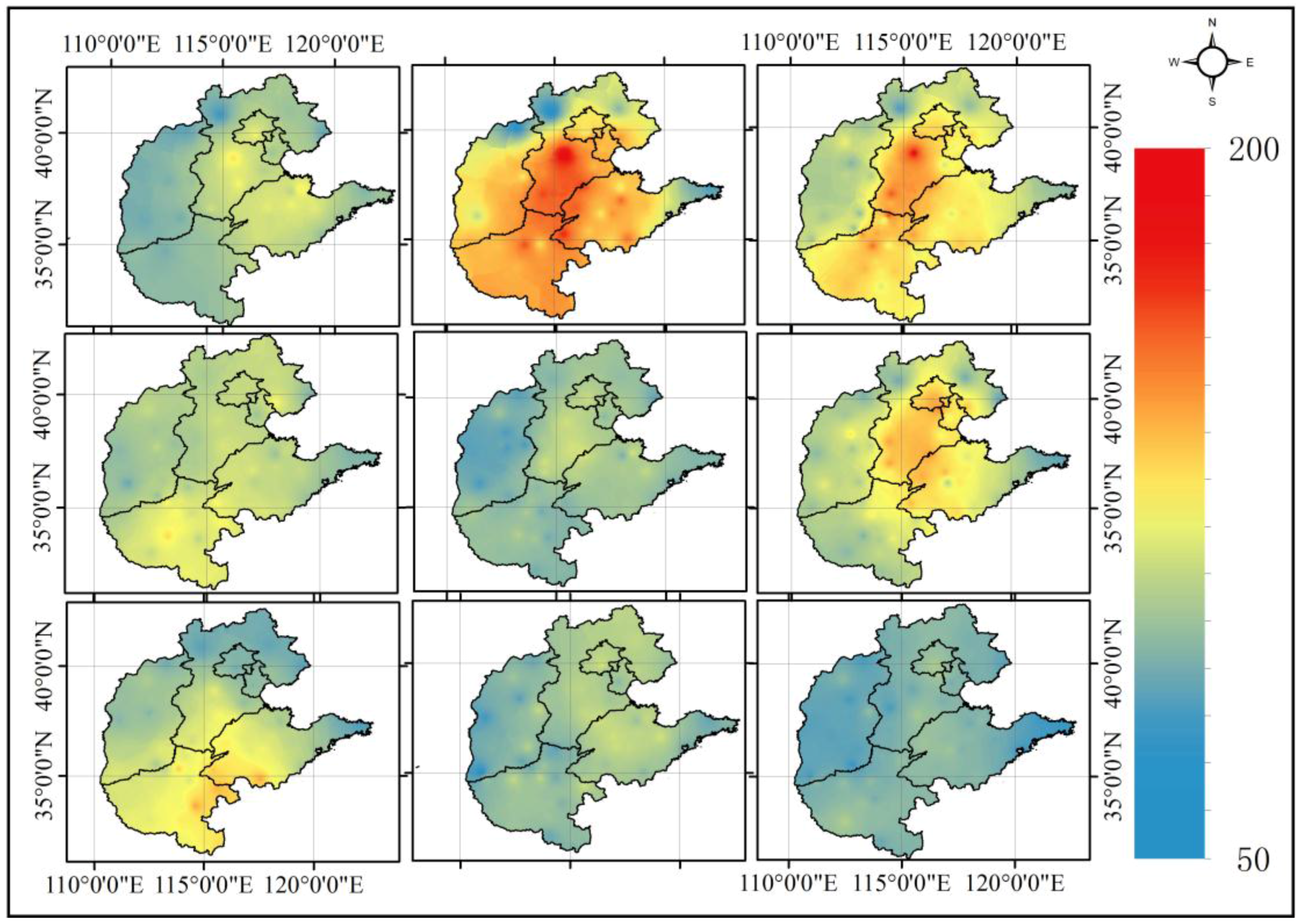
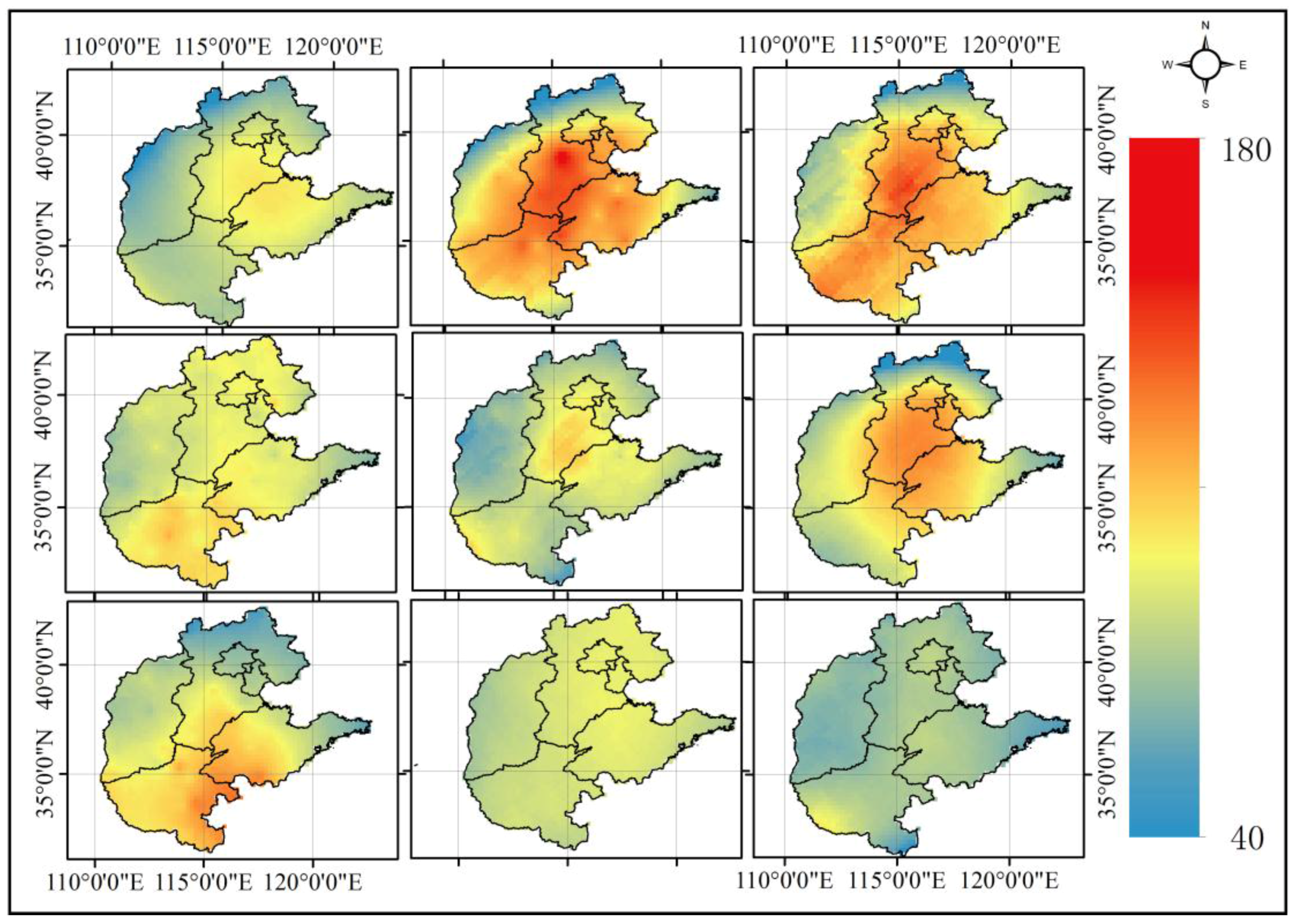
4.2. AQI Mapping with IDW
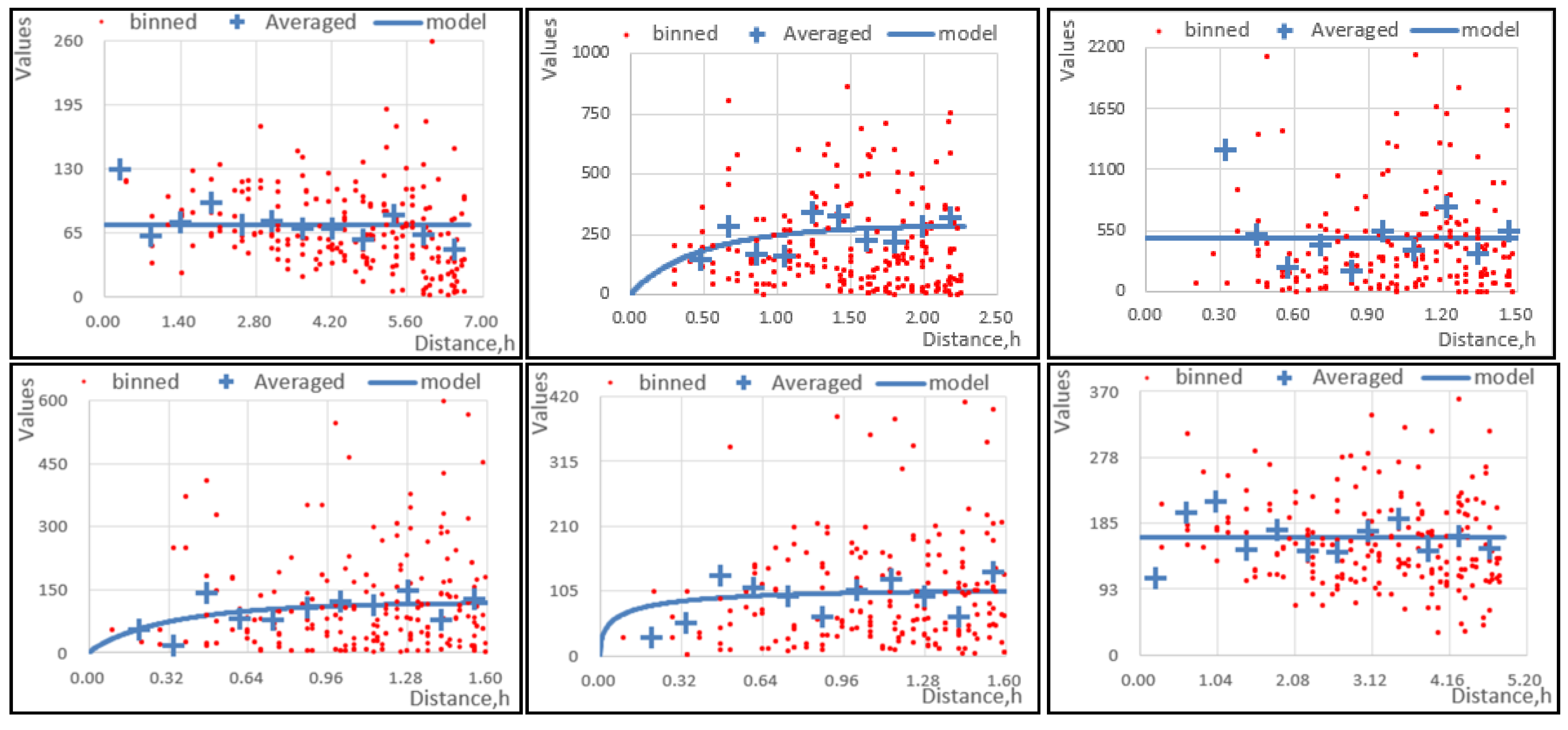
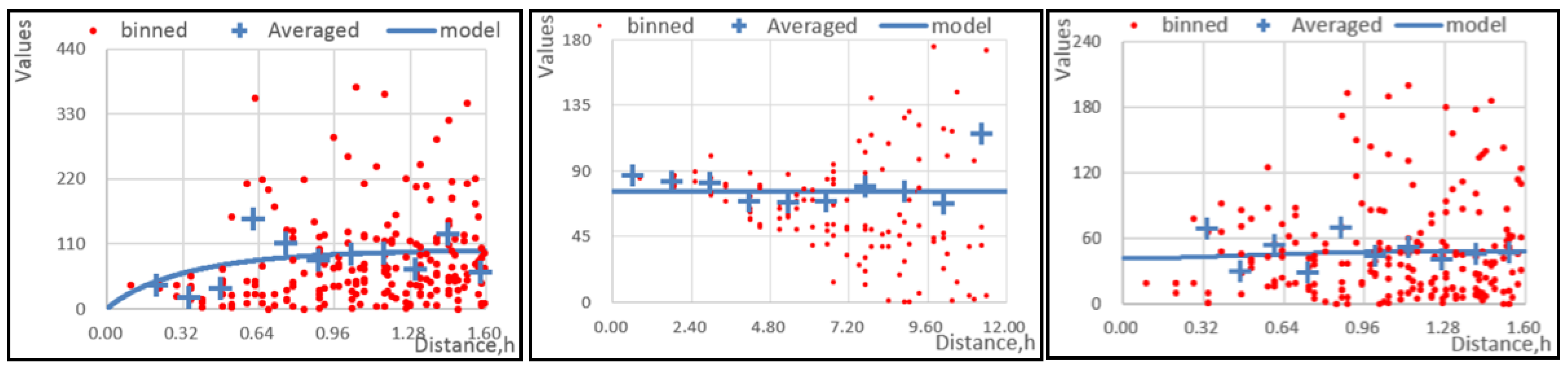
4.3. AQI Mapping with Kriging
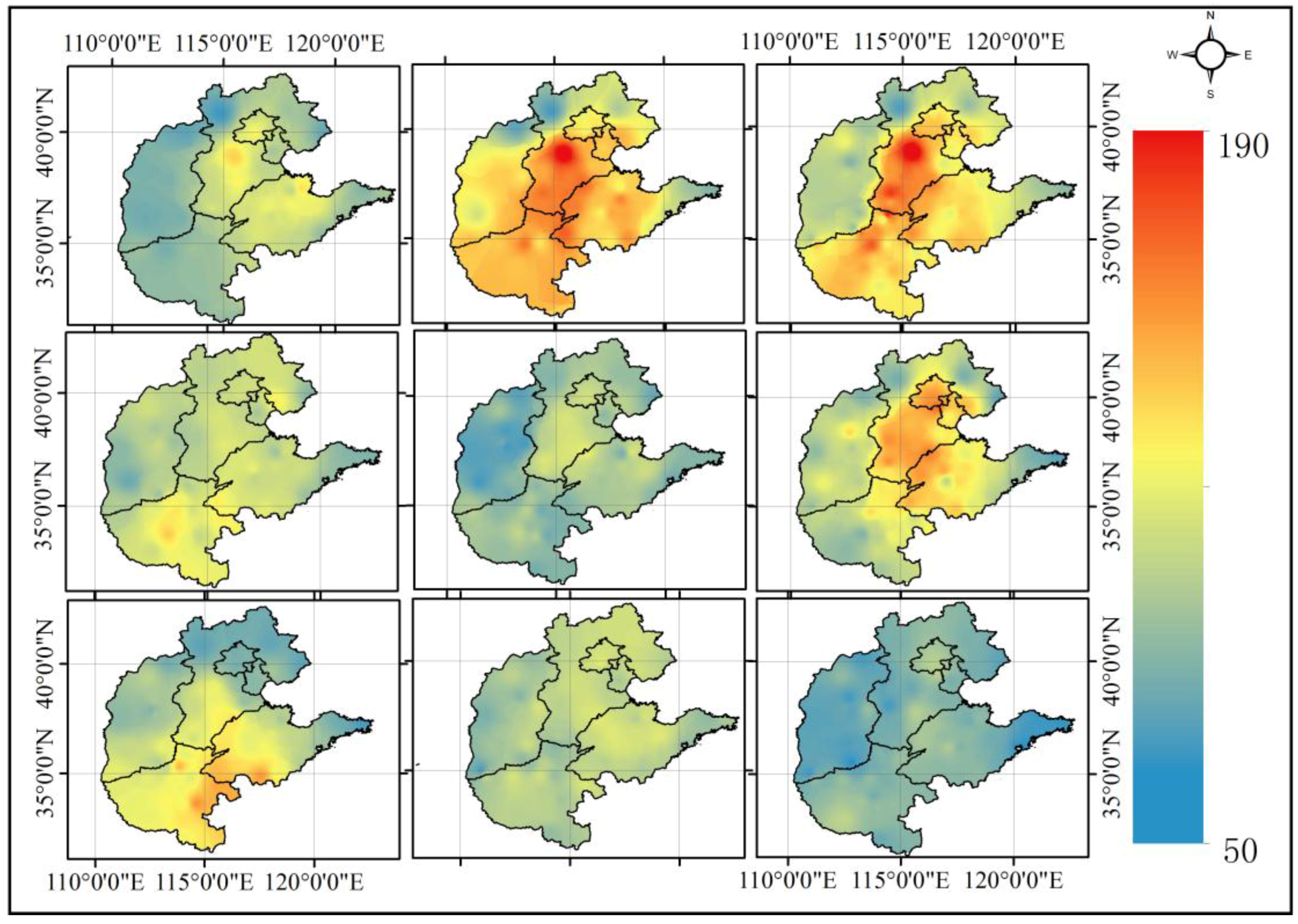
4.4. AQI Mapping with BME
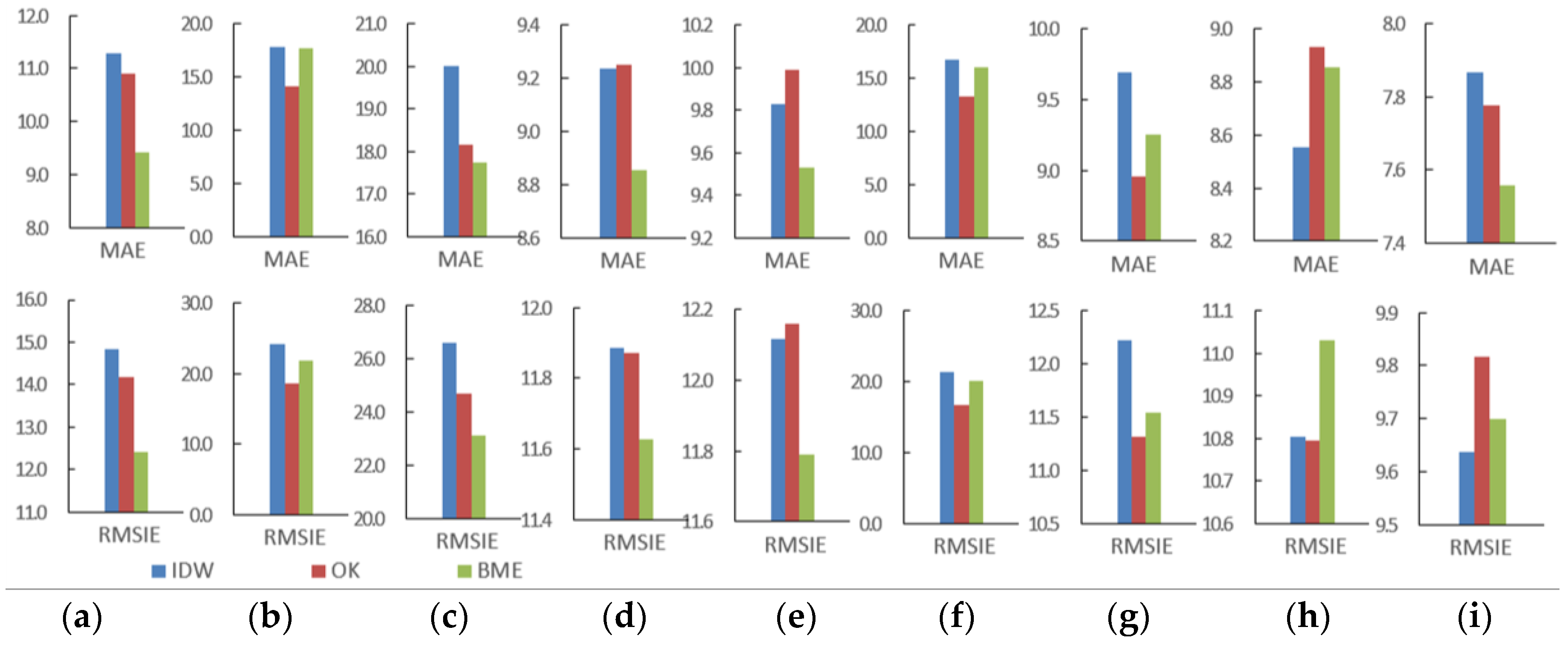
4.5. Cross-Validation and Comparison
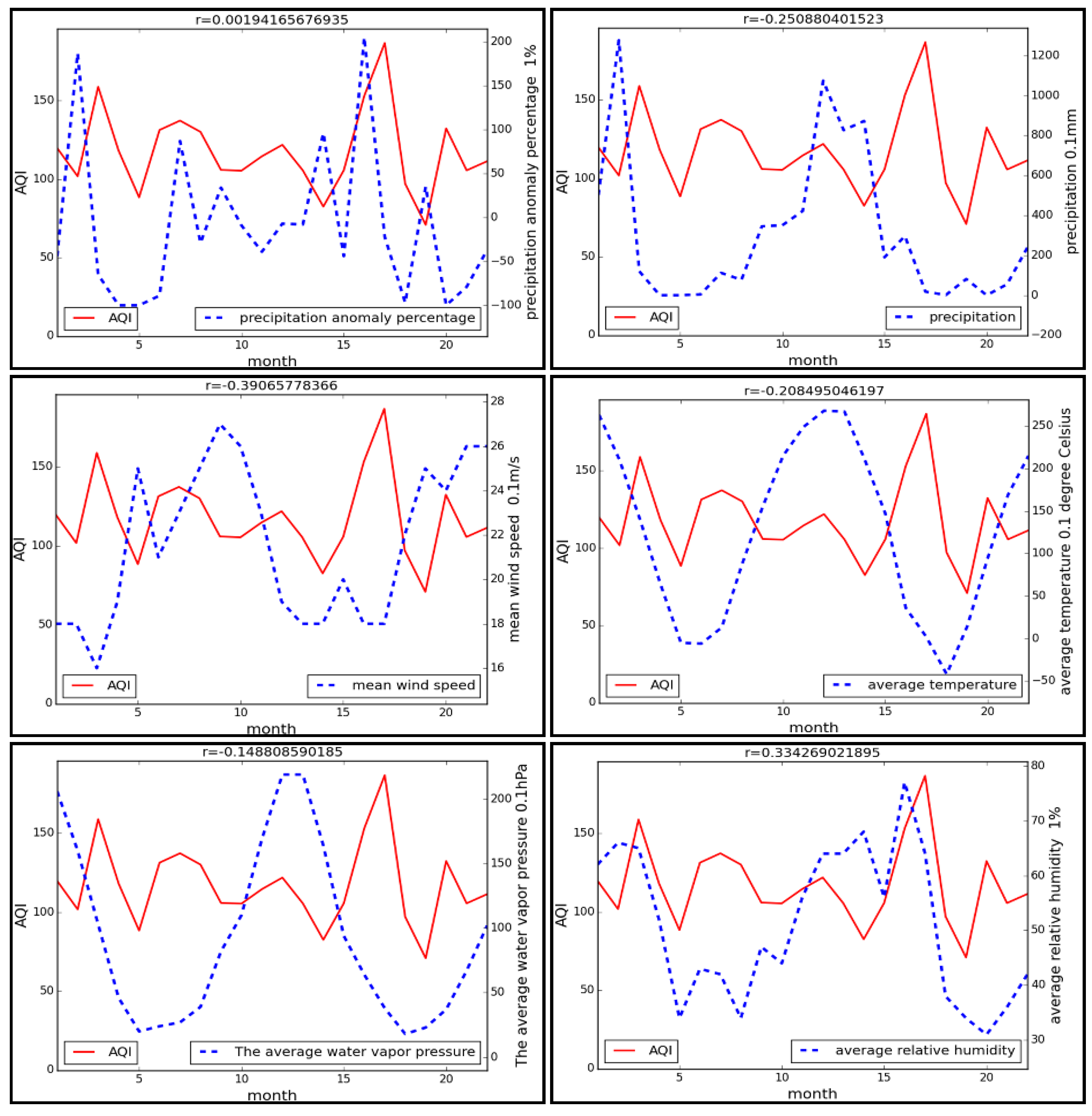
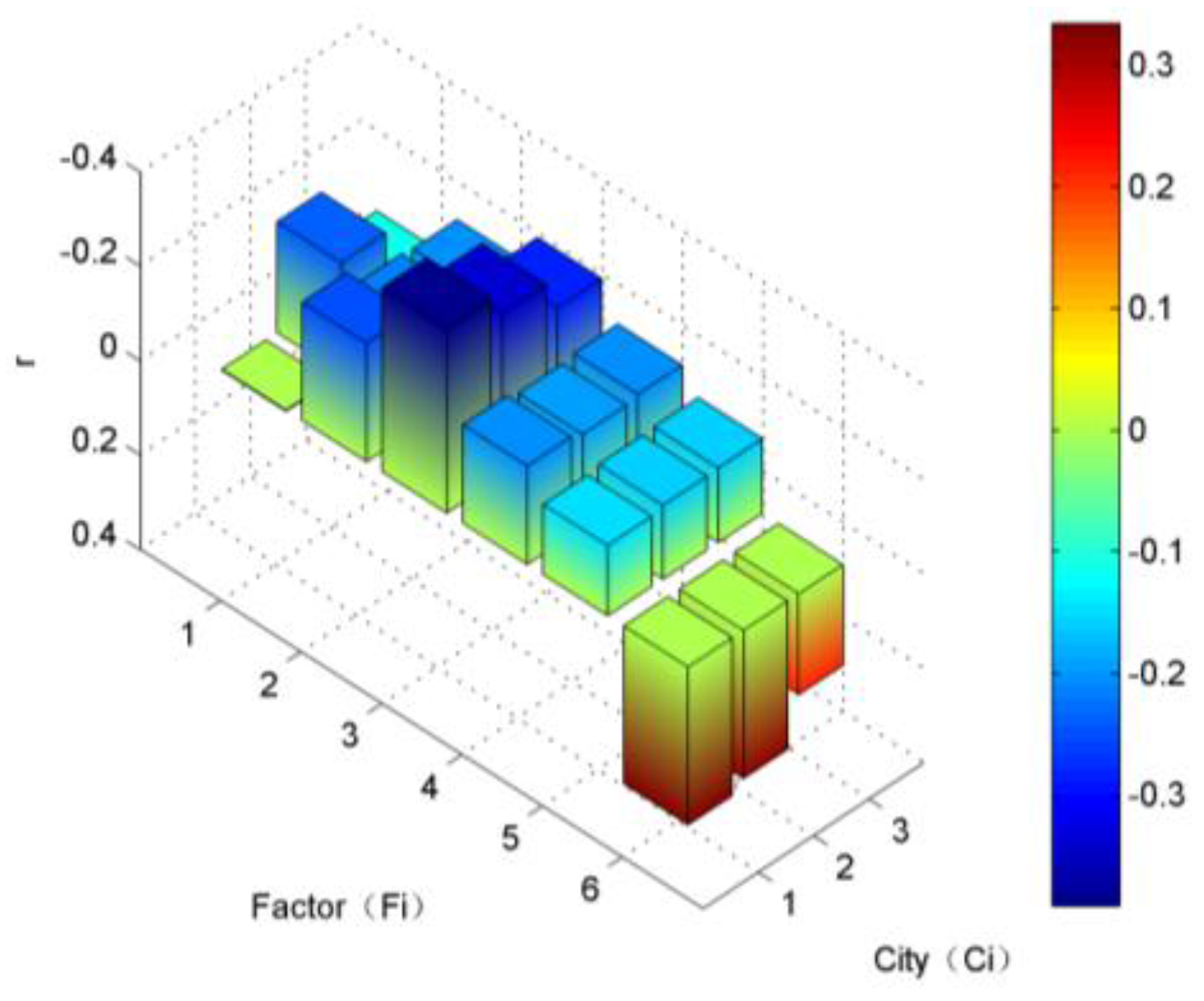
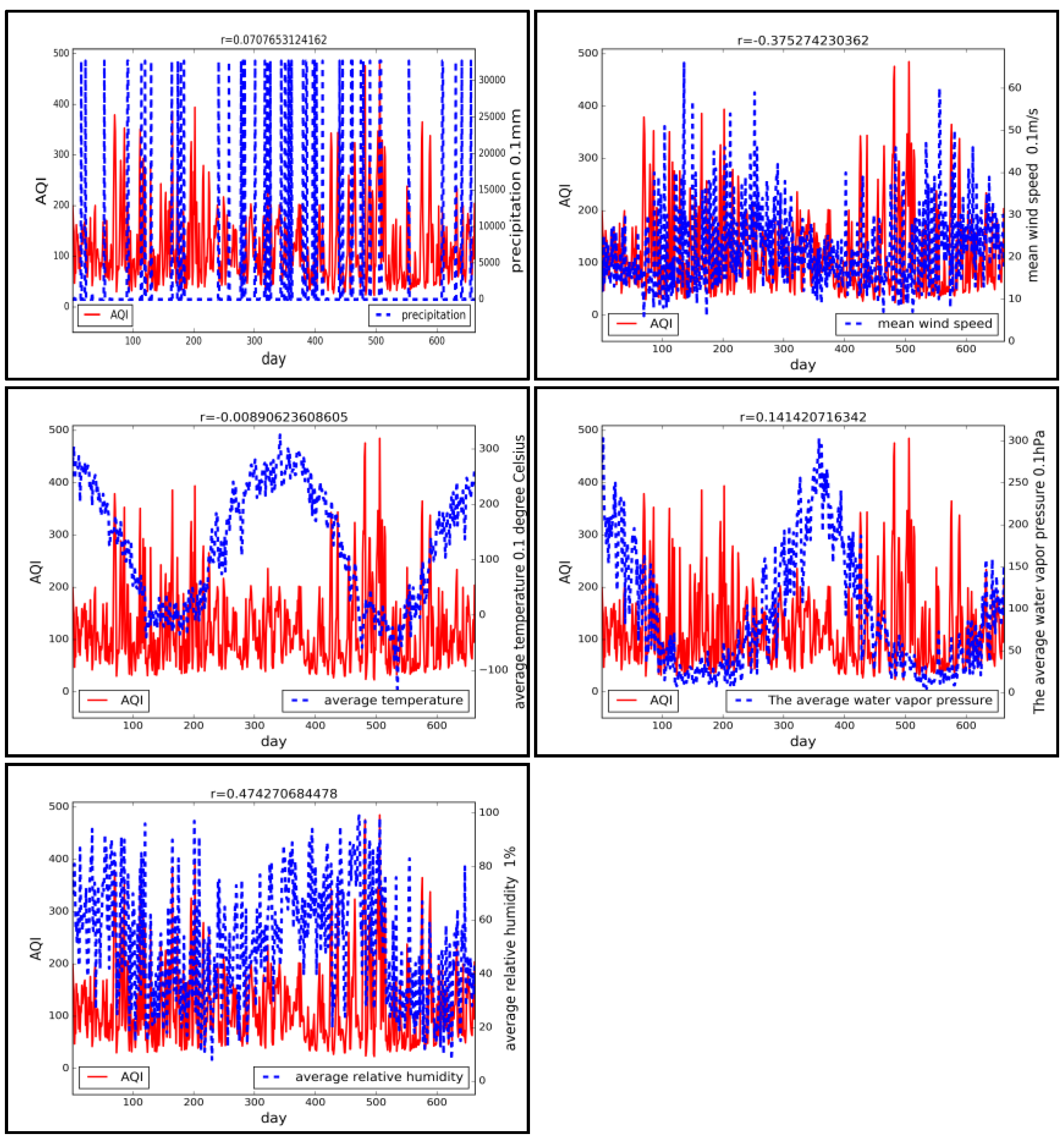
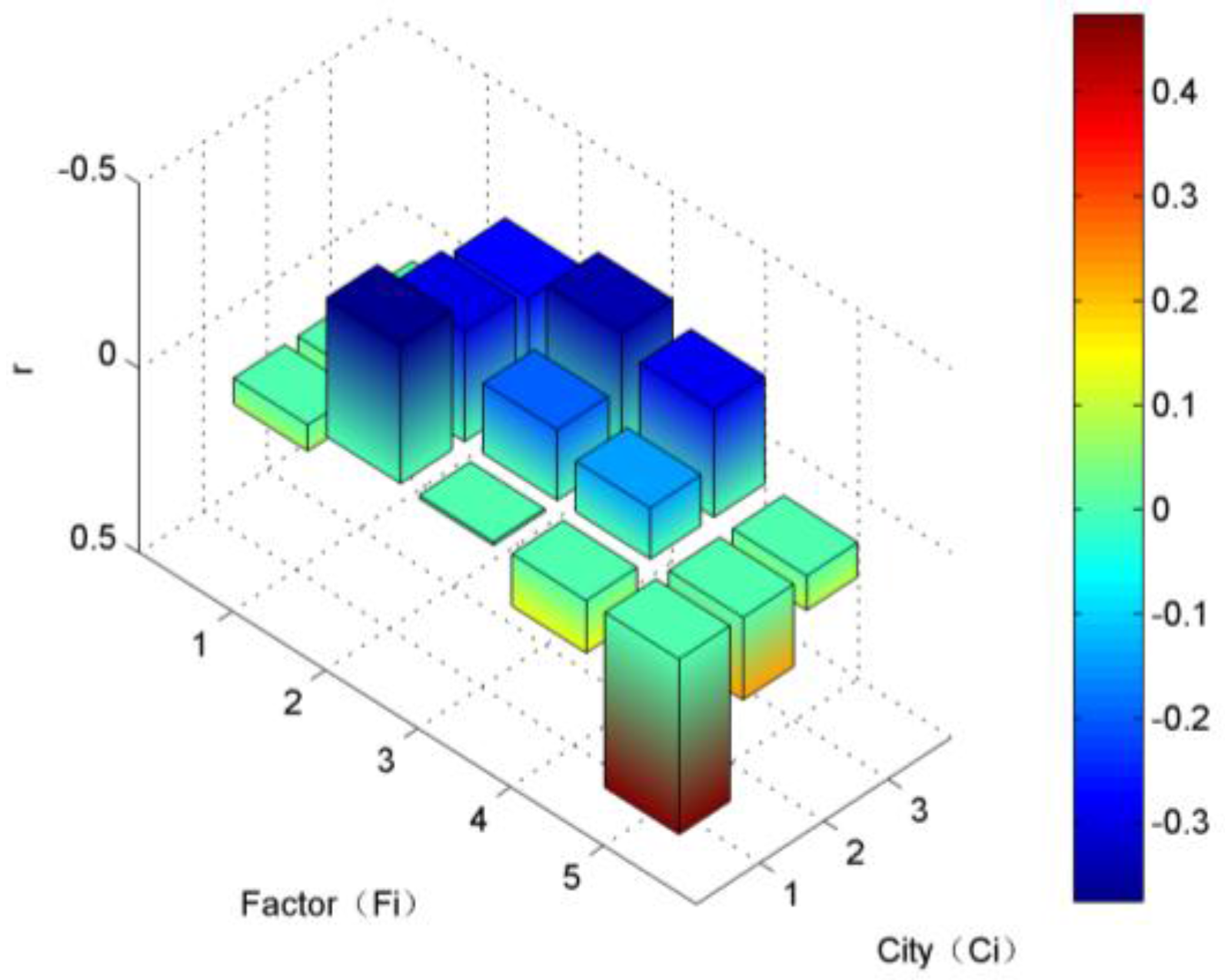
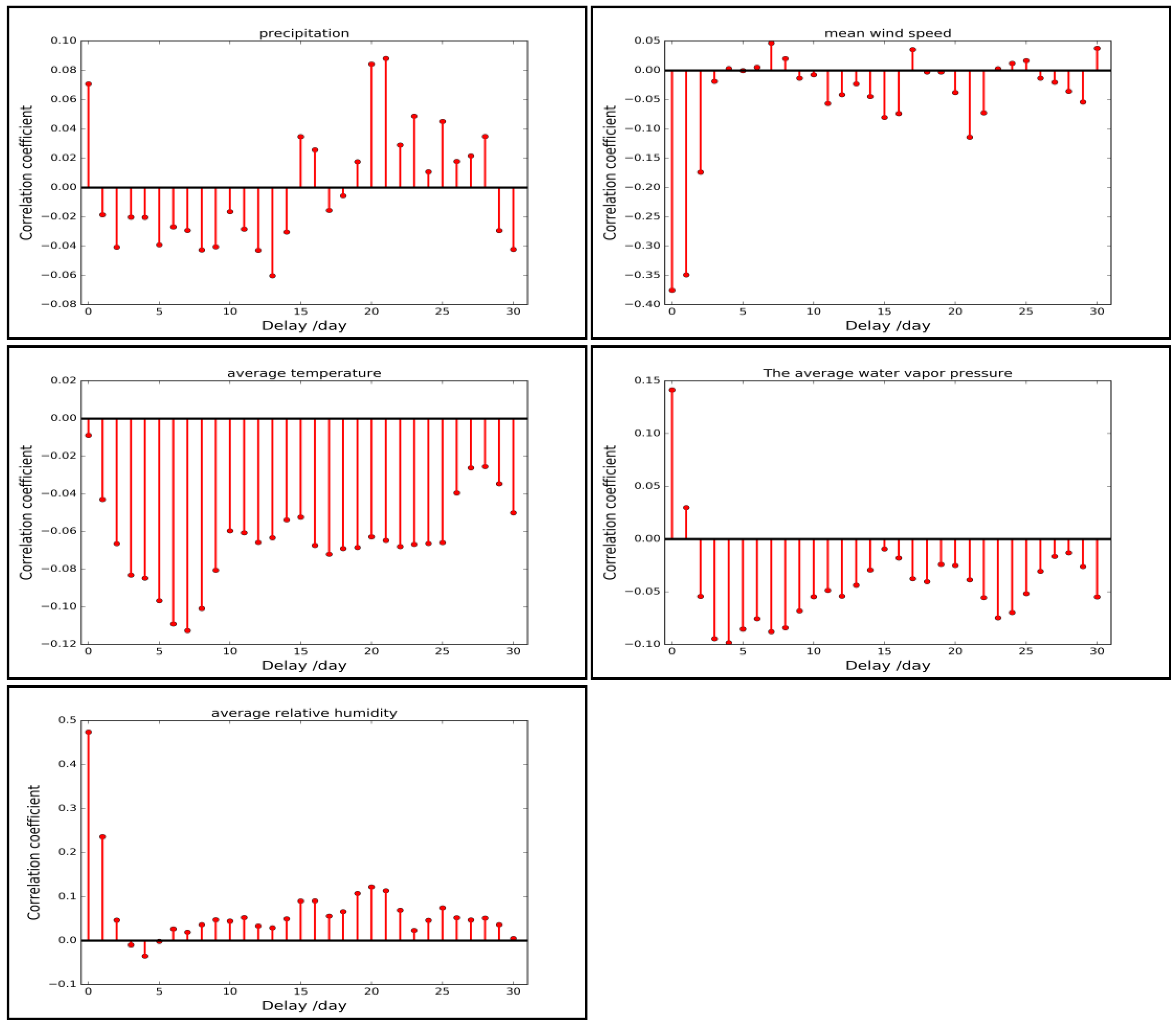
5. Relationship between AQI and Meteorological Conditions
6. Conclusions
- (1)
- In recent years, AQI shows a clear periodicity, although overall, it has a downward trend. AQI fluctuates more drastically over time; the peak of AQI appeared in November, December and January.
- (2)
- Bayesian maximum entropy interpolation has a higher accuracy than kriging. IDW has the maximum error.
- (3)
- In the same year, the AQI of winter (November) and spring (February) is much worse than summer (May) and autumn (August). Additionally, the air quality has improved every quarter for three years. It proves that the government’s air quality management strategy has been effective in recent years.
- (4)
- The distribution of AQI has obvious spatial characteristics. For the study area, the most polluted areas of air quality are concentrated in Beijing, the southern part of Tianjin, the central-southern part of Hebei, the central-northern part of Henan and the western part of Shandong.
- (5)
- The average wind speed and average relative humidity have a real correlation. The calculated correlation coefficients using daily data provide support for association analysis on a finer scale. The effect of meteorological factors, such as wind, precipitation and humidity, on AQI is putative to have a temporal lag to different extents.
- (6)
- The AQI of a city with poor air quality will fluctuate greater than others when weather changes and has higher correlation with meteorological factors.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sæther, B.E.; Grøtan, V.; Tryjanowski, P. Climate and spatio-temporal variation in the population dynamics of a long distance migrant, the white stork. J. Anim. Ecol. 2006, 75, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Kyriakidis, P.C.; Journel, A.G. Stochastic modeling of atmospheric pollution: A spatial time-series framework. Part I: Methodology. Atmos. Environ. 2001, 35, 2331–2337. [Google Scholar] [CrossRef]
- Varotsos, C.; Cartalis, C. Re-evaluation of surface ozone over Athens, Greece, for the period 1901–1940. Atmos. Res. 1991, 26, 303–310. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Varotsos, C.; Kaltsounides, N.A.; Petrakis, M.; Lalas, D.P. Atmospheric turbidity parameters in the highly polluted site of Athens basin. Renew. Energy 1994, 4, 465–470. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Karalis, J.D. Broad-band turbidity parameters and spectral band resolution of solar radiation for the period 1954–1991, in Athens, Greece. Int. J. Clim. 1996, 16, 229–242. [Google Scholar] [CrossRef]
- Brook, R.D.; Franklin, B.; Cascio, W.; Hong, Y.; Howard, G.; Lipsett, M.; Luepker, R.; Mittleman, M.; Samet, J.; Smith, S.C.; et al. Air pollution and cardiovascular disease. Curr. Probl. Cardiol. 2012, 40, 207–238. [Google Scholar]
- Wong, T.W.; Lau, T.S.; Yu, T.S.; Neller, A.; Wong, S.L.; Tam, W.; Pang, S.W. Air pollution and hospital admissions for respiratory and cardiovascular diseases in Hong Kong. Occup. Environ. Med. 1999, 56, 679–683. [Google Scholar] [CrossRef] [PubMed]
- Barnett, A.G.; Williams, G.M.; Schwartz, J.; Best, T.L.; Neller, A.H.; Petroeschevsky, A.L.; Simpson, R.W. The Effects of Air Pollution on Hospitalizations for Cardiovascular Diseasein Elderly People in Australian and New Zealand Cities. Environ. Health Perspect. 2006, 114, 1018–1023. [Google Scholar] [CrossRef] [PubMed]
- Koken, P.J.; Piver, W.T.; Ye, F.; Elixhauser, A.; Olsen, L.M.; Portier, C.J. Temperature, air pollution, and hospitalization for cardiovascular diseases among elderly people in Denver. Environ. Health Perspect. 2003, 111, 1312–1317. [Google Scholar] [CrossRef] [PubMed]
- Feretis, E.; Theodorakopoulos, P.; Varotsos, C.; Efstathiou, M.; Tzanis, C.; Xirou, T.; Alexandridou, N.; Aggelou, M. On the plausible association between environmental conditions and human eye damage. Environ. Sci. Pollut. Res. 2002, 9, 163–165. [Google Scholar] [CrossRef]
- Katsambas, A.; Andoniou, C.; Stratigos, J.; Arvanitis, I.; Zolota, F.; Varotsos, C.; Cartalis, C.; Asimakopoulos, D.N. A simple algorithm for simulating the solar ultraviolet radiation at the Earth’s surface: An application in determining the minimum erythema dose. Earth Moon Planets 1991, 53, 191–204. [Google Scholar] [CrossRef]
- An, J.-L.; Wang, Y.-S.; Li, X.; Sun, Y.; Shen, S.H. Relationship between surface UV radiation and air pollution in Beijing. Environ. Sci. 2008, 29, 1053–1058. [Google Scholar]
- Shi, Y. Ambient Air Quality Standard. J. China Environ. Manag. Cadre Coll. 2012, 1, 71. [Google Scholar]
- Li, A.; Bo, Y. The interpolation of precipitation based on Bayesian Maximum Entropy. J. Desert Res. 2012, 32, 1408–1416. [Google Scholar]
- Bao, Z.; Liu, T.; Luo, J. Analysis of the Space and Time Distribution of China’s Environmental Quality Index. Geomat. World 2014, 21, 17–21. [Google Scholar]
- Zhang, B.; Li, W.; Yang, Y. The Bayesian Maximum Entropy geostatistical approach and its application in soil and environmental sciences. Acta Pedol. Sin. 2011, 48, 831–839. [Google Scholar]
- Zhang, Y.; Yan, H. Analysis of influencing factor of air quality in Urumqi. Math. Pract. Theory 2015, 45, 149–154. [Google Scholar]
- Ashraf, M.; Loftis, J.C.; Hubbard, K.G. Application of geostatistics to evaluate partial weather station networks. Agric. Forest Meteorol. 1997, 84, 255–271. [Google Scholar] [CrossRef]
- Peng, S. Development of Spatio-Temporal Interpolation Methods for Meteorological Elements. Master Dissertation, Central South University, Changsha, China, 1 June 2010. [Google Scholar]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Cressie, N. Spatial prediction and ordinary kriging. Math. Geosci. 1988, 20, 405–421. [Google Scholar] [CrossRef]
- Pereira, J.J.; Schultz, E.T.; Auster, P.J. Geospatial analysis of habitat use in yellowtail flounder Limanda ferruginea on Georges Bank. Mar. Ecol. Prog. 2012, 468, 279–290. [Google Scholar] [CrossRef]
- Zhang, F.S.; Zhong, S.B.; Yang, Z.T.; Sun, C.; Wang, C.L.; Huang, Q.Y. Spatial Estimation of Losses Attributable to Meteorological Disasters in a Specific Area (105.0° E–115.0° E, 25° N–35° N) Using Bayesian Maximum Entropy and Partial Least Squares Regression. Adv. Meteorol. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Christakos, G. A Bayesian/maximum-entropy view to the spatial estimation problem. Math. Geol. 1990, 22, 763–777. [Google Scholar] [CrossRef]
- Christakos, G.; Serre, M.L. BME analysis of spatiotemporal particulate matter distributions in North Carolina. Atmos. Environ. 2000, 34, 3393–3406. [Google Scholar] [CrossRef]
- Christakos, G.; Serre, M.L.; Kovitz, J.L. BME representation of particulate matter distributions in the state of California on the basis of uncertain measurements. J. Geophys. Res. Atmos. 2001, 106, 9717–9731. [Google Scholar] [CrossRef]
- Xia, X.L.; Qi, Q.W.; Liang, H.; Zhang, A.; Jiang, L.; Ye, Y.; Liu, C.; Huang, Y. Pattern of Spatial Distribution and Temporal Variation of Atmospheric Pollutants during 2013 in Shenzhen, China. ISPRS Int. J. Geo-Inf. 2017, 6, 2. [Google Scholar] [CrossRef]
- Matheron, G. The Intrinsic Random Functions and Their Applications. Adv. Appl. Probab. 1973, 5, 439–468. [Google Scholar] [CrossRef]
- Bilonick, R.A. The space-time distribution of sulfate deposition in the northeastern United States. Atmos. Environ. 1985, 19, 1829–1845. [Google Scholar] [CrossRef]
- Bilonick, R.A. Monthly hydrogen ion deposition maps for the northeastern US from July 1982 to September 1984. Atmos. Environ. 1988, 22, 1909–1924. [Google Scholar] [CrossRef]
- Sampson, P.D.; Guttorp, P. Nonparametric Estimation of Nonstationary Spatial Covariance Structure. J. Am. Stat. Assoc. 1992, 87, 108–119. [Google Scholar] [CrossRef]
- Dale, L.; Zimmerman, M.; Bridget, Z. A Comparison of Spatial Semivariogram Estimators and Corresponding Ordinary Kriging Predictors. Technometrics 1991, 33, 77–91. [Google Scholar]
- Seymour, G. The Predictive Sample Reuse Method with Application. J. Am. Stat. Assoc. 1975, 70, 320–328. [Google Scholar]
- Peng, B.; Zhong, S.; Su, X.; Li, X. Analysis on Rainfall Spatial Interpolation Precision in Lijiang River Basin. J. Meteorol. Res. Appl. 2011, 32, 30–33. [Google Scholar]
- Ziegel, E.R.; Chatfield, C. The Analysis of Time Series. In The Analysis of Time Series; Chapman and Hall: Boca Raton, FL, USA, 2004; pp. 199–227. [Google Scholar]
- Jabro, J.D.; Stevens, W.B.; Evans, R.G. Spatial Variability and Correlation of Selected Soil Properties in the Ap Horizon of a CRP Grassland. Appl. Eng. Agric. 2010, 26, 419–428. [Google Scholar] [CrossRef]

| Station | Mean | Mean (2014) | Mean (2015) | Variance | Variance (2014) | Variance (2015) | Max | Min |
|---|---|---|---|---|---|---|---|---|
| Beijing | 117.68 | 119.20 | 116.17 | 5457.34 | 4640.34 | 6275.74 | 485 | 23 |
| Tianjin | 104.38 | 108.90 | 99.89 | 3316.49 | 3228.31 | 3372.55 | 391 | 27 |
| Baoding | 145.85 | 160.73 | 131.10 | 7485.18 | 8055.78 | 6501.22 | 500 | 35 |
| Yangquan | 98.33 | 100.54 | 96.14 | 2083.73 | 1853.59 | 2308.03 | 360 | 26 |
| Linfen | 87.65 | 84.36 | 90.90 | 1964.32 | 1747.82 | 2163.05 | 346 | 20 |
| Zhengzhou | 129.78 | 134.62 | 124.98 | 4245.17 | 3755.58 | 4695.95 | 500 | 38 |
| Month | Nugget | Parameter | Major Range | Partial Sill | Lag Size |
|---|---|---|---|---|---|
| August 2014 | 72.562 | 0.2 | 4.5 | 0 | 0.56249 |
| November 2014 | 0 | 0.91016 | 1.6529 | 290.05 | 0.18965 |
| February 2015 | 486.36 | 0.2 | 1.0211 | 0 | 0.12764 |
| May 2015 | 0 | 0.88027 | 1.1841 | 120.27 | 0.13472 |
| August 2015 | 0 | 0.43906 | 1.1841 | 108.53 | 0.13474 |
| November 2015 | 165.83 | 0.2 | 3.2688 | 0 | 0.40860 |
| February 2016 | 0 | 0.90488 | 1.1841 | 100.52 | 0.13717 |
| May 2016 | 75.69 | 0.2 | 14.213 | 0 | 1.18445 |
| August 2016 | 42.136 | 2 | 1.1841 | 6.6152 | 0.13353 |
| Time | Method | MAE | RMSIE | Time | Method | MAE | RMSIE |
|---|---|---|---|---|---|---|---|
| August 2014 | IDW | 11.2923 | 14.8369 | November 2015 | IDW | 16.8145 | 21.3827 |
| OK | 10.9151 | 14.1755 | OK | 13.3573 | 16.6038 | ||
| BME | 9.4169 | 12.4072 | BME | 16.0600 | 20.0600 | ||
| November 2014 | IDW | 17.8546 | 24.1299 | February 2016 | IDW | 9.6880 | 12.2206 |
| OK | 14.0996 | 18.6090 | OK | 8.9560 | 11.3090 | ||
| BME | 17.6734 | 21.8362 | BME | 9.2500 | 11.5400 | ||
| February 2015 | IDW | 20.0113 | 26.6201 | May 2016 | IDW | 8.5534 | 10.8039 |
| OK | 18.1584 | 24.6983 | OK | 8.9295 | 10.7937 | ||
| BME | 17.7400 | 23.1100 | BME | 8.8525 | 11.0317 | ||
| May 2015 | IDW | 9.2370 | 11.8869 | August 2016 | IDW | 7.8679 | 9.6368 |
| OK | 9.2512 | 11.8708 | OK | 7.7776 | 9.8154 | ||
| BME | 8.8569 | 11.6275 | BME | 7.5564 | 9.6982 | ||
| August 2015 | IDW | 9.8277 | 12.1164 | ||||
| OK | 9.9885 | 12.1584 | |||||
| BME | 9.5299 | 11.7899 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Zhong, S.; Wang, C.; Yang, Y.; Yao, G.; Huang, Q. Mapping Comparison and Meteorological Correlation Analysis of the Air Quality Index in Mid-Eastern China. ISPRS Int. J. Geo-Inf. 2017, 6, 52. https://doi.org/10.3390/ijgi6020052
Yu Z, Zhong S, Wang C, Yang Y, Yao G, Huang Q. Mapping Comparison and Meteorological Correlation Analysis of the Air Quality Index in Mid-Eastern China. ISPRS International Journal of Geo-Information. 2017; 6(2):52. https://doi.org/10.3390/ijgi6020052
Chicago/Turabian StyleYu, Zhichen, Shaobo Zhong, Chaolin Wang, Yongsheng Yang, Guannan Yao, and Quanyi Huang. 2017. "Mapping Comparison and Meteorological Correlation Analysis of the Air Quality Index in Mid-Eastern China" ISPRS International Journal of Geo-Information 6, no. 2: 52. https://doi.org/10.3390/ijgi6020052
APA StyleYu, Z., Zhong, S., Wang, C., Yang, Y., Yao, G., & Huang, Q. (2017). Mapping Comparison and Meteorological Correlation Analysis of the Air Quality Index in Mid-Eastern China. ISPRS International Journal of Geo-Information, 6(2), 52. https://doi.org/10.3390/ijgi6020052





