Integrating Decentralized Indoor Evacuation with Information Depositories in the Field

Abstract

The lonelier evacuees find themselves, the riskier become their wayfinding decisions. This research supports single evacuees in a dynamically changing environment with risk-aware guidance. It deploys the concept of decentralized evacuation, where evacuees are guided by smartphones acquiring environmental knowledge and risk information via exploration and knowledge sharing by peer-to-peer communication. Peer-to-peer communication, however, relies on the chance that people come into communication range with each other. This chance can be low. To bridge between people being not at the same time at the same places, this paper suggests information depositories at strategic locations to improve information sharing. Information depositories collect the knowledge acquired by the smartphones of evacuees passing by, maintain this information, and convey it to other passing-by evacuees. Multi-agent simulation implementing these depositories in an indoor environment shows that integrating depositories improves evacuation performance: It enhances the risk awareness and consequently increases the chance that people survive and reduces their evacuation time. For evacuating dynamic events, deploying depositories at staircases has been shown more effective than deploying them in corridors.

1. Introduction

When disasters strike, such as a fire, a gas leak, a chemical spill, an earthquake, a flooding, or a roaming sniper, the first and foremost action is to get people out of the disaster area. This paper focuses on those evacuees who find themselves without organized help when the alarm goes off. For them, environmental knowledge, knowledge about the dynamically changing event, and thus some risk awareness in their decision making is essential [1]. For these situations, decentralized evacuation has been embraced by recent research due to its robustness and scalability [2,3].

In decentralized evacuations evacuees are guided by their smartphones that are acquiring environmental knowledge and risk information as the evacuees explore the environment. These smartphones are sharing their collected knowledge by peer-to-peer communication with other smartphones within communication range. Decentralized evacuation has the advantage that no further infrastructure is required, i.e., it is applicable in any environment. In simulation, it has proven to work well where there are good chances that evacuees come into communication range with each other. In reality, however, the chance that evacuees encounter may be low due to the following facts.

• Encounters happen when two people walk in opposite directions; however, in evacuation situations people tend to move in similar directions, i.e., from their current positions to where they guess the closest exit is.
• Even when people move towards each other, for example, trying to get to the same staircase from opposite directions, they may still miss each other if one person reaches the staircase earlier than the other. More formally, even if their two trajectories have a joint point in space, they still can miss each other by time.
• High density of evacuees, although desirable in the context of exchanging knowledge, is also leading to congestions and panic situations [4], and thus risk-aware evacuees might actively avoid crowded spaces.

The success of a single evacuee depends on up-to-date knowledge of the dynamics in the environment. A recently proposed ‘fading memory’ method, distrusting older knowledge, introduces some aspects of risk awareness, and generally improves evacuation success [2]. However, the fading memory method produces can even decrease evacuation success when older information is discarded that is still valid. The research question of this paper is how to effectively maintain the spatial and temporal information of the dynamic environment within the environment, and how to robustly keep evacuees updated.

To bridge the spatial and temporal gaps in the communication of single evacuees in decentralized evacuations, and inspired by ants that communicate by pheromone traces that keep being updated by passers-by, this paper suggests information depositories in the field for decentralized evacuation. Information depositories enable the environment to maintain information and interact with passing-by evacuees. They record and update the environmental and risk information deposited by passing-by evacuees, and provide this information to later passers-by. They are sharing points in the environment for evacuees passing the same location at different times, enabling asynchronous communication [5,6]. Thus information depositories add to peer-to-peer communication, can address all three challenges listed above, and therefore are expected to produce better evacuation outcomes.

The hypothesis is that even a small number of information depositories will enhance risk awareness of evacuees and improve the evacuation results.

The hypothesis will be verified through agent-based simulation by adding information depositories to a decentralized evacuation of an indoor environment. Simulation results will be evaluated with the success rates of evacuees, the number of steps required to exits, and the amount of knowledge that has been updated. The contributions of this paper are as follows.

• This paper proposes information depositories for asynchronous communication in decentralized evacuation.
• This paper verifies that integrating information depositories benefits decentralized evacuation.
• This paper shows that already a small number of information depositories make a difference if these depositories are deployed at strategic locations such as staircases.
• This paper compares the alternative approaches of fading memory and information depositories, showing that their mutual advantages can be combined.

The research scope of this paper is to investigate a conceptual model of decentralized indoor evacuation with information depositories, while it leaves aside specific implementations of technologies. For example, a conceptual model may involve multiple modules such as simulation of the emergency event, localization and navigation, the sensing of the environment, risk assessment, and ad-hoc communication. This paper does not limit the implementation of each module to specific technologies. Any existing or emerging technologies can be plugged in. In this paper, sensing is assumed to happen on a mobile device in the background and is taken for granted. To explain and to investigate the conceptual model of evacuation with information depositories, this paper assumes that each evacuee carries a mobile device such as a smartphone, and evacuation happens in a departmental building after a fire broke out. The fire is spatially extended and varying over time.

The rest of this paper is organized as follows. Section 3 develops the concept of immobile information depositories for roving, self-localizing and mapping agents. Section 4 implements the information depositories in an agent-based simulation of decentralized evacuation from an indoor environment. Section 5 presents the results of simulations, which are discussed in Section 6. Section 7 concludes this paper.

2. Related Work

Evacuation is the overarching task for disaster management [3,7], which generally relocates people from a risky area to safe areas due to emergencies, such as fire, a gas leak, a hurricane, or an earthquake (e.g., [8,9]). The area in emergencies can be an office building, a theater, a railway station (e.g., [10,11]), a shopping mall, or an urban region (e.g., [12,13,14]). Research on pedestrian and evacuation can be divided into three streams: (a) the study of pedestrian behavior and crowd dynamics, (b) the development of descriptive models to represent pedestrian dynamics as realistically as possible, and (c) the optimization-based method to determine optimal evacuation plans or design solutions [15]. Most of the research falls under the first two categories.

2.1. Evacuation Models and Crowd Dynamics

Alvear et al. [16] identified three purposes of evacuation models: (a) performance-based analysis for new and existing buildings in order to evaluate the design and evacuation procedures (e.g., [17,18]), (b) forensic analysis to reconstruct historical evacuation processes in order to analyze possible failures and inefficiencies (e.g., [19]), and (c) management during evacuation procedures (e.g., [20]). The detailed assessments of the existing modeling approaches and simulation models can be found in the literature [21,22,23,24].

Evacuation models can be roughly categorized into microscopic models and macroscopic models, which simulate crowd movement in emergency situations with different levels of abstraction. In microscopic models, the evacuating population is considered to be discrete individuals, and collective phenomena emerge from the interactions between individuals. Macroscopic models capture the evacuation situation from a global perspective and represent collective phenomena directly [21,22].

Examples of microscopic models are cellular automata models (e.g., [10,25,26,27,28,29,30,31]), lattice gas models (e.g., [32]), social force models (e.g., [4,11,33,34,35]), motion planning with velocity obstacles (e.g., [36,37]), agent-based models (e.g., [38,39,40]), game theoretic models (e.g., [41,42,43]), approaches based on experiments with animals (e.g., [44,45,46,47]), and hybrid models (e.g., [48]). Cellular automata models and lattice gas models partition the space into grids or hexagons. Evacuees are supposed to move from one cell to another. A social force model was first proposed by Helbing and Molnar [49], describing pedestrians as particles that are subject to forces of attraction and repulsion. Helbing et al. [4] then developed another social force model to study the collective phenomenon of escape panic, where a mixture of socio-psychological and physical forces was assumed, which includes interaction forces, body force and siding friction force. Velocity obstacle models have been originally developed for robot motion planning. They assume that other robots in the environment maintain their current velocity and thus may define velocity obstacles; such models enable a robot to plan for collision avoidance. Agent-based models describe the evacuation system by simulating each evacuee (or a household [40]) as an autonomous agent with certain behavior and situated in an environment, and studying the emergent system behavior. In contrast, approaches based on experiments with animals study escape dynamics with real biological agents such as mice [44] or ants [45,46,47]. Hybrid models combine the previously mentioned microscopic models to benefit from their advantages and to avoid their drawbacks.

In contrast to microscopic models describing the crowds as discrete individuals, macroscopic models treat the crowd as a continuous medium characterized by averaged quantities such as density and velocity [50,51]. Fluid dynamic models are the most recognized macroscopic models [52,53], which use the analogy of fluid dynamics to describe the crowd flow in the form of partial differential equations [54]. Fluid-dynamic models and social force models are continuous in space and time, compared to cellular automata models and lattice gas models, where space and time are discrete [22]. Agent-based models can have both continuous and discrete representations in space and time.

Typical phenomena that can be reproduced in simulations include kin behavior, arching, effect of obstacles, jamming, friction effects, clogging, “freezing by heating", “faster-is-slower", counterflow, choking flow, mass behavior, pushing behavior, panic propagation, impatience, repulsion behavior, competitive behavior, queuing behavior, and herding behavior [22]. Zheng et al. [22] identified two reasons that may cause people being injured or killed during evacuations: either due to failing to evacuate timely, or due to the crowd’s behavior such as shuffling, pushing, crushing, and trampling. Sivers et al. [19] argued that most models for evacuation dynamics consider individuals as particles, so they added social identity to pedestrian simulation. They take helping others as an example to investigate whether psychological models and computer models of pedestrian motion can be combined so that simulation results correspond to observations from crowd psychology. Davidich et al. [10] found that standing pedestrians affect crowd dynamics strongly and should be considered when designing critical infrastructures such as railway stations. Kneidl et al. [48] developed a hybrid model which combines a dynamic navigation field with a navigation graph. Space and time are discretized using cellular automata, which act as the underlying grid for constructing the navigation field. The dynamic navigation field employs the analogy of an expanding wave which estimates the travel times of pedestrians traveling between an origin and a given destination considering congestions. Such a dynamic navigation field allows evacuees (a) to follow a direction which is subject to minimization of estimated travel times, and (b) to steer around congestions even when the congestions are not visible from their actual position. However, Kneidl et al. [48] aimed to provide a realistic simulation of crowd dynamics rather than optimizing evacuation paths, so they also added a navigation graph constructed on top of the scenarios’ geometry which acts as a visibility graph to help distinguish between visible and invisible areas.

In contrast to building evacuation, other research deals with optimizing traffic during evacuations on an urban scale [25,55]. So and Daganzo [25] proposed a decentralized strategy that evacuated the maximum number of people at all times. Feng and Miller-Hooks [20] proposed a network optimization-based methodology to support crowd movement during large public gatherings held in venues such as complex buildings, transportation stations, football stadiums, and commercial malls. Yin et al. [40] presented an agent-based travel demand modeling system to generate household activity-travel plans for hurricane evacuation simulation, in which each agent represented a household. They considered the ultimate evacuation trips of a household as the result of a series of demands and the thereafter decisions, such as whether to evacuate, when, to where, by which mode, as well as pre-evacuation preparation activities such as purchasing fuel and food, or family gathering. Another model addressing the simulation of pre-evacuation behavior has been studied by Lovreglio et al. [56], which adopted Random Utility Theory. Compared with indoor evacuation which involves pedestrians, evacuation planning in urban areas involves different tasks: such as deciding shelter locations, routing for public transport and for individual traffic simultaneously [13]. A review of highway-based evacuation modeling and simulation has been provided as well [57].

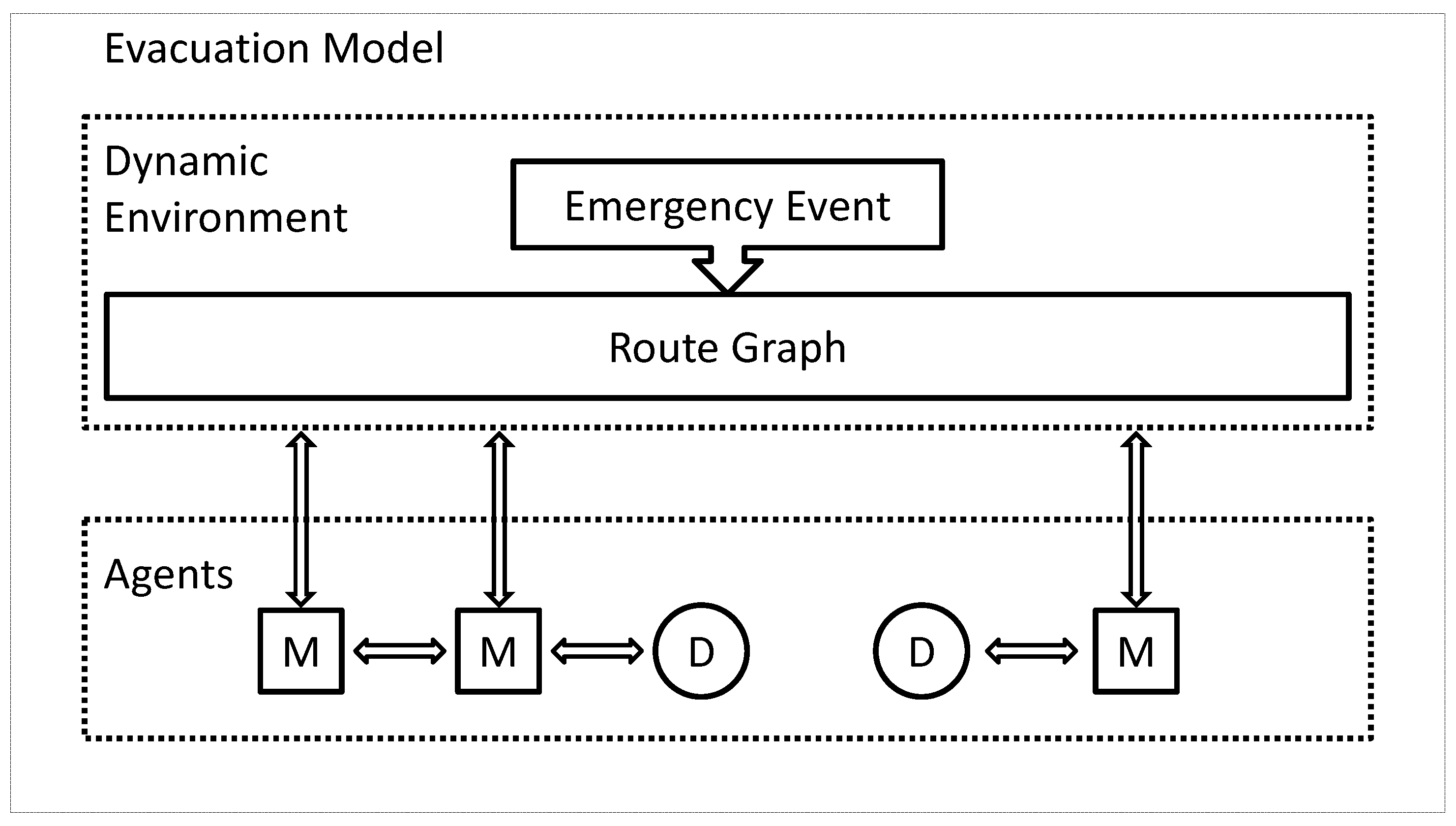
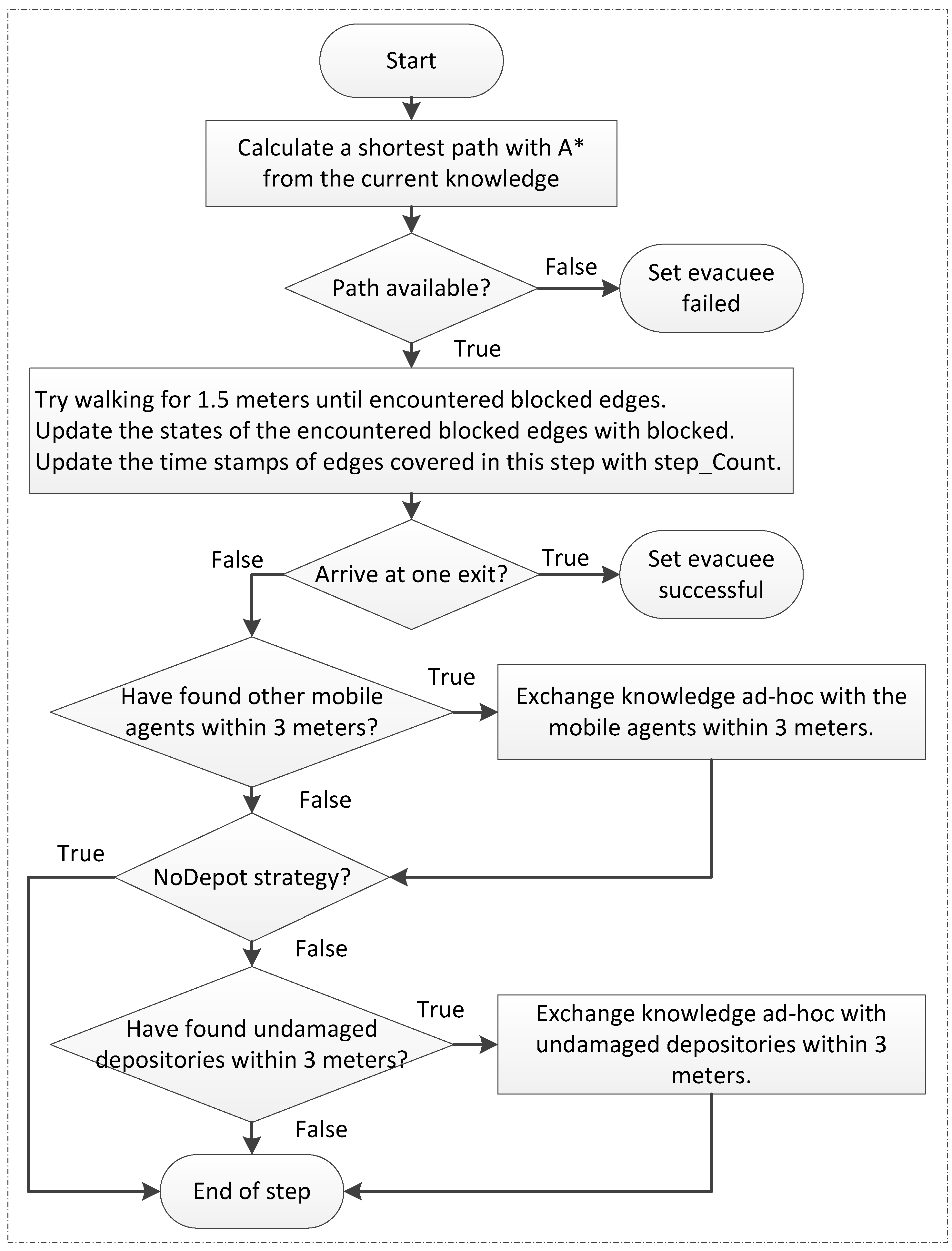
This paper focuses on simulating the heterogeneous characters of each evacuee and their interactions by using an agent-based model. Each evacuee acts as an autonomous agent which independently explores the environment and acquires different knowledge. In particular, this paper aims to investigate optimal evacuation strategies when the density of evacuees is very low and chances for encounters are rare, thus crowd behavior has been neglected in all the simulations.

2.2. Evacuation Optimization

Compared with evacuation models and crowd dynamics, evacuation optimization has received less attention from researchers. A recent review of optimization models for evacuation problems has been provided [15].

The purpose of evacuation optimization is to improve the evacuation process, aiming at two objectives: reducing the number of deaths and accelerating the evacuation process [7]. Research efforts for evacuation optimization fall into two categories: either to improve the evacuation process by improving the environmental factors (e.g., optimizing the room structures, finding the optimal number, width and placement of doors), or by improving the path choice of evacuees [58].

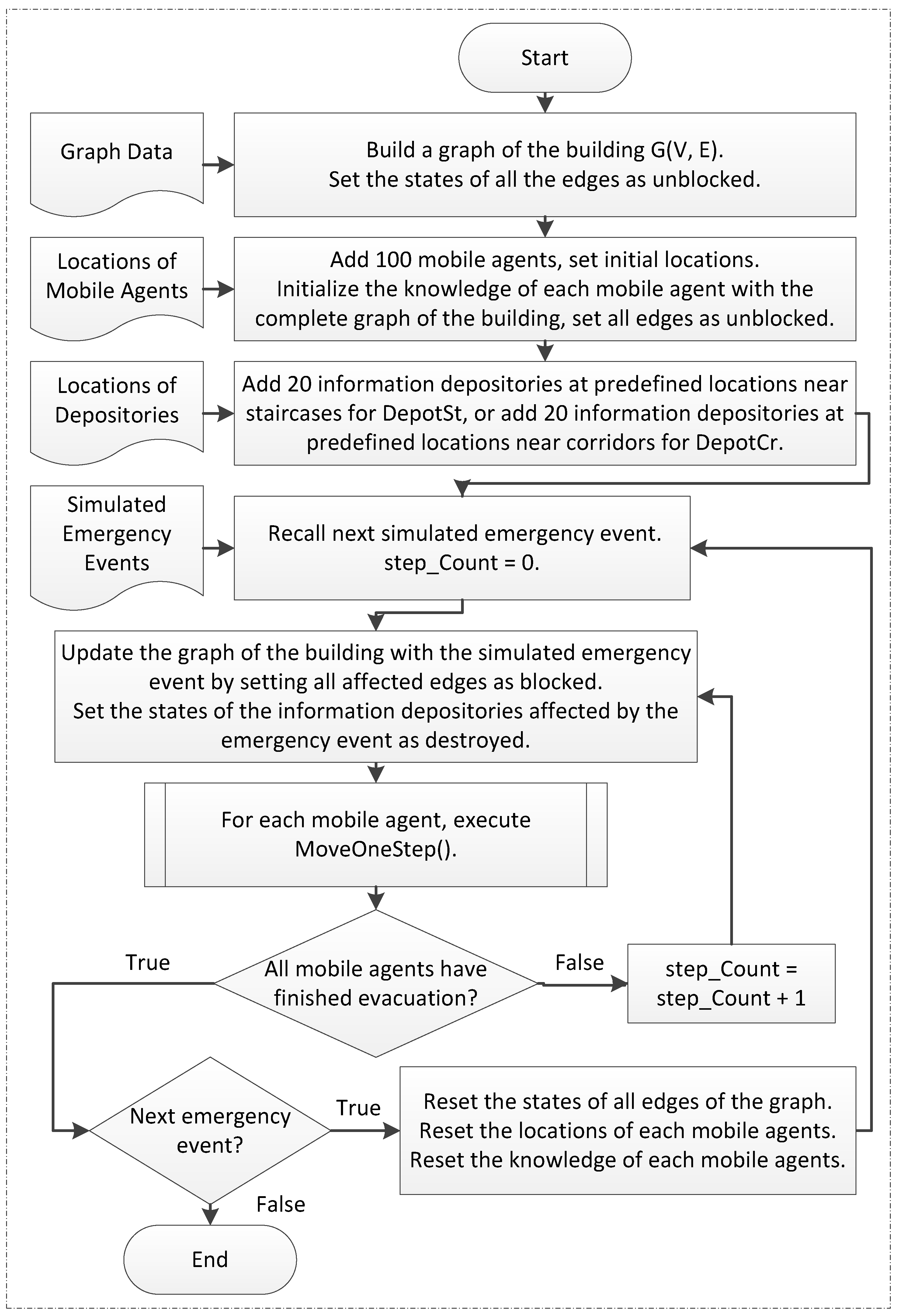
Optimization models gravitate to graphs to represent the paths available to pedestrian evacuees [59,60]. A graph is defined by a set of nodes representing rooms or decision points, and edges representing doors, corridors, or other paths connecting the spaces represented by nodes [61]. Edges are associated with weights, which can be the distance between the connected nodes or the time required to travel between the connected nodes. A time-expanded graph includes a graph and states of nodes and edges at different time steps [59,62]. Optimization of path choices has been studied either by optimizing the flow of pedestrians (or vehicles) based on evacuation graph, or by finding evacuation paths with minimum cost algorithms such as Dijkstra’s, A*, Ant Colony Optimization, D*, or D* Lite.

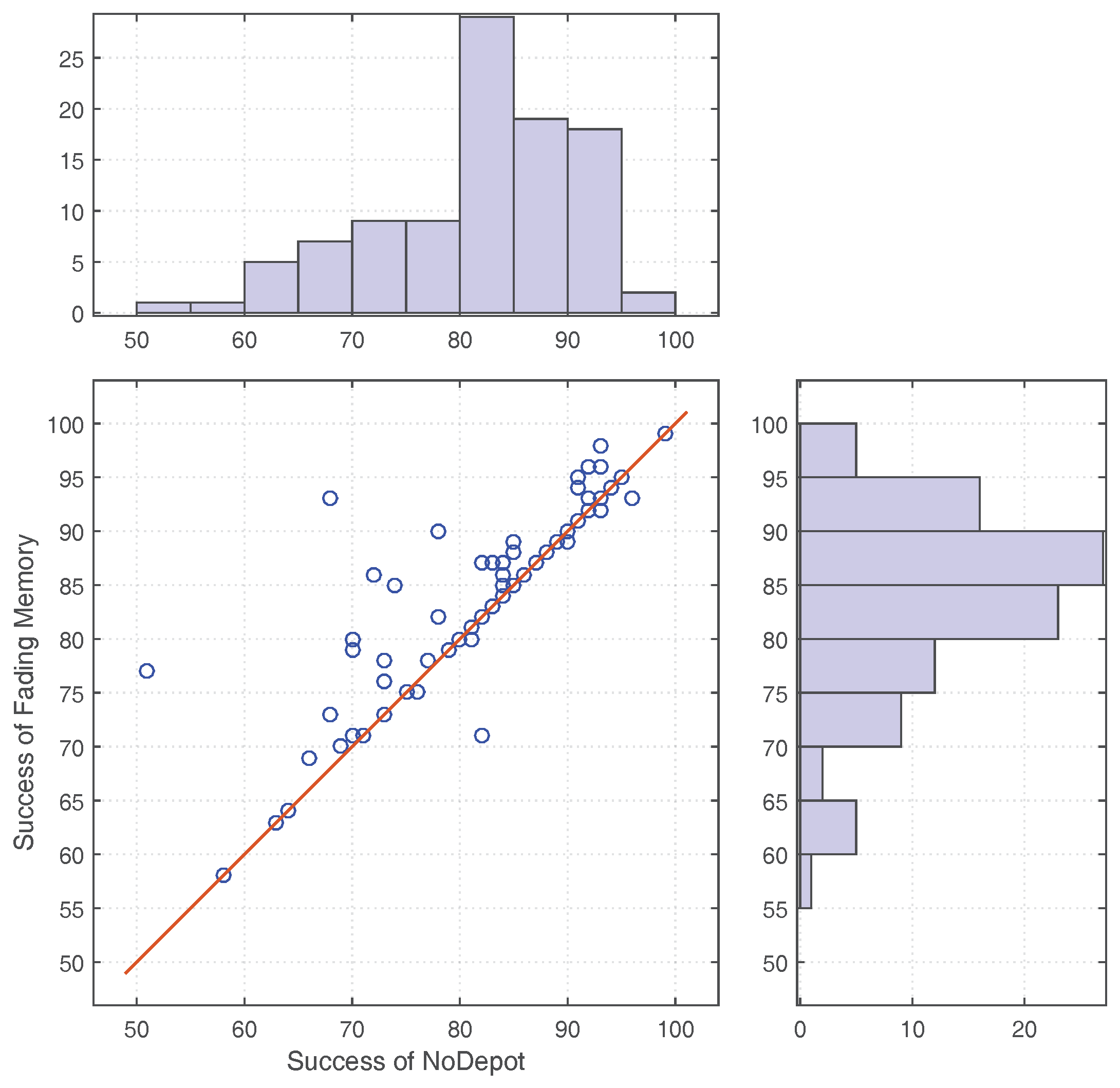
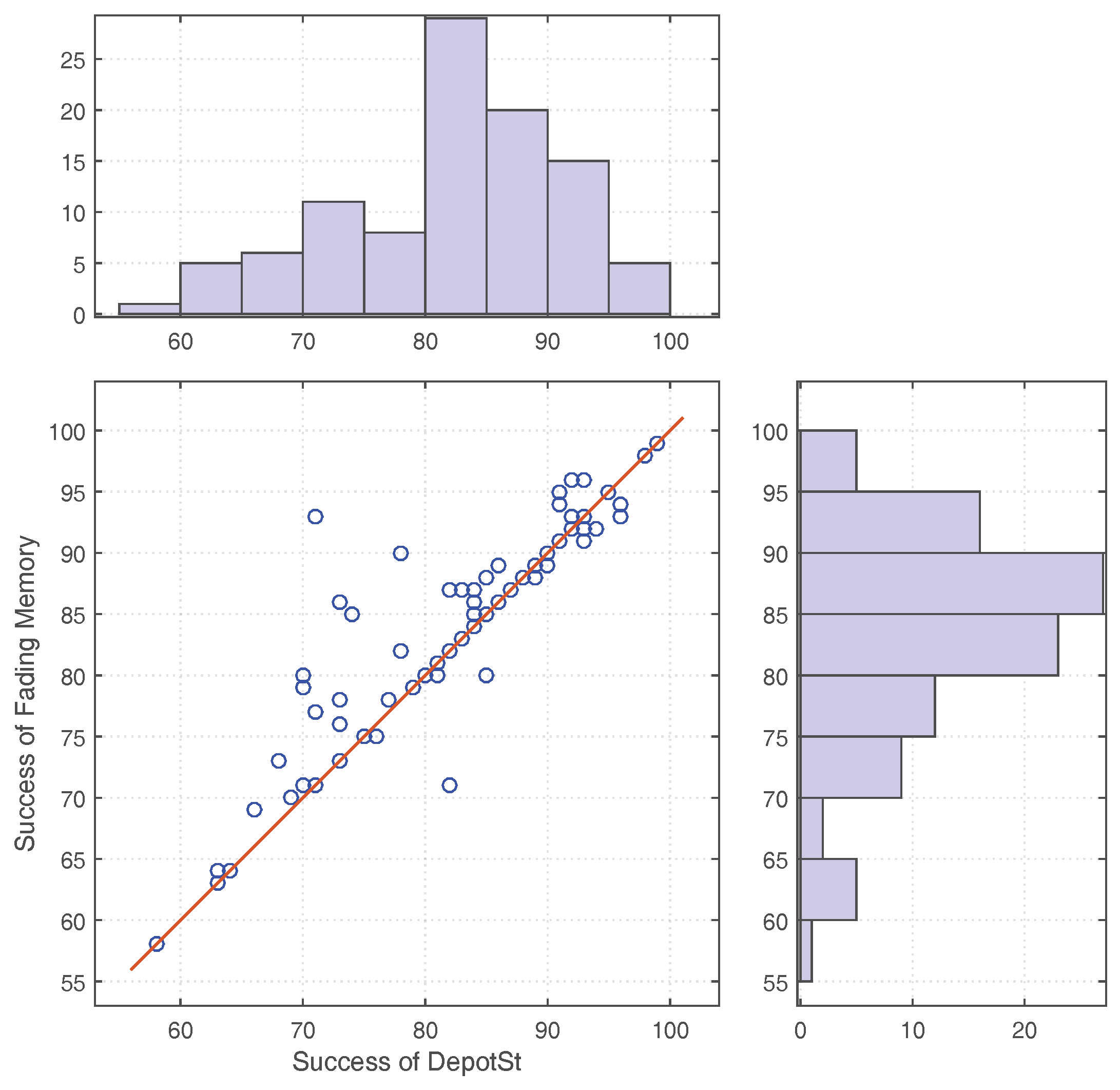
For path planning, evacuees may either have the global knowledge of the graph or only have a limited view of the graph. All the knowledge is time stamped and may have become out of date due to the evolution of the disaster, thus introducing uncertainty to the knowledge. Zhao and Winter [2] addressed the uncertainty of knowledge by developing a fading memory model which trusted less the older knowledge. They found that the fading memory model generally improved the evacuation process. However, such a model also poses a risk of devaluing knowledge that is still valid. Another research that considers the impact of the dynamics of disasters on the evacuation process was conducted by Tan et al. [63]. They considered both the stationary environment during a normal situation and the predictable spatial change caused by the activated fire safety facilities during emergency situations, such as a fire rolling shutter that would be shut off during emergency situations.

Wang et al. [1] and Wang et al. [62] addressed the evacuation optimization problem by suggesting a centralized evacuation framework incorporating multiple sensors and mobile phones. Such a centralized system carries out computations on a central server and makes decisions based on real-time awareness of the state of the environment, thus producing optimal evacuation paths. However, such centralized systems share a common shortcoming: They require system infrastructure and expect that their infrastructure is not affected by the disaster.

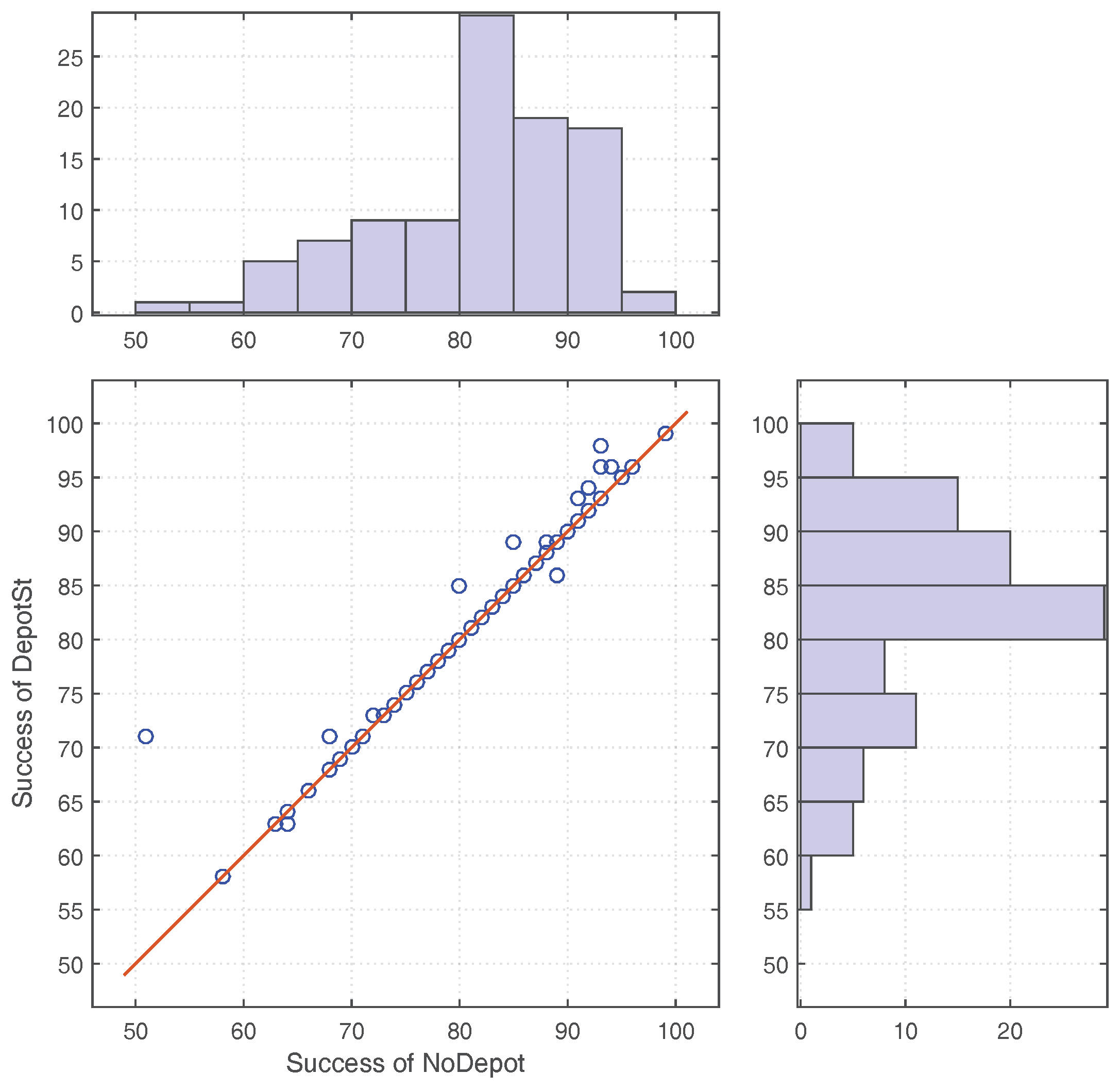
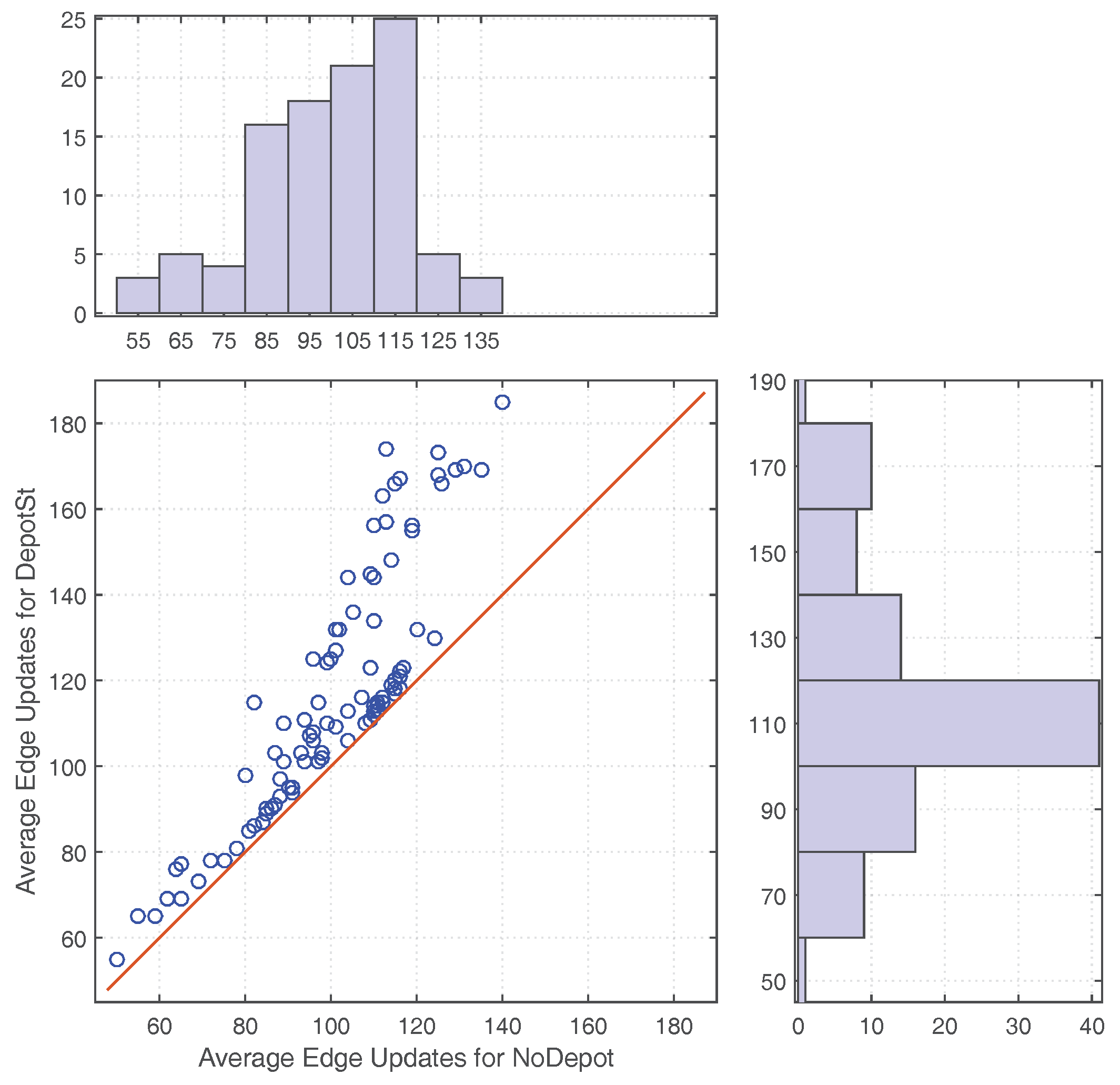
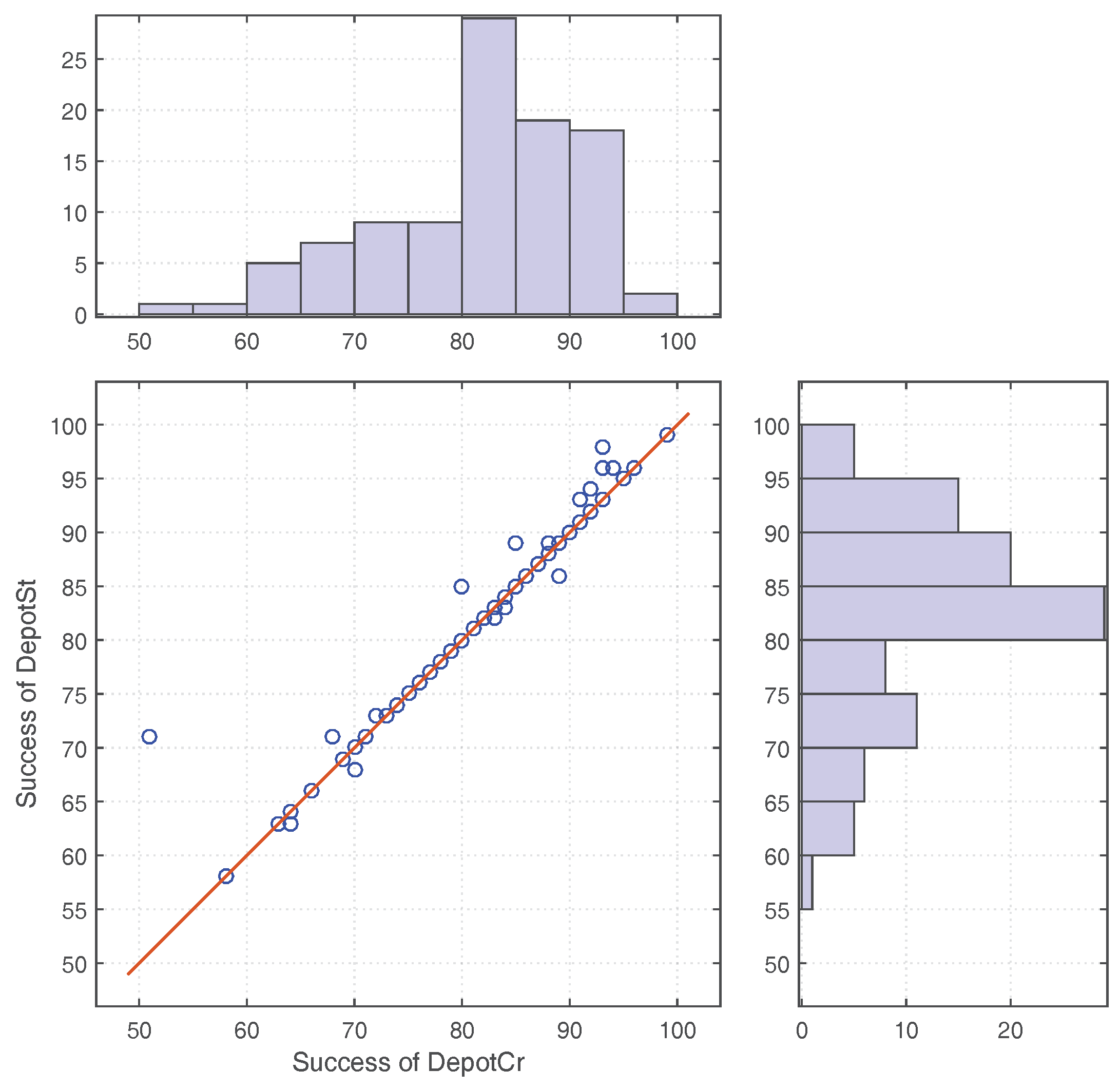
In contrast to evacuation models aiming for realistic simulation of crowd dynamics, evacuation optimization aims to investigate efficient evacuation strategies, which is to be addressed in this paper. In particular, this paper focuses on evacuation strategies in a decentralized manner. Further, this paper prioritizes the number of successful evacuees over minimizing evacuation times, since not all the evacuees are guaranteed to be successfully evacuated.

2.3. Decentralized Evacuation

Advances in technology such as sensors and smartphones make decentralized spatial computing possible. Existing sensors can detect acoustic, chemical, electromagnetic, optical, thermal, or mechanical stimuli, and convert such environmental stimuli into digital signals to be processed by a computer [64]. Such sensors can measure environmental data such as humidity, $C{O}_2$ concentration, temperature, or even location [65]. A number of these sensors can be found on-board of smartphones, and thus, smartphones can be considered a node in a mobile sensor network. A sensor node has a microcontroller for computing, a wireless radio for communication, and one or more sensors for capturing data about its environment. Mobile sensor networks are examples of decentralized systems. A decentralized system is a special case of a distributed system where no single component knows the entire system state and each node in a decentralized system acts independently and autonomously. In general, decentralized spatial computing is advantageous over centralized spatial computing in six aspects: energy constraints, information overload, scalability, sensor/actuator networks, latency, and information privacy [64].

Richter et al. [3] proposed a decentralized system for collaborative evacuation. This system utilizes smartphones with their sensors and their capacity for peer-to-peer communication where computation is performed directly on the devices held by evacuees and guidance is provided by a mobile service. The advantage of peer-communication and -collaboration correlates positively with the density of evacuees in the environment: The more evacuees exist in a certain environment, the more opportunity exists for exchanging knowledge. However, a larger number of evacuees also implies an increased risk of congestions [58]. Similar work has been done by Fujihara and Miwa [66]. They considered the opportunistic communication of mobile nodes in Mobile Opportunistic Networks (MONs), and assumed also a navigation service. Evacuees share disaster information by opportunistic encounter and short-range wireless communication. In their scenario the disaster information is finally gathered by a database server in the refuge and forwarded out of the disaster area by delay tolerant network technologies such as satellite-based communications. Komatsu et al. [67] also introduced cooperation between evacuees with mobile sensor nodes. Each mobile node senses the environment and tries to navigate its evacuee by presenting an evacuation route. The mobile node estimates a road segment as blocked when it detects the difference between a recommended route and actual evacuation behavior. Then it recalculates an alternative evacuation route, which does not include the blocked road segments discovered. They focus specifically on reducing the network load. Iizuka et al. [68] presented a method for decentralized evacuation, which considers evacuation as a distributed constraint optimization problem and estimates the location of evacuees so as to relieve congestion.

Due to the fundamental property of opportunistic communication, all the wireless mobile sensor networks share a shortcoming that the effects of opportunistic communication become weaker when the number of users in the network is smaller. None of the previous work has addressed this issue. Thus, improving decentralized evacuation management for less occupied buildings is the object to be addressed in this paper.

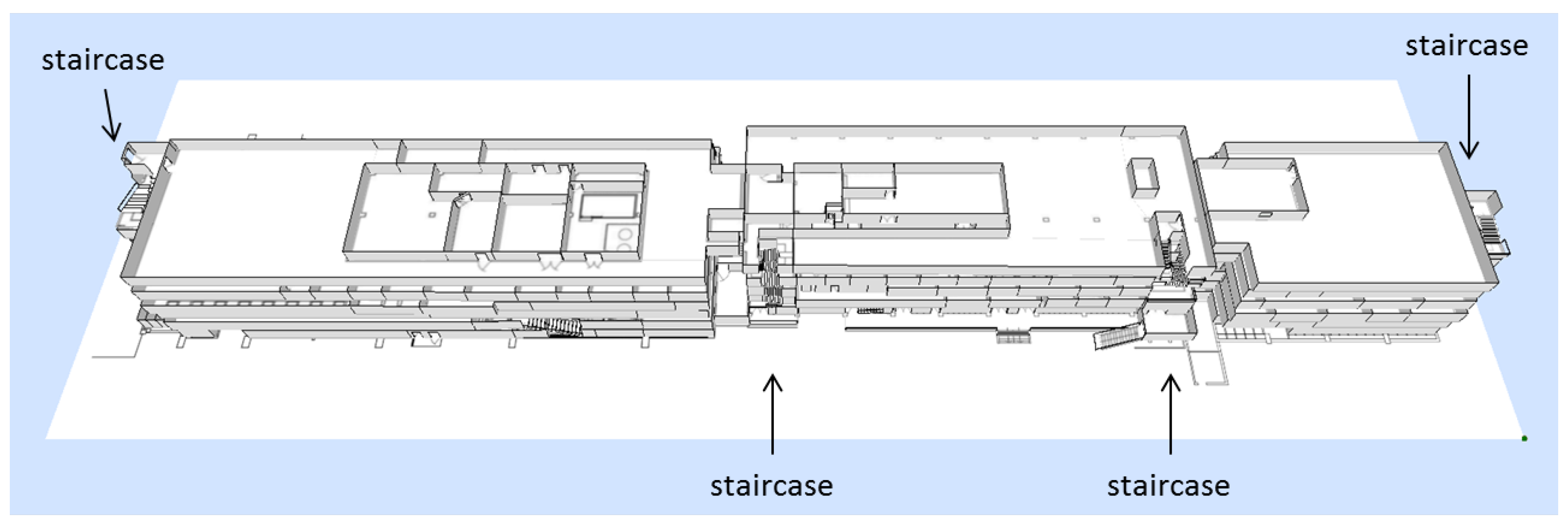
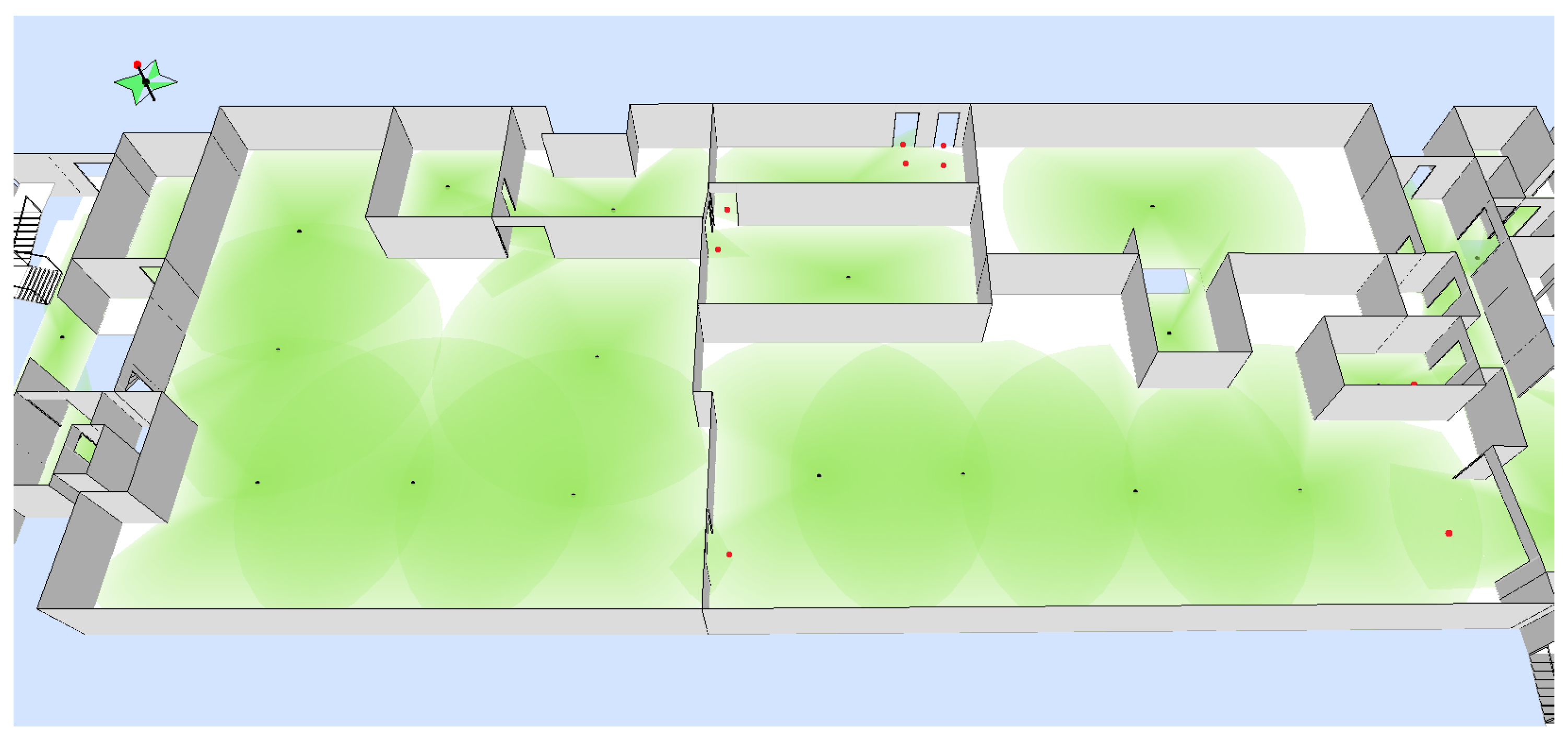
While static sensor networks can detect the extent of phenomena such as fires or concentrations of pollutants, and can delineate the boundaries of such regions, low-density in situ sensor networks may not suffice to estimate the boundaries, especially in evacuation situations where the sensor nodes are outside of these hazardous regions. Brink [69] suggest adding mobile sensors with an intelligent and adaptive sampling strategy to collect the missing information for monitoring the boundaries of highly dynamic phenomena such as plumes. In contrast, this paper will suggest static depositories at strategic locations that collect the knowledge acquired by the smartphones of evacuees passing by, merging data over time.

3. Information Depositories

3.1. Awareness of the Indoor Environment

The indoor space of a building can be represented by a navigable graph $G(V,E)$, where V is a set of vertices $v_i$ with a total count of $\parallel V\parallel =m$, and E is a set of edges $e_j$ with a total count of $\parallel E\parallel =n$. Nodes represent locations, and edges represent a possibility to move directly between two locations. Moving agents (evacuees) can have partial or complete knowledge of this graph, depending on their individual familiarity with the environment. The partial or complete awareness of the indoor space during evacuation consists of at least three dimensions:

• The (partial or complete) original graph of the indoor environment. It represents the connectivity of the indoor environment before being affected by a disaster.
• The state of the original graph. States of nodes and edges track the changes caused by the disaster that evolves dynamically. This paper assumes two possible states of each edge or node: unblocked and blocked. A blocked edge is not passable for evacuees, while an unblocked edge allows evacuees to pass through freely. A blocked node can be represented by setting all its adjacent edges as blocked. In decentralized evacuation different evacuees can have different knowledge of the states of the graph.
• The time stamp of the state. It labels when that state of an edge or node has been lastly updated. Since the only sensors in decentralized evacuation are the (smartphones of the) evacuees, edges and nodes are only updated when encountered and found in a different state by an evacuee. Thus, these times are transaction times of individual sensors, not valid times of changes in the environment. Furthermore, in decentralized evacuation different sensor nodes can obtain the same information at different times.

Awareness of the indoor environment can be represented by a set of triplets:

$$\{{(e,stat{e}_e,t_e)}_j\},j\in \{1,2,\cdots ,n\}$$

(1)

where e denotes an edge of the graph, $stat{e}_e$ denotes the state of that edge, and $t_e$ denotes the time when that $stat{e}_e$ has been obtained.

Such awareness of the indoor environment is an enhanced graph for computing shortest evacuation paths while avoiding the known-to-be-blocked edges.

3.2. Update of Awareness

In decentralized evacuation, evacuees generally update their awareness in two ways:

• By exploration. Awareness of the indoor environment can be updated when an evacuee encounters new locations or passages, or new states of already known locations or passages.
• By peer-to-peer communication. Two evacuees exchange their awareness of the indoor environment when they get close (technically: into short-range radio communication range). Their awareness of the environment may differ in completeness and in currency. After the exchange, both evacuees will have the same knowledge, where the merging operation ensures that among duplicates only the awareness with the more recent time stamp will be retained.

3.3. The Role of Information Depositories

This paper assumes the indoor space has also been deployed with disconnected static information depositories. Such static depositories are capable of the same peer-to-peer communication with their surroundings and hence work in two ways.

• As a repository. The static information depositories work as repositories that collect the awareness of evacuees that pass by.
• As a service station. A static information depository shares with passing-by evacuees the collective awareness in its repository.

Such a concept of static information depositories enables the space itself to maintain awareness information and interact with passers-by.

4. Evacuation Simulation Model

4.1. The Building

Simulations adopt a five level departmental building, which has already been used for testing (purely) decentralized evacuation [2]. This building consists of three rectangular blocks. Each block includes the ground floor, level one, level two, level three, level four and the roof level. There are mainly four staircases starting from the ground floor and ending at the roof level, two of which are located on the left side and the right side of this building, and the other two are located near the joint parts of two blocks (Figure 1). These four staircases direct to the four main exits of this building. There are another six exits accessible only to evacuees on the ground floor. This building is mostly dedicated to staff use (offices), apart from labs on level one, two lecture theaters on level four, and a computer lab on the ground floor.

4.2. Route Graph

A route graph associates evacuation routes with the building structure. This paper adopts the method developed by Wang et al. [1], Stahl [70], to generate a route graph. The nodes of the route graph are mainly placed pair-wise on both sides of an entrance, at the beginning, end, and turning points of staircases, or at the shifted boundary vertices of concave regions. The graph for this building consists of 1739 edges and 1120 nodes (Figure 2). Before the emergency, all the edges are initially unblocked and are allocated with a weight of their actual length. However, during the emergency, the edges of this graph will be continually affected by the emergency events: Some edges will become blocked by allocating a weight of infinity.

4.3. Emergency Event

The simulation assumes that the building is affected by a spatially-extended and temporally-varying event such as a fire emergency, and adopts the emergency simulation developed by Zhao and Winter [2]. This emergency simulation assumes a virtual sensor network covering the whole area of the indoor environment (Figure 3). Each sensor captures the environmental factors within a circular detecting area (radius r = 6 m) if no walls shield the reception of this sensor. Otherwise, the detection area of the sensor is the intersection between the circular area and the boundary of the region where the virtual sensor is located. The sensor network is generated by adding an edge between two sensor nodes if their detection areas are intersecting. Two sensor nodes are neighboring each other if they are connected with an edge. Each sensor node has two possible states: normal and active. A sensor stays in the normal state when its detecting area is safe, and will shift to active when its detecting area is blocked by the emergency event. Before the event, all sensors should be in the normal state. The event is marked by setting one sensor to be active. As the event expands, the next active sensors should be one or more neighbored sensors of the already active one. Every two steps, this simulation randomly picks up one of the already active sensors, and set all its neighboring sensors as active. Thus, an extended emergency process has been simulated through simulating the state transfer of the virtual sensors. The main parameter that differentiates a simulated emergency event is the location where the first virtual sensor that detects the emergency events.

The emergency event is modeled independently from the route graph, so that the virtual sensors can be distributed equidistantly and can cover also spaces that are not directly covered by the route graph. Such simulations represent spatially-extended events, starting from a single location and continuing to expand. Events of other characteristics, such as earthquakes that impact at multiple locations at the same time or bomb explosions that do not expand after going off, will not be covered by this particular simulation, but could be tested in the same way in differently designed simulations.

4.4. Mobile Agent

100 agents (evacuees) are randomly located in this building before the emergency. Each agent is capable of simulating an evacuee carrying a mobile device equipped with sensors. Each mobile device saves a local version of the graph of the building, which will be used to compute the shortest path independently during evacuations. The local graph can be updated by:

• Identify whether the edge being visited by this evacuee is blocked (e.g., by temperature, smoke, or visibility, or by the fact that the owner turns around and seeks alternative paths [67]), and save this updated awareness in their memory.
• Communicate ad-hoc with devices that have come close (e.g., 3 m in the simulation), and exchange their individual awareness of the environment. These other devices can be other evacuees’ mobile devices, or static information depositories.
• Fuse the received awareness of another agent or depository with its own awareness. The merging operation ensures that among duplicates only the awareness with the more recent time stamp will be retained.

During evacuations, each mobile device computes a shortest path locally using A* algorithm, and provides evacuation guidance to the evacuee. The evacuee is supposed to follow the path suggested by the mobile device unless the evacuee finds the edge in front has been blocked. The mobile device senses this situation, allocates the blocked edge with a weight of infinity, and recalculates a new shortest path.

In the simulation, each device has been initialized with awareness of the complete original graph of this building. Such awareness is valid until a disaster strikes and the emergency evacuation is initiated. During the evacuation, the individual agents’ awareness will be updated by continuously sensing the environment and exchanging knowledge with peer agents and depositories.

4.5. Evacuation Strategies

In order to find out (a) whether adding static information depositories will improve the evacuation performance, and (b) whether deployment of these depositories in staircases or corridors makes a difference, simulations compare three evacuation strategies during evacuation:

• Decentralized evacuation with no static information depositories (denoted by $NoDepot$), in order to establish the baseline. Evacuees update awareness of the dynamic environment only through exploration and peer-to-peer communication with other agents.
• Decentralized evacuation with information depositories at staircases (denoted by $DepotSt$). Evacuees update awareness of the dynamic environment not only through exploration and peer-to-peer communication with other agents, but also through peer-to-peer communication with close information depositories. In this strategy, twenty static depositories have been deployed, placed at each floor at locations near the four staircases of this building.
• Decentralized evacuation with information depositories in corridors (denoted by $DepotCr$). In this strategy, twenty static depositories have been deployed at random locations along the corridors of this building.

The locations of the information depositories are labeled with red squares (for DepotSt) and blue circles (for DepotCr) in Figure 4. Level one has been occupied by spacious labs. In this case, information depositories for DepotCr have been placed at graph nodes that are close to the doors of the rooms.

4.6. Evacuation Simulation

There are mainly four components in the evacuation simulation (Figure 5): the route graph, the emergency event, the mobile agents and the depositories. The route graph represents the indoor space of the building. All the edges are unblocked before the emergency. The emergency event acts as a stimulus that changes the states of the edges in the route graph. The emergency event and the route graph together create a route graph with changing states over time, which forms the ground truth of the dynamic indoor environment in the simulation. Each mobile agent senses the dynamic changes by visiting certain part of the environment, and keeps a partially out-of-date version of this graph, which forms their local knowledge. Their local knowledge can also be updated by the short-range communication with encountered peer mobile agents and depositories. Information depositories also save a local version of the dynamic graph, but they cannot sense the blocked edges and are immobile. Information depositories are considered to be set up before any event, as a fix part of the infrastructure of a building. In contrast to any centralized communication infrastructure, local depositories are robust towards any type of event and capacity. In this simulation, mobile agents are only blocked by blocked edges. Since this paper assumes that the density of evacuees is low, the effect of congestions between mobile agents will not be considered. The route graph, the simulated emergency events, the locations of mobile agents, and the locations of depositories have been predefined and saved to files, so that each pair of comparison simulations refer to identical experiment conditions.

The agent-based simulation tool Repast Simphony has been used. Figure 6 shows a flow chart of the simulation process. Before an emergency, the states of edges in the (global) route graph are unblocked, and the mobile agents are placed at predefined locations. All the mobile agents are initialized with the complete graph of the building as their prior knowledge. Evacuees are assumed to start evacuation simultaneously and immediately after the emergency alarm. The emergency event expands every two steps, and affects certain edges of the (global) graph, making them blocked. Also the information depositories will be destroyed if the emergency event expands to where the depository locates. The independence of each depository contributes to the robustness of the “system”.

The flow in Figure 6 describes necessarily a simplified model of human behavior. In a real evacuation scenario, people may not evacuate immediately after they hear the emergency alarm, which causes pre-evacuation delays. The start time of evacuation for each evacuee is uncertain, and can be affected by physiological and psychological factors. For example, some people may insist on gathering family members (known as kin behavior [71]) before they start evacuation. Such human behavior aspects are not modeled in this paper since they would add some noise to the results, conflicting with a desire to control the parameters of a simulation for comparison purposes.

Figure 7 describes the subprocess of how a mobile agent acts in each step. Each mobile agent who has not finished the evacuation tries to compute a shortest path from the current local knowledge. If no path is available, evacuation of this mobile agent is considered to be failing, otherwise this mobile agent tries to move along the evacuation path for 1.5 m unless it encounters blocked edges. The mobile agent updates its knowledge with the current states of the edges that have been visited in this step. Updating happens by overriding older information with newer ones. If other mobile agents or depositories are found within the communication range, they exchange and fuse their knowledge. If the mobile agent has arrived an exit, the mobile agent is considered to be successful. A mobile agent is considered to have finished the evacuation if it has failed or has been successful.

In this simulation, the moment when the emergency starts is considered as time zero, and the time for each step is considered as one second. The evacuation time of a mobile agent is represented by the steps consumed by this mobile agent. The timestamps of edges in the knowledge of a mobile agent are represented by the step counts when those edges were visited.

The experiments simulate each of the three evacuation strategies with 100 independent but identical emergency events, i.e., the evacuees start always from the same locations, but the emergency events start from different locations and spread continuously in some random fashion that has been recorded.

5. Results

The simulations evaluate the performance of the different strategies in three dimensions:

• Success rate. It is measured by the total number of successful evacuees for each emergency event.
• Evacuation time. It is measured by the total evacuation steps of all successful evacuees.
• Currency of situation awareness. It is measured by the average number of edges that have been updated during evacuations.

The success rate and the situation awareness have been measured based on all the 100 emergency events, while the evacuation time has been compared only when the success rates for different strategies were the same.

5.1. Success Rate

Success rate measured by the total number of successful evacuees, is the uppermost factor to be used for evaluating the performance of different evacuation strategies.

5.1.1. NoDepot vs. DepotSt

Figure 8 shows 100 paired comparisons of DepotSt and NoDepot in their evacuation success. Each point in the scatter plot corresponds to a simulated emergency event. The coordinates of each point shows the evacuation success of the two compared evacuation strategies simulated under that emergency event. Points on the red line indicate the two evacuation strategies have saved equal number of evacuees in those emergency events. The histogram shows the distribution of evacuation success for the 100 emergency events.

Comparing NoDepot and DepotSt, for 87 events (i.e., 87% of the total 100 events) both strategies have saved the same number of evacuees, while for the remaining thirteen events (i.e., 13% of the total 100 events) the number of successful evacuees shows differences (Figure 8). For these thirteen events, DepotSt on average saved 3.4 more people than NoDepot. Specifically, in eleven of these events (84.6% of the thirteen events showing differences in the number of successful evacuees) DepotSt saved more people (4.4 people per event on average) than NoDepot, and only in the other two events (15.4% of the thirteen events showing differences in the number of successful evacuees), DepotSt saved less people (two people per event on average) (

Table 1. The advantages of DepotSt and NoDepot in terms of success rate when the numbers of the successful evacuees for DepotSt and NoDepot differ.

	Number of Cases	Proportion	More Saved Per Case
DepotSt’s Advantageous	11	84.6%	4.4
NoDepot’s Advantageous	2	15.4%	2

).

5.1.2. NoDepot vs. DepotCr

Comparing NoDepot and DepotCr, in 97 events (i.e., 97% of the 100 events) both strategies have saved the same number of evacuees, while in the remaining three events (i.e., 3% of the 100 events) the number of successful evacuees shows differences (Figure 9). DepotCr has saved more people in each of these three events (on average 1.3 more people per event) (

Table 2. The advantages of DepotCr and NoDepot in terms of success rate when the numbers of the successful evacuees for DepotCr and NoDepot differ.

	Number of Cases	Proportion	More Saved Per Case
DepotCr’s Advantageous	3	100%	1.3
NoDepot’s Advantageous	0	0%	0

).

5.1.3. Combined Depositories

A combined depository scenario has also been simulated. In this scenario, 40 information depositories have been deployed, twenty of which have been placed at the same locations as DepotSt, and the other twenty depositories were placed at the same locations as DepotCr. Result shows that in the cases (eleven emergency cases) where DepotSt has saved more people than NoDepot and the two emergency cases where DepotCr has saved more people than NoDepot, a combined depository scenario also saved more people than NoDepot. In the two emergency cases where DepotSt has saved fewer people than NoDepot, a combined depository scenario also has saved fewer people (

Table 3. The advantages of a combined depository scenario in terms of success rate when the numbers of the successful evacuees differ.

	Number of Cases	Proportion	More Saved Per Case
Depository’s Advantageous	14	87.5%	3.7
NoDepot’s Advantageous	2	12.5%	2

).

Compared with DepotSt, a combined depository scenario shows advantages over NoDepot in three more emergency cases, which attributes to the contribution of the additional twenty depositories near corridors.

5.2. Evacuation Time

The evacuation time has been compared only when different evacuation strategies have saved the same number of evacuees. It is always preferable to save more people even with increased average evacuation time. Therefore, the evacuation time has been considered as a supplementary factor of success rate to evaluate the advantages of different evacuation strategies. Simulation results indicate that deploying depositories has generally accelerated the evacuation process in many simulated emergency cases.

For the 87 events (i.e., 87% of the 100 events) where DepotSt saved the same number of evacuees as NoDepot, the total steps for each event show differences in 28 events. In 27 events (i.e., 96.4% of the 28 events showing differences in the evacuation time), DepotSt reduced the total steps of all successful evacuees by 70 steps. Only in one event (i.e., 3.6% of the 28 events showing differences in the evacuation time), DepotSt used one step more than NoDepot (

Table 4. The advantages of DepotSt and NoDepot in terms of evacuation time when the numbers of the successful evacuees for DepotSt and NoDepot are the same.

	Number of Cases	Proportion	Fewer Steps Per Case
DepotSt’s Advantageous	27	96.4%	70
NoDepot’s Advantageous	1	3.6%	1

).

For the 97 events (i.e., 97% of the 100 events) where DepotCr saved the same number of evacuees as NoDepot, the total steps for each event show differences in ten events (i.e., 10% of the 100 events). Compared with NoDepot, DepotCr allowed evacuees to consume less time in all the ten events and has decreased the total steps by 15 steps on average for each of the ten events (

Table 5. The advantages of DepoCr and NoDepot in terms of evacuation time when the numbers of the successful evacuees for DepotCr and NoDepot are the same.

	Number of Cases	Proportion	Fewer Steps Per Case
DepotCr’s Advantageous	10	100%	15
NoDepot’s Advantageous	0	0%	0

).

5.3. Situation Awareness

5.3.1. NoDepot vs. DepotSt

Situation awareness of an evacuee is measured by the number of edges that have been updated in knowledge during the evacuation. Figure 10 compares the average updated edges for each evacuee. The line is the boundary where the figure for DepotSt and NoDepot are identical. In all the 100 events, DepotSt allowed evacuees to update more of their knowledge. Compared with NoDepot, DepotSt leads to an increase of 15% on average of the edge updates (15.4 more edges updated per person for each event) (

Table 6. The advantages of DepotSt and NoDepot in terms of situation awareness when the numbers of the updated edges for DepotSt and NoDepot differ.

	Number of Cases	Proportion	More Updated Edges Per Case
DepotSt’s Advantageous	100	100%	15.4
NoDepot’s Advantageous	0	0%	0

).

5.3.2. NoDepot vs. DepotCr

Figure 11 shows that in no event people with DepotCr were less aware of changes in the environment. In most of the events (77% of the 100 emergency events as in

Table 7. The advantages of DepotCr and NoDepot in terms of situation awareness when the numbers of the updated edges for DepotCr and NoDepot differ.

	Number of Cases	Proportion	More Updated Edges Per Case
DepotCr’s Advantageous	77	100%	4.3
NoDepot’s Advantageous	0	0%	0

), people with DepotCr had more updates of their awareness than with NoDepot. On average, DepotCr allowed evacuees to be more updated by 3.3% (3.3 more edges per person on average for each of the 100 emergency events).

5.4. Staircase vs. Corridor

Figure 12 compares static depositories deployed at staircases and static depositories deployed in corridors. For strategies with depositories, in eleven events (i.e., 11% of the 100 events) DepotSt saved more people than DepotCr (4.4 people per event on average). In five events (i.e., 5% of the 100 events), DepotCr saved more people (1.6 people per event on average) (

Table 8. The advantages of DepotSt and DepotCr in terms of success rate when the numbers of the successful evacuees for DepotSt and DepotCr differ.

	Number of Cases	Proportion	More Saved Per Case
DepotSt’s Advantageous	11	68.8%	4.4
DepotCr’s Advantageous	5	31.2%	1.6

). A Wilcoxon signed ranks test shows that the differences between the successful evacuees of DepotSt and DepotCr are statistically significant with a confidence interval of 95% (p = 0.0352).

Generally, deploying depositories at staircases has allowed people to be more situational aware than deploying the sensors in corridors (Figure 13). Specifically, DepotSt demonstrated advantages over DepotCr in 98% of the 100 events (by 12.4 edges per person). Only in 2% of the 100 events, DepotCr was better than DepotSt, allowing on average 1.5 more edges to be updated (

Table 9. The advantages of DepotSt and DepotCr in terms of situation awareness when the numbers of the updated edges for DepotSt and DepotCr differ.

	Number of Cases	Proportion	More Updated Edges Per Case
DepotSt’s Advantageous	98	98%	12.4
DepotCr’s Advantageous	2	2%	1.5

). Overall, deploying depositories at staircases allowed evacuees to be more updated about the environment by 11.7% (12.1 edges per person per event). To find out whether the differences between the average edge updates for DepotSt and DepotCr are significant, a Wilcoxon signed ranks test has been applied. Test results reject with a confidence interval of 95% (p = $3.6782\times {10}^{-5}$) the null hypothesis that DepotSt and DepotCr are not significantly different in their average number of updated edges.

5.5. Information Depositories vs. Fading Memory

Information depositories improve evacuation by enhancing the knowledge exchange and thus allow for more current awareness. The current awareness, however, has been acquired based on visiting certain parts of the environment by some agent. This means, any agent’s situation awareness has some age, compared to a continuously changing environment. In order to introduce the information age into decision making, a ‘fading memory’ model has been proposed [2]: It improves evacuation success by relying more on more recent information.

To find out whether information depositories improve evacuation in a more robust way than the fading memory, additional simulations have been run implementing the fading memory model and applying the same 100 emergency events.

Figure 14 shows the number of successful evacuees for NoDepot and the fading memory strategy. The line separates the pairs of comparison for each emergency event. On the left side of the line, fading memory saved more people than NoDepot. On the right side of the line, fading memory saved fewer people than NoDepot.

Generally, both the fading memory strategy and DepotSt saved more people than NoDepot. Fading memory outperformed DepotSt in both the quantity and the magnitude of evacuation success. Specifically, in 29 events (i.e., 29% of the total 100 events) fading memory has saved more people (6.1 more persons on average per event), which is more than twice the number of events when DepotSt saved more evacuees than NoDepot (Section 5.1). However, fading memory also saved fewer people than NoDepot (3 persons on average per event) in more cases (6 events). Thus in this simulation, fading memory is less predictable than DepotSt (

Table 10. The advantages of NoDepot and fading memory in terms of success rate when the numbers of the successful evacuees for NoDepot and fading memory differ.

	Number of Cases	Proportion	More Saved Per Case
FadingMemory’s Advantageous	29	82.9%	6.1
NoDepot’s Advantageous	6	17.1%	3

).

Figure 15 compares evacuations with DepotSt and using fading memory. In 29 events (i.e., 29% of the total 100 events), fading memory saved more people than DepotSt (5.1 persons per event on average). In twelve events (i.e., 12% of the total 100 events), DepotSt saved more people than fading memory (2.8 persons per event on average) (

Table 11. The advantages of DepotSt and fading memory in terms of success rate when the numbers of the successful evacuees for DepotSt and fading memory differ.

	Number of Cases	Proportion	More Saved Per Case
FadingMemory’s Advantageous	29	70.7%	5.1
DepotSt’s Advantageous	12	29.3%	2.8

). A two-tailed Wilcoxon signed-rank test shows that the differences between the number of successful evacuees for DepotSt and fading memory strategies are statistically significant (p = 0.0011).

6. Discussion

Table 12. Comparisons among different evacuation strategies in three dimensions: success rate, evacuation time, and situation awareness. Each figure represents the number of simulated emergency cases where the evacuation strategy is advantageous over the evacuation strategy in the comparison base because of saving more evacuees (the number of the more evacuees saved per case in parentheses), or because it has saved the same number of evacuees but has consumed less time (the number of the fewer steps used per case in parentheses), or because it has allowed more edge updates (the number of the more updated edges per case in parentheses). The total number of simulated emergency cases is one hundred.

Evaluation Factor	Comparison Base	NoDepot	DepotSt	DepotCr	FadingMemory
Success Rate	NoDepot	–	11 (4.4)	3 (1.3)	29 (6.1)
	DepotSt	2 (2.0)	–	5 (1.6)	29 (5.1)
	DepotCr	0 (0.0)	11 (4.4)	–	29 (6.0)
	FadingMemory	6 (3.0)	12 (2.8)	6 (3.2)	–
Evacuation Time	NoDepot	–	27 (70.5)	10 (14.6)	16 (120.4)
	DepotSt	1 (1.0)	–	5 (25.6)	12 (68.4)
	DepotCr	0 (0.0)	24 (75.0)	–	16 (117.4)
	FadingMemory	5 (24.2)	13 (72.0)	9 (14.3)	–
Situation Awareness	NoDepot	–	100 (15.4)	77 (4.3)	33 (5.5)
	DepotSt	0 (0.0)	–	2 (1.5)	4 (8.0)
	DepotCr	0 (0.0)	98 (12.4)	–	9 (11.0)
	FadingMemory	20 (3.1)	96 (15.1)	60 (5.1)	–

shows a summary of the comparisons among different evacuation strategies in three dimensions: success rate, evacuation time, and situation awareness. For the success rate, the figures show the numbers of simulated emergency cases where one evacuation strategy has saved more evacuees than another evacuation strategy, and the figures in parentheses represent the numbers of the more evacuees saved per case. For the evacuation time, the figures are the numbers of simulated emergency cases where one evacuation strategy used less evacuation time than another evacuation strategy, and the figures in parentheses represent the numbers of the fewer steps used per case. For situation awareness, the figures are the numbers of simulated emergency cases where one evacuation strategy has more edge updates than another evacuation strategy, and the figures in parentheses represent the numbers of the more edges updated per case. The evacuation times were computed based on the cases when two evacuation strategies have saved the same number of evacuees but have consumed different evacuation times.

Table 13. The average success rate and the average edge updates calculated from the total 100 simulated emergency cases. Statistical significant differences (Wilcoxon p < 0.05) are indicated with (*), and standard deviations are labeled in parentheses.

	NoDepot	DepotSt	DepotCr	FadingMemory
Average Success Rate	82.1 (9.3)	82.5 * (9.0)	82.1 (9.3)	83.7 * (8.6)
Average Edge Updates	100.3 (18.0)	115.7 * (28.2)	103.6 * (19.4)	101.5 (17.5)

shows the average success rates and the average edge updates calculated from the total 100 simulated emergency cases. To find out whether the differences of success rates and edge updates between NoDepot and other evacuation strategies are statistically significant, the Wilcoxon signed-rank test has been applied.

Table 13 shows that the edge updates of DepotSt and DepotCr were significantly different from the edge updates of NoDepot, which means that integrating information depositories has made a significant difference in situation awareness. Table 12 shows that, in all the one hundred simulated emergency events, DepotSt has more edge updates than NoDepot, and DepotCr has improved edge updates in 77% of the simulated emergency events. In no cases, DepotSt or DepotCr has fewer edge updates than NoDepot. It is safe to conclude that integrating information depositories has improved the situation awareness in terms of the edge updates.

The Wilcoxon signed-rank test also shows that a significant difference between the success rate of DepotSt and NoDepot was observed. Table 12 shows that deploying information depositories at staircases has guaranteed to save no fewer evacuees in 98% of the simulated emergency events, and to consume no more evacuation time in 99% of the simulated emergency events. It has improved the evacuation results in 38% of the simulated emergency events, either by saving more evacuees (11 simulated emergency cases), or by reducing the evacuation time (27 simulated emergency cases).

Noticeably, although DepotSt has more edge updates in all the simulated emergency events than NoDepot, there are still two cases where DepotSt has saved fewer evacuees and one case where DepotSt has increased the evacuation time. This can be explained by the complexity of the evacuation problem per se. Evacuation dynamics is very complex, where multiple factors are involved and interact non-linearly to produce an output shown as features such as the success rate and evacuation time [15]. In some cases, even if the situation awareness has been more current due to the new strategy, such improvements may not always trigger an increased number of successful evacuees or decreased evacuation steps. In very few cases, such improvements of situation awareness may still accidentally lead to decreased evacuation success due to the effect of non-linear interactions between different evacuees, and the interactions between evacuees and the dynamically changing environment. This also explains why there are more cases where integrating information depositories has increased edge updates and decreased evacuation steps, but less so many cases where integrating information depositories has saved more people.

Compared with the significant improvements by deploying information depositories at staircases, depositories in corridors have made less significant improvements. The comparison of the Wilcoxon signed-rank tests for DepotSt and DepotCr also indicates that the information depositories should be strategically distributed. Simulation results suggest information depositories at staircases lead to better evacuation outcome than information depositories in corridors. Compared with corridors where evacuees’ route choices are largely restricted, staircases may allow evacuees to have more alternatives towards the exits and more likely to make decisions that have a significant impact on the evacuation outcome. A combined depository scenario of DepotSt and DepotCr shares the advantages and disadvantages on both sides. Comparison of evacuation success between a combined depository scenario and DepotSt suggests that increased number of depositories leads to more evacuation success.

The fading memory, as another approach to bridging the temporal gap of knowledge exchange in decentralized evacuations, has also improved the evacuation success significantly. Compared with DepotSt, fading memory has improved the evacuation success in a larger number of cases (29 cases), and has a larger average success rate (83.7). At the same time, in more cases (6 cases), it has saved fewer evacuees than DepotSt (2 cases), which fundamentally attributes to the mechanism of fading memory model per se: Fading memory devalues older knowledge because of losing trust in its continuing validity, which involves risks of devaluing knowledge that is still valid. In such life-critical situations as evacuations, the uncertainty of leading to fewer people saved should be minimized at strategic level. An evacuation strategy that almost guarantees saving no fewer people is much reliable than a strategy that involves large uncertainty. In this sense, deploying information depositories is more robust than fading memory method in terms of improving the evacuation performance.

DepotSt has also outperformed fading memory in the number of updated edges. In 96% of the cases, DepotSt has more edge updates than the fading memory, while only in four cases does fading memory have more edge updates. Compared with fading memory, DepotSt has added information depositories and allows asynchronous communication for awareness sharing in decentralized evacuations. More situation awareness contributes to better prediction, which is essential for fading memory method. So it can be anticipated that a hybrid model that integrates information depositories and fading memory can benefit from the advantages of both sides.

In summary, information depositories generally improve evacuation performance on all measures:

• In terms of the number of successful evacuees, information depositories guaranteed almost always no less successful evacuees than NoDepot. In a portion of events, information depositories saved significantly more people.
• In terms of the time consumed by the evacuees, information depositories allow evacuees to almost always use no more steps than NoDepot. In a number of events, information depositories allow evacuees to complete evacuation within fewer steps.
• In terms of the update of knowledge, simulation results indicate that information depositories guaranteed that no fewer edges were updated during evacuations, especially when the information depositories were deployed at staircases, where the number of updated edges has increased by 15.3% on average.
• In terms of the location of depositories, deploying information depositories at staircases can improve evacuation more than deploying sensors in corridors.

7. Conclusions

The paper develops a concept of information depositories for decentralized evacuation. The information depositories bridge the temporal gap of asynchronous communication for awareness sharing in decentralized evacuations. Depositories collect the environmental and risk information from passing by agents, maintain this information by fusion, and convey the fused information to passing-by evacuees. Simulations verify that information depositories enhance the spatial awareness of the environment and risk awareness by tracking states and updating information, thus raising the chance that people survive and or can reduce their evacuation time. This paper also suggests that the information depositories should be deployed at strategic locations such as staircases. A comparison of the alternative approaches of fading memory and information depositories shows that information depositories are more reliable than the fading memory when improving the evacuation outcome. However, fading memory also has advantages that can be combined by information depositories. Overall, simulation results support the hypothesis that even a small number of information depositories will enhance risk awareness of evacuees and improve the evacuation results.

Without explicitly tested, it is anticipated that there will be an upper bound of the density of information depositories. Beyond that bound, no significant improvements will occur by increasing further the number of information depositories. Deploying information depositories at strategic locations such as staircases are advantageous possibly because staircases are “bottlenecks”, or, generally, have a high centrality in the evacuation graph, which can be investigated in the future. Future work may also explore whether information depositories work equally well in decentralized evacuation for events with substantially different behavior, such as earthquakes or a roaming sniper, and whether deploying depositories near staircases or in corridors are better options for these kinds of disasters. Since depositories improve situation awareness, and more situation awareness may contribute to better prediction, it is expected a hybrid model combining information depositories and fading memory will significantly improve the evacuation performance.