Hall Effect Sensors Design, Integration and Behavior Analysis

Abstract

The present paper focuses on various aspects regarding Hall Effect sensors’ design, integration, and behavior analysis. In order to assess their performance, different Hall Effect geometries were tested for Hall voltage, sensitivity, offset, and temperature drift. The residual offset was measured both with an automated measurement setup and by manual switching of the individual phases. To predict Hall sensors performance prior to integration, three-dimensional physical simulations were performed.

1. Introduction

Hall Effect sensors are widely used in industrial applications for a series of low power applications, including current-sensing, position detection, and contactless switching. Such magnetic sensors, integrated in regular CMOS technology, prove to be cost-effective and offer high performance [1]. In order to guarantee Hall Effect sensors optimal behavior, high sensitivity, low offset, and low temperature drift are performance aspects that need to be achieved. Previous papers by the authors investigated the temperature effects on both sensitivity and offset [2,3]. The present paper is highly focused on Hall Effect sensors design, integration, and performance investigation. To achieve good results while still preserving the integration process, the sensors geometrical configuration is to be exploited [4,5]. As the extensive measurements performed and presented by the authors [6] prove, there is offset variance with geometry. The project specifications, a few times better than the actual state-of-the-art in terms of offset and its drift, have been reached and various good candidates have been revealed. The present paper is structured as follows. The second section is intended to offer an overview on Hall Effect sensors basic considerations and the most important equations governing their behavior. Within this section, arguments for sensors geometry selection and design details are presented. Extensive measurements results concerning the sensors sensitivity, offset, and its temperature drift are incorporated in the third part of the present paper. The fourth section is devoted to presenting three-dimensional physical simulations used to predict the sensors’ behavior. The results and discussion are part of the fifth section of this work. Finally, the conclusions are drawn.

2. Hall Effect Sensors Design and Integration

2.1 Hall Effect Sensors Basic Considerations

Figure 1 presents the classical Greek-cross shape of a Hall Effect sensor. We can observe the symmetrical and orthogonal character of the shape. The figure also depicts the biasing and sensing contacts. If a current is applied between two contacts (let us say b and d) and the probe is placed under a magnetic field, the carriers will be deviated by the Lorentz force and a voltage drop which is called the Hall voltage will appear between the other two opposite contacts (a and c).

Figure 1. Classical Greek-cross Hall Effect sensor representation.

Figure 1. Classical Greek-cross Hall Effect sensor representation.

In Hall Effect sensors performance assessment, the Hall voltage and sensitivity are important parameters. By consequence, the Hall voltage is defined by the relation:

(1)

where G is the geometrical correction factor, r_H is the scattering factor of Silicon, (usually 1.15), n is the carrier density, t is the thickness of the active region, I_bias is the biasing current, and B is the magnetic field induction, [7].

For a cross-like Hall cell, the geometrical correction factor G is defined as follows:

(2)

where L and W are the sensor’s length and width respectively, according to Figure 1, and θ_H is the Hall angle [8].

The above equation has an accuracy better that 0.5% if , where is the length of the arms.

The absolute, current-related, and voltage-related sensitivities of a Hall sensor are given by the following relations:

(3)

From Equations (1) and (3) we can see that the Hall voltage and absolute sensitivity are inversely proportional to the n-well doping concentration. Therefore, in order to achieve high sensitivities, a lightly doped n-well is normally used in the fabrication process of these magnetic sensors.

2.2. Hall Effect Sensors Geometry Selection and Design Guidelines

Nine different Hall shapes have been designed and integrated in a CMOS 0.35 μm technology in two different runs. The basic cell is a classical Greek-cross shape. It is primarily integrated as a reference shape, but it might suffer from a difference in the piezoresistance due to the orientation of the axes. The L and XL Hall cells are scaled versions of the basic cell. For these cells, the selection criterion relies on the fact that any errors on the contour will be less due to an averaging on a bigger size. The 45° cell is actually the basic cell turned 45° in order to cancel out the effect of the piezoresistance effect with respect to the Si crystallographic axes. Further on, the borderless cell is a square structure that has small contacts located further away from the p-n junction. This particular geometry might minimize the influence of any errors that could appear on the borders. In this case, the sensitivity is affected as well due to the decrease of the effective active region by the position of the contacts. The low doped Hall cells have a more lightly doped n-well, so there is an increase of the sensitivity, according to Equation (3). The optimum cell is a combination of increased square dimensions with contacts situated halfway between the n-well center and borders respectively.

In order to achieve maximum sensitivity, a geometrical correction factor G maximization was performed for rectangular Hall structures with small sensing contacts s. The analysis was initiated by the authors and presented in a recent paper [9]. G was maximized when design specifications act as constraints, such as imposed sensing contacts length s and area A = LW. Further on, in order to guarantee maximum sensitivity, a guiding procedure for selecting the Hall cells dimensions L and W respectively is represented in a flow-like sequence diagram in Figure 2. In this particular case, an approximation of the G is used which is valid for relatively long Hall plates, with L/W > 1.5, small sensing contacts s/W < 0.18 and small Hall angles [7].

Figure 2. Guiding procedure for L and W selection for rectangular Hall Effect structures with small sensing contacts.

Figure 2. Guiding procedure for L and W selection for rectangular Hall Effect structures with small sensing contacts.

Figure 3 presents the choice of the length-to-width ratio plotted versus the area for different small sensing contacts length s. This analysis can guide the designer in selecting the best Hall cells’ dimensions for getting maximum sensitivity, in the case of area A and sensing contacts length constraints.

Figure 3. Variation of L/W with respect to the area A, for different small sensing contact sizes, s.

Figure 3. Variation of L/W with respect to the area A, for different small sensing contact sizes, s.

3. Experimental Section

3.1. Hall Effect Sensor Measurements

In order to accurately test the Hall Effect sensors, an automated measurements setup has been built [6]. Previous papers in the literature were devoted to Hall sensors current measurements [10].

The nine integrated Hall cells are presented in Table 1. Part 1 of the table refers to the cross-like Hall cells, while Part 2 focuses on the square Hall cells. The table summarizes both geometrical design parameters and measurements results for the input resistance at room temperature R₀, absolute sensitivity S_A, offset drift, etc. The design parameters include L, W, and s, which stand for sensors length, width, and sensing contacts length respectively.

The information for the offset refers to the four-phases residual offset and it is an average on eleven tested samples. For offset drift measurements, a TEMPTRONICS temperature control system was used and the temperature was cycled from 0 to 90 °C.

From the measurements results, we can see that there is offset and sensitivity variance with geometry. The XL cell proved to have the best performance in terms of offset drift. There is a decrease of the borderless sensitivity compared to the other cells due to the position of contacts with respect to the borders.

Table 1. Integrated Hall Effect devices characterization.

Geometry Type	Basic	Low-doped	L	XL	45 Deg	Narrow Contacts	Borderless	Square	Optimum
Shape
R0 (kΩ) @ T=300 K, B=0 T	2.3	5.6	2.2	2.2	2.1	2.5	1.3	4.9	1.5
SA (V/T) @ Ibias = 1 mA	0.0807	0.3392	0.0804	0.0806	0.0807	0.0822	0.0325	0.0884	0.0635
Offset drift (μT/°C) (4-phases current spinning)	0.409	0.067	0.264	0.039	0.373	0.344	0.526	0.082	0.328
L, W (μm) of the Active Area (n-well)	L = 21.6	L = 21.6	L = 32.4	L = 43.2	L = 21.6	L = 21.6	L = 50	L = 20	L = 50
	W = 9.5	W = 9.5	W = 14.25	W = 19	W = 9.5	W = 9.5	W = 50	W = 20	W = 50
L/W	2.27	2.27	2.27	2.27	2.27	2.27	1	1	1
s (μm) for Sensing Contacts	8.8	8.8	13.55	18.3	8.8	1.5	2.3	2.3	4.7

Table 1. Integrated Hall Effect devices characterization.

Geometry Type	Basic	Low-doped	L	XL	45 Deg	Narrow Contacts	Borderless	Square	Optimum
Shape
R0 (kΩ) @ T=300 K, B=0 T	2.3	5.6	2.2	2.2	2.1	2.5	1.3	4.9	1.5
SA (V/T) @ Ibias = 1 mA	0.0807	0.3392	0.0804	0.0806	0.0807	0.0822	0.0325	0.0884	0.0635
Offset drift (μT/°C) (4-phases current spinning)	0.409	0.067	0.264	0.039	0.373	0.344	0.526	0.082	0.328
L, W (μm) of the Active Area (n-well)	L = 21.6	L = 21.6	L = 32.4	L = 43.2	L = 21.6	L = 21.6	L = 50	L = 20	L = 50
	W = 9.5	W = 9.5	W = 14.25	W = 19	W = 9.5	W = 9.5	W = 50	W = 20	W = 50
L/W	2.27	2.27	2.27	2.27	2.27	2.27	1	1	1
s (μm) for Sensing Contacts	8.8	8.8	13.55	18.3	8.8	1.5	2.3	2.3	4.7

3.2. Offset Temperature Drift Measurement Results Using a DC Measurement Setup and Manual Phase Switching

The offset is a parasitic effect that adds to the total Hall voltage. The offset was measured in the absence of magnetic field (B = 0 T), by using a zero-Gauss chamber. The offset is defined as follows:

(4)

In order to have information on the offset of each individual phase, manual phase switching was performed. Both two-phases and four-phases residual offsets were measured.

The four-phases residual offset in V is computed as follows:

(5)

where V_p1,2,3,4 are the individual phases offsets.

The magnetic-equivalent offset (measured in T) is defined by dividing the four-phases residual offset in V by the absolute sensitivity, as follows:

(6)

Figure 4. Hall cells polarization for Greek-cross cells (a), borderless cell (b) and optimum cell (c).

Figure 4. Hall cells polarization for Greek-cross cells (a), borderless cell (b) and optimum cell (c).

In Figure 4, the specifical Hall cells polarization is represented, for the Greek-cross cells, borderless and optimum cells respectively.

Further on, Table 2 presents the four phases used for Hall cells polarization, including biasing and sensing contacts.

Table 2. The corresponding polarization phases.

Phases	Ibias	VHALL
	(biasing)	(sensing)
Phase 1	a to c	b to d
Phase 2	d to b	a to c
Phase 3	c to a	d to b
Phase 4	b to d	c to a

Table 2. The corresponding polarization phases.

Phases	Ibias	VHALL
	(biasing)	(sensing)
Phase 1	a to c	b to d
Phase 2	d to b	a to c
Phase 3	c to a	d to b
Phase 4	b to d	c to a

In Figure 5, Figure 6, Figure 7, the magnetic equivalent residual offset vs. absolute temperature for four different Hall Effect sensors is depicted. Two different biasing currents were taken into account, I_bias = 0.5 mA and I_bias = 1 mA respectively. The samples were placed into an oven and the temperature was cycled between −40 and 125 °C. We can observe the parabolic temperature dependence of the residual offset.

Figure 5. Magnetic-equivalent offset vs. absolute temperature for the basic (left) and L (right) Hall cells, for I_bias = 0.5 mA.

Figure 5. Magnetic-equivalent offset vs. absolute temperature for the basic (left) and L (right) Hall cells, for I_bias = 0.5 mA.

Figure 6. Magnetic-equivalent offset vs. absolute temperature for the XL Hall cell, for I_bias = 0.5 mA (left) and I_bias = 1 mA (right).

Figure 6. Magnetic-equivalent offset vs. absolute temperature for the XL Hall cell, for I_bias = 0.5 mA (left) and I_bias = 1 mA (right).

Figure 7. Magnetic-equivalent offset vs. absolute temperature for the borderless Hall cell, for I_bias = 0.5 mA (left) and I_bias = 1 mA (right).

Figure 7. Magnetic-equivalent offset vs. absolute temperature for the borderless Hall cell, for I_bias = 0.5 mA (left) and I_bias = 1 mA (right).

3.3. Room Temperature Offset Measurement Results Using an Automated AC Measurement Setup

Using an automated measurement setup presented in detail by the authors in a recent paper [6], the proposed Hall cells have been tested and subsequently evaluated. In this sense eleven samples, each one containing 64 cells (the first eight different geometries in Table 1 times eight locations), were tested. The positioning of the eight cells as repetitions of eight is presented in Figure 8. We wanted to have the same cell several times, and at different locations on the chip in order to investigate possible offset variation due to position. Therefore, the same cell was tested eight times on the same chip.

Figure 8. Location of the eight analyzed Hall cells on a tested chip.

Figure 8. Location of the eight analyzed Hall cells on a tested chip.

Figure 9, Figure 10 present the 4-phases residual offset in T at room temperature versus the absolute sensitivity for four of the integrated Hall cells. The indications in the legend represent the specific positions of the tested cell within a chip containing 64 cells. To obtain the data in Figure 9, Figure 10, the biasing current was ramped, and the residual offset measured. It is to be mentioned that the residual offset is not a direct function of the sensitivity, but an implicit one via the biasing current. However, for more meaningfulness, we decided to display this information versus the absolute sensitivity, as it is useful to know how much residual offset corresponds to certain sensitivity.

Figure 9. Room temperature residual offset for basic (a) and 45° (b) Hall cells.

Figure 9. Room temperature residual offset for basic (a) and 45° (b) Hall cells.

Figure 10. Room temperature residual offset for XL (a) and Narrow contacts (b) Hall cells.

Figure 10. Room temperature residual offset for XL (a) and Narrow contacts (b) Hall cells.

By the green band we understand the project specifications in terms of offset at room temperature, which falls in the interval ±30 μT. We can observe that the best behavior is obtained for the XL cell.

4. Three-Dimensional Physical Simulations

Regarding Hall Effect sensors behavior analysis, a finite element lumped circuit model was recently developed by the authors in [3]. Other models, based on six-resistance approach were proposed [11].

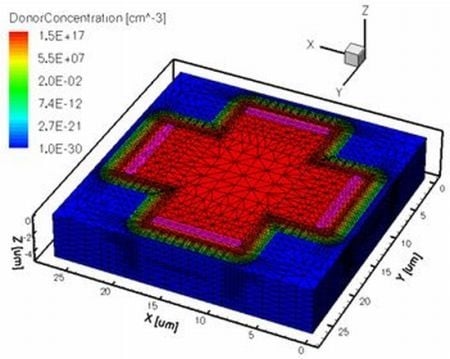
A powerful tool to predict the Hall Effect sensor’s performance is based on three-dimensional physical simulations. In a recent paper, the authors presented 3D simulations as an instrument to assess Hall sensors behavior [12]. In this work, five different cells, including basic, L, XL, borderless, and optimum, were simulated and evaluated using TCAD Sentaurus Synopsys tool [13]. In Figure 11, the three dimensional structure of the basic cell with the donor concentration profile is displayed.

Figure 11. Three-dimensional simulated structure of the basic Hall cell.

Figure 11. Three-dimensional simulated structure of the basic Hall cell.

The structure is also endowed with four electrical contacts, located at the extremities of the arms. For the p-substrate, a Boron concentration of 10¹⁵ cm⁻³ is used while the active n-well region is implanted with an Arsenic doping concentration of 1.5 × 10¹⁷ cm⁻³ with a Gaussian profile. The thickness of the p-substrate is 5 μm while the n-profile implantation depth is 1 μm. In this case, the average mobility is 0.0630 m²·V⁻¹·s⁻¹.

5. Results and Discussion

The three-dimensional structures for three of the five simulated Hall cells are incorporated in Figure 12, Figure 13, Figure 14, also depicting the electrostatic potential (V) distribution. A current in the range 0–1 mA was used to bias the Hall structures from a to c contacts and the Hall voltage was recorded between the opposite b and d contacts. For the cross Hall cells, the current has an orthogonal flow, while for the borderless and optimum cells, the current flow is on a diagonal path, according to Figure 4. In Table 3, the design parameters of the five simulated cells are summarized. L, W, and s stand for sensors length, width, and sensing contacts length respectively.

Figure 12. The three-dimensional representation of the simulated basic Hall cell.

Figure 12. The three-dimensional representation of the simulated basic Hall cell.

Figure 13. The three-dimensional representation of the simulated XL Hall cell.

Figure 13. The three-dimensional representation of the simulated XL Hall cell.

Figure 14. The three-dimensional representation of the simulated borderless Hall cell.

Figure 14. The three-dimensional representation of the simulated borderless Hall cell.

Table 3. Simulated Hall Effect devices geometrical parameters.

Hall Structure	L (μm)	W (μm)	s (μm)
Basic	21.6	9.5	8.8
L	32.4	14.25	13.55
XL	43.2	19	18.3
Borderless	50	50	4.7
Optimum	50	50	2.3

Table 3. Simulated Hall Effect devices geometrical parameters.

Hall Structure	L (μm)	W (μm)	s (μm)
Basic	21.6	9.5	8.8
L	32.4	14.25	13.55
XL	43.2	19	18.3
Borderless	50	50	4.7
Optimum	50	50	2.3

Figure 15. Hall voltage (V) vs. biasing current for the five simulated Hall cells.

Figure 15. Hall voltage (V) vs. biasing current for the five simulated Hall cells.

The five Hall cells were simulated for Hall voltage, by considering the influence of a magnetic field of strength B = 0.5 T. The following results were obtained as presented in Figure 15.

In Figure 16, the absolute sensitivity versus the biasing current is displayed for the five simulated Hall structures. We can observe that the cross Hall cells have the highest sensitivity, while there is a decrease in sensitivity for borderless and optimum cells, as confirmed by the measurements results presented in Table 1.

The sensitivity is directly related to the geometrical correction factor and G is in turn directly proportional to the length-to-width ratio. By consequence, it is expected for basic, L, and XL Hall cells to have approximately the same absolute sensitivity, as they are scaled up versions of a classical Greek-cross.

To explain the Hall voltage and sensitivity reduction in the square Hall cells compared to the cross structures, one has to take into consideration the geometrical correction factor G which is lower in the case of the square cells. Moreover, contacts on square structures located further away from the p-n junction considerably reduce the effective active n-well area, so they also produce a decrease in the sensitivity.

Figure 16. Absolute sensitivity (V/T) vs. biasing current for the five simulated Hall cells.

Figure 16. Absolute sensitivity (V/T) vs. biasing current for the five simulated Hall cells.

6. Conclusions

Different Hall effect sensors were integrated in a CMOS technology, and their performance, were evaluated. The measurements results corresponding to the sensitivity, residual offset, and its behavior with the temperature were presented, with a comparative analysis on different Hall cell types. To achieve the highest sensitivity, geometrical correction factor maximization was performed for long rectangular Hall structures with small sensing contacts. To model the Hall Effect sensors behavior and predict their performance, three-dimensional physical simulations were performed. This procedure can guide the designer in selecting the best integration process, adequate Hall cell shapes and dimensions.