The results of the previous section allow us to construct asymptotic confidence intervals for the population and income shares of the middle class, according to the different definitions considered. However, because we can also construct asymptotically pivotal functions, it is possible to construct bootstrap confidence intervals, and to perform bootstrap tests of specific hypotheses about these shares.
3.2. Confidence Intervals
The confidence intervals given in this section are either asymptotic, using the estimates of asymptotic variances derived in the previous section, or bootstrap intervals, of the sort usually called percentile-
t, or bootstrap-
t; see for instance
DiCiccio and Efron (
1996),
Davison and Hinkley (
1997), and
Hall (
1992) for a discussion of the relative merits of different types of bootstrap confidence interval.
A bootstrap-t interval is constructed as follows using a resampling bootstrap. For a suitable number B of bootstrap repetitions, a bootstrap sample is created by resampling from the original sample. Let the parameter of interest be denoted by , its estimate from the original sample by , and its standard error by . If the true, or population, value is , an asymptotically pivotal quantity is . A bootstrap sample yields a parameter estimate and a standard error . Then, the bootstrap counterpart of is , since is the “true” parameter value for the resampling bootstrap data-generating process (DGP).
If non-uniform weights are associated with the sample observations, then the reampling should also be non-uniform, whereby observation
i is resampled with probability
, where
is the weight associated with the observation. This amounts to generating bootstrap samples from the weighted EDF (
17). Then, each bootstrap sample is to treated as though it were a genuinely random sample, so that the weights do not appear in the estimation of the shares or in their standard errors. However, since, in some of the samples analysed here, there are no weights, and, even if they are present, they are very nearly, if not exactly, uniform, all of the empirical results are computed without use of weighting.
The distribution of
is estimated by the empirical distribution of its
B realisations. For an equal-tailed confidence interval of confidence level
, the
and
quantiles of the distribution are estimated by the order statistics
and
of the realisations of
. Let these estimated quantiles be
and
. The bootstrap-
t confidence interval is then
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8 present point estimates as well as asymptotic and bootstrap confidence intervals, at nominal confidence level of 95%, of the population and income shares, for the median-based definition of the middle class in 1971, 1981, 1991, 2001, and 2006.
Remark 2. In many cases, the asymptotic and bootstrap intervals very nearly coincide. The bootstrap intervals are a bit wider for 1971. For 2001 and 2006, however, the bootstrap population-share and income-share intervals for males extend far to the left of the asymptotic ones. For females, the pattern is different. In 2001, the asymptotic and bootstrap intervals are very close, but, in 2006, the bootstrap intervals extend far to the right of the asymptotic ones.
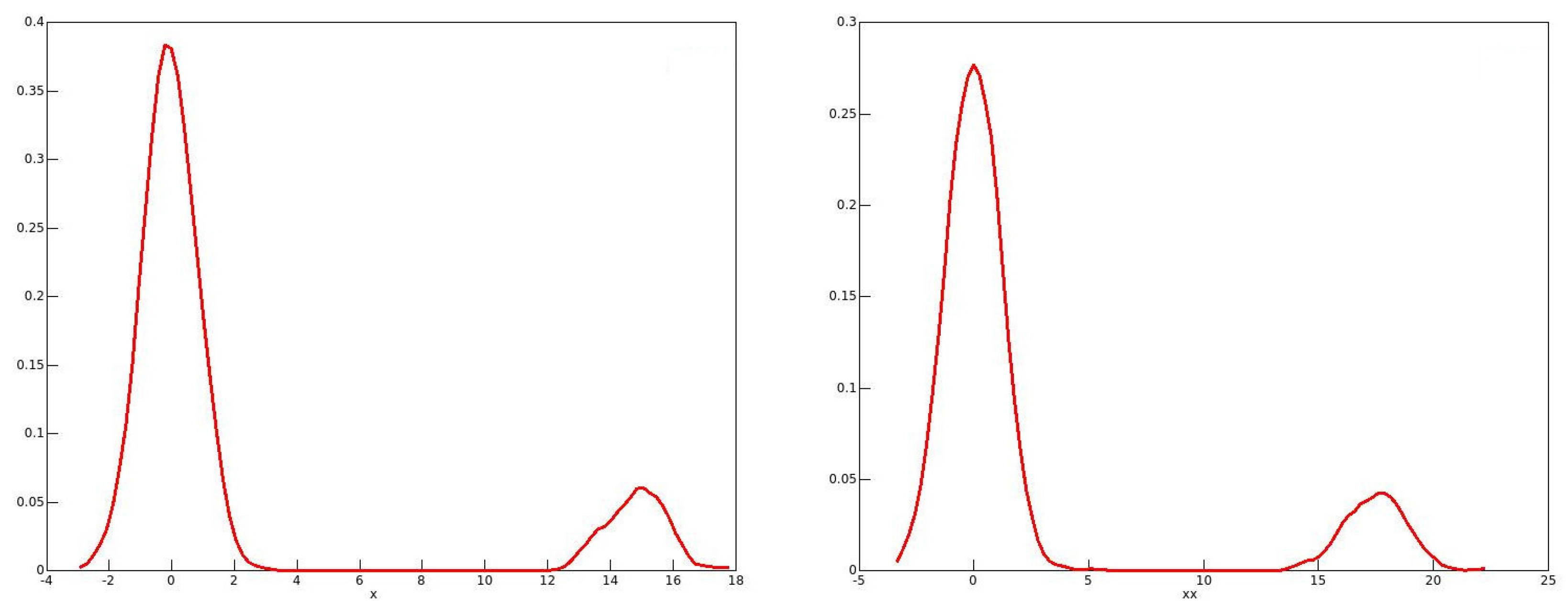
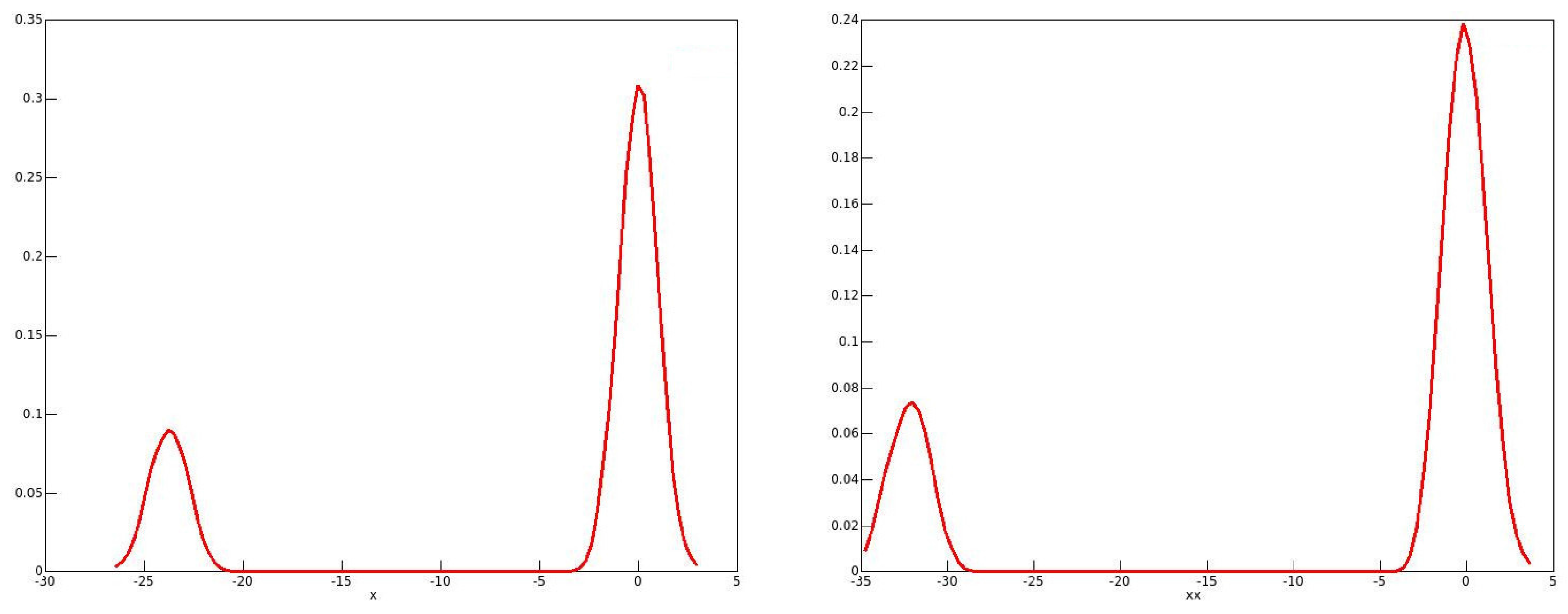
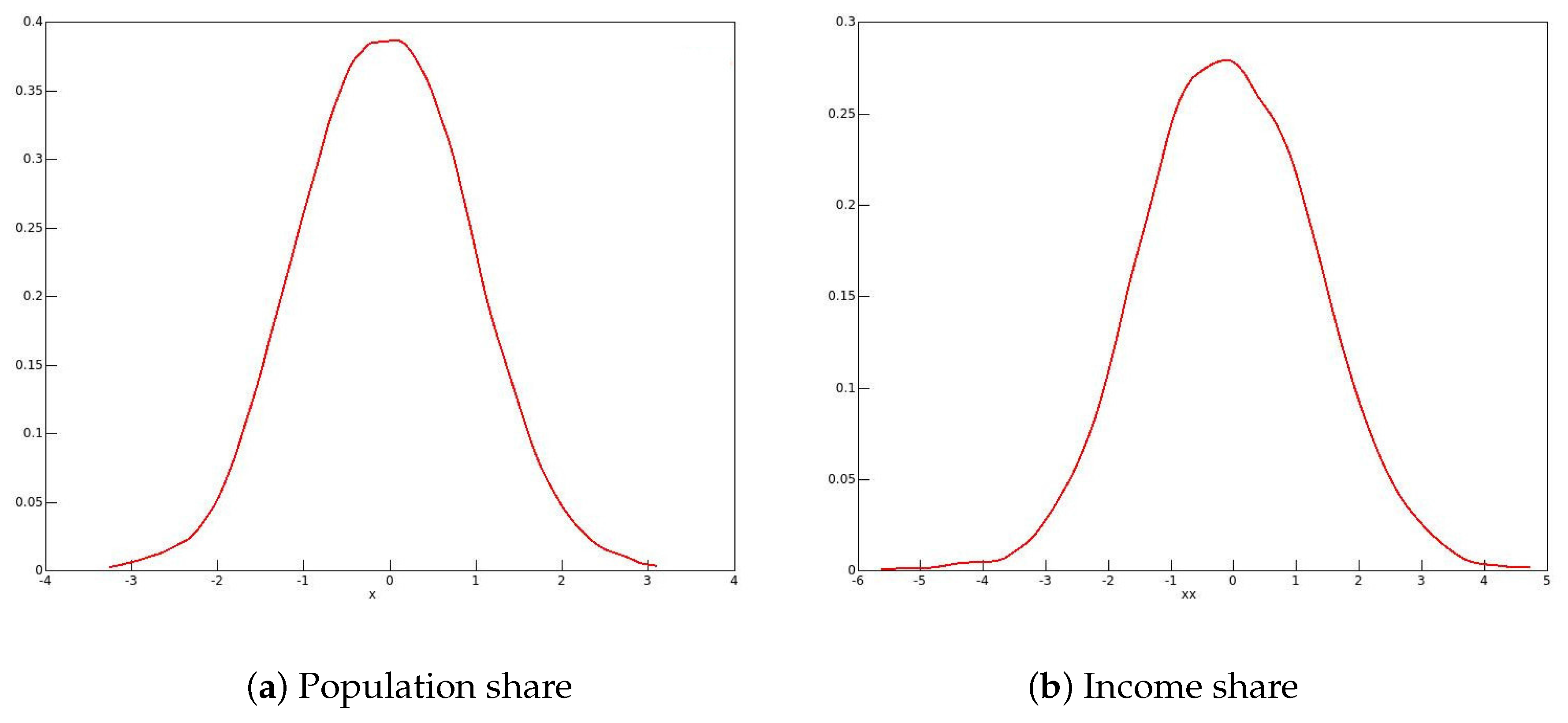
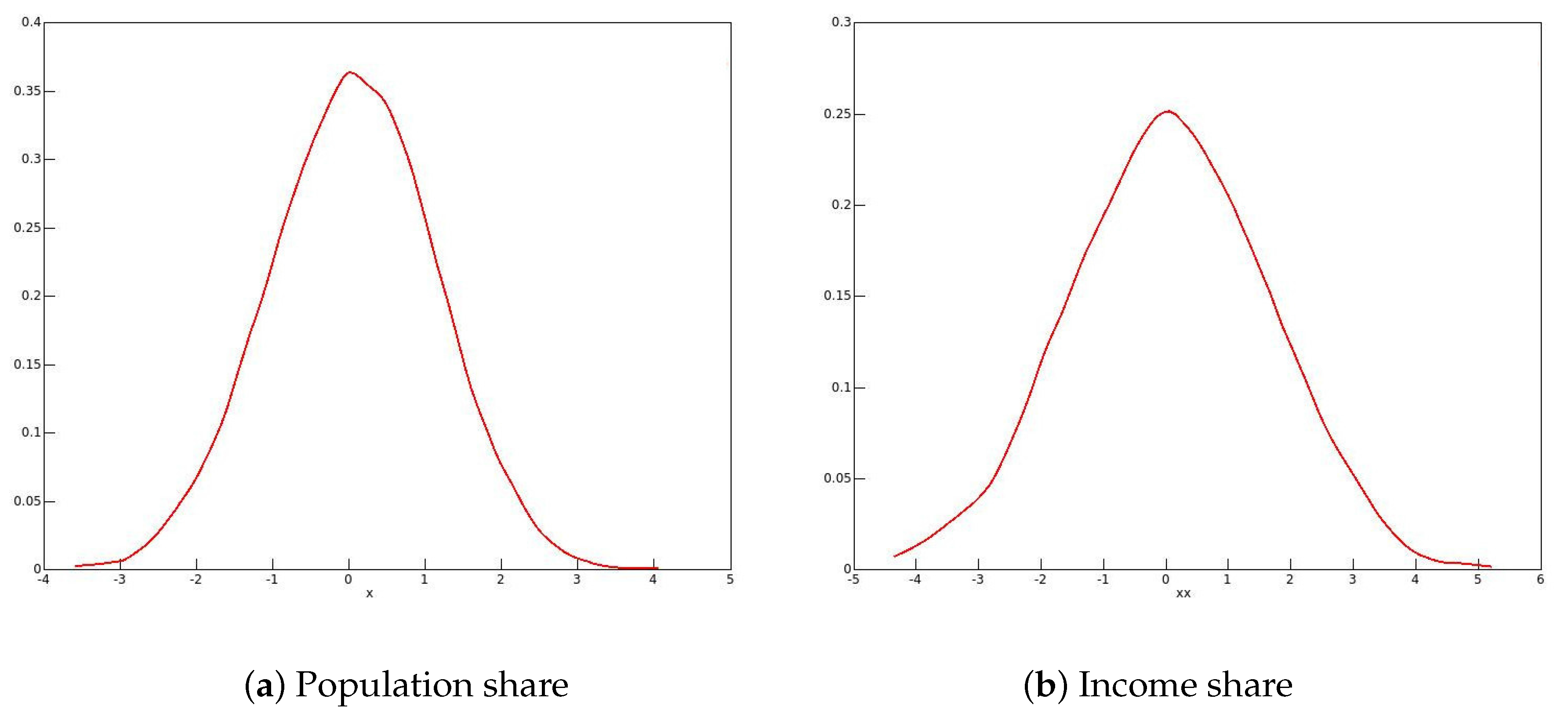
The reason for these phenomena with the 2001 and 2006 data emerges from looking at the distributions of the bootstrap statistics, of which kernel density plots in 2006 for males and for females are shown in Figure 1 and Figure 2 respectively. One might expect the plots to resemble roughly a plot of the standard normal density. This would be the case if the long right-hand tail for men, and the long left-hand tail for women, each with a second mode, are neglected. It is well known that the resampling bootstrap can give highly misleading results with heavy-tailed data; see for instance Davidson (2012). By looking at kernel density plots in Figure 3 of the sample income distributions for men and women in 2006, one can see evidence of the heavy right-hand tails for both sexes. In addition, for all of the twenty-first century data, there is clear evidence of top-coding, since, in all cases, there are several observations equal to the largest income in the sample, while the next highest income is much lower. For instance, in the 2006 male sample, out of the 238,356 observations, there are 121 equal to the highest income of $1,202,480, while the next highest income in the sample is $872,522.
However, there is no reason to think that top-coding would have any effect on the estimated population shares, since their exact values do not matter. They do, of course, for the income shares, and so these are overestimated with top-coding. It turns out that the reason for the bimodal distributions of the bootstrap statistics is quite unrelated to top-coding. A closer look at the data for 2006 shows that a phenomenon that we may call “heaping” occurs in the data. What this means is that, for each recorded income, there are multiple instances, with comparatively large gaps between the distinct recorded incomes. While there is some measure of a similar heaping in the twentieth-century data, the phenomenon is much less marked. As an example, there is only one observation in the 1971 male data equal to the maximum value.
The consequences of this heaping are most salient with the 2006 data. For men, the median income is $35,000, and there are no fewer than 3228 observations of incomes apparently exactly equal to $35,000. The upper and lower limits for middle-class incomes that have been used in this study are $52,500 and $17,500, respectively. There are no observations of incomes equal to either of these limits, and this follows inevitably from the fact that all incomes no greater than $200,000 are recorded as exact integer multiples of $1000.
The data for women present a different picture, because the limits of $12,000 and $36,000 are integer multiples of $1000, and all incomes no greater than $100,000 are recorded as integer multiples of $1000. The maximum income of $310,136 is assigned to 99 observations; the median of $24,000 to 3316 observations; the lower limit of $12,000 to 4282 observations; and the upper limit of $36,000 to 2694 observations. The second highest recorded income is $306,763.
What this has meant for the bootstrap is that, of the 999 bootstrap repetitions with the data for men, all but 146 had a median of $35,000, the others having a median of $36,000. For the latter, the limits for middle-class income were $18,000 and $54,000, and including the 2052 observations of $54,000 in the numbers of the middle class greatly increases the population and income shares in those bootstrap samples relative to the shares of the 853 samples with a median of $35,000. At the other end, increasing the limit from $17,500 to $18,000 made no difference to the numbers, since there are no observations recorded in the interior of the range of the increase.
A similar analysis can be conducted with the data for women, but the reason for the bimodal distributions of the bootstrap statistics is clear: it arises on account of the data heaping. With the 2001 data, a bimodal distribution might have been expected, but all but five out of 999 bootstrap samples had a median equal to that of the original data, and, as expected, the distribution of the bootstrap statistics is unimodal in that case.
The data for years before 2001 have a much lesser amount of heaping and have unimodal bootstrap distributions. This no doubt implies that the bootstrap results are credible, although this conclusion is not of much worth since the bootstrap and asymptotic confidence intervals are nearly coincident.
3.3. Smoothing
An obvious remedy for the heaping in the later datasets is to smooth them. The smoothed sample distribution may well be a better estimate of the population distribution than the heaped estimate, since the heaping is manifestly an artefact of the way in which the datasets were constructed. As always with smoothing, a troublesome question is the choice of bandwidth. Since the heaping occurs at integer multiples of
$1000, the bandwidth
h should be of a comparable magnitude in order to avoid an excessively discrete distribution. For
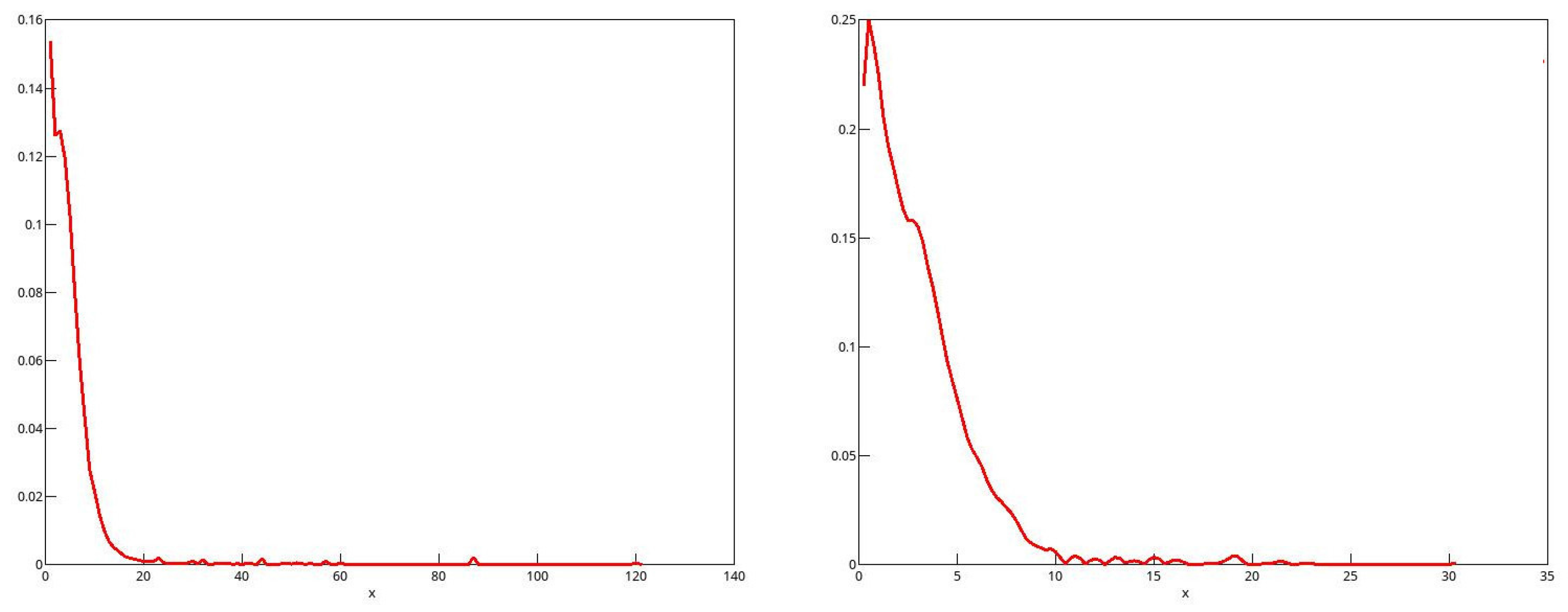
, the raw EDFs of the 2006 data for men and women are plotted in
Figure 4 along with the smoothed EDFs, for the range of incomes from half the median to 1.5 times the median. The heaped nature of the data for both sexes is quite evident in the green, unsmoothed, plots.
The (cumulative) kernel used for smoothing was the integrated Epanechnikov kernel. The smoothed estimate of the distribution is
where
h is the bandwidth, and the cumulative kernel
K is defined as
where
h is the bandwidth. Other choices of
h greater than around 500 give qualitatively similar results.
For bootstrapping, resampling from the unsmoothed EDF is replaced by resampling from the smoothed EDF. Since the heaping phenomenon is banished by the smoothing, we can expect dramatically different results, in particular, a unimodal distribution of the bootstrap statistics. The CDF (
20) describes a mixture distribution which assigns a weight of
to the each of the distributions characterised by the terms in the sum. It is easily checked that
K in (
21) is a valid CDF, with support
. The term indexed by
i in (
20) has support
.
To draw from the distribution (
21), one starts from a uniform variate
p from the U(0,1) distribution, and the draw is then
. The analytic form of
is not, I think, well known, and so I give it here for reference. It is
2Thus, to draw from distribution (
20), one may first draw the index
i from the uniform distribution on
, then draw
p from U(0,1), and get the draw
The effect is to resample from the unsmoothed distribution and then add some smoothing “noise” from the Epanechnikov distribution.
Although the smoothing preserves the mean of the distribution, it does not preserve the median, nor the population or income shares. If we accept the argument that the smoothed CDF is a better estimate of the true distribution than the unsmoothed one, then the smoothed median, and the shares in the smoothed distribution are also better estimators. In addition, the smoothed shares are the “true” values for the bootstrap DGP, and so the bootstrap statistics should test the hypothesis that they are true, not the hypothesis that the unsmoothed shares are true.
With the 2006 data for men, the new estimates of the shares are 0.421 for the population and 0.307 for income, slightly higher than the estimates from the raw data. The bootstrap confidence intervals are, for the population share, and, for the income share, . They are of roughly the same width as the asymptotic intervals.
With the data for women, the new share estimates are 0.393 and 0.298, substantially lower than the unsmoothed estimates, and the confidence interval for the population share is , and, for the income share . Unsurprisingly, the smoothed share estimates are roughly in the middle of the respective intervals.
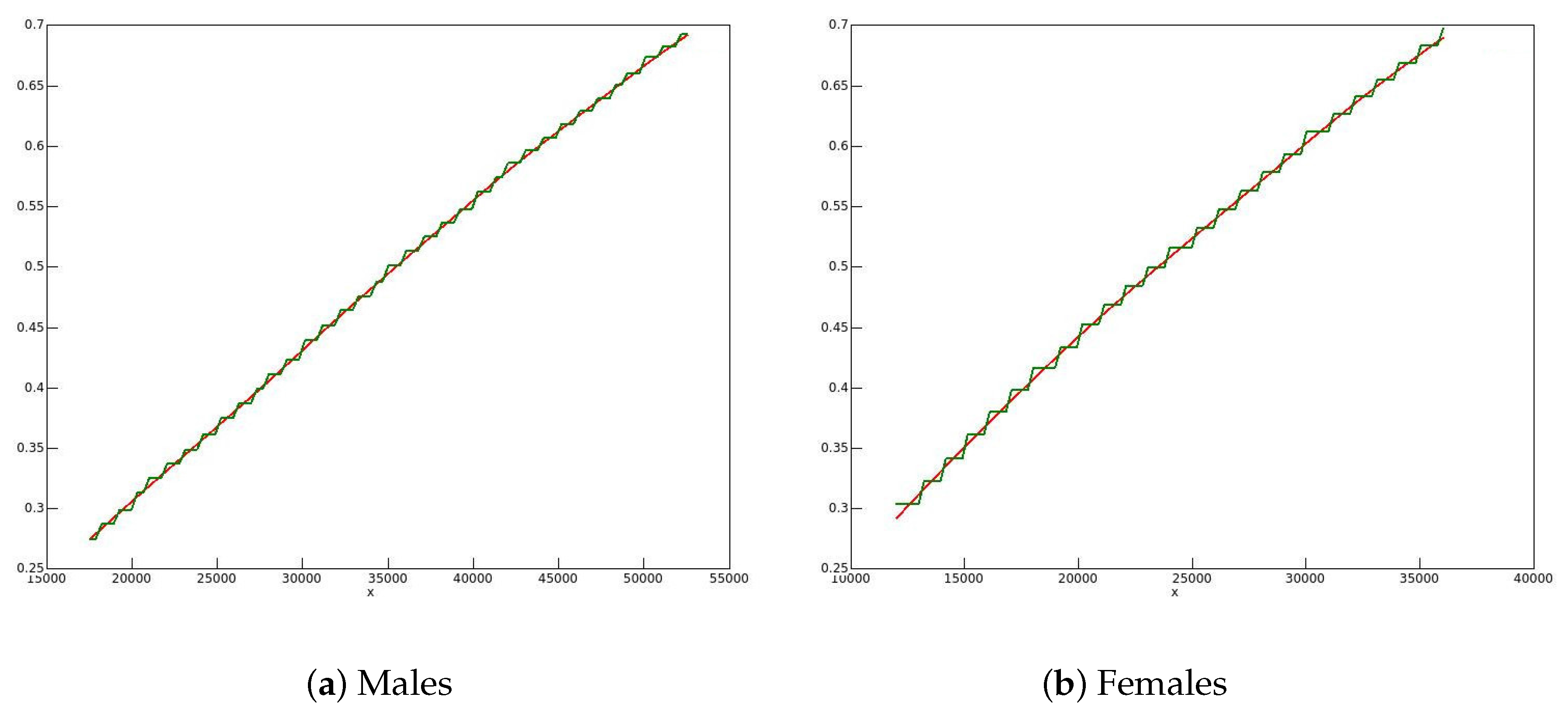
In
Figure 5 (men) and
Figure 6 (women), kernel density plots are shown for the distribution of the bootstrap statistics. There is no trace of bimodality, and so it seems that smoothing has indeed corrected the heaping problem.
3.4. Hypothesis Tests
In this section, the results of testing various hypotheses are found. All of the test statistics are asymptotic, as we have seen that when bootstrap inference differs greatly from asymptotic, the unsmoothed bootstrap, at least, is likely to be unreliable.
First are tests of hypotheses that the population and income shares for each sex did not change from one census until the next one. For instance, can one reject the hypothesis that the population share of the male middle class did not change from 1981 to 1991? Next are tests of hypotheses that the shares of men and women are the same in each census. For instance, can one reject the hypothesis that the income shares of men and women were the same in 2001?
The test results are expressed as asymptotic t statistics, rather than asymptotic p values, since in most cases the hypothesis is rejected strongly, and a p value very close to zero does not let one judge just how strong the rejection is. However, in some cases, the hypotheses are not rejected, and in some other cases, the sign of the statistic differs from the signs of the other statistics for the same sort of hypothesis.
For the first group of tests, the results of which are found in
Table 9, the sign of the statistic is positive if the decline in a share from the earlier to the later census is positive. A negative statistic indicates that the estimated share rose between the two censuses.
Remark 3. All but two hypotheses of no change between two censuses are strongly rejected. The two exceptions concern the female population share, which did not change significantly either between 1981 and 1991 or between 2001 and 2006. There are two significantly positive increases, for the female population and income shares from 1991 to 2001.
In
Table 10 are found the statistics for testing the hypothesis that the share of men and women is the same for a given census. A positive statistic means that the estimated male share is greater than the female.