Electromagnetic Simulation and Alignment of Dual-Polarized Array Antennas in Multi-Mission Phased Array Radars ^†

Abstract

Electromagnetic (EM) simulation of dual-polarized antennas is necessary for precise initial alignments, calibration and performance predictions of multi-function phased array radar systems. To achieve the required flexibility and scalability, a novel Finite-Difference Time-Domain (FDTD) solution is developed for rectangular, cylindrical and non-orthogonal coordinate systems to simulate various types of array antenna manifolds. Scalable array pattern predictions and beam generations are obtained by combining the FDTD simulation solutions with the Near-Field (NF) chamber measurements. The effectiveness and accuracy of this approach are validated by comparing different simulations and comparing simulations with measurements.

1. Introduction

Traditionally, the approximation-approach based on array factors and typical element patterns is sufficient for designing and testing many large-scale array antenna systems [1,2,3]. The recent developments on more advanced and sophisticated phased array radar systems, which can perform aerospace surveillance, weather observation and target discrimination, demand more accurate electromagnetic characterizations of the radiation patterns and interactions between antennas and electronics. As an example, precise knowledge of the three-dimensional cross-polarization radiation patterns is needed to predict and calibrate the future dual-polarized multifunction array radar [4,5,6], regardless of analog or digital array system architectures. In addition, the impacts of mutual coupling and the surface wave on optimal beam-forming [7] are important considerations in phased array antenna designing.

The challenges of this electromagnetic (EM) characterization are significant in the following aspects: (i) the immense disparity between the small-scale testbeds and larger, full-scale systems, which are necessarily characterized by both simulations and measurements: We may simulate infinite array with Periodic Boundary Conditions (PBC), but the reflection of surface currents (end currents) is absent in those computations. The end currents (edge current) and interference of the surface current wave with Floquet currents give unique characteristics to finite arrays [7]. Then, we need to investigate the surface wave impacts on array performances changing from a small-sized array to a larger array. For the measurements, although we have developed a laboratory-scale testbed and measurement procedures [8,9,10,11] for different types of manifolds, the method to extend small-scale array measurements to a large array with thousands of elements still needs more investigations and verifications; (ii) The diversity of design options being evaluated and compared, especially for cylindrical arrays [12], due to multiple and different choices in the manifold implementations: Other examples include dipole vs. radiating patch elements, faceted geometries vs. fully-conformal geometries for array antenna implementations and hybrid configurations. Electromagnetic simulations are essential in the prediction, comparison and verification of larger EM structure applications. However, the existing approaches are limited to address the challenge. Commercial solvers, such as ANSYS HFSS (In this work, HFSS is used to validate and compare the efficiency of the new algorithm and simulator. Since the new solver does not have the capability to use all of the computational power, HFSS uses one core to solve the equivalent model or structure simulated by the program developed in this work.), can solve active element in a planar array antenna very accurately and reliably through master-slave boundary conditions. However, The precise modeling of periodic boundaries is questionable when the elements are conformal to a cylindrical surface; (iii) Initial alignments of the actual system and measurements: After we have the pattern characterizations through combined simulation and measurements, the challenge is how to use this information for initial alignment of the array system, which is also more complicated for larger arrays; (iv) As most of the existing simulations are frequency-domain solutions, time-domain solutions are more desirable for a system level simulation, for example considering the trend in wider bandwidth waveforms, pulse compression technologies and electronics’ calibrations.

To address these challenges, simulation and laboratory measurement approaches are developed. An in-house and EM solver was developed, which is based on the Finite-Difference Time-Domain (FDTD) algorithm and PBC in the rectangular, cylindrical and unstructured nonorthogonal coordinate systems. Active Element Patterns (AEPs) for linear (one-by-infinite), planar (infinite-by-infinite) and cylindrical (finite-by-infinite) array systems can be simulated effectively. For validations, the array radiation patterns generated from the simulated AEPs are synthesized for the radiation patterns of the full array, which are then compared with the measured patterns of a full array in a near-field chamber. A synthesis process is also applied to obtain optimized patterns using both simulation and measurement data. The laboratory part involves measurement for AEPs of small-scale array manifolds that can fit into the near-field chamber facility. In this measurement process, the 3D radiation patterns of each element were measured while all of the other elements are properly terminated with match loads. The novel aspects of this approach lie in the application of the time-domain EM solution, the configuration of boundary conditions for different array configurations and a method to extend smaller scale array characterizations to a full-scale radar system, meanwhile achieving the right balance between accuracy and complexity.

Predicting the antenna radiation patterns for a large-scale system is still a big challenge for the radar system community. The capability to make an accurate prediction of finite array antenna patterns has an inherently significant effect on the success of designing large-scale array antennas for the future generation of air-surveillance radar. In particular, this work is related to the Multi-functional Phased Array Radar (MPAR), which is a critical R&D program by Federal Aviation Administration (FAA) and National Oceanic and Atmospheric Administration (NOAA) in the USA and will be the new multi-function radar system platform for both weather surveillance and air-traffic control.

This paper is organized as follows: Section 2 introduces the theoretical foundation of the time-domain EM solver used in this study; Section 3 describes the simulations of AEPs in a specific array configuration; Section 4 outlines measurements of the AEP using the Configurable Polarimetric Array Demonstrator (CPAD) in the near-field range; and Section 5 shows how the array radiation patterns are characterized based on AEP. In Section 6, a novel technique of extending the smaller scale array pattern characterization to a larger scale or full-size array is presented. A summary and conclusions are provided in Section 7.

2. Theory

The EM simulation for radiation pattern prediction is implemented with the FDTD updating equations [13,14,15] for calculating electric and magnetic field components in a grid space. The standard FDTD solution is based on rectangular coordinates. The FDTD updating equations for a cylindrical grid [15] can be used to simulate a fully-conformal cylindrical phased array antenna. However, the cylindrical array as part of CPAD fabricated in this work is based on column sub-arrays, which is not a fully-conformal array, but rather a faceted array. The simulation of a faceted-cylindrical array is achieved by FDTD solution in a non-orthogonal grid. The solution of an array with a larger number of columns approaches the expected EM characterization of a true cylindrical grid. The goal of EM simulation is to estimate the co-polarization and cross-polarization of active elements precisely. To achieve good approximation for AEP of the middle element of a large array (with a size larger than nine-by-nine elements), an infinite-by-infinite array is usually assumed [16]. When we apply this assumption, a periodically-arranged patch antenna is modeled as a unit cell. The FDTD model for the unit cell of a planar phased array is depicted as in Figure 1. In Figure 1, the Yee cells in the $\widehat{x}$ and $\widehat{y}$ directions in the mesh only contain the patch antenna without any air gap. By switching among appropriate boundary conditions, this array model can also be used to obtain the AEP of any elements in a semi-infinite array in the $\widehat{x}$ or $\widehat{y}$ directions.

Figure 1. Unit cell for finite-difference time-domain (FDTD) simulation for a planar array. Convolutional perfectly matched layer (CPML) and Periodic Boundary Condition (PBC) are the boundaries of the problem space. This unit cell has one patch antenna of an infinite planar array. The red color area is the metal patch and gray color area is the substrate material.

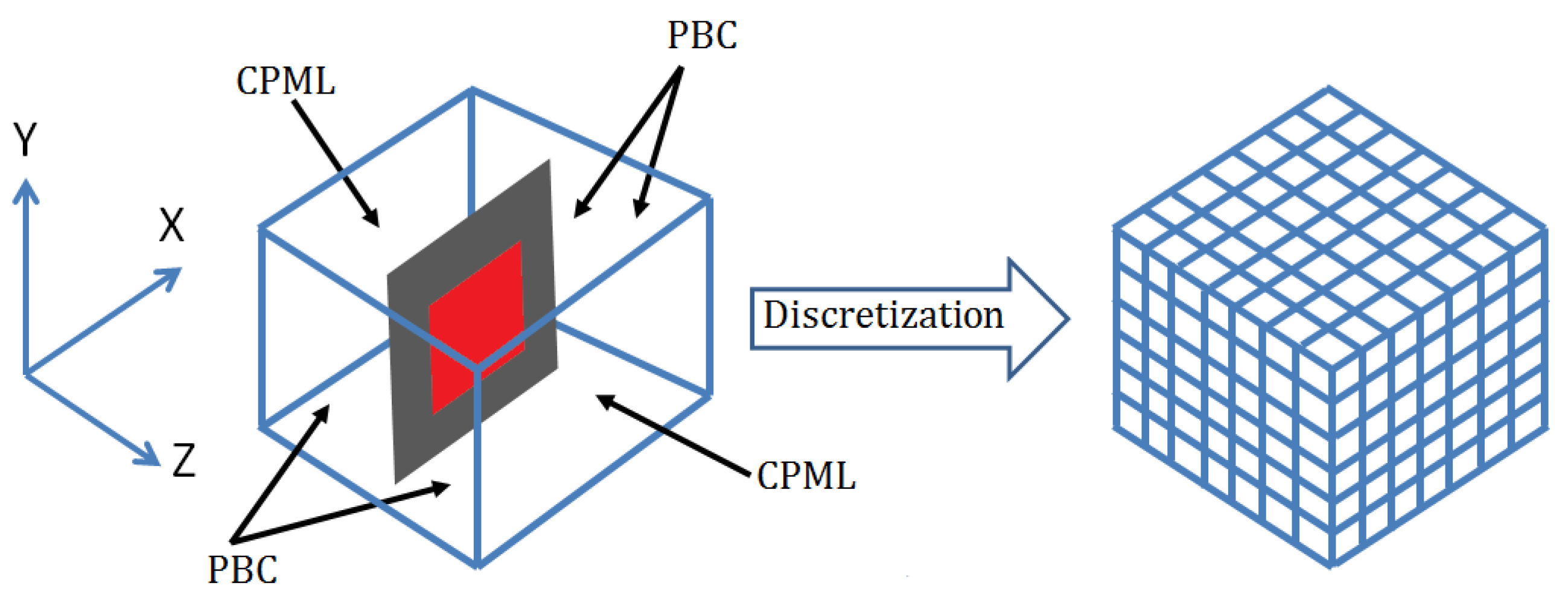
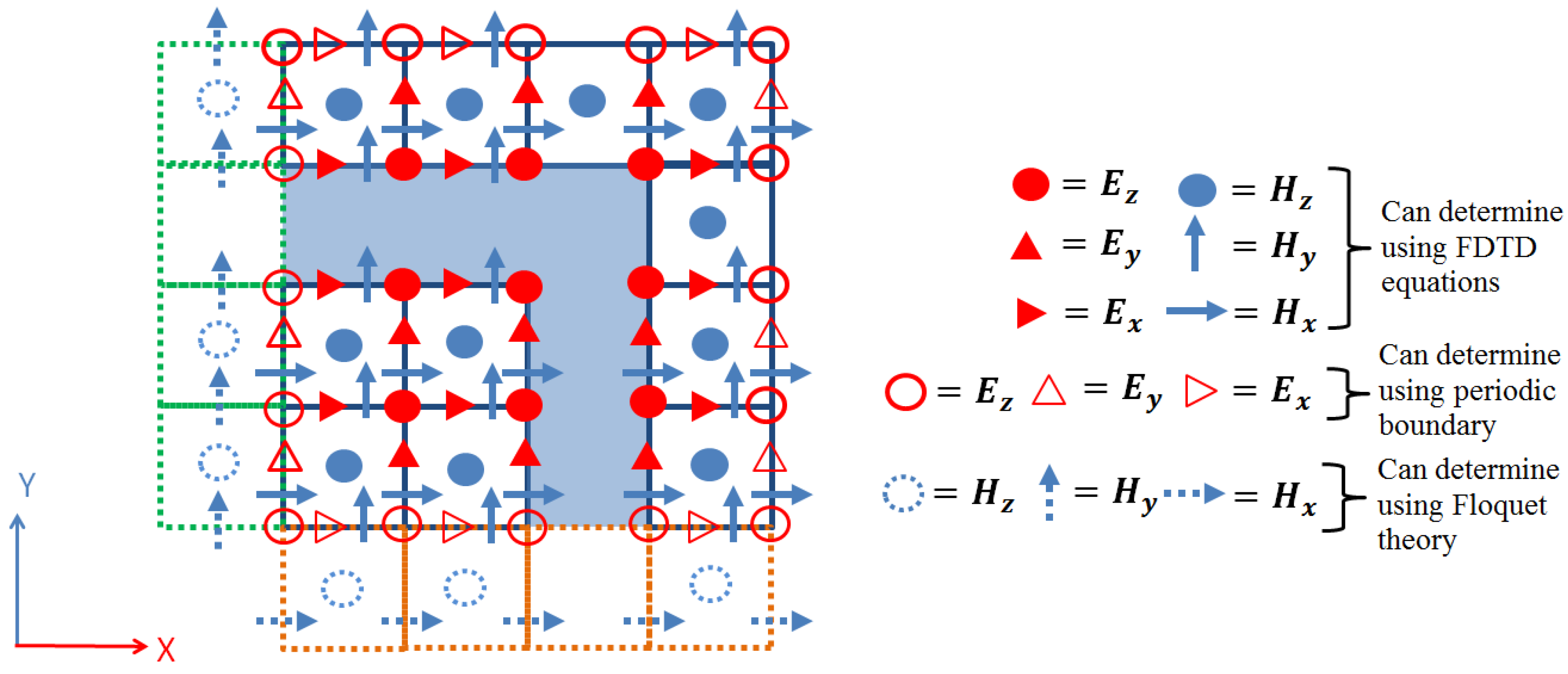
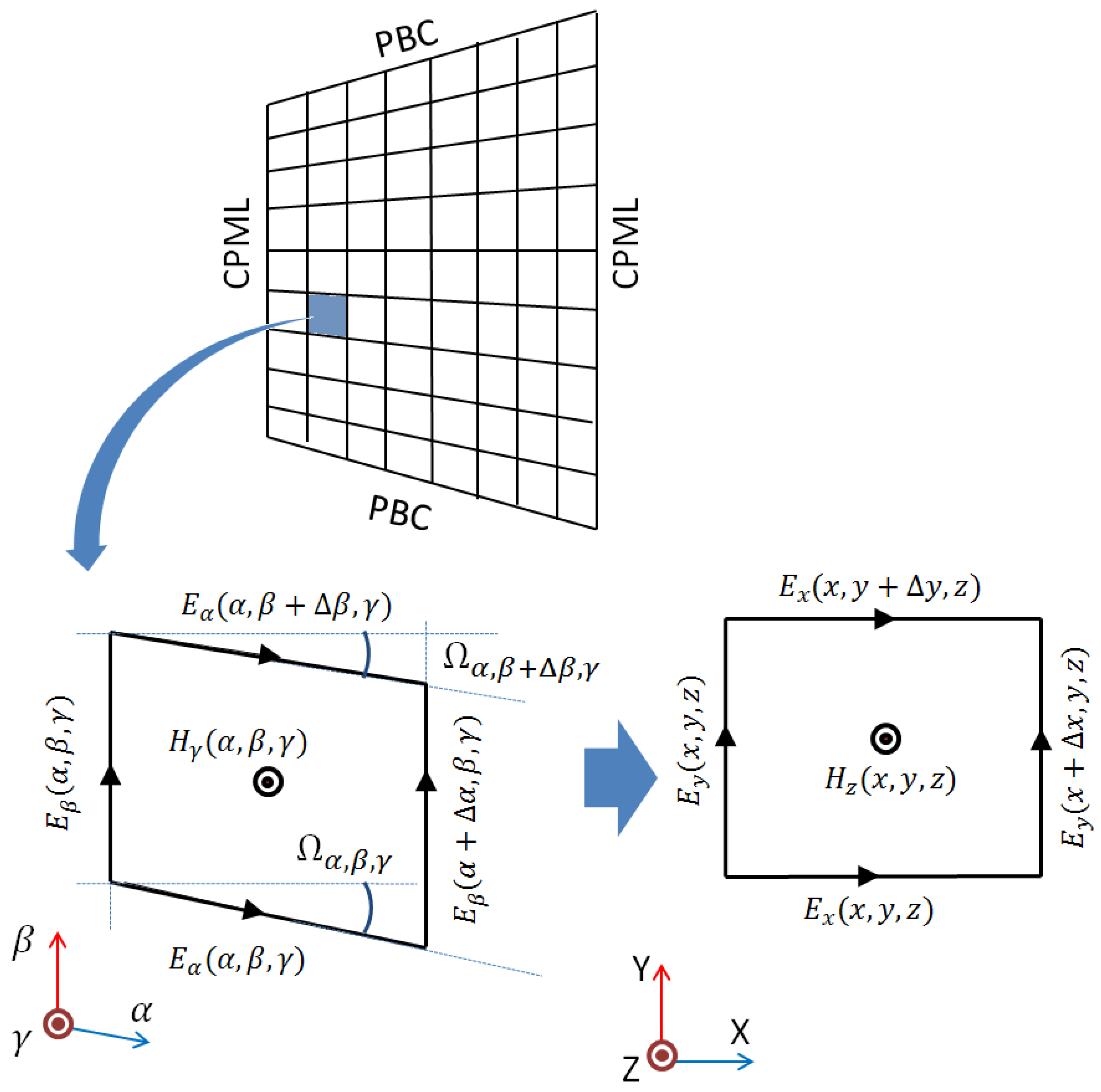
2.1. Rectangular Grid

The detailed mathematical formulation for this case is omitted as it is the standard scenario. Indeed, the updating equations, absorbing boundaries model and voltage source model to calculate field components $E_x$, $E_y$, $E_z$, $H_x$, $H_y$ and $H_z$ in a rectangular grid can be found in [14,15]. In this EM simulator, the Yee cell is a cubic shape, then ${\Delta }_x={\Delta }_y={\Delta }_z=\Delta$. These updating equation are altered to realize the periodic boundaries as in [17,18]. Yee cells at $i_x=1$, $i_y=1$, $i_x=N_x$ and $i_y=N_y$ are used to form the periodic boundaries. In the $+\widehat{z}$ and $-\widehat{z}$ directions, Convolutional Perfectly Matched Layers (CPML) are implemented with proper air gaps to truncate the problem space in a finite region. As illustrated in Figure 2, field components can be found using traditional FDTD equations, the nature of periodic boundary and Floquet theory. This method is called the constant horizontal wavenumber approach, and an exclusive discussion can be found in [14]. In Figure 2, filled blue-colored circles, solid blue-colored arrows, filled red-colored circles, and filled red-colored triangles are representing magnetic and electric field components in $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$ directions which can be computed using FDTD updating equations based on rectangular coordinate system. At the boundaries of the problem space, the electric field components (red-colored circles and triangles) in $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$ direction can not be computed using standard FDTD equations since one of the magnetic fields in $\widehat{x}$, $\widehat{y}$, or $\widehat{z}$ does not exist in the problem space. Those missing magnetic fields represented by The blue-colored circles and dashed blue-colored arrows can be determined by the Floquet theory. The blue-colored solid lines are representing the cells in the problem space. The green colored and orange colored dashed lines are representing Yee cells, which does not exist in the problem space.

Figure 2. Field components in one unit cell.

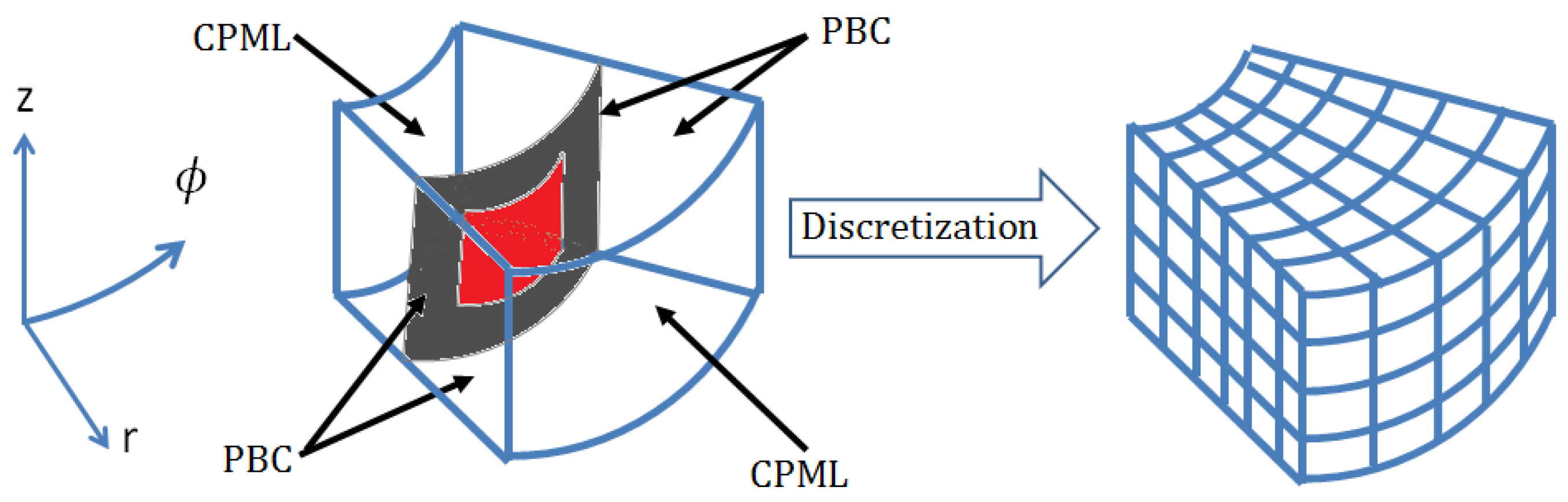
2.2. Cylindrical Grid

In our solution, the simulation model for a fully-conformal cylindrical phased array antenna has been implemented using absorbing boundaries and periodic boundaries in the cylindrical coordinate system. The PBC implementation utilized in the rectangular grid can be adapted for PBC in the cylindrical grid, as well. The detailed computing procedure is presented in the rest of this section. The periodic boundaries are implemented in the $+\widehat{\varphi }$, $-\widehat{\varphi }$, $+\widehat{z}$ and $-\widehat{z}$ directions and the Convolutional Perfectly Matched Layers (CPML) are implemented in the $+\widehat{r}$ and $-\widehat{r}$ directions (Figure 3). A circular array or an isolated element in cylindrical coordinates can be simulated by switching the PBC to CPML of the unit cell, to achieve the objective of simulating the AEP of a cylindrical array antenna. The FDTD updating equations for the cylindrical grid are provided in Appendix A.

Figure 3. Unit cell for FDTD simulation for a cylindrical array. This unit cell has one patch antenna of an infinite cylindrical array. The red color area is the metal patch and gray color area is the substrate material.

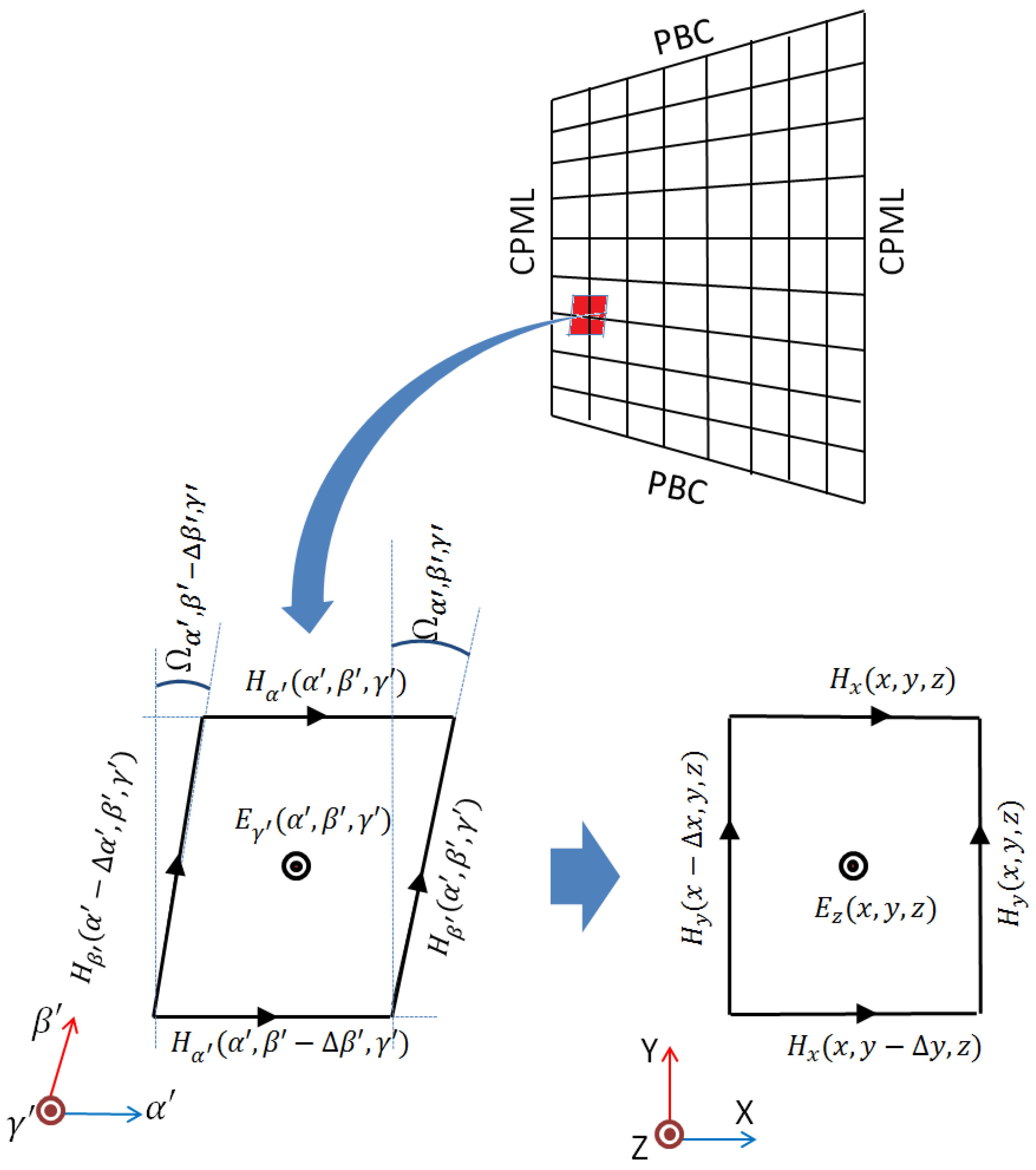
2.2.1. Periodicity in the $\widehat{z}$ Direction

Equation (1) is for calculating the field components $E_{\varphi }$ at the lower bound of z ($i_z=1$). The field components $E_{\varphi }^{n+1}(i_r,i_{\varphi },1)$ are computed using $E_{\varphi }^n(i_r,i_{\varphi },1)$ and the magnetic field components in the $\widehat{z}$ and $\widehat{r}$ directions, which are $H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },1)$, $H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$, $H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)$ and $H_z^{n+\frac{1}{2}}(i_r-1,i_{\varphi },1)$. The updating coefficients $C_{e\varphi e}(i_r,i_{\varphi },1)$, $C_{e\varphi hr}(i_r,i_{\varphi },1)$ and $C_{e\varphi hz}(i_r,i_{\varphi },1)$ of Equation (1) can be computed using Equation (A4).

$$\begin{array}{cc}\hfill E_{\varphi }^{n+1}& (i_r,i_{\varphi },1)=C_{e\varphi e}(i_r,i_{\varphi },1)\times E_{\varphi }^n(i_r,i_{\varphi },1)\hfill \\ & +C_{e\varphi hr}(i_r,i_{\varphi },1)\times \left(H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },1)-H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },0)\right)\hfill \\ & -C_{e\varphi hz}(i_r,i_{\varphi },1)\times \left(H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)-H_z^{n+\frac{1}{2}}(i_r-1,i_{\varphi },1)\right)\hfill \end{array}$$

(1)

The magnetic field components $H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$ do not exist in the problem space. Using the Floquet theory, $H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$ can be calculated as in Equation (2). $k_z$ is the wave number in the $\widehat{z}$ direction and can be computed as $k_z=\frac{\omega }{c}sin{\varpi }_z$ (${\varpi }_z$ is the incident angle of the wave in the $\widehat{z}$ direction):

$$\begin{array}{c}\hfill H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },0)=H_r^{n+\frac{1}{2}}(i_r,i_{\varphi },N_z)e^{j{k}_z{N}_z{\Delta }_z}\end{array}$$

(2)

A similar procedure can be carried out to compute $E_{\varphi }^{n+1}(i_r,i_{\varphi },N_z+1)$. However, using the Floquet theory, $E_{\varphi }^{n+1}(i_r,i_{\varphi },N_z+1)$ can be computed using $E_{\varphi }^{n+1}(i_r,i_{\varphi },1)$ as Equation (3).

$$\begin{array}{c}\hfill E_{\varphi }^{n+1}(i_r,i_{\varphi },N_z+1)=E_{\varphi }^{n+1}(i_r,i_{\varphi },1)e^{j{k}_z{N}_z{\Delta }_z}\end{array}$$

(3)

Equation (4) is for calculating the $E_r$ field components at the lower bound of ϕ ($i_{\varphi }=1$). The field components $E_r^{n+1}(i_r,i_{\varphi },1)$ are computed using $E_r^n(i_r,i_{\varphi },1)$ and the magnetic field components in the z and ϕ directions, which are $H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)$, $H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)$, $H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },1)$ and $H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },1)$. The magnetic field components $H_z^{n+\frac{1}{2}}(i_r,1,i_z)$ are at $\varphi =0$. The updating coefficients $C_{ere}(i_r,N_{\varphi },i_z)$, $C_{erhz}(i_r,N_{\varphi },i_z)$ and $C_{erh\varphi }(i_r,N_{\varphi },i_z)$ of Equation (4) can be computed using Equation (A2).

$$\begin{array}{cc}\hfill E_r^{n+1}& (i_r,i_{\varphi },1)=C_{ere}(i_r,N_{\varphi },i_z)E_r^n(i_r,i_{\varphi },1)\hfill \\ \hfill +& C_{erhz}(i_r,i_{\varphi },1)\times \left(H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)-H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)\right)\hfill \\ \hfill +& C_{erh\varphi }(i_r,i_{\varphi },i_z)\times \left(H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },1)-H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },1)\right)\hfill \end{array}$$

(4)

The magnetic field components $H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$ do not exist in the problem space. Using the Floquet theory, $H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$ can be calculated as in Equation (5). $k_{\varphi }$ is the wave number in the $\widehat{\varphi }$ direction and can be computed as $k_{\varphi }=\frac{\omega }{c}sin{\varpi }_{\varphi }$ (${\varpi }_{\varphi }$ is the incident angle of the wave in the $\widehat{\varphi }$ direction):

$$\begin{array}{c}\hfill H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },0)=H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },N_z)e^{j{k}_z{N}_z{\Delta }_z}\end{array}$$

(5)

Using the Floquet theory, $E_r^{n+1}(i_r,i_{\varphi },N_z+1)$ can be computed using $E_r^{n+1}(i_r,i_{\varphi },1)$ as Equation (6).

$$\begin{array}{c}\hfill E_r^{n+1}(i_r,i_{\varphi },N_z+1)=E_r^{n+1}(i_r,i_{\varphi },1)e^{j{k}_z{N}_z{\Delta }_z}\end{array}$$

(6)

2.2.2. Periodicity in the $\widehat{\varphi }$ Direction

Equation (7) is for calculating the $E_z$ field components at the lower bound of ϕ ($i_{\varphi }=1$). The field components $E_z^{n+1}(i_r,1,i_z)$ are computed using $E_z^n(i_r,1,i_z)$ and the magnetic field components in the $\widehat{\varphi }$ and $\widehat{r}$ directions, which are $H_{\varphi }^{n+\frac{1}{2}}(i_r,1,i_z)$, $H_{\varphi }^{n+\frac{1}{2}}(i_r-1,1,N_z)$, $H_r^{n+\frac{1}{2}}(i_r,1,i_z)$, $H_r^{n+\frac{1}{2}}(i_r,0,i_z)$. The updating coefficients of Equation (7) $C_{eze}(i_r,1,i_z)$, $C_{ezhr}(i_r,1,i_z)$ and $C_{ezh\varphi }(i_r,1,i_z)$ can be computed using Equation (A6).

$$\begin{array}{cc}\hfill E_z^{n+1}& (i_r,1,i_z)=C_{eze}(i_r,1,i_z)E_z^n(i_r,1,i_z)\hfill \\ \hfill +& C_{ezh\varphi }(i_r,1,i_z)\times \left(r{H}_{\varphi }^{n+\frac{1}{2}}(i_r,1,i_z)-(r-\Delta r)H_{\varphi }^{n+\frac{1}{2}}(i_r-1,1,i_z)\right)\hfill \\ \hfill +& C_{ezhr}(i_r,1,i_z)\times \left(H_r^{n+\frac{1}{2}}(i_r,1,i_z)-H_r^{n+\frac{1}{2}}(i_r,0,i_z)\right)\hfill \end{array}$$

(7)

The magnetic field components $H_r^{n+\frac{1}{2}}(i_r,0,i_z)$ do not exist in the problem space. Using the Floquet theory, $H_r^{n+\frac{1}{2}}(i_r,0,i_z)$ can be calculated as in Equation (8). $k_{\varphi }$ is the wave number in the $\widehat{\varphi }$ direction and can be computed as $k_{\varphi }=\frac{\omega }{c}sin{\varpi }_{\varphi }$ (${\varpi }_{\varphi }$ is the incident angle of the wave in the $\widehat{\varphi }$ direction):

$$\begin{array}{c}\hfill H_r^{n+\frac{1}{2}}(i_r,0,i_z)=H_r^{n+\frac{1}{2}}(i_r,N_{\varphi },i_z)e^{j{k}_{\varphi }{N}_{\varphi }{\Delta }_{\varphi }}\end{array}$$

(8)

Using the Floquet theory, $E_z^{n+1}(i_r,i_{\varphi },N_z+1)$ can be computed using $E_z^{n+1}(i_r,i_{\varphi },1)$ as Equation (9).

$$\begin{array}{c}\hfill E_z^{n+1}(i_r,N_{\varphi }+1,i_z)=E_z^{n+1}(i_r,1,i_z)e^{j{k}_{\varphi }{N}_{\varphi }{\Delta }_{\varphi }}\end{array}$$

(9)

Equation (10) is for calculating the $E_r$ field components at the lower bound of ϕ ($i_{\varphi }=1$). The field components $E_r^{n+1}(i_r,1,i_z)$ are computed using $E_r^n(i_r,1,i_z)$ and the magnetic field components in the $\widehat{z}$ and $\widehat{\varphi }$ directions, which are $H_z^{n+\frac{1}{2}}(i_r,1,i_z)$, $H_z^{n+\frac{1}{2}}(i_r,N_{\varphi },i_z)$, $H_{\varphi }^{n+\frac{1}{2}}(i_r,1,i_z)$ and $H_{\varphi }^{n+\frac{1}{2}}(i_r,1,i_z-1)$. The updating coefficients $C_{ere}(i_r,N_{\varphi },i_z)$, $C_{erhz}(i_r,N_{\varphi },i_z)$ and $C_{erh\varphi }(i_r,N_{\varphi },i_z)$ of Equation (10) can be computed using Equation (A2).

$$\begin{array}{cc}\hfill E_r^{n+1}& (i_r,i_{\varphi },1)=C_{ere}(i_r,N_{\varphi },i_z)E_r^n(i_r,i_{\varphi },1)\hfill \\ \hfill +& C_{erhz}(i_r,i_{\varphi },1)\times \left(H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)-H_z^{n+\frac{1}{2}}(i_r,i_{\varphi },1)\right)\hfill \\ \hfill +& C_{erh\varphi }(i_r,i_{\varphi },i_z)\times \left(H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },1)-H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },1)\right)\hfill \end{array}$$

(10)

The magnetic field components $H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$ do not exist in the problem space. Using the Floquet theory, $H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },0)$ can be calculated as in Equation (11). $k_{\varphi }$ is the wave number in the $\widehat{\varphi }$ direction and can be computed as $k_{\varphi }=\frac{\omega }{c}sin{\varpi }_{\varphi }$ (${\varpi }_{\varphi }$ is the incident angle of the wave in the $\widehat{\varphi }$ direction):

$$\begin{array}{c}\hfill H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },0)=H_{\varphi }^{n+\frac{1}{2}}(i_r,i_{\varphi },N_z)e^{j{k}_z{N}_z{\Delta }_z}\end{array}$$

(11)

Using the Floquet theory, $E_r^{n+1}(i_r,i_{\varphi },N_z+1)$ can be computed using $E_r^{n+1}(i_r,i_{\varphi },1)$ as Equation (12).

$$\begin{array}{c}\hfill E_r^{n+1}(i_r,i_{\varphi },N_z+1)=E_r^{n+1}(i_r,i_{\varphi },1)e^{j{k}_z{N}_z{\Delta }_z}\end{array}$$

(12)

2.2.3. At the Corners

At the corners of the cell (the FDTD mesh of the patch antenna), $E_r$ has to be updated using (13) and (15)–(17).

$$\begin{array}{cc}\hfill E_r^{n+1}& (i_r,1,1)=C_{ere}(i_r,1,1)E_r^n(i_r,1,1)\hfill \\ \hfill +& C_{erhz}(i_r,1,1)\times \left(H_z^{n+\frac{1}{2}}(i_r,1,1)-H_z^{n+\frac{1}{2}}(i_r,0,1)\right)\hfill \\ \hfill +& C_{erh\varphi }(i_r,1,1)\times \left(H_{\varphi }^{n+\frac{1}{2}}(i_r,1,1)-H_{\varphi }^{n+\frac{1}{2}}(i_r,1,0)\right)\hfill \end{array}$$

(13)

The magnetic field components $H_{\varphi }^{n+\frac{1}{2}}(i_r,1,0)$ and $H_z^{n+\frac{1}{2}}(i_r,0,1)$ do not exist in the problem space. They can be calculated as in Equation (14).

$$H_{\varphi }^{n+\frac{1}{2}}(i_r,1,0)=H_{\varphi }^{n+\frac{1}{2}}(i_r,1,N_z)\times e^{j{k}_{\varphi }{N}_{\varphi }{\Delta }_{\varphi }}$$

(14a)

$$H_z^{n+\frac{1}{2}}(i_r,0,1)=H_{\varphi }^{n+\frac{1}{2}}(i_r,N_{\varphi },1)\times e^{j{k}_z{N}_z{\Delta }_z}$$

(14b)

After electric field components $\left\{E_r^{n+1}(i_r,1,1)\right\}$ are computed using Equation (13), all of the electric field components $E_r^{n+1}(i_r,N_{\varphi }+1,1)$, $E_r^{n+1}(i_r,1,N_z+1)$ and $E_r^{n+1}(i_r,N_{\varphi }+1,N_z+1)$ at other corners can be computed using Equations (15)–(17).

$$E_r^{n+1}(i_r,N_{\varphi }+1,1)=E_r^{n+1}(i_r,1,1)\times e^{j{k}_{\varphi }{N}_{\varphi }{\Delta }_{\varphi }}$$

(15)

$$E_r^{n+1}(i_r,1,N_z+1)=E_r^{n+1}(i_r,1,1)\times e^{j{k}_z{N}_z{\Delta }_z}$$

(16)

$$E_r^{n+1}(i_r,N_{\varphi }+1,N_z+1)=E_r^{n+1}(i_r,1,1)\times e^{j{k}_{\varphi }{N}_{\varphi }{\Delta }_{\varphi }}\times e^{j{k}_z{N}_z{\Delta }_z}$$

(17)

In all of the above equations, from Equation (1) to Equation (17), $i_r$, $i_{\varphi }$ and $i_z$ are indexes of r, ϕ and z. The updating coefficients depend on the material properties (${ϵ}_r$, ${ϵ}_{\varphi }$, ${ϵ}_z$, ${\sigma }_r^e$, ${\sigma }_{\varphi }^e$ and ${\sigma }_z^e$), the lattice increment at the location of the field component and the time increment ($\Delta t$). They are constant in time for the material used in patch antenna fabrication. The CPML for the cylindrical grid [19,20,21,22] will be located in the direction of $+\widehat{r}$ and $-\widehat{r}$ in all of the simulations presented in this work. If a finite-by-infinite array needs to be simulated, CPMLs will be located in the direction of $+\widehat{r}$, $-\widehat{r}$, $+\widehat{z}$ and $-\widehat{z}$.

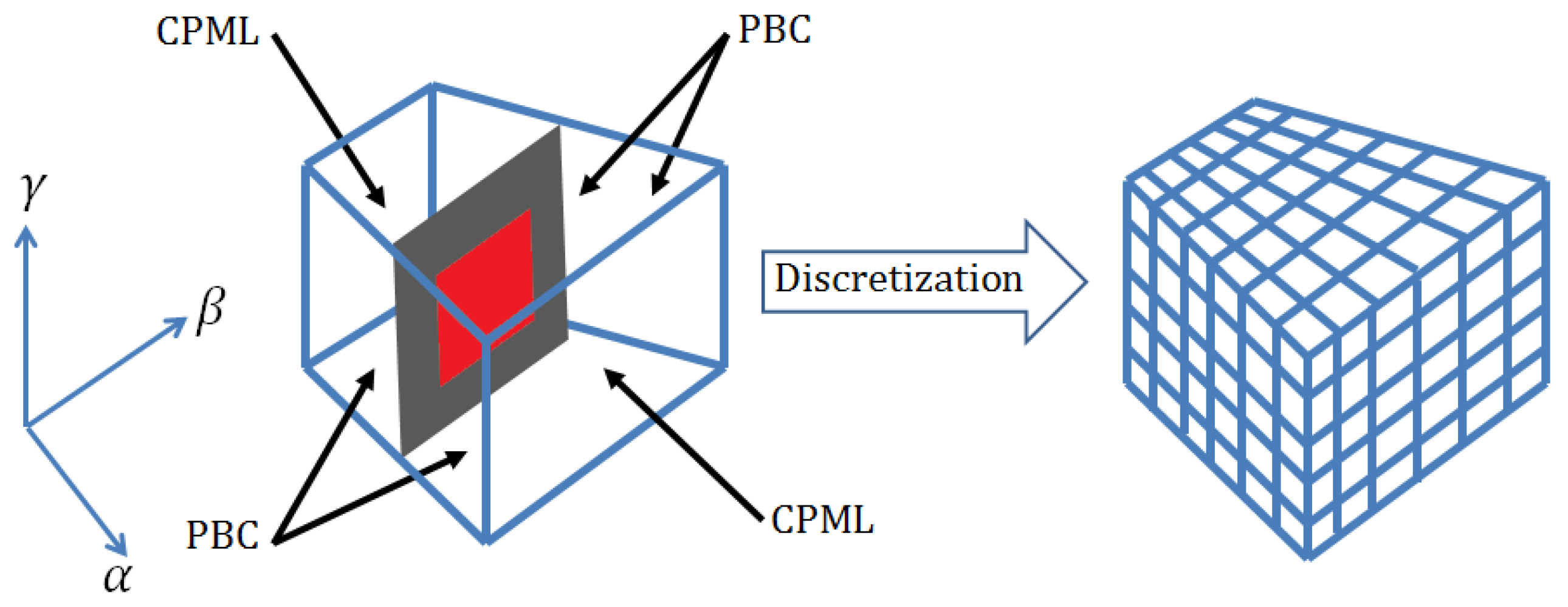
2.3. Nonorthogonal Grid

As mentioned before, a facet array is a better manifold model for some existing system testbeds [6], and the radiating elements in this configuration are planar. The consequence of the facet array is that the unit cell is located in a non-orthogonal grid, as is shown in Figure 4, Figure 5 and Figure 6. The updating equations based on the proper projection scheme of a non-orthogonal grid are developed and used to simulate AEP [11]. Our formulation of the project scheme takes advantage of the specific nature of the geometry of the unit cell. Since the non-orthogonality only manifests in a two-dimensional plane, modified equations from the rectangular grid model are used to reduce the computational load. Compared to the update equations in the rectangular grid, the equations to calculate the field components in the $\widehat{y}$ direction are the same. The field components the $\widehat{x}$ and $\widehat{z}$ directions are computed with an irregular nonorthogonal structured grid [15]; more details of these equations are shown in Appendix B. Since the field components are not orthogonal to each other, the intersection of two and three CPMLs does not create a boundary, which can allow the perfect transmission of EM waves from one CPML to another. Therefore, this grid can only be used in the simulation of an active element in infinite arrays.

Figure 4. Unit cell for FDTD simulation for a faceted cylindrical array.

Figure 5. Illustration of the process of transforming the electric field component in the nonorthogonal grid into the electric field in the orthogonal grid.

Figure 6. Illustration of the process of transforming the magnetic field component in the nonorthogonal grid into the magnetic field in the orthogonal grid.

Even though the FDTD updating equations can be derived for the nonorthogonal grid starting from Maxwell’s equation, the derivation process is simplified by taking the geometry into consideration. Figure 5 and Figure 6 illustrate the derivation of FDTD equations for electric field components using the FDTD equations for a rectangular grid. Let us consider that the nonorthogonal coordinate system (Figure 5) is represented by $\widehat{\alpha }$, $\widehat{\beta }$ and $\widehat{\gamma }$ unit vectors for representing electric field components. Notice that $\widehat{\alpha }$ depends on the location $(\alpha ,\beta ,\gamma )$, which makes this grid unstructured. By inspection of the geometry (Figure 5), one can write Equations (18a)–(18c) to express $E_x$, $E_y$ and $E_z$ in terms of $E_{\alpha }$, $E_{\beta }$ and $E_{\gamma }$.

$$E_x(x,y,z)=E_{\alpha }(\alpha ,\beta ,\gamma )cos{\Omega }_{\alpha ,\beta ,\gamma }$$

(18a)

$$E_y(x,y,z)=E_{\beta }(\alpha ,\beta ,\gamma )-E_{\alpha }(\alpha ,\beta ,\gamma )sin{\Omega }_{\alpha ,\beta ,\gamma }$$

(18b)

$$E_z(x,y,z)=E_{\gamma }(\alpha ,\beta ,\gamma )$$

(18c)

$$J_x(x,y,z)=J_{\alpha }(\alpha ,\beta ,\gamma )cos{\Omega }_{\alpha ,\beta ,\gamma }$$

(18d)

$$J_y(x,y,z)=J_{\beta }(\alpha ,\beta ,\gamma )-J_{\alpha }(\alpha ,\beta ,\gamma )sin{\Omega }_{\alpha ,\beta ,\gamma }$$

(18e)

$$J_z(x,y,z)=J_{\gamma }(\alpha ,\beta ,\gamma )$$

(18f)

In the same way, let us consider that the nonorthogonal coordinate system (Figure 6) is represented by $\widehat{{\alpha }^{\prime }}$, $\widehat{{\beta }^{\prime }}$ and $\widehat{{\gamma }^{\prime }}$ unit vectors for representing magnetic field components. As the electric field component was determined, one can write Equations (19a)–(19c) to express $E_x$, $E_y$ and $E_z$ in terms of $E_{{\alpha }^{\prime }}$, $E_{{\beta }^{\prime }}$ and $E_{{\gamma }^{\prime }}$ by inspection of the geometry in Figure 6.

$$H_x(x,y,z)=H_{{\alpha }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })+H_{{\beta }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })sin{\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$$

(19a)

$$H_y(x,y,z)=H_{{\beta }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })cos{\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$$

(19b)

$$H_z(x,y,z)=H_{{\gamma }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })$$

(19c)

$$M_x(x,y,z)=M_{{\alpha }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })+M_{{\beta }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })sin{\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$$

(19d)

$$M_y(x,y,z)=M_{{\beta }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })cos{\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$$

(19e)

$$M_z(x,y,z)=M_{{\gamma }^{\prime }}({\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime })$$

(19f)

${\Omega }_{\alpha ,\beta ,\gamma }$ and ${\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$ are measured with respect to the blue colored dashed line. The positive sign will be assigned if it is measured in the clockwise direction, and the negative sign will be assigned if it is measured counterclockwise. Notice that ${\Omega }_{\alpha ,\beta ,\gamma }$ (${\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$) is independent of spacial variables α (${\alpha }^{\prime }$) and γ (${\gamma }^{\prime }$), and ${\Omega }_{\alpha ,\beta ,\gamma }$ and ${\Omega }_{{\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }}$ are equal in magnitude and sign. By substituting $E_x(x,y,z)$, $E_y(x,y,z)$, $E_z(x,y,z)$, $H_x(x,y,z)$, $H_y(x,y,z)$, $H_z(x,y,z)$ in the FDTD updating equation for the rectangular grid [15,17], a new set of FDTD updating equations has been derived for this nonorthogonal and unstructured grid (Appendix B).

3. Simulation of Active Element Patterns

3.1. Computational Load

The computational load and speed of computing for FDTD depend on the step size, far-field frequency band (the number of frequency points used to do the near-to-far-field calculation), Yee’s cell size, the boundary condition, the size of the computing domain and the size of the memory as a result of these parameters. It also depends on the tradeoffs involved in the accuracies. Using PBC, for example, reduces the AEP computation time to a single cell with an approximation of infinite array size, because the air gaps in the $+\widehat{x}$, $-\widehat{x}$, $+\widehat{y}$ and $-\widehat{y}$ directions are absent. For finite arrays, we may simulate the entire array on a powerful computing platform or use other techniques to reduce the computational load [7,23]. More discussion of computational load and benchmarks of this program, in general, can be found in [10]. In this study, we only focus on getting reasonable convergences in a manageable amount of time rather than optimizing the computational aspects.

Our specific simulation scenarios involve hundreds of thousands of Yee cells and about twenty thousand iterations of the time marching loop, which is CPU time and memory consuming. To keep a balance between computational efficiency and the ease of debugging, the Java programming language is used to implement the EM solver. A computer with Intel Core i7-4770K CPU @3.50 GHz and 32 GB memory (RAM) is used to run the simulation. To compute a single AEP, the receiving power was detected for planar waves from different directions. The same simulation needs to run N times to obtain the complete three-dimensional AEP. The N will be determined by the step sizes and range of θ and ϕ in the spherical coordinate system. As an example, let us consider that we want to have a two-degree resolution in the 3D radiation pattern plot. Therefore, we need 90 samples for θ and 180 samples for ϕ. To record all of the data point, 16,200 ($=90\times 180$) simulations will have to be performed. It is a very CPU time-consuming process ($\sim 4000$ h). Even though simulating AEP is not the target of this work, active elements of infinite planar, cylindrical and faceted-cylindrical arrays are simulated and presented in Section 3.2.

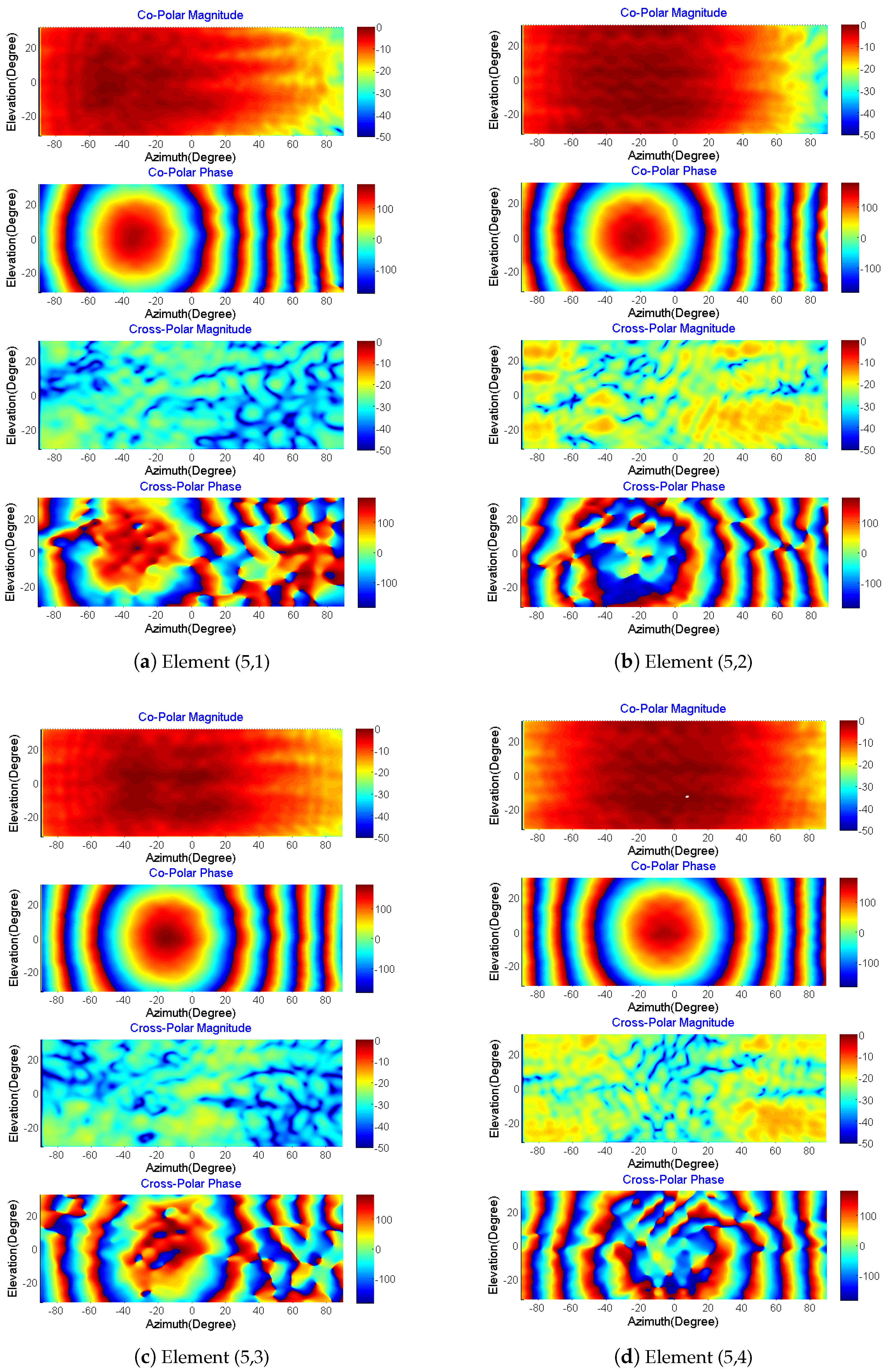
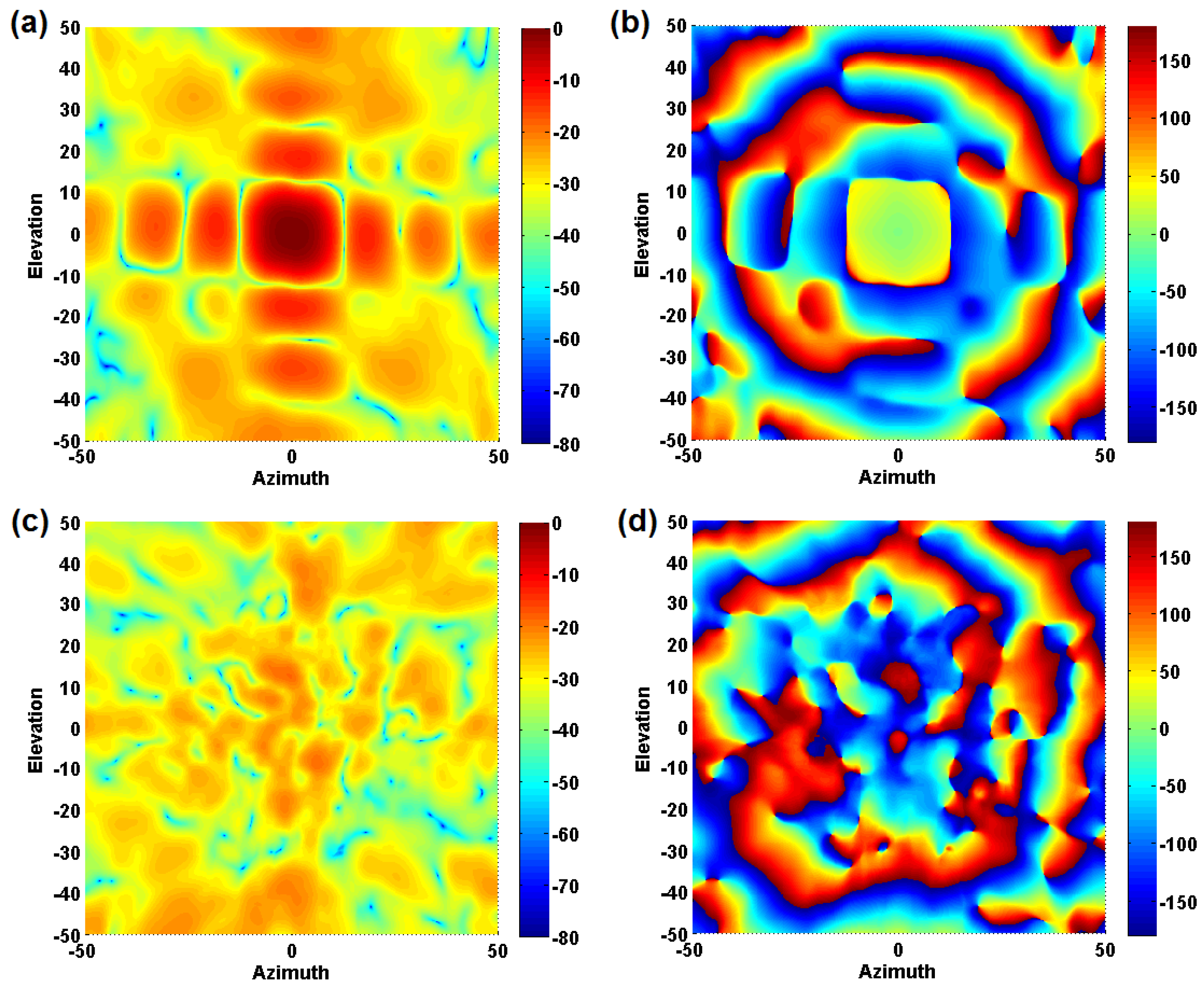
3.2. Example Results of Simulated AEP

To support comparative studies, we simulated AEPs for identical radiating elements embedded in different manifolds. Some of the simulated AEPs can be compared with measurements to be validated; others are evaluated based on comparing with other simulations or expected physical features. More details are explained in Section 4 and Section 5.

The planar wave source was created near the top CPML of the model. The receiving power was detected at one of two ports of the active element, and the other ports are terminated with the match load. The planar waves from different directions ($-{180}^{\circ }<\varphi <+{180}^{\circ }$) were created in each simulation to collect received power for the planar wave coming from a different angle. That received power information will be used to construct the AEP. This procedure is a CPU time hungry process, which will do the same simulation 360 times (the increment of ϕ is $1^{\circ }$). The approximated elapsed time to predict a principal plane cut was around 350 min.

Figure 7 shows an example of the principal plane cut for AEP from an infinite-by-infinite planar array, $100\lambda$-diameter (λ is the wavelength of the operating frequency or the center frequency of a bandwidth) cylindrical array and $100\lambda$-diameter faceted-cylindrical array. The material specifications (Section 4) and dimensions (Figure 8) are the same as the specifications and dimensions of the array being measured. One thousand two hundred fifty seven radiating elements with $\frac{\lambda }{2}$ spacing can occupy one ring (the circumference of the cylinder) of the $100\lambda$-diameter cylindrical array. One thousand two hundred fifty six radiating elements with $\frac{\lambda }{2}$ spacing can occupy one ring of the $100\lambda$-diameter faceted-cylindrical array.

Figure 7. Simulation of an AEP of planar, cylindrical ($100\lambda$ radius) and faceted-cylindrical ($100\lambda$ radius) arrays.

Figure 8. Specifications of the array antenna.

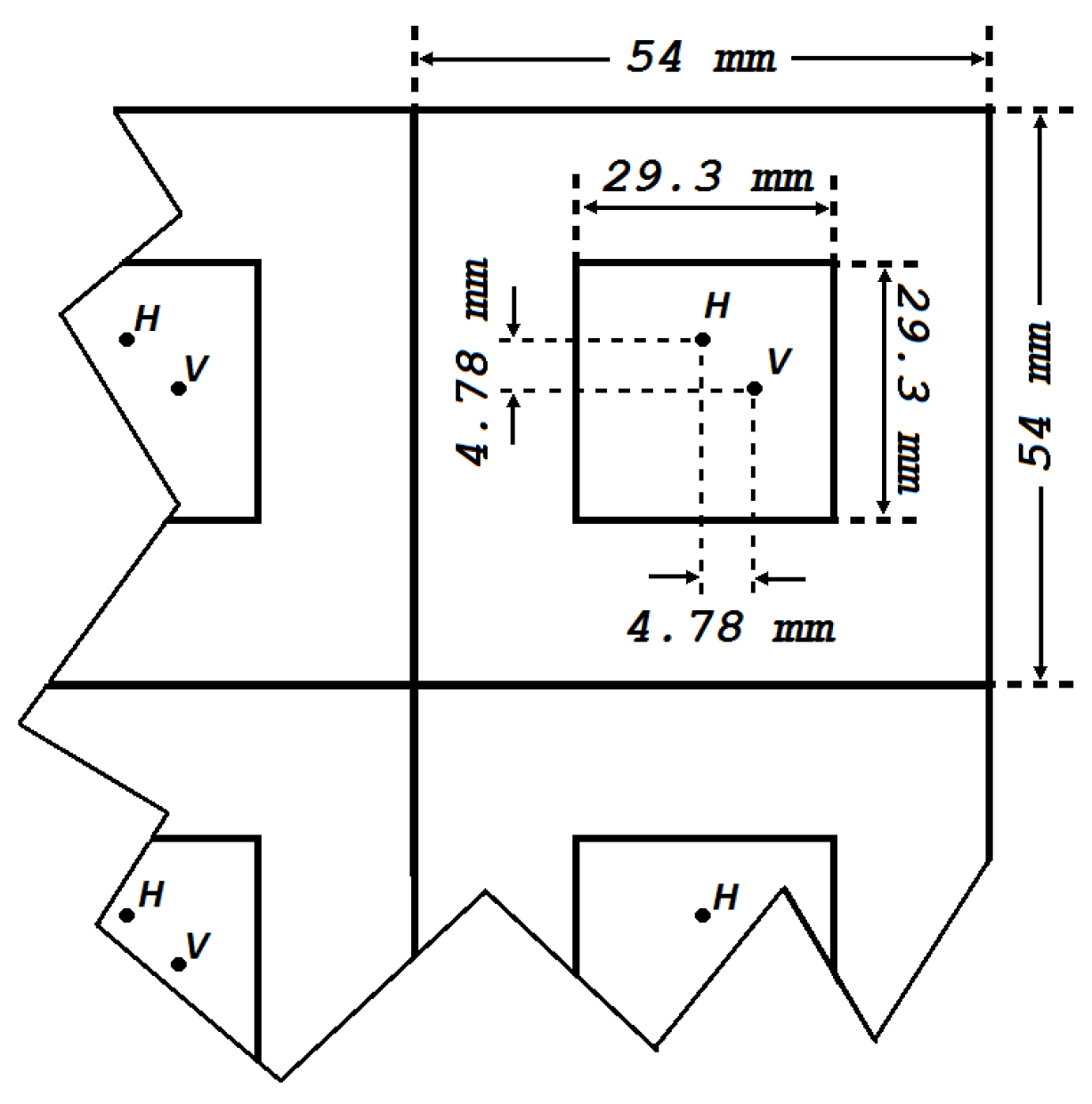
4. Measurements of Active Element Patterns

In-chamber measurement of AEPs is the most accurate approach for array system characterization and prediction. However, it is limited to certain sizes of arrays that fit into the chamber environment. In later sections, we will describe our solution to extend small-scale system measurement to larger system predictions. For dual-polarized pattern measurements, we also need to be careful with the coordinate systems. The azimuth-over-elevation coordinate system with the Ludwig II definition of cross-polarization [24] is used for all of the chamber measurements in this work, which is consistent with the EM simulations.

In the measurement testbed setup, the patch antennas are dual polarized single layer elements with $\frac{\lambda }{2}$ separation. The patch antennas (Figure 8) used in the CPAD configuration was fabricated on the RT/Duroid 5880 substrate with 1.575 mm thickness and $\frac{1}{2}$ oz copper ($17 \mathsf{\mu }$m thickness of copper) cladding. The operating frequency was selected in S-band, which is common in many antennas used in weather radar systems [6]. The CPAD allows the same set of radiating elements to be configured to either planar or faceted-cylindrical manifolds with similar aperture sizes.

To measure the AEPs, one port of a test patch antenna element is excited while all other ports are terminated with matched load (50 Ω). In near-field measurements, the complex AEP, measured directly as the amplitude and phase of co-polar and cross-polar electrical field sampled at the near-field range, is obtained first, and then, it is transformed to far-field as needed. The planar and faceted-cylindrical array measurement system set up in the near-field chamber is shown in Figure 9. The results clearly show that the AEPs vary with the location of the element due to the effects of surface currents, mutual coupling and edge currents, as presented in Figure 10 for elements in the planar array antenna and Figure 11 for elements in the cylindrical array antenna. As expected, at the middle section of the arrays, the measured AEPs are similar to simulated AEPs with PBC. The following subsections provide more detailed information for these results.

Figure 9. Measurement setup for 10-by-eight planar (left) and cylindrical (right) phased array antennas.

Figure 10. Measured AEPs of the (5,1) (a), (5,2) (b), (5,3) (c) and (5,4) (d) elements in the eight-by-eight planar phased array antenna; co-polar magnitude in dB (first row), co-polar phase in degrees (second row), cross-polar magnitude in dB (third row) and cross-polar phase in degrees (forth row).

Figure 11. Measured AEPs of the (5,1) (a), (5,2) (b), (5,3) (c) and (5,4) (d) elements in the eight-by-eight faceted-cylindrical phased array antenna; co-polar magnitude in dB (first row), co-polar phase in degrees (second row), cross-polar magnitude in dB (third row) and cross-polar phase in degrees (forth row).

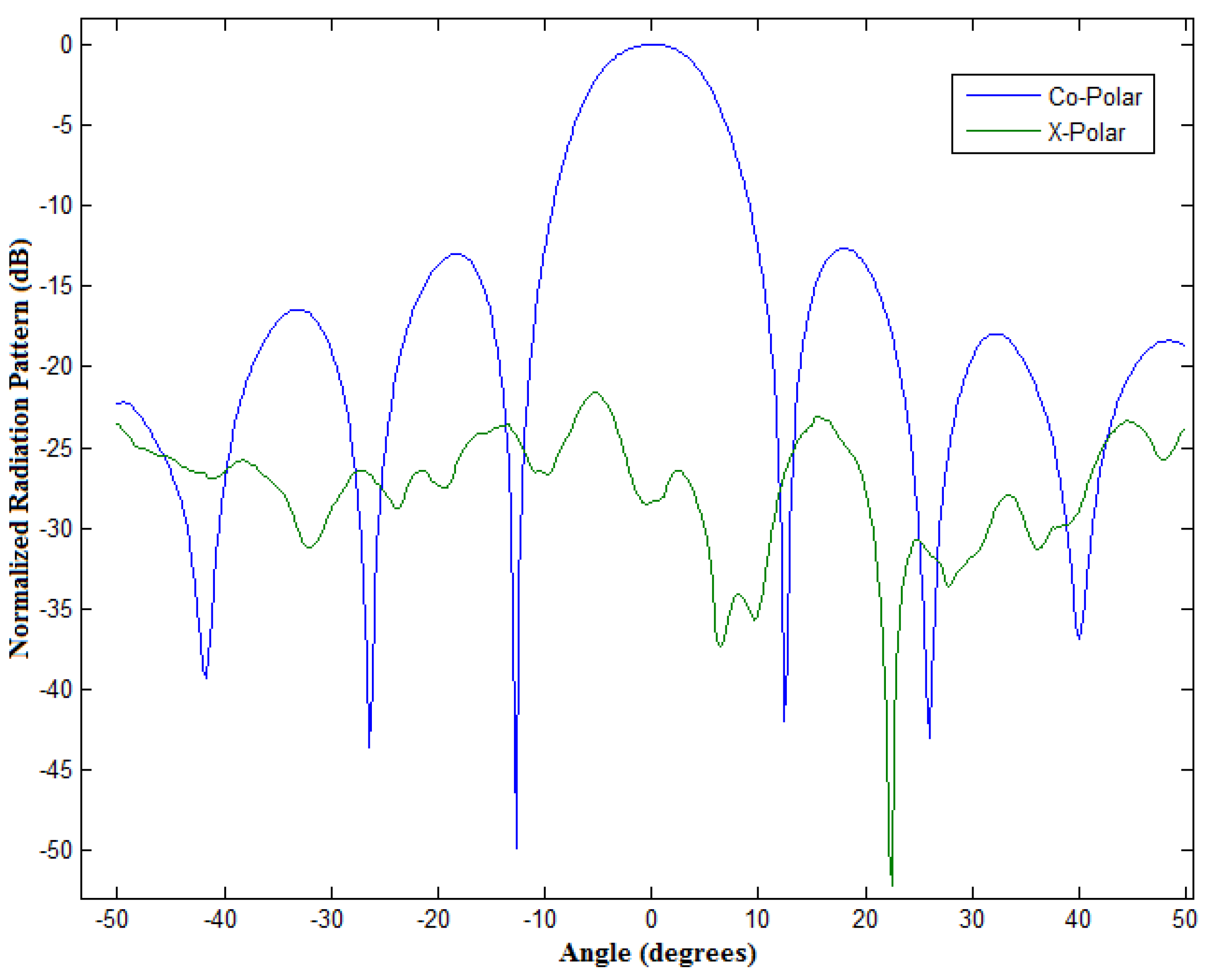
4.1. Planar Array Example Measurement Results

In this example, the CPAD is configured as an eight-by-eight planar array with an aperture size of 432 mm. The results of AEPs are illustrated in Figure 10. The average directivities of the measured AEPs are 9.81 dB and 9.98 dB at 3.1 GHz for the H and V channels, respectively. The probe model (OEWG WR284) can be used in the [2.6 GHz, 3.96 Hz] frequency band. This probe model is employed in both the near-field measurement process and the near-to-far-field conversion process. Since the Near Field (NF) scanner is five feet in height, the system can measure $[-{50}^{\circ },+{50}^{\circ }]$ in both the azimuth range and elevation ranges. The co-polar (up) and cross polar (down) AEPs of elements (4, 1), (4, 2), (4, 3) and (4, 4) are shown in Figure 10a–d, respectively. The cross-polar level in AEP is around 15 dB below the maximum of the co-polar level.

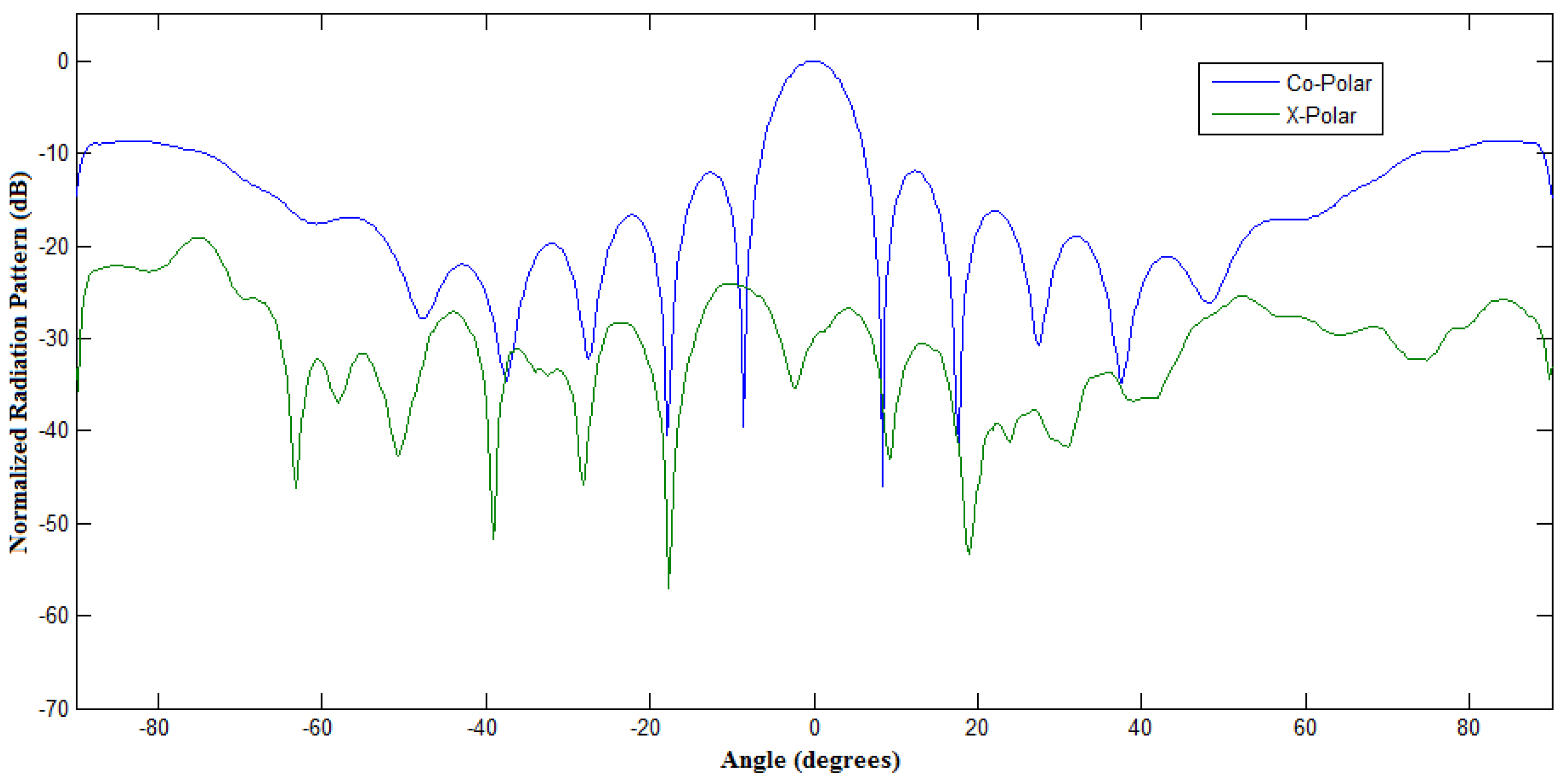
4.2. Faceted-Cylindrical Array Example Measurement Results

For the next example, the CPAD is configured as a partial faceted-cylindrical array with a diameter of 385 mm, which has an identical planar aperture size as the planar array example. The average directivities of the measured AEPs are $10.50$ dB and $10.46$ dB at $3.1$ GHz for the H and V channels, respectively. The probe model is the same model used for planar array measurements. Given the system geometry, the azimuth range of measurement is $[-{90}^{\circ },+{90}^{\circ }]$, and the elevation range is $[-{32}^{\circ },+{32}^{\circ }]$. The co-polar (up) and cross polar (down) AEPs of elements (4,1), (4,2), (4,3) and (4,4) are shown in Figure 11a–d , respectively. The cross-polarization level is around 25 dB below the maximum of the co-polarization level. The AEPs are more directive than the planar case AEPs.

5. Generation of The Array Pattern from Measured AEP

The radiation pattern of an array without including the mutual coupling is related to the isolated element pattern through a simple equation: $E(\vartheta ,\phi )$ = array factor × isolated element pattern. Implementing the same concept, a rigorous relation in which the mutual coupling effects are already included can be presented using the AEPs as in Equation (20). The theory to generate array patterns for planar and faceted-cylindrical arrays using AEPs from near-field measurements is presented in this section. The radiation pattern is related to AEPs, which takes into account the mutual coupling effects, through the equations from (20) to (23), to provide mathematical formulas for the pattern generation using the MATLAB®program:

$$E(\vartheta ,\phi )=\sum _{\forall n,m}{a}_{m,n}{c}_{m,n}{E}_{m,n}(\vartheta ,\phi )e^{jk{\overrightarrow{r}}_{m,n}·{\widehat{r}}_{\vartheta ,\phi }}$$

(20)

where $E_{m,n}(\vartheta ,\phi )$ is the complex electric field in the ${\widehat{r}}_{\vartheta ,\phi }$ direction, which can be measured or simulated as the phase and magnitude of each element’s AEP. k is the wave number, which is $2\pi /\lambda$.

$$a_{m,n}=\left|a_{m,n}\right|e^{-jk{\overrightarrow{r}}_{m,n}·{\widehat{r}}_{{\vartheta }_0,{\phi }_0}}$$

(21)

where:

$${\overrightarrow{r}}_{\vartheta ,\phi }=u\widehat{x}+v\widehat{y}+cos\vartheta \widehat{z}$$

u and v are the direction cosines and they are defined as $u=sin\vartheta cos\phi$ and $v=sin\vartheta sin\phi$. ${\vartheta }_0$ and ${\phi }_0$ define the beam steering direction.

$c_{m,n}$ is the calibration value for each element. This value can be measured with a proper test procedure. In this work, the mean value (${\alpha }_{m,n}$) of a small zone ($4\times 4$ data points) at the center of the co-polarization phase pattern is processed in each element to compute the $8\times 8$ calibration matrix: $\left[c_{m,n}\right]$.

$$c_{m,n}=\left|c_{m,n}\right|e^{-j{\alpha }_{m,n}}$$

(22)

$$\begin{array}{c}\hfill {\overrightarrow{r}}_{m,n}=x_{m,n}\widehat{x}+y_{m,n}\widehat{y}+z_{m,n}\widehat{z}\end{array}$$

(23)

5.1. The Planar Array (Case I)

Since the elements of the planar array are arranged on the $XY$ plane, $z_{n,n}=0$. The other parameters $x_{m,n}$ and $y_{m,n}$ can be calculated with Equation (24). The patch antenna elements under measurement are square-shaped, then the element separation distance is the same in the $\widehat{x}$ and $\widehat{y}$ directions. Therefore, d is used to represent the element size of the array.

$$x_{m,n}=(2n-1){\displaystyle \frac{d}{2}}$$

(24a)

$$y_{m,n}=(2m-1){\displaystyle \frac{d}{2}}$$

(24b)

The generated planar phased array pattern using 64 AEPs for the H channel (horizontal polarization) is shown in Figure 12. The azimuth principal plane cut is shown in Figure 13. In the same manner, the radiation pattern can be generated for the V channel using AEPs for V channels.

Figure 12. Measured patterns of an eight-by-eight planar phased array antenna (based on AEPs and software calibration) : (a) co-polar magnitude in dB; (b) co-polar phase in degrees; (c) cross-polar magnitude; and (d) cross-polar phase in degrees.

Figure 13. The azimuth principal plane cut of measured co-polar and cross-polar patterns of an eight-by-eight planar phased array antenna (based on AEPs and software calibration).

5.2. The Faceted-Cylindrical Array (Case II)

The parameters $x_{m,n}$, $y_{m,n}$ and $z_{m,n}$ can be calculated with Equation (25). These equations were derived using the geometry of the faceted-cylindrical array.

$$x_{m,n}={\displaystyle \frac{d}{2}}\left(sin\frac{(2n-1){\Delta }_{\xi }}{2}cot\frac{{\Delta }_{\xi }}{2}\right)$$

(25a)

$$y_{m,n}=(2m-1){\displaystyle \frac{d}{2}}$$

(25b)

$$z_{m,n}={\displaystyle \frac{d}{2}}\left(csc{\displaystyle \frac{{\Delta }_{\xi }}{2}}-cos\frac{(2n-1){\Delta }_{\xi }}{2}cot\frac{{\Delta }_{\xi }}{2}\right)$$

(25c)

The radius of the partially-populated faceted-cylindrical array being measured in the near-field chamber is $4\lambda$, and the element spacing is $0.7\lambda$. The generated faceted-cylindrical phased array pattern using 64 AEPs for the H channel (horizontal polarization) is shown in Figure 14. The azimuth principal plane cut is shown in Figure 15. In the same manner, radiation patterns for V-channels are generated using AEPs for V channels.

Figure 14. Measured patterns of an eight-by-eight faceted-cylindrical phased array antenna (based on AEPs and software-calibration) (a) co-polar magnitude in dB; (b) co-polar phase in degrees; (c) cross-polar magnitude in dB; and (d) cross-polar phase in degrees.

Figure 15. The azimuth principal plane cut of the measured co-polar and cross-polar magnitude patterns of an eight-by-eight faceted-cylindrical phased array antenna (based on AEPs and software calibration).

For the CPAD configuration in this study, we have 128 measured AEPs for each dual polarized eight-by-eight array (either planar or faceted-cylindrical array). The above equations based on the measured AEPs are used to generate the dual-polarized array radiation pattern. Figure 12 and Figure 14 show the generated 3D array patterns for planar and faceted-cylindrical arrays, respectively. Based on the locations, phase calibration factors are extracted and are applied to each AEP. The alignment algorithm tunes the phase excitation of each element until the maximum radiation power toward the desired direction is achieved. The calibration beam-forming and alignment were done in MATLAB. It should be noted here that this is a very straightforward and basic beam-forming/calibration approach, which only uses phase alignment; the purpose is to prove the concept and to compare with simulation results. There is no beam-forming optimization technique applied here.

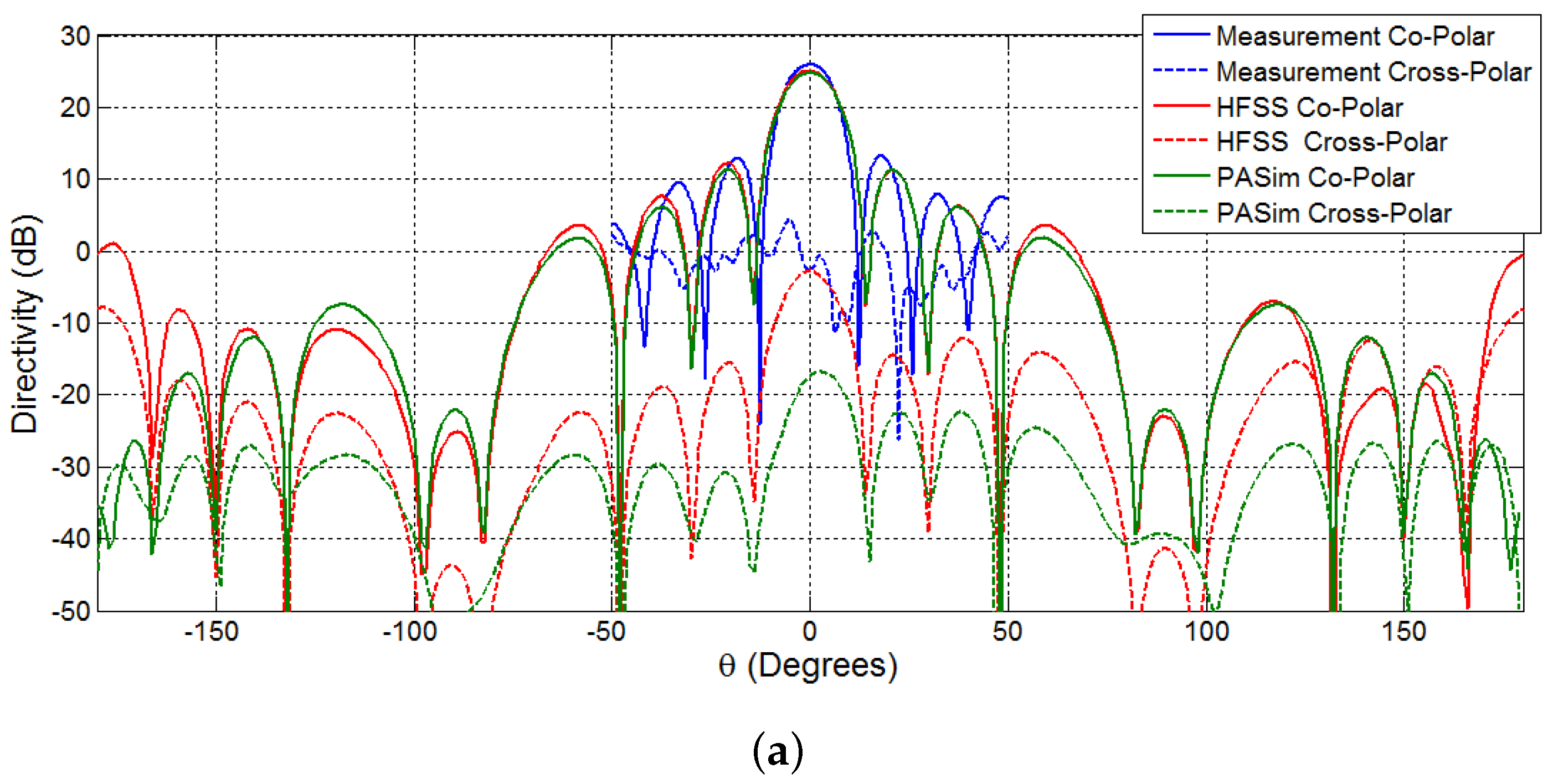
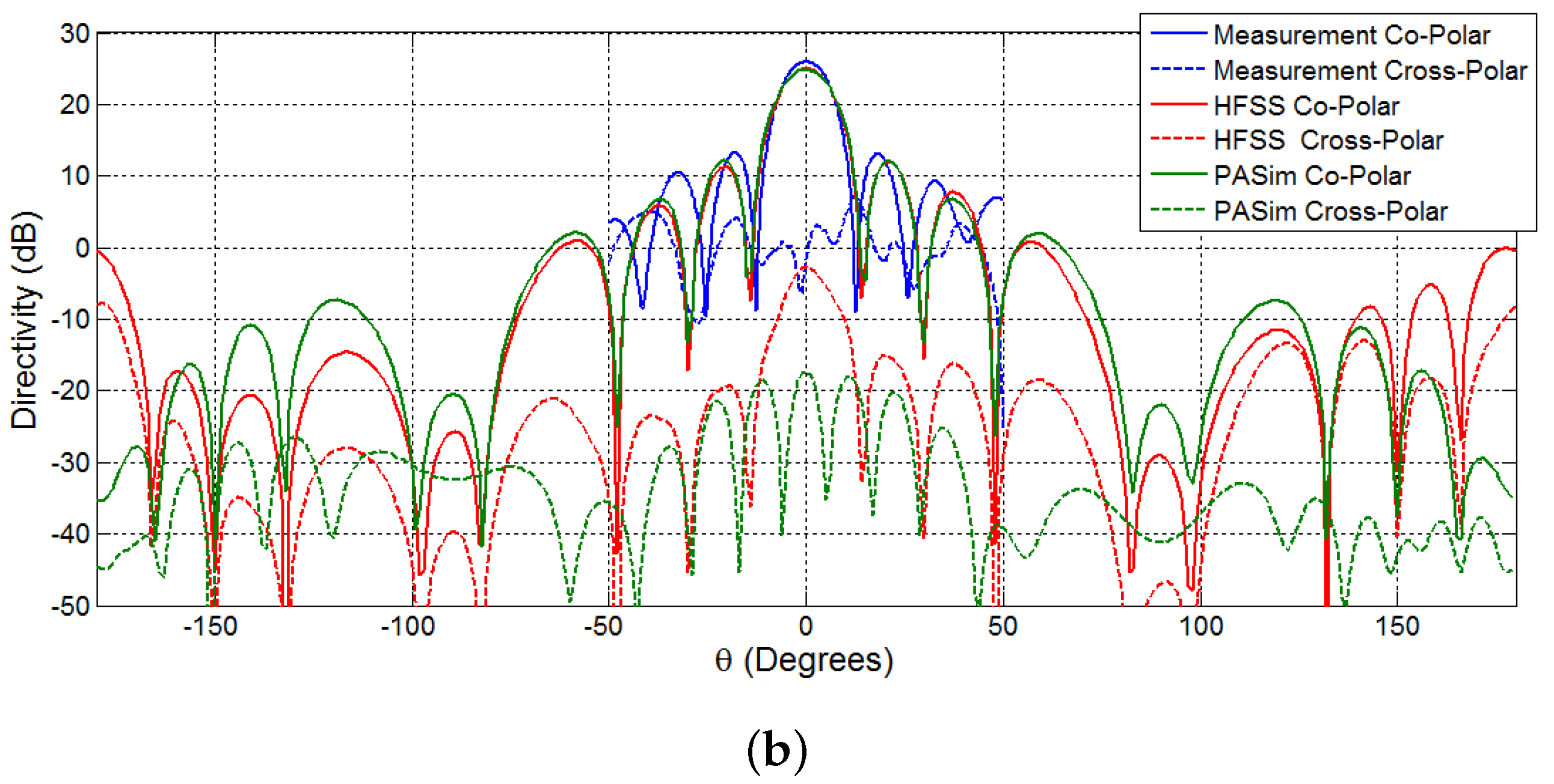
5.3. Comparison of the Results of the Planar Array vs. the Facet Cylindrical Array

It is interesting to compare the results from the planar and the cylindrical/facet array since they have the same radiating elements and the same (projected) planar aperture size. For the planar array, the focused array beam pattern has the sidelobes and cross-polarization levels below −18 dB and −27 dB, respectively. Comparing Figure 13 and Figure 15, in the principal planes, the faceted-cylindrical array patterns have lower cross-polarizations in some directions, while the radiation pattern of the cylindrical array has some higher sidelobes at $-{90}^{\circ }$ and ${90}^{\circ }$ locations, which is mainly due to the surface curvature [25]. Associated EM simulations show that with the increased size of the diameter, the sidelobe levels at $-{90}^{\circ }$ and ${90}^{\circ }$ locations decrease, while the cross-polarized power levels around broadside directions are not much affected.

6. Large Finite Array Antennas

Numerous methods have been proposed by researchers to predict the finite array pattern with the knowledge of mutual coupling, radar cross-section, infinite array data and small array data from both simulation and measurements [7,23]. In this section, we propose a new approach that extends the near-field FDTD characterization of small sub-arrays to larger scale arrays. The solution applies to both planar and cylindrical arrays. To implement this method for facet-cylindrical arrays, there is a fundamental issue since the intersection of CPMLs with the nonorthogonal grid cannot support orthogonal field components in those regions. This issue can be resolved by using the local sub-gridding technique, which is beyond the scope of this research.

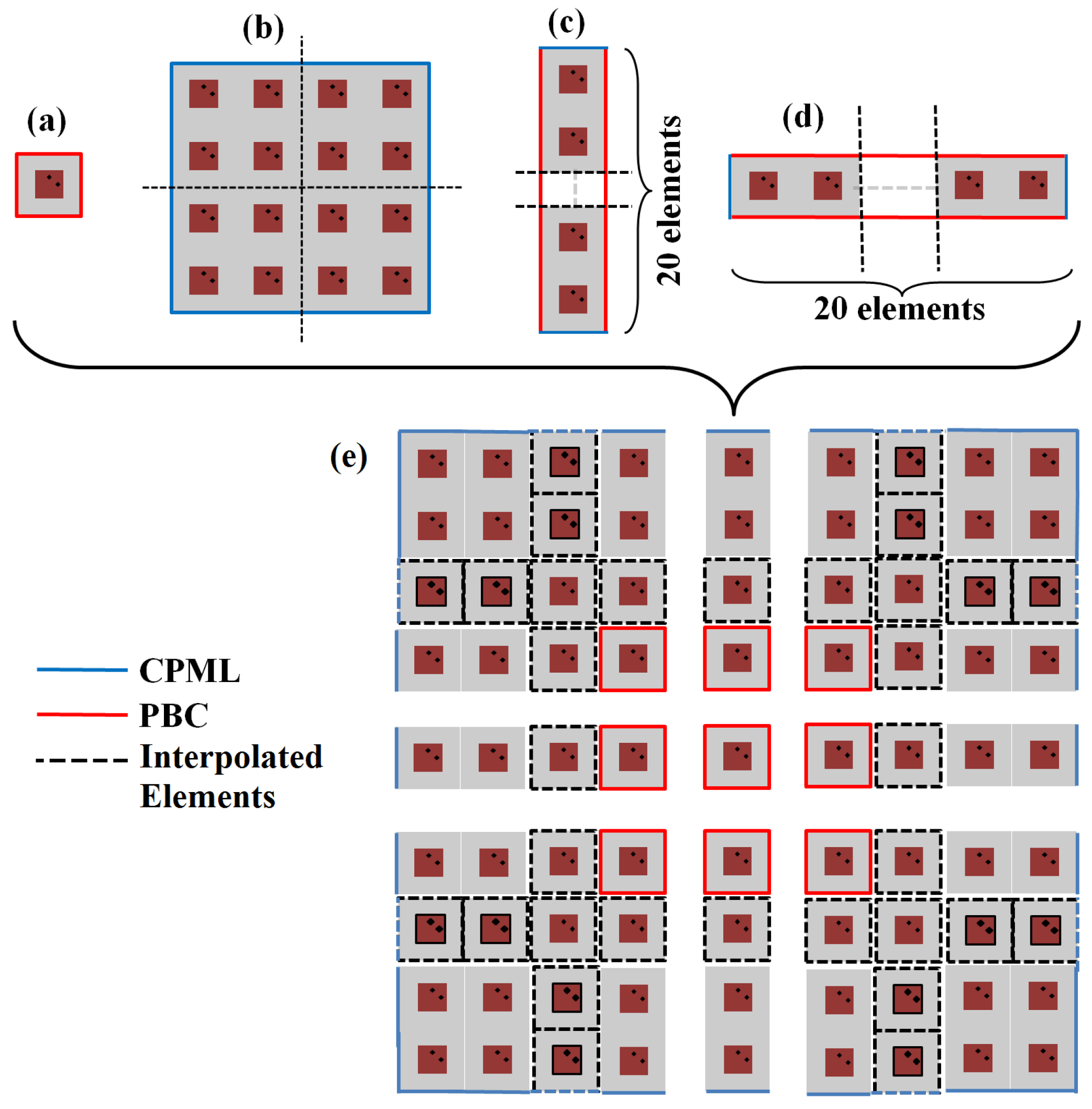
6.1. Near-Field Aperture Merging Technique

Given a radiating element design, an approach is developed that can merge the near-field patterns of smaller subarrays to arbitrarily-sized large arrays and achieve a good compromise between computational loads and full-wave accuracies. Within the FDTD time marching loop, the electric and magnetic current densities on the designated imaginary surface are collected in the first step, which is used to calculate the near-field to far-field transformation. The frequency domain or time domain current densities can also be collected. For the proposed procedure herein, the frequency domain current values are used for the near-field to far-field transformation calculations. Four separate simulations are performed firstly as the building blocks, and they are illustrated, in Figure 16a–d. The first building block is an active element in an infinite array (infinite-by-infinite array with periodicities in both the $\widehat{x}$ and $\widehat{y}$ directions). The second and third are semi-infinite arrays (20-by-infinite array with the periodicity in the $\widehat{y}$ direction and infinite-by-20 array, which periodically repeats in the $\widehat{x}$ direction). The fourth building block is a finite array (four-by-four). These four simulations can be done simultaneously using four cores of a computer. For each of the simulation runs, the current densities in the frequency domain are collected at strategic locations. For example, in the simulation illustrated by the array (a) in Figure 16, current densities on the surfaces in the $+\widehat{z}$ and $-\widehat{z}$ directions are collected. The edges of a large array are constructed with the array simulation illustrated with the array (b) and the array (c) in Figure 16. The current distribution on surfaces in the $+\widehat{z}$ and $-\widehat{z}$ directions is gathered for the first two and the last two elements of both arrays in the frequency domain. The 20-by-infinite building block has CPMLs in the $+\widehat{x}$ and $-\widehat{x}$ directions, and the infinite-by-20 building block has CPMLs in the $+\widehat{y}$ and $-\widehat{y}$ directions. These current densities are used to merge and combine the near-field samples (current density components) of a large finite array. During the merging process, the current distributions over the entire surface of the large finite array are re-constructed based on the current densities collected from the building blocks. In addition, the current distributions on the surfaces next to the periodic boundaries are discarded, and the current distributions on the surfaces next to the CPML are used.

Figure 16. Illustration of the finite array antenna simulation. (a) Infinite-by-infinite array; (b) small finite-by-finite array; (c) finite-by-infinite array; (d) infinite-by-finite array; and (e) large finite-by-finite array computation using (a), (b), (c), and (d).

The array (e) in Figure 16 shows the assembly of all of the near-field current densities in the frequency domain for a planar array. The elements indicated with dashed lines represent surfaces with interpolated current densities using adjacent elements, which ensure a smooth transition from one element to the next throughout the array. After this assembly, the process of near-field to far-field transformation is computed to simulate the far-field radiation pattern of an arbitrarily large finite-by-finite array.

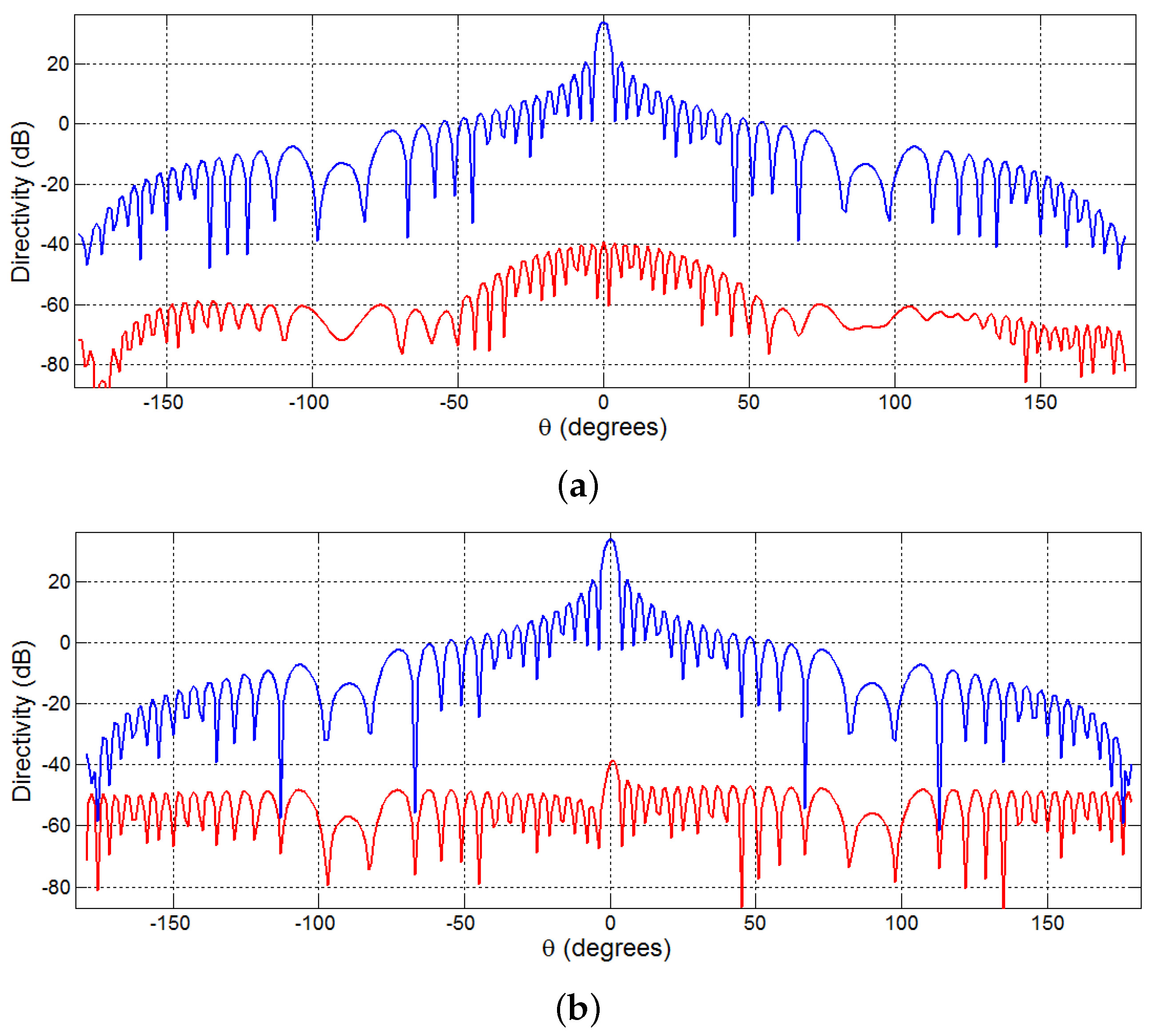
6.2. Simulation of Larger Scale Cylindrical and Facet Arrays

Compared to planar arrays, large-scale faceted-cylindrical or cylindrical arrays can take better advantage of the PBC in the azimuth direction. As a result, the technique from the previous section is only needed for the vertical direction of a faceted-cylindrical array or partially-populated faceted-cylindrical arrays. As PBC is used, the computational load for a larger cylindrical array is not significantly greater than a smaller-sized array, and convergence may be easier to achieve since there is less curvature effect. As an example, Figure 7 shows the principal plane cut of a simulated AEP from a large size $100\lambda$ diameter cylindrical array. For this case, there is no testbed system of that size yet, and other commercial simulators cannot provide comparable results. However, the AEP is consistent with some theoretical and analytical predictions, such as the zoom-in area of the main lobe, which shows the expected ripples generated in AEP due to the conformal surface.

6.3. Simulation of Larger Scale Planar Arrays

Figure 17 compares results from HFSS simulation and the proposed solution for an eight-by-eight dual-polarized patched antenna array. The cross-polarization patterns of the horizontal and vertical principal plane cuts are similar to the HFSS results, while for the Phased Array Simulator (PASim) simulation results, more ripples are shown in the broadside direction. Both results show lower cross-pol levels than measurements due to the modeling process. We need to point out that the grid scheme in PASim is not as sophisticated as the one used in commercially available software. In future work, PASim will be improved with locally none-structured and nonorthogonal grids, which can model the electromagnetic structure more accurately.

Figure 17. Principal plane cuts of eight-by-eight array simulations and measurements. Simulation patterns were generated by HFSS and PASim. Measured patterns were generated using near field measurements of each active element of the array. (a) Horizontal principal plane cut; (b) Vertical principal plane cut.

Figure 18 shows both the azimuth principal plane cut (Figure 18a) and elevation principal plane cut (Figure 18b) of a 32-by-32 planar array simulation (1024 elements). Both HFSS and PASim simulations were done only for calculation principal plane cut results, and only one CPU core is used for both. For PASim, this 32-by-32 array simulation used the similar computational resources as that of the eight-by-eight simulation. For our particular PC platform (i7-5960X CPU with 64 GB RAM), the simulations of eight-by-eight and 32-by-32 arrays are done in 334 and 354 min, respectively, while for HFSS, the simulation of the eight-by-eight array was done in about 96 h (four days), and the 32-by-32 array simulation was not performed for the current experiment.

Figure 18. Principal plane cut of 32-by-32 array simulations using the PASim program. The blue and red plots are respectively co-polar and cross-polar directivity patterns of each principal plans. (a) Horizontal principal plane cut; (b) Vertical principal plane cut.

7. Summary and Conclusions

This work introduces an approach that combines FDTD-EM simulation and chamber-laboratory measurements for the challenges of the precise characterization of dual-polarized array antennas for multi-functional radars. The traditional FDTD for different coordinate systems and domain termination boundary conditions are implemented in a Java language-based, computationally-efficient software. This unique character of the software tool enables full-wave simulation of a wide variety of array configurations from the small laboratory scale to large field system scales, such as planar arrays, fully-conformal cylindrical arrays and faceted-cylindrical arrays. The fidelity of the EM simulation is validated by using a laboratory array testbed (CPAD) and a near-field chamber measurement. A simple array alignment approach is used to generate dual-polarized, three-dimensional and focused radiation beams from both simulated and measured AEPs. The EM simulation is then extended to large-scale array systems through a new near-field aperture merging technique, and reasonable results are obtained.

An interesting contribution of this work is comparing the dual-polarized pattern characteristics for planar and faceted-cylindrical arrays. CPAD allows both configurations with the same aperture size in hardware. The comparison reveals that the far-end sidelobes of cylindrical array radiation patterns are more significant for a smaller cylinder radius, which is consistent with theoretical predictions and EM simulations. On the other hand, there are no real significant advantages of cross-polarization levels for a particular radiation direction.

There is much future work expected related to this study. Since the simulation and measurements are based on AEP, array pattern optimizations are naturally next steps to improve the co-pol and cross-pol pattern performance generated using simple alignments. Computational speed needs to be enhanced through more efficient, C-language implementation and applications on the General-Purpose Graphic Processing Unit (GPGPU). Validations through measurements will be more comprehensive as larger field-scale systems and chambers become available.