Testing-Based Approach to Determining the Divergence Speed of Slung Loads
Abstract
:1. Introduction
2. Review on Approaches to Slung-Load Aeromechanics
2.1. Flight Test Data
2.2. Wind-Tunnel Data
2.3. Dynamics Analysis
2.4. Computational Analyses
2.5. Need for Comprehensive Analyses
2.6. Control Approaches
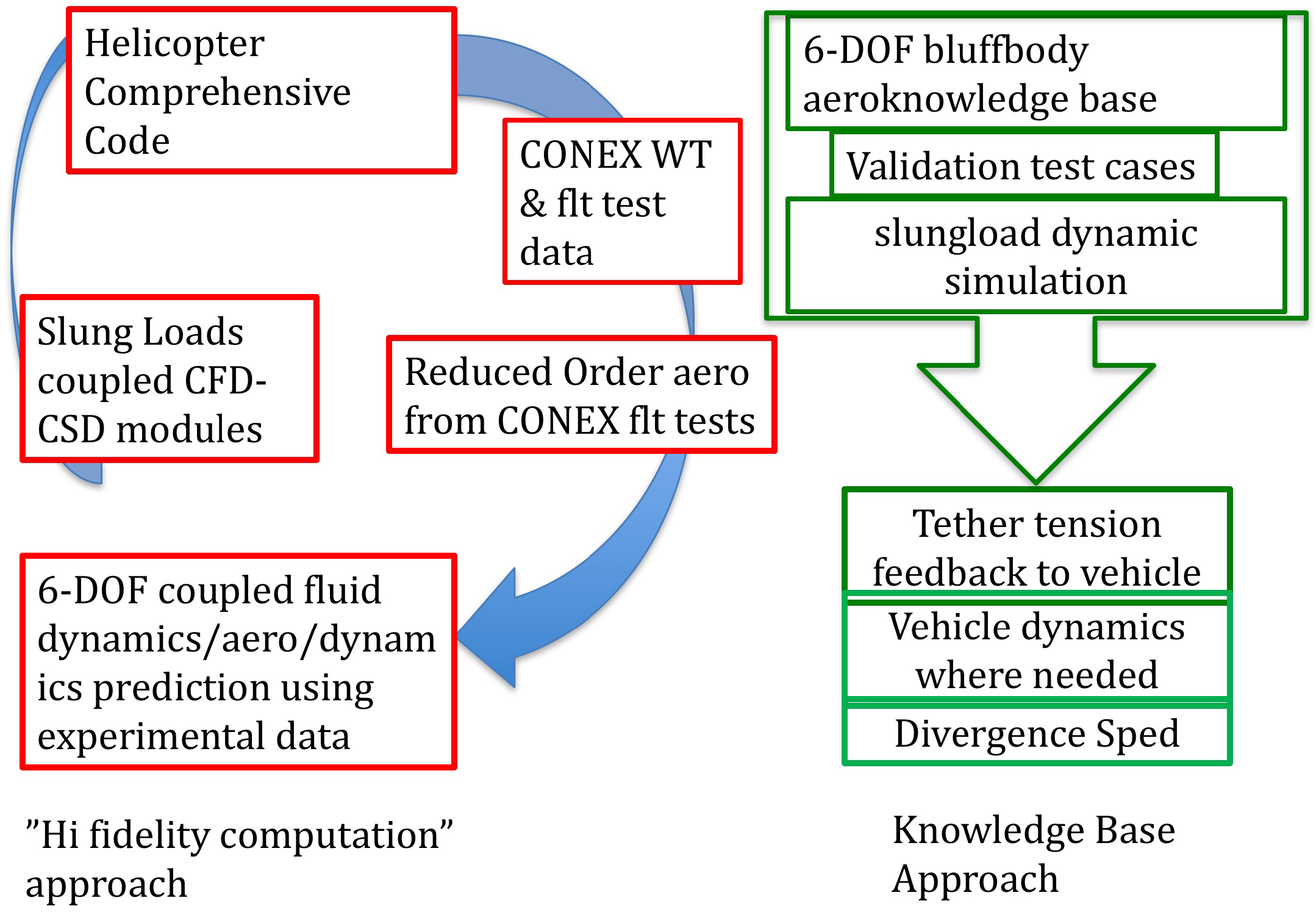
3. Status Summary and Evolution of Approach
- There is a very large and rising number of combinations of flight vehicle and slung objects, where certification of the limiting speed must be performed and available for each mission.
- The full problem involves two-body dynamics (3 in the case of artillery pieces that have their ammunition slung below the weapon) of the vehicle and the slung load.
- Prediction of the aeromechanics of a slung load was presumed to require a coupled fluid–structure interaction high-fidelity computation.
- High spatial and temporal resolution was required from the computational grid because of the complex geometry and the high Reynolds number.
- Wind-tunnel experiments provided a low-cost but tedious avenue to provide datasets to validate computational fluid dynamics codes at moderate Reynolds numbers, with limited flight experiments to validate high-Reynolds-number flight conditions.
4. Simplified Problem Statement
- Froude number scaling holds accurately between flight tests and wind-tunnel tests, across a wide spectrum of Reynolds numbers. This is primarily due to the bluff body shapes with sharp edges used in validation. Some doubt remained about smooth-surface separation and vortex shedding from cylindrical tanks.
- Military experience indicates that for loads that are less than 1/3 of the gross weight of the vehicle, the effects of the dynamics of the swinging load on the vehicle dynamics are minimal. Thus, slung-load dynamics can be decoupled for a first iteration from those of the vehicle. This assumption is usually satisfied with human-piloted rotorcraft since either the external load capability, or the flight speed, is limited by performance. Obviously the assumption may be violated in case of violent oscillations, but the purpose of prediction is to stay at speeds where such oscillations cannot occur.
- The Froude number results lead to the belief that aerodynamic coefficients obtained in wind-tunnel tests should be reasonably representative of high-Reynolds-number flight results, once tunnel-wall and support interference effects are held to negligible levels.
- The frequencies and rates encountered in slung-load operations stay well within the regime of low-reduced-frequency, quasi-steady aerodynamics.
- Structural deformations such as tether elastic deformation are negligible, and tethers may be assumed to be rigid. Two exceptions occur: the first is when the tethers wind up in cases of rigid mounting points, and the second is where the oscillations become violent. The first regime is typically limited to hover and low-speed operation where the wake swirl causes steady yaw in one direction. For high-speed flight, experience shows that having a free-to-spin bearing at the attachment point enables operation to significantly higher speeds. The other regime must be avoided by staying below the speed where significant amplification occurs.
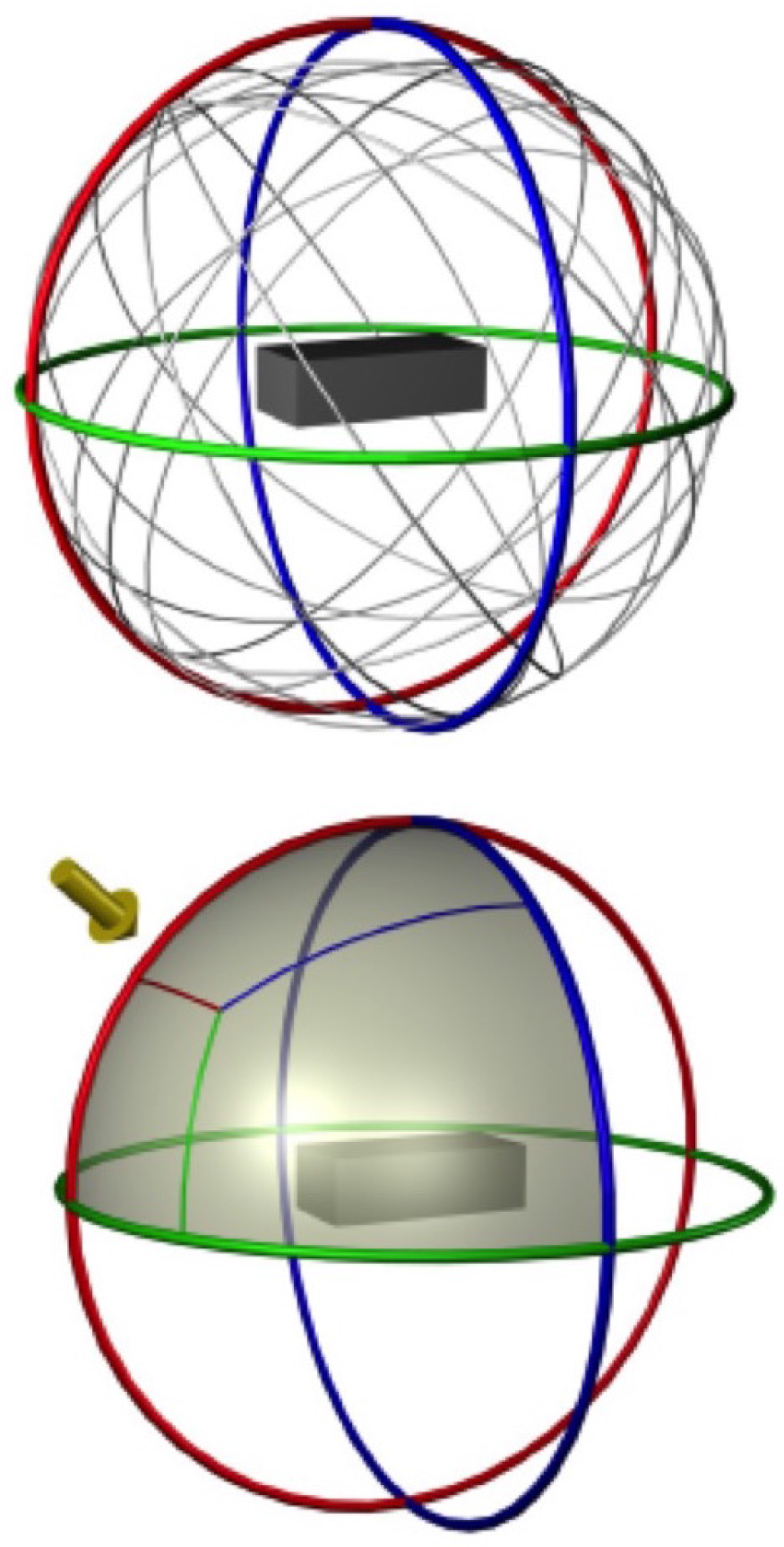
5. Continuous Rotation Method
- Models with sharp edges and flat sides may be highly sensitive to yaw, and this is key to understanding the onset of interactions causing instabilities. This requires many yaw points to define slopes and transitions.
- For each yaw setting, the model must be set precisely at a given attitude for data acquisition, and the attitude verified. This requires accounting for support deflection under load.
- For the above reasons, data come with non-uniform spacing, requiring a lookup table and interpolation of doubtful validity during dynamic simulation. This is because sharp changes can occur, for instance in side force and moments, over a small change in orientation. For instance, if one interpolated from degrees to +8 degrees angle of attack, for the lift coefficient of a sharp-edged flat plate, a 16-degree interval typical of those used in bluff body wind tunnel tests and computational fluid dynamics (CFD), one might entirely miss the region of greatest importance to aerodynamics. Most cases are not that extreme, but we do not know enough yet to generalize and be sure.
- Symmetry assumptions are generally not valid.
- Reynolds number effects are hard to predict.
- Interactions between degrees of freedom are hard to predict.
6. Divergence Prediction
7. Conclusions
- For loads that are less than 30 percent of the gross weight of the rotorcraft, the feedback from the dynamics of the load to the rotorcraft is negligible. This is primarily because the main rotor has a very large moment of inertia, and this dominates the moment of inertia of the vehicle. Human-piloted rotorcraft have fairly low payload fractions. Most situations where divergence is a concern are cases where the slung load is light and has low inertia, so that the vehicle can fly fast. This means that where divergence is a concern with human-piloted rotorcraft, the load is significantly below 30 percent of gross weight.
- The continuous rotation method has been used with high productivity to capture air loads, likely modes of instability, and divergence speeds of several shapes.
- Aerodynamic coefficient maps have been obtained covering all relevant attitudes with excellent resolution and accuracy, on several classes of canonical and practical shapes. These enable rapid interpolation and synthesis of aerodynamic data for new shapes, for a first estimate of divergence speed, preceding actual wind-tunnel tests. Errors up to 10 percent error in aerodynamic loads have little effect on the divergence speed.
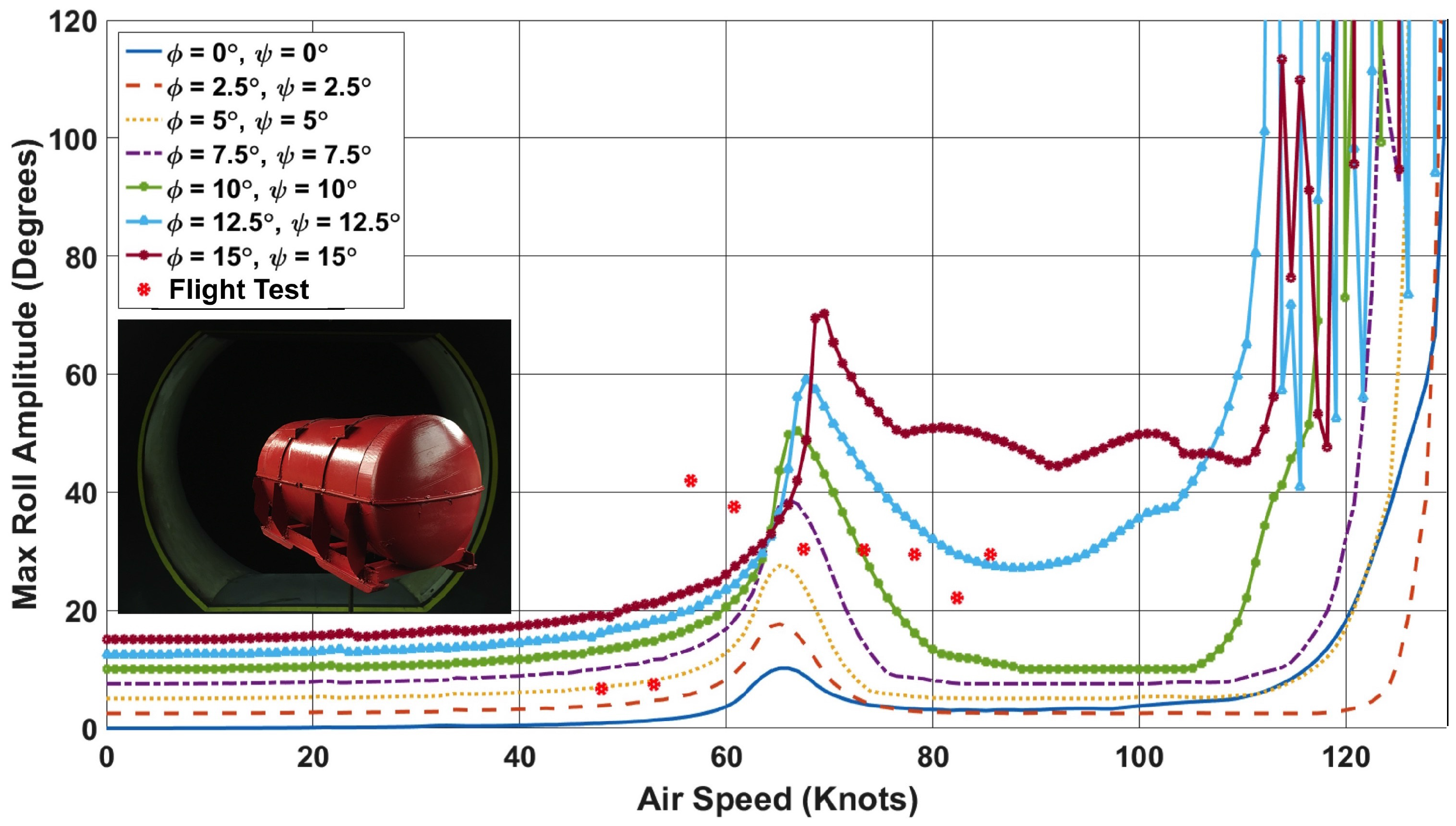
- Froude-scaled model results from a small low-speed wind tunnel have correlated well with full-scale flight tests on cuboid (CONEX) containers.
- Where the vehicle has a high payload fraction, amplification of roll oscillations occurring due to air disturbances occurring while flying near the divergence speed could be suppressed using fast vehicle maneuvers. Such maneuvers require high bandwidth and are hence better suited to uninhabited aerial vehicles (UAVs).
- For the test case of a cylindrical engine canister, measurements of the object geometry were made from a technical description. An initial approximation of the geometry was made immediately, and the aerodynamic load map obtained by interpolating the existing Continuous Rotation (CR) knowledge base. Dynamic simulations were run using these data, and correctly captured the roll and pitch angle excursions that led to the flight test being ended.
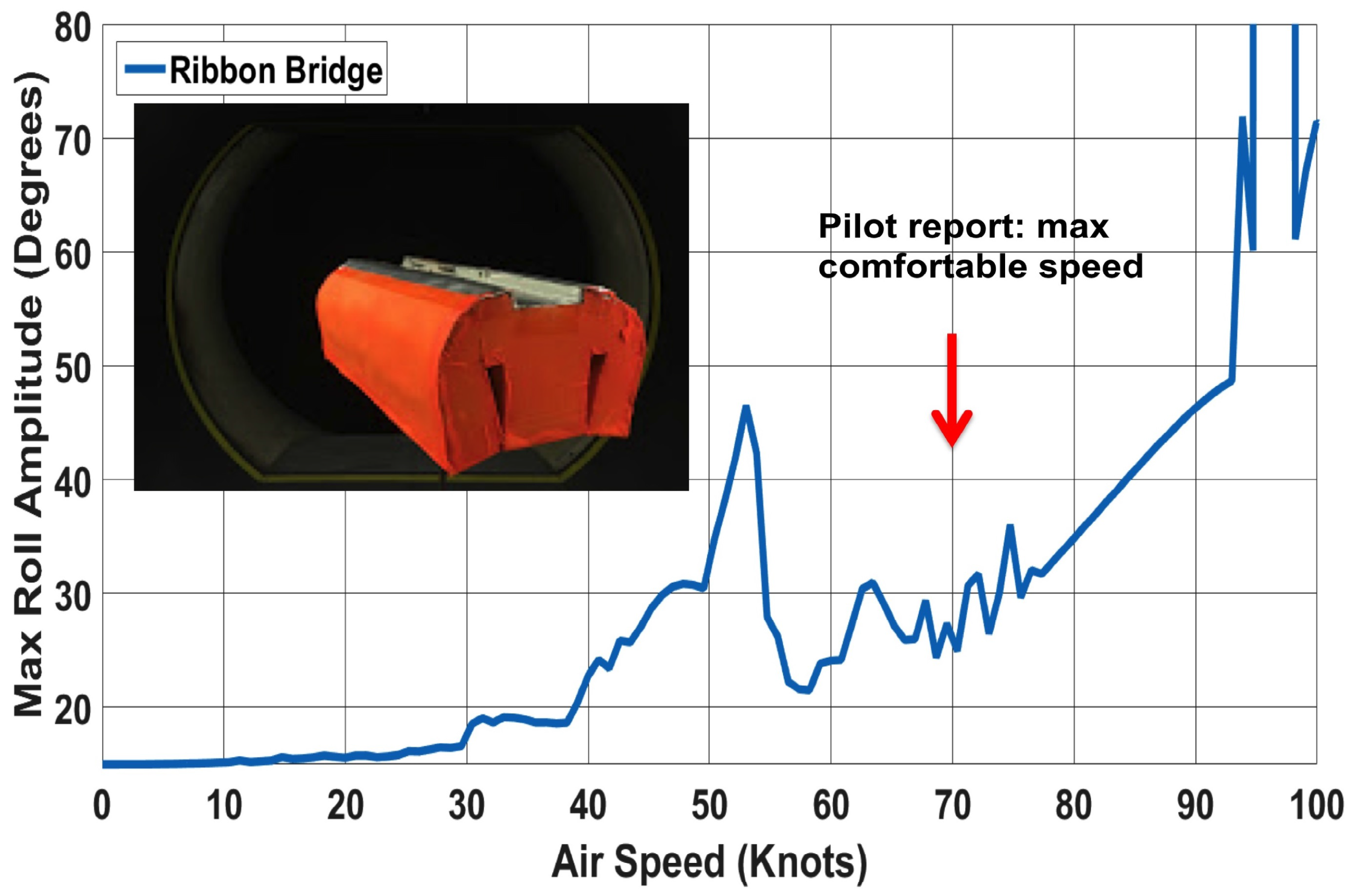
- For the test case of a ribbon bridge, wind-tunnel tests were conducted with a scale model, and the data were used in the simulation to successfully capture the roll and trail angle history. This was shown up to the speed where the actual flight test was stopped, and beyond.
- The instabilities that amplify appear to stem from a very few classes of interactions.
- With these demonstrations, it appears that the original problem of predicting the safe flight envelope of helicopters carrying arbitrary slung-load shapes is solved.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Anon. Multiservice Helicopter Sling Load: Single-Point Load Rigging Procedures; Technical Report; US Air Force: Washington, DC, USA, 2003.
- Anon. Multiservice Helicopter Sling Load: Basic Operations and Equipment. In Technical Memorandum TM 4-48.09 (FM 4-20.197) MCRP 4-11.3, Vol. INTTP 3-04.11 AFMAN 11-223 (I), Vol I COMDINST M13482.2B; United States Department of Defense, Headquarters, Departments of the Army, Navy, Marine Corps and Air Force: Washington, DC, USA, 2012. [Google Scholar]
- Dudley, M.; Greenhoe, G. Fifty years of helicopter firefighting. Fire Manag. Notes 1998, 58, 6–7. [Google Scholar]
- Matheson, N. Helicopter Slung Load Instabilities; Aerodynamics Note 364; Department of Defence, Defense Science and Technology Organisation, Aeronautical Research Laboratories: Melbourne, VIC, Australia, 1976. [Google Scholar]
- Starr, G.; Wood, J.; Lumia, R. Rapid Transport of Suspended Payloads. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2005; pp. 1394–1399. [Google Scholar]
- Grigel, J. Role of the Helitanker in Forest Fire Control; Information Report NOR-X-123; Enviroment Canada, Northern Forest Research Centre, Canadian Forestry SErvice: Edmonton, AB, Canada, 1974. [Google Scholar]
- De Voogt, A.J.; Uitdewilligen, S.; Eremenko, N. Safety in high-risk helicopter operations: The role of additional crew in accident prevention. Saf. Sci. 2009, 47, 717–721. [Google Scholar] [CrossRef]
- Stuckey, R. Dynamic Simulation of the CH-47D Helicopter and Externally Slung Boat. In Proceedings of the 3rd Australia Pacific Vertiflite Conference on Helicopter Technology, American Helicopter Society (AHS), Melbourne, Australia, 18–19 December 2000. [Google Scholar]
- Key, D.L. Airworthiness Qualification Criteria for Rotorcraft With External Sling Loads; Technical Report; NASA Ames Research Center: Moffett Field, CA, USA, 2002. [Google Scholar]
- Cicolani, L.S.; McCoy, A.H.; Sahai, R.; Tyson, P.H.; Tischler, M.B.; Rosen, A.; Tucker, G.E. Flight Test Identification and Simulation of a UH-60A Helicopter and Slung Load. J. Am. Helicopter Soc. 2001, 46, 140–160. [Google Scholar] [CrossRef]
- Cicolani, L.; Kanning, G. General Equilibrium Characteristics of a Dual-Lift Helicopter System; TP 2615; NASA: Washington, DC, USA, 1986. [Google Scholar]
- Cicolani, L.; Raz, R.; Rosen, A.; Gordon, R.; Cone, A.; Theron, J.; Lusardi, J.; Tischler, M.; Robinson, D. Flight Test, Simulation and Passive Stabilization of a Cargo Container Slung Load in Forward Flight. In Proceedings of the American Helicopter Society Annual Forum, Virginia Beach, VA, USA, 1–3 May 2007; Volume 63, p. 2177. [Google Scholar]
- Cicolani, L.; Lusardi, J.; Greaves, L.; Robinson, D.; Rosen, A.; Raz, R. Flight Test Results for the Motions and Aerodynamics of a Cargo Container and a Cylindrical Slung Load; Technical Paper TP 216380; NASA: Washington, DC, USA, 2010. [Google Scholar]
- Cicolani, L.; Kanning, G. A Comprehensive Estimate of the Static Aerodynamic Forces and Moments of the 8- by 8- by 20-Foot Cargo Container; Technical Report 89433; NASA: Washington, DC, USA, 1987. [Google Scholar]
- Thompson, T.; Thorpe, K. Final Report of Helicopter Sling-Load Working Working Group; Technical Report AMR-AE-06-01; Aviation and Missile Research, Development and Engineering Center: Huntsville, AL, USA, 2006. [Google Scholar]
- Cicolani, L.; Ivler, C.; Ott, C.; Raz, R.; Rosen, A. Rotational stabilization of cargo container slung loads. J. Am. Helicopter Soc. 2015, 60, 1–13. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Hoerner Fluid Dynamics: Midland Park, NJ, USA, 1965. [Google Scholar]
- Warner, E.P.; Norton, F.H. Wind Tunnel Balances; Report 72; National Advisory Committee for Aeronautics, Bureau of Construction and Repair (Navy): Washington, DC, USA, 1920. [Google Scholar]
- Zham, A. The Six-Component Wind Balance; Report 146; Aerodynamical Laboratory, U.S. Navy: Washington, DC, USA, 1922. [Google Scholar]
- Goldberg, C. Wind Tunnel Balance. U.S. Patent 2,380,516, 31 July 1945. [Google Scholar]
- Trimble, G.S. Six Component Balance for Wind Tunnels. U.S. Patent 2,768,526, 30 October 1956. [Google Scholar]
- Gieseler, L.P. Wind Tunnel Roll-Moment Balance. U.S. Patent 2,865,200, 23 December 1958. [Google Scholar]
- Ormond, A.N. Force Measuring Instrument. U.S. Patent 2,918,816, 29 December 1959. [Google Scholar]
- Kutsay, A.U. Strain Detecting Load Cell. U.S. Patent 3,695,096, 3 October 1959. [Google Scholar]
- Zipin, R.B. Multi-Axis Load Cell. U.S. Patent 3,939,704, 24 January 1976. [Google Scholar]
- Wasko, B. Precision Balance. U.S. Patent 3,955,638, 11 May 1976. [Google Scholar]
- Dubois, M. Six-Component Strain-Gage Balances for Large Wind Tunnels. Exp. Mech. 1981, 21, 401–407. [Google Scholar] [CrossRef]
- Meyer, R.A.; Olson, D.J. Six Axis Load Cell. U.S. Patent 5,315,882, 31 May 1994. [Google Scholar]
- Almeida, R.A.; Vaz, D.C.; Urgueira, A.P.; Borges, A.J. Using ring strain sensors to measure dynamic forces in wind-tunnel testing. Sens. Actuators A Phys. 2012, 185, 44–52. [Google Scholar] [CrossRef]
- Green, J.; Quest, J. A short history of the European Transonic Wind Tunnel ETW. Prog. Aerosp. Sci. 2011, 47, 319–368. [Google Scholar] [CrossRef]
- Habéis, T.A. The 7 by 10 Foot Wind Tunnel of the National Advisory Committee for Aeronautics; Report; NASA: Washington, DC, USA, 1933. [Google Scholar]
- Pope, A.; Harper, J.J. Low Speed Wind Tunnel Testing; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1966. [Google Scholar]
- Horanoff, E.V. Wind Tunnel Balance. U.S. Patent 3,447,369, 3 June 1969. [Google Scholar]
- Pinier, J.; Hanke, J.L.; Tomek, W.G. Ares I Aerodynamic Testing at the Boeing Polysonic Wind Tunnel. J. Spacecr. Rocket. 2012, 49, 853–863. [Google Scholar] [CrossRef]
- Mehta, R.D. Aerodynamics of sports balls. Ann. Rev. Fluid Mech. 1985, 17, 151–189. [Google Scholar] [CrossRef]
- Jones, T.W.; Lunsford, C.B.; Graves, S.S. Design and development of a real-time model attitude measurement system for hypersonic facilities. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- DeLoach, R. The modern design of experiments: A technical and marketing framework. In Proceedings of the 21st AIAA Advanced Measurement Technology and Ground Testing Conference, Denver, CO, USA, 19–22 June 2000; Volume 2691. [Google Scholar]
- Raz, R.; Rosen, A.; Carmeli, A.; Lusardi, J.; Cicolani, L.; Robinson, D. Wind Tunnel and Flight Evaluation of Passive Stabilization of a Cargo Container Slung Load. J. Am. Helicopter Soc. 2010, 55, 032001. [Google Scholar] [CrossRef]
- Rosen, A.; Cecutta, S.; Yaffe, R. Wind Tunnel Tests of Cube and CONEX Models. Technion Inst. Technol. Dep. Aerospace Eng. Haifa Israel TAE 1999. [Google Scholar]
- Gabel, R.; Wilson, G.J. Test approaches to external sling load instabilities. J. Am. Helicopter Soc. 1968, 13, 44–55. [Google Scholar]
- Nakamura, Y. Bluff-Body Aerodynamics and Turbulence. J. Wind Eng. Ind. Aerodyn. 1993, 49, 65–78. [Google Scholar] [CrossRef]
- Zdravkovich, M.; Brand, V.; Mathew, G.; Weston, A. Flow past short circular cylinders with two free ends. J. Fluid Mech. 1989, 203, 557–575. [Google Scholar] [CrossRef]
- Zdravkovich, M.; Flaherty, A.; Pahle, M.; Skelhorne, I. Some aerodynamic aspects of coin-like cylinders. J. Fluid Mech. 1998, 360, 73–84. [Google Scholar] [CrossRef]
- Greenwell, D. Modelling of static aerodynamics of helicopter underslung loads. Aeronaut. J. 2011, 115, 201–219. [Google Scholar] [CrossRef]
- Koenig, K.; Roshko, A. An experimental study of geometrical effects on the drag and flow field of two bluff bodies separated by a gap. J. Fluid Mech. 1985, 156, 167. [Google Scholar] [CrossRef]
- Lee, B. Some Observations of the Effect of Aspect Ratio on the Influence of Turbulence on the Drag of Rectangular Cylinders. J. Wind Eng. Ind. Aerodyn. 1990, 33, 107–111. [Google Scholar] [CrossRef]
- Windsor, R. Wind Tunnel Tests of Two Models of Rectangular Containers; Report 573; Glenn Martin Wind Tunnel, University of Maryland: College Park, MD, USA, 1970. [Google Scholar]
- Roshko, A. Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech 1961, 10, 345–356. [Google Scholar] [CrossRef]
- Matsumoto, M. Vortex Shedding of Bluff Bodies: A Review. J. Fluids Struct. 1999, 13, 791–811. [Google Scholar] [CrossRef]
- Komatsu, S.; Kobayashi, H. Vortex-Induced Oscillation of Bluff Cylinders. J. Wind Eng. Ind. Aerodyn. 1980, 6, 335–362. [Google Scholar] [CrossRef]
- King, R. A Review of Vortex Shedding Research and Its Application. Ocean Eng. 1977, 4, 141–171. [Google Scholar] [CrossRef]
- Barnes, F.H.; Grant, I. Vortex Shedding in Unsteady Flow. J. Wind Eng. Ind. Aerodyn. 1983, 11, 335–344. [Google Scholar] [CrossRef]
- Bearman, P.; Morel, T. Effect of free stream turbulence on the flow around bluff bodies. Prog. Aerosp. Sci. 1983, 20, 97–123. [Google Scholar] [CrossRef]
- Bentley, J.; Mudd, J. Vortex Shedding Mechanisms in Single and Dual Bluff Bodies. Flow Meas. Instrum. 2003, 14, 23–31. [Google Scholar] [CrossRef]
- Wei, C.; Chang, J. Wake and Base-Bleed Flow Downstream of Bluff Bodies with Different Geometry. Exp. Therm. Fluid Sci. 2002, 26, 39–52. [Google Scholar] [CrossRef]
- Bearman, P.; Tombazis, N. The Effects of Three-Dimensional Imposed Disturbances on Bluff Body Near Wake Flows. J. Wind Eng. Ind. Aerodyn. 1993, 49, 339–350. [Google Scholar] [CrossRef]
- Sharma, S.; Komerath, N.; Raghav, V. Aerodynamic Instability Modes for a Load Slung From a Helicopter. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Houston, TX, USA, 9–15 November 2012; pp. 481–489. [Google Scholar]
- Sharma, S.; Raghav, V.; Komerath, N. Efficient Modeling of Dynamic Blockage Effects for Unsteady Wind Tunnel Testing. In Proceedings of the 69th American Helicopter Society Annual Forum, Phoenix, AZ, USA, 21–23 May 2013. [Google Scholar]
- Swanson, W. The Magnus effect: A summary of investigations to date. J. Basic Eng. 1961, 83, 461–470. [Google Scholar] [CrossRef]
- Szepessy, S.; Bearman, P. Aspect ratio and end plate effects on vortex shedding from a circular cylinder. J. Fluid Mech. 1992, 234, 191–217. [Google Scholar] [CrossRef]
- Norberg, C. An experimental investigation of the flow around a circular cylinder: Influence of aspect ratio. J. Fluid Mech. 1994, 258, 287–316. [Google Scholar] [CrossRef]
- Sheldon, D.; Pryor, J. Study in Depth of a Single Point and Two Point Lateral and Tandem Suspension of Rectangular Box Loads; Technical Note AM 38; The Royal Military College of Science: Shrivenham, UK, 1973. [Google Scholar]
- Nagabhushan, B.L. Systematic Investigation of Models of Helicopter With a Slung Load. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1977. [Google Scholar]
- Micale, E.C.; Poli, C. Dynamics of Sling Bodies using a Rotating Wheel for Stability. J. Aircr. 1973, 10, 80–86. [Google Scholar] [CrossRef]
- Watkins, T.; Sinacori, J.; Kesler, D. Stabilization of Externally Slung Helicopter Loads; Technical Report TR-74-42; USAAMRDL: Moffett Field, CA, USA, 1974. [Google Scholar]
- Reddy, K.; Truong, T.; Stuckey, R.; Bourne, K. Dynamic simulation of a helicopter carrying a slung load. In Proceedings of the International Congress on Modeling and Simulation, University of Canterbury, Christchurch, New Zealand, 10–13 December 2007; pp. 2740–2746. [Google Scholar]
- Feaster, L.; Poli, C.; Kirchhoff, R. Dynamics of a Slung Load. J. Aircr. 1977, 14, 115–121. [Google Scholar] [CrossRef]
- Tyson, P.; Cicolani, L.; Tischler, M.; Rosen, A.; Levine, D.; Dearing, M. Simulation Prediction and Flight Validation of the UH-60A Black Hawk Slung Load Characteristics. In Proceedings of the American Helicopter Society Annual Forum, Montreal, QC, Canada, 25–27 May 1999; Volume 55, pp. 2075–2100. [Google Scholar]
- Bernard, M.; Kondak, K. Generic slung load transportation system using small size helicopters. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3258–3264. [Google Scholar]
- Bisgaard, M.; Bendtsen, J.D.; Cour-Harbo, L.; Anders. Modelling of Generic Slung Load System. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Bisgaard, M.; la Cour-Harbo, A.; Bendtsen, J.D. Adaptive control system for autonomous helicopter slung load operations. Control Eng. Pract. 2010, 18, 800–811. [Google Scholar] [CrossRef]
- Cicolani, L.S.; Cone, A.; Theron, J.N.; Robinson, D.; Lusardi, J.; Tischler, M.B.; Rosen, A.; Raz, R. Flight test and simulation of a cargo container slung load in forward flight. J. Am. Helicopter Soc. 2009, 54, 32006. [Google Scholar] [CrossRef]
- Fusato, D.; Guglieri, G.; Celi, R. Flight Dynamics of an Articulated Rotor Helicopter with an External Slung Load. In Proceedings of the 55th American Helicopter Society Annual Forum, Montreal, QC, Canada, 25–27 May 1999. [Google Scholar]
- Oktay, T.; Sultan, C. Modeling and control of a helicopter slung-load system. Aerosp. Sci. Technol. 2013, 29, 206–222. [Google Scholar] [CrossRef]
- Palunko, I.; Fierro, R.; Cruz, P. Trajectory generation for swing-free maneuvers of a quadrotor with suspended payload: A dynamic programming approach. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 2691–2697. [Google Scholar]
- Stuckey, R.A. Mathematical Modelling of Helicopter Slung-Load Systems; Technical Report DSTO-TR-1257; Australian Government Department of Defence, Defence Science and Technology Organisation: Melbourne, VIC, Australia, 2001.
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Bonhaus, D. An Upwind Multigrid Method For Solving Viscous Flows On Unstructured Triangular Meshes. Master’s Thesis, George Washington University, Washington, DC, USA, 1993. [Google Scholar]
- Theron, J.; Gordon, R.; Rosen, A.; Cicolani, L.; Duque, E.; Halsey, R. Simulation of Helicopter Slung Load Aerodynamics: Wind tunnel validation of two computational fluid dynamics codes. In Proceedings of the 36th AIAA Fluid Dynamics Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Mantri, R.; Raghav, V.; Komerath, N.; Smith, M.J. Stability Prediction of Sling Load Dynamics Using Wind Tunnel Models. In Proceedings of the 67th American Helicopter Society Annual Forum, Virginia Beach, VA, USA, 3–5 May 2011. [Google Scholar]
- Prosser, D.; Smith, M. Navier-Stokes-Based Dynamic Simulations of Sling Loads. In Proceedings of the 54th AIAA Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar]
- Raghav, V.; Mantri, R.; Komerath, N.; Smith, M. Study of Factors Driving Pitch, Roll and Yaw Coupling in Bluff Body Aerodynamics. In Proceedings of the AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar]
- Beard, R. Quadrotor Dynamics and Control Rev 0.1; Technical Report; Brigham Young University: Provo, UT, USA, 2008. [Google Scholar]
- De Crousaz, C.; Farshidian, F.; Neunert, M.; Buchli, J. Unified motion control for dynamic quadrotor maneuvers demonstrated on slung load and rotor failure tasks. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2223–2229. [Google Scholar]
- Ivler, C. Design and Flight Test of a Cable Angle Feedback Control System for Improving Helicopter Slung Load Operations at Low Speed; Technical Report; AMRDEC, Aeroflightdynamics Directorate: Moffett Field, CA, USA, 2014. [Google Scholar]
- Lee, S.J.; Kim, H.J. Autonomous swing-angle estimation for stable slung-load flight of multi-rotor UAVs. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4576–4581. [Google Scholar]
- Krishnamurthi, J.; Horn, J.F. Helicopter Slung Load Control Using Lagged Cable Angle Feedback. J. Am. Helicopter Soc. 2015, 60, 1–12. [Google Scholar] [CrossRef]
- Johnson, N.A. Control of a Folding Quadrotor with a Slung Load Using Input Shaping. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2017. [Google Scholar]
- Kui, Y.; Feng, G.; Liying, Y.; Yuqing, H.; Jianda, H. Sliding mode control for a quadrotor slung load system. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 3697–3703. [Google Scholar]
- Mo, R.; Geng, Q.; Lu, X. Study on control method of a rotor UAV transportation with slung-load. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 3274–3279. [Google Scholar]
- Nonnenmacher, D.; Kim, H.; Götz, J.; Weber, P.; von Hinüber, E.; Knedlik, S. System architecture of HALAS—A helicopter slung load stabilisation and positioning system. CEAS Aeronaut. J. 2014, 5, 127–143. [Google Scholar] [CrossRef]
- Pereira, P.O.; Herzog, M.; Dimarogonas, D.V. Slung load transportation with a single aerial vehicle and disturbance removal. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 671–676. [Google Scholar]
- Pollini, L.; Metrangolo, A. Simulation and Robust Backstepping Control of a Quadrotor Aircraft. In Proceedings of the Guidance, Navigation, and Control and Co-located Conferences, American Institute of Aeronautics and Astronautics, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Raptis, I.; Valavanis, K.; Moreno, W. A Novel Nonlinear Backstepping Controller Design for Helicopters Using the Rotation Matrix. IEEE Trans. Control Syst. Technol. 2011, 19, 465–473. [Google Scholar] [CrossRef]
- Tartaglione, G.; D’Amato, E.; Ariola, M.; Rossi, P.S.; Johansen, T.A. Model predictive control for a multi-body slung-load system. Robot. Auton. Syst. 2017, 92, 1–11. [Google Scholar] [CrossRef]
- Vargas, A.; Ireland, M.L.; Anderson, D. Swing-Free Manoeuvre Controller for Rotorcraft Unmanned Aerial Vehicle Slung-Load System Using Echo State Networks. Int. J. Unmanned Syst. Eng. 2015, 3, 26. [Google Scholar] [CrossRef]
- Vargas, A.; Anderson, D. Computer vision technique to estimate the slung load dynamics when coupled to a Multirotor Unmanned Aerial Vehicle. Rev. Int. Investig. e Innov. Tecnol. (RIIIT) 2017, 1–10. Available online: https://www.researchgate.net/publication/318458252_Computer_vision_technique_to_estimate_the_slung_load_dynamics_when_coupled_to_a_Multirotor_Unmanned_Aerial_Vehicle (accessed on 25 February 2018).
- Zuo, Z.; Zhu, M.; Zheng, Z. Trajectory Tracking Control of a Quadrotor Unmanned Mini-Helicopter. In Proceedings of the Aerospace Sciences Meetings, American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Gibson, J. Blackhawk helicopter with sling–loaded Humvee. US Army Photo by Staff Sgt. Joel Gibson; 13th SC(E) Public Affairs. Courtesy US Army, 2014. [Google Scholar]
- Hiremath, N.; Shukla, D.; Hale, E.; Sparacello, T.; Komerath, N. Slung Load Amplification Detector. In Proceedings of the ASME 2017 International Mechanical Engineering Conference and Exposition IMECE2017, Tampa, FL, USA, 3–9 November 2017. Number IMECE2017-70252. [Google Scholar]
- Motahari, N.; Hiremath, N.; Komerath, N. Aerodynamic Load Maps of Bluff-Body Combinations in Incompressible Flow. In Proceedings of the ASME 2016 Fluids Engineering Division Summer Meeting (ASME), Washington, DC, USA, 10–14 July 2016. Number FEDSM2016-7683. [Google Scholar]
- Motahari, N.; Hiremath, N.; Komerath, N. Towards Generalized Certification of Slung Load Flight Envelopes. In Proceedings of the 72nd Forum of AHS International American Helicopter Society, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
- Motahari, N.; Hiremath, N.; Komerath, N. Generalized Approach for Slung-Load Aerodynamics. In Proceedings of the 72nd Forum of AHS International American Helicopter Society, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
- Motahari, N.; D’Turbeville, F.; Hiremath, N.; Komerath, N. Airload Maps of Vehicle Shapes at Arbitrary Attitude. In Proceedings of the SAE Aerotech Conference, Seattle, WA, USA, 22–24 September 2015. Paper Number 2015-01-15ATC-0198. [Google Scholar]
- Komerath, N.; Raghav, V.; Hiremath, N. Aerodynamics of Arbitrary Shapes. In Aerodynamic Loads on Arbitrary Shapes; SCV Inc.: Alpharetta, GA, USA, 2016. [Google Scholar]
- Komerath, N.; Hiremath, N. Closed Circular Cylinders in Yaw; Number Book 2 in Aerodynamics of Arbitrary Shapes; SCV Inc.: Alpharetta, GA, USA, 2016. [Google Scholar]
- Forbes, A.; Raghav, V.; Mayo, M.; Komerath, N. Rotation Effects on Hub Drag. In Proceedings of the ASME 2013 International Mechanical Engineering Congress & Exposition, San Diego, CA, USA, 15–21 November 2013. [Google Scholar]
- Mastinu, G.; Gobbi, M.; Previati, G. A new six-axis load cell. Part I: Design. Exp. Mech. 2011, 51, 373–388. [Google Scholar] [CrossRef]
- Forbes, A.; Raghav, V.; Komerath, N. Continuous Rotation Technique to Measure Aerodynamic Loads ona Bluff Body; Data Report ADLP-2013090501; Experimental Aerodynamics and Concepts Group, School of AE, Georgia Institute of Technology: Atlanta, GA, USA, 2013. [Google Scholar]
- Forbes, A.; Pirau, S.; Liberi, B.; Raghav, V.; Komerath, N. Testing-Based Approach to Determining the Divergence Speed of Slung Loads. In Proceedings of the 70th American Helicopter Society Forum, Montreal, QC, Canada, 20–22 May 2014. [Google Scholar]
- Pirau, S.; Forbes, A.; Liberi, B.; Raghav, V.; Komerath, N. Quasi-Steady Air Loads Report: CUBOID; Data Report ADLP2015022401; Experimental Aerodynamics and Concepts Group, School of AE, Georgia Institute of Technology: Atlanta, GA, USA, 2015. [Google Scholar]
- Pirau, S.; Forbes, A.; Liberi, B.; Raghav, V.; Komerath, N. Quasi-Steady Air Loads Report: Flat Plate with Central Load; Data Report ADLP2015022402; Experimental Aerodynamics and Concepts Group, School of AE, Georgia Institute of Technology: Atlanta, GA, USA, 2015. [Google Scholar]
- Pirau, S.; Forbes, A.; Liberi, B.; Raghav, V.; Komerath, N. Quasi-Steady Air Loads Report: Porous Box; Data Report ADLP2015022403; Experimental Aerodynamics and Concepts Group, School of AE, Georgia Institute of Technology: Atlanta, GA, USA, 2015. [Google Scholar]
- Shukla, D.; Hiremath, N.; Motahari, N.; Komerath, N. Genesis of the Airload Variations on Cylinders of Small Aspect Ratios. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Hiremath, N.; Shukla, D.; Robinson, J.; Jha, A.; Palaniappan, A.; Komerath, N. Aerodynamic Loads on Arbitrary Configurations: Measurements, Computations and Geometric Modeling. In Proceedings of the SAE AeroTech Conference on Society of Automotive Engineers, Ft. Worth, TX, USA, 26–28 September 2017. Paper Number 2017-01-02162. [Google Scholar]
- Pirau, S.; Raghav, V.; Forbes, A.; Liberi, B.; Komerath, N. Efficient Airload Determination For Bluff Body Aeromechanics. In Proceedings of the ASME 2014 International Mechanical Engineering Congress & Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Liberi, B.; Pirau, S.; Raghav, V.; Komerath, N. Determination Of Slung Load Divergence Speed Using Airloa Measurement And Simulation. In Proceedings of the ASME 2014 International Mechanical Engineering Congress & Exposition, Montreal, QC, Canada, 14–20 November 2014. Number IMECE2014-38260 in ASME Paper. [Google Scholar]
- Liberi, B.; Ton, C.; Komerath, N. Divergence Speed Prediction For Practical Slung Load Shapes. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference, Seoul, Korea, 26–31 July 2015. Number AJK2015-27543 in Paper. [Google Scholar]
- Liberi, B.; Kijjakarn, P.; Komerath, N. Slung Load Divergence Speed Predictions for Vehicle Shapes. In Proceedings of the SAE AeroTech Conference, Seattle, WA, USA, 22–24 September 2015. [Google Scholar]
- Liberi, B.; Pirau, S.; Komerath, N.; Ton, C. Effects of Uncertainty on Slung Load Divergence Speed Determination. In Proceedings of the 71st American Helicopter Society Forum, Virginia Beach, VA, USA, 5–7 May 2015. [Google Scholar]
- Ton, C.; Mackunis, W. Robust Attitude Tracking Control of a Quadrotor Helicopter in the Presence of Uncertainty. In Proceedings of the IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 937–942. [Google Scholar]
- Pirau, S.; Liberi, B.; Barbely, N.; Komerath, N. Generalized Prediction of Bluff-Body Aerodynamic Load Maps. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference AJK2015-FED, Number 15542 in AJK2015, Seoul, Korea, 26–31 July 2015. [Google Scholar]
- Motahari, N.; Hiremath, N.; Shukla, D.; Liberi, B.; Thorell, N.; Komerath, N. Generalized Airloads Prediction for Bluff Bodies Transported as Slung Loads. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Houston, TX, USA, 13–19 November 2015. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komerath, N.; Hiremath, N.; Shukla, D. Testing-Based Approach to Determining the Divergence Speed of Slung Loads. Aerospace 2018, 5, 24. https://doi.org/10.3390/aerospace5010024
Komerath N, Hiremath N, Shukla D. Testing-Based Approach to Determining the Divergence Speed of Slung Loads. Aerospace. 2018; 5(1):24. https://doi.org/10.3390/aerospace5010024
Chicago/Turabian StyleKomerath, Narayanan, Nandeesh Hiremath, and Dhwanil Shukla. 2018. "Testing-Based Approach to Determining the Divergence Speed of Slung Loads" Aerospace 5, no. 1: 24. https://doi.org/10.3390/aerospace5010024
APA StyleKomerath, N., Hiremath, N., & Shukla, D. (2018). Testing-Based Approach to Determining the Divergence Speed of Slung Loads. Aerospace, 5(1), 24. https://doi.org/10.3390/aerospace5010024




