On Predictive Modeling Using a New Flexible Weibull Distribution and Machine Learning Approach: Analyzing the COVID-19 Data
Abstract
:1. Introduction
2. A New Modified Flexible Weibull Extension
3. The HT Characteristics
Regular Variational Property
A Supportive Example of RVP
4. Estimation and Simulation
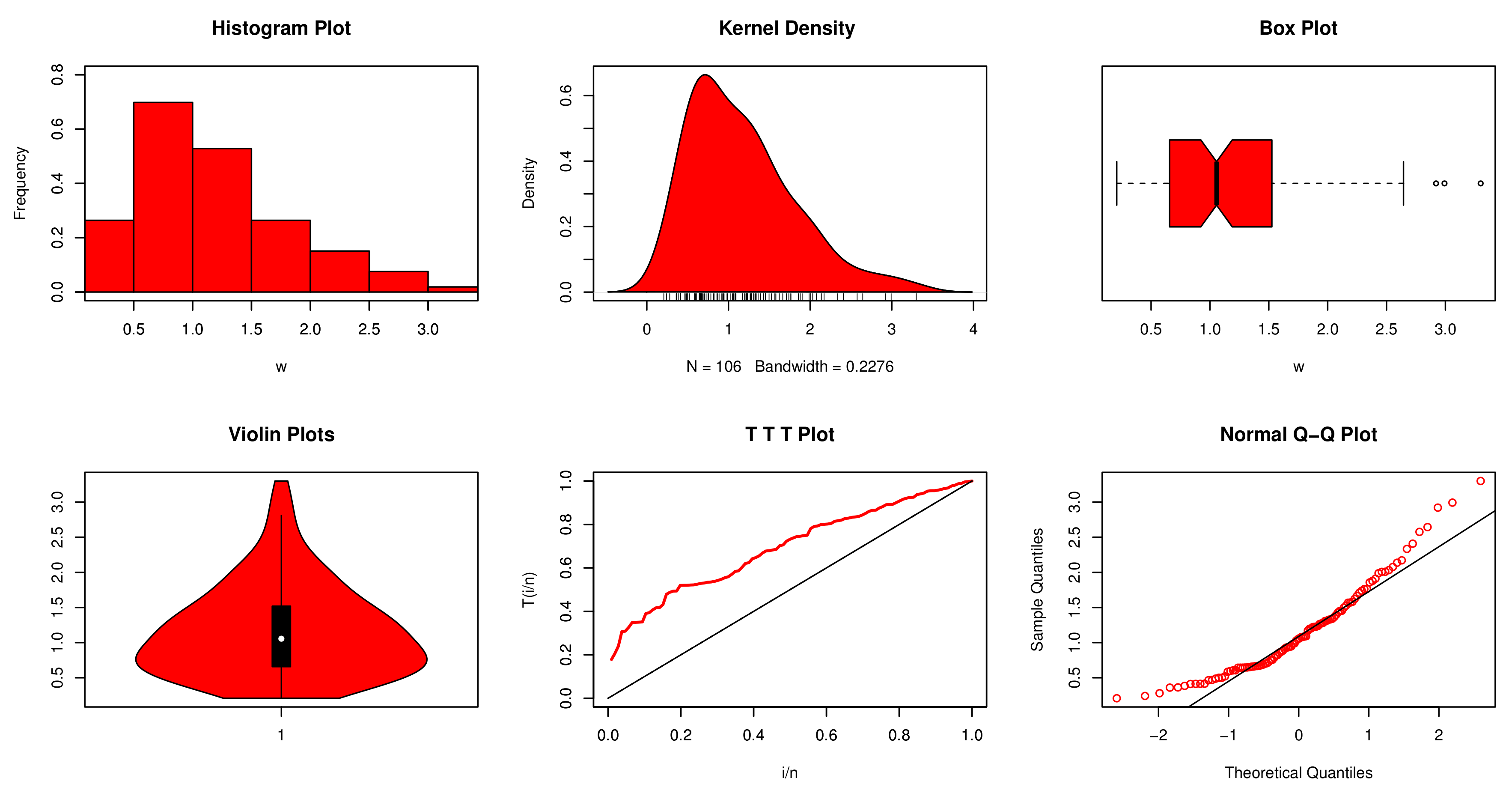
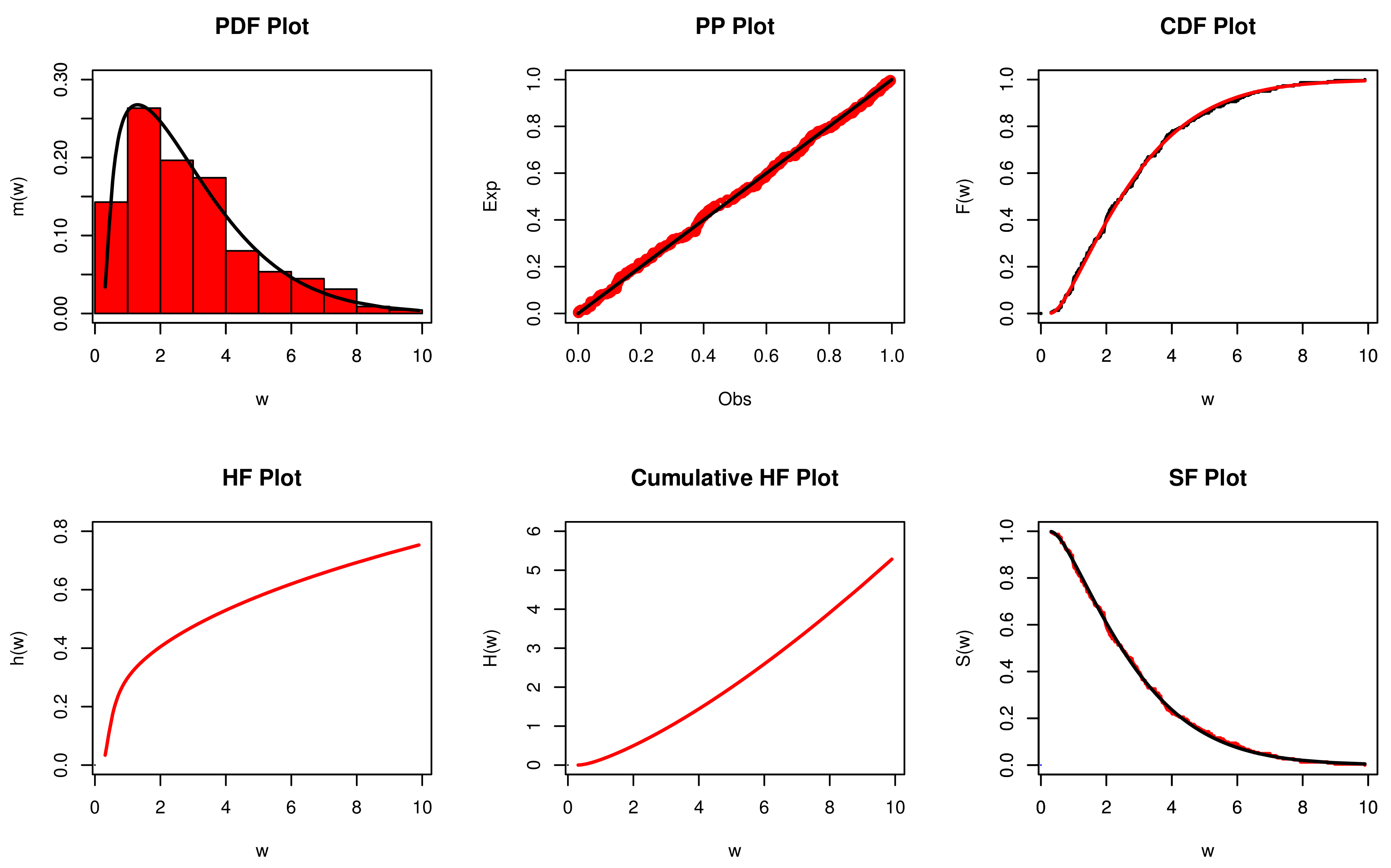
5. Data Analysis
- FWE:where and ;
- E-FWE:where , , and ;
- Weibull:where and ;
- E-Weibull:where , , and ;
- K-Weibull:where , , and .
- AIC (Akaike information criterion), obtained as
- CAIC (corrected Akaike information criterion), calculated by
- BIC (Bayesian information criterion), computed as
- HQIC (Hannan–Quinn information criterion), obtained using the formula
- AD (Anderson–Darling) test, having a mathematical expression given by
- CM (Cramér-von Mises) test, obtained using the formula
- KS (Kolmogorov–Smirnov) test, whose value is computed using the expression
6. An Econometric Approach
6.1. The ARMA Model
6.2. The NP-ARMA Method
6.3. The NNAR Method
6.4. The SVR Method
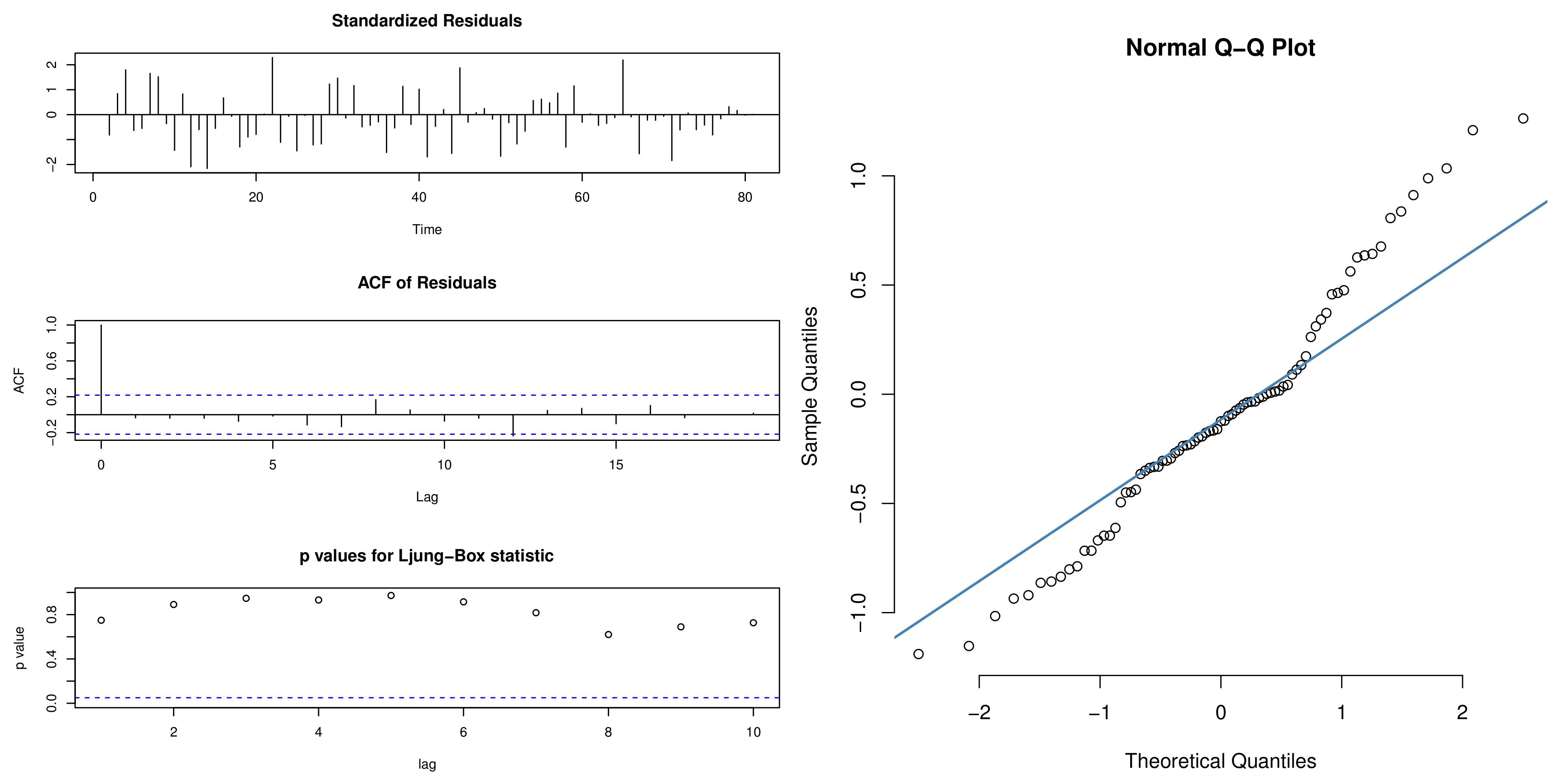
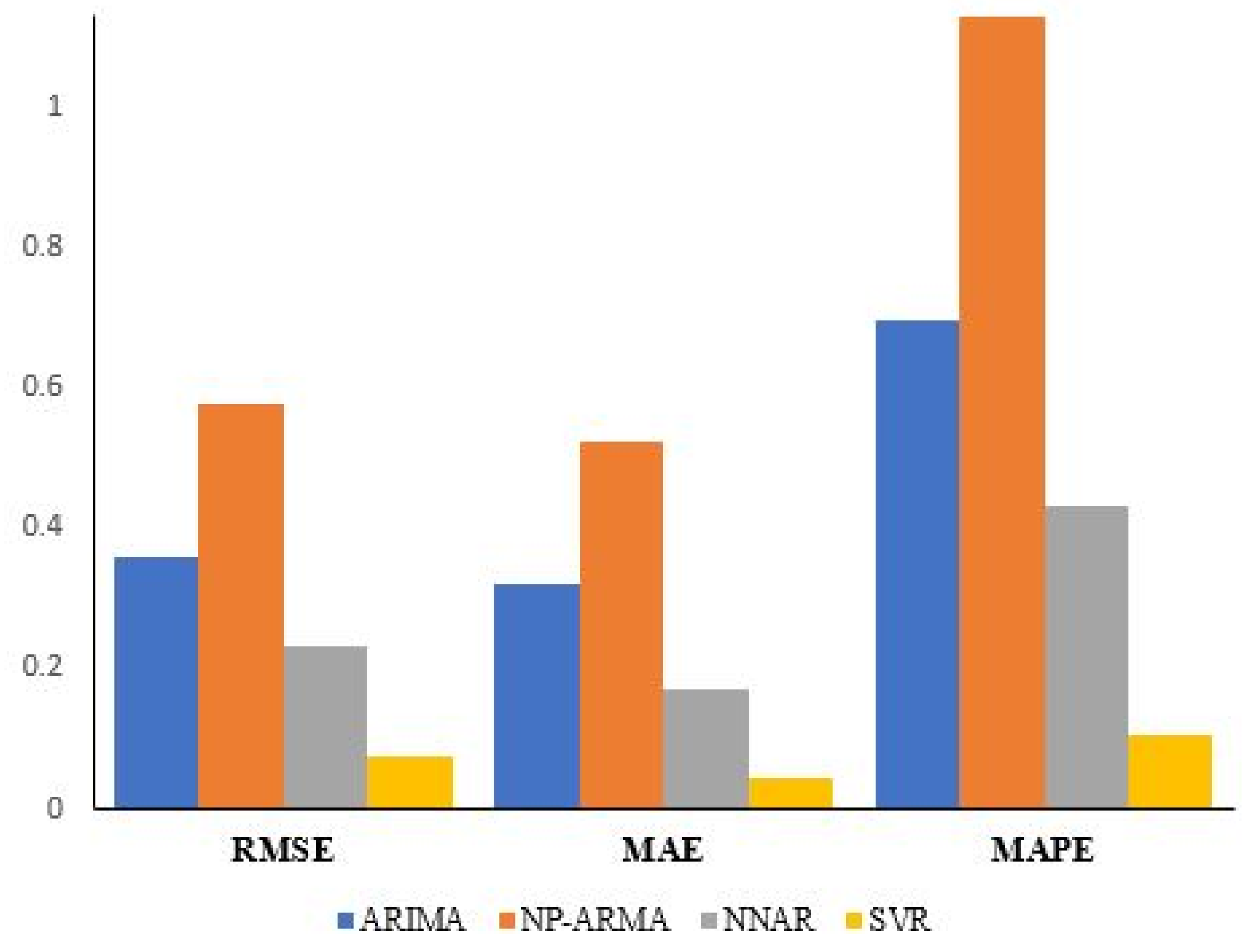
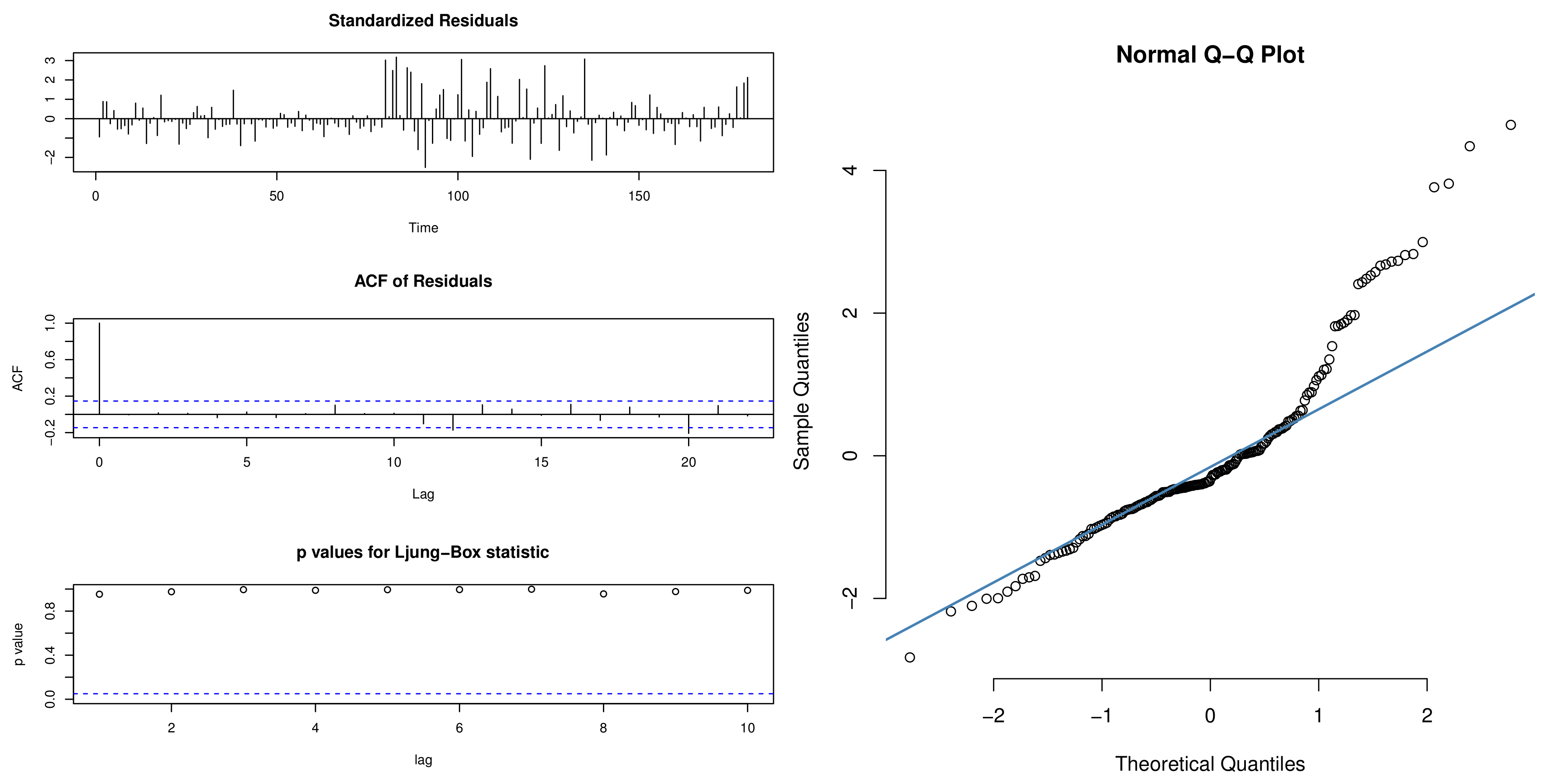
6.5. Empirical Results
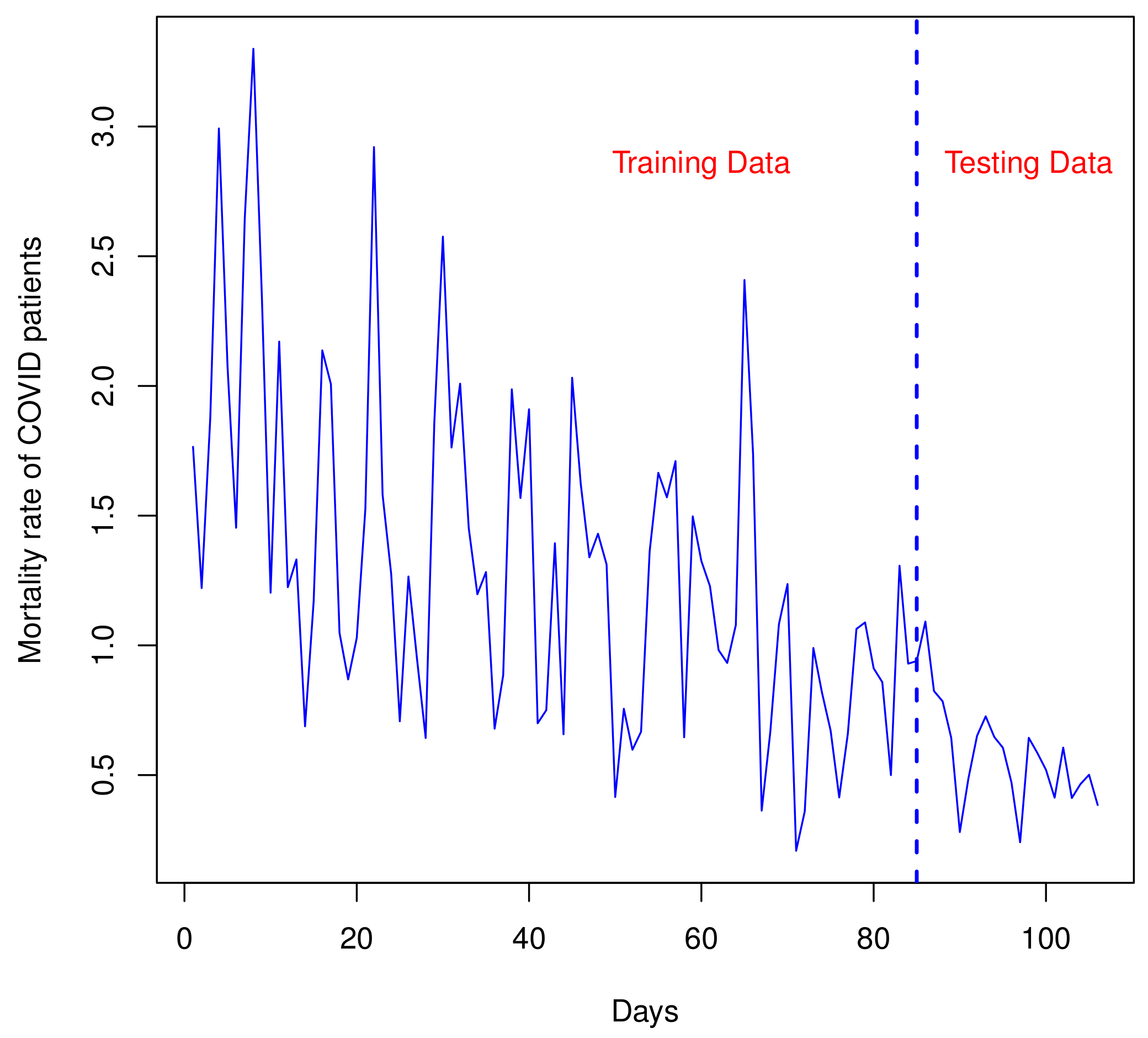
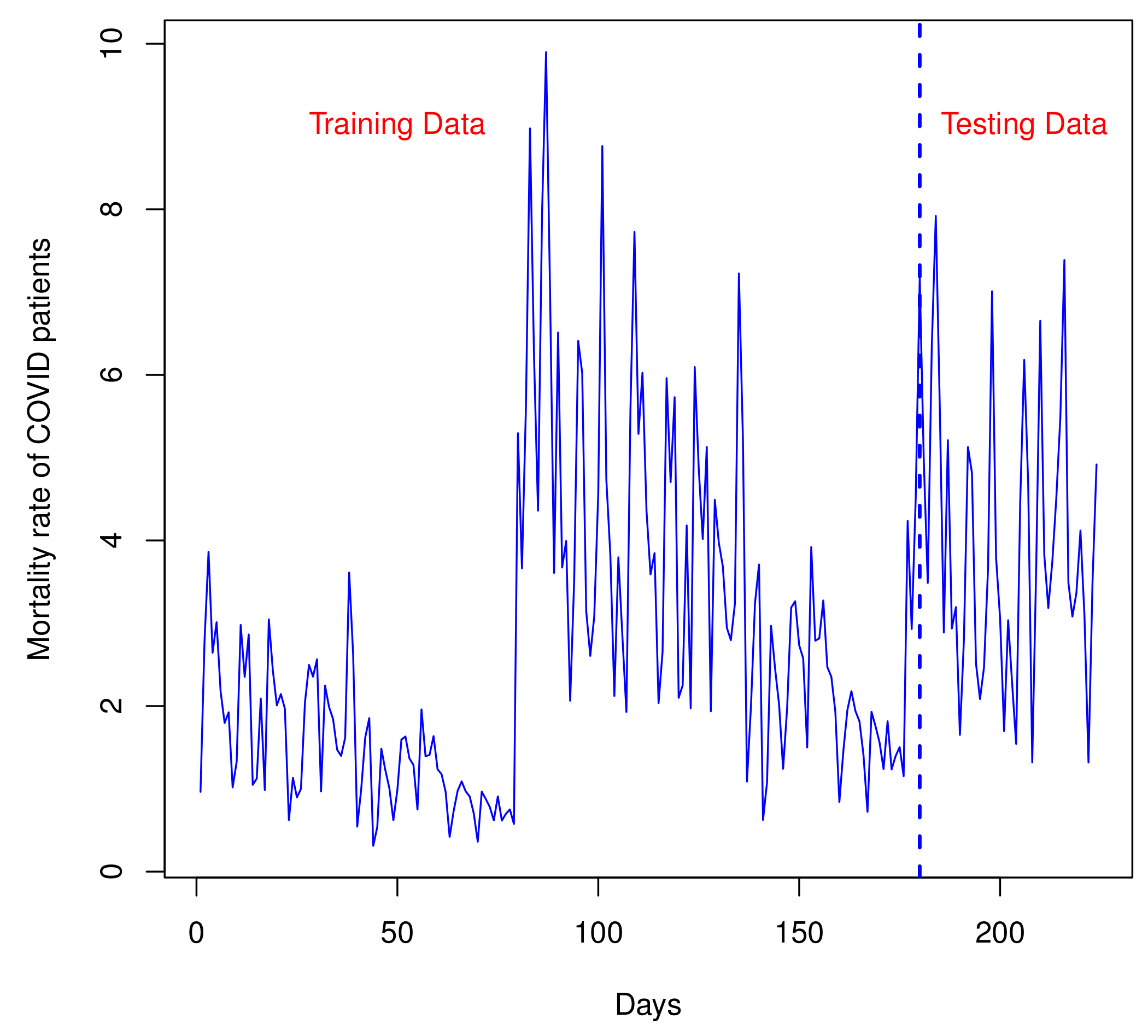
6.5.1. Analyzing the COVID-19 Data Taken from Mexico
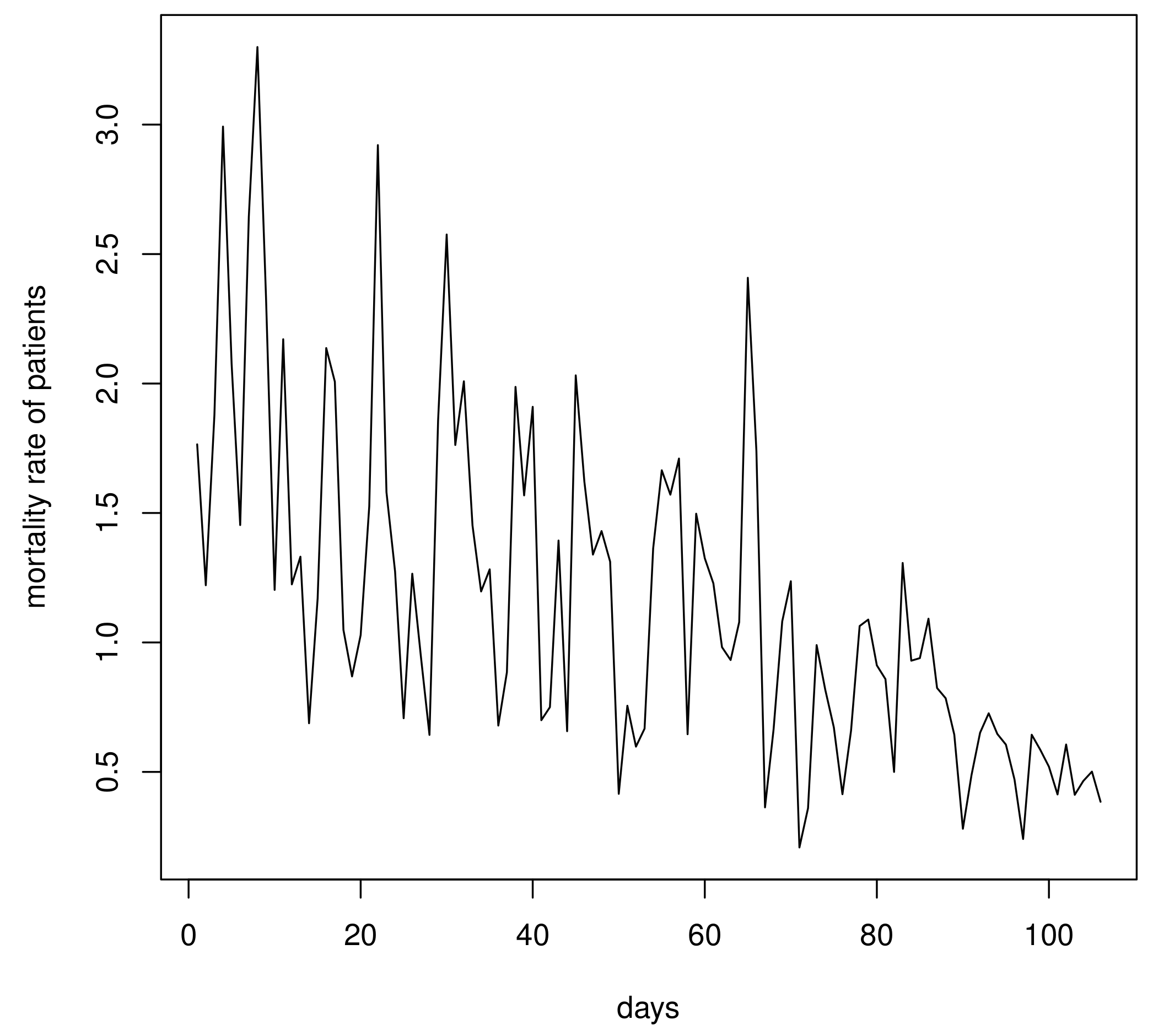
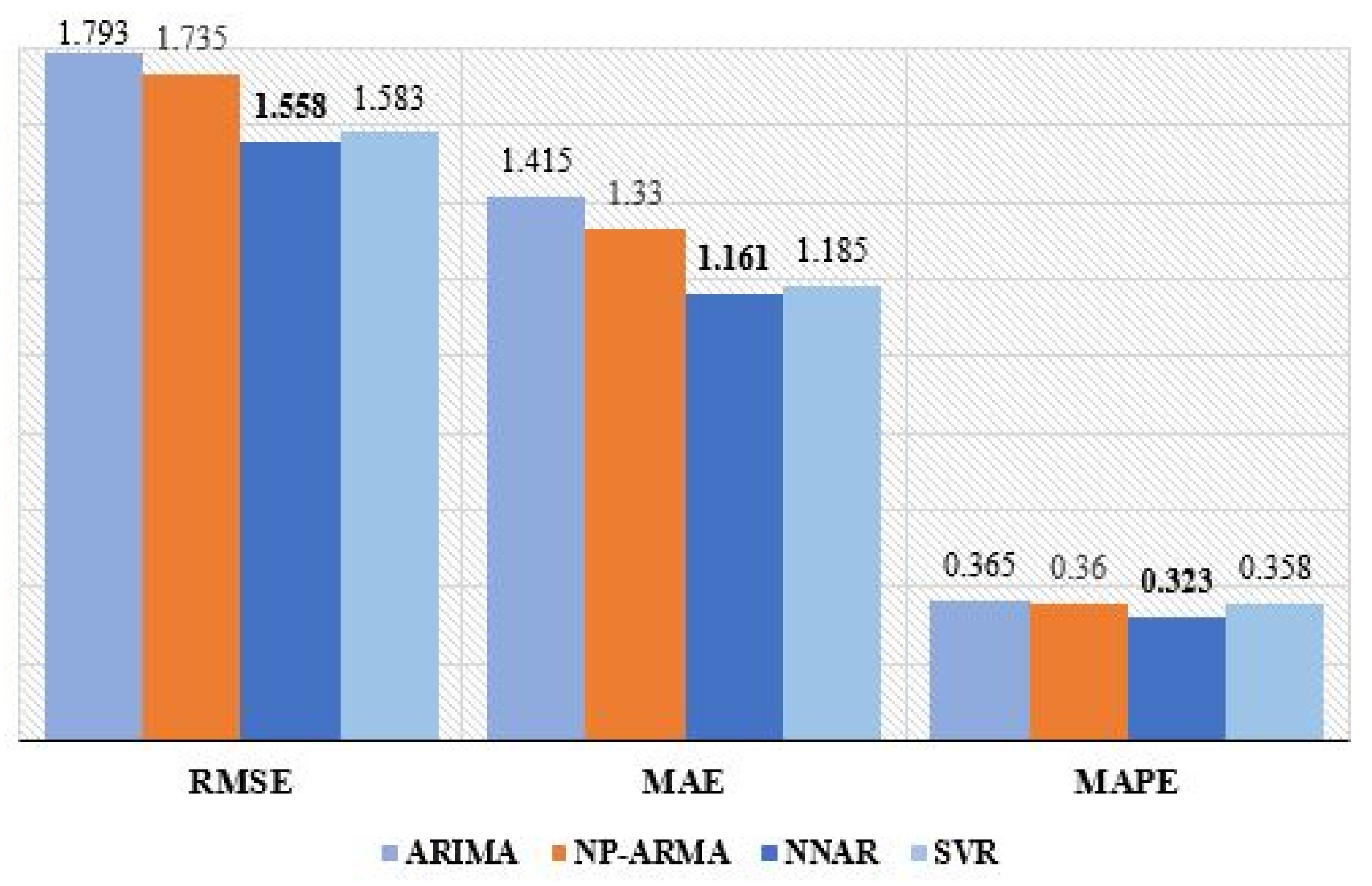
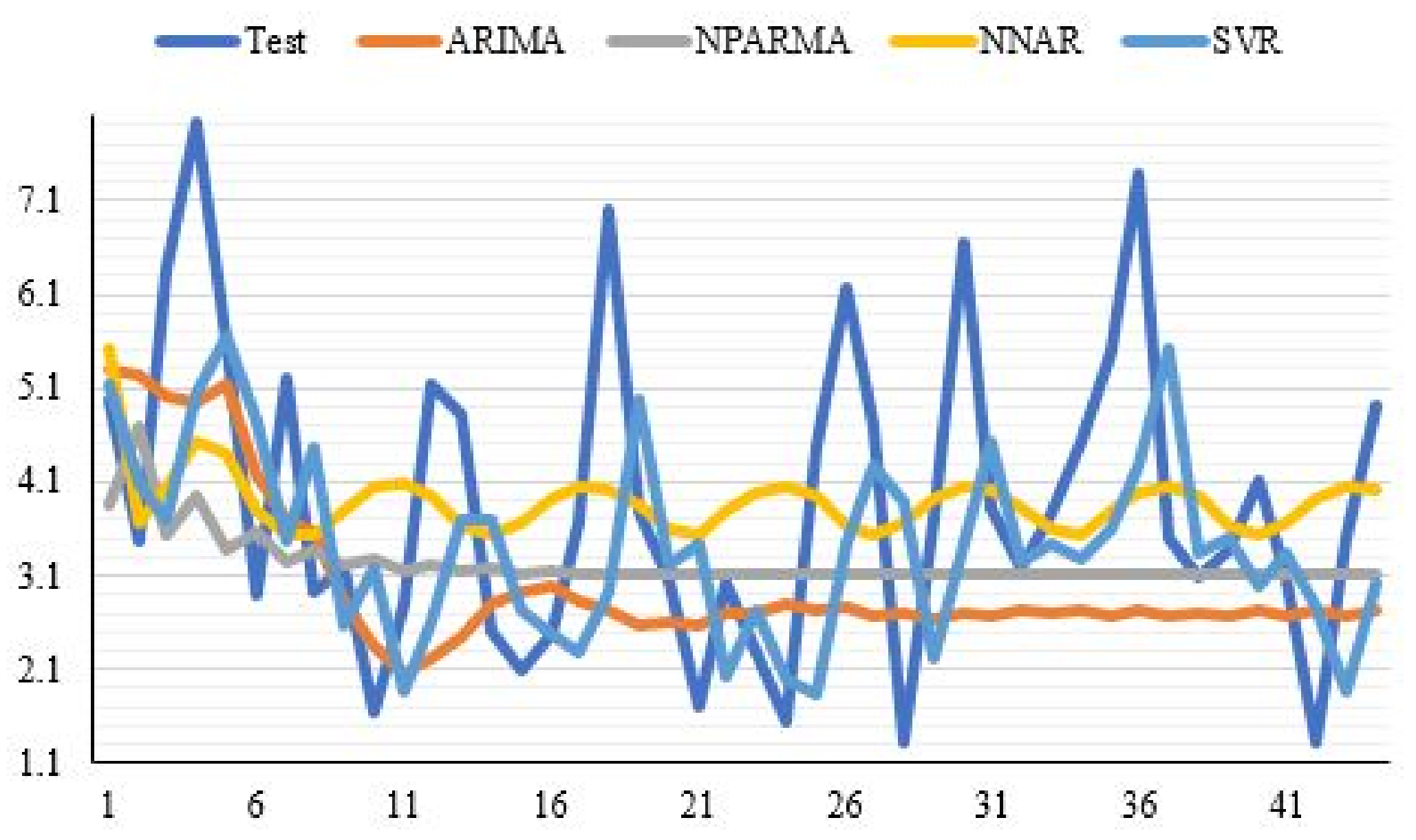
6.5.2. Analyzing the COVID-19 Data Taken from Canada
7. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hogan, C.A.; Sahoo, M.K.; Pinsky, B.A. Sample pooling as a strategy to detect community transmission of SARS-CoV-2. JAMA 2020, 323, 1967–1969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 10, 2000180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ilyas, N.; Azuine, R.E.; Tamiz, A. COVID-19 pandemic in Pakistan. Int. J. Transl. Med. Res. Public Health 2020, 4, 37–49. [Google Scholar] [CrossRef]
- Rao, G.S.; Aslam, M. Inspection plan for COVID-19 patients for Weibull distribution using repetitive sampling under indeterminacy. BMC Med. Res. Methodol. 2020, 21, 229. [Google Scholar] [CrossRef] [PubMed]
- Singhal, A.; Singh, P.; Lall, B.; Joshi, S.D. Modeling and prediction of COVID-19 pandemic using Gaussian mixture model. Chaos Solitons Fractals 2020, 138, 110023. [Google Scholar] [CrossRef]
- Qin, J.; You, C.; Lin, Q.; Hu, T.; Yu, S.; Zhou, X.H. Estimation of incubation period distribution of COVID-19 using disease onset forward time: A novel cross-sectional and forward follow-up study. Sci. Adv. 2020, 6, eabc1202. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Alharbi, R.; Alnagar, D.; Hafez, E.H. A new inverted topp-leone distribution: Applications to the COVID-19 mortality rate in two different countries. Axioms 2021, 10, 25. [Google Scholar] [CrossRef]
- Almongy, H.M.; Almetwally, E.M.; Aljohani, H.M.; Alghamdi, A.S.; Hafez, E.H. A new extended Rayleigh distribution with applications of COVID-19 data. Results Phys. 2021, 23, 104012. [Google Scholar] [CrossRef]
- Liu, X.; Ahmad, Z.; KKhosa, S.; Yusuf, M.; Alamri, O.A.; Emam, W. A New Flexible Statistical Model: Simulating and Modeling the Survival Times of COVID-19 Patients in China. Complexity 2021, 2021, 6915742. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M.; Eliwa, M.S.; Alqahtani, K.M.; EL-Morshedy, M. Asymmetric randomly censored mortality distribution: Bayesian framework and parametric bootstrap with application to COVID-19 data. J. Math. 2022, 2022, 8300753. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Altun, E.; El-Dawoody, M.; El-Morshedy, M. A new three-parameter discrete distribution with associated INAR (1) process and applications. IEEE Access 2020, 8, 91150–91162. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; Altun, E. Discrete Burr-Hatke distribution with properties, estimation methods and regression model. IEEE Access 2020, 8, 74359–74370. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Altun, E.; Eliwa, M.S. A new statistical approach to model the counts of novel coronavirus cases. Math. Sci. 2020, 16, 37–50. [Google Scholar] [CrossRef]
- Altun, H.K.; Ermumcu, M.S.K.; Kurklu, N.S. Evaluation of dietary supplement, functional food and herbal medicine use by dietitians during the COVID-19 pandemic. Public Health Nutr. 2021, 24, 861–869. [Google Scholar] [CrossRef]
- Altun, E.; El-Morshedy, M.; Eliwa, M.S. A new regression model for bounded response variable: An alternative to the beta and unit-Lindley regression models. PLoS ONE 2021, 16, e0245627. [Google Scholar]
- Bebbington, M.; Lai, C.D.; Zitikis, R. A flexible Weibull extension. Reliab. Eng. Syst. Saf. 2007, 92, 719–726. [Google Scholar] [CrossRef]
- El-Morshedy, M.; El-Bassiouny, A.H.; El-Gohary, A. Exponentiated inverse flexible Weibull extension distribution. J. Stat. Appl. Probab. 2017, 6, 169–183. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; El-Gohary, A.; Almetwally, E.M.; EL-Desokey, R. Exponentiated Generalized Inverse Flexible Weibull Distribution: Bayesian and Non-Bayesian Estimation Under Complete and Type II Censored Samples with Applications. Commun. Math. Stat. 2021, 1–22. [Google Scholar] [CrossRef]
- Abubakari, A.G.; Kandza-Tadi, C.C.; Moyo, E. Modified Beta Inverse Flexible Weibull Extension Distribution. Ann. Data Sci. 2021, 7, 1–29. [Google Scholar] [CrossRef]
- El-Gohary, A.; El-Bassiouny, A.H.; El-Morshedy, M. Exponentiated flexible Weibull extension distribution. Int. J. Math. Its Appl. 2015, 3, 1–12. [Google Scholar]
- El-Damcese, M.A.; Mustafa, A.; El-Desouky, B.S.; Mustafa, M.E. The Kumaraswamy flexible Weibull extension. Int. J. Math. Its Appl. 2016, 4, 1–14. [Google Scholar]
- Ahmad, Z.; Mahmoudi, E.; Dey, S. A new family of heavy tailed distributions with an application to the heavy tailed insurance loss data. Commun. Stat.-Simul. Comput. 2020, 49, 1–24. [Google Scholar] [CrossRef]
- Gardiner, J.C.; Luo, Z.; Tang, X.; Ramamoorthi, R.V. Fitting heavy-tailed distributions to health care data by parametric and Bayesian methods. J. Stat. Theory Pract. 2014, 8, 619–652. [Google Scholar] [CrossRef]
- Zhao, W.; Khosa, S.K.; Ahmad, Z.; Aslam, M.; Afify, A.Z. Type-I heavy tailed family with applications in medicine, engineering and insurance. PLoS ONE 2020, 15, e0237462. [Google Scholar] [CrossRef]
- Bhati, D.; Ravi, S. On generalized log-Moyal distribution: A new heavy tailed size distribution. Insur. Math. Econ. 2018, 79, 247–259. [Google Scholar] [CrossRef]
- Ahmad, Z.; Mahmoudi, E.; Hamedani, G.G.; Kharazmi, O. New methods to define heavy-tailed distributions with applications to insurance data. J. Taibah Univ. Sci. 2020, 14, 359–382. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, Z.; Mahmoudi, E.; Alizadeh, M.; Roozegar, R.; Afify, A.Z. The exponential TX family of distributions: Properties and an application to insurance data. J. Math. 2021, 2021, 3058170. [Google Scholar] [CrossRef]
- Seneta, E. Karamata’s characterization theorem, feller and regular variation in probability theory. Publications de l’Institut Mathématique 2002, 71, 79–89. [Google Scholar] [CrossRef]
- Qi, M.; Zhang, G.P. An investigation of model selection criteria for neural network time series forecasting. Eur. J. Oper. Res. 2001, 132, 666–680. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. An artificial neural network (p, d, q) model for timeseries forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Bibi, N.; Shah, I.; Alsubie, A.; Ali, S.; Lone, S.A. Electricity Spot Prices Forecasting Based on Ensemble Learning. IEEE Access 2021, 9, 150984–150992. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S. Modeling and forecasting medium-term electricity consumption using component estimation technique. Forecasting 2020, 2, 163–179. [Google Scholar] [CrossRef]
- Khashei, M.; Hajirahimi, Z. A comparative study of series arima/mlp hybrid models for stock price forecasting. Commun. Stat.-Simul. Comput. 2019, 48, 2625–2640. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. In Advance in Neural Information Processing System; Mozer, M., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; Volume 9, pp. 281–287. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Ribeiro MH, D.M.; da Silva, R.G.; Mariani, V.C.; dos Santos Coelho, L. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. Chaos Solitons Fractals 2020, 135, 109853. [Google Scholar] [CrossRef]
- Lu, C.J.; Lee, T.S.; Chiu, C.C. Financial time series forecasting using independent component analysis and support vector regression. Decis. Support Syst. 2009, 47, 115–125. [Google Scholar] [CrossRef]

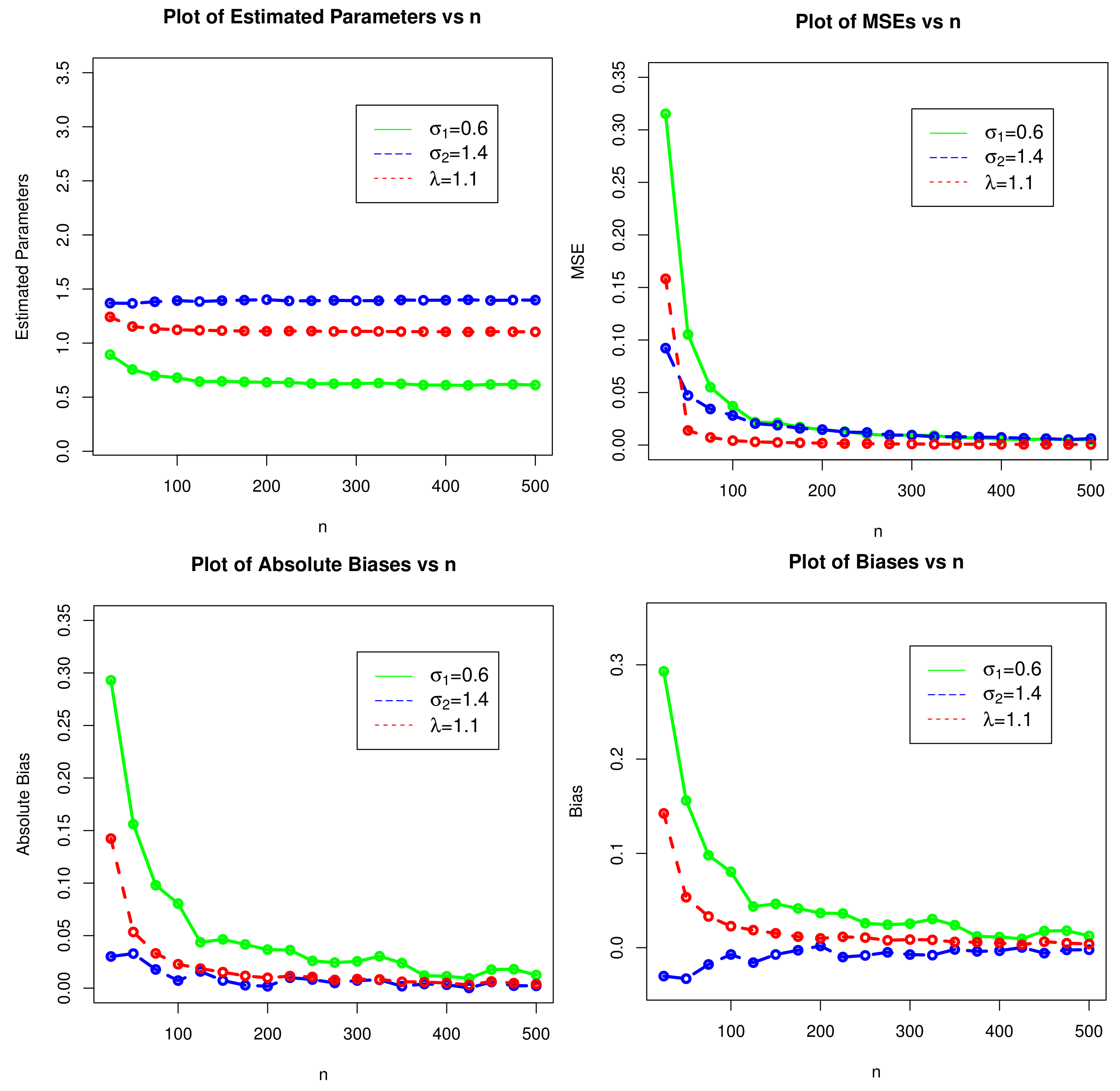

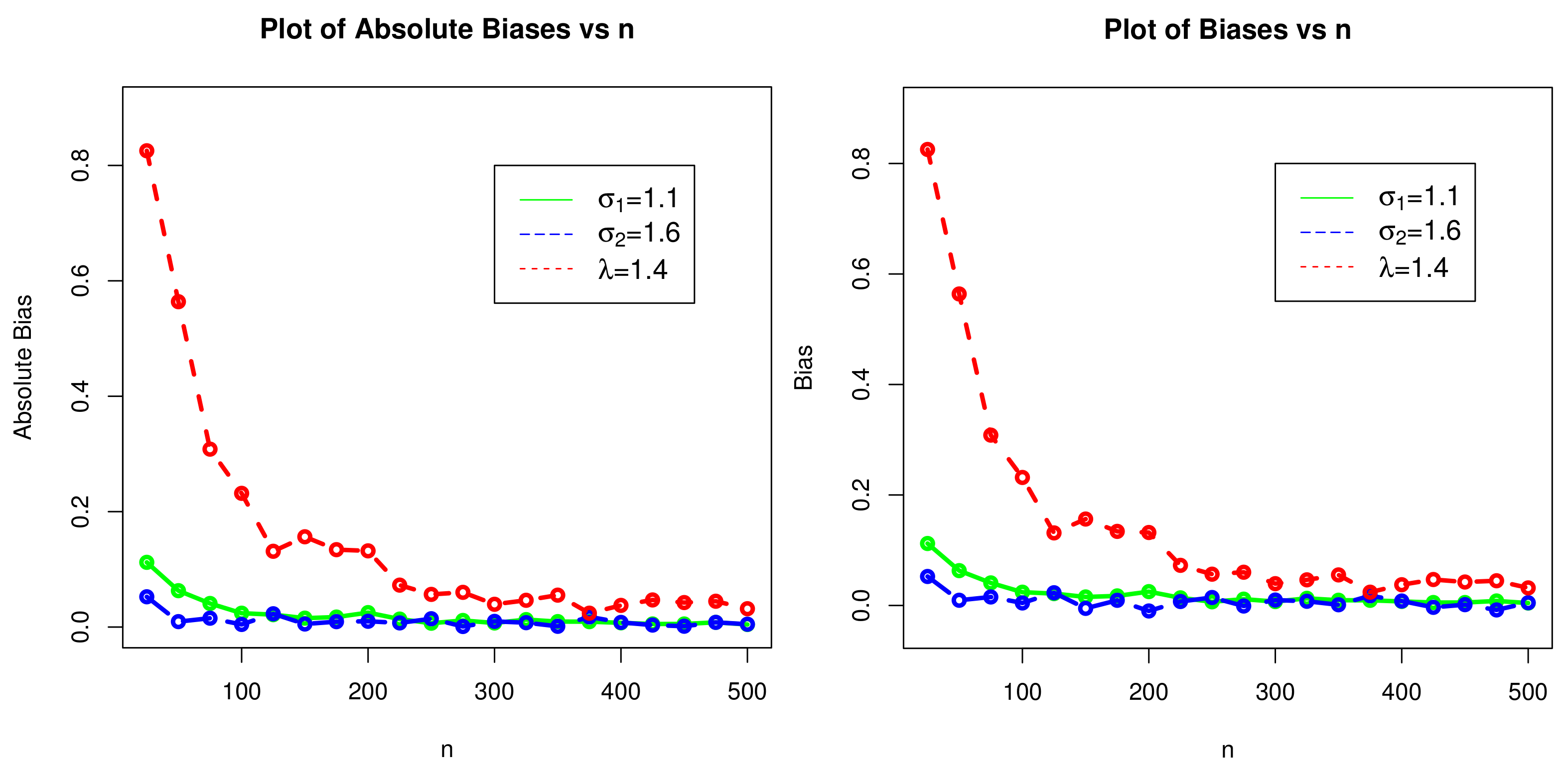





| n | Parameters | MLEs | MSEs | Biases |
|---|---|---|---|---|
| 0.89302560 | 0.315274822 | 0.293025560 | ||
| 25 | 1.36985000 | 0.092232346 | −0.03015010 | |
| 1.24237000 | 0.158247051 | 0.142369775 | ||
| 0.75604460 | 0.105204950 | 0.156044587 | ||
| 50 | 1.36711800 | 0.047163494 | −0.03288202 | |
| 1.15347600 | 0.013885900 | 0.053475874 | ||
| 0.69801090 | 0.055053130 | 0.098010942 | ||
| 75 | 1.38220000 | 0.034336224 | −0.01779995 | |
| 1.13308800 | 0.007274670 | 0.033088078 | ||
| 0.68048360 | 0.037073941 | 0.080483598 | ||
| 100 | 1.39280200 | 0.028143866 | −0.00719760 | |
| 1.12277300 | 0.004239282 | 0.022773367 | ||
| 0.64644740 | 0.021180684 | 0.046447381 | ||
| 150 | 1.39273800 | 0.018909237 | −0.00726232 | |
| 1.11521500 | 0.002497769 | 0.015214547 | ||
| 0.63668930 | 0.014568689 | 0.036689263 | ||
| 200 | 1.40180900 | 0.014734874 | 0.001809424 | |
| 1.10985700 | 0.001831123 | 0.009857116 | ||
| 0.62596330 | 0.010368965 | 0.025963329 | ||
| 250 | 1.39177300 | 0.011995360 | −0.00822708 | |
| 1.11065800 | 0.001393079 | 0.010658350 | ||
| 0.62550910 | 0.009587663 | 0.025509126 | ||
| 300 | 1.39270200 | 0.009345810 | −0.00729828 | |
| 1.10861100 | 0.001066879 | 0.008610622 | ||
| 0.62391800 | 0.006948299 | 0.023917996 | ||
| 350 | 1.39811500 | 0.008009759 | −0.00188529 | |
| 1.10609300 | 0.000808322 | 0.006093125 | ||
| 0.61132940 | 0.005626040 | 0.011329370 | ||
| 400 | 1.39673000 | 0.007298053 | −0.00327033 | |
| 1.10493100 | 0.000693269 | 0.004930592 | ||
| 0.61765410 | 0.005751539 | 0.017654106 | ||
| 450 | 1.39418200 | 0.006140556 | −0.00581764 | |
| 1.10637100 | 0.000606152 | 0.006371330 | ||
| 0.61250040 | 0.004853576 | 0.012500388 | ||
| 500 | 1.39779400 | 0.006180866 | −0.00220605 | |
| 1.10388200 | 0.000549189 | 0.003882268 |
| n | Parameters | MLEs | MSEs | Biases |
|---|---|---|---|---|
| 1.21214000 | 0.109696162 | 0.112139576 | ||
| 25 | 1.65247100 | 0.211066950 | 0.052471477 | |
| 2.22540700 | 2.677630360 | 0.825406630 | ||
| 1.16302800 | 0.046138277 | 0.063028001 | ||
| 50 | 1.60940600 | 0.127701240 | 0.009405599 | |
| 1.96382400 | 1.630116700 | 0.563823750 | ||
| 1.14084100 | 0.029142804 | 0.040841203 | ||
| 75 | 1.61535700 | 0.080794640 | 0.015357220 | |
| 1.70831400 | 0.785862990 | 0.308313730 | ||
| 1.12400600 | 0.018225475 | 0.024006192 | ||
| 100 | 1.60450400 | 0.065363500 | 0.004504030 | |
| 1.63171300 | 0.494613440 | 0.231713380 | ||
| 1.11539700 | 0.012912002 | 0.015397237 | ||
| 150 | 1.59474700 | 0.048261320 | −0.005252810 | |
| 1.55643900 | 0.268352060 | 0.156439100 | ||
| 1.12505500 | 0.009975488 | 0.025054780 | ||
| 200 | 1.59002600 | 0.031762970 | −0.00997431 | |
| 1.53205300 | 0.172517940 | 0.132052860 | ||
| 1.10665200 | 0.007469320 | 0.006651779 | ||
| 250 | 1.61439400 | 0.028265080 | 0.014393549 | |
| 1.45660500 | 0.079107080 | 0.056605210 | ||
| 1.10702000 | 0.005739174 | 0.007019600 | ||
| 300 | 1.60981400 | 0.022193800 | 0.009813938 | |
| 1.43945700 | 0.037317540 | 0.039456630 | ||
| 1.10944500 | 0.005131958 | 0.009445283 | ||
| 350 | 1.60127800 | 0.019648730 | 0.001277727 | |
| 1.45528500 | 0.056621610 | 0.055285400 | ||
| 1.10729900 | 0.004561712 | 0.007299329 | ||
| 400 | 1.60803700 | 0.017440070 | 0.008037465 | |
| 1.43753900 | 0.036744330 | 0.037538550 | ||
| 1.10532200 | 0.003908403 | 0.005322438 | ||
| 450 | 1.60144000 | 0.016748580 | 0.001439921 | |
| 1.44244400 | 0.033483900 | 0.042444350 | ||
| 1.10438500 | 0.003518714 | 0.004384936 | ||
| 500 | 1.60492800 | 0.013190150 | 0.004928443 | |
| 1.43178200 | 0.024440440 | 0.031781690 |
| Data 1 | 1.7652, 1.2210, 1.8782, 2.9924, 2.0766, 1.4534, 2.6440, 3.2996, 2.3330, 1.2030, 2.1710, 1.2244, 1.3312, 0.6880, 1.1708, 2.1370, 2.0070, 1.0484, 0.8688, 1.0286, 1.5260, 2.9208, 1.5806, 1.2740, 0.7074, 1.2654, 0.9460, 0.6430, 1.8568, 2.5756, 1.7626, 2.0086, 1.4520, 1.1970, 1.2824, 0.6790, 0.8848, 1.9870, 1.5680, 1.9100, 0.6998, 0.7502, 1.3936, 0.6572, 2.0316, 1.6216, 1.3394, 1.4302, 1.3120, 0.4154, 0.7556, 0.5976, 0.6672, 1.3628, 1.6650, 1.5708, 1.7102, 0.6456, 1.4972, 1.3250, 1.2280, 0.9818, 0.9322, 1.0784, 2.4084, 1.7392, 0.3630, 0.6654, 1.0812, 1.2364, 0.2082, 0.3600, 0.9898, 0.8178, 0.6718, 0.4140, 0.6596, 1.0634, 1.0884, 0.9114, 0.8584, 0.5000, 1.3070, 0.9296, 0.9394, 1.0918, 0.8240, 0.7844, 0.6438, 0.2804, 0.4876, 0.6514, 0.7264, 0.6466, 0.6054, 0.4704, 0.2410, 0.6436, 0.5852, 0.5202, 0.4130, 0.6058, 0.4116, 0.4652, 0.5012, 0.3846 |
| Data 2 | 0.9636, 2.7852, 3.8628, 2.6436, 3.0120, 2.1780, 1.7952, 1.9236, 1.0176, 1.3272, 2.9796, 2.3520, 2.8644, 1.0488, 1.1244, 2.0904, 0.9852, 3.0468, 2.4324, 2.0088, 2.1444, 1.9680, 0.6228, 1.1328, 0.8964, 1.0008, 2.0436, 2.4972, 2.3556, 2.5644, 0.9684, 2.2452, 1.9872, 1.8420, 1.4724, 1.3980, 1.6176, 3.6120, 2.6088, 0.5436, 0.9972, 1.6212, 1.8540, 0.3120, 0.5400, 1.4844, 1.2264, 1.0068, 0.6204, 0.9888, 1.5948, 1.6320, 1.3668, 1.2876, 0.7500, 1.9596, 1.3944, 1.4088, 1.6368, 1.2360, 1.1760, 0.9648, 0.4200, 0.7308, 0.9768, 1.0896, 0.9696, 0.9072, 0.7056, 0.3612, 0.9648, 0.8772, 0.7800, 0.6192, 0.9084, 0.6168, 0.6972, 0.7512, 0.5760, 5.2956, 3.6624, 5.6340, 8.9772, 6.2292, 4.3596, 7.9320, 9.8988, 6.9984, 3.6084, 6.5124, 3.6732, 3.9936, 2.0640, 3.5124, 6.4104, 6.0204, 3.1452, 2.6064, 3.0852, 4.5780, 8.7624, 4.7412, 3.8220, 2.1216, 3.7956, 2.8380, 1.9284, 5.5704, 7.7268, 5.2872, 6.0252, 4.3560, 3.5904, 3.8472, 2.0364, 2.6544, 5.9604, 4.7040, 5.7300, 2.0988, 2.2500, 4.1808, 1.9716, 6.0948, 4.8648, 4.0176, 5.1300, 1.9368, 4.4916, 3.9744, 3.6840, 2.9448, 2.7960, 3.2352, 7.2252, 5.2176, 1.0884, 1.9956, 3.2436, 3.7092, 0.6240, 1.0800, 2.9688, 2.4528, 2.0148, 1.2420, 1.9788, 3.1896, 3.2652, 2.7336, 2.5752, 1.5000, 3.9204, 2.7888, 2.8176, 3.2748, 2.4720, 2.3532, 1.9308, 0.8412, 1.4628, 1.9536, 2.1792, 1.9392, 1.8156, 1.4112, 0.7224, 1.9308, 1.7556, 1.5600, 1.2384, 1.8168, 1.2348, 1.3956, 1.5036, 1.1532, 4.2360, 2.9304, 4.5072, 7.1808, 4.9836, 3.4872, 6.3456, 7.9188, 5.5992, 2.8872, 5.2104, 2.9376, 3.1944, 1.6512, 2.8092, 5.1288, 4.8168, 2.5152, 2.0844, 2.4684, 3.6624, 7.0092, 3.7932, 3.0576, 1.6968, 3.0360, 2.2704, 1.5432, 4.4556, 6.1812, 4.6764, 1.3188, 3.7068, 6.6516, 3.8244, 3.1848, 3.7476, 4.5180, 5.4912, 7.3872, 3.4908, 3.0804, 3.3684, 4.1184, 3.0912, 1.3176, 3.4884, 4.9176 |
| Model | |||||
|---|---|---|---|---|---|
| NMFWE | 0.61568 (0.06012) | 1.33469 (0.20807) | 2.86140 (1.76820) | - | - |
| FWE | 0.64201 (0.05039) | 1.11759 (0.10961) | - | - | - |
| E-FWE | 0.65089 (0.11588) | 1.35112 (2.14650) | - | 0.82677 (1.39368) | - |
| Weibull | 1.92159 (0.14090) | 0.58694 (0.07121) | - | - | - |
| E-Weibull | 1.00398 (0.32020) | 1.78865 (0.75560) | - | 4.02508 (3.10070) | - |
| K-Weibull | 1.44294 (0.14370) | 3.76192 (NaN) | - | 3.13605 (1.63131) | 0.24665 (NaN) |
| Model | AIC | CAIC | BIC | HQIC |
|---|---|---|---|---|
| NMFWE | 186.12600 | 186.36130 | 194.11630 | 189.36450 |
| FWE | 189.04580 | 189.16230 | 196.37270 | 191.20480 |
| E-FWE | 187.01970 | 187.25500 | 195.01000 | 190.25820 |
| Weibull | 191.38590 | 191.50240 | 196.71280 | 193.54490 |
| E-Weibull | 188.2469 0 | 188.48220 | 196.23720 | 191.48540 |
| K-Weibull | 189.18680 | 189.58290 | 199.84060 | 193.50490 |
| Model | CM | AD | KS | p-Value |
|---|---|---|---|---|
| NMFWE | 0.03276 | 0.20485 | 0.05085 | 0.94680 |
| FWE | 0.03963 | 0.26343 | 0.05313 | 0.92580 |
| E-FWE | 0.03866 | 0.25671 | 0.05589 | 0.89500 |
| Weibull | 0.10233 | 0.65790 | 0.06967 | 0.68220 |
| E-Weibull | 0.05380 | 0.29853 | 0.06758 | 0.71820 |
| K-Weibull | 0.04335 | 0.24179 | 0.06477 | 0.76540 |
| Model | |||||
|---|---|---|---|---|---|
| NMFWE | 0.21080 (0.02141) | 2.14767 (0.01293) | 10.42059 (2.72864) | - | - |
| FWE | 0.64201 (0.05039) | 1.11759 (0.10961) | - | - | - |
| E-FWE | 0.21612 (0.01809) | 3.86071 (1.84962) | - | 0.54707 (0.27101) | - |
| Weibull | 1.61908 (0.08247) | 0.14782 (0.02037) | - | - | - |
| E-Weibull | 0.89210 (0.69863) | 0.81533 (0.69098) | - | 3.72610 (2.65132) | - |
| K-Weibull | 1.20004 (NaN) | 2.22247 (NaN) | - | 4.63532 (0.13187) | 0.14624 (0.01021) |
| Model | AIC | CAIC | BIC | HQIC |
|---|---|---|---|---|
| NMFWE | 848.33910 | 848.44800 | 858.57400 | 852.47040 |
| FWE | 851.87659 | 851.90876 | 863.87654 | 856.75648 |
| E-FWE | 850.06480 | 850.17658 | 861.29978 | 854.19629 |
| Weibull | 859.51210 | 859.56640 | 866.33540 | 862.26630 |
| E-Weibull | 855.16730 | 855.27630 | 865.40220 | 859.29860 |
| K-Weibull | 852.71950 | 852.90220 | 866.36610 | 858.22800 |
| Model | CM | AD | KS | p-Value |
|---|---|---|---|---|
| NMFWE | 0.03762 | 0.21668 | 0.04217 | 0.82040 |
| FWE | 0.04076 | 0.25807 | 0.04746 | 0.71927 |
| E-FWE | 0.03975 | 0.24540 | 0.04819 | 0.67560 |
| Weibull | 0.13201 | 0.92260 | 0.05400 | 0.53080 |
| E-Weibull | 0.05951 | 0.40453 | 0.04895 | 0.65640 |
| K-Weibull | 0.04285 | 0.26641 | 0.04345 | 0.79130 |
| Test | p-Value | |
|---|---|---|
| Box–Ljung test | 23.697 | 0.10 |
| JB test | 1.932 | 0.38 |
| Criteria | ARIMA | NP-ARMA | NNAR | SVR |
|---|---|---|---|---|
| RMSE | 0.359 | 0.576 | 0.230 | 0.073 |
| MAE | 0.320 | 0.525 | 0.169 | 0.043 |
| MAPE | 0.696 | 1.127 | 0.431 | 0.104 |
| Test | p-Value | |
|---|---|---|
| Box–Ljung test | 17.95 | 0.59 |
| JB test | 0.172 | 0.91 |
| Criteria | ARIMA | NP-ARMA | NNAR | SVR |
|---|---|---|---|---|
| RMSE | 1.793 | 1.735 | 1.558 | 1.583 |
| MAE | 1.415 | 1.330 | 1.161 | 1.185 |
| MAPE | 0.365 | 0.360 | 0.323 | 0.358 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, Z.; Almaspoor, Z.; Khan, F.; El-Morshedy, M. On Predictive Modeling Using a New Flexible Weibull Distribution and Machine Learning Approach: Analyzing the COVID-19 Data. Mathematics 2022, 10, 1792. https://doi.org/10.3390/math10111792
Ahmad Z, Almaspoor Z, Khan F, El-Morshedy M. On Predictive Modeling Using a New Flexible Weibull Distribution and Machine Learning Approach: Analyzing the COVID-19 Data. Mathematics. 2022; 10(11):1792. https://doi.org/10.3390/math10111792
Chicago/Turabian StyleAhmad, Zubair, Zahra Almaspoor, Faridoon Khan, and Mahmoud El-Morshedy. 2022. "On Predictive Modeling Using a New Flexible Weibull Distribution and Machine Learning Approach: Analyzing the COVID-19 Data" Mathematics 10, no. 11: 1792. https://doi.org/10.3390/math10111792






