Growth Recovery and COVID-19 Pandemic Model: Comparative Analysis for Selected Emerging Economies
Abstract
:1. Introduction
2. Theoretical Framework and Mathematical Modeling
2.1. The Kermack–McKendrick Model
2.2. The Wonderland Model
2.3. The Proposed Model
2.3.1. Extension of the SIR Model
α = 1.94597445654447; b = 0.0247039444045711;
c = 0.0619984179153856; d = 0.00807089279296773.
2.3.2. Applying the “Wonderland Model”
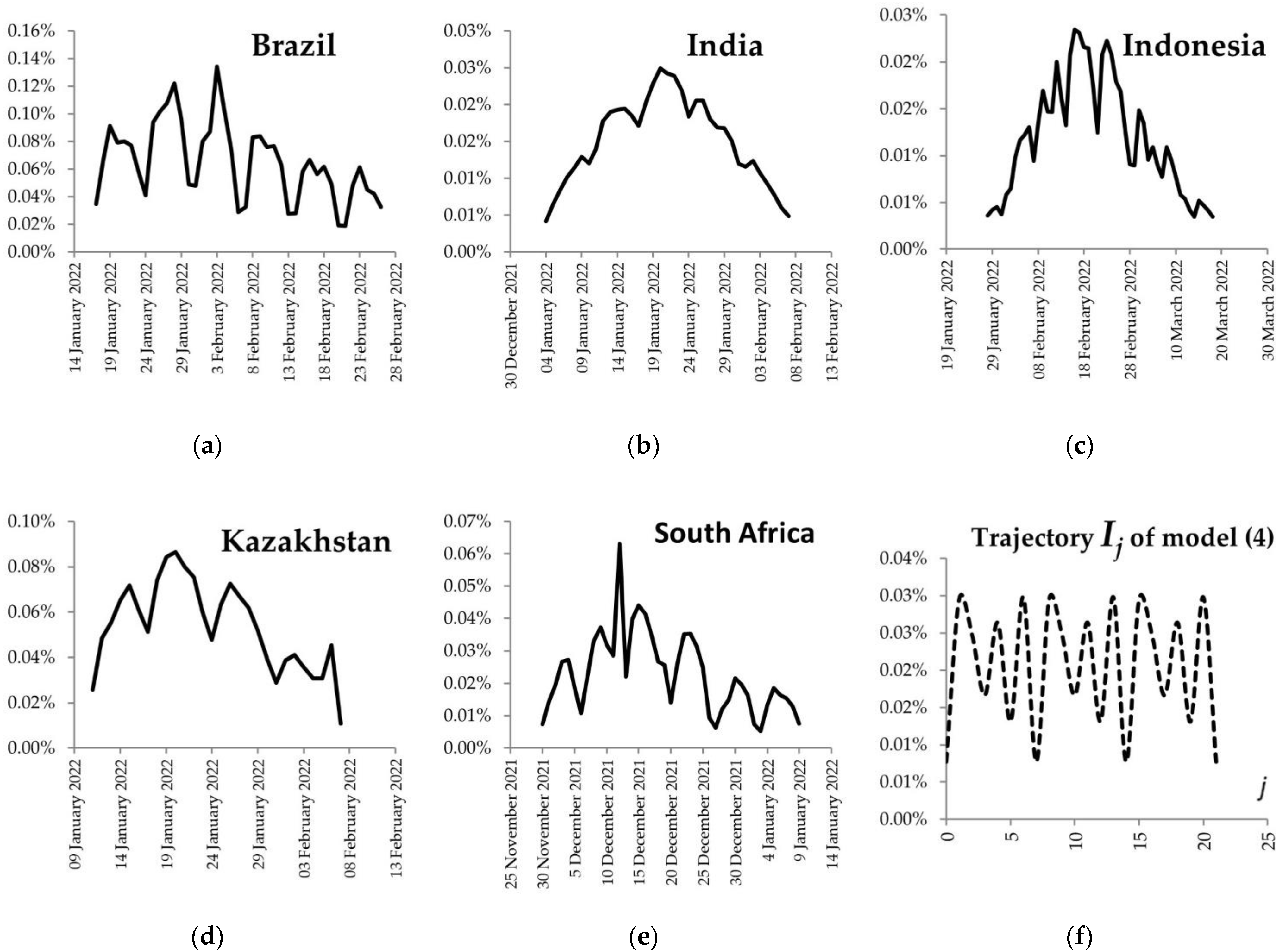
3. Data
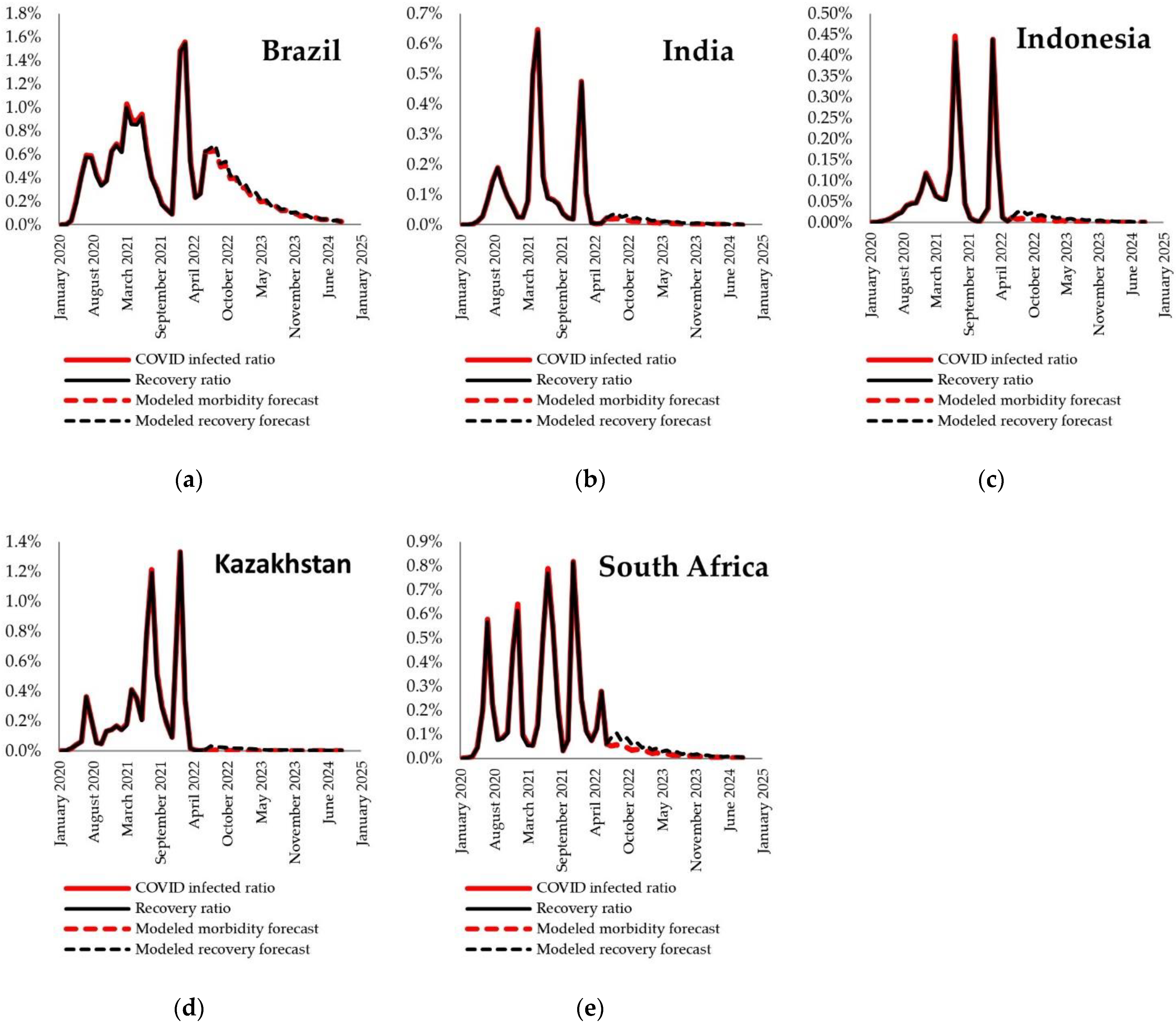
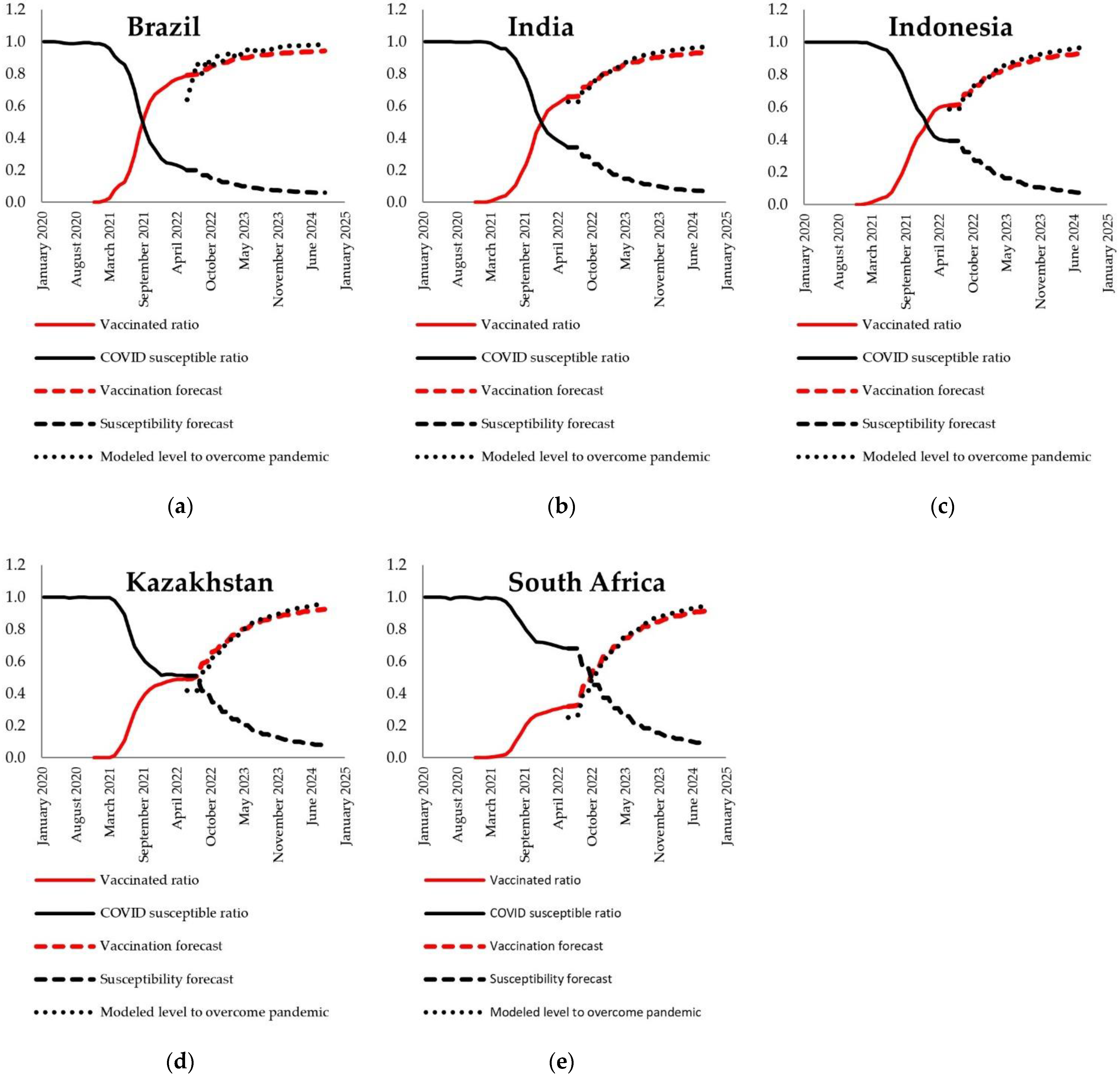
4. Model-Based Estimates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, P.; Zheng, X.; Li, J.; Zhu, B. Prediction of epidemic trends in COVID-19 with logistic model and machine learning technics. Chaos Solitons Fractals 2020, 139, 110058. [Google Scholar] [CrossRef] [PubMed]
- Barlow, N.S.; Weinstein, S.J. Accurate closed-form solution of the SIR epidemic model. Phys. Nonlinear Phenom. 2020, 408, 132540. [Google Scholar] [CrossRef] [PubMed]
- Marinov, T.T.; Marinova, R.S. Dynamics of COVID-19 using inverse problem for coefficient identification in SIR epidemic models. Chaos Solitons Fractals X 2020, 5, 100041. [Google Scholar] [CrossRef]
- Nkwayep, C.H.; Contreras, S.; Tewa, J.J.; Kurths, J. Short-term forecasts of the COVID-19 pandemic: A study case of Cameroon. Chaos Solitons Fractals 2020, 140, 110106. [Google Scholar] [CrossRef] [PubMed]
- Contreras, S.; Villavicencio, H.A.; Medina-Ortiz, D.; Biron-Lattes, J.P.; Olivera-Nappa, Á. A multi-group SEIRA model for the spread of COVID-19 among heterogeneous populations. Chaos Solitons Fractals 2020, 136, 109925. [Google Scholar] [CrossRef] [PubMed]
- World Bank Group. Global Economic Prospects. January 2022; The World Bank Group: Washington, DC, USA, 2022; Available online: https://openknowledge.worldbank.org/bitstream/handle/10986/36519/9781464817601.pdf (accessed on 15 May 2022).
- International Labour Organization. ILO Monitor: COVID-19 and the World of Work. Seventh Edition. International Labour Organization, 2021. Available online: https://www.ilo.org/wcmsp5/groups/public/---dgreports/---dcomm/documents/briefingnote/wcms_767028.pdf (accessed on 5 May 2022).
- International Labour Office. World Social Protection Report 2020-22 Social Protection at the Crossroads—In Pursuit of a Better Future; International Labour Organisation (ILO): Genève, Switzerland, 2021. [Google Scholar]
- Baldwin, R. Keeping the Lights on: Economic Medicine for a Medical Shock. CEPR. Available online: https://cepr.org/voxeu/columns/keeping-lights-economic-medicine-medical-shock (accessed on 22 September 2021).
- Baldwin, R.E.; di Mauro, B.W. Economics in the Time of COVID-19; VoxEU.org eBook; CEPR Press: London, UK, 2020; Available online: https://www.sensiblepolicy.com/download/2020/2020_CEPR_McKibbin_Fernando_COVD-19.pdf (accessed on 5 May 2022).
- Furceri, D.; Loungani, P.; Ostry, J.D.; Pizzuto, P. COVID-19 Will Raise Inequality if Past Pandemics Are a Guide. CEPR. Available online: https://cepr.org/voxeu/columns/covid-19-will-raise-inequality-if-past-pandemics-are-guide (accessed on 11 September 2021).
- Balleer, A.; Gehrke, B.; Hochmuth, B.; Merkl, C. Guidelines for Cost-Effective Use of SURE: Rule-Based Short-Time Work with Workers’ Consent and Aligned Replacement Rates. CEPR. Available online: https://cepr.org/voxeu/columns/guidelines-cost-effective-use-sure-rule-based-short-time-work-workers-consent-and (accessed on 1 September 2021).
- Belhadi, A.; Kamble, S.; Jabbour, C.J.C.; Gunasekaran, A.; Ndubisi, N.O.; Venkatesh, M. Manufacturing and service supply chain resilience to the COVID-19 outbreak: Lessons learned from the automobile and airline industries. Technol. Forecast. Soc. Change 2021, 163, 120447. [Google Scholar] [CrossRef]
- Škare, M.; Soriano, D.R.; Porada-Rochoń, M. Impact of COVID-19 on the travel and tourism industry. Technol. Forecast. Soc. Change 2021, 163, 120469. [Google Scholar] [CrossRef]
- Devezas, T. The struggle SARS-CoV-2 vs. homo sapiens–Why the earth stood still, and how will it keep moving on? Technol. Forecast. Soc. Change 2020, 160, 120264. [Google Scholar] [CrossRef]
- Devezas, T. Aeronautics and COVID-19: A Reciprocal Cause-and-Effect Phenomenon. J. Aerosp. Technol. Manag. 2020, 12, e3420. [Google Scholar] [CrossRef]
- Stiglitz, J.E. The proper role of government in the market economy: The case of the post-COVID recovery. J. Gov. Econ. 2021, 1, 100004. [Google Scholar] [CrossRef]
- Haleem, A.; Javaid, M.; Vaishya, R. Effects of COVID-19 pandemic in daily life. Curr. Med. Res. Pract. 2020, 10, 78–79. [Google Scholar] [CrossRef] [PubMed]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef]
- Sintunavarat, W.; Turab, A. Mathematical analysis of an extended SEIR model of COVID-19 using the ABC-fractional operator. Math. Comput. Simul. 2022, 198, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Sanderson, W.C. Simulation Models of Demographic, Economic, and Environmental Interactions. In Population—Development—Environment; Lutz, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 33–71. [Google Scholar] [CrossRef]
- Lutz, W. (Ed.) Population—Development—Environment: Understanding their Interactions in Mauritius; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar] [CrossRef]
- Anderson, J.; Begamini, E.; Brekelmans, S.; Cameron, A.; Darvas, Z.; Domíngez Jiménez, M. The Fiscal Response to the Economic Fallout from the Coronavirus. Bruegel|The Brussels-Based Economic Think Tank. Available online: https://www.bruegel.org/publications/datasets/covid-national-dataset/ (accessed on 1 May 2022).
- RBK. The Accounts Chamber Estimated the Cost of Fighting the Pandemic, Cчeтнaя пaлaтa Oцeнилa вeличинy Pacxoдoв нa бopьбy c пaндeмиeй (In Russian). Available online: https://www.rbc.ru/economics/24/02/2021/6034d7659a7947b5e4403bdd (accessed on 1 May 2022).
- Asian Development Bank (ADB). Homepage|ADB COVID-19 Policy Database. 2020. Available online: https://covid19policy.adb.org/ (accessed on 12 May 2022).
- KPMG. Brazil—Government and Institution Measures in Response to COVID-19. 2020. Available online: https://home.kpmg/xx/en/home/insights/2020/04/brazil-government-and-institution-measures-in-response-to-covid.html (accessed on 1 May 2021).
- Comunian, A.; Gaburro, R.; Giudici, M. Inversion of a SIR-based model: A critical analysis about the application to COVID-19 epidemic. Phys. Nonlinear Phenom. 2020, 413, 132674. [Google Scholar] [CrossRef] [PubMed]
- Zvyagintsev, А.I. On a Nonlinear Differential System Modeling the Dynamics of the COVID-19 Pandemic, O HEЛИHEЙHOЙ ДИФФEPEHЦИAЛbHOЙ CИCTEME, MOДEЛИPYЮЩEЙ ДИHAMИKY ПAHДEMИИ COVID-19 (In Russian). Int. Res. J. Meждyнapoдный Hayчнo-Иccлeдoвameльcкuй Жypнaл 2022, 7, 116–121. [Google Scholar] [CrossRef]
- Sadovnichiy, V.A.; Akaev, A.A.; Zvyagintsev, A.I.; Sarygulov, A.I. Mathematical Modeling of Overcoming the COVID-19 Pandemic and Restoring Economic Growth. Dokl. Math. 2022, 106, 30–235. [Google Scholar] [CrossRef]
- Leonov, G.A.; Zvyagintseva, K.A. Piragas stabilization of discrete delayed feedback systems with a periodic pulse gain, Cтaбилизaция пo Пиpaгacy диcкpeтныx cиcтeм зaпaздывaющeй oбpaтнoй cвязью c пepиoдичecким импyльcным кoэффициeнтoм ycилeния (In Russian). Vestn. St. Petersburg Univ. Math. 2015, 48, 147–156. [Google Scholar] [CrossRef]
- Leonov, G.A.; Zvyagintseva, K.A.; Kuznetsova, O.A. Pyragas stabilization of discrete systems via delayed feedback with periodic control gain. IFAC-Pap. 2016, 49, 56–61. [Google Scholar] [CrossRef]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 1992, 170, 421–428. [Google Scholar] [CrossRef]
- Ritchie, H.; Mathieu, E.; Rodés-Guirao, L.; Appel, C.; Giattino, C.; Ortiz-Ospina, E.; Hasell, J.; Macdonald, B.; Beltekian, D.; Roser, M. Coronavirus Pandemic (COVID-19). Our World Data. 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 27 August 2022).
- Our World in Data. COVID Live—Coronavirus Statistics—Worldometer. Coronavirus Pandemic (COVID-19). Available online: https://www.worldometers.info/coronavirus/ (accessed on 5 May 2022).
- International Monetary Fund. World Economic Outlook, April 2022: War Sets Back the Global Recovery; IMF: Washington, DC, USA, 2022; Available online: https://www.imf.org/en/Publications/WEO/Issues/2022/04/19/world-economic-outlook-april-2022 (accessed on 5 May 2022).
- World Bank. GDP (Constant 2015 US$)—India, Indonesia, Brazil, South Africa, Kazakhstan|Data. Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.KD?end=2020&locations=IN-ID-BR-ZA-KZ&start=2014 (accessed on 1 May 2022).
- World Bank. Population, Total—India, Indonesia, Brazil, South Africa, Kazakhstan | Data. The Worldbank. Available online: https://data.worldbank.org/indicator/SP.POP.TOTL?end=2020&locations=IN-ID-BR-ZA-KZ&start=2014 (accessed on 1 May 2022).
- Organization for Economic Cooperation and Development. Quarterly National Accounts. Available online: https://stats.oecd.org/Index.aspx?DataSetCode=QNA (accessed on 12 May 2022).
- Dime, R.; Ginting, E.; Zhuang, J. Estimating Fiscal Multipliers in Selected Asian Economies. ADB Econ. Work. Pap. Ser. 2021, 638, 1–32. [Google Scholar] [CrossRef]
- Raga, S. Fiscal Multipliers: A Review of Fiscal Stimulus Options and Impact on Developing Countries. IDRC. 2022. Available online: https://set.odi.org/fiscal-multipliers-a-review-of-fiscal-stimulus-options-and-impact-on-developing-countries/ (accessed on 5 May 2022).

| Brazil | India | Indonesia | Kazakhstan | South Africa | |
|---|---|---|---|---|---|
| (Susceptible, %) | 0.198118 | 0.343269 | 0.390949 | 0.509977 | 0.68141 |
| (Infected, %) | 0.006257 | 0.000221 | 0.000121 | 0.000052 | 0.00059 |
| (Recovered, %) | 0.006235 | 0.00022 | 0.00012 | 0.000051 | 0.00058 |
| (Vaccinated, %) | 0.78939 | 0.65629 | 0.60881 | 0.48992 | 0.31742 |
| (Epidemiological level of infection) | 0.63818 | 0.6251 | 0.58678 | 0.41644 | 0.25091 |
| (GDP per capita, USD) | 8549.62 | 1953.94 | 3855.9 | 11269.4 | 5864.0 |
| Brazil | India | Indonesia | Kazakhstan | South Africa | |
|---|---|---|---|---|---|
| a | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| b | 0.5 | 5 | 10 | 50 | 5 |
| c | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| d | 0.000005263157895 | 0.000005263157895 | 0.000005263157895 | 0.000005263157895 | 0.000005263157895 |
| r | 1 | 10 | 20 | 100 | 10 |
| v | 0.35 | 0.8 | 1.3 | 5.3 | 0.8 |
| q | 0.0011 | 0.0011 | 0.0011 | 0.0011 | 0.0011 |
| γ | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 |
| η | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| λ | 2 | 2 | 2 | 2 | 2 |
| δ | 0.190487385822133 | 0.00458002457714418 | 0.00447593310948182 | 0.00247737693036435 | 0.013011433457796 |
| ω | −0.2 | −0.2 | −0.2 | −0.2 | −0.2 |
| ρ | 3 | 3 | 3 | 3 | 3 |
| k | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| Scale of Vaccination (% of Country’s Population) | Additional Investments in the Economy (bln USD) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Date | BRA | IND | IDN | KAZ | ZAF | BRA | IND | IDN | KAZ | ZAF |
| 07.22 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 32.70 | 21.71 | 10.15 | 1.14 | 3.34 |
| 08.22 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 14.80 | 21.52 | 10.05 | 1.13 | 3.25 |
| 09.22 | 3.4 | 6.2 | 7.2 | 9.7 | 13.4 | 17.12 | 35.60 | 15.20 | 1.33 | 3.62 |
| 10.22 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9.63 | 14.16 | 6.60 | 0.73 | 2.11 |
| 11.22 | 2.7 | 5.0 | 5.8 | 7.8 | 10.7 | 13.11 | 25.46 | 10.73 | 0.90 | 2.42 |
| 12.22 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6.25 | 9.26 | 4.31 | 0.47 | 1.37 |
| 01.23 | 2.2 | 4.0 | 4.6 | 6.2 | 8.6 | 10.10 | 18.33 | 7.63 | 0.61 | 1.63 |
| 02.23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4.04 | 6.03 | 2.80 | 0.31 | 0.89 |
| 03.23 | 1.7 | 3.2 | 3.7 | 5.0 | 6.9 | 7.83 | 13.29 | 5.46 | 0.41 | 1.10 |
| 04.23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.61 | 3.91 | 1.82 | 0.20 | 0.57 |
| 05.23 | 1.4 | 2.5 | 3.0 | 4.0 | 5.5 | 6.10 | 9.73 | 3.94 | 0.28 | 0.74 |
| 06.23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.68 | 2.53 | 1.17 | 0.13 | 0.37 |
| 07.23 | 1.1 | 2.0 | 2.4 | 3.2 | 4.4 | 4.77 | 7.19 | 2.88 | 0.20 | 0.51 |
| 08.23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.08 | 1.63 | 0.76 | 0.08 | 0.24 |
| 09.23 | 0.9 | 1.6 | 1.9 | 2.6 | 3.5 | 3.75 | 5.36 | 2.12 | 0.14 | 0.35 |
| 10.23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.69 | 1.05 | 0.49 | 0.05 | 0.15 |
| 11.23 | 0.7 | 1.3 | 1.5 | 2.0 | 2.8 | 2.95 | 4.04 | 1.58 | 0.10 | 0.24 |
| 12.23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.45 | 0.68 | 0.31 | 0.03 | 0.10 |
| 01.24 | 0.6 | 1.0 | 1.2 | 1.6 | 2.2 | 2.33 | 3.07 | 1.19 | 0.07 | 0.17 |
| 02.24 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.29 | 0.44 | 0.20 | 0.02 | 0.06 |
| 03.24 | 0.5 | 0.8 | 1.0 | 1.3 | 1.8 | 1.85 | 2.35 | 0.90 | 0.05 | 0.12 |
| 04.24 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.18 | 0.28 | 0.13 | 0.01 | 0.04 |
| 05.24 | 0.4 | 0.7 | 0.8 | 1.0 | 1.4 | 1.47 | 1.81 | 0.69 | 0.04 | 0.09 |
| 06.24 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.12 | 0.18 | 0.08 | 0.01 | 0.03 |
| 07.24 | 0.3 | 0.5 | 0.6 | 0.8 | 1.1 | 1.17 | 1.40 | 0.53 | 0.03 | 0.06 |
| 08.24 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.08 | 0.12 | 0.05 | 0.01 | 0.02 |
| 09.24 | 0.2 | 0.4 | 0.5 | 0.7 | 0.9 | 0.93 | 1.09 | 0.41 | 0.02 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akaev, A.; Zvyagintsev, A.I.; Sarygulov, A.; Devezas, T.; Tick, A.; Ichkitidze, Y. Growth Recovery and COVID-19 Pandemic Model: Comparative Analysis for Selected Emerging Economies. Mathematics 2022, 10, 3654. https://doi.org/10.3390/math10193654
Akaev A, Zvyagintsev AI, Sarygulov A, Devezas T, Tick A, Ichkitidze Y. Growth Recovery and COVID-19 Pandemic Model: Comparative Analysis for Selected Emerging Economies. Mathematics. 2022; 10(19):3654. https://doi.org/10.3390/math10193654
Chicago/Turabian StyleAkaev, Askar, Alexander I. Zvyagintsev, Askar Sarygulov, Tessaleno Devezas, Andrea Tick, and Yuri Ichkitidze. 2022. "Growth Recovery and COVID-19 Pandemic Model: Comparative Analysis for Selected Emerging Economies" Mathematics 10, no. 19: 3654. https://doi.org/10.3390/math10193654
APA StyleAkaev, A., Zvyagintsev, A. I., Sarygulov, A., Devezas, T., Tick, A., & Ichkitidze, Y. (2022). Growth Recovery and COVID-19 Pandemic Model: Comparative Analysis for Selected Emerging Economies. Mathematics, 10(19), 3654. https://doi.org/10.3390/math10193654







