Gain-Scheduled Sliding-Mode-Type Iterative Learning Control Design for Mechanical Systems
Abstract
:1. Introduction
- The proposed controller is synthesized involving a feedback regulation item, a feedforward learning item, and a robust switching item. By combining the advantages of both SM control and IL control, the proposed controller has strong robustness against model uncertainties and disturbances.
- The gain-scheduled mechanism is employed for both the feedback regulation item and feedforward learning item. Benefiting from this design, the proposed controller can achieve relatively fast convergence speed.
- Convergence analysis is theoretically provided. The proposed controller can ensure the position and velocity tracking errors can eventually regulate to zero even in the presence of model uncertainties and disturbances.
2. Problem Description
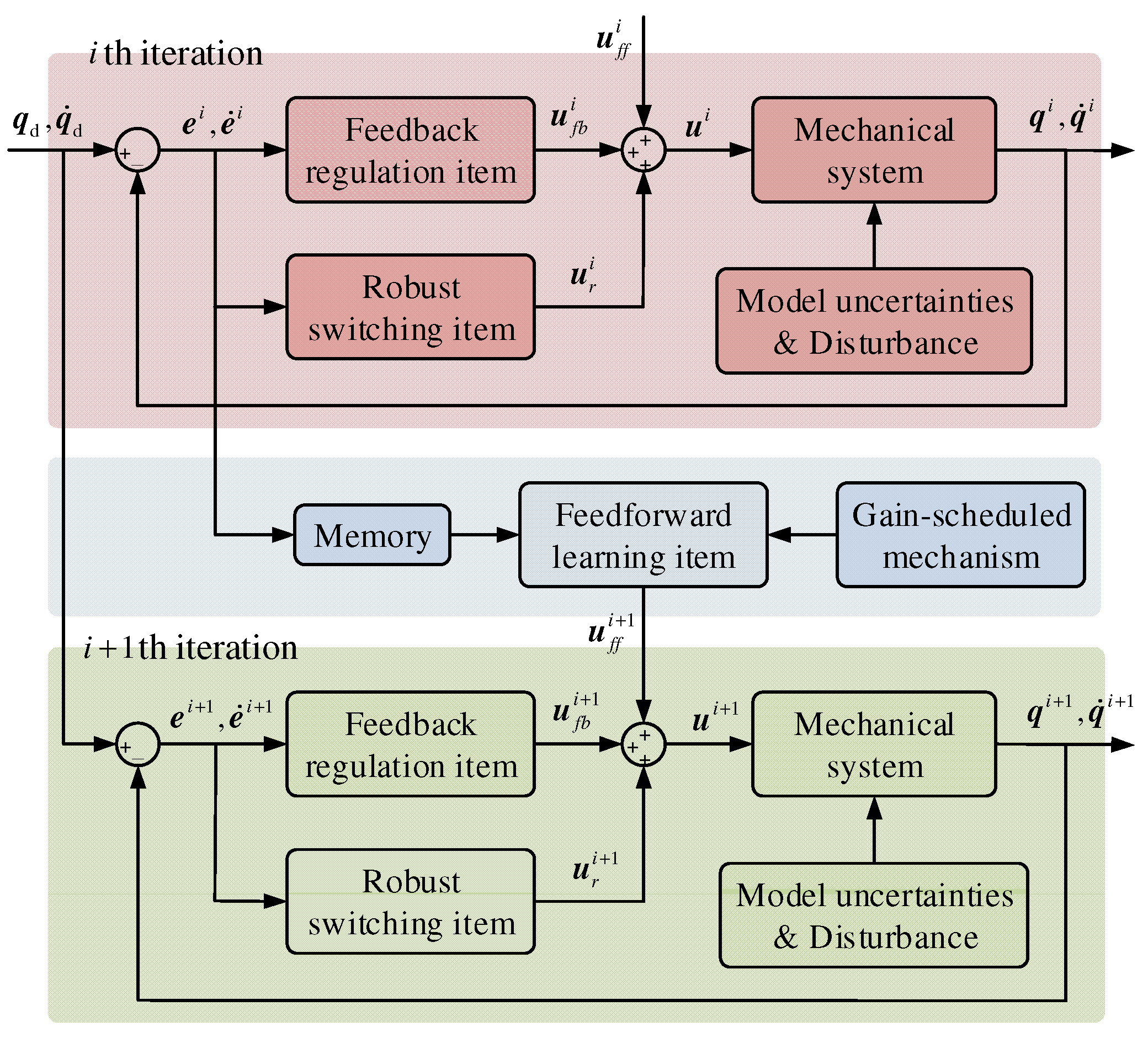
3. Controller Design
4. Convergence Analysis
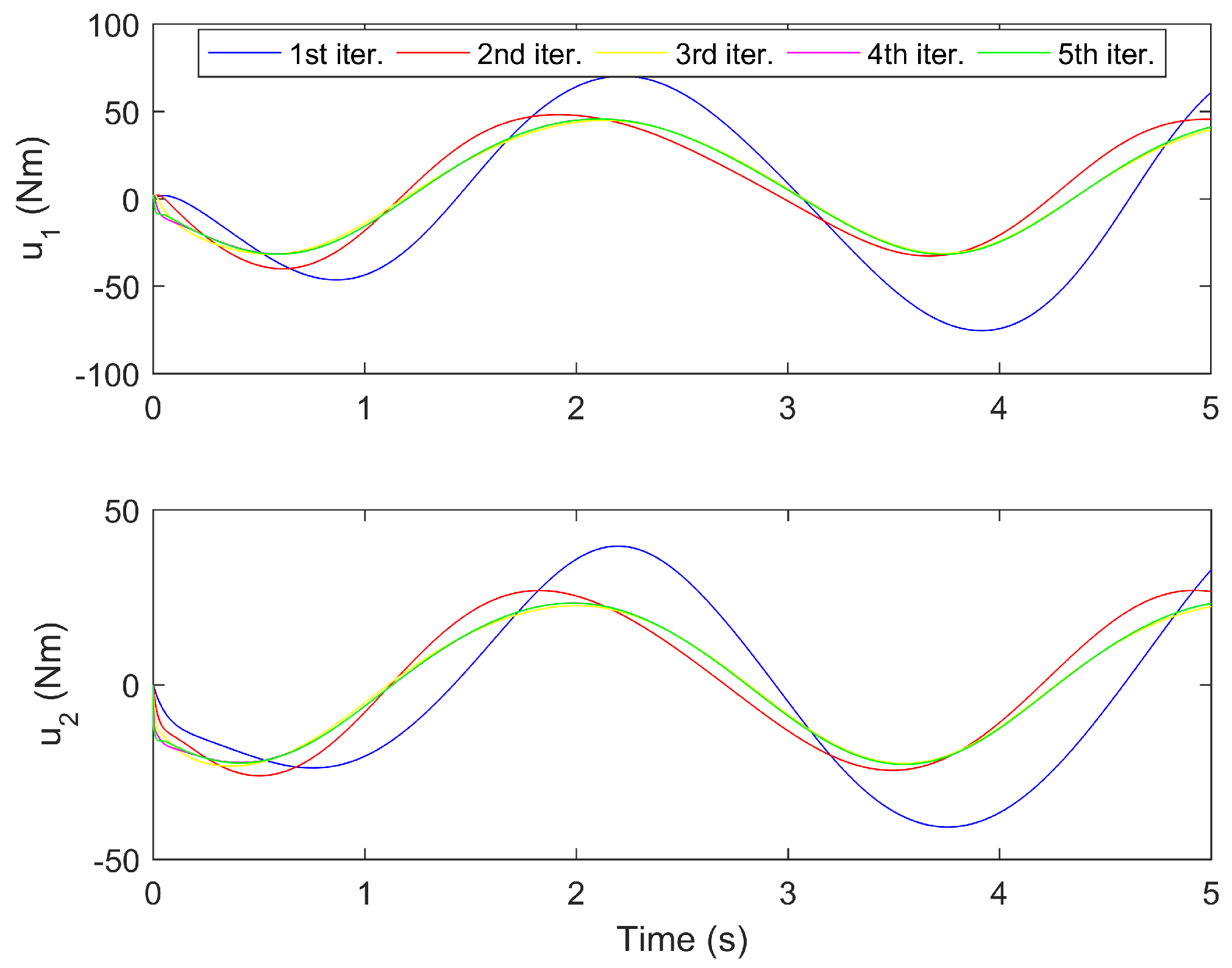
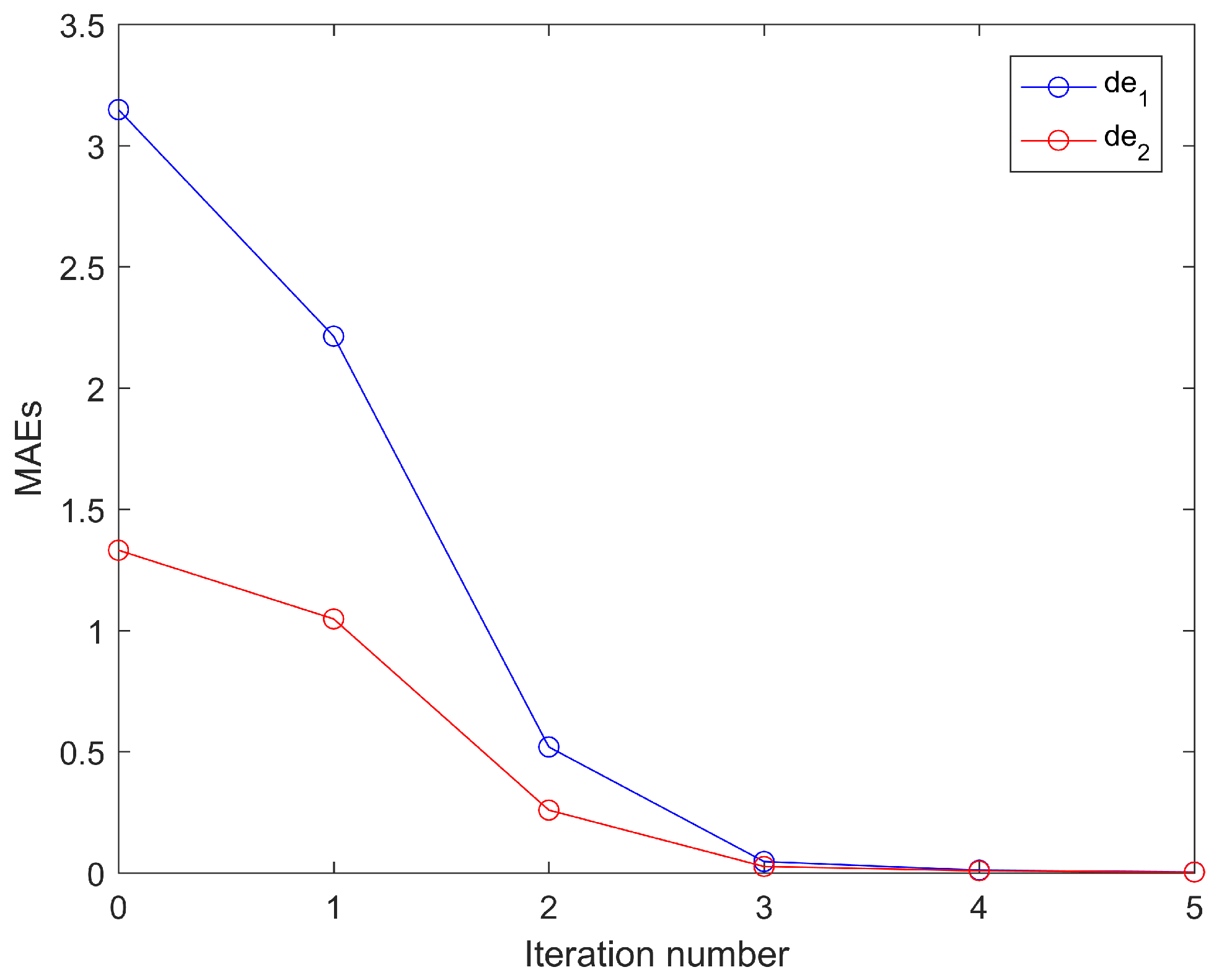
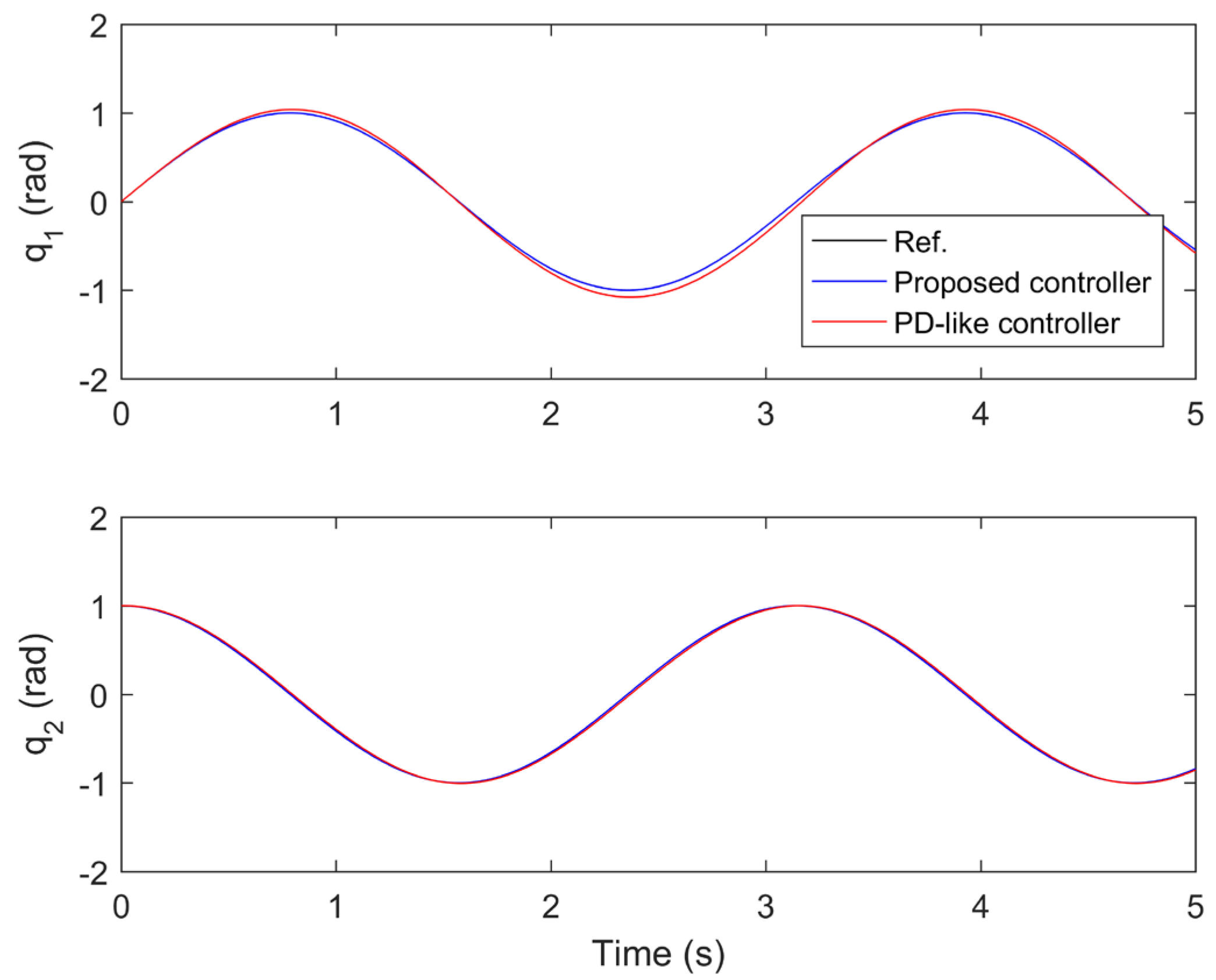
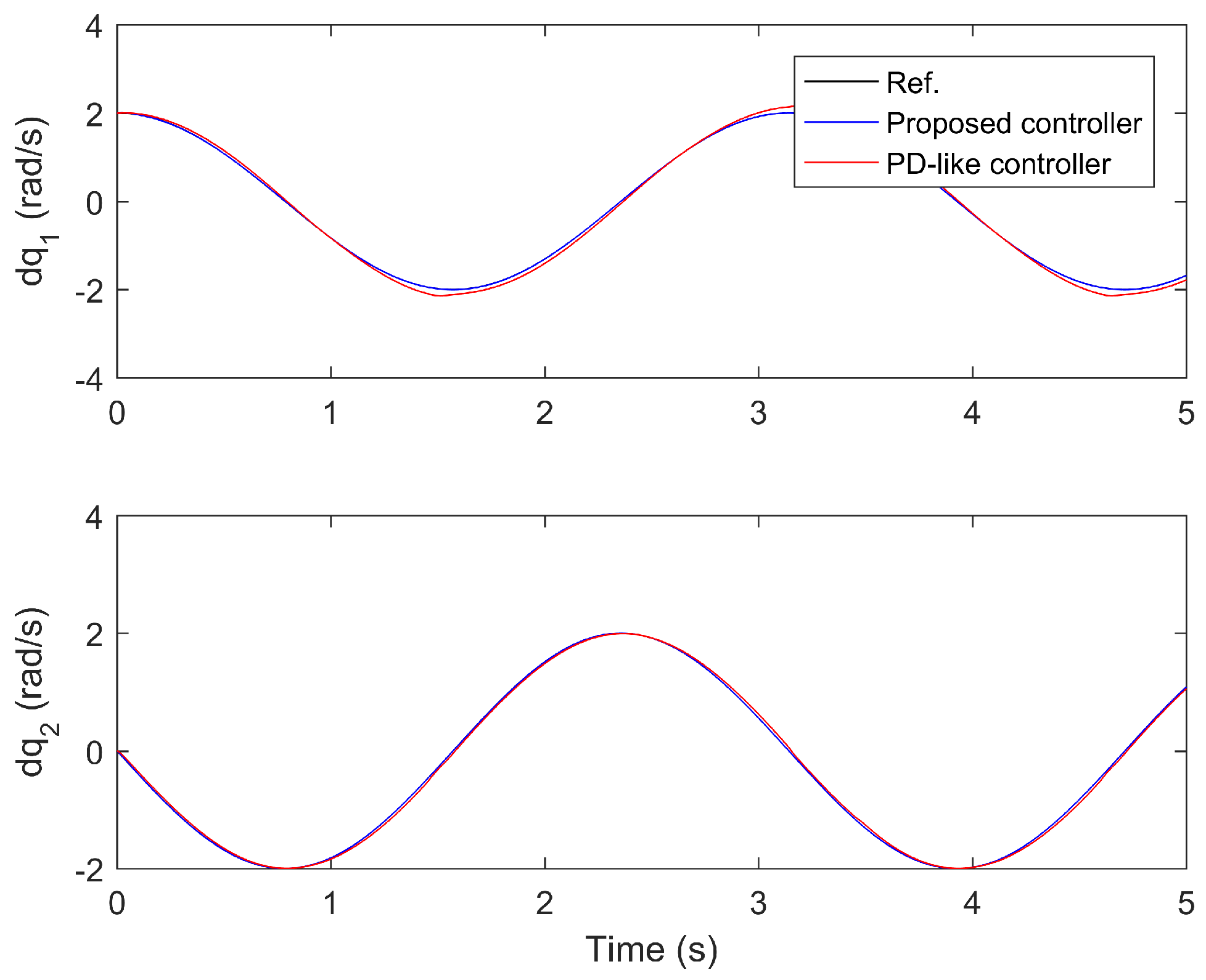
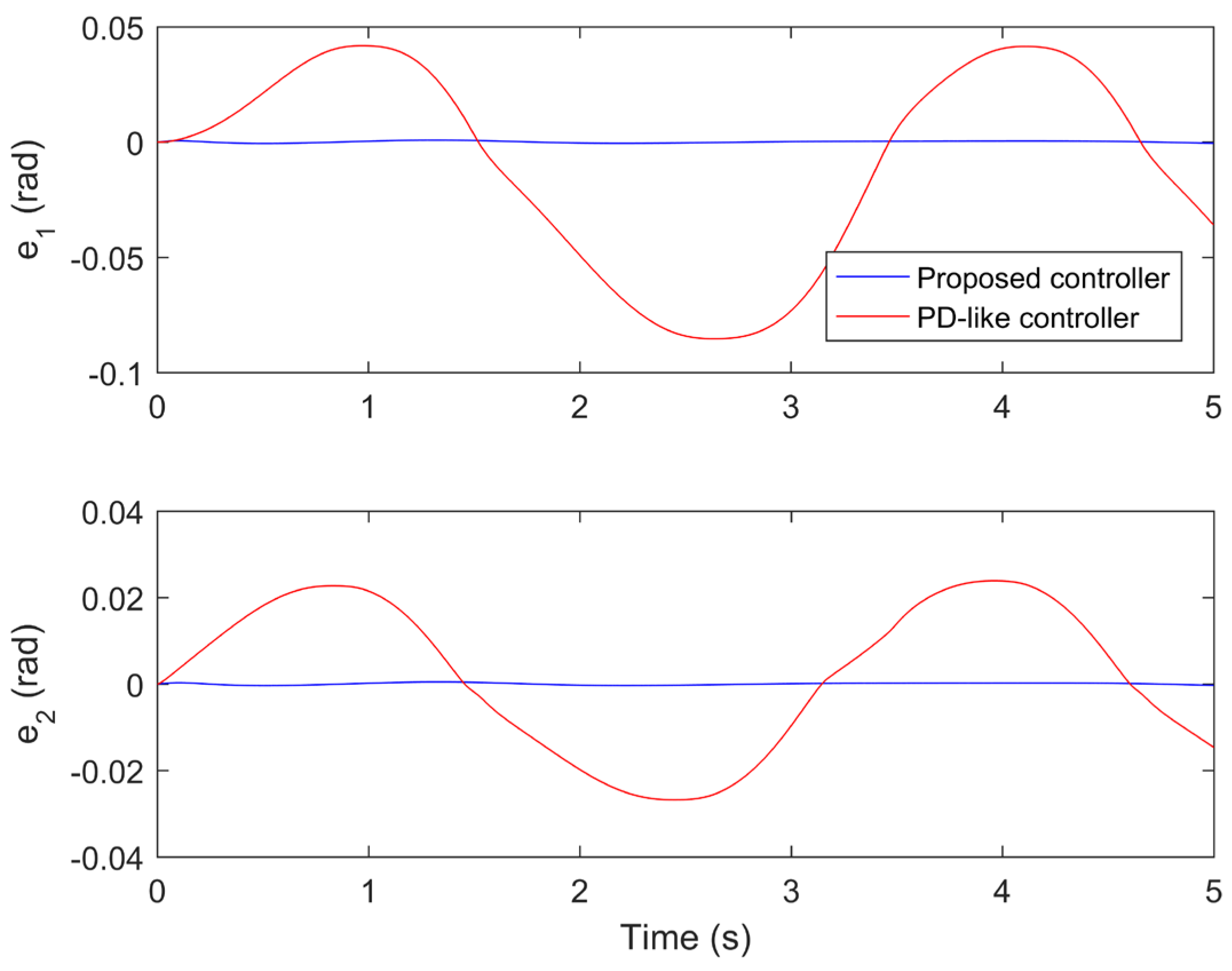
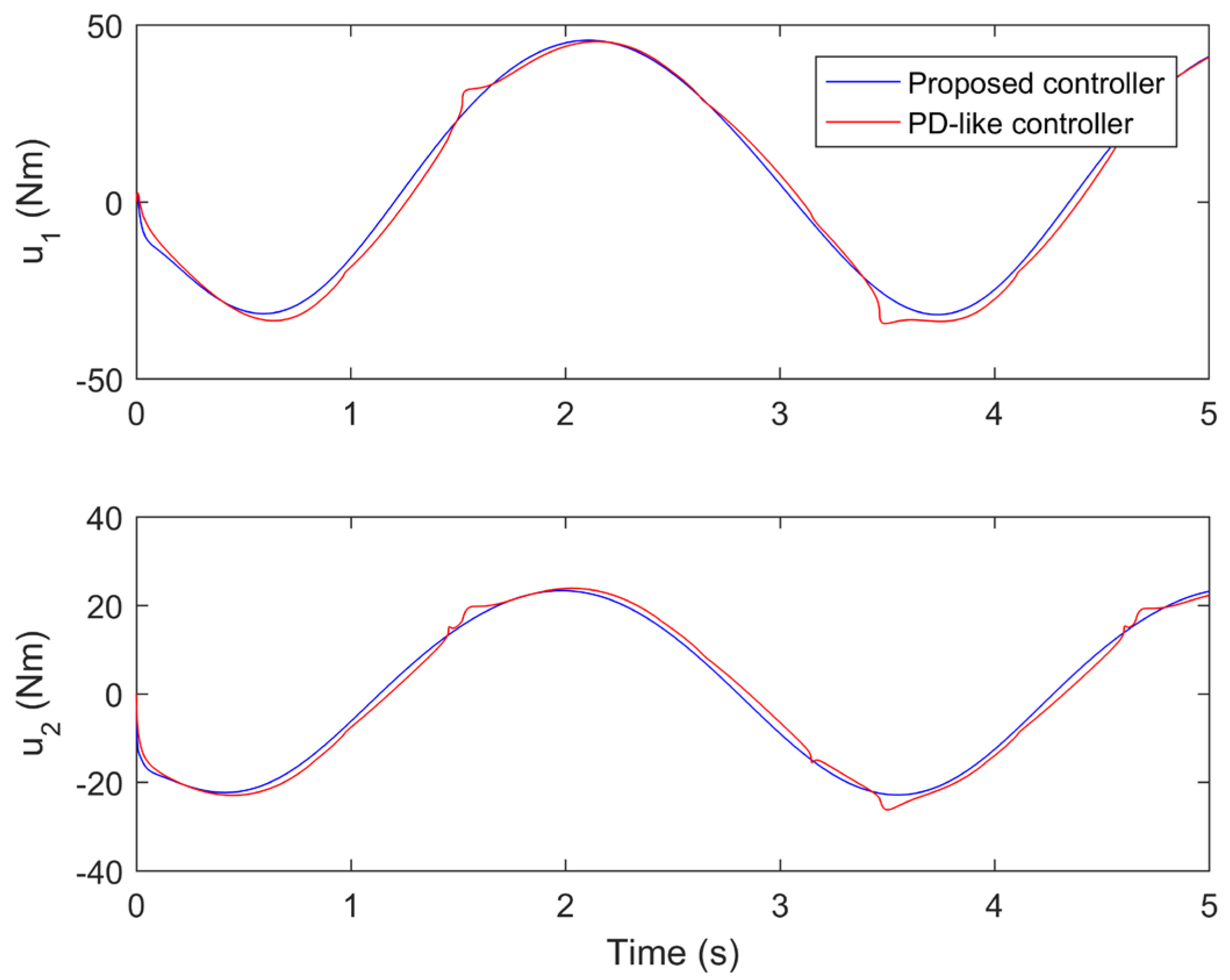
5. Simulations and Comparisons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Jahanshahi, H.; Volos, C.; Bekiros, S.; Khan, M.A.; Agarwal, P.; Aly, A.A. A new RBF neural network-based fault-tolerant active control for fractional time-delayed systems. Electronics 2021, 10, 1501. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.-M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. An optimal fuzzy PID control approach for docking maneuver of two spacecraft: Orientational motion. Eng. Sci. Technol. Int. J. 2017, 20, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Li, J.-F.; Jahanshahi, H.; Kacar, S.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alotaibi, N.D.; Alharbi, K.H. On the variable-order fractional memristor oscillator: Data security applications and synchronization using a type-2 fuzzy disturbance observer-based robust control. Chaos Solitons Fractals 2021, 145, 110681. [Google Scholar] [CrossRef]
- Wang, B.; Jahanshahi, H.; Arıcıoğlu, B.; Boru, B.; Kacar, S.; Alotaibi, N.D. A variable-order fractional neural network: Dynamical properties, Data security application, and synchronization using a novel control algorithm with a finite-time estimator. J. Frankl. Inst. 2022. [Google Scholar] [CrossRef]
- Alsaade, F.W.; Jahanshahi, H.; Yao, Q.; Al-zahrani, M.S.; Alzahrani, A.S. A new neural network-based optimal mixed H2/H∞ control for a modified unmanned aerial vehicle subject to control input constraints. Adv. Space Res. 2022. [Google Scholar] [CrossRef]
- Zhou, S.-S.; Jahanshahi, H.; Din, Q.; Bekiros, S.; Alcaraz, R.; Alassafi, M.O.; Alsaadi, F.E.; Chu, Y.-M. Discrete-time macroeconomic system: Bifurcation analysis and synchronization using fuzzy-based activation feedback control. Chaos Solitons Fractals 2021, 142, 110378. [Google Scholar] [CrossRef]
- Xiong, P.-Y.; Jahanshahi, H.; Alcaraz, R.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alsaadi, F.E. Spectral entropy analysis and synchronization of a multi-stable fractional-order chaotic system using a novel neural network-based chattering-free sliding mode technique. Chaos Solitons Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Soradi-Zeid, S.; Castillo, O. A review on design and implementation of type-2 fuzzy controllers. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Zambrano-Serrano, E.; Bekiros, S.; Wei, Z.; Volos, C.; Castillo, O.; Aly, A.A. On the dynamical investigation and synchronization of variable-order fractional neural networks: The Hopfield-like neural network model. Eur. Phys. J. Spec. Top. 2022, 231, 1757–1769. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.-T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Rajagopal, K.; Akgul, A.; Sari, N.N.; Namazi, H.; Jafari, S. Complete analysis and engineering applications of a megastable nonlinear oscillator. Int. J. Non-Linear Mech. 2018, 107, 126–136. [Google Scholar] [CrossRef]
- Bekiros, S.; Jahanshahi, H.; Bezzina, F.; Aly, A.A. A novel fuzzy mixed H2/H∞ optimal controller for hyperchaotic financial systems. Chaos Solitons Fractals 2021, 146, 110878. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Shahriari-Kahkeshi, M.; Alcaraz, R.; Wang, X.; Singh, V.P.; Pham, V.-T. Entropy analysis and neural network-based adaptive control of a non-equilibrium four-dimensional chaotic system with hidden attractors. Entropy 2019, 21, 156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jahanshahi, H. Smooth control of HIV/AIDS infection using a robust adaptive scheme with decoupled sliding mode supervision. Eur. Phys. J. Spec. Top. 2018, 227, 707–718. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sajjadi, S.S.; Bekiros, S.; Aly, A.A. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller. Chaos Solitons Fractals 2021, 144, 110698. [Google Scholar] [CrossRef]
- Xu, J.-X. A survey on iterative learning control for nonlinear systems. Int. J. Control 2011, 84, 1275–1294. [Google Scholar] [CrossRef]
- Ahn, H.-S.; Chen, Y.; Moore, K.L. Iterative learning control: Brief survey and categorization. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1099–1121. [Google Scholar] [CrossRef]
- Bristow, D.A.; Tharayil, M.; Alleyne, A.G. A survey of iterative learning control. IEEE Control Syst. Mag. 2006, 26, 96–114. [Google Scholar]
- Moore, K.L.; Dahleh, M.; Bhattacharyya, S.P. Iterative learning control: A survey and new results. J. Robot. Syst. 1992, 9, 563–594. [Google Scholar] [CrossRef]
- Arimoto, S.; Kawamura, S.; Miyazaki, F. Bettering operation of robots by learning. J. Robot. Syst. 1984, 1, 123–140. [Google Scholar] [CrossRef]
- Saab, S.S.; Shen, D.; Orabi, M.; Kors, D.; Jaafar, R.H. Iterative learning control: Practical implementation and automation. IEEE Trans. Ind. Electron. 2021, 69, 1858–1866. [Google Scholar] [CrossRef]
- Bouakrif, F.; Zasadzinski, M. Trajectory tracking control for perturbed robot manipulators using iterative learning method. Int. J. Adv. Manuf. Technol. 2016, 87, 2013–2022. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Lin, Y.; Xi, F.; Guo, S. Calibration-based iterative learning control for path tracking of industrial robots. IEEE Trans. Ind. Electron. 2014, 62, 2921–2929. [Google Scholar] [CrossRef]
- Bouakrif, F.; Boukhetala, D.; Boudjema, F. Velocity observer-based iterative learning control for robot manipulators. Int. J. Syst. Sci. 2013, 44, 214–222. [Google Scholar] [CrossRef]
- Tayebi, A.; Abdul, S.; Zaremba, M.B.; Ye, Y. Robust iterative learning control design: Application to a robot manipulator. IEEE/ASME Trans. Mechatron. 2008, 13, 608–613. [Google Scholar] [CrossRef] [Green Version]
- Tayebi, A.; Islam, S. Adaptive iterative learning control for robot manipulators: Experimental results. Control Eng. Pract. 2006, 14, 843–851. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, P.R.; Zhang, W.J.; Gupta, M.M. An adaptive switching learning control method for trajectory tracking of robot manipulators. Mechatronics 2006, 16, 51–61. [Google Scholar] [CrossRef]
- Tayebi, A. Adaptive iterative learning control for robot manipulators. Automatica 2004, 40, 1195–1203. [Google Scholar] [CrossRef]
- Norrlof, M. An adaptive iterative learning control algorithm with experiments on an industrial robot. IEEE Trans. Robot. Autom. 2002, 18, 245–251. [Google Scholar] [CrossRef] [Green Version]
- Kuc, T.-Y.; Nam, K.; Lee, J.S. An iterative learning control of robot manipulators. IEEE Trans. Robot. Autom. 1991, 7, 835–842. [Google Scholar]
- Li, X.; Ren, Q.; Xu, J.-X. Precise speed tracking control of a robotic fish via iterative learning control. IEEE Trans. Ind. Electron. 2015, 63, 2221–2228. [Google Scholar] [CrossRef]
- Hu, T.; Low, K.H.; Shen, L.; Xu, X. Effective phase tracking for bioinspired undulations of robotic fish models: A learning control approach. IEEE/ASME Trans. Mechatron. 2012, 19, 191–200. [Google Scholar] [CrossRef]
- Qian, S.; Zi, B.; Ding, H. Dynamics and trajectory tracking control of cooperative multiple mobile cranes. Nonlinear Dyn. 2016, 83, 89–108. [Google Scholar] [CrossRef]
- Yu, C.; Chen, X. Trajectory tracking of wheeled mobile robot by adopting iterative learning control with predictive, current, and past learning items. Robotica 2015, 33, 1393–1414. [Google Scholar] [CrossRef]
- Gui, Y.; Jia, Q.; Li, H.; Cheng, Y. Reconfigurable fault-tolerant control for spacecraft formation flying based on iterative learning algorithms. Appl. Sci. 2022, 12, 2485. [Google Scholar] [CrossRef]
- Yao, Q. Robust adaptive iterative learning control for high-precision attitude tracking of spacecraft. J. Aerosp. Eng. 2021, 34, 04020108. [Google Scholar] [CrossRef]
- Wu, B.; Wang, D.; Poh, E.K. High precision satellite attitude tracking control via iterative learning control. J. Guid. Control Dyn. 2015, 38, 528–534. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W.; Liu, J.; Wen, C. A robust adaptive iterative learning control for trajectory tracking of permanent-magnet spherical actuator. IEEE Trans. Ind. Electron. 2015, 63, 291–301. [Google Scholar] [CrossRef]
- Patan, K.; Patan, M. Neural-network-based iterative learning control of nonlinear systems. ISA Trans. 2020, 98, 445–453. [Google Scholar] [CrossRef]
- Bensidhoum, T.; Bouakrif, F. Adaptive P-type iterative learning radial basis function control for robot manipulators with unknown varying disturbances and unknown input dead zone. Int. J. Robust Nonlinear Control 2020, 30, 4075–4094. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Chien, C.-J.; Teng, C.-C. Direct adaptive iterative learning control of nonlinear systems using an output-recurrent fuzzy neural network. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 1348–1359. [Google Scholar] [CrossRef]
- Jiang, P.; Unbehauen, R. Iterative learning neural network control for nonlinear system trajectory tracking. Neurocomputing 2002, 48, 141–153. [Google Scholar] [CrossRef]
- Gopinath, S.; Kar, I.N.; Bhatt, R.K.P. Experience inclusion in iterative learning controllers: Fuzzy model based approaches. Eng. Appl. Artif. Intell. 2008, 21, 578–590. [Google Scholar] [CrossRef]
- Chien, C.-J. A combined adaptive law for fuzzy iterative learning control of nonlinear systems with varying control tasks. IEEE Trans. Fuzzy Syst. 2008, 16, 40–51. [Google Scholar] [CrossRef]
- Simba, K.R.; Bui, B.D.; Msukwa, M.R.; Uchiyama, N. Robust iterative learning contouring controller with disturbance observer for machine tool feed drives. ISA Trans. 2018, 75, 207–215. [Google Scholar] [CrossRef]
- Maeda, G.J.; Manchester, I.R.; Rye, D.C. Combined ILC and disturbance observer for the rejection of near-repetitive disturbances, with application to excavation. IEEE Trans. Control Syst. Technol. 2015, 23, 1754–1769. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.-Q.; Yeh, C.-P. Robust iterative learning control via continuous sliding-mode technique with validation on an SRV02 rotary plant. Mechatronics 2012, 22, 588–593. [Google Scholar] [CrossRef]
- Lu, J.-S.; Cheng, M.-Y.; Su, K.-H.; Tsai, M.-C. Wire tension control of an automatic motor winding machine—an iterative learning sliding mode control approach. Robot. Comput. Integr. Manuf. 2018, 50, 50–62. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, Y.; Zou, Y. An adaptive sliding-mode iterative constant-force control method for robotic belt grinding based on a one-dimensional force sensor. Sensors 2019, 19, 1635. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.V.; Phung, M.D.; Ha, Q.P. Iterative Learning Sliding Mode Control for UAV Trajectory Tracking. Electronics 2021, 10, 2474. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.; Yang, P.; Guo, S. Iterative learning sliding mode control for output-constrained upper-limb exoskeleton with non-repetitive tasks. Appl. Math. Model. 2021, 97, 366–380. [Google Scholar] [CrossRef]
- Wang, W.; Ma, J.; Li, X.; Cheng, Z.; Zhu, H.; Teo, C.S.; Lee, T.H. Iterative super-twisting sliding mode control for tray indexing system with unknown dynamics. IEEE Trans. Ind. Electron. 2020, 68, 9855–9865. [Google Scholar] [CrossRef]
- Wang, W.; Ma, J.; Cheng, Z.; Li, X.; de Silva, C.W.; Lee, T.H. Global iterative sliding mode control of an industrial biaxial gantry system for contouring motion tasks. IEEE/ASME Trans. Mechatron. 2021, 27, 1617–1628. [Google Scholar] [CrossRef]
- Liu, W.; Shu, F.; Xu, Y.; Ding, R.; Yang, X.; Li, Z.; Liu, Y. Iterative learning based neural network sliding mode control for repetitive tasks: With application to a PMLSM with uncertainties and external disturbances. Mech. Syst. Signal Process. 2022, 172, 108950. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Chi, R.; Hou, Z.; Xu, J. Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition. Automatica 2008, 44, 2207–2213. [Google Scholar] [CrossRef]
- Park, K.-H. An average operator-based PD-type iterative learning control for variable initial state error. IEEE Trans. Autom. Control 2005, 50, 865–869. [Google Scholar] [CrossRef]
- Xu, J.-X.; Yan, R.; Chen, Y. On initial conditions in iterative learning control. IEEE Trans. Autom. Control 2005, 50, 1349–1354. [Google Scholar]
- Sun, M.; Wang, D. Iterative learning control with initial rectifying action. Automatica 2002, 38, 1177–1182. [Google Scholar] [CrossRef]
- Hong, Y.; Xu, Y.; Huang, J. Finite-time control for robot manipulators. Syst. Control Lett. 2002, 46, 243–253. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Q.; Jahanshahi, H.; Bekiros, S.; Mihalache, S.F.; Alotaibi, N.D. Gain-Scheduled Sliding-Mode-Type Iterative Learning Control Design for Mechanical Systems. Mathematics 2022, 10, 3005. https://doi.org/10.3390/math10163005
Yao Q, Jahanshahi H, Bekiros S, Mihalache SF, Alotaibi ND. Gain-Scheduled Sliding-Mode-Type Iterative Learning Control Design for Mechanical Systems. Mathematics. 2022; 10(16):3005. https://doi.org/10.3390/math10163005
Chicago/Turabian StyleYao, Qijia, Hadi Jahanshahi, Stelios Bekiros, Sanda Florentina Mihalache, and Naif D. Alotaibi. 2022. "Gain-Scheduled Sliding-Mode-Type Iterative Learning Control Design for Mechanical Systems" Mathematics 10, no. 16: 3005. https://doi.org/10.3390/math10163005






