Analysis of the Stability and Optimal Control Strategy for an ISCR Rumor Propagation Model with Saturated Incidence and Time Delay on a Scale-Free Network
Abstract
:1. Introduction
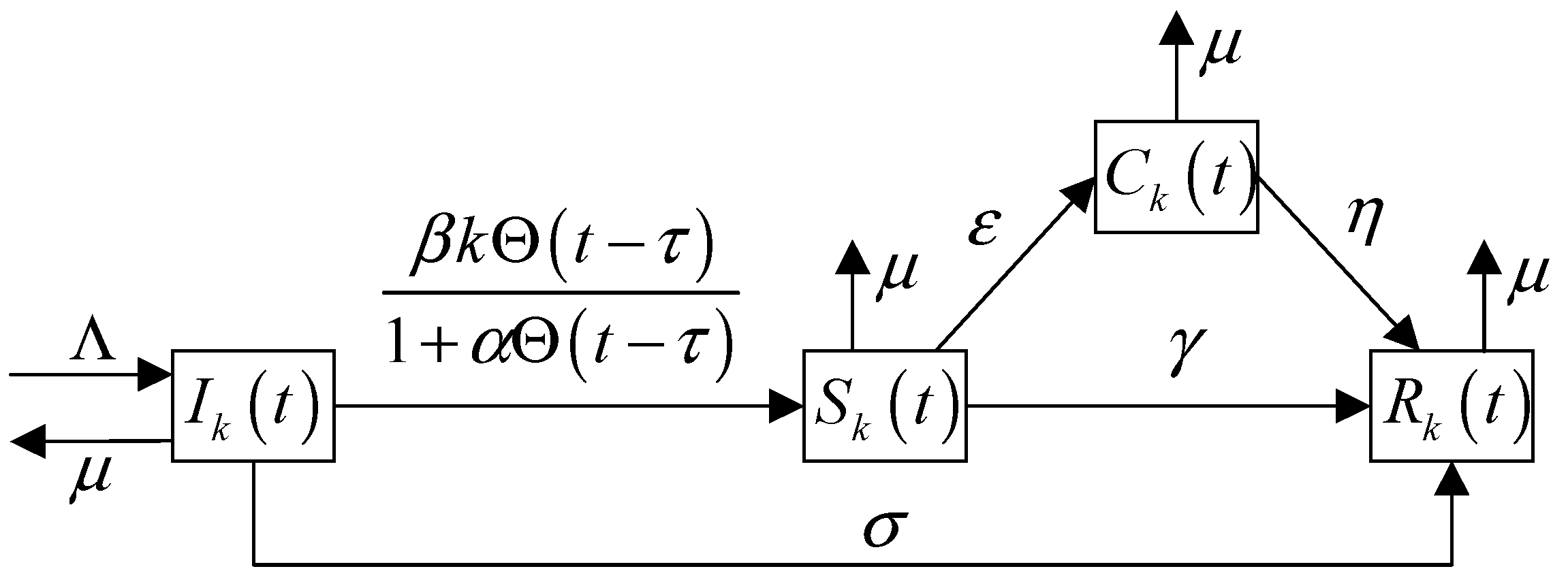
2. The Rumor Spreading Model
2.1. Model Formulation
2.2. The Basic Reproduction Number of the System (1)
3. The Stability of the Rumor Propagate Model
4. Optimal Control Strategy for Rumor Propagation
5. Numerical Simulations
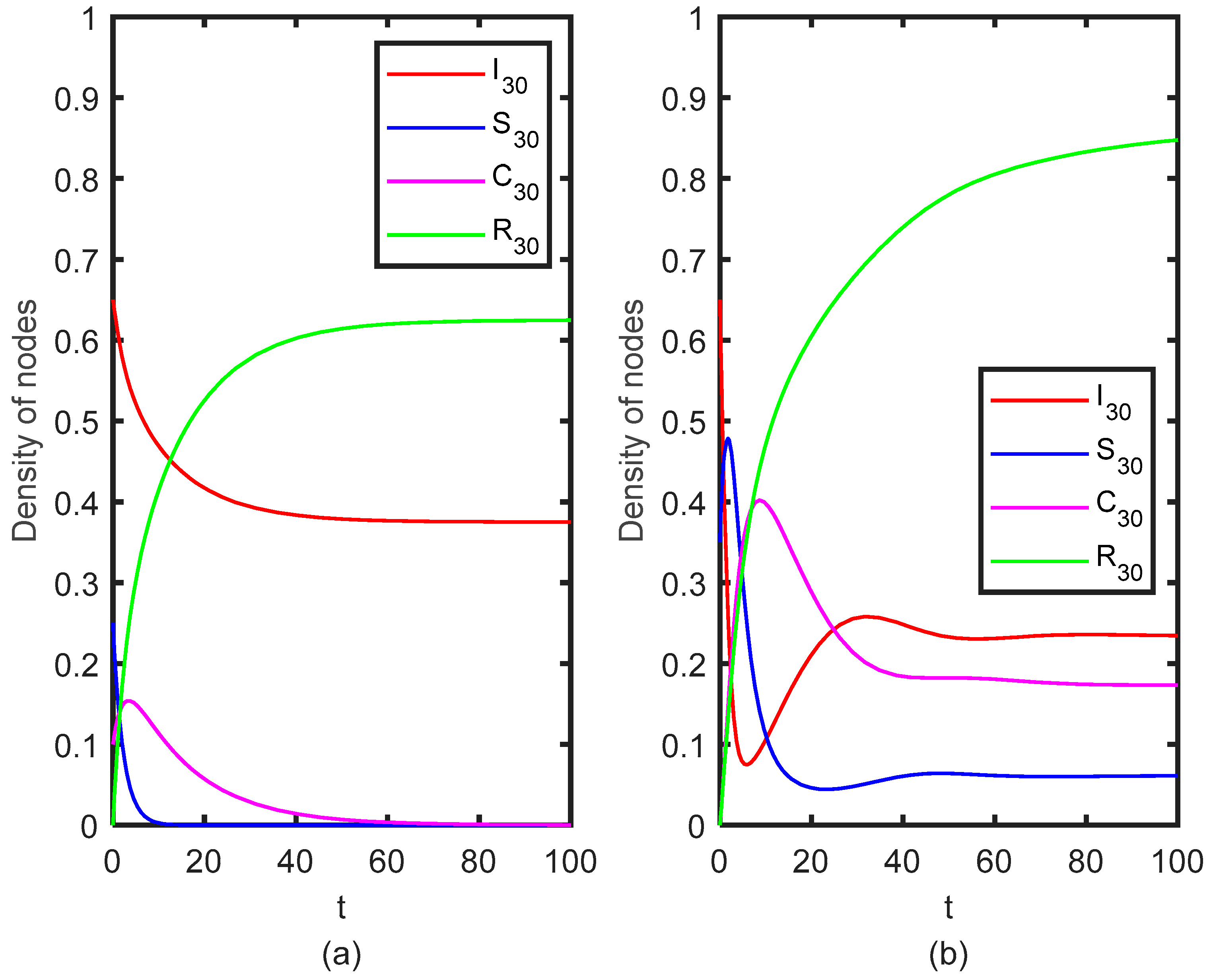
5.1. Dynamical Behavior of System (1) on the Scale-Free Network
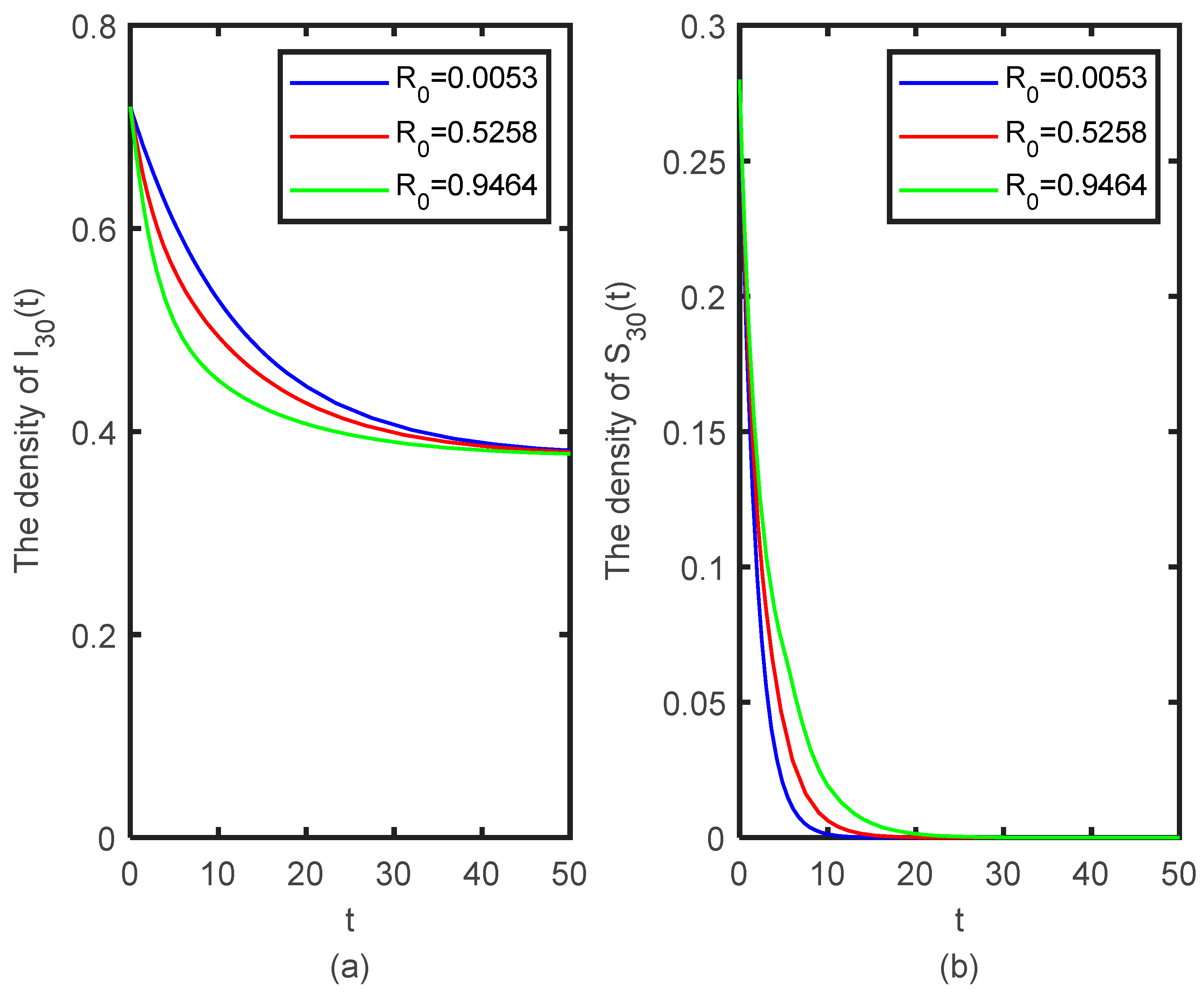
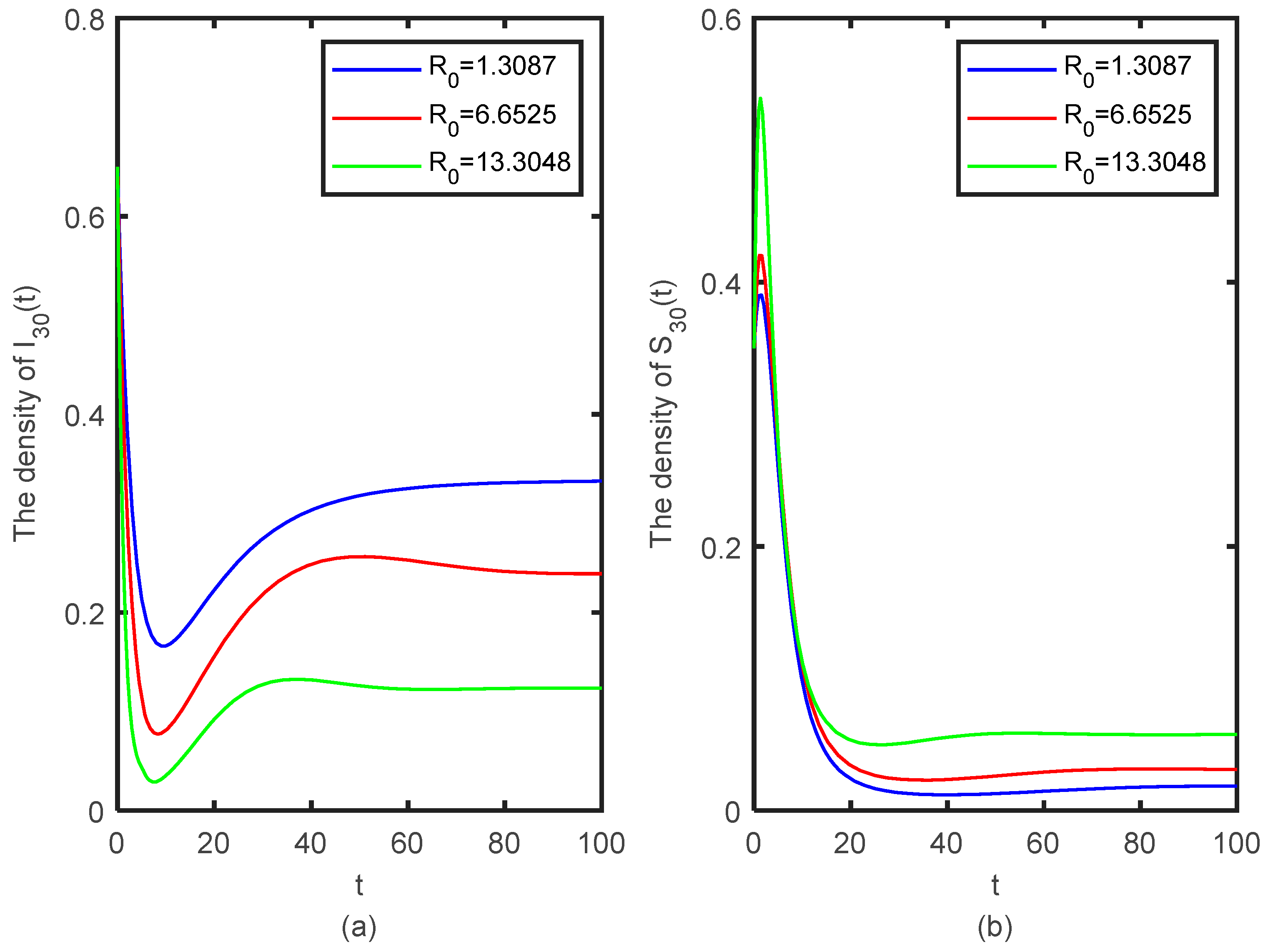
5.2. The Effect of Node Degree on Rumor Propagation
5.3. The Effect of Psychological Inhibition Factor on Rumor Propagation
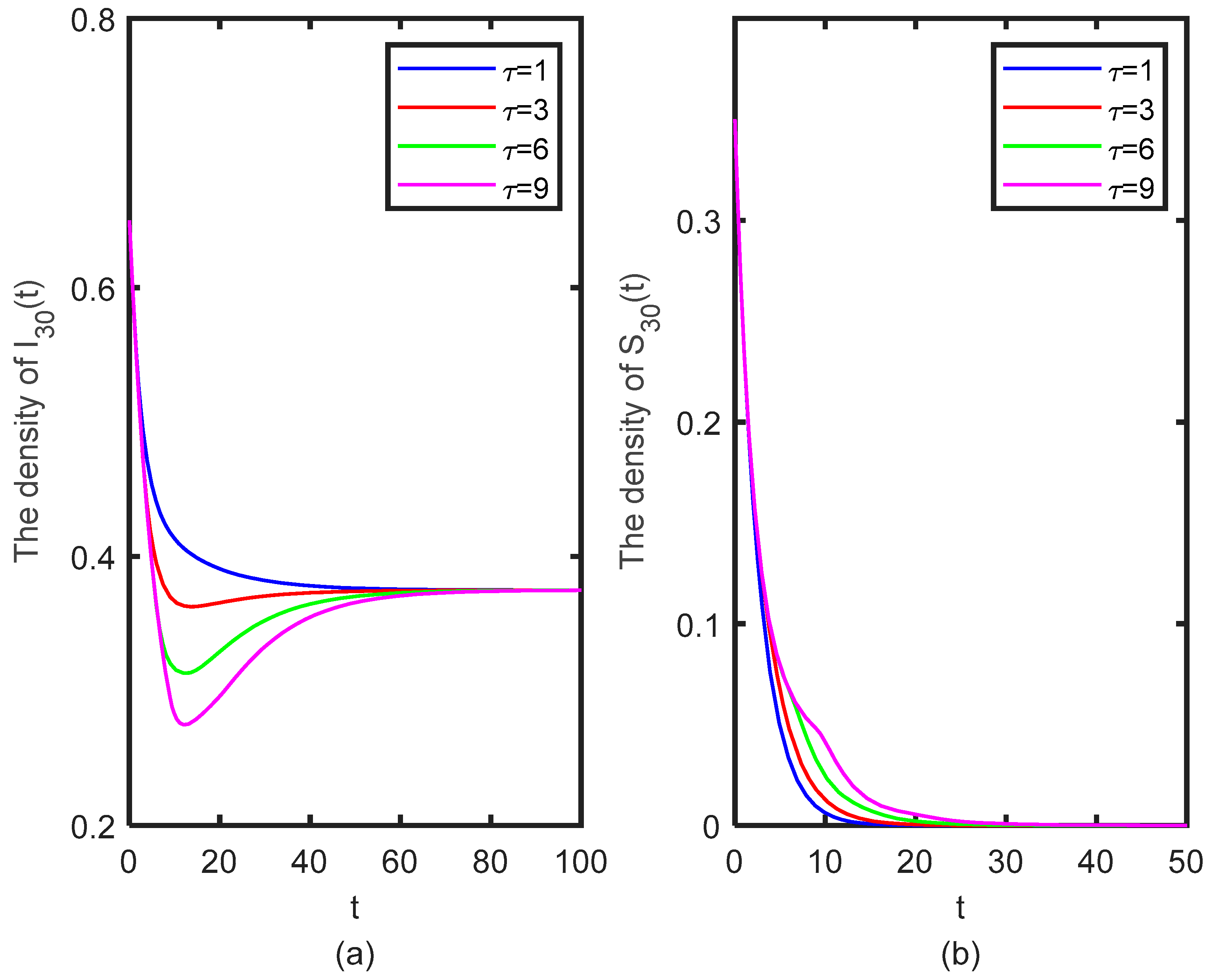
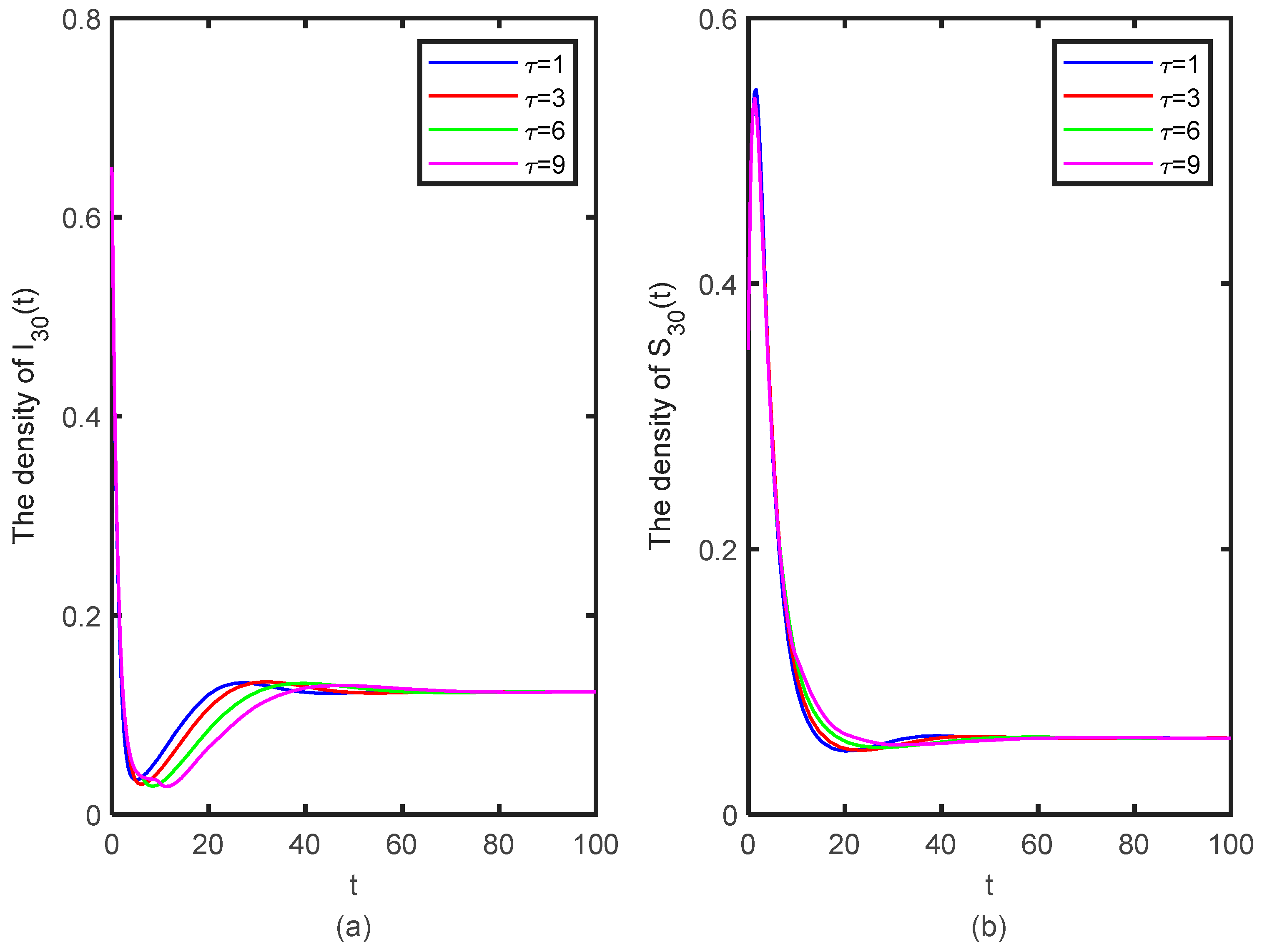
5.4. The Effect of Time Delay
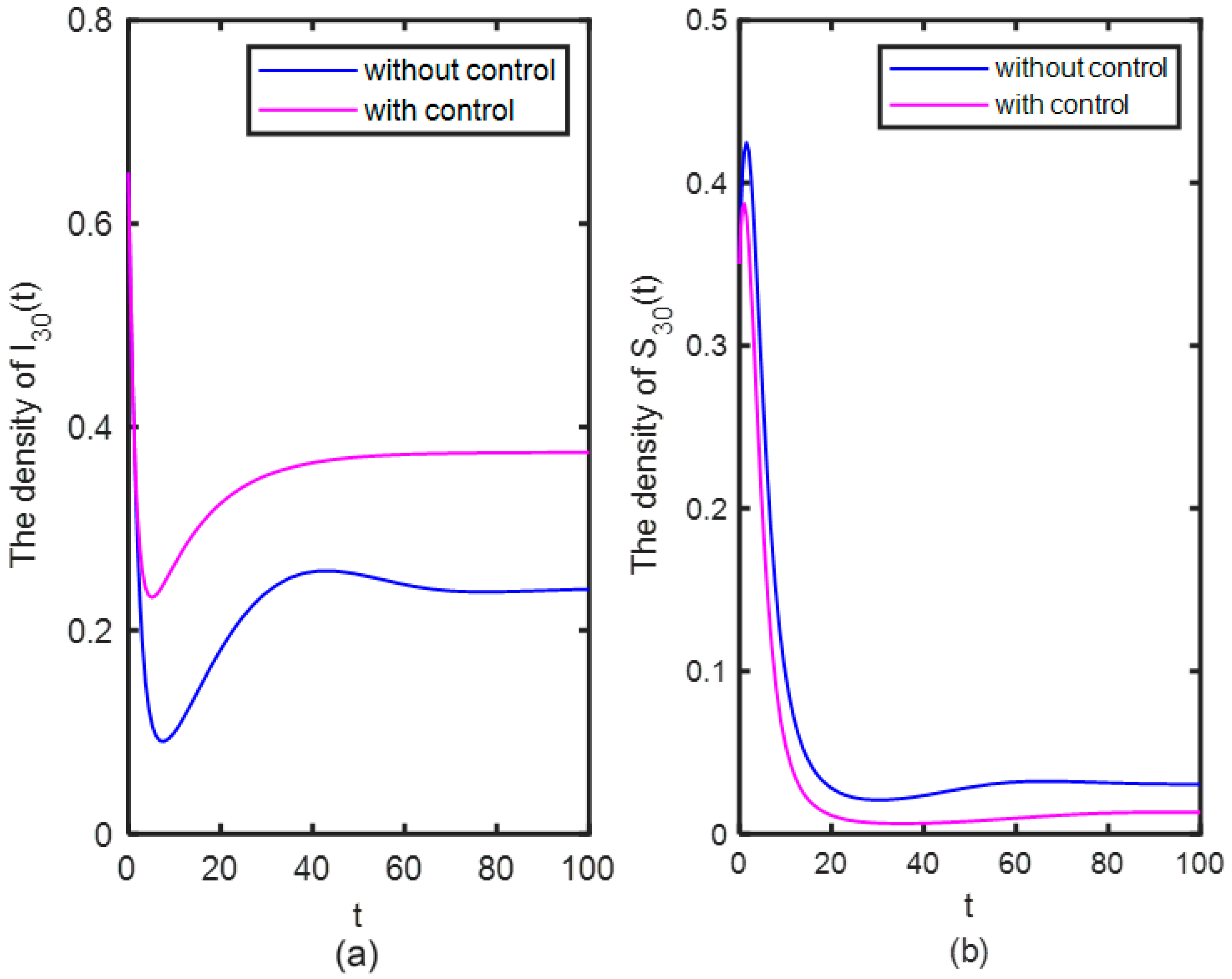
5.5. The Effect of Optimal Control Strategy on Rumor Propagation
5.6. Comparative Analysis of ISR Model and ISCR Model
6. Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Lu, S.; Wang, D.; Li, Z. Modeling and analysis of rumor propagation in social networks. Inf. Sci. 2021, 580, 857–873. [Google Scholar] [CrossRef]
- Cui, Y.; Ni, S.; Shen, S.; Wang, Z. Modeling the dynamics of information dissemination under disaster. Phys. A Stat. Mech. Its Appl. 2019, 537, 122822. [Google Scholar] [CrossRef]
- Daley, D.J.; Kendall, D.G. Epidemics and Rumours. Nature 1964, 204, 1118. [Google Scholar] [CrossRef] [PubMed]
- Maki, D.P.; Maki, D.P.; Mali, D.; Thompson, M.; Thompson, M. Mathematical Models and Applications: With Emphasis on the Social, Life, and Management Sciences; Prentice Hall: Hoboken, NJ, USA, 1973. [Google Scholar]
- Kawachi, K.; Seki, M.; Yoshida, H.; Otake, Y.; Warashina, K.; Ueda, H. A rumor transmission model with various contact interactions. J. Theor. Biol. 2008, 253, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Xiao, X.; Zhang, C.; Dou, C.; Xia, S. Stability analysis of an SDILR model based on rumor recurrence on social media. Phys. A Stat. Mech. Its Appl. 2019, 535, 122236. [Google Scholar] [CrossRef]
- Zhou, X.; Qiu, L.; Hao, T. SCIR rumor propagation model with the chord mechanism in social networks. Int. J. Mod. Phys. C 2021, 33, 2250014. [Google Scholar] [CrossRef]
- Zanette, D.H. Critical behavior of propagation on small-world networks. Phys. Rev. E 2001, 64, 050901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno, Y.; Nekovee, M.; Pacheco, A.F. Dynamics of rumor spreading in complex networks. Phys. Rev. E 2004, 69, 066130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Jiang, H.; Mei, X.; Hu, C.; Zhang, G. Dynamical analysis of rumor spreading model in multi-lingual environment and heterogeneous complex networks. Inf. Sci. 2020, 536, 391–408. [Google Scholar] [CrossRef]
- Ai, S.; Hong, S.; Zheng, X.; Wang, Y.; Liu, X. CSRT rumor spreading model based on complex network. Int. J. Intell. Syst. 2021, 36, 1903–1913. [Google Scholar] [CrossRef]
- Vega-Oliveros, D.A.; Da F Costa, L.; Rodrigues, F.A. Rumor propagation with heterogeneous transmission in social networks. arXiv 2016. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Liu, Z.; Li, B. Influence of network structure on rumor propagation. Phys. Lett. A 2007, 368, 458–463. [Google Scholar] [CrossRef]
- Xia, L.-L.; Jiang, G.-P.; Song, B.; Song, Y.-R. Rumor spreading model considering hesitating mechanism in complex social networks. Phys. A Stat. Mech. Its Appl. 2015, 437, 295–303. [Google Scholar] [CrossRef]
- Zhao, L.; Qiu, X.; Wang, X.; Wang, J. Rumor spreading model considering forgetting and remembering mechanisms in inhomogeneous networks. Phys. A Stat. Mech. Its Appl. 2013, 392, 987–994. [Google Scholar] [CrossRef]
- Sun, X.-L.; Wang, Y.-G.; Cang, L.-Q. Correlation and trust mechanism-based rumor propagation model in complex social networks. Chin. Phys. B 2022, 31, 050202. [Google Scholar] [CrossRef]
- Tian, Y.; Ding, X. Rumor spreading model with considering debunking behavior in emergencies. Appl. Math. Comput. 2019, 363, 124599. [Google Scholar] [CrossRef]
- Huo, L.; Chen, S. Rumor propagation model with consideration of scientific knowledge level and social reinforcement in heterogeneous network. Phys. A Stat. Mech. Its Appl. 2020, 559, 125063. [Google Scholar] [CrossRef]
- Liu, W.; Wu, X.; Yang, W.; Zhu, X.; Zhong, S. Modeling cyber rumor spreading over mobile social networks: A compartment approach. Appl. Math. Comput. 2018, 343, 214–229. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, Y.; Weigang, L.; Liu, H. Rumor and authoritative information propagation model considering super spreading in complex social networks. Phys. A Stat. Mech. Its Appl. 2018, 506, 395–411. [Google Scholar] [CrossRef]
- Vosoughi, S.; Roy, D.; Aral, S. The spread of true and false news online. Science 2018, 359, 1146–1151. [Google Scholar] [CrossRef]
- Qiu, X.; Zhao, L.; Wang, J.; Wang, X.; Wang, Q. Effects of time-dependent diffusion behaviors on the rumor spreading in social networks. Phys. Lett. A 2016, 380, 2054–2063. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, M.; Zhang, Z. Dynamical Analysis and Control Strategies of Rumor Spreading Models in Both Homogeneous and Heterogeneous Networks. J. Nonlinear Sci. 2020, 30, 2545–2576. [Google Scholar] [CrossRef]
- Guan, G.; Guo, Z. Stability behavior of a two-susceptibility SHIR epidemic model with time delay in complex networks. Nonlinear Dyn. 2021, 106, 1083–1110. [Google Scholar] [CrossRef]
- Yu, S.; Yu, Z.; Jiang, H.; Yang, S. The dynamics and control of 2I2SR rumor spreading models in multilingual online social networks. Inf. Sci. 2021, 581, 18–41. [Google Scholar] [CrossRef]
- Cheng, Y.; Huo, L.; Zhao, L. Dynamical behaviors and control measures of rumor-spreading model in consideration of the infected media and time delay. Inf. Sci. 2021, 564, 237–253. [Google Scholar] [CrossRef]
- Cheng, Y.; Huo, L.; Zhao, L. Stability analysis and optimal control of rumor spreading model under media coverage considering time delay and pulse vaccination. Chaos Solitons Fractals 2022, 157, 111931. [Google Scholar] [CrossRef]
- Chen, G. ILSCR rumor spreading model to discuss the control of rumor spreading in emergency. Phys. A Stat. Mech. Its Appl. 2018, 522, 88–97. [Google Scholar] [CrossRef]
- Chang, Z.; Jiang, H.; Yu, S.; Chen, S. Dynamic Analysis and Optimal Control of ISCR Rumor Propagation Model with Nonlinear Incidence and Time Delay on Complex Networks. Discret. Dyn. Nat. Soc. 2021, 2021, 3935750. [Google Scholar] [CrossRef]
- Huo, L.; Wang, L.; Zhao, X. Stability analysis and optimal control of a rumor spreading model with media report. Phys. A Stat. Mech. Its Appl. 2018, 517, 551–562. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, B. Stability analysis of a SAIR rumor spreading model with control strategies in online social networks. Inf. Sci. 2020, 526, 1–19. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, M.; Liu, Y.; Zhang, Z. Nonlinear dynamic analysis and optimum control of reaction-diffusion rumor propagation models in both homogeneous and heterogeneous networks. J. Math. Anal. Appl. 2021, 502, 125260. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Hu, C.; Yu, Z.; Li, J. Stability and Hopf bifurcation analysis of multi-lingual rumor spreading model with nonlinear inhibition mechanism. Chaos Solitons Fractals 2021, 153, 111464. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, H.; Li, L.; Li, J. Dynamical behaviors and optimal control of rumor propagation model with saturation incidence on heterogeneous networks. Chaos Solitons Fractals 2020, 140, 110206. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, F.; Guan, G.; Zhang, Z. Modeling the dynamics of rumor diffusion over complex networks. Inf. Sci. 2021, 562, 240–258. [Google Scholar] [CrossRef]
- Ding, L.; Hu, P.; Guan, Z.-H.; Li, T. An Efficient Hybrid Control Strategy for Restraining Rumor Spreading. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6779–6791. [Google Scholar] [CrossRef]
- Li, T.; Guo, Y. Nonlinear Dynamical Analysis and Optimal Control Strategies for a New Rumor Spreading Model with Comprehensive Interventions. Qual. Theory Dyn. Syst. 2021, 20, 84. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Qin, T.; Sun, Q.; Li, S.; Song, H.H.; Chen, Z. SIRQU: Dynamic Quarantine Defense Model for Online Rumor Propagation Control. IEEE Trans. Comput. Soc. Syst. 2022, 9, 1–12. [Google Scholar] [CrossRef]
- Yu, S.; Yu, Z.; Jiang, H.; Mei, X.; Li, J. The spread and control of rumors in a multilingual environment. Nonlinear Dyn. 2020, 100, 2933–2951. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Jiang, H.; Yu, Z. Global dynamics of ILSR rumor spreading model with general nonlinear spreading rate in multi-lingual environment. Chaos Solitons Fractals 2021, 154, 111698. [Google Scholar] [CrossRef]
- Nekovee, M.; Moreno, Y.; Bianconi, G.; Marsili, M. Theory of rumour spreading in complex social networks. Phys. A Stat. Mech. Its Appl. 2007, 374, 457–470. [Google Scholar] [CrossRef]
- Ma, Y.; Cui, Y.; Wang, M. Global stability and control strategies of a SIQRS epidemic model with time delay. Math. Methods Appl. Sci. 2022, 45, 8269–8293. [Google Scholar] [CrossRef]
- Yang, P.; Wang, Y. Dynamics for an SEIRS epidemic model with time delay on a scale-free network. Phys. A Stat. Mech. Its Appl. 2019, 527, 121290. [Google Scholar] [CrossRef]
- La Salle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Huo, L.; Dong, Y. Analyzing the dynamics of a stochastic rumor propagation model incorporating media coverage. Math. Methods Appl. Sci. 2020, 43, 6903–6920. [Google Scholar] [CrossRef]
- Zhu, L.; He, L. Pattern formation in a reaction–diffusion rumor propagation system with Allee effect and time delay. Nonlinear Dyn. 2022, 107, 3041–3063. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J. Cross-network propagation model of public opinion information and its control in coupled double-layer online social networks. Aslib J. Inf. Manag. 2021, 74, 354–376. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Ouyang, Y. Rumor Transmission in Online Social Networks under Nash Equilibrium of a Psychological Decision Game. Netw. Spat. Econ. 2022, 2, 1–24. [Google Scholar] [CrossRef]
- Yang, S.; Wang, S.; Yiwen, Y. Internet Rumor Audience Response Prediction Algorithm Based on Machine Learning in Big Data Environment. Wirel. Commun. Mob. Comput. 2022, 2022, 3632679. [Google Scholar] [CrossRef]
- Lee, J.; Britt, B.C.; Kanthawala, S. Taking the lead in misinformation-related conversations in social media networks during a mass shooting crisis. Internet Res. 2022; ahead-of-print. [Google Scholar] [CrossRef]
- Huo, L.-A.; Dong, Y.-F.; Lin, T.-T. Dynamics of a stochastic rumor propagation model incorporating media coverage and driven by Levy noise. Chin. Phys. B 2021, 30, 080201. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, X.; Huo, L. Analysis of the Stability and Optimal Control Strategy for an ISCR Rumor Propagation Model with Saturated Incidence and Time Delay on a Scale-Free Network. Mathematics 2022, 10, 3900. https://doi.org/10.3390/math10203900
Yue X, Huo L. Analysis of the Stability and Optimal Control Strategy for an ISCR Rumor Propagation Model with Saturated Incidence and Time Delay on a Scale-Free Network. Mathematics. 2022; 10(20):3900. https://doi.org/10.3390/math10203900
Chicago/Turabian StyleYue, Xuefeng, and Liangan Huo. 2022. "Analysis of the Stability and Optimal Control Strategy for an ISCR Rumor Propagation Model with Saturated Incidence and Time Delay on a Scale-Free Network" Mathematics 10, no. 20: 3900. https://doi.org/10.3390/math10203900





