Fixed/Predefined-Time Synchronization of Complex-Valued Stochastic BAM Neural Networks with Stabilizing and Destabilizing Impulse
Abstract
:1. Introduction
2. System Description and Preliminary Knowledge
- (1)
- For any initial condition , there exists a ST function such that .
- (2)
- Stability in probability: for every pair of and , there exists a such that , whenever .
- (3)
- The mathematical expectation of is bounded by a constant such that
3. Main Results
3.1. Fixed Time Synchronization
3.2. Predefined Time Synchronization
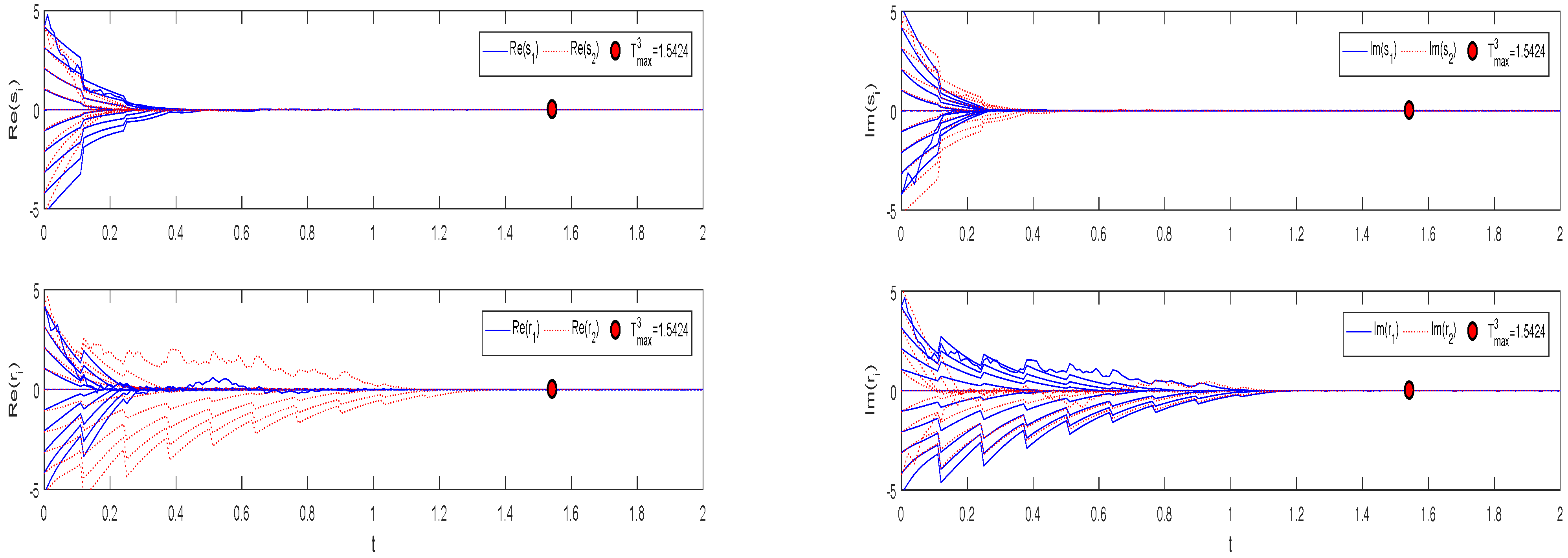
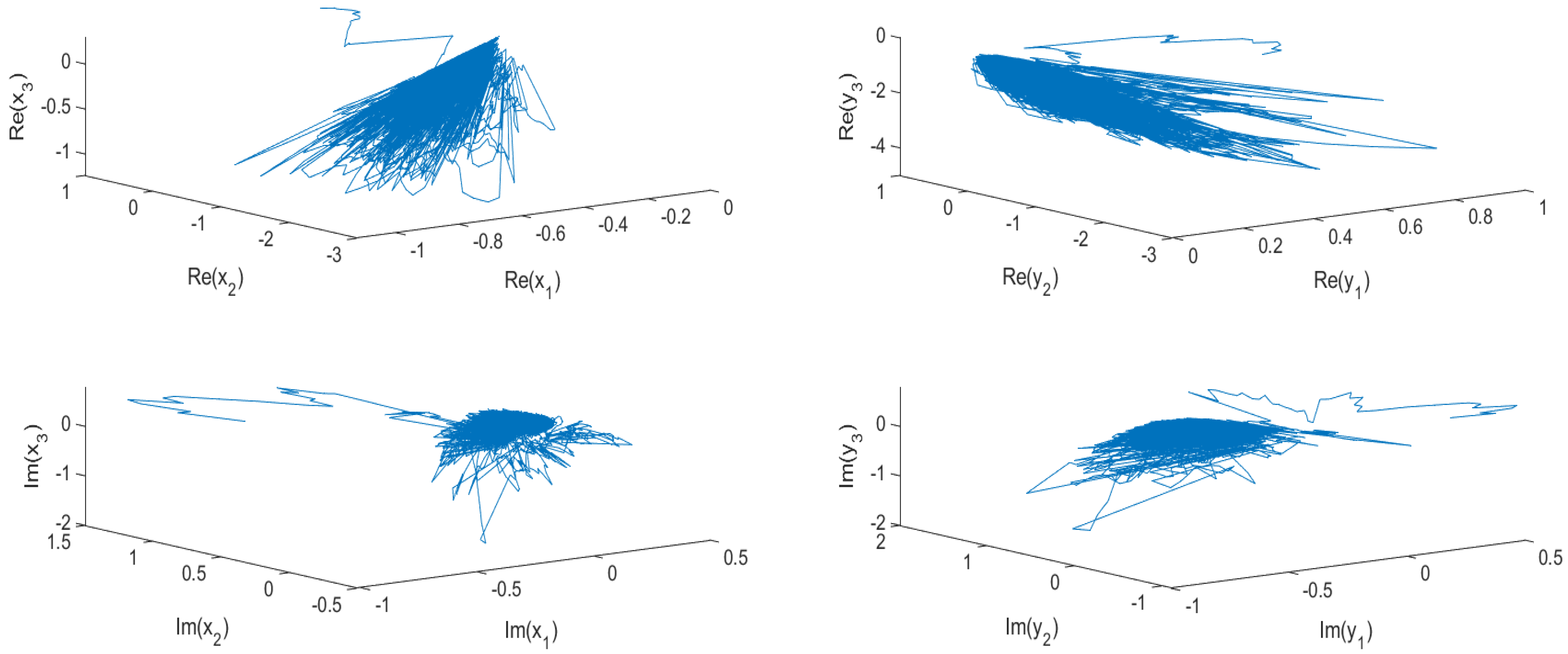
4. Numerical Examples and Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kosko, B. Adaptive bidirectional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.S.; Vadivel, R.; Kwon, O.M. Decentralized event-triggered stability analysis of neutral-type BAM neural networks with Markovian jump parameters and mixed time varying delays. Int. J. Control Autom. Syst. 2018, 16, 983–993. [Google Scholar] [CrossRef]
- Dong, T.; Xiang, W.; Huang, T. Pattern formation in a reaction-diffusion BAM neural network with time delay: (k1, k2) mode Hopf-zero bifurcation case. IEEE Trans. Neural Netw. Learn. Syst. 2021, 3, 15–28. [Google Scholar] [CrossRef]
- Ali, M.S.; Saravanakumar, R.; Cao, J. New passivity criteria for memristor-based neutral-type stochastic BAM neural networks with mixed time-varying delays. Neurocomputing 2016, 171, 1533–1547. [Google Scholar]
- Guo, Y.; Luo, Y.; Wang, W. Fixed-time synchronization of complex-valued memristive BAM neural network and applications in image encryption and decryption. Int. J. Control Autom. Syst. 2020, 18, 462–476. [Google Scholar] [CrossRef]
- Yuan, M.; Wang, W.; Luo, X. Asymptotic anti-synchronization of memristor-based BAM neural networks with probabilistic mixed time-varying delays and its application. Mod. Phys. Lett. Condens. Matter Phys. Stat. Phys. Appl. Phys. 2018, 32, 1850278. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Luo, X. Finite-time projective synchronization of memristor-based BAM neural networks and applications in image encryption. IEEE Access 2018, 6, 56457–56476. [Google Scholar] [CrossRef]
- Nejadgholi, I.; Seyyedsalehi, S.A.; Chattier, S. A chaotic feature extracting BAM and its application in implementing memory search. Neural Process. Lett. 2012, 36, 69–99. [Google Scholar] [CrossRef]
- Abdurahman, A.; Jiang, H.; Teng, Z. Finite-time synchronization for memristor-based neural networks with time-varying delays. Neural Netw. 2015, 69, 20–28. [Google Scholar] [CrossRef]
- Liu, X.; Cao, J.; Yu, W. Nonsmooth finite-time synchronization of switched coupled neural networks. IEEE Trans. Cybern. 2015, 46, 2360–2371. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of homogeneous systems. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 6 June 1997; IEEE: Piscataway, NJ, USA, 1997; Volume 4, pp. 2513–2514. [Google Scholar]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Fixed-time cluster synchronization for complex networks via pinning control. arXiv 2015, arXiv:1509.03350. [Google Scholar]
- Wan, Y.; Cao, J.; Wen, G. Robust fixed-time synchronization of delayed Cohen-Grossberg neural networks. Neural Netw. 2016, 73, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Lam, J.; Ho, D.W.C. Fixed-time synchronization of complex networks with impulsive effects via nonchattering control. IEEE Trans. Autom. Control 2017, 62, 5511–5521. [Google Scholar] [CrossRef]
- Jia, H.; Luo, D.; Wang, J.; Shen, H. Fixed-time synchronization for inertial CohenC-Grossberg delayed neural networks: An event-triggered approach. Knowl.-Based Syst. 2022, 250, 109104. [Google Scholar] [CrossRef]
- Pang, M.; Zhang, Z.; Wang, X.; Wang, Z.; Lin, C. Fixed/Preassigned-time synchronization of high-dimension-valued fuzzy neural networks with time-varying delays via nonseparation approach. Knowl.-Based Syst. 2022, 255, 109774. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.W.; Xiao, J.W. Predefined-time secondary control for DC microgrid. IEEE Trans. Ind. Electron. 2021, 69, 13504–13513. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S. Predefined-time vector-polynomial-based synchronization among a group of chaotic systems and its application in secure information transmission. AIMS Math. 2021, 6, 11005–11028. [Google Scholar] [CrossRef]
- Nitta, T. Solving the XOR problem and the detection of symmetry using a single complex-valued neuron. Neural Netw. 2003, 16, 1101–1105. [Google Scholar] [CrossRef]
- Gibbon, J.D.; Mcguinness, M.J. The real and complex Lorenz equations in rotating fluids and lasers. Physical D 1982, 5, 108–122. [Google Scholar] [CrossRef]
- Bolognani, S.; Smyshlyaev, A.; Krstic, M. Adaptive output feedback control for complex-valued reaction-advection-diffusion systems. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 961–966. [Google Scholar]
- Sun, K.; Zhu, S.; Wei, Y. Finite-time synchronization of memristor-based complex-valued neural networks with time delays. Phys. Lett. A 2019, 383, 2255–2263. [Google Scholar] [CrossRef]
- Ding, X.; Cao, J.; Alsaedi, A. Robust fixed-time synchronization for uncertain complex-valued neural networks with discontinuous activation functions. Neural Netw. 2017, 90, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Guo, R.; Liu, X.; Zhong, M.; Lin, C.; Chen, B. Fixed-time synchronization for complex-valued BAM neural networks with time delays. Asian J. Control 2019, 23, 298–314. [Google Scholar] [CrossRef]
- Feng, L.; Yu, J.; Hu, C. Nonseparation method-based finite/fixed-time synchronization of fully complex-valued discontinuous neural networks. IEEE Trans. Cybern. 2021, 51, 3212–3223. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Cao, J. Stability analysis of Markovian jump stochastic BAM neural networks with impulse control and mixed time delays. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 467–479. [Google Scholar] [PubMed]
- Shi, P.; Zhang, Y.; Agarwal, R.K. Stochastic finite-time state estimation for discrete time-delay neural networks with Markovian jumps. Neurocomputing 2015, 151, 168–174. [Google Scholar] [CrossRef]
- Xu, D.; Liu, Y.; Liu, M. Finite-time synchronization of multi-coupling stochastic fuzzy neural networks with mixed delays via feedback control. Fuzzy Sets Syst. 2021, 411, 85–104. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S.; Li, J. Fixed-time stability theorem of stochastic nonlinear systems. Int. J. Control 2019, 92, 2194–2200. [Google Scholar] [CrossRef]
- Li, L.; Xu, R.; Gan, Q. A switching control for finite-time synchronization of memristor-based BAM neural networks with stochastic disturbances. Nonlin. Anal. Control 2020, 25, 958–979. [Google Scholar] [CrossRef]
- Ren, H.; Peng, Z.; Gu, Y. Fixed-time synchronization of stochastic memristor-based neural networks with adaptive control. Neural Netw. 2020, 130, 165–175. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, Y. Exponential stability of impulsive discrete-time stochastic BAM neural networks with time-varying delay. Neurocomputing 2014, 131, 323–330. [Google Scholar] [CrossRef]
- Gu, H. Mean square exponential stability in high-order stochastic impulsive BAM neural networks with time-varying delays. Neurocomputing 2011, 74, 720–729. [Google Scholar] [CrossRef]
- Abudusaimaiti, M.; Abdurahman, A.; Jiang, H. Fixed/predefined-time synchronization of fuzzy neural networks with stochastic perturbations. Chaos Solitons Fractals 2022, 154, 111596. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, H.; Liu, A. Predefined-time Synchronization of Stochastic Memristor-based Bidirectional Associative Memory Neural Networks with Time-varying Delays. IEEE Trans. Cogn. Dev. Syst. 2021. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; She, K. Pinning impulsive synchronization of complex dynamical networks with various time-varying delay sizes. Nonlin. Anal. Syst. 2017, 26, 307–318. [Google Scholar] [CrossRef]
- Rajchakit, G.; Sriraman, R. Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays. Neural Process. Lett. 2021, 53, 581–606. [Google Scholar] [CrossRef]
- Hu, H.; Gao, B.; Xu, L. Finite-Time and Fixed-Time Attractiveness for Nonlinear Impulsive Systems. IEEE Trans. Autom. Control. 2021, 67, 5586–5593. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Huang, T. Fixed-time stability and stabilization of impulsive dynamical systems. J. Frankl. Inst. 2017, 354, 8626–8644. [Google Scholar] [CrossRef]
- Jamal, M.A.; Kumar, R.; Mukhopadhyay, S. Fixed-time stability of dynamical systems with impulsive effects. J. Frankl. Inst. 2022, 359, 3164–3182. [Google Scholar] [CrossRef]
- Lee, L.; Liu, Y.; Liang, J. Finite time stability of nonlinear impulsive systems and its applications in sampled-data systems. ISA Trans. 2015, 57, 172–178. [Google Scholar] [CrossRef]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Yin, J.; Khoo, S.; Man, Z. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Plya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Anguiano-Gijón, C.A.; Muñoz-Vázquez, A.J.; Sxaxnchez-Torres, J.D. On predefined-time synchronisation of chaotic systems. Chaos Solitons Fractals 2019, 122, 172–178. [Google Scholar] [CrossRef]
- Song, Q.; Yan, H.; Zhao, Z. Global exponential stability of complex-valued neural networks with both time-varying delays and impulsive effects. Neural Netw. 2016, 79, 108–116. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, J.; Abdurahman, A.; Sadik, H. Fixed/Predefined-Time Synchronization of Complex-Valued Stochastic BAM Neural Networks with Stabilizing and Destabilizing Impulse. Mathematics 2022, 10, 4384. https://doi.org/10.3390/math10224384
You J, Abdurahman A, Sadik H. Fixed/Predefined-Time Synchronization of Complex-Valued Stochastic BAM Neural Networks with Stabilizing and Destabilizing Impulse. Mathematics. 2022; 10(22):4384. https://doi.org/10.3390/math10224384
Chicago/Turabian StyleYou, Jingjing, Abdujelil Abdurahman, and Hayrengul Sadik. 2022. "Fixed/Predefined-Time Synchronization of Complex-Valued Stochastic BAM Neural Networks with Stabilizing and Destabilizing Impulse" Mathematics 10, no. 22: 4384. https://doi.org/10.3390/math10224384



