Chaotic Oscillations in Cascoded and Darlington-Type Amplifier Having Generalized Transistors
Abstract
:1. Introduction
2. Mathematical Models
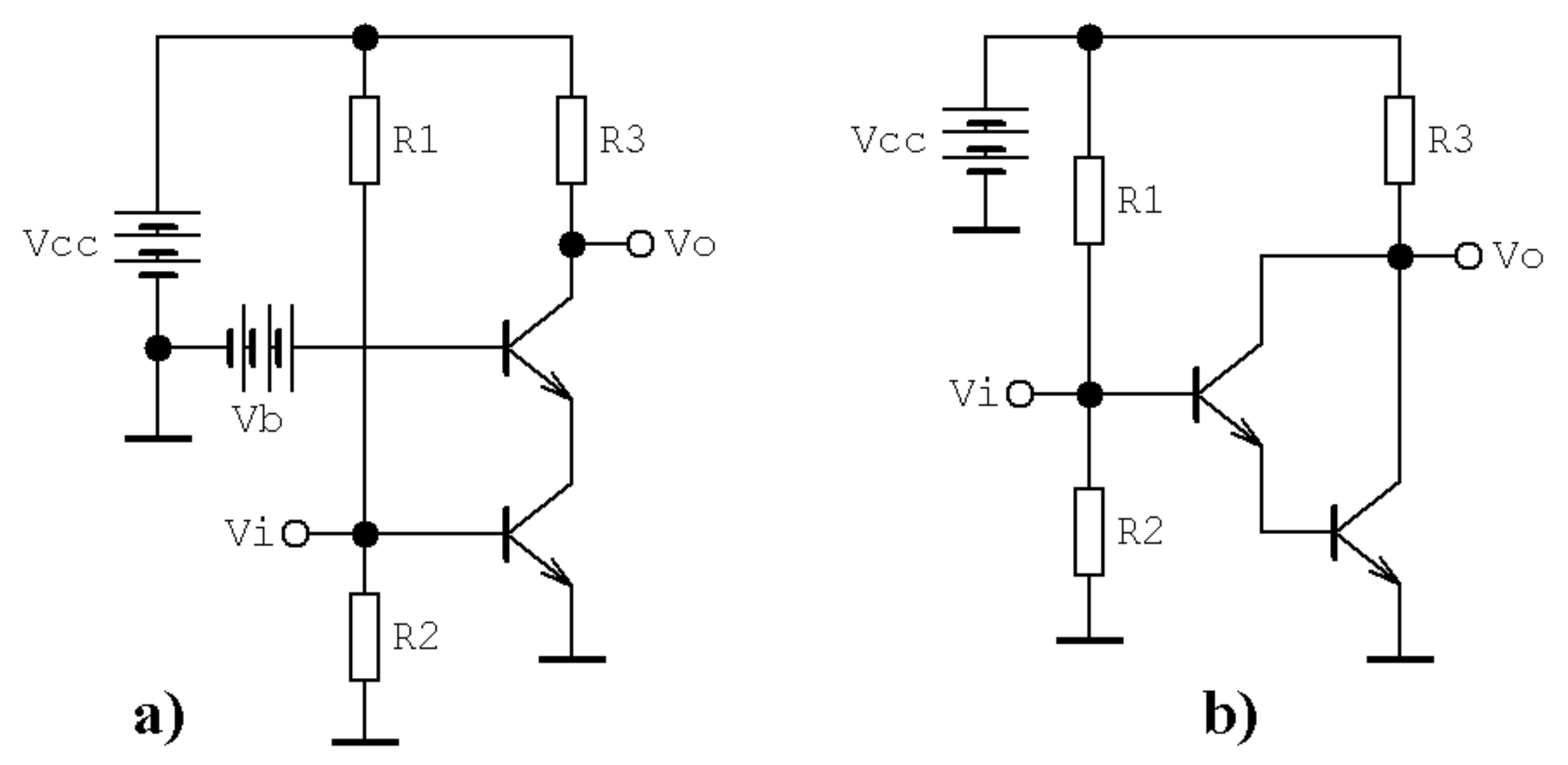
2.1. Cascoded Class C Amplifier
2.2. Resonant Amplifier with Darlington’s Subcircuit
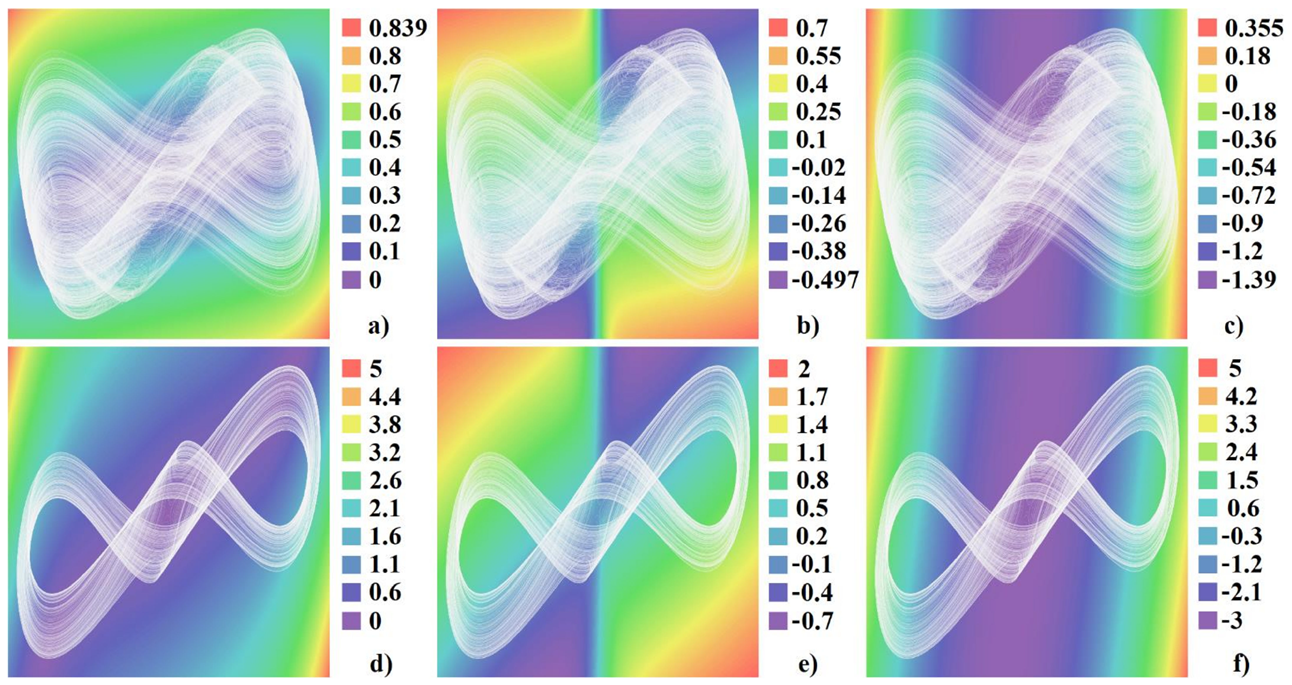
3. Numerical Analysis
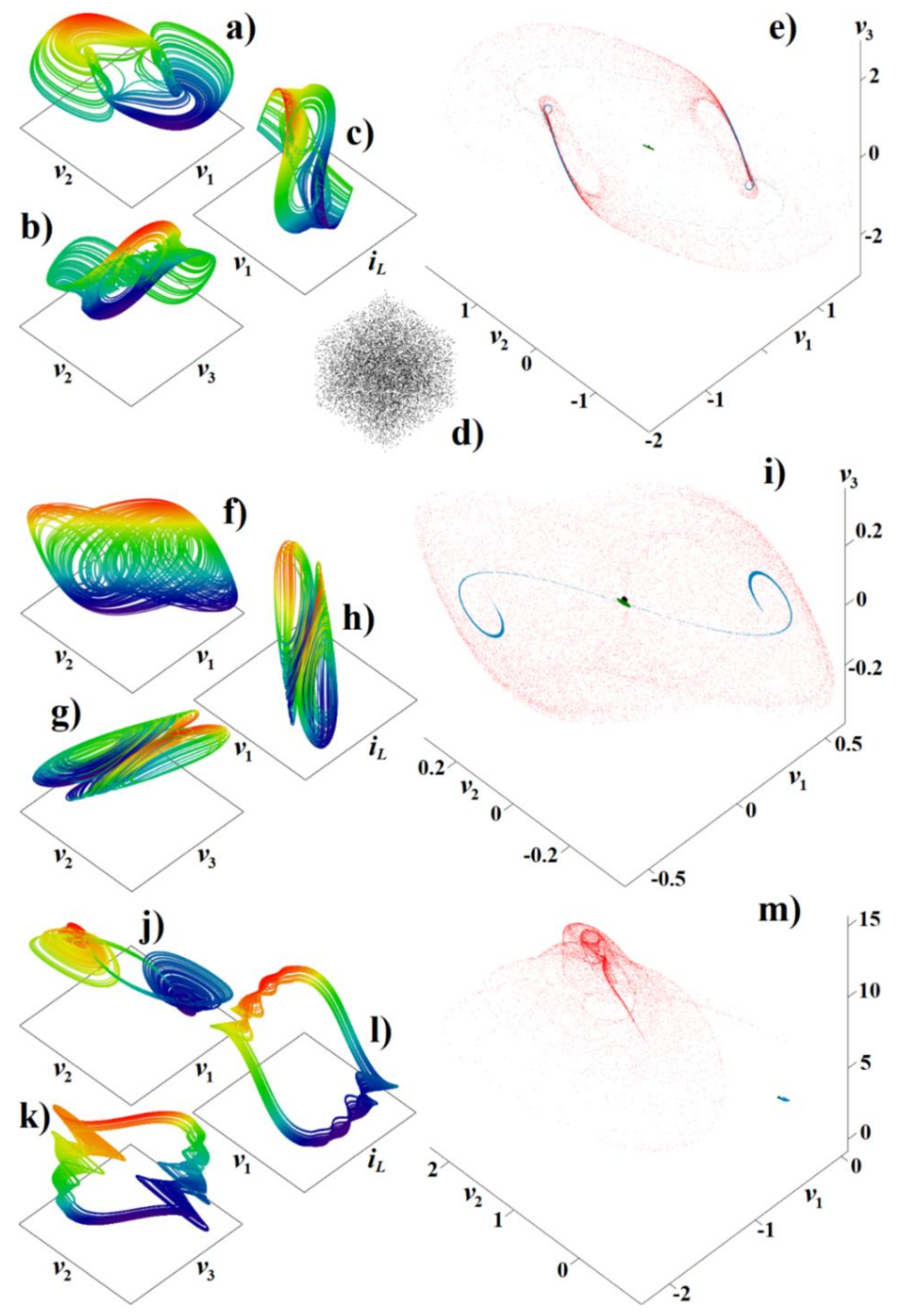
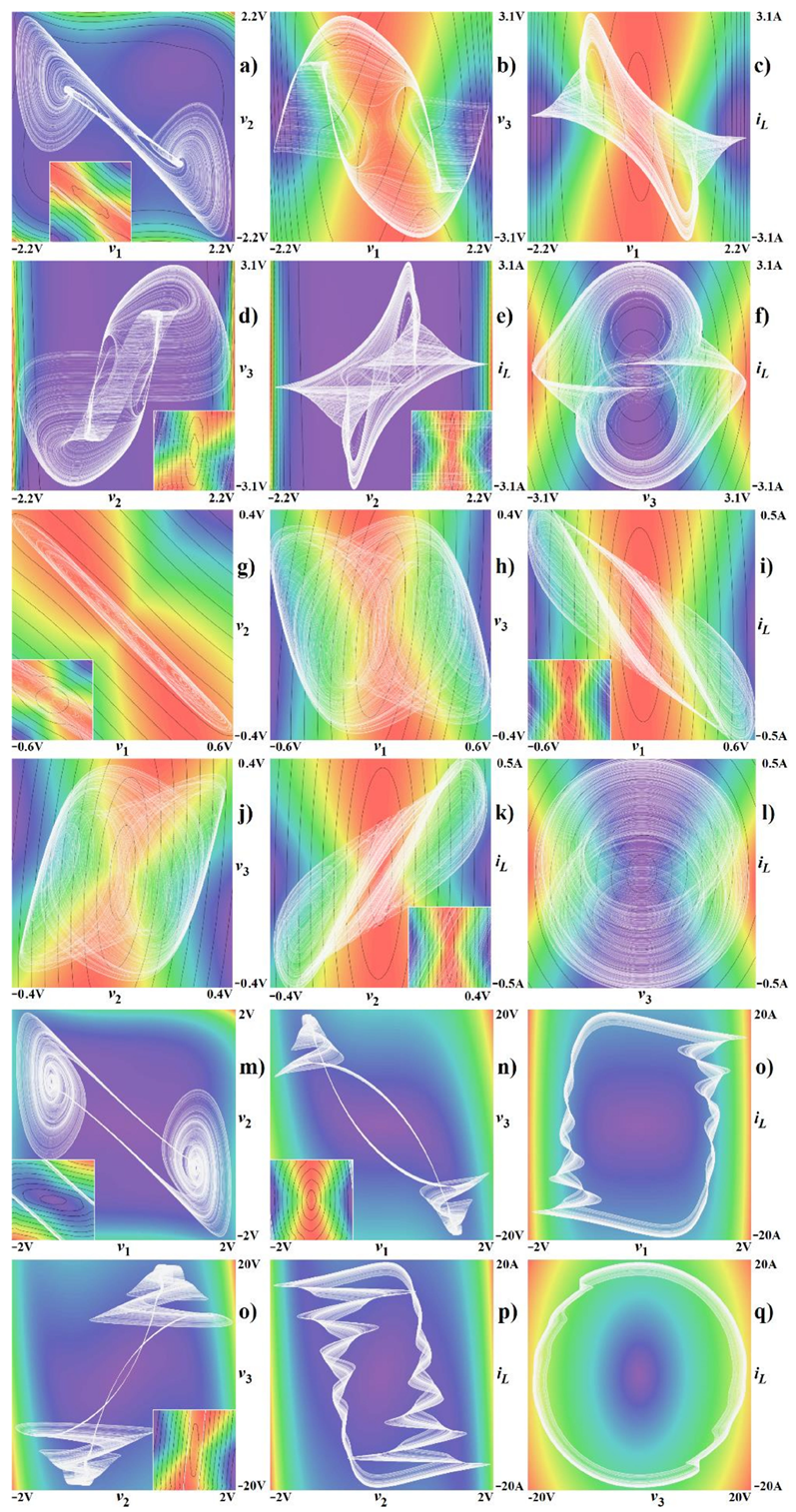
3.1. Cascoded Class C Amplifier
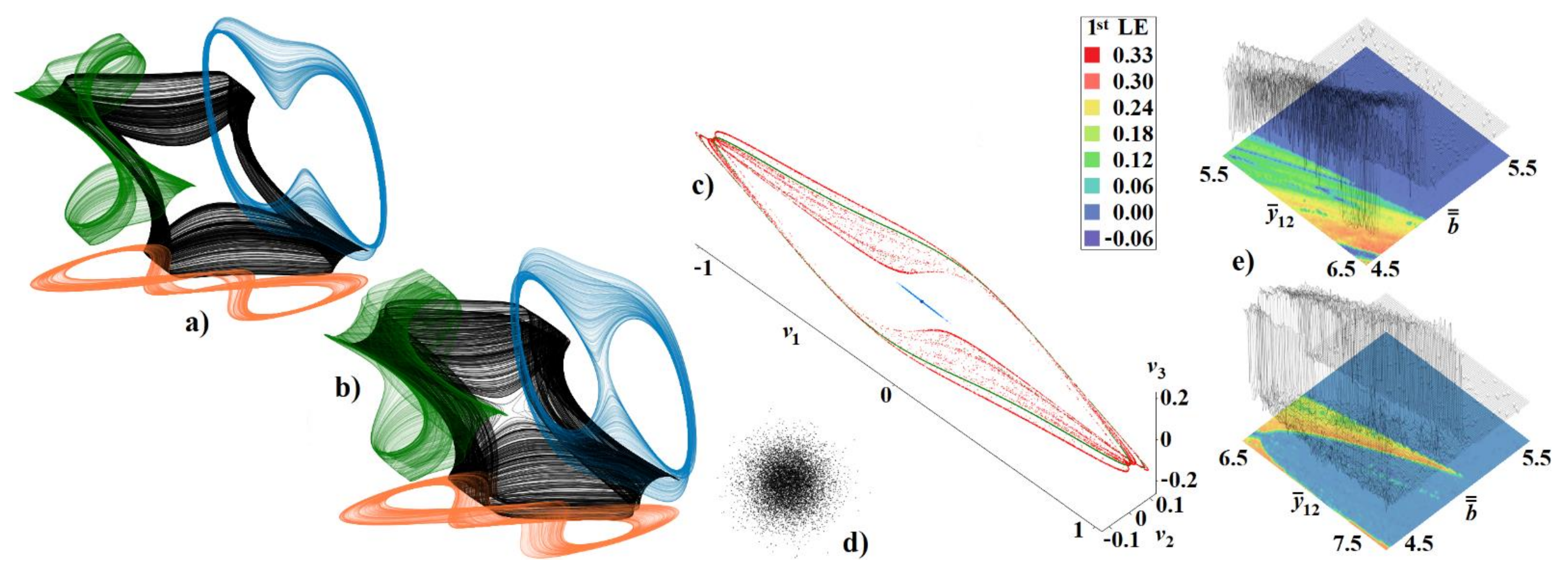
3.2. Resonant Amplifier with Darlington-Type Subcircuit
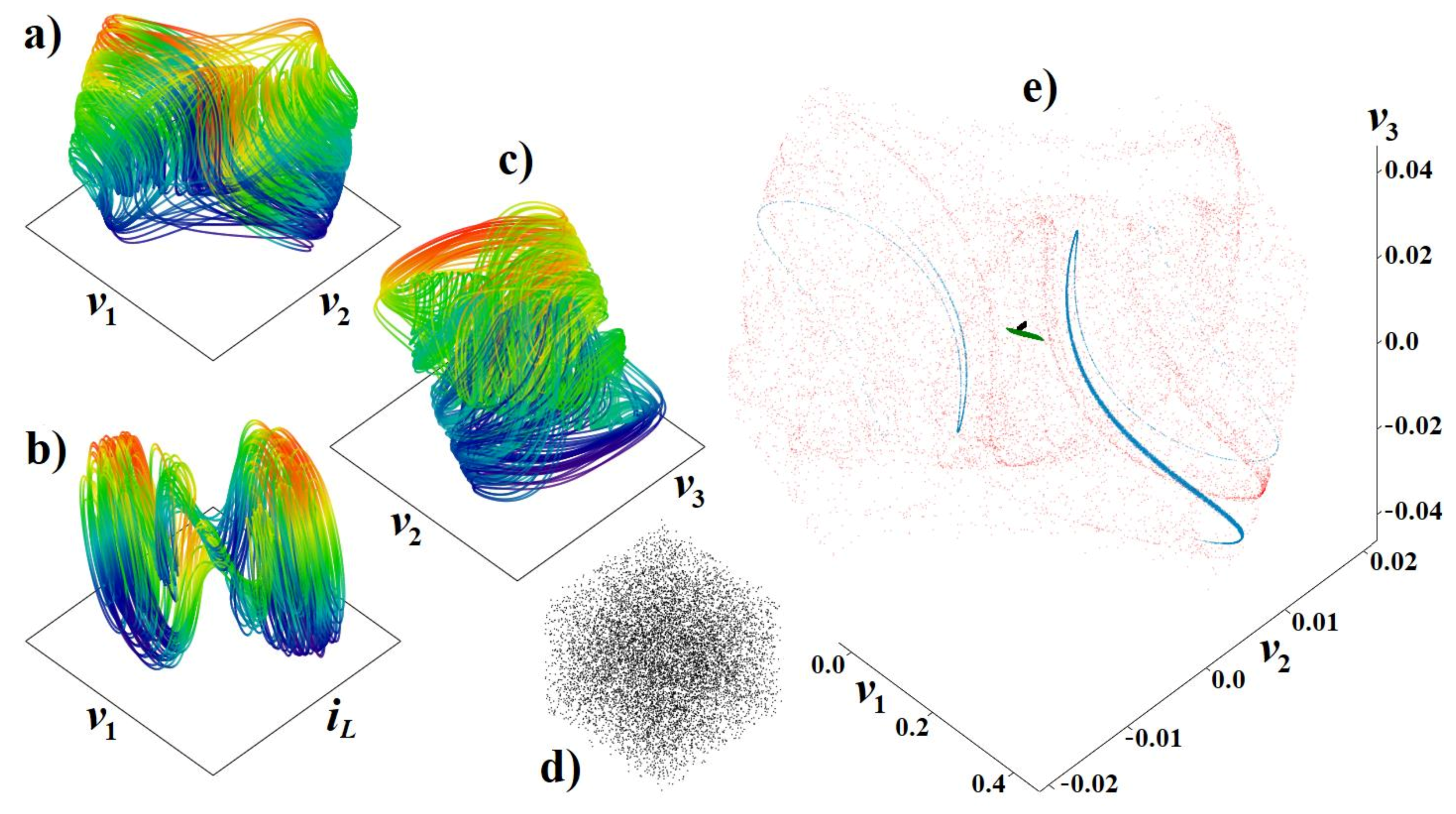
3.3. Fractional-Order Modification of Analyzed GBT-Based Functional Blocks
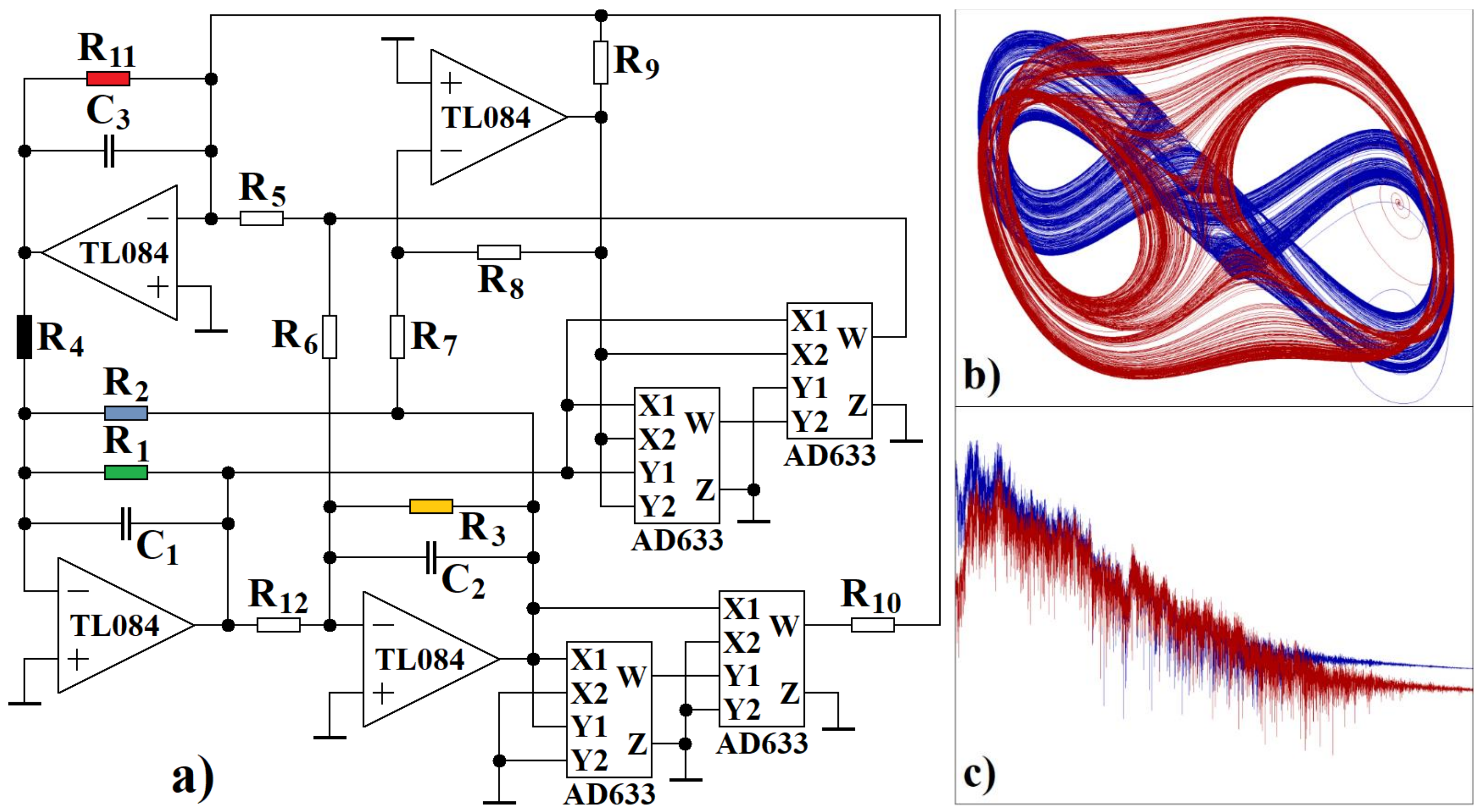
4. Experimental Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Common Function of Two-Transistor Cascoded Amplifier
References
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Huang, A.; Pivka, L.; Wu, C.W.; Franz, M. Chua’s equation with cubic nonlinearity. Int. J. Bifurc. Chaos 1996, 6, 2175–2222. [Google Scholar] [CrossRef]
- Zhong, G.-Q. Implementation of Chua’s circuit with a cubic nonlinearity. IEEE Trans. Circuits Syst. I 1994, 41, 934–941. [Google Scholar] [CrossRef] [Green Version]
- Chua, L.O. Global unfolding of Chua’s circuit. IEICE Trans. Fundam. 1993, 76, 704–734. [Google Scholar]
- Bilotta, E. A Gallery of Chua Attractors; World Scientific: Singapore, 2008; 600p. [Google Scholar]
- Guzan, M. Variations of boundary surface in Chua’s circuit. Radioengineering 2015, 24, 814–823. [Google Scholar] [CrossRef]
- Spany, V.; Galajda, P.; Guzan, M.; Pivka, L.; Olejar, M. Chua’s singularities: Great miracle in circuit theory. Int. J. Bifurc. Chaos 2010, 20, 2993–3006. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Kuznetsova, O.A.; Leonov, G.A.; Mokaev, T.N.; Stankevich, N.V. Hidden attractors localization in Chua circuit via the describing function method. IFAC-PapersOnLine 2017, 50, 2651–2656. [Google Scholar] [CrossRef]
- Galias, Z. Positive topological entropy of Chua’s circuit: A computer assisted proof. Int. J. Bifurc. Chaos 1997, 7, 331–349. [Google Scholar] [CrossRef] [Green Version]
- Tsay, S.-C.H.; Huang, C.H.-K.; Chen, W.-T.; Wu, Y.-R. Synchronization of Chua chaotic circuits with application to the bidirectional secure communication systems. Int. J. Bifurc. Chaos 2005, 15, 605–616. [Google Scholar] [CrossRef]
- Itoh, M. Spread spectrum communication via chaos. Int. J. Bifurc. Chaos 1999, 9, 155–213. [Google Scholar] [CrossRef]
- Endo, T.; Chua, L.O. Chaos from phase-locked loops. IEEE Trans. Circuits Syst. 1988, 35, 987–1003. [Google Scholar] [CrossRef]
- Fossas, E.; Olivar, G. Study of chaos in the buck converter. IEEE Trans. Circuits Syst. 1996, 43, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Bernardo, M.; Tse, C.H.-K. Chaos in Power Electronics; World Scientific Series: Singapore, 2002; pp. 317–340. [Google Scholar] [CrossRef]
- Kennedy, M.P. Chaos in the Colpitts oscillator. IEEE Trans. Circuits Syst. 1994, 41, 771–774. [Google Scholar] [CrossRef]
- Kvarda, P. Chaos in Hartley’s oscillator. Int. J. Bifurc. Chaos 2002, 12, 2229–2232. [Google Scholar] [CrossRef]
- Kilic, R.; Yildrim, F. A survey of Wien bridge-based chaotic oscillator: Design and experimental issues. Chaos Solitons Fractals 2008, 38, 1394–1410. [Google Scholar] [CrossRef]
- Keuninckx, L.; Van der Sande, G.; Danckaert, J. Simple two-transistor single-supply resistor-capacitor chaotic oscillator. IEEE Trans. Circuits Syst. II 2015, 62, 891–895. [Google Scholar] [CrossRef]
- Rajagopal, K.; Li, C.H.; Nazarimehr, F.; Karthikeyan, A.; Duraisamy, P.; Jafari, S. Chaotic dynamics of modified Wien bridge oscillator with fractional order memristor. Radioengineering 2019, 28, 165–174. [Google Scholar] [CrossRef]
- Petrzela, J. Multi-valued static memory cell with resonant tunneling diodes as natural source of chaos. Nonlinear Dyn. 2018, 94, 1867–1887. [Google Scholar] [CrossRef]
- Petrzela, J. On the existence of chaos in the electronically adjustable structures of state variable filters. Int. J. Circuit Theory Appl. 2016, 44, 1779–1797. [Google Scholar] [CrossRef]
- Kvarda, P. Identifying the deterministic chaos by using the Lyapunov exponents. Radioengineering 2000, 10, 38–40. [Google Scholar]
- Kvarda, P. Identifying the deterministic chaos by using the Lorenz maps. Radioengineering 2000, 9, 32–33. [Google Scholar]
- Minati, L.; Frasca, M.; Oswiecimka, P.; Faes, L.; Drozd, S. Atypical transistor-based chaotic oscillators: Design, realization, and diversity. Chaos 2017, 27, 073113. [Google Scholar] [CrossRef]
- Silva-Juarez, A.; Tlelo-Cuautle, E.; Gerardo de la Fraga, L.; Li, R. Optimization of the Kaplan-Yorke dimension in fractional-order chaotic oscillators by metaheuristic. Appl. Math. Comput. 2021, 394, 125831. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Pham, V.-T.; Reza Hashemi Golpayegani, M. A new cost function for parameter estimation of chaotic systems using return maps as fingerprints. Int. J. Bifurc. Chaos 2014, 24, 1450134. [Google Scholar] [CrossRef]
- Petrzela, J. New chaotic oscillator derived from class C single transistor-based amplifier. Math. Probl. Eng. 2020, 2020, 2640629. [Google Scholar] [CrossRef]
- Petrzela, J. Chaotic and hyperchaotic self-oscillations of lambda diode composed by generalized bipolar transistors. Appl. Sci. 2021, 11, 3326. [Google Scholar] [CrossRef]
- Petrzela, J. Hyperchaotic self-oscillations of two-stage class C amplifier with generalized bipolar transistors. IEEE Access 2021, 9, 62182–62194. [Google Scholar] [CrossRef]
- Valencia-Ponce, M.A.; Tlelo-Cuautle, E.; Gerrardo de la Fraga, L. Estimating the highest time-step in numerical methods to enhance the optimization of chaotic oscillators. Mathematics 2021, 9, 1938. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, G.; Lin, D.; Sun, X.-K. Global attractive sets of a novel bounded chaotic system. Neural Comput. Appl. 2014, 25, 1177–1183. [Google Scholar] [CrossRef]
- Zhang, F. Analysis of a Lorenz-like chaotic system by Lyapunov functions. Complexity 2019. [Google Scholar] [CrossRef]
- Ul Abadin Zafar, Z.; Sene, N.; Rezazadeh, H.; Esfandian, N. Tangent nonlinear equation in context of fractal fractional operators with nonsingular kernel. Math. Sci. 2021, 10, 1–11. [Google Scholar] [CrossRef]
- Zhou, M.-X.; Ravi Kanth, A.S.V.; Aruna, K.; Raghavendar, K.; Rezazadeh, H.; Inc, M.; Aly, A.A. Numerical solutions of time fractional Zakharov-Kuznetsov equation via natural transform decomposition method with nonsingular kernel derivatives. J. Funct. Spaces 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Petras, I. Tuning and implementation methods for fractional-order controllers. Fract. Calc. Appl. Anal. 2012, 15, 282–303. [Google Scholar] [CrossRef]
- Kadlcik, L.; Horsky, P. A low-dropout voltage regulator with a fractional-order control. Radioengineering 2016, 25, 312–320. [Google Scholar] [CrossRef]
- Yao, J.; Wang, K.; Huang, P.; Chen, L.; Machado, J.T. Analysis and implementation of fractional-order chaotic system with standard components. J. Adv. Res. 2020, 25, 97–109. [Google Scholar] [CrossRef]
- Petrzela, J. Fractional-order chaotic memory with wideband constant phase elements. Entropy 2020, 22, 422. [Google Scholar] [CrossRef] [Green Version]
- Kartci, A.; Herencsar, N.; Machado, J.T. History and progress of fractional-order element passive emulators: A review. Radioengineering 2020, 29, 296–304. [Google Scholar] [CrossRef]
- Valencia-Ponce, M.A.; Castaneda-Avina, P.R.; Tlelo-Cuautle, E.; Carbajal-Gomez, V.H.; Gonzalez-Diaz, V.R.; Sandoval-Ibarra, Y.; Nunez-Perez, J.-C. CMOS OTA-based filters for designing fractional-order chaotic oscillators. Fractal Fract. 2021, 5, 122. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. FPAA-based realization of filters with fractional Laplace operators of different orders. Fractal Fract. 2021, 5, 218. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Said, L.A.; Radwan, A.G. Reconfigurable FPGA realization of fractional-order chaotic systems. IEEE Access 2021, 9, 89376–89389. [Google Scholar] [CrossRef]
- Sprott, J.C. A proposed standard for the publication of new chaotic systems. Int. J. Bifurc. Chaos 2011, 21, 2391–2394. [Google Scholar] [CrossRef] [Green Version]
- Itoh, M. Synthesis of electronic circuits for simulating nonlinear dynamics. Int. J. Bifurc. Chaos 2001, 11, 605–653. [Google Scholar] [CrossRef]
- Petrzela, J.; Gotthans, T.; Guzan, M. Current-mode network structures dedicated for simulation of dynamical systems with plane continuum of equilibrium. J. Circuits Syst. Comput. 2018, 27, 1830004. [Google Scholar] [CrossRef]
- Valencia-Ponce, M.A.; Tlelo-Cuautle, E.; Gerrardo de la Fraga, L. On the sizing of CMOS operational amplifiers by applying many-objective optimization algorithms. Electronics 2021, 10, 3148. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Pham, V.-T.; Volos, C.H.; Jafari, S.; Kapitaniak, T. Coexistence of hidden attractors in a novel no-equilibrium system. Nonlinear Dyn. 2017, 87, 2001–2010. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrzela, J.; Rujzl, M. Chaotic Oscillations in Cascoded and Darlington-Type Amplifier Having Generalized Transistors. Mathematics 2022, 10, 532. https://doi.org/10.3390/math10030532
Petrzela J, Rujzl M. Chaotic Oscillations in Cascoded and Darlington-Type Amplifier Having Generalized Transistors. Mathematics. 2022; 10(3):532. https://doi.org/10.3390/math10030532
Chicago/Turabian StylePetrzela, Jiri, and Miroslav Rujzl. 2022. "Chaotic Oscillations in Cascoded and Darlington-Type Amplifier Having Generalized Transistors" Mathematics 10, no. 3: 532. https://doi.org/10.3390/math10030532





