Tunable Multi-Band-Stop Filters Using Generalized Fibonacci Photonic Crystals for Optical Communication Applications
Abstract
:1. Introduction
2. Method and Problem Formulation
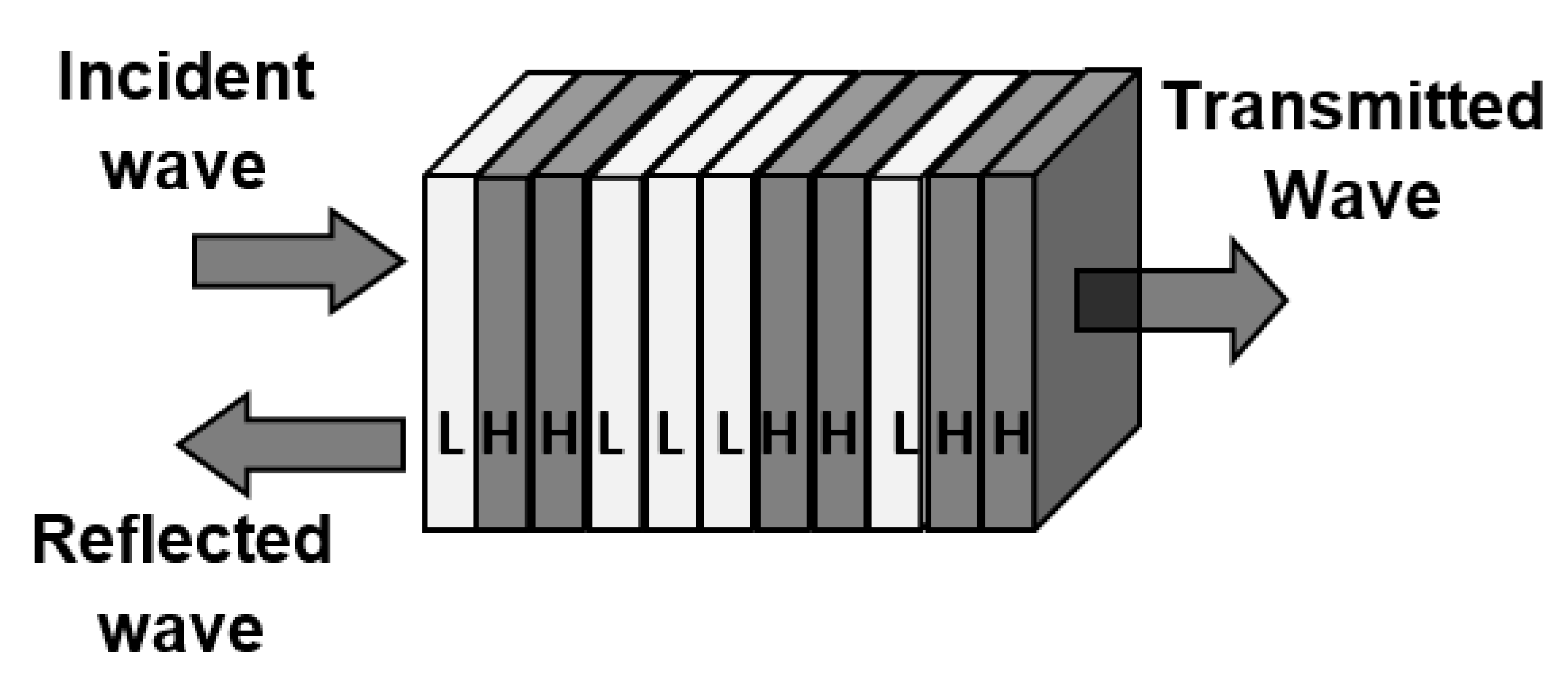
2.1. Transfer Matrix Method
2.2. Fibonacci and Generalized Fibonacci Quasi-Crystals Models
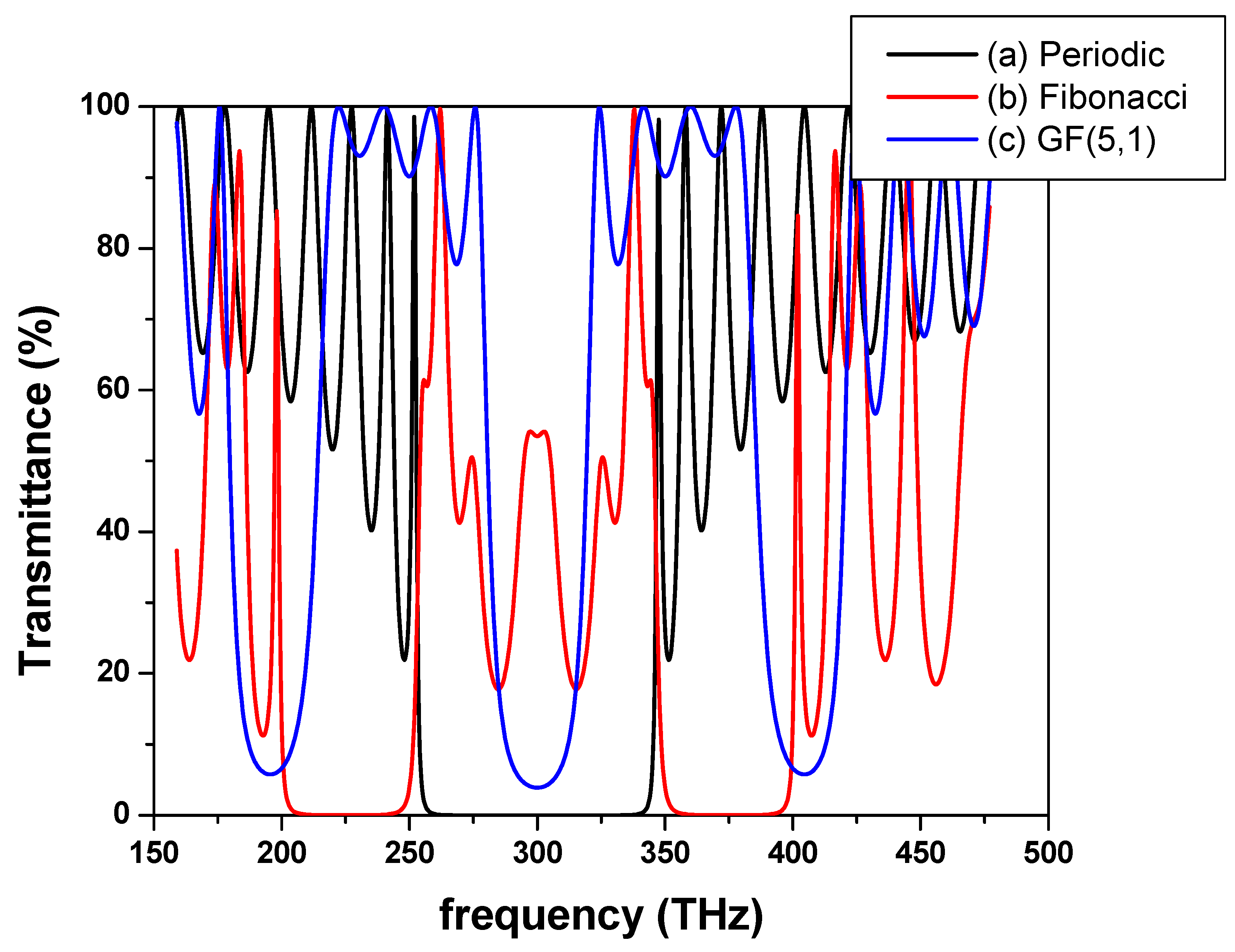
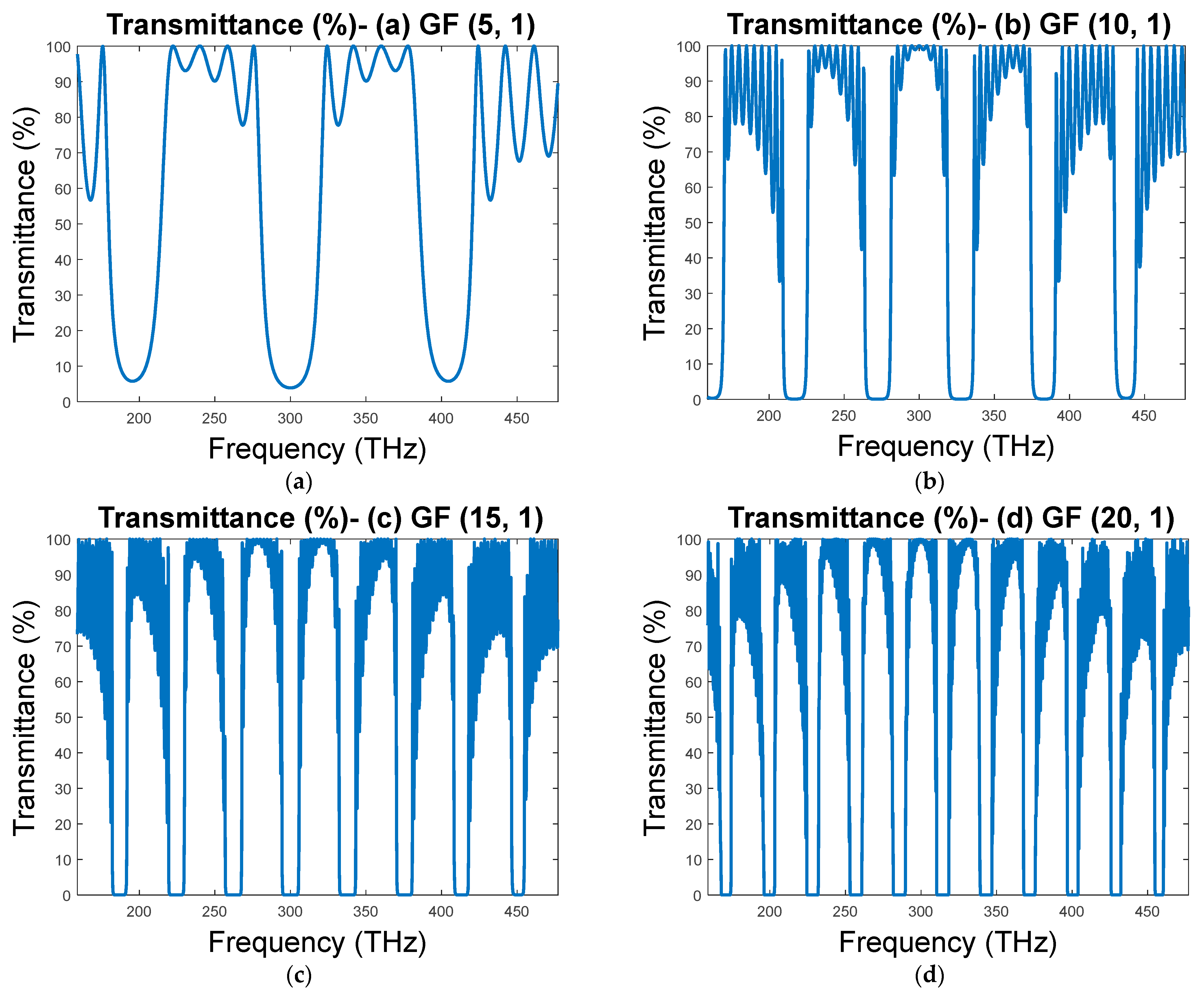
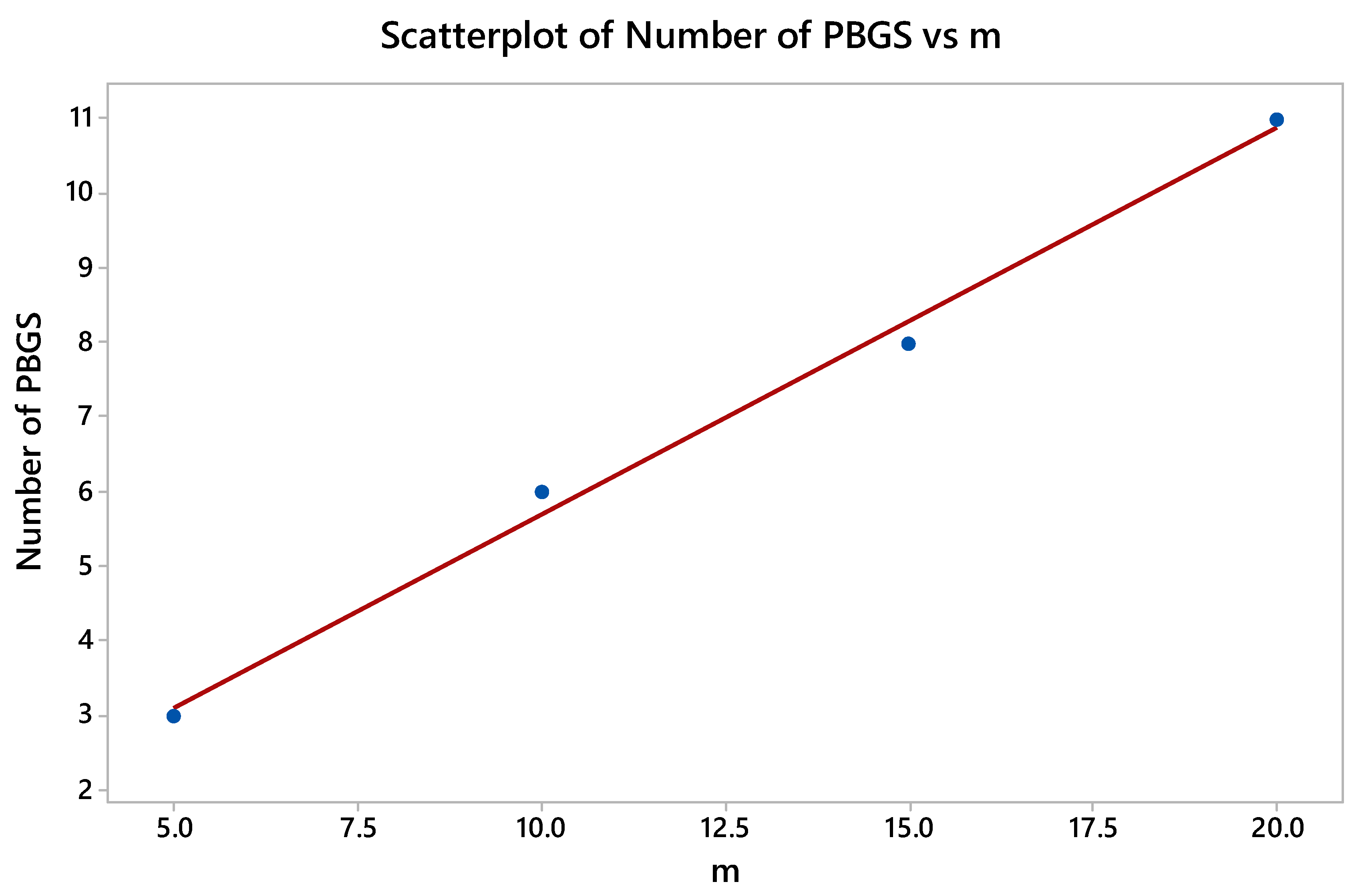
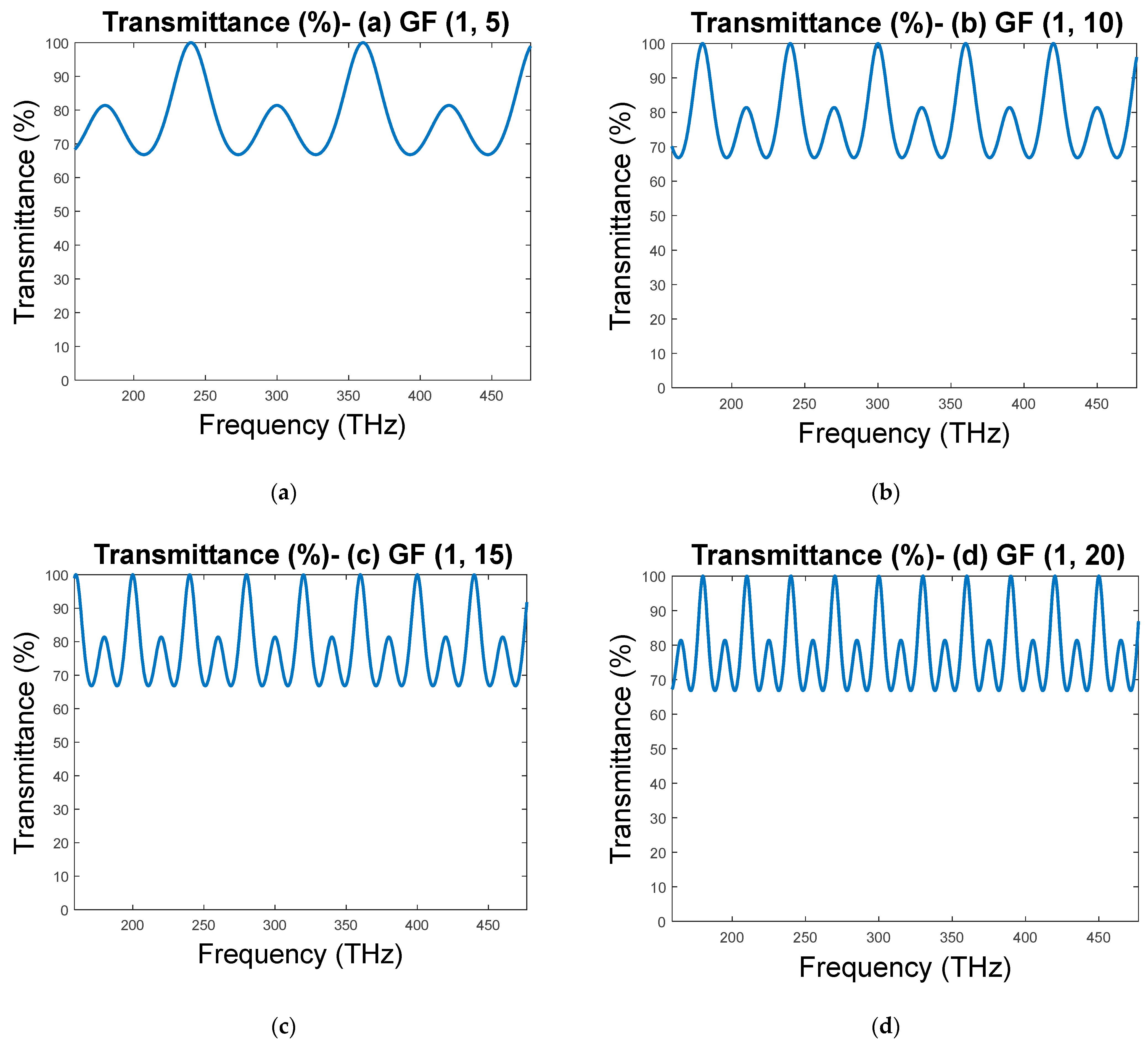
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Augustyniak, A.; Zdanowicz, M.; Osuch, T. Self-Similarity Properties of Complex Quasi-Periodic Fibonacci and Cantor Photonic Crystals. Photonics 2021, 8, 558. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Iguchi, K. Localization in Optics: Quasiperiodic Media. Phys. Rev. Lett. 1987, 58, 2436. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.B.; Zaghdoudi, J.; Kanzari, M.; Kuszelewicz, R. The slowing of light in one-dimensional hybrid periodic and non-periodic photonic crystals. J. Opt. 2010, 12, 045402. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ali, N.B.; Segovia-Chaves, F.; Posada, H.V. Photonic band gap properties of one-dimensional photonic quasicrystals containing Nematic liquid crystals. Results Phys. 2020, 19, 103600. [Google Scholar] [CrossRef]
- Ali, N.B.; Trabelsi, Y.; Kanzari, M. Stop band filter by using hybrid quasi-periodic one dimensional photonic crystal in microwave domain. IJMOT 2009, 4, 195–204. [Google Scholar]
- Ali, N.B.; Dhasarathan, V.; Alsaif, H.; Trabelsi, Y.; Nguyenb, T.; Bouazzi, Y.; Kanzari, M. Design of output-graded narrow polychromatic filter by using photonic quasicrystals. Phys. B Condens. Matter 2020, 582, 411918. [Google Scholar] [CrossRef]
- Ali, N.B.; Kanzari, M. omni-directional high reflectors using one-dimensional deformed quasi-periodic Cantor band gap structure at optical telecommunication wavelength band. Mediterr. J. Electron. Commun. 2010, 6, 1–6. [Google Scholar]
- Segovia-Chaves, F.; Posada, H.V.; Trabelsi, Y.; Ali, N.B. Transmittance spectrum in a one-dimensional photonic crystal with Fibonacci sequence superconductor–semiconductor. Optik 2020, 217, 164803. [Google Scholar] [CrossRef]
- Han, P.; Wang, H.Z. Effect of invariant transformation in one-dimensional randomly-perturbed photonic crystal. Chin. Phys. Lett. 2003, 20, 1520. [Google Scholar]
- Merlin, R.; Bajema, K.; Clarke, R.; Juang, F.Y.; Bhattacharya, P.K. Quasiperiodic GaAs-AlAs heterostructures. Phys. Rev. Lett. 1985, 55, 1768. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B. Critical wave functions and a Cantor-set spectrum of a one-dimensional quasicrystal model. Phys. Rev. B 1987, 35, 1020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sibilia, C.; Bertolotti, M. Trends in Optics and Photonics. In ICO Book IV Trends in Optics and Photonics; Asakura, T., Ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Chakrabarti, A. Field induced delocalization in a Koch fractal. Phys. Rev. B 1999, 60, 10576–10579. [Google Scholar] [CrossRef]
- Gellermann, W.; Kohmoto, M.; Sutherland, B.; Taylor, P.C. Localization of light waves in Fibonacci dielectric multilayers. Phys. Rev. Lett. 1994, 72, 633–636. [Google Scholar] [CrossRef] [PubMed]
- Barry, G.G.; Howard, H.; Ramzi, H.N. Optical processors for smart structures. In Proceedings of the Advances in Optical Information Processing IV, Orlando, FL, USA, 1 September 1990; Volume 1296. [Google Scholar] [CrossRef]
- Luo, D.; Hao, Q. Optical transmission link between microprocessors and memories. In Proceedings of the Asia Communications and Photonics Conference, Shanghai, China, 11–14 November 2014; ISBN 978-1-55752-852-0. [Google Scholar] [CrossRef]
- Alexoudi, T.; Kanellos, G.T.; Pleros, N. Optical RAM and integrated optical memories: A survey. Light Sci. Appl. 2020, 9, 91. [Google Scholar] [CrossRef]
- Leonardo, D.B.; Niall, M.; Pascal, D. Optical memories and switching dynamics of counterpropagating light states in microresonators. Opt. Express 2021, 29, 2193–2203. [Google Scholar] [CrossRef]
- Heim, B.; Soeken, M.; Marshall, S.; Granade, C.; Roetteler, M.; Geller, A.; Troyer, M.; Svore, K. Quantum programming languages. Nat. Rev. Phys. 2020, 2, 709–722. [Google Scholar] [CrossRef]
- LeeAnn, M.S.; Scott, E.S.; David, A.M. Preparation of an exciton condensate of photons on a 53-qubit quantum computer. Phys. Rev. Res. 2020, 2, 043205. [Google Scholar] [CrossRef]
- Jin, C.J.; Cheng, B.Y.; Man, B.Y.; Li, Z.L.; Zhang, D.Z. Two-dimensional dodecagonal and decagonal quasiperiodic photonic crystals in the microwave region. Phys. Rev. B 2000, 61, 10762–10767. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ali, N.B.; Segovia-Chaves, F.; Posada, H.V. Tunable 1D nano-photonic filter using Nematic liquid crystal and high-Tc superconductors. Opt. Quant. Electron. 2021, 53, 712. [Google Scholar] [CrossRef]
- Huang, X.Q.; Jiang, S.S.; Peng, R.W.; Hu, A. Perfect transmission and self-similar optical transmission spectra in symmetric Fibonacci-class multilayers. J. Phys. Rev. E 2001, 59, 245104. [Google Scholar] [CrossRef]
- Belhadj, W.; Ali, N.B.; Dakhlaoui, H.; Alsalmi, O.H.; Alsaif, H.; Torchani, A. Characterization of spectral features of cavity modes in one-dimensional graphene-based photonic crystal structures, Eur. Phys. J. B 2021, 94, 198. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ben Ali, N.; Belhadj, W.; Kanzari, M. Photonic Band Gap Properties of One-dimensional Generalized Fibonacci Photonic Quasicrystal Containing Superconductor Material. J. Supercond. Nov. Magn. 2019, 32, 3541–3547. [Google Scholar] [CrossRef]
- Gahef, T.; Bouazzi, Y.; Kanzari, M. Omnidirectional mirror at 1.3 and 1.55 μm for optical fiber communication by specific deformation of Bragg reflector. Opt. Quant. Electron. 2017, 49, 95. [Google Scholar] [CrossRef]
- Chittaranjan, N.; Alireza, A.; Ardhendu, S.; Narottam, D. Near- and mid-infrared bandgaps in a 1D photonic crystal containing superconductor and semiconductor-metamaterial. Int. J. Mod. Phys. B 2019, 33, 1950219. [Google Scholar] [CrossRef]
- Augusto, D.A.F.; Luis, M.G.S.; Vivechana, A. Study of the omnidirectional photonic bandgap for dielectric mirrors based on porous silicon: Effect of optical and physical thickness. Nanoscale Res. Lett. 2012, 7, 391. [Google Scholar] [CrossRef] [Green Version]
- Ali, N.B.; Kanzari, M. Designing of omni-directional high reflectors by using one-dimensional modified hybrid Fibonacci/Cantor band-gap structures at optical telecommunication wavelength band. J. Mod. Opt. 2010, 57, 287–294. [Google Scholar] [CrossRef]
- Sanjeev, S.; Rajender, K.; Singh, K.S.; Kumar, V.; Deepti, J. Design of a Narrow-Band Photonic Crystal Based Omni-Directional Mirror for Optical Fiber Communication. IJECSE 2012, 1, 1825–1832. [Google Scholar]
- Ali, N.B.; Trabelsi, Y.; Alsaif, H.; Badawi, I.; Gal, S. Omnidirectional High Reflectors Using Silica/Superconductor Fibonacci Photonic Crystal for Optical Communication Applications. Phys. C: Supercond. Its Appl. 2022, 594, 1354021. [Google Scholar] [CrossRef]
- Ahmad, I.; Ullah, S.; Ullah, S.; Habib, U.; Ahmad, S.; Ghaffar, A.; Alibakhshikenari, M.; Khan, S.; Limiti, E. Design and Analysis of a Photonic Crystal Based Planar Antenna for THz Applications. Electronics 2021, 10, 1941. [Google Scholar] [CrossRef]
- Mao, H.; Lu, G. Enhancement of THz Photoconductive Antenna Gain based on a Photonic Crystal Fiber Substrate. In Proceedings of the IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (APS/URSI), Singapore, 16 February 2022. [Google Scholar] [CrossRef]
- Geler-Kremer, J.; Eltes, F.; Stark, P.; Sharma, A.; Caimi, D.; Offrein, B.J.; Fompeyrine, J.; Abel, S. A Non-Volatile Optical Memory in Silicon Photonics. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC) IEEE, San Francisco, CA, USA, 6–10 June 2021. [Google Scholar]
- Mohammadi, M.; Farahmand, M.; Olyaee, S.; Seifouri, M. An Overview of All-Optical Memories Based on Periodic Structures Used in Integrated Optical Circuits. Silicon 2022, 14, 54. [Google Scholar] [CrossRef]
- Bartlett, B.; Dutt, A.; Fan, S. Deterministic photonic quantum computation in a synthetic time dimension. Optica 2021, 8, 1515–1523. [Google Scholar] [CrossRef]
- Ochoa, M.; Algorri, J.F.; Roldán-Varona, P.; Rodríguez-Cobo, L.; López-Higuera, J.M. Recent Advances in Biomedical Photonic Sensors: A Focus on Optical-Fibre-Based Sensing. Sensors 2021, 21, 6469. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.B.; Alsaif, H.; Trabelsi, Y.; Chughtai, M.T.; Dhasarathan, V.; Kanzari, M. High Sensitivity to Salinity-Temperature Using One-Dimensional Deformed Photonic Crystal. Coatings 2021, 11, 713. [Google Scholar] [CrossRef]
- Yu, B.; Luo, Y.; Chen, L.; Chu, Z.; Li, K.H. An optical humidity sensor: A compact photonic chip integrated with artificial opal. Sens. Actuators B Chem. 2021, 349, 130763. [Google Scholar] [CrossRef]
- Lio, G.E.; Ferraro, A. LIDAR and Beam Steering Tailored by Neuromorphic Metasurfaces Dipped in a Tunable Surrounding Medium. Photonics 2021, 8, 65. [Google Scholar] [CrossRef]
- Shaltout, A.M.; Kim, J.; Boltasseva, A.; Shalaev, V.M.; Kildishev, A.V. Ultrathin and multicolour optical cavities with embedded metasurfaces. Nat. Commun. 2018, 9, 2673. [Google Scholar] [CrossRef] [Green Version]
- Lio, G.E.; Ferraro, A.; Giocondo, M.; Caputo, R.; De Luca, A. Color Gamut Behavior in Epsilon Near-Zero Nanocavities during Propagation of Gap Surface Plasmons. Adv. Opt. Mater. 2020, 8, 2000487. [Google Scholar] [CrossRef]
- Tibuleac, S.; Magnusson, R.; Maldonado, T.A.; Young, P.P.; Holzheimer, T.R. Dielectric frequency-selective structures incorporating waveguide gratings. IEEE Trans. Microw. Theory Tech. 2000, 48, 553–561. [Google Scholar] [CrossRef]
- Tsitsas, N.L.; Uzunoglu, N.K.; Kaklamani, D.I. Diffraction of plane waves incident on a grated dielectric slab: An entire domain integral equation analysis. Radio Sci. 2007, 42, RS6S22. [Google Scholar] [CrossRef]
- Norton, S.M.; Turan, E.; Michael, G.M. Coupled-mode theory of resonant-grating filters. J. Opt. Soc. Am. A 1997, 14, 629–639. [Google Scholar] [CrossRef]
- Tsitsas, N.L. Efficient integral equation modeling of scattering by a gradient dielectric metasurface. EPJ Appl. Metamater. 2017, 43, 3. [Google Scholar] [CrossRef] [Green Version]
| Optical Fiber Wavelengths | ||||
|---|---|---|---|---|
| Structures | 650 nm | 850 nm | 1300 nm | 1550 nm |
| GF (5, 1) | 100 | 92.0 | 93 | 6 |
| GF (10, 1) | 70 | 87.0 | 100 | 75 |
| F (15, 1) | 96 | 96.0 | 64 | 90 |
| GF (20, 1) | 26 | 77.8 | 0 | 55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, N.B.; Alshammari, S.; Trabelsi, Y.; Alsaif, H.; Kahouli, O.; Elleuch, Z. Tunable Multi-Band-Stop Filters Using Generalized Fibonacci Photonic Crystals for Optical Communication Applications. Mathematics 2022, 10, 1240. https://doi.org/10.3390/math10081240
Ali NB, Alshammari S, Trabelsi Y, Alsaif H, Kahouli O, Elleuch Z. Tunable Multi-Band-Stop Filters Using Generalized Fibonacci Photonic Crystals for Optical Communication Applications. Mathematics. 2022; 10(8):1240. https://doi.org/10.3390/math10081240
Chicago/Turabian StyleAli, Naim Ben, Serhan Alshammari, Youssef Trabelsi, Haitham Alsaif, Omar Kahouli, and Zied Elleuch. 2022. "Tunable Multi-Band-Stop Filters Using Generalized Fibonacci Photonic Crystals for Optical Communication Applications" Mathematics 10, no. 8: 1240. https://doi.org/10.3390/math10081240
APA StyleAli, N. B., Alshammari, S., Trabelsi, Y., Alsaif, H., Kahouli, O., & Elleuch, Z. (2022). Tunable Multi-Band-Stop Filters Using Generalized Fibonacci Photonic Crystals for Optical Communication Applications. Mathematics, 10(8), 1240. https://doi.org/10.3390/math10081240






