Optimizing Inventory Management: A Comprehensive Analysis of Models Integrating Diverse Fuzzy Demand Functions

Abstract

This review study provides a comprehensive analysis of the classification of inventory models, with a focus on incorporating various fuzzy demand functions. The incorporation of fuzzy sets theory within inventory models is highlighted as a significant advancement in the field. The study emphasizes the importance of efficiently locating pertinent publications on this topic, rendering it a valuable resource for individuals interested in exploring inventory models that incorporate fuzzy demand functions. There was a need for a systematic and complete examination of recent breakthroughs in fuzzy inventory management. Our objective was to provide an illuminating overview of the significant developments in this field and offer insights into the probable future directions of research. Our evaluation of various model components has unveiled new and underexplored territories that may warrant further exploration. Perhaps it would be prudent to consider the possibility of establishing simpler models or incorporating qualitative methods into existing models and initiating a discourse on this topic.

1. Introduction

Effective inventory management requires the utilization of sophisticated inventory models to determine optimal order quantities, reorder points, and inventory holding costs. Among these models, the economic order quantity (EOQ) and economic production quantity (EPQ) are the most commonly employed. The EOQ model, a traditional inventory management framework, was first developed in the early 20th century. Over time, deterministic models have evolved from this original concept through several extensions. Harris [1] introduced management issue modeling in 1915, while Hanssmann [2] in 1962 and Hadley and Whitin [3] in 1963 focused on inventory system development. Ghare and Schrader [4] studied the exponentially decaying inventory model in 1963. Haneveld and Teunter [5] analyzed the impact of discount and demand rate variations on the EOQ model in 1998, while Hariga [6] examined an EOQ model for degrading goods with time-varying demand in 1996. However, it is important to acknowledge that these models operate under the assumption of a predetermined, deterministic environment, which is not always the case in today’s competitive and dynamic corporate setting.

Exploring fuzzy set theory (FST), created by Zadeh [7], can be beneficial as it allows for the transformation of ill-defined information into mathematical expressions and may help address some of the inherent shortcomings of traditional inventory models. Bellman and Zadeh [8] used them to solve a decision-making problem. Since then, numerous researchers have been engaged to describe the fuzzy sets’ actual characteristics. The inventory system has been evolving naturally in a fuzzy environment, guided by great thinkers. Lee and Yao [9] created a fuzzy EOQ model without backorder. Bjork [10] developed an analytical solution for the fuzzy EOQ model with backorder. In a different study, Mahata [11] investigated the learning effect of the unit production time on optimal lot size for an imperfect production process with partial backlogs of shortage quantity in fuzzy random environments. The learning and forgetting effects on fuzzy parameters for the backorder EOQ model, taking into account imperfect quality items, were recently discussed by Kazemi et al. [12,13,14]. However, Yager’s [15] contribution to de-fuzzification analysis, particularly on ranking fuzzy numbers, has maintained an unquestionable place. Jaggi et al. [16] propose a fuzzy EOQ model that integrates a flexible payment approach, price-dependent demand, and discounts for early payments and allows full backlog shortages. An integrated inventory model for an imperfect production accounting for time-varying demand, repair and production rates, and inflationary pressures was introduced by Jain and Tiwari [17] in 2018. A sophisticated fuzzy inventory model that accounts for item deterioration, variable demand, delayed payments, and partial backlogging was developed by Shaikh et al. [18] in the same year.

Fuzzy set theory can be particularly helpful in calibrating inventory-related data, resulting in the improved handling of real-world situations. This is especially useful when estimating demand projections and costs associated with holding, replenishing, shortages, and backorders, which can be challenging to estimate with precision in practical applications. Figure 1 displays the general frameworks of fuzzy inventory models, which are widely utilized algorithms for integrating the concept of fuzziness into models. In order to ensure effective inventory management in dynamic and competitive business environments, it is imperative to carefully consider various aspects and techniques when implementing fuzzy inventory models.

A suggested framework in Figure 1 can be utilized to study the impact of uncertainty in quantity or demand. Once the model is formulated and all uncertain parameters and variables are taken into account, the fuzzification process can commence. During the third phase, the model’s behavior in an uncertain environment can be analyzed using appropriate fuzzy tools such as membership functions and related operators. Feedback derived from this analysis must be applicable to decision makers in the real world. Therefore, it is necessary to de-fuzzify the results in the final phase (Phase 4) to ensure that they can be effectively used for decision-making purposes.

Further, various extensions in the classification of inventory models, with a focus on incorporating fuzzy demand functions, have been developed. One such development is the introduction of cloudy fuzzy, an innovative inventory management system that is transforming the industry. De and Mahata [19] studied the cloudy fuzzy numbers on a backordered inventory model. Recently, Barman [20] introduced a backordered inventory model with inflation in a cloudy fuzzy environment; unlike traditional models that were prone to inaccuracies due to uncertain demand patterns, lead times, and fluctuating replenishment quantities, cloudy fuzzy factors in these uncertainties. Type 2 fuzzy logic addresses the limitations of traditional type 1 fuzzy in handling higher levels of uncertainty and imprecision. Type 2 fuzzy logic extends type 1 fuzzy logic by allowing for the modeling and manipulation of uncertainty in the membership degrees themselves. It introduces a second level of uncertainty, known as the footprint of uncertainty, which captures the uncertainty associated with the primary membership degrees. The triangular dense fuzzy set (TDFS) was first introduced by De and Beg [21] using the learning experience over the fuzzy set. Karmakar et al. [22] used the TDFS on an EOQ model that was sensitive to pollution. De [23] developed a triangular dense fuzzy lock set and expanded the TDFS. It has proven to be a valuable tool in a wide range of applications. These include decision making, psychological testing, military selection, cryptography, photography, crime research, filtering of noisy environments, and risk analysis. In addition, Atanassov [24] created the intuitionistic fuzzy set (IFS) by including non-membership and hesitant degree in the fuzzy set itself.

For single or multiple items, several researchers developed EPL models that took into account either a uniform or variable production rate (dependent on time, demand, and/or the level of on-hand inventory). The development of their inventory models took into account either a uniform or variable production rate by Bhunia and Maiti [25], Balkhi and Benkherouf [26], Abad [27], Mandal and Maiti [28], Roy, Kar, and Maiti [29], Das et al. [30,31,32,33], and others.

While there have been some review papers addressing fuzzy set theory in inventory management, there is still a gap in the literature regarding inventory models under other various fuzzy environments.

2. Literature Review

To establish the necessity of this study, it is imperative to examine the relevant literature on inventory management.

Table 1. Previous review papers on fuzzy inventory models.

Study Published	Area of Research	Aspects of Research	Year
Guiffrida and Nagi [34]	Production management	Fuzzy set theory	Until 1977
Mula et al. [35]	Production planning	Uncertain models	1983–2004
Aissaoui et al. [36]	Operational research models	Supply selection and order allocation	Until 2005
Ko et al. [37]	Supply chain management	Soft computing applications	1990–2009
Khan et al. [38]	Economic order quantity	Imperfect quality items	2000–2011
Wong and Lai [39]	Production and operations	Fuzzy set theory applications	1998–2009
Bakker et al. [40]	Inventory systems	Deteriorating items	2001–2011
Aloulou et al. [41]	Lot-sizing models	Non-deterministic models	2000–2013
Andriolo et al. [42]	Lot-sizing models	Deterministic, stochastic and fuzzy models	1913–2012
Janssen et al. [43]	Inventory models	Deteriorating items	2012–2017
Shekarian et al. [44]	Inventory models	Fuzzy set theory	Until 2017
Lakshmi et al. [45]	Inventory models	Fuzzy environment	2018
Present review	Inventory models	Various fuzzy demand functions	Until 2023

provides a summary of review papers that have analyzed a range of fuzzy inventory models.

In conclusion, it is evident that there is a gap in the literature on inventory management regarding the extensions of fuzzy demand functions. No review study has exclusively focused on this area. Despite the numerous works that have been performed in this field, the lack of a systematic review makes it difficult to analyze the advancements made and identify research gaps for further exploration. Therefore, this study aims to fill the presented gaps and provide a comprehensive analysis of the progress made in this area. The last row of Table 1 outlines the role of this study in addressing the identified research gaps.

In our research, we employed a variety of search terms, including “cloudy fuzzy demand* AND inventory”, “dense fuzzy demand* AND inventory”, “type-2 fuzzy demand* AND inventory”, and “Intuitionistic dense fuzzy demand* AND inventory”, utilizing the logical link “AND” between the two search words. To ensure the comprehensiveness of our scope, we conducted searches across a selection of reputable databases and websites, such as researchgate.net, sciencedirect.com, tandfonline.com, inderscienceonline.com, springerlink.com, scholar.google.com, onlinelibrary.wiley.com, and more. We also carefully examined proposed papers from various publishers.

The initial sample underwent thorough scrutiny to ensure its relevance to the review’s topic. To maintain focus and comprehensiveness, we established criteria to exclude papers that did not meet the following characteristics:

• The study’s primary theme must center around developing a fuzzy mathematical model rather than solely applying a fuzzy solution approach. Therefore, we excluded papers that only applied fuzzy solution procedures from our analysis;
• Additionally, the study must exclusively study a problem within the inventory management field. Our objective was to account for all relevant papers in the field up to 2023 while adhering to these established criteria. We did so to ensure the review’s thoroughness and accuracy.

The primary motivation behind this review is to develop sophisticated models that can effectively manage the complexities associated with inventory management in real-world scenarios, particularly when dealing with uncertainties. By harnessing the power of fuzzy logic, the review endeavors to provide decision makers with reliable tools that can facilitate the navigation of uncertainties while simultaneously optimizing resource utilization, preserving service levels, and improving predictive capabilities for superior demand forecasting. The review also aims to foster innovation and encourage the creation of adaptable models that can be widely applied across various industries. Additionally, it aims to bridge the gap between theory and practice by proposing models that are both theoretically sound and practically feasible in real-world situations.

Classification of the inventory models under various fuzzy demand functions has been performed, as shown in Figure 2.

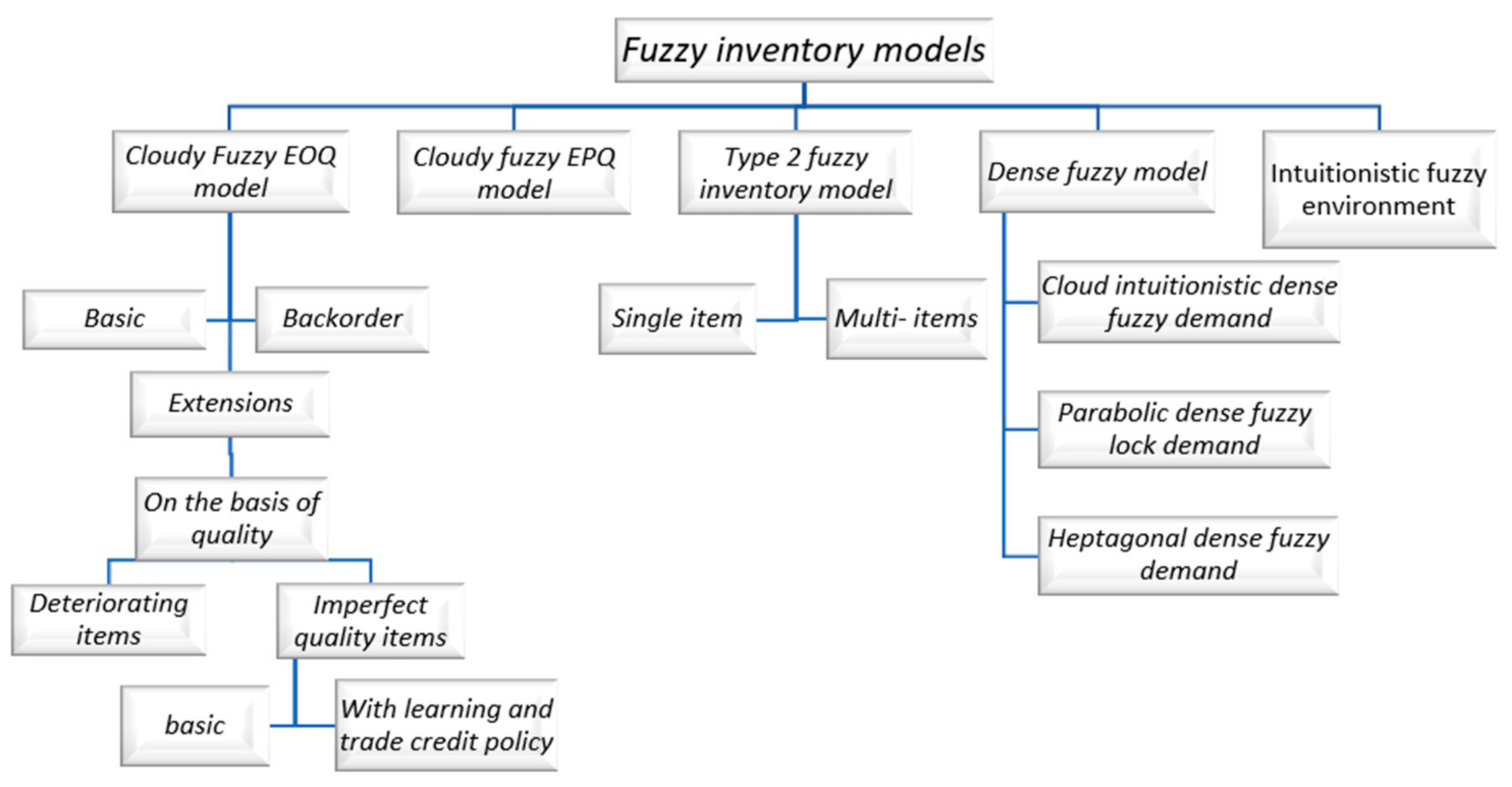
3. Content Analysis

The papers in our sample are examined in the sections that follow in accordance with the classification scheme shown in the previous figure. To retain the length of the article within reasonable bounds, we refrain from discussing papers in-depth and instead make an effort to present studies succinctly by outlining their main contributions and conclusions.

3.1. Cloudy Fuzzy Economic Order Quantity Model

The cloudy fuzzy EOQ model is an extension of the traditional EOQ model that incorporates uncertainty and imprecision in the demand and other parameters. This model considers a range of possible demand values instead of a single deterministic value. Each demand level is associated with a membership degree that represents the likelihood or possibility of that demand level occurring. This model provides a more realistic approach to inventory management by considering the inherent uncertainty in demand.

In the cloudy fuzzy EOQ model without backorders, it is assumed that demand cannot exceed the available inventory, and customers will not wait for the product. If demand exceeds the available inventory, it is considered lost sales. The objective, in this case, is to minimize the total cost, which includes inventory holding costs and ordering costs but not backorder costs. In this graph, the total cost curve will also have a U shape, but the backorder cost component is not present. The curve represents the total cost, including only inventory holding costs and ordering costs.

When backorders are allowed, it means that demand can exceed the available inventory, and customers are willing to wait for the product to be restocked. In the cloudy fuzzy EOQ model with backorders, the objective is to find the optimal quantity that minimizes the total cost, which includes inventory holding costs, ordering costs, and backorder costs. In this graph, the total cost curve will have a U shape, with a minimum point indicating the optimal order quantity. The cost components involved are inventory holding costs, ordering costs, and backorder costs. The backorder cost curve will increase as the order quantity decreases, while the other cost curves will exhibit a U-shaped curve.

3.1.1. Basic Cloudy Fuzzy EOQ Model without Backorder

For the classic EOQ model inventory management problem, Karmakar [46] introduced a new fuzzy number called the cloudy fuzzy and its new de-fuzzification method. By using the demand rate as a general fuzzy number as well as a cloudy fuzzy number, he first solved the crisp model. He then solved the general fuzzy and cloudy fuzzy problem using the standard Yager’s index method and the extension of Yager’s index method, respectively.

Figure 3, obtained from the results of Karmakar’s [46] study, shows that when the fuzzy and crisp solutions follow an exponential path, cloudy fuzzy follows a hyperbolic path. In the cloudy fuzzy case, inventory costs were very high, which began to decrease with cycle time, and the minimum value was obtained at 7 days cycle time only. Here, the fuzzy objective path meets the cloudy objective path, indicating that the fuzzy objective gives better results.

Hence, it was demonstrated how general fuzzy solutions and crisp solutions can both be better in some situations, but they do not always follow reality. The general fuzzy model’s primary flaw is that it consistently incorporates the same uncertainties, which is an unrealistic premise. The cloudy fuzzy method gives lower inventory costs in the long run. As a result, the cloudy fuzzy method, which takes into account all uncertainties, provides the correct answer.

3.1.2. Cloudy Fuzzy EOQ Model with Backorder

De and Mahata [19] (2016) deal with the classical backorder economic order quantity inventory model under a cloudy fuzzy environment. A crisp model is taken, which is later fuzzified to obtain a decision under the cloudy fuzzy demand rate, and a new de-fuzzification method has been utilized for ranking the fuzzy numbers.

Figure 4, obtained from the results of ref. [19]’s study shows that there is a substantial difference between the average inventory costs of the crisp and general fuzzy methods and the cloudy fuzzy model. The lowest value of inventory costs is given using the cloudy fuzzy model, hence making it a better choice.

It can be concluded that the average inventory costs of the crisp and general fuzzy models have significantly differed from those of the cloudy fuzzy models. It was also discovered that the general fuzzy model offered the maximum value of the objective function, but the cloudy fuzzy model gave the lowest value everywhere. Therefore, the solution in a cloudy fuzzy environment is a preferable option for an inventory practitioner, especially a decision maker.

3.1.3. Extensions

On the Basis of Quality

• Deteriorating items

Deterioration has been considered as one of the most vital factors in inventory systems. Deteriorating items are those that lose their utility as time progresses. Shah and Patel [47] developed a cloudy fuzzy EOQ model with deteriorating items. It is observed that there is a significant difference among the solutions in crisp, fuzzy, and cloudy fuzzy environments.

By analyzing Figure 5 based on the results of Shah and Patel’s [48] study, it can be seen that there is not much difference between the optimal solutions in a crisp and fuzzy environment, but a significant difference can be observed in the case of the cloudy fuzzy model.

In a cloudy fuzzy environment, if we consider the higher cycle time, the total inventory cost will be much lower than in other environments. As time increases, the decision maker gains more experience, and the decision will be much more accurate. Hence, the concept of cloudy fuzzy is a very close approach to reality.

• Imperfect quality

• Basic cloudy fuzzy EOQ model for imperfect quality items

De and Mahata [47] created a cloudy fuzzy EOQ model for items with low quality within allowable proportionate discounts. In this study, a cloudy fuzzy EOQ model with imperfect quality items is developed where a 100% screening process is performed, and the imperfect quality items are sold as a single batch later with a proportionate discount rate. A new de-fuzzification method has been introduced on the EOQ model with imperfect quality items developed by Salameh and Jaber [49]. Crisp, general, and cloudy fuzzy environments have been used to describe the model.

On the basis of the results obtained, Figure 6 shows that the average inventory costs in the case of the general fuzzy model are inferior to the crisp and cloudy fuzzy models. However, a numerical study shows the superiority of the cloudy fuzzy model compared to the general fuzzy model.

The following managerial observations were made from this study:

(1)

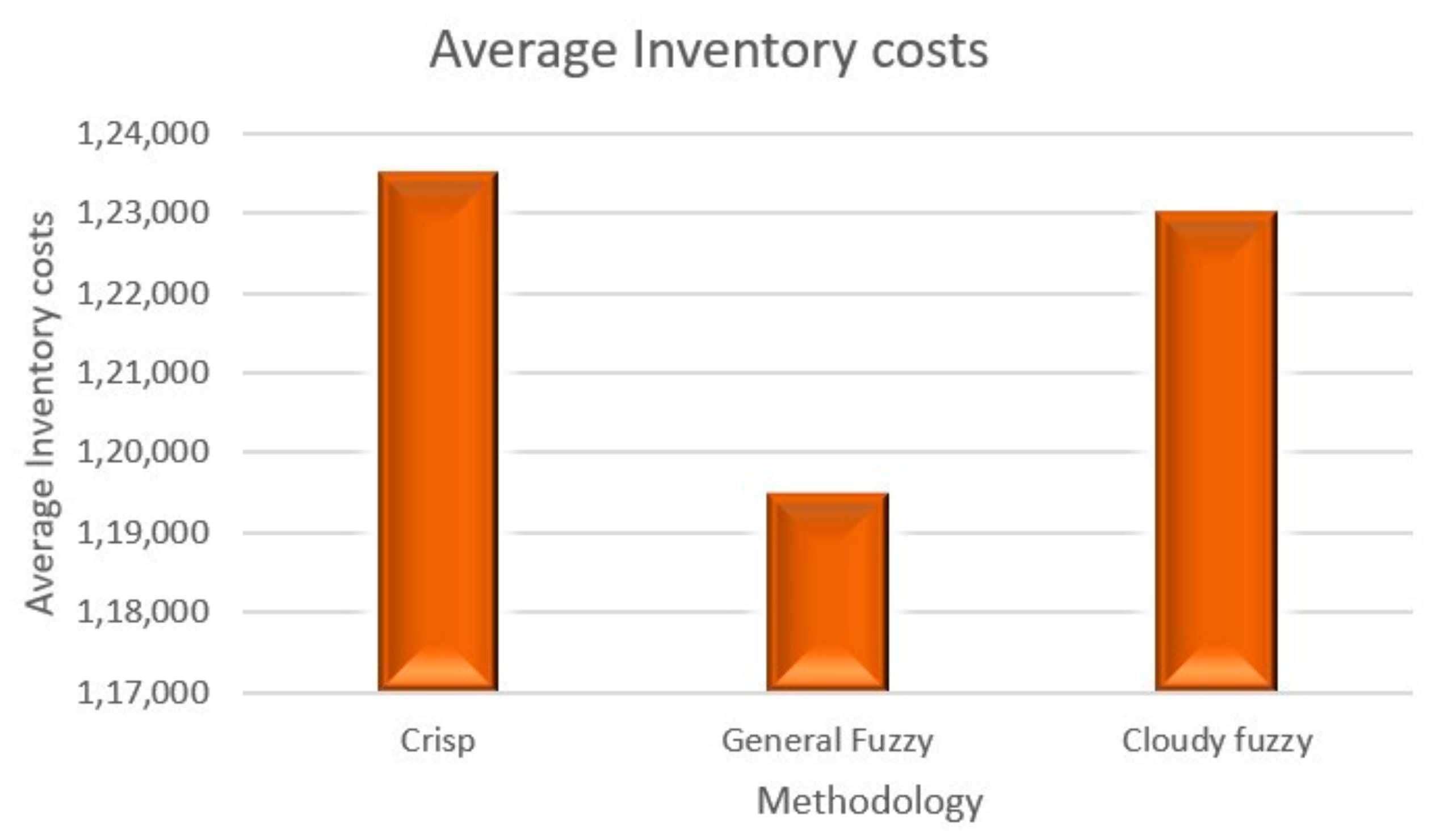
The average maximum profit value of the model is always provided by the cloudy fuzzy model;

(2)

A model’s profitability is not increased by having fewer ambiguities (fuzziness);

(3)

Not all cost factors contribute equally to the improvement of the profit curve;

(4)

The ideal order amount and the chosen cycle duration can affect the overall choice made during the inventory process.

2.

Cloudy fuzzy EOQ model for imperfect quality items with learning and trade-credit policy

An inventory model with a trade-credit policy and learning was created by M.K. Jayaswal and Mandeep Mittal [50], and it assumes demand to be a cloudy fuzzy number for goods of low-quality products. Due to the inclusion of concepts related to learning and trade-credit financing, this study differs from that of De and Mahata [47].

It was seen that as compared to the crisp and fuzzy environments, the cloudy fuzzy environment has a lower order quantity but a longer cycle and higher overall profit. In the case of the cloudy fuzzy environment, the retailer made a greater profit. The cloudy fuzzy environment can control the demand rate, which is better for the retailer.

The model’s findings eventually led to the conclusion that the cost and number of defective units decrease when learning increases and takes on a shape resembling a logistic curve. It is advised to order lots less frequently because learning became faster, and slow learning led to ordering quantities that were larger than their EOQ values. A large, permitted delay period encourages the retailer to place a large order, which ultimately yields a higher profit. The cloudy fuzzy model will always provide the average consumer with the maximum profit. The results and mathematical analysis clearly demonstrate the positive influence of trade credit and the learning effect on retailer ordering policy.

3.2. Cloudy Fuzzy Economic Production Quantity Model

A fuzzy economic production lot-size model under an imperfect production process with a cloudy fuzzy demand rate was the focus of Ajoy Kumar Maiti’s [51] research. The production process of a single product or multiple ones is believed to be rigid and predetermined in the traditional economic production lot-size (EPL) model. But, in practice, it is seen that demand has an impact on output. Customers consume more when the demand rises, and manufacturers must expand their output to keep up with the additional demands of the market.

Here, a cloudy fuzzy demand rate model is built under an imperfect production process, and the production rate is demand-dependent. Using Yager’s index approach and De and Beg’s ranking index method for de-fuzzification, the model is solved in crisp, general fuzzy, and cloudy fuzzy environments, and later, the outcomes are compared in each of these three environments. His main goal is to use the dominance-based particle swarm optimization (PSO) method to minimize average total cost in order to discover the best order quantity and cycle time for the decision maker (DM).

Comparing the results (Figure 7), it has been observed from the graphical representations that a cloudy fuzzy model predicts minimum average cost. The cloudy fuzzy model shows a U-shaped curve, i.e., the curve is convex. So, it can be noted that the cloudy fuzzy model is more reliable. In the same year, Barman et al. [20] developed a model for items subject to deterioration with time-dependent demand and shortages that were partially backordered in a cloudy fuzzy environment. Initially, a crisp model was created, taking into account linearly time-dependent demand with a constant deterioration rate, constant inflation rate, and shortages under a partially backordered environment. The model was later fuzzified to obtain results under the cloudy fuzzy demand rate, inflation rate, deterioration rate, and partially backordered rate. The primary objective of their research was to minimize the total inventory cost by applying the ranking index method of fuzzy and cloudy fuzzy numbers. Rajput et al. [52] introduced an economic production quantity model that incorporates a trade-credit policy. The model presented a classical approach but considered a fuzzy demand rate in a cloudy fuzzy environment. The economic production quantity (EPQ) model introduced by Rajput et al. [53] is a noteworthy contribution that addresses the challenge of managing uncertainty in real-life situations using fuzzy numbers. The research effort aims to develop a mathematical model that optimizes EPQ in different environments, including crisp, general fuzzy, and cloudy fuzzy situations. The method used for the de-fuzzification of the EPQ is Yager’s ranking index method, and the triangular-shaped fuzzy numbers with different types of left and right membership functions are assumed for the constraint goal and inventory cost parameters. Additionally, the study highlights the potential applications and future scope of the cloudy normalized triangular fuzzy number (CNTFN) model in realistic situations.

3.3. Dense Fuzzy Inventory Model

In 2016, De and Beg [21] introduced triangular dense fuzzy sets and a new de-fuzzification technique that corresponds to them. These sets are defined by a sequence of functions that are generated from the mapping of natural numbers with a crisp number x, and if all the components converge to the crisp number x as n → ∞, then the sets are known as dense fuzzy sets (DFS). Figure 8 represents the graphical representation of DFS.

The dense fuzzy inventory model is an extension of traditional inventory models that incorporates the concept of fuzzy logic to handle uncertainties and imprecise information in inventory management. It allows for more robust decision making by considering the ambiguity and imprecision associated with inventory-related parameters such as demand, lead time, and costs.

3.3.1. Intuitionistic Dense Fuzzy Demand Rate

Intuitionistic fuzzy sets, introduced by Krassimir Atanassov [24] in 1986, in which the membership function is generalized to include three components: the degree of membership, degree of non-membership, and degree of hesitancy. This additional component, the degree of hesitancy, captures the level of uncertainty or indecisiveness associated with the membership or non-membership of an element in a set. Intuitionistic dense fuzzy sets further extend the concept of intuitionistic fuzzy sets by allowing for the representation of uncertain or vague information using interval-valued membership degrees. This means that the membership, non-membership, and hesitancy values are expressed as intervals rather than crisp values.

In the learning–forgetting domain, Maity, De, and Mondal [54] proposed a simple backorder EOQ model with an intuitionistic dense fuzzy environment, where the learning curves pertaining to the (non)membership function that resembles that of the cloud drop model. This study demonstrates that the dense fuzzy technique outperforms the crisp approach. Furthermore, the idea of the learning–forgetting process using an intuitionistic dense fuzzy method pays particular attention to the decision makers who are meant to gain expertise under non-random uncertain systems. It has been noted that extreme optimality arises when the learning frequency (experience gained day by day) outweighs the forgetting frequency (complexity grows day by day). Although learning–forgetting curves have a finite form and hence all decisions are user-friendly, cloud drop distribution curves do not provide a proper boundary. Any managerial system must account for learning and forgetting, and any decision can be made in an environment with intuitionistic dense fuzzy data. Anything outside of this model is unrealistic.

The implementation of a non-linear pentagonal intuitionistic fuzzy approach has been employed in an economic production quantity (EPQ) model by Chakraborty et al. [55]. This model accounts for the production of imperfect goods and the reworking of defective items. Furthermore, the model has been applied in a learning and forgetting domain to enhance its efficacy. The study published by Swetha and Afelix [56] in 2022 presents a new method for ranking intuitionistic dense fuzzy sets. By utilizing Haar’s ranking and Yager’s ranking, the proposed method achieves accurate results that were previously difficult to obtain in the field of fuzzy logic. In 2023, Maity et al. [57] introduced a new inventory model called the Green inventory model. This model accounts for various factors such as demand, price, stock, and green concern. It also incorporates a quadratic function of time to represent holding cost and preservation technology to control carbon emissions. The demand rate is represented using a pentagonal intuitionistic dense fuzzy number.

A more adaptable and expressive framework for dealing with uncertainty and ambiguity in decision-making and pattern recognition tasks is provided using intuitionistic dense fuzzy sets. It enables more sophisticated modeling of challenging real-world problems by permitting a better representation of uncertain information.

3.3.2. EOQ Model of Growing Items with a Parabolic Dense Fuzzy Lock Demand Rate

Triangular fuzzy numbers are created in a way that only allows their membership function to reach their maximum value inside an interval. When triangular parabolic fuzzy numbers reach their peak value near the middle of an interval, they are said to be parabolic in shape. Arithmetic operations on generalized parabolic fuzzy numbers and their application were first introduced by H. Garg and Ansha [58] in 2016. The economic order quantity (EOQ) model with shortages was further established by Faritha Asma. A and Priya G. [59] by generating α-cut from a triangular parabolic membership function and employing triangle-shaped values. In their study of an EOQ model of growing items with a parabolic dense fuzzy lock demand rate, Maity, De, Pal, and Mondal [60] used non-linear equations to solve a triangular parabolic membership function.

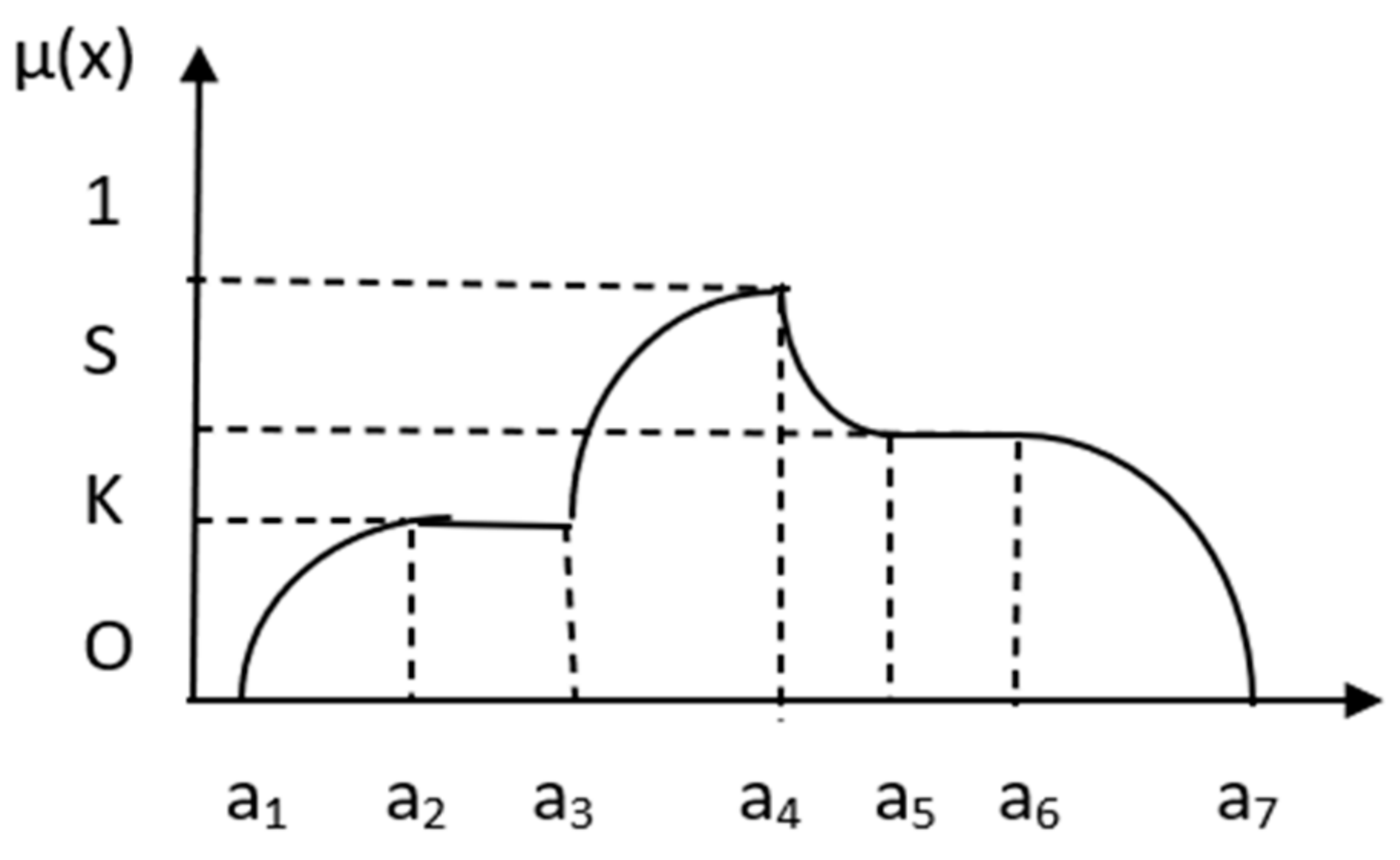
3.3.3. Backlogging EOQ Model with a Non-Linear Heptagonal Dense Fuzzy Environment

Maity, De, and Mondal [61] introduced the concept of linear (Figure 9) and as well as non-linear (Figure 10) for both symmetric and asymmetric heptagonal dense fuzzy numbers. They said, “A fuzzy number A = (a₁, a₂, a₃, a₄, a₅, a₆, a₇) is said to be Heptagonal fuzzy number” if it satisfies the following conditions:

• µ_A(x) is a continuous function in the interval [0, 1];
• µ_A(x) is strictly increasing and continuous function on [a₁, a₂] and [a_3, a₄];
• µ_{A (x)} takes value k in the interval [a₂, a₃] and [a₅, a₆] where 0 < k < 1;
• µ_{A (x)} is strictly decreasing and continuous function on [a₄, a₅] and [a₆, a₇];
• µ_{A (x)} takes value 1 at the point a₄.

They talked about a simple backorder EOQ model in a non-linear heptagonal dense fuzzy environment. It explored how heptagonal dense fuzzy numbers can help us understand the impact of learning experiences on demand rate. The team even conducted a comparative study and found that the demand rate could be triangularly dense fuzzy, trapezoidal dense fuzzy, pentagonal dense fuzzy, and hexagonal dense fuzzy. It was fascinating to consider all the variables at play in this model.

Figure 11 shows the study of a backlogging EOQ model under different dense fuzzy environments. In comparison to other prevailing fuzzy environments, it was found that the non-linear heptagonal dense fuzzy environment is far more suitable for any decision maker of an inventory management problem, and whenever we enhance the learning effects, the average inventory costs gradually decrease.

Later, the application of a pentagonal dense fuzzy set (PDFS) and a novel de-fuzzification method based on the cut was applied to inventory management, utilizing an economic order quantity (EOQ) model by Shah et al. [62] in 2022. To mitigate the uncertainty associated with the EOQ model, the use of a pentagonal fuzzy number was employed, and a cloud pentagonal fuzzy number (CPFN) based on PDFS was introduced. The model was developed by considering demand as CPFN. An optimal replenishment strategy for a two-echelon inventory model in a fuzzy environment that aims to minimize the total inventory cost, considering carrying cost, ordering cost, and replenishment processing cost as pentagonal fuzzy numbers was introduced by Hemalatha et al. [63] in the following year. He proposed two inventory models, one with crisp models and fuzzy total inventory cost and the other with a fuzzy model that formulates both fuzzy total inventory cost and fuzzy optimal order quantity.

3.4. Inventory Models under a Type 2 Fuzzy Environment

Type 2 fuzzy sets are a sophisticated extension of type 1 fuzzy sets, originally introduced by Zadeh [7,64]. Typically, the membership grade of a type 1 fuzzy set is a real number that falls within the range [0, 1]. However, in situations where the membership function of a type 1 fuzzy set is imprecise, a type 2 fuzzy set can be formulated. The membership grade of a type 2 fuzzy set is represented as a fuzzy number with a support that is bounded by the interval of [0, 1]. The logical operations of type 2 fuzzy sets have been explored by a number of eminent researchers, including Mizumoto and Tanaka [65] and Dubois and Prade [66]. Over the years, numerous theoretical research works have been undertaken to examine the properties of type 2 fuzzy sets and their applications, for example [67,68]. In the case of a type 2 fuzzy set, the complete de-fuzzification process consists of two parts: type reduction and de-fuzzification. Type reduction is the procedure by which a type 2 fuzzy set is transformed into a corresponding type 1 fuzzy set, known as a type-reduced set (TRS). The TRS is then easily de-fuzzified to a crisp value. Various reduction methods have been proposed to reduce type 2 fuzzy sets into type 1 fuzzy sets, including the centroid type of reduction method proposed by Karnik and Mendel [69] and the CV reduction methods introduced by Qin et al. [70]. The extension principle forms a robust methodology for extending mathematical concepts from crisp sets to fuzzy sets, which has been applied to many operations and extended to interval-valued fuzzy sets. Many researchers have studied the concept of type 2 fuzziness over the years. For instance, Castillo and Melin [71] conducted a review of optimization methods used in the design of type 2 fuzzy sets. Chen et al. [72] extended the QUALIFLEX method to handle multiple criteria decision-making problems in the context of interval type 2 fuzzy sets. Fuzzy arithmetic about the linear combinations of common type 2 fuzzy variables was discussed by Liu and Bai [73]. Bai and Liu [74] explored the impact of uncertain transportation costs and customers’ demands, where the uncertain parameters were characterized by type 2 fuzzy variables. Turk et al. [75] presented a two-stage integrated approach to supplier selection and inventory planning, in which suppliers were ranked based on various criteria using interval type 2 fuzzy sets.

3.4.1. Inventory Models under a Type 2 Fuzzy Environment with Imperfect Quality Items and Backlogging

In 2018, an inventory system model was introduced by Ravi Shankar Kumar [76], titled “Type-2 fuzzy inventory system considering items with imperfect quality and shortage backlogging”. The model is built to operate in a fuzzy environment where shortages can occur and be backlogged. For businesses, demand is a crucial factor, and it can be predicted using historical data. However, predicting future scenarios comes with a lot of uncertainties, such as incomplete data sets, ambiguous scenarios, and imprecise demand. To tackle these uncertainties, a more effective technique called the interval type 2 fuzzy demand rate is used here. The number of items in a lot that will be of poor quality is difficult to estimate, so the percentage of such products is regarded as a type 2 fuzzy variable. The study offers a de-fuzzification approach to type 2 fuzzy variables concerning interval approximation. The suggested method is used to calculate the equivalent crisp total average profit function, and it has been discovered that type 2 fuzzy variable parameters have a significant impact on the decision-making process.

3.4.2. Inventory Model under Type 2 Fuzzy with Trade Credit Policy

In a recent study by Debnath et al. [77], they explored an inventory model that utilizes type 2 fuzzy parameters under a trade-credit policy. They employed the generalized Hukuhara derivative approach to solve the model. The main contributions of the study can be summarized in three aspects. Firstly, they discussed the CV-based reduction method suggested by Qin et al. [70] and successfully used it to obtain the total variable cost for the proposed model. Secondly, they presented a type 2 fuzzy number for demand in an economic order quantity model with stock and selling price-dependent demand. The model was solved for the retailer’s lowest cost using the CV-based reduction approach and the α-cut of a pentagonal fuzzy number. Lastly, they looked at type 1 and crisp demand, which are specific cases of type 2 demand, and the outcomes of the current inventory model. The study’s approaches are quite general and can be used to solve type 2 fuzzy parameter decision-making issues in a variety of contexts. However, one limitation of the suggested model is that it only takes into account pentagonal type 2 fuzzy numbers. Despite this, the model can still be useful in launching new products on the market. The study is particularly relevant for retailers in multinational emerging countries. With the use of this information, decision makers are able to make wiser and more accurate decisions.

3.4.3. Multi-Item Inventory Problem under a Type 2 Fuzzy Environment

A type 2 fuzzy optimization technique was invented by Yanan Li [78] and used to solve a multi-item inventory problem. He began by discussing the expected value of type 2 fuzzy variables under typical possibility distributions using mean reduction methods.

The following points are included in the main conclusions:

(i)

The mean reduction methods were used to determine the expected value concerning the reciprocal of type 2 discrete and triangular fuzzy variables after discussing the expected value of the fuzzy variable;

(ii)

He created a multi-item single-period expected profit model, where type 2 fuzzy variations are used to characterize the uncertain demands in the inventory problem.

3.5. Optimization in an Intuitionistic Fuzzy Environment

Intuitionistic fuzzy sets, a generalization of fuzzy sets, were first introduced by Krassimir Atanassov [24] in 1986. Plamen P. Angelov [79] later introduced optimization in an intuitionistic fuzzy environment in 1997. Following this, Nayak and Pal [80,81] described an intuitionistic fuzzy optimization, crisp transformation, and solution procedure based on intuitionistic fuzzy sets. In 2011, Chakrabortty, Pal, and Nayak [82] presented an approach to an inventory model with shortages. The method assumes fuzzy numbers for carrying cost, shortage cost, ordering or setup cost, and demand, making the inventory model more realistic. They converted the fuzzy numbers into interval numbers and used an intuitionistic fuzzy optimization model to give a solution procedure. In 2013, the same authors [83] introduced an intuitionistic fuzzy optimization technique for Pareto’s optimal solution of manufacturing inventory models with shortages. A year later, De, Goswami, and Sana [84] developed a solution procedure for an intuitionistic fuzzy backorder inventory model that considered all the parameters as fuzzy numbers. Later, in 2014, the intuitionistic fuzzy optimization technique in the EOQ model with two types of imperfect quality items by Bhaya, Pal, and Nayak [85] analyzed the EOQ model with scrap and reworkable items and proposed a solution using the intuitionistic fuzzy programming technique. A deterministic single objective economic order quantity (EOQ) model with space constraint in an intuitionistic fuzzy environment was presented by Mondal, Garai, and Roy [86] in 2018. The proposed model offers a novel approach to solving the EOQ problem in an intuitionistic fuzzy environment, where space constraint poses a significant challenge. In 2022, Singh and Kumar [87] proposed an intuitionistic fuzzy inventory model with a waste disposal cost to determine the total inventory cost. In the same year, Sahoo, Acharya, and Patnaik [88] focused on minimizing the total costs by describing a fuzzy model using a generalized pentagonal intuitionistic fuzzy number for per unit holding cost and a ranking generalized pentagonal intuitionistic fuzzy number for de-fuzzification purposes.

4. Conclusions and Future Scope

This comprehensive review has thoroughly examined and compared various fuzzy inventory models, with a particular focus on the efficacy of cloudy fuzzy models in handling uncertainties inherent in real-world scenarios. The study delved extensively into the cloudy fuzzy economic order quantity (EOQ) models, both with and without backorders, and compared them against traditional crisp and fuzzy models. The findings consistently supported the superiority of cloudy fuzzy approaches in providing more accurate, practical, and cost-efficient solutions for inventory management. The models account for uncertainties comprehensively, offering decision makers a more reliable framework. The review also explored extensions into deteriorating items, imperfect quality items, and the integration of learning and trade credit policies within cloudy fuzzy environments. The analysis highlights the significant improvements achieved by these extensions over traditional crisp and fuzzy approaches, thereby emphasizing the relevance and applicability of cloudy fuzzy models in addressing complex real-world inventory management challenges. Furthermore, the review explores other fuzzy models, including dense fuzzy, intuitionistic dense fuzzy, and type 2 fuzzy models and optimization in an intuitionistic fuzzy environment, which show their potential to provide more expressive frameworks to handle uncertainties and vague information. These models can enable more accurate representations of real-world inventory management complexities.

Hence, following an exhaustive analysis, this report highlights the benefits of adopting cloudy fuzzy models for inventory management. Compared to their traditional crisp or fuzzy counterparts, cloudy fuzzy models are more pragmatic, precise, and effective, especially in uncertain situations, and also acknowledge the potential of other fuzzy models.

There are many avenues for further research in fuzzy inventory models. These include refining existing models to improve accuracy and computational efficiency, developing adaptive models, integrating multiple sources of uncertainty, exploring multi-objective optimization, conducting empirical studies, developing systems that learn from historical data, and designing models for risk analysis and mitigation. User-friendly decision support systems that leverage fuzzy inventory models can assist decision makers in understanding complex scenarios. Research in this field can also contribute to sustainable inventory management practices and expand the scope of research in healthcare, service industries, and emerging technologies. However, it is important to note that our search was limited to papers available through the Web of Science and only considered journal articles and books; thus, the current comparison between fuzzy models and traditional models appears to have limitations in terms of depth. A more comprehensive comparative analysis would be advisable to provide greater clarity in the review. This would help to clearly outline the specific advantages and limitations of fuzzy models when compared to certain traditional models, providing a more complete picture of the strengths and weaknesses of both types of models. Such an analysis could be of value to a wider audience and contribute to a better understanding of this area of study.