Multidimensional Diffusion-Wave-Type Solutions to the Second-Order Evolutionary Equation
Abstract
:1. Introduction
2. Formulation
3. Heat-Wave-Type Solutions
3.1. Polynomial in Powers of
3.2. Series in Powers of t
3.3. Series in Powers of
- 1.
- If , there is a trivial solution .
- 2.
- If , there is a non-trivial solution having the Taylor series form.
4. Separation of Variables
- 1.
- If , there is a trivial solution .
- 2.
- If , there is a non-trivial solution in the Maclaurin series form.
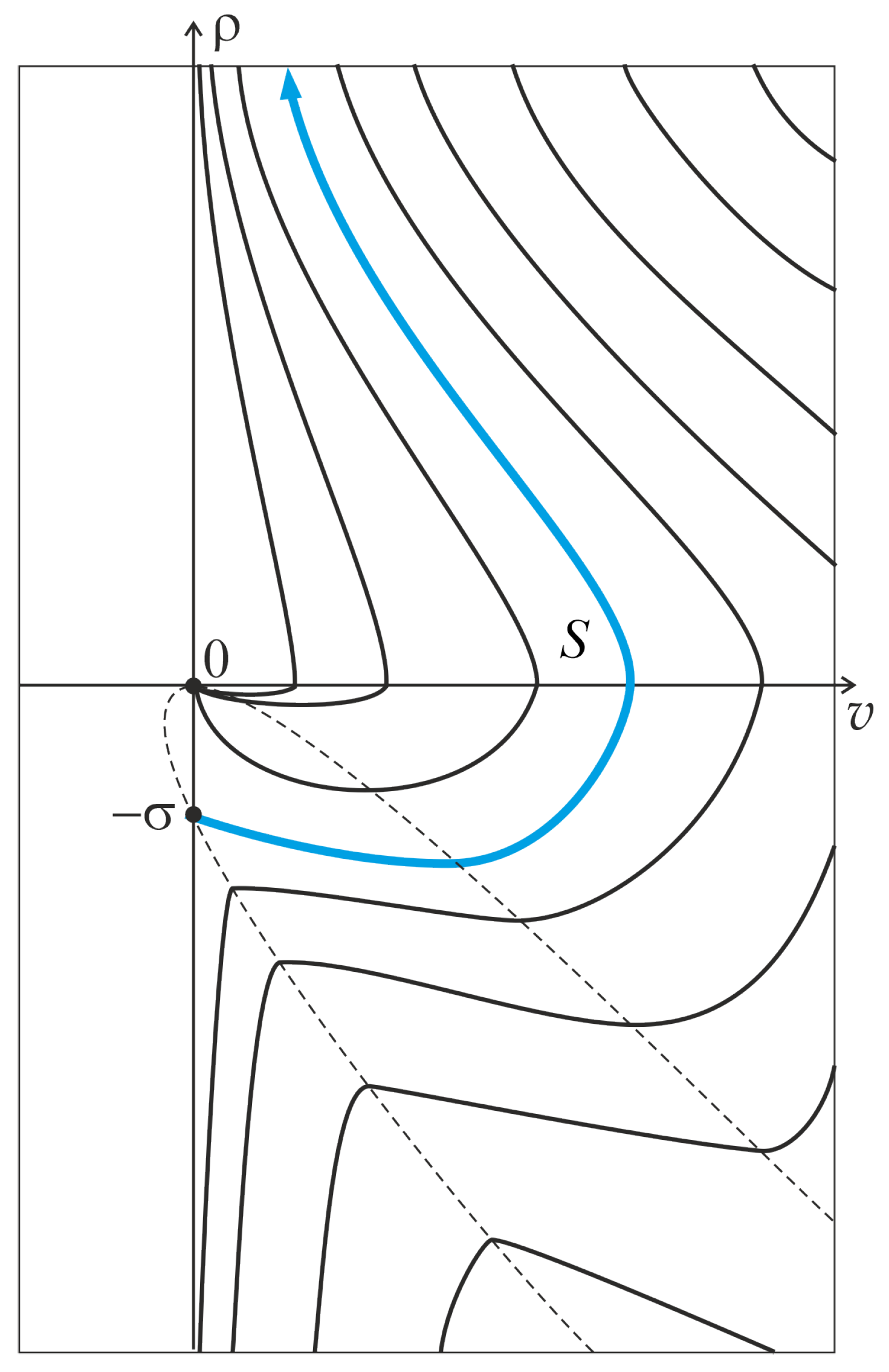
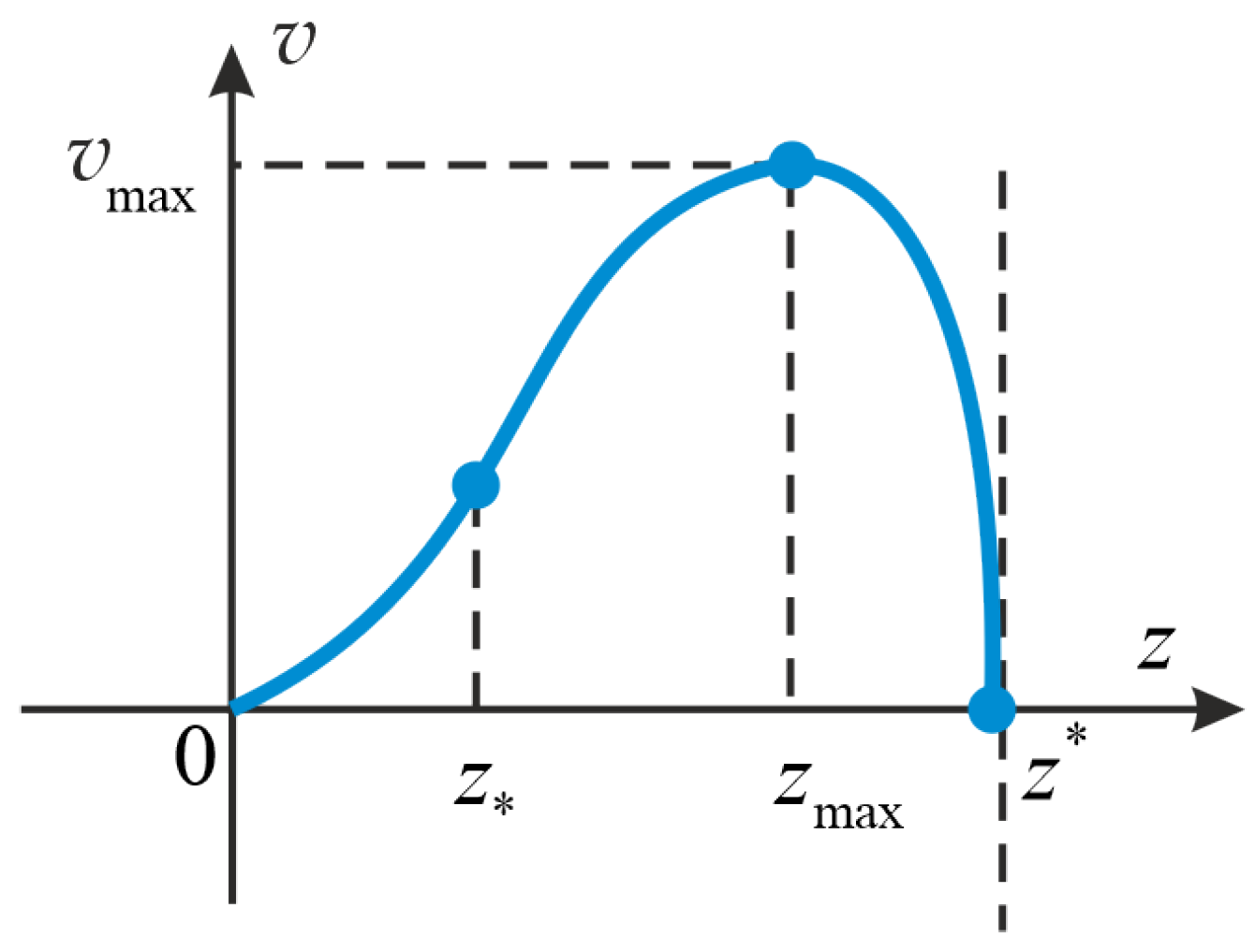
5. Qualitative Analysis
5.1. Analysis of Singular Points
5.2. Phase Portrait
6. Existence and Uniqueness Theorem
- 1.
- , are analytical functions in some neighborhood of the point and , , , .
- 2.
- , are analytical functions in some neighborhood of the point and , .
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Friedman, A. Partial Differential Equations of Parabolic Type; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Vazquez, J. The Porous Medium Equation: Mathematical Theory; Clarendon Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Samarskii, A.; Galaktionov, V.; Kurdyumov, S.; Mikhailov, A. Blow-Up in Quasilinear Parabolic Equations; Walter de Gruyte: Berlin, Germany, 1995. [Google Scholar] [CrossRef]
- Ladyzenskaja, O.; Solonnikov, V.; Ural’ceva, N. Linear and Quasi-Linear Equations of Parabolic Type. Translations of Mathematical Monographs, Vol. 23; American Mathematical Society: Providence, RI, USA, 1988. [Google Scholar]
- Grindrod, P. Patterns and Waves: Theory and Applications of Reaction-Diffusion Equations; Oxford Applied Mathematics and Computing Science Series; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Boussinesq, J. Essai sur la Theorie des Eaux Courantes; Imprimerie Nationale: Paris, France, 1877. [Google Scholar]
- Evans, L. Partial Differential Equations; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics. Vol. II: Partial Differential Equations; Interscience Publishers, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Andreev, V.K.; Gaponenko, Y.A.; Goncharova, O.N.; Pukhnachev, V.V. Mathematical Models of Convection; Walter de Gruyte: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Murray, J. Mathematical Biology: I. An Introduction, 3rd ed.; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2002; Volume 17. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Dover Publications: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Barenblatt, G.; Entov, V.; Ryzhik, V. Theory of Fluid Flows Through Natural Rocks; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- DiBenedetto, E. Degenerate Parabolic Equations; Springer: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Chetverushkin, B.; Olkhovskaya, O.; Gasilov, V. An explicit difference scheme for non-linear heat conduction equation. Mat. Model. 2022, 34, 3–19. [Google Scholar] [CrossRef]
- Cassol, G.O.; Dubljevic, S. Hyperbolicity of the heat equation. IFAC-PapersOnLine 2019, 52, 63–67. [Google Scholar] [CrossRef]
- Sidorov, A.F. Analytic representations of solutions of nonlinear parabolic equations of time-dependent filtration type. Sov. Math. Dokl. 1985, 31, 40–44. [Google Scholar]
- Filimonov, M.Y.; Korzunin, L.G.; Sidorov, A.F. Approximate Methods for Solving Nonlinear Initial Boundary-Value Problems Based on Special Constructions of Series. Russ. J. Numer. Anal. Math. Model. 1993, 8, 101–126. [Google Scholar] [CrossRef]
- Filimonov, M.Y. Representation of solutions of boundary value problems for nonlinear evolution equations by special series with recurrently calculated coefficients. J. Phys. Conf. Ser. 2019, 1268, 012071. [Google Scholar] [CrossRef]
- Rubina, L.I.; Ul’yanov, O.N. On some method for solving a nonlinear heat equation. Sib. Math. J. 2012, 53, 872–881. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Separation of Variables and Exact Solutions to Nonlinear PDEs; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Chmykhov, M.A. Approximate solutions to one-dimensional nonlinear heat conduction problems with a given flux. Comput. Math. Math. Phys. 2007, 47, 107–117. [Google Scholar] [CrossRef]
- Kudryashov, N.; Zakharchenko, A. A note on solutions of the generalized Fisher equation. Appl. Math. Lett. 2014, 32, 53–56. [Google Scholar] [CrossRef]
- Kudryashov, N.; Zakharchenko, A. Painlevé analysis and exact solutions of a predator–prey system with diffusion. Math. Methods Appl. Sci. 2015, 38, 1418–1427. [Google Scholar] [CrossRef]
- Sinelshchikov, D.I.; Kudryashov, N.A. Integrable Nonautonomous Lienard-Type Equations. Theor. Math. Phys. 2018, 196, 1230–1240. [Google Scholar] [CrossRef]
- Galaktionov, V.A.; Shishkov, A.E. Self-similar boundary blow-up for higher-order quasilinear parabolic equations. Proc. R. Soc. Edinb. Sect. A Math. 2005, 135, 1195–1227. [Google Scholar] [CrossRef]
- Stepanova, E.V.; Shishkov, A.E. Initial evolution of supports of solutions of quasilinear parabolic equations with degenerate absorption potential. Mat. Sb. 2013, 204, 79–106. [Google Scholar] [CrossRef]
- Shishkov, A.E.; Yevgenieva, Y.A. Localized Blow-Up Regimes for Quasilinear Doubly Degenerate Parabolic Equations. Math. Notes 2019, 106, 639–650. [Google Scholar] [CrossRef]
- Bui, D.; Nguyen, H.; Qin, X.; Wang, Y. On maximal solution to a degenerate parabolic equation involving in time fractional derivative. Electron. J. Appl. Math. 2023, 1, 62–80. [Google Scholar] [CrossRef]
- Gurefe, Y.; Le, D.L.; Kumar, D. Regularization of nonlocal pseudo-parabolic equation with random noise. Electron. J. Appl. Math. 2023, 1, 40–61. [Google Scholar] [CrossRef]
- Antontsev, S.; Shmarev, S. Evolution PDEs with Nonstandard Growth Conditions. Existence, Uniqueness, Localization, Blow-Up; Atlantis Press: Paris, France, 2015. [Google Scholar] [CrossRef]
- Antontsev, S.; Shmarev, S. Global Estimates for Solutions of Singular Parabolic and Elliptic Equations with Variable Nonlinearity. Nonlinear Anal.-Theory Methods Appl. 2020, 195, 111724. [Google Scholar] [CrossRef]
- Feo, F.; Vázquez, J.L.; Volzone, B. Anisotropic p-Laplacian Evolution of Fast Diffusion Type. Adv. Nonlinear Stud. 2021, 21, 523–555. [Google Scholar] [CrossRef]
- Feo, F.; Vázquez, J.L.; Volzone, B. Anisotropic fast diffusion equations. Nonlinear Anal. 2023, 233, 113298. [Google Scholar] [CrossRef]
- Vazquez, J.L. Asymptotic behaviour for the porous medium equation posed in the whole space. J. Evol. Equ. 2003, 3, 67–118. [Google Scholar] [CrossRef]
- Carrillo, J.A.; Gomez-Castro, D.; Vazquez, J.L. Infinite-time concentration in aggregation–diffusion equations with a given potential. J. Math. Pures Appl. 2022, 157, 346–398. [Google Scholar] [CrossRef]
- Kazakov, A. Solutions to Nonlinear Evolutionary Parabolic Equations of the Diffusion Wave Type. Symmetry 2021, 13, 871. [Google Scholar] [CrossRef]
- Kazakov, A.; Lempert, A. Diffusion-Wave Type Solutions to the Second-Order Evolutionary Equation with Power Nonlinearities. Mathematics 2022, 10, 232. [Google Scholar] [CrossRef]
- Kazakov, A.L. On exact solutions to a heat wave propagation boundary-value problem for a nonlinear heat equation. Sib. Electron. Math. Rep. 2019, 16, 1057–1068. [Google Scholar] [CrossRef]
- Kazakov, A.; Spevak, L. Constructing Exact and Approximate Diffusion Wave Solutions for a Quasilinear Parabolic Equation with Power Nonlinearities. Mathematics 2022, 10, 1559. [Google Scholar] [CrossRef]
- Kazakov, A.L.; Nefedova, O.A.; Spevak, L.F. Solution of the Problem of Initiating the Heat Wave for a Nonlinear Heat Conduction Equation Using the Boundary Element Method. Comput. Math. Math. Phys. 2019, 59, 1015–1029. [Google Scholar] [CrossRef]
- Kozlov, V.V. Sofya Kovalevskaya: A mathematician and a person. Russ. Math. Surv. 2000, 55, 1175–1192. [Google Scholar] [CrossRef]
- Andronov, A.A.; Leontovich, E.A.; Gordon, I.I.; Maier, A.G. Qualitative Theory of Second-Order Dynamic Systems; Israel Program for Scientific Translations; Halstead Press: Jerusalem, Israel, 1973. [Google Scholar]
- El-Mikkawy, M.E. On the inverse of a general tridiagonal matrix. Appl. Math. Comput. 2004, 150, 669–679. [Google Scholar] [CrossRef]
- Kazakov, A.; Lempert, A. Existence and Uniqueness of the Solution of the Boundary-Value Problem for a Parabolic Equation of Unsteady Filtration. J. Appl. Mech. Tech. Phys. 2013, 54, 251–258. [Google Scholar] [CrossRef]
- Kazakov, A.L.; Kuznetsov, P.A. On the Analytic Solutions of a Special Boundary Value Problem for a Nonlinear Heat Equation in Polar Coordinates. J. Appl. Ind. Math. 2018, 812, 227–235. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazakov, A.; Lempert, A. Multidimensional Diffusion-Wave-Type Solutions to the Second-Order Evolutionary Equation. Mathematics 2024, 12, 354. https://doi.org/10.3390/math12020354
Kazakov A, Lempert A. Multidimensional Diffusion-Wave-Type Solutions to the Second-Order Evolutionary Equation. Mathematics. 2024; 12(2):354. https://doi.org/10.3390/math12020354
Chicago/Turabian StyleKazakov, Alexander, and Anna Lempert. 2024. "Multidimensional Diffusion-Wave-Type Solutions to the Second-Order Evolutionary Equation" Mathematics 12, no. 2: 354. https://doi.org/10.3390/math12020354





