Stability and Synchronization of Delayed Quaternion-Valued Neural Networks under Multi-Disturbances
Abstract
:1. Introduction
- (1)
- Considering the existing uncertain QVNNs, studies [8,14,27,56] only considered impulsive disturbances, and the researchers of [12,57] only investigated stochastic disturbances. Furthermore, the stochastic disturbance introduced in the QVNNs in [12] does not exert any influence on connecting neurons.
- (2)
- Decomposition is a common method when dealing with multivalued NNs. Studies [7,9,10,11,13,14,19,20,21,23,24,25,26,27] decomposed QVNNs and proposed relevant criteria to ensure system stability or synchronization. However, decomposable quaternion activation functions are rare, and the assumptions associated with decomposable activation functions are strict.
- (3)
- The scalar Lyapunov function method is the most commonly used method for investigating the stability and synchronization of NNs [6,7,8,10,11,13,14,15,16,17,18,19,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,57]. Compared with vector Lyapunov functions, scalar Lyapunov functions are difficult to construct using this method.
- (4)
- The synchronization analysis of chaotic NNs based on the concept of the drive-response system is equivalent to the stability problem of a synchronization error system. Only a few studies have simultaneously investigated the stability and synchronization of QVNNs.
- (5)
- (1)
- We will consider both impulsive and stochastic disturbances in mixed-delay QVNNs and examine the interaction of connected neurons after introducing stochastic disturbances.
- (2)
- The non-decomposition method, which retains the coupling characteristics of each part of the quaternion, is used to conduct the research.
- (3)
- To avoid the difficulty of constructing the scalar Lyapunov functions, this study combines the vector Lyapunov function method with mathematical induction and differential integration theory and proposes sufficient criteria to ensure the mean-squared exponential stability of the equilibria of the system.
- (4)
- For a type of chaotic QVNNs with mixed delays as well as impulsive and stochastic disturbances, judgment conditions for ensuring the mean-square exponential synchronization of the drive-response system with a linear feedback controller are obtained using the established mean-square exponential stability conditions.
- (5)
- In this study, the correctness and feasibility of the stability and synchronization criteria are demonstrated in examples 1 and 2, respectively. Furthermore, the applicability of the criterion for realizing image associative memory is validated via example 3.
2. Model Description and Preliminaries
- where:
3. Main Results of Stability
4. Main Results of Synchronization
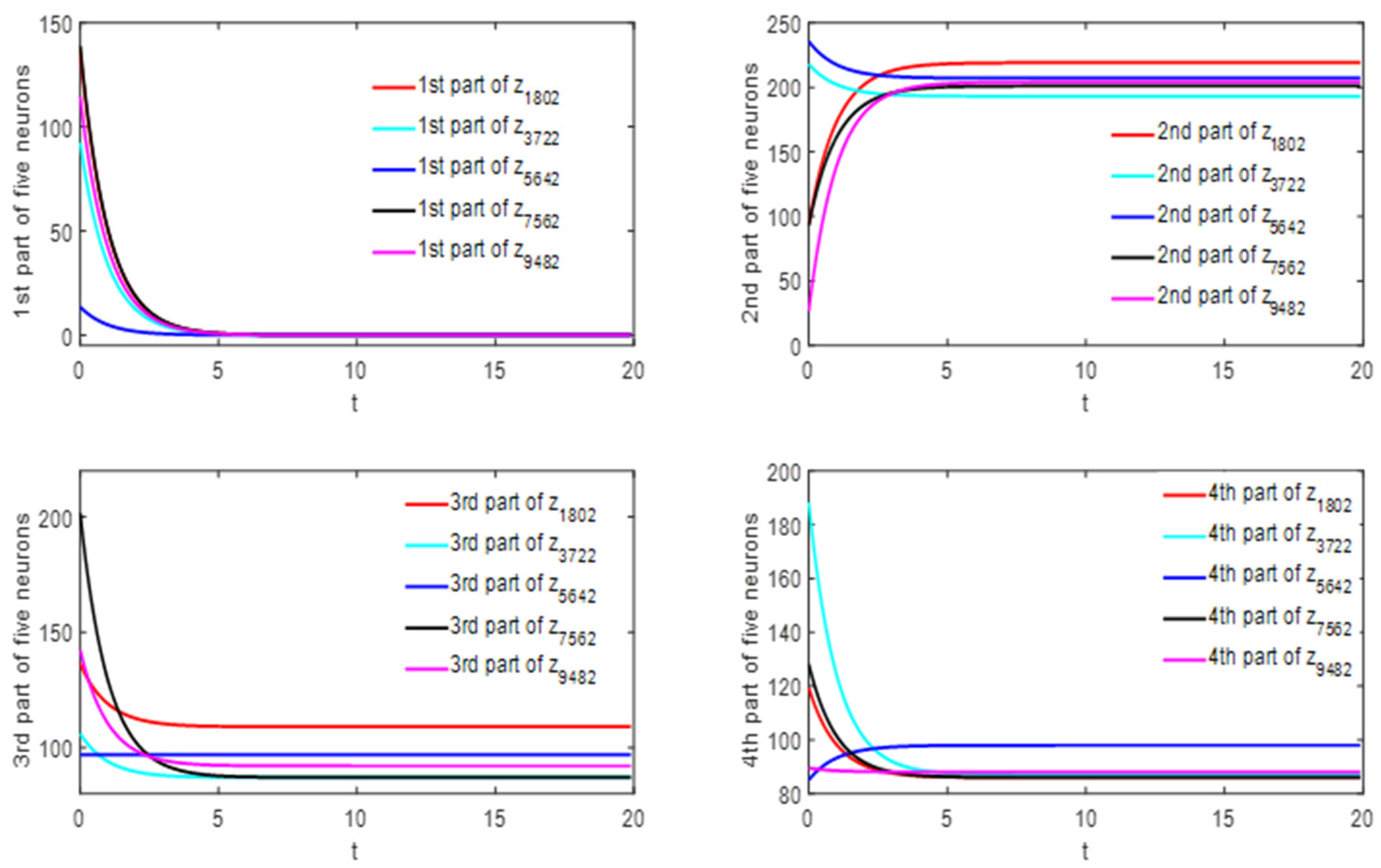
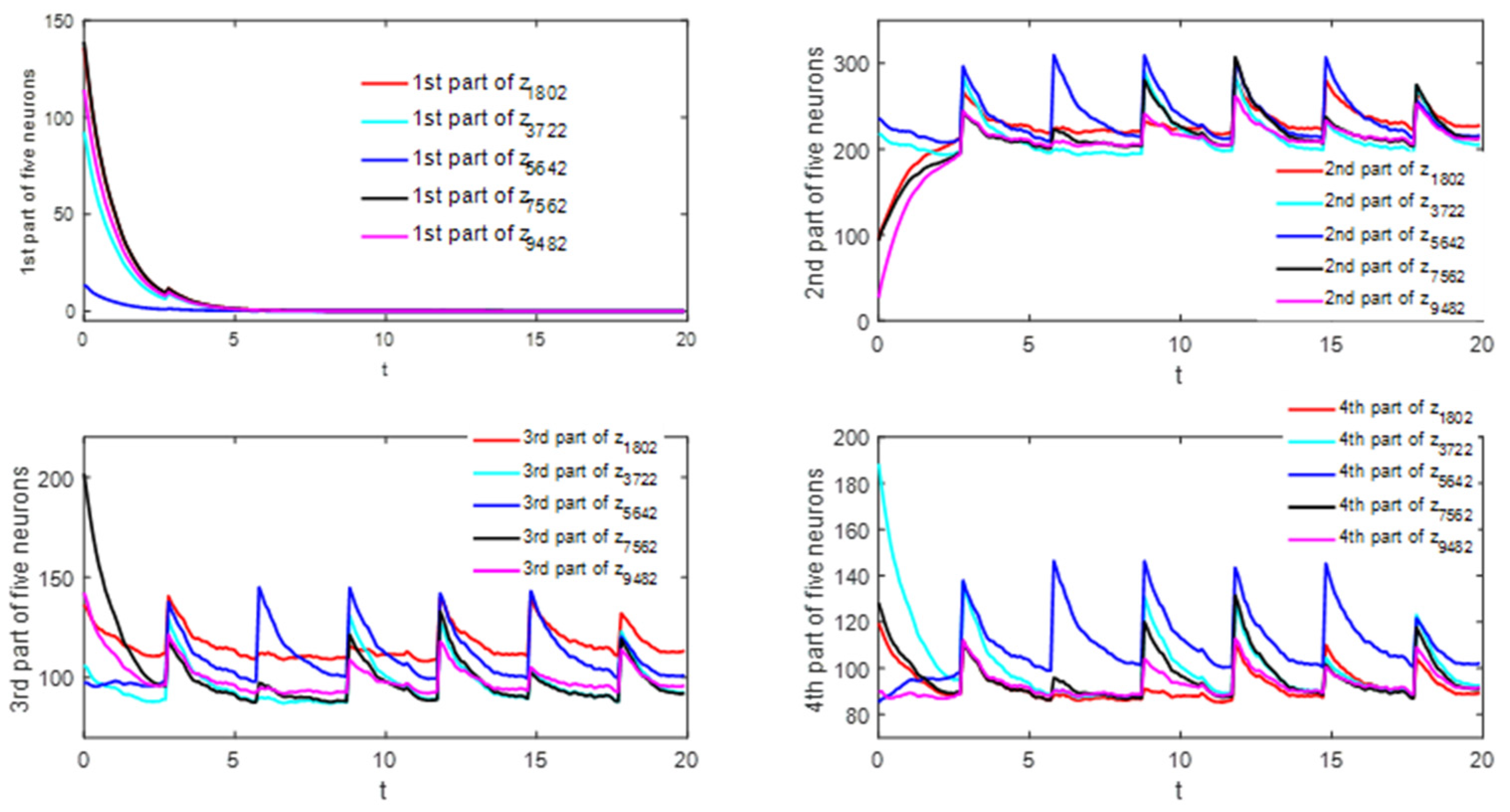
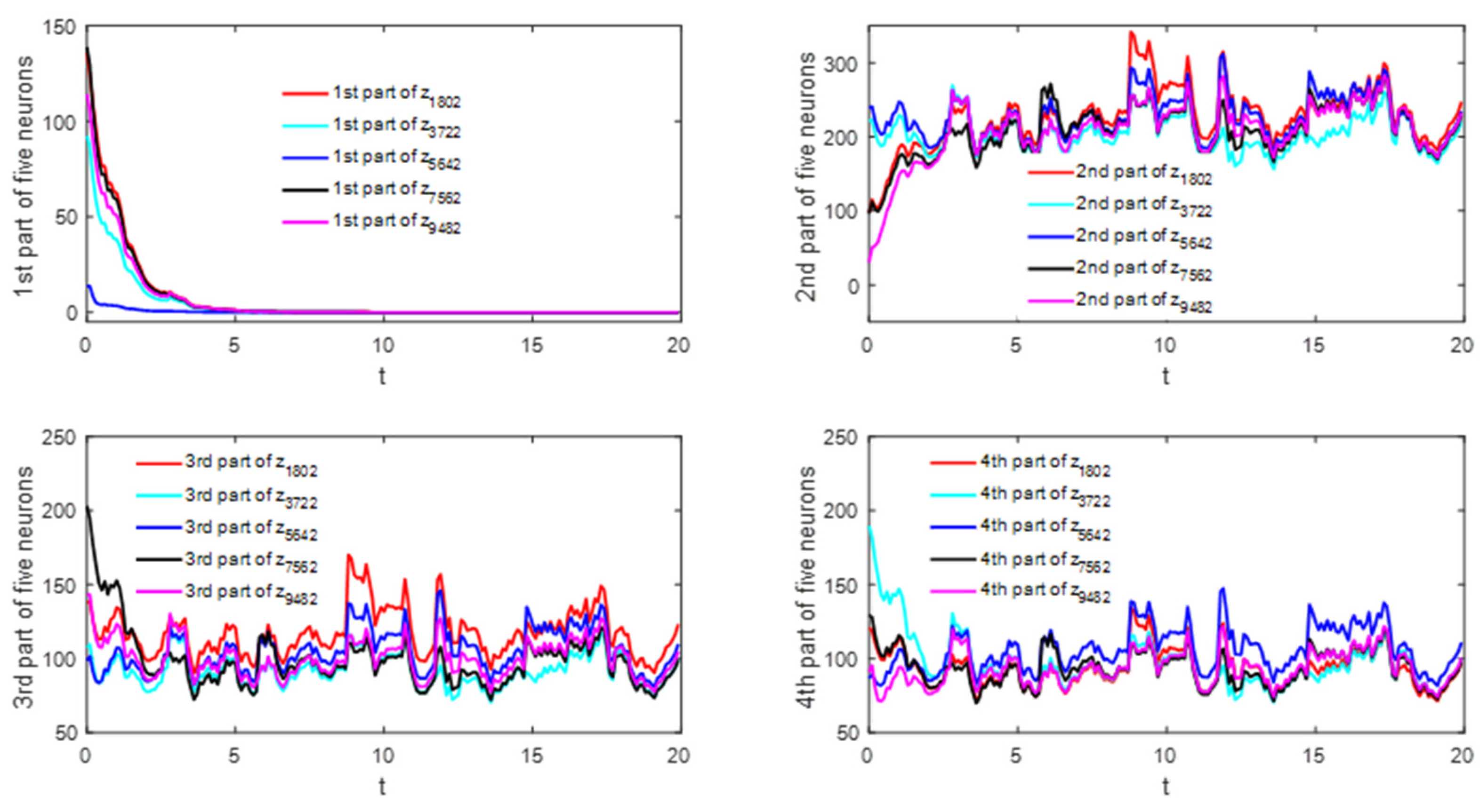
5. Examples
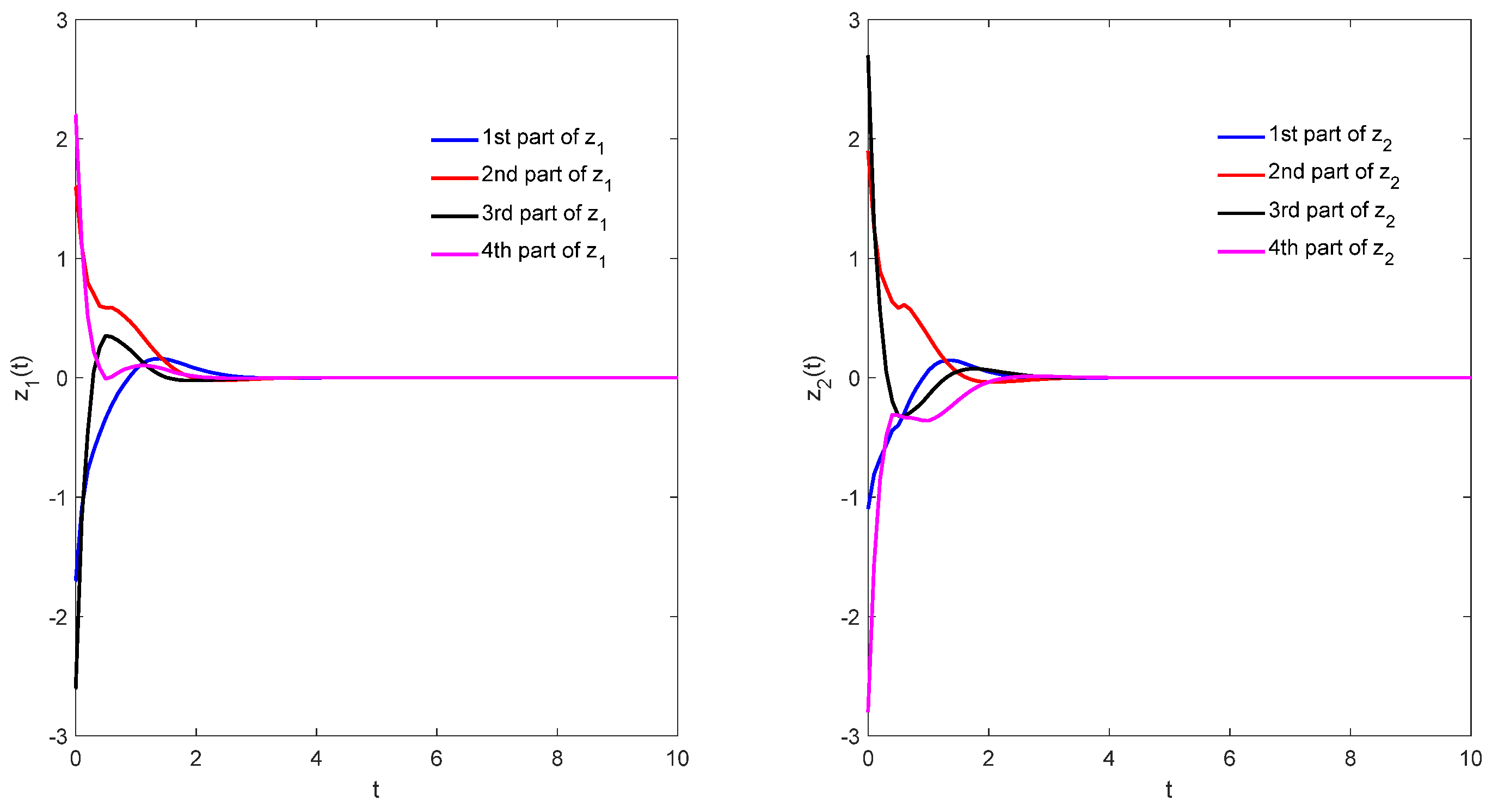
5.1. Example 1
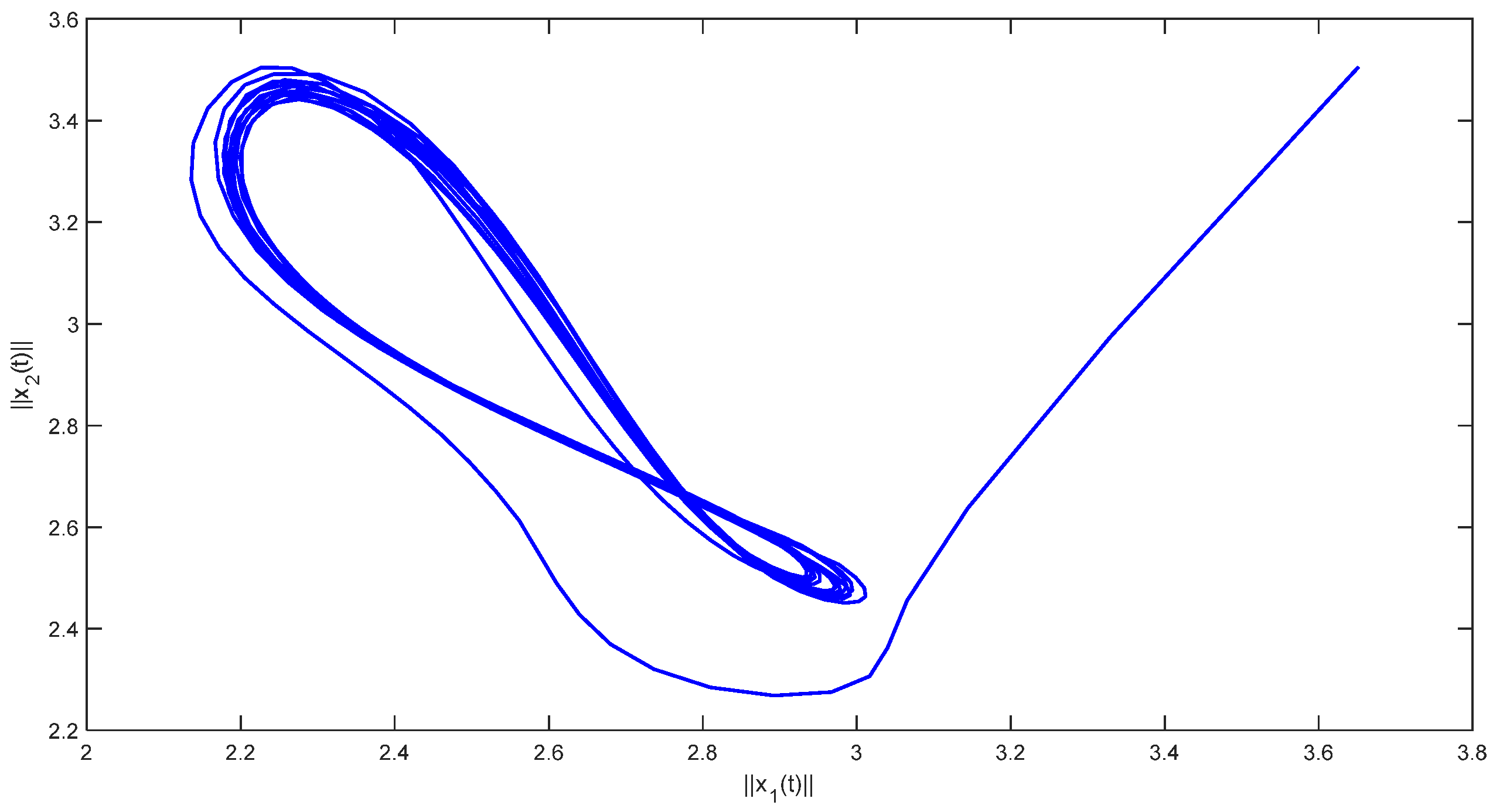
5.2. Example 2
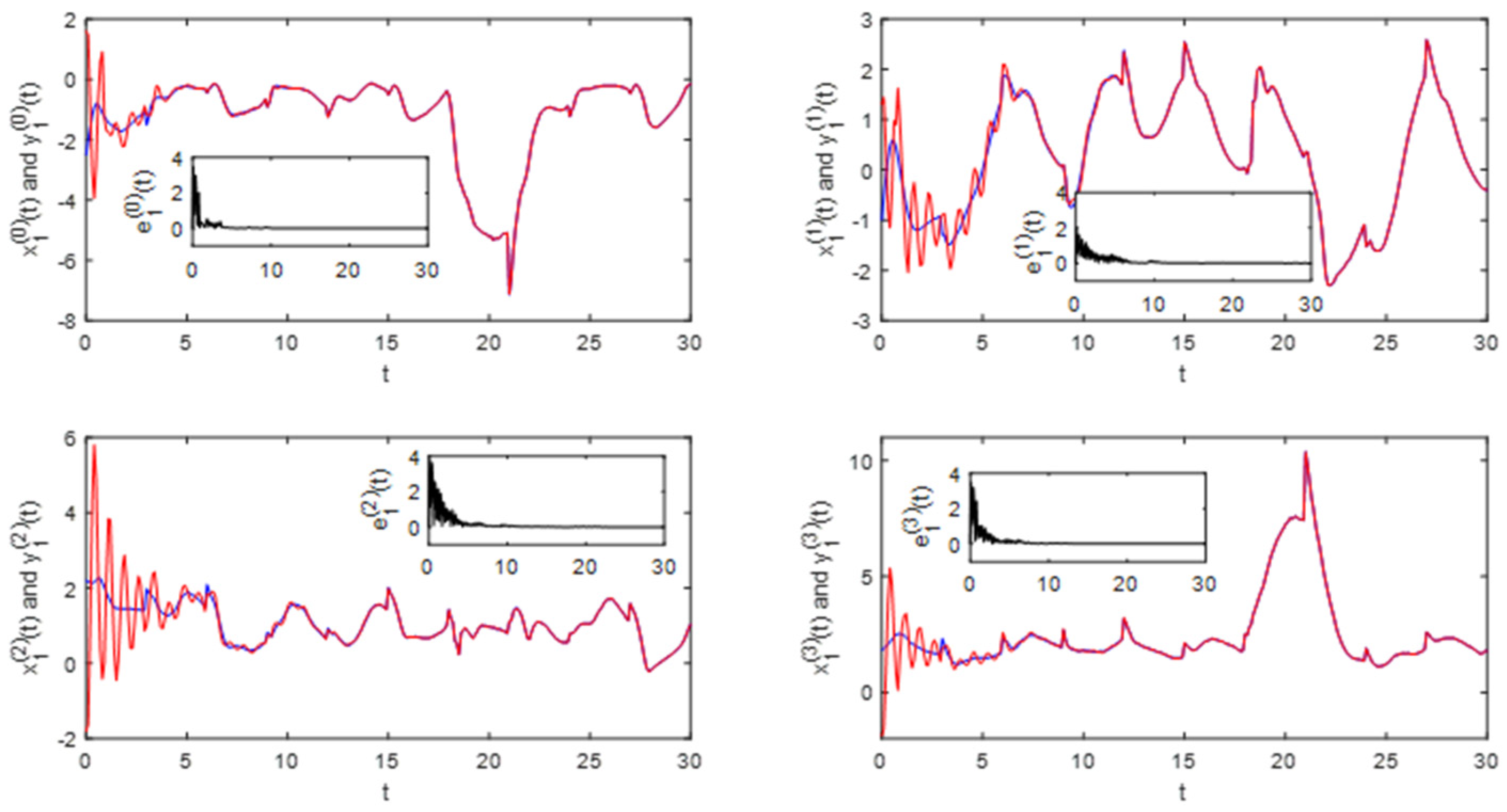
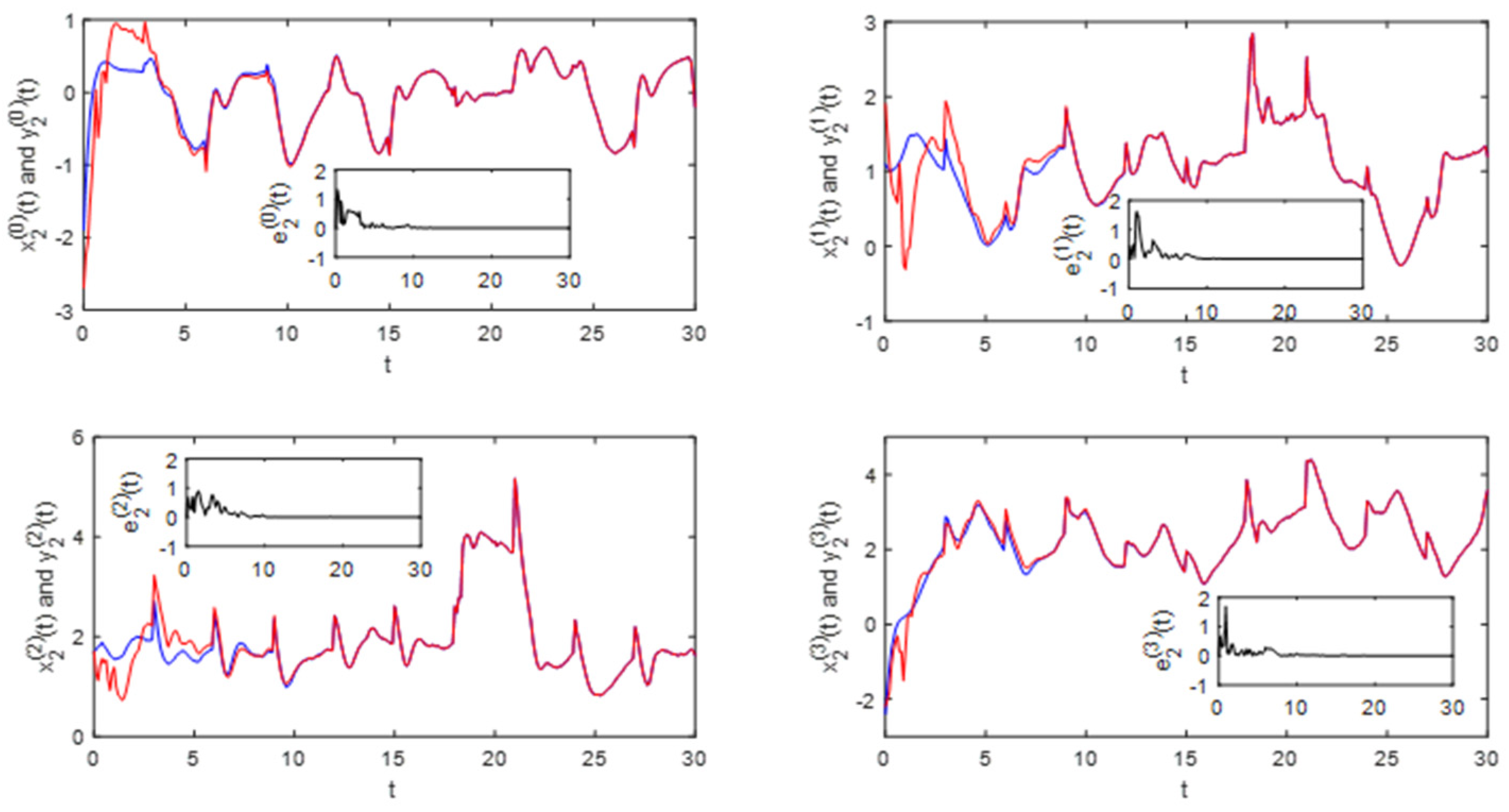
5.3. Example 3
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Isokawa, T.; Kusakabe, T.; Matsui, N.; Peper, F. Quaternion neural network and its application. In Proceedings of the Knowledge-Based Intelligent Information and Engineering Systems, 7th International Conference, Berlin, Germany, 3 September 2003. [Google Scholar]
- Chen, X.F.; Song, Q.K.; Li, Z.S. Design and analysis of quaternion-valued neural networks for associative memories. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2305–2314. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, Z.J.; Wang, Y.C.; Wang, W. Quaternion-based adaptive trajectory tracking control of a rotormissile with unknown parameters identification. Def. Technol. 2024, 31, 375–386. [Google Scholar] [CrossRef]
- Xian, B.; Diao, C.; Zhao, B.; Zhang, Y. Nonlinear robust output feedback tracking control of a quadrotor UAV using quaternion representation. Nonlinear Dyn. 2015, 79, 2735–2752. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, X.; Wei, J.W.; Xie, N.; Shao, J.; Yang, Y. Quaternion representation learning for cross-modal matching. Knowl.-Based Syst. 2023, 270, 110505. [Google Scholar] [CrossRef]
- Yan, H.Y.; Qiao, Y.H.; Duan, L.J.; Miao, J. New inequalities to finite-time synchronization analysis of delayed fractional-order quaternion-valued neural networks. Neural Comput. Appl. 2022, 34, 9919–9930. [Google Scholar] [CrossRef]
- Aouiti, C.; Bessifi, M. Periodically intermittent control for finite-time synchronization of delayed quaternion-valued neural networks. Neural Comput. Appl. 2021, 33, 6527–6547. [Google Scholar] [CrossRef]
- Lin, D.Y.; Chen, X.F.; Yu, G.P.; Li, Z.S.; Xia, Y.N. Global exponential synchronization via nonlinear feedback control for delayed inertial memristor-based quaternion-valued neural networks with impulses. Appl. Math. Comput. 2021, 401, 126093. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.D.; Lu, J.Q. Global exponential stability for quaternion-valued recurrent neural networks with time-varying delays. Nonlinear Dyn. 2017, 87, 553–565. [Google Scholar] [CrossRef]
- Shu, J.L.; Wu, B.W.; Xiong, L.L. Stochastic stability criteria and event-triggered control of delayed Markovian jump quaternion-valued neural networks. Appl. Math. Comput. 2022, 420, 126904. [Google Scholar] [CrossRef]
- Shu, J.L.; Wu, B.W.; Xiong, L.L.; Wu, T.; Zhang, H.Y. Stochastic stabilization of markov jump quaternion-valued neural network using sampled-data control. Appl. Math. Comput. 2021, 400, 126041. [Google Scholar] [CrossRef]
- Song, Q.K.; Zeng, R.T.; Zhao, Z.J.; Liu, Y.R.; Alsaadi, F.E. Mean-square stability of stochastic quaternion-valued neural networks with variable coefficients and neutral delays. Neurocomputing 2022, 471, 130–138. [Google Scholar] [CrossRef]
- Wang, H.M.; Wei, G.L.; Wen, S.P.; Huang, T.W. Impulsive disturbance on stability analysis of delayed quaternion-valued neural networks. Appl. Math. Comput. 2021, 390, 125680. [Google Scholar] [CrossRef]
- Qi, X.N.; Bao, H.B.; Cao, J.D. Synchronization criteria for quaternion-valued coupled neural networks with impulses. Neural Netw. 2020, 128, 150–157. [Google Scholar] [CrossRef]
- Zhang, T.T.; Jian, J.G. Quantized intermittent control tactics for exponential synchronization of quaternion-valued memristive delayed neural networks. ISA Trans. 2021, 126, 288–299. [Google Scholar] [CrossRef]
- Li, R.X.; Cao, J.D.; Xue, C.F.; Manivannan, R. Quasi-stability and quasi-synchronization control of quaternion-valued fractional-order discrete-time memristive neural networks. Appl. Math. Comput. 2021, 395, 125851. [Google Scholar] [CrossRef]
- Zhang, J.S.; Ma, X.L.; Li, Y.K.; Gan, Q.T.; Wang, C.L. Synchronization in fixed/preassigned-time of delayed fully quaternion-valued memristive neural networks via non-separation method. Commun. Nonlinear Sci. Numer. Simul. 2022, 113, 106581. [Google Scholar] [CrossRef]
- Peng, T.; Zhong, J.; Tu, Z.W.; Lu, J.Q.; Lou, J.G. Finite-time synchronization of quaternion-valued neural networks with delays: A switching control method without decomposition. Neural Netw. 2022, 148, 37–47. [Google Scholar] [CrossRef]
- Wei, W.L.; Yu, J.; Wang, L.M.; Hu, C.; Jiang, H.J. Fixed/Preassigned-time synchronization of quaternion-valued neural networks via pure power-law control. Neural Netw. 2022, 146, 341–349. [Google Scholar] [CrossRef]
- Chen, Y.H.; Zhang, X.; Xue, Y. Global exponential synchronization of high-order quaternion hopfield neural networks with unbounded distributed delays and time-varying discrete delays. Math. Comput. Simul. 2022, 193, 173–189. [Google Scholar] [CrossRef]
- Xu, X.H.; Xu, Q.; Yang, J.B.; Xue, H.B.; Xu, Y.H. Further research on exponential stability for quaternion-valued neural networks with mixed delays. Neurocomputing 2020, 400, 186–205. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Yang, Z. Asymptotic stability for quaternion-valued fuzzy BAM neural networks via integral inequality approach. Chaos Soliton Fractals 2023, 169, 113227. [Google Scholar] [CrossRef]
- Xia, Y.N.; Chen, X.F.; Lin, D.Y.; Li, B.; Yang, X.J. Global exponential stability analysis of commutative quaternion-valued neural networks with time delays on time scales. Neural Process. Lett. 2023, 55, 6339–6360. [Google Scholar] [CrossRef]
- Chouhan, S.S.; Das, S.; Singh, S.; Shen, H. Multiple mu-stability analysis of time-varying delayed quaternion-valued neural networks. Math. Methods Appl. Sci. 2023, 46, 9853–9875. [Google Scholar] [CrossRef]
- Yu, S.Y.; Li, H.; Chen, X.F.; Lin, D.Y. Multistability analysis of quaternion-valued neural networks with cosine activation functions. Appl. Math. Comput. 2023, 445, 127849. [Google Scholar] [CrossRef]
- Tan, G.Q.; Wang, Z.S.; Shi, Z. Proportional–integral state estimator for quaternion-valued neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1074–1079. [Google Scholar] [CrossRef]
- Mo, W.J.; Bao, H.B. Finite-time synchronization for fractional-order quaternion-valued coupled neural networks with saturated impulse. Chaos Soliton Fractals 2022, 164, 112714. [Google Scholar] [CrossRef]
- Kiruthika, R.; Krishnasamy, R.; Lakshmanan, S.; Prakash, M.; Manivannan, A. Non-fragile sampled-data control for synchronization of chaotic fractional-order delayed neural networks via LMI approach. Chaos Soliton Fractals 2023, 169, 113252. [Google Scholar] [CrossRef]
- Tao, P.; Wu, Y.Q.; Tu, Z.W.; Alofi, A.S.; Lu, J.Q. Fixed-time and prescribed-time synchronization of quaternion-valued neural networks: A control strategy involving Lyapunov functions. Neural Netw. 2023, 160, 108–121. [Google Scholar]
- Lv, X. A new approach to stability analysis for stochastic hopfield neural networks with time delays. IEEE Trans. Autom. Control 2022, 67, 5278–5288. [Google Scholar] [CrossRef]
- Yang, D.; Li, X.D.; Song, S.J. Design of state-dependent switching laws for stability of switched stochastic neural networks with time-delays. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1808–1819. [Google Scholar] [CrossRef]
- Chen, T.; Peng, S.G.; Hong, Y.H.; Mai, G.Z. Finite-time stability and stabilization of impulsive stochastic delayed neural networks with rous and rons. IEEE Access 2020, 8, 87133–87141. [Google Scholar] [CrossRef]
- Sheng, Y.; Zhang, H.; Zeng, Z.G. Stability and robust stability of stochastic reaction–diffusion neural networks with infinite discrete and distributed delays. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1721–1732. [Google Scholar] [CrossRef]
- Wang, L.M.; Ge, M.F.; Hu, J.H.; Zhang, G.D. Global stability and stabilization for inertial memristive neural networks with unbounded distributed delays. Nonlinear Dyn. 2019, 95, 943–955. [Google Scholar] [CrossRef]
- Tian, Y.F.; Wang, Z.S. Stochastic stability of markovian neural networks with generally hybrid transition rates. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7390–7399. [Google Scholar] [CrossRef]
- Liu, X.Z.; Wu, K.N.; Ding, X.H.; Zhang, W.H. Boundary stabilization of stochastic delayed cohen–grossberg neural networks with diffusion terms. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3227–3237. [Google Scholar] [CrossRef]
- Wei, Y.L.; Park, J.H.; Karimi, H.R.; Tian, Y.C.; Jung, H. Improved stability and stabilization results for stochastic synchronization of continuous-time semi-markovian jump neural networks with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2488–2501. [Google Scholar] [CrossRef]
- Chen, L.J.; Wan, L.Y.; Wei, X.L.; Wang, L.M.; He, H.Q. Adaptive synchronization of reaction diffusion neural networks with infinite distributed delays and stochastic disturbance. IEEE Access 2020, 8, 180411–180421. [Google Scholar] [CrossRef]
- Chen, H.B.; Shi, P.; Lim, C.C. Exponential synchronization for markovian stochastic coupled neural networks of neutral-type via adaptive feedback control. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1618–1632. [Google Scholar] [CrossRef]
- Bao, H.B.; Park, J.H.; Cao, J.D. Exponential synchronization of coupled stochastic memristor-based neural networks with time-varying probabilistic delay coupling and impulsive delay. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 190–201. [Google Scholar] [CrossRef]
- Zhang, X.L.; Li, H.L.; Kao, Y.G.; Zhang, L.; Jiang, H.J. Global mittag-leffler synchronization of discrete-time fractional-order neural networks with time delays. Appl. Math. Comput. 2022, 433, 127417. [Google Scholar] [CrossRef]
- Zhang, H.G.; Wang, J.Y.; Wang, Z.S.; Liang, H.J. Mode-dependent stochastic synchronization for markovian coupled neural networks with time-varying mode-delays. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2621–2634. [Google Scholar] [CrossRef]
- Li, X.F.; Bi, D.J.; Xie, X.; Xie, Y.L. Multi-synchronization of stochastic coupled multi-stable neural networks with time-varying delay by impulsive control. IEEE Access 2019, 7, 15641–15653. [Google Scholar] [CrossRef]
- Pan, L.J.; Song, Q.K.; Cao, J.D.; Ragulskis, M. Pinning impulsive synchronization of stochastic delayed neural networks via uniformly stable function. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4491–4501. [Google Scholar] [CrossRef]
- Wang, Q.J.; Zhao, H.; Liu, A.D.; Li, L.X.; Niu, S.J.; Chen, C. Predefined-time synchronization of stochastic memristor-based bidirectional associative memory neural networks with time-varying delays. IEEE Trans. Cogn. Dev. Syst. 2022, 14, 1584–1593. [Google Scholar] [CrossRef]
- Chen, G.L.; Xia, J.W.; Park, J.H.; Shen, H.; Zhuang, G.M. Sampled-data synchronization of stochastic markovian jump neural networks with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3829–3841. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Z.; Huang, X.; Li, Y.X.; Ma, Q.; Shen, H. Stochastic sampled-data exponential synchronization of markovian jump neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 909–920. [Google Scholar] [CrossRef]
- Cao, Z.R.; Li, C.D.; He, Z.L.; Zhang, X.Y.; You, L. Synchronization of coupled stochastic reaction-diffusion neural networks with multiple weights and delays via pinning impulsive control. IEEE Trans. Netw. Sci. Eng. 2022, 9, 820–833. [Google Scholar] [CrossRef]
- Zhou, W.N.; Zhu, Q.Y.; Shi, P.; Su, H.Y.; Fang, J.A.; Zhou, L.W. Adaptive synchronization for neutral-type neural networks with stochastic perturbation and markovian switching parameters. IEEE Trans. Cybern. 2014, 44, 2848–2860. [Google Scholar] [CrossRef]
- Yuan, J.X.; Zhang, C.; Chen, T. Command filtered adaptive neural network synchronization control of nonlinear stochastic systems with lévy noise via event-triggered mechanism. IEEE Access 2021, 9, 146195–146202. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Xie, H.; Wang, J. Finite-time and fixed-time synchronization of coupled switched neural networks subject to stochastic disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6511–6532. [Google Scholar] [CrossRef]
- Liu, M.J.; Wang, X.R.; Zhang, Z.Y.; Wang, Z. Global synchronization of complex-valued neural networks with stochastic disturbances and time-varying delay. IEEE Access 2019, 7, 182600–182610. [Google Scholar] [CrossRef]
- Liang, T.; Yang, D.G.; Lei, L.; Zhang, W.L.; Pan, J. Preassigned-time bipartite synchronization of complex networks with quantized couplings and stochastic perturbations. Math. Comput. Simul. 2022, 202, 559–570. [Google Scholar] [CrossRef]
- Wang, H.Q.; Ai, Y.D. Adaptive fixed-time control and synchronization for hyperchaotic Lü systems. Appl. Math. Comput. 2022, 433, 127388. [Google Scholar] [CrossRef]
- Hu, Z.P.; Ren, H.R.; Shi, P. Synchronization of complex dynamical networks subject to noisy sampling interval and packet loss. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3216–3226. [Google Scholar] [CrossRef]
- Peng, T.; Lu, J.Q.; Xiong, J.; Tu, Z.W.; Liu, Y.; Lou, J.G. Fixed-time synchronization of quaternion-valued neural networks with impulsive effects: A non-decomposition method. Commun. Nonlinear Sci. Numer. Simul. 2024, 132, 107865. [Google Scholar] [CrossRef]
- Zeng, R.T.; Song, Q.K. Mean-square exponential input-to-state stability for stochastic neutral-type quaternion-valued neural networks via Itô’s formula of quaternion version. Chaos Soliton Fractals 2024, 178, 114341. [Google Scholar] [CrossRef]
- Xu, X.H.; Yang, J.B.; Yang, H.L.; Sun, S.L. Effect of impulses on robust exponential stability of delayed quaternion-valued neural networks. Neural Process. Lett. 2023, 55, 9615–9634. [Google Scholar] [CrossRef]
- Oksendal, B. Stochastic differential equations—An introduction with applications plications applications. In Springer Science & Business Media; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Song, Q.K.; Yu, Q.Q.; Zhao, Z.J.; Liu, Y.R.; Alsaadi, F.E. Dynamics of complex-valued neural networks with variable coefficients and proportional delays. Neurocomputing 2018, 275, 2762–2768. [Google Scholar] [CrossRef]
- Jia, S.F.; Chen, Y.H. Discrete analogue of impulsive recurrent neural networks with both discrete and finite distributive asynchronous time-varying delays. Cogn. Neurodynamics 2022, 16, 733–744. [Google Scholar] [CrossRef] [PubMed]
- Cai, T.; Cheng, P.; Yao, F.Q.; Hua, M.G. Robust exponential stability of discrete-time uncertain impulsive stochastic neural networks with delayed impulses. Neural Netw. 2023, 160, 227–237. [Google Scholar] [CrossRef]




| Notations | Means | Notations | Means |
|---|---|---|---|
| real number domain | |||
| complex number domain | |||
| skew field of quaternions | |||
| natural number set | conjugate of defined as | ||
| set defined as | modulus of vector defined as | ||
| transpose of a vector or matrix | norm of defined as | ||
| imaginary unit | modulus of the matrix defined as | ||
| expectation function | complete probability space | ||
| Types of Assumption | Decomposition Method | Non-Decomposition Method |
|---|---|---|
| Lipschitz condition | 9, 11, 13, 14, 19–21, 26 | 8, 12, 15–18, 22 |
| Boundedness | 10, 24 | none |
| Three Cases | PSNR Value (dB) at Different Times (s) | |||||
|---|---|---|---|---|---|---|
| t = 0 | t = 1 | t = 3 | t = 5 | t = 10 | t = 20 | |
| case 0 (only impulsive disturbances) | 8.662 | 17.348 | 34.720 | 52.091 | 95.521 | 182.380 |
| case 1 (weak stochastic disturbances) | 8.662 | 17.266 | 16.880 | 31.904 | 24.492 | 31.141 |
| case 2 (strong stochastic disturbances) | 8.662 | 16.302 | 15.969 | 21.953 | 20.914 | 21.573 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Xu, X.; Xu, Q.; Yang, H.; Yu, M. Stability and Synchronization of Delayed Quaternion-Valued Neural Networks under Multi-Disturbances. Mathematics 2024, 12, 917. https://doi.org/10.3390/math12060917
Yang J, Xu X, Xu Q, Yang H, Yu M. Stability and Synchronization of Delayed Quaternion-Valued Neural Networks under Multi-Disturbances. Mathematics. 2024; 12(6):917. https://doi.org/10.3390/math12060917
Chicago/Turabian StyleYang, Jibin, Xiaohui Xu, Quan Xu, Haolin Yang, and Mengge Yu. 2024. "Stability and Synchronization of Delayed Quaternion-Valued Neural Networks under Multi-Disturbances" Mathematics 12, no. 6: 917. https://doi.org/10.3390/math12060917




