Real-Time EtherCAT-Based Control Architecture for Electro-Hydraulic Humanoid
Abstract
:1. Introduction
2. Previous Works
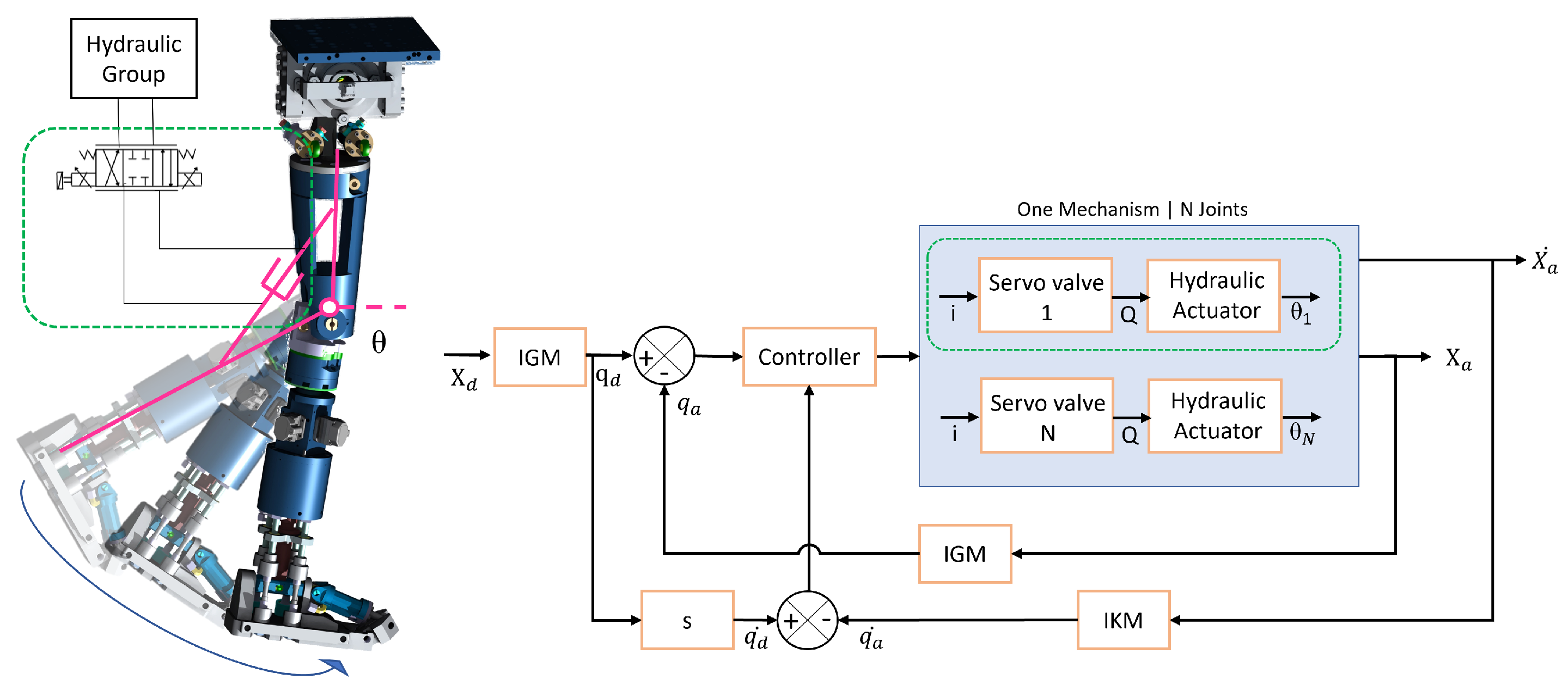
3. HYDROïD’s Mechatronics Overview
4. Control Architecture Development Methodology
4.1. Kinematic and Inverse Geometric Model of Hybrid Mechanism
4.1.1. Inverse Geometric Model
- The jth closed kinematic chain is designated as a chain for j = 1, 2, 3, 4. The mechanism outputs are grouped into a vector q = (, , ).
- The linear joint positions are the mechanism inputs and are named for j = 1, 2, 3, 4.
- The rotation of the ith joint in the jth closed loop is represented by .
- All the joints are passive joints except for and are the active joint variables.
4.1.2. Inverse Kinematic Model
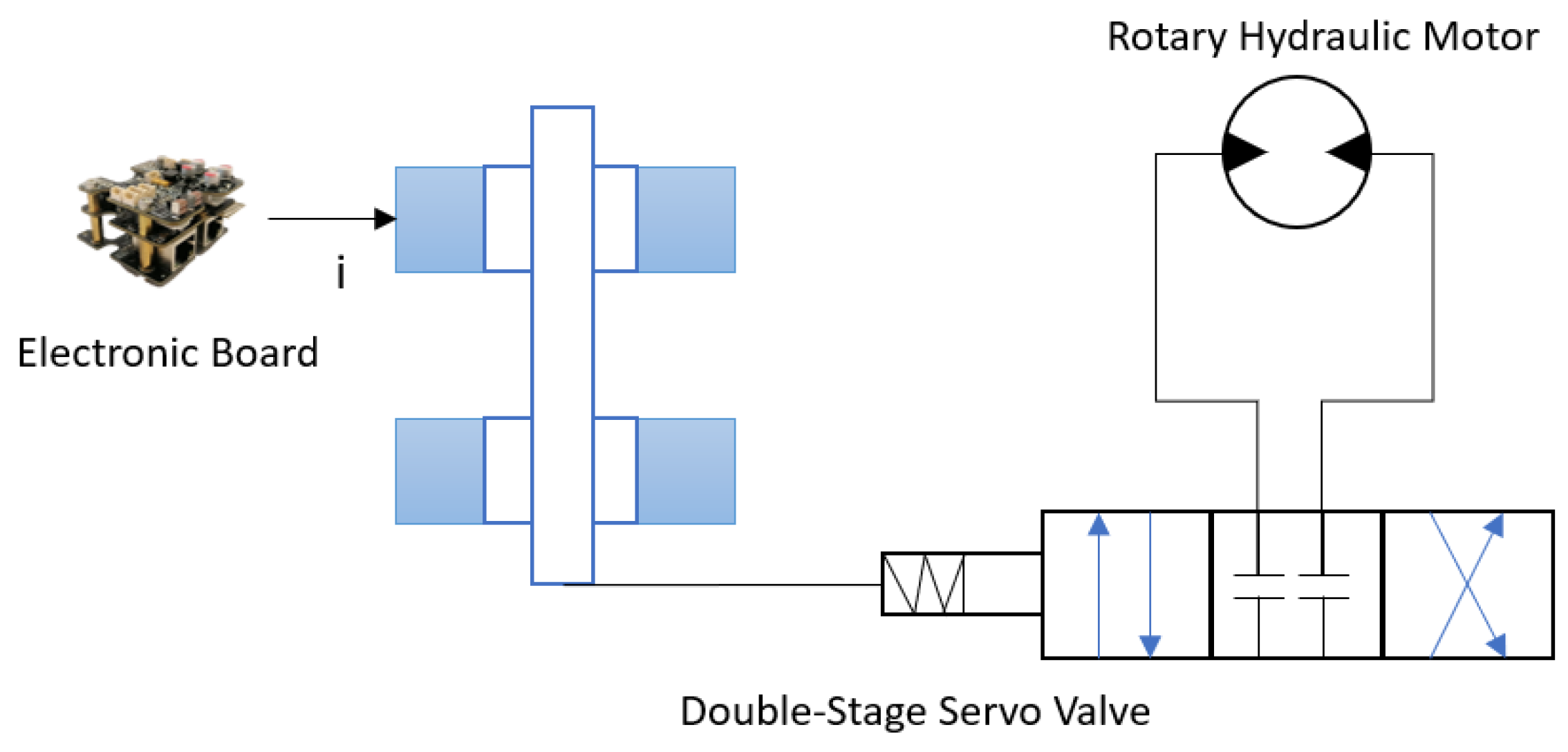
4.2. Modeling and Simulation of Electro-Hydraulic Actuator
4.3. Computational Cost Estimations
5. Proposed Real-Time Control Architecture
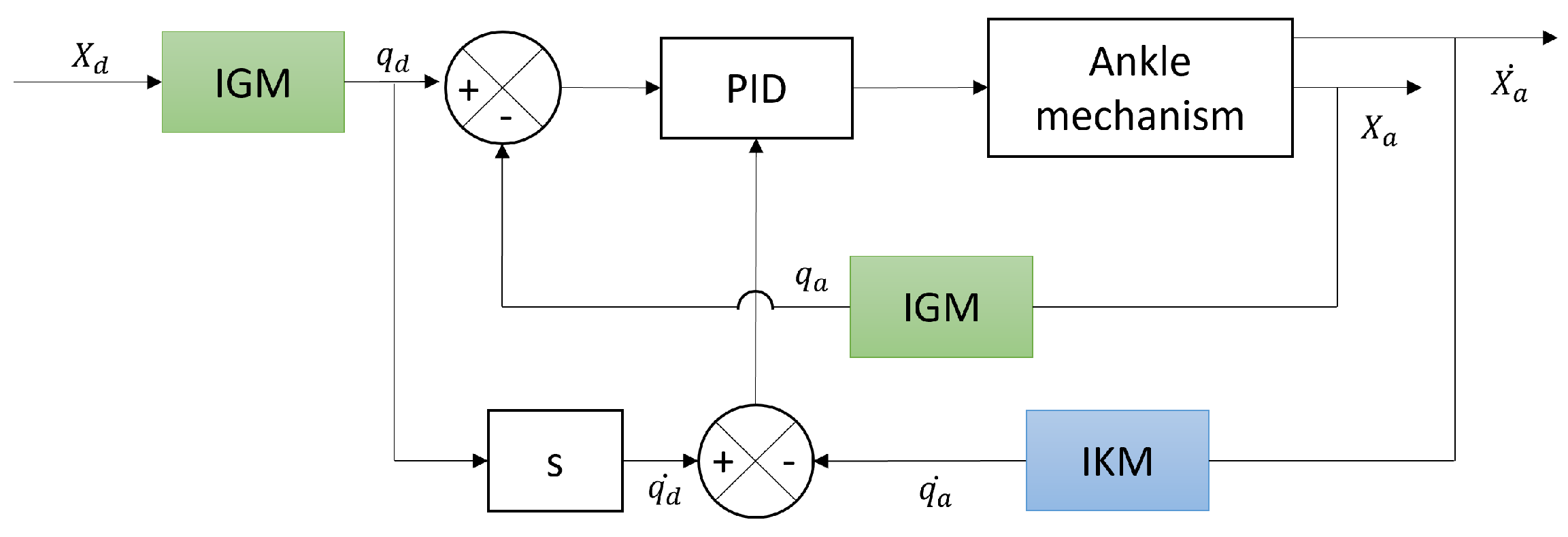
5.1. Joint Controller
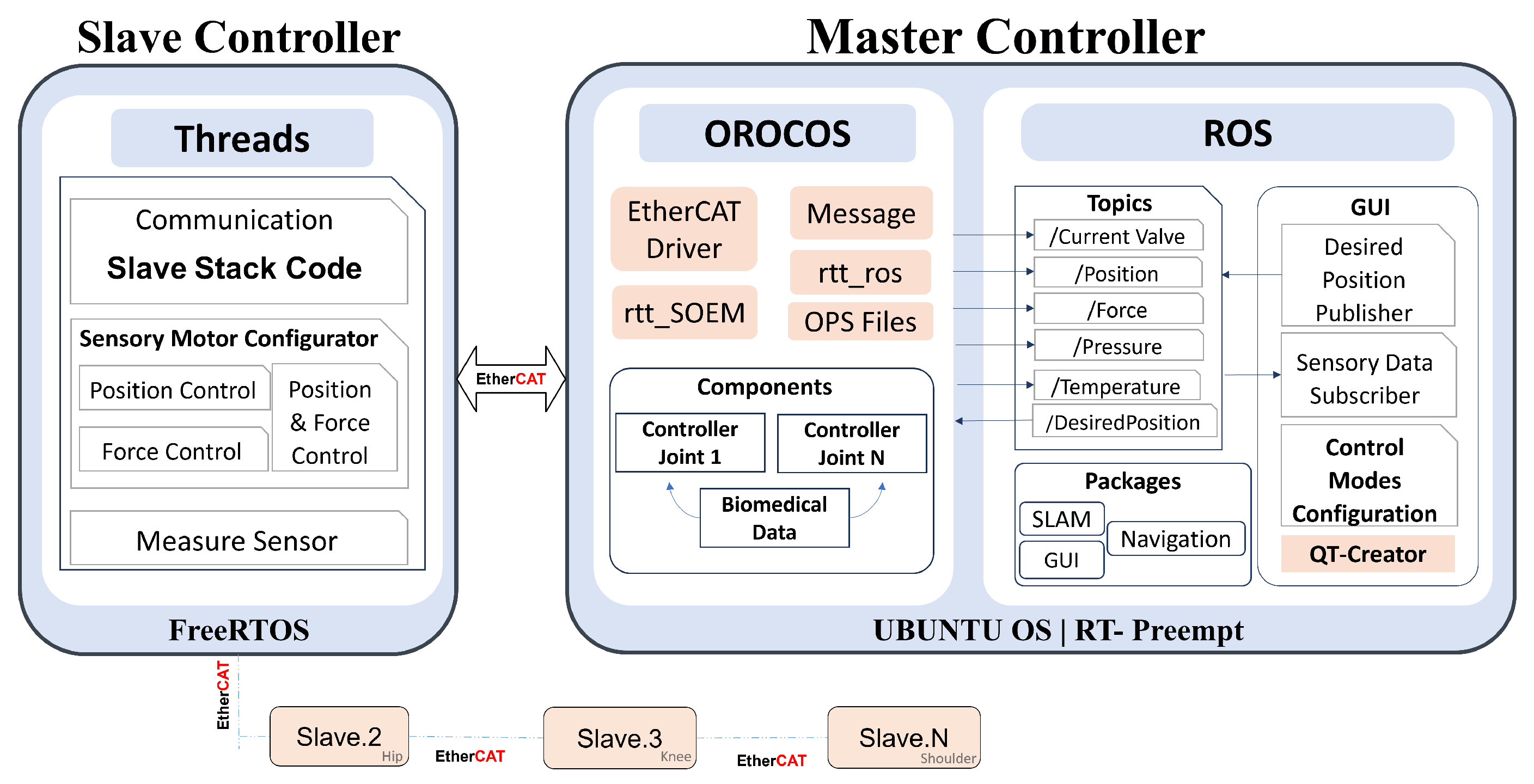
5.2. Joint Controller Distribution
5.3. Communication Protocol
5.4. Real-Time EtherCAT Joint Controller
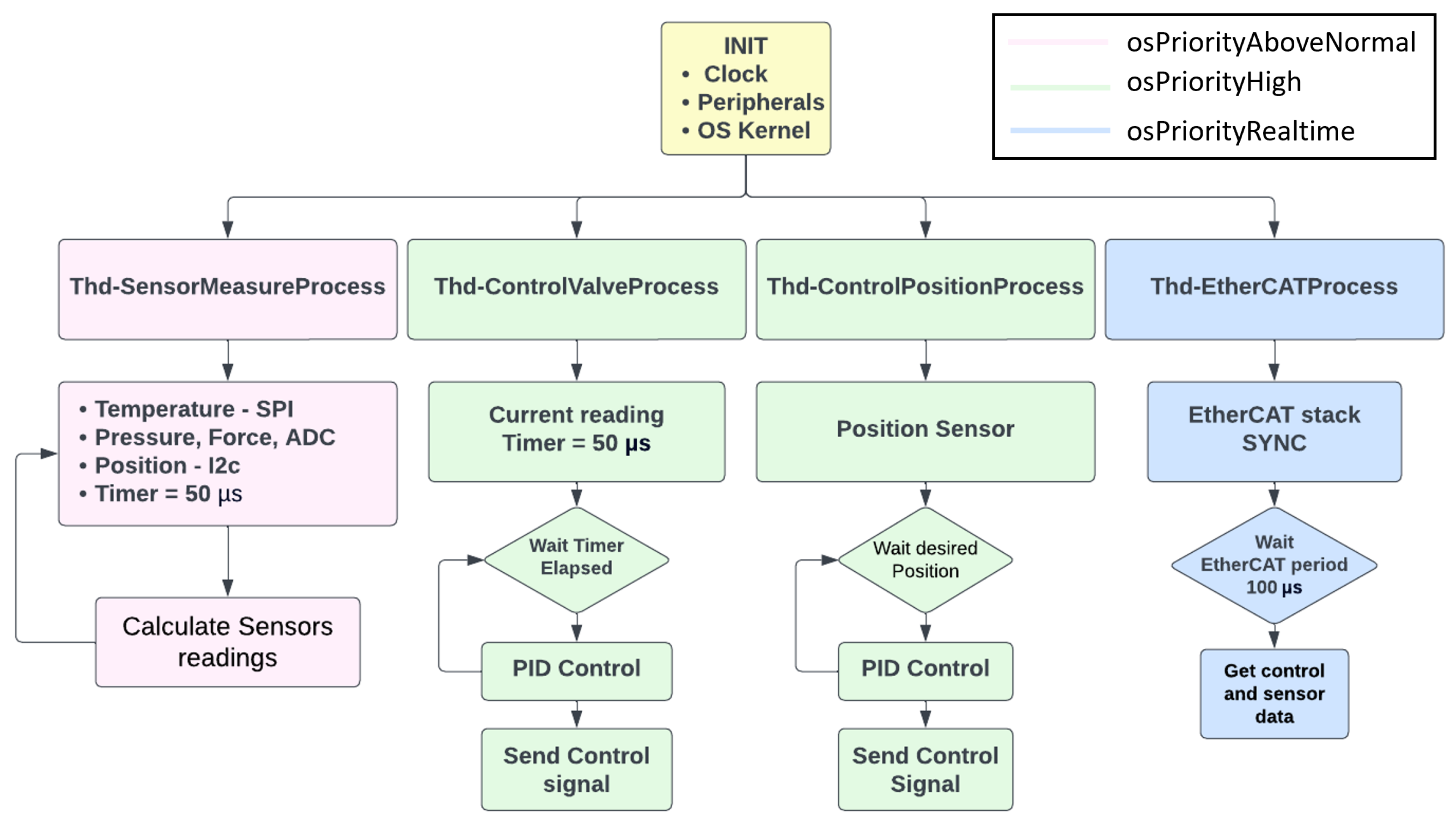
5.5. Real-Time Software
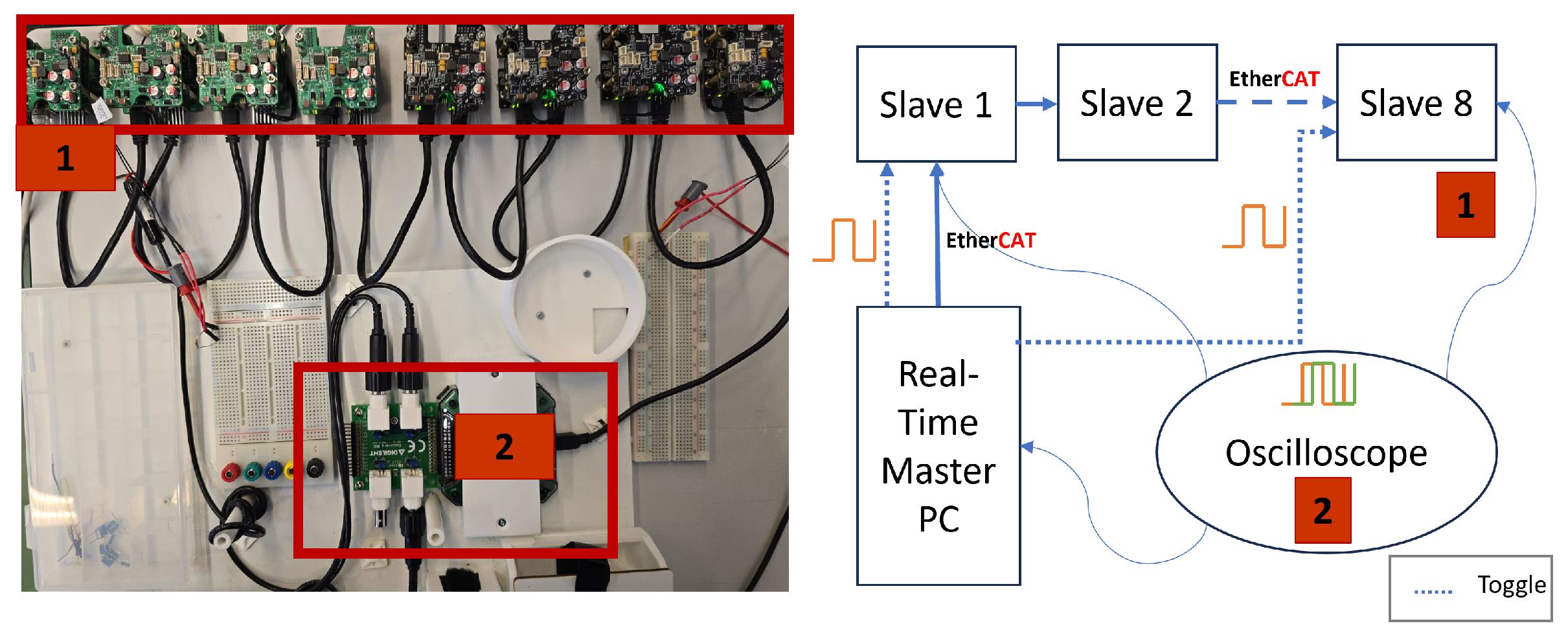
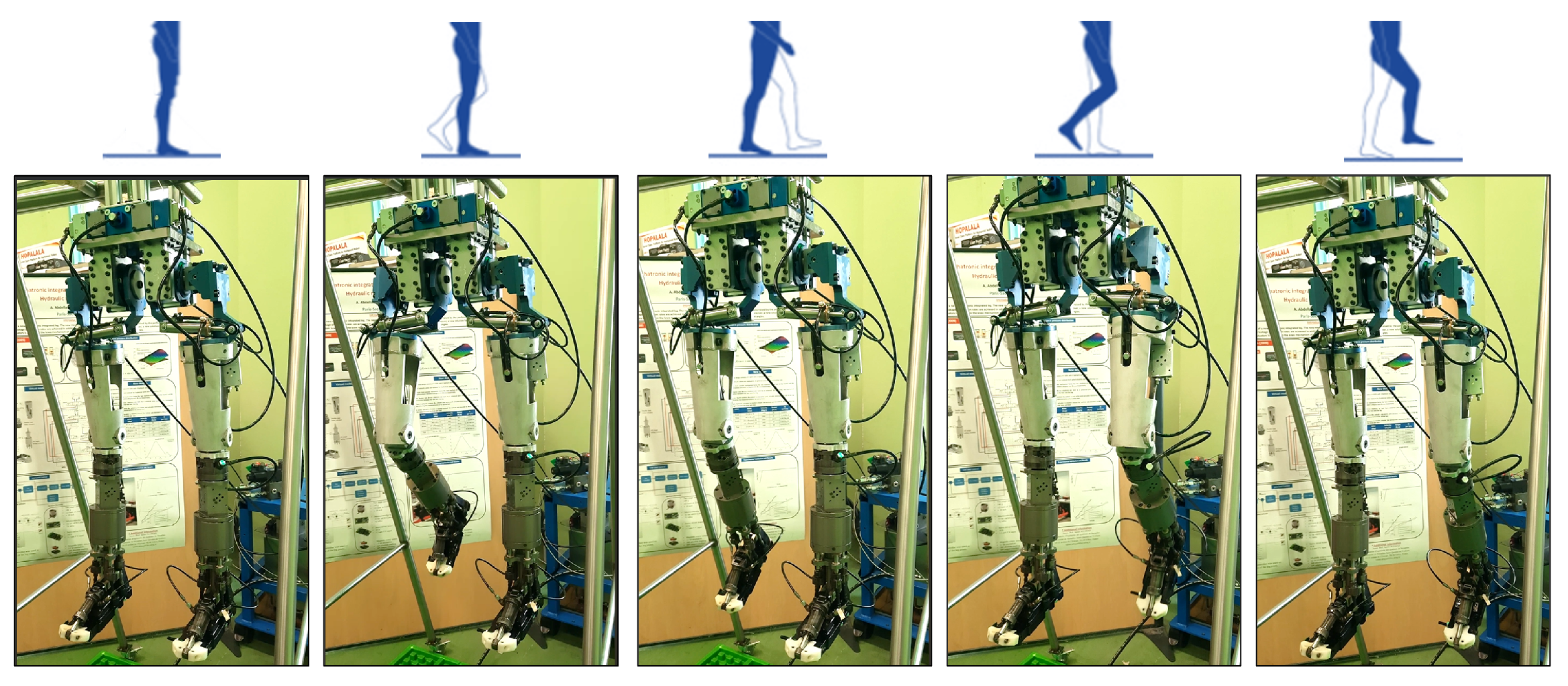
6. Experimental Validation
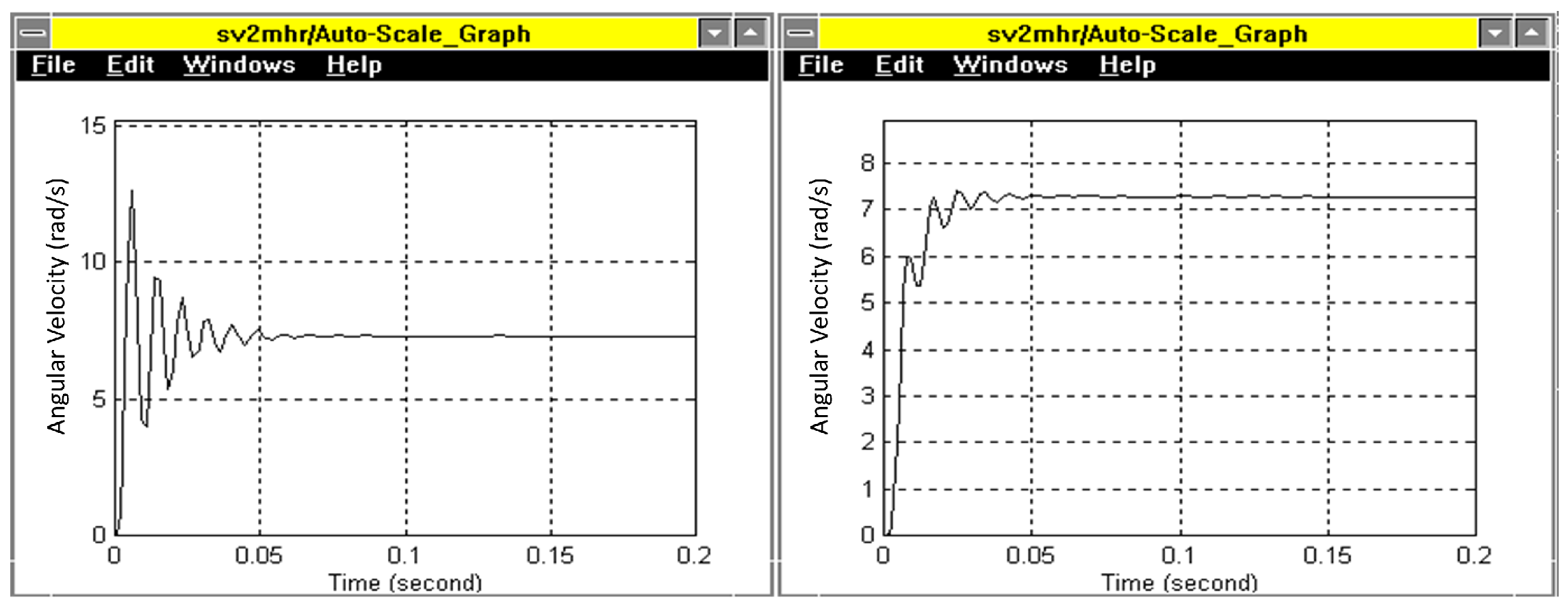
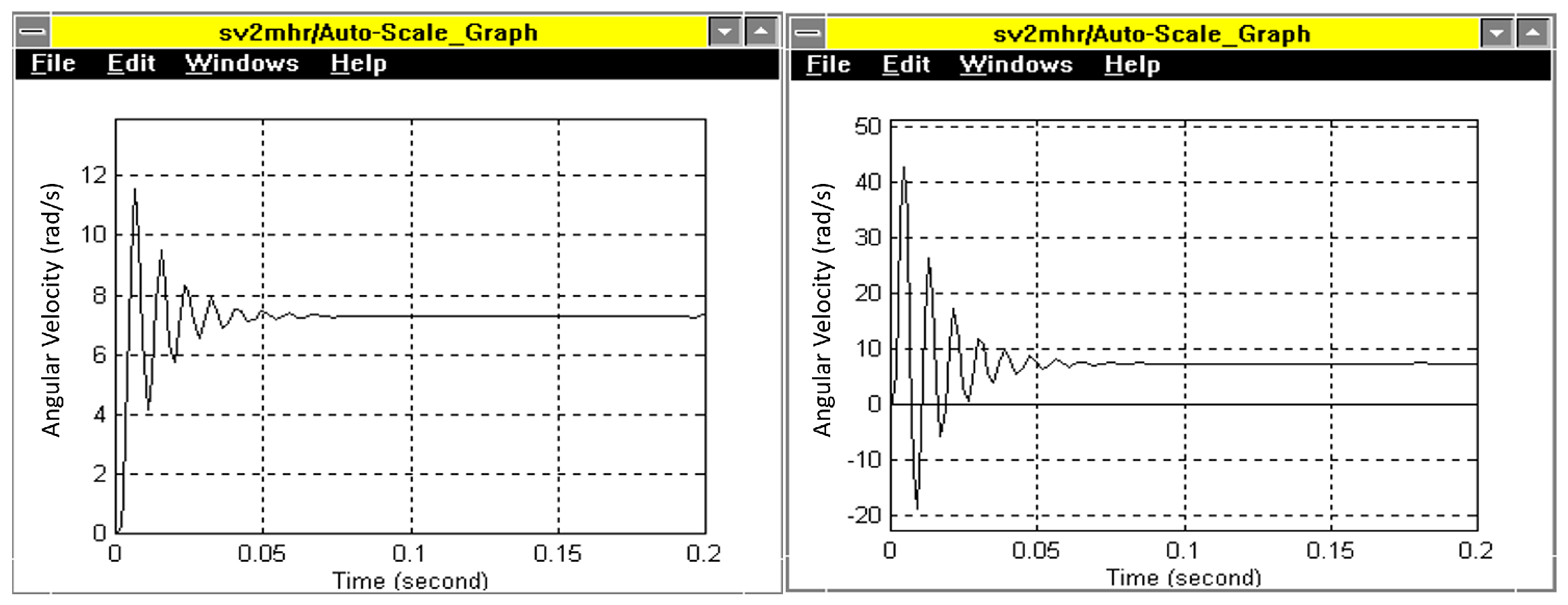
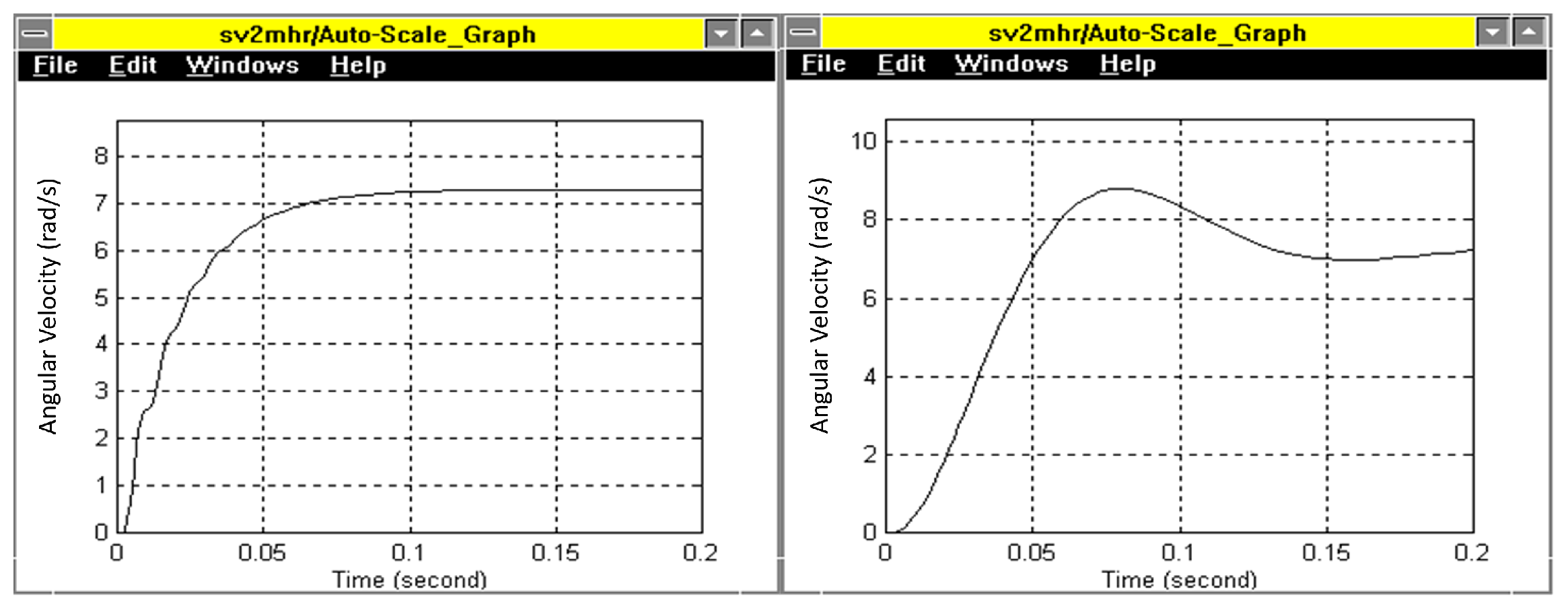
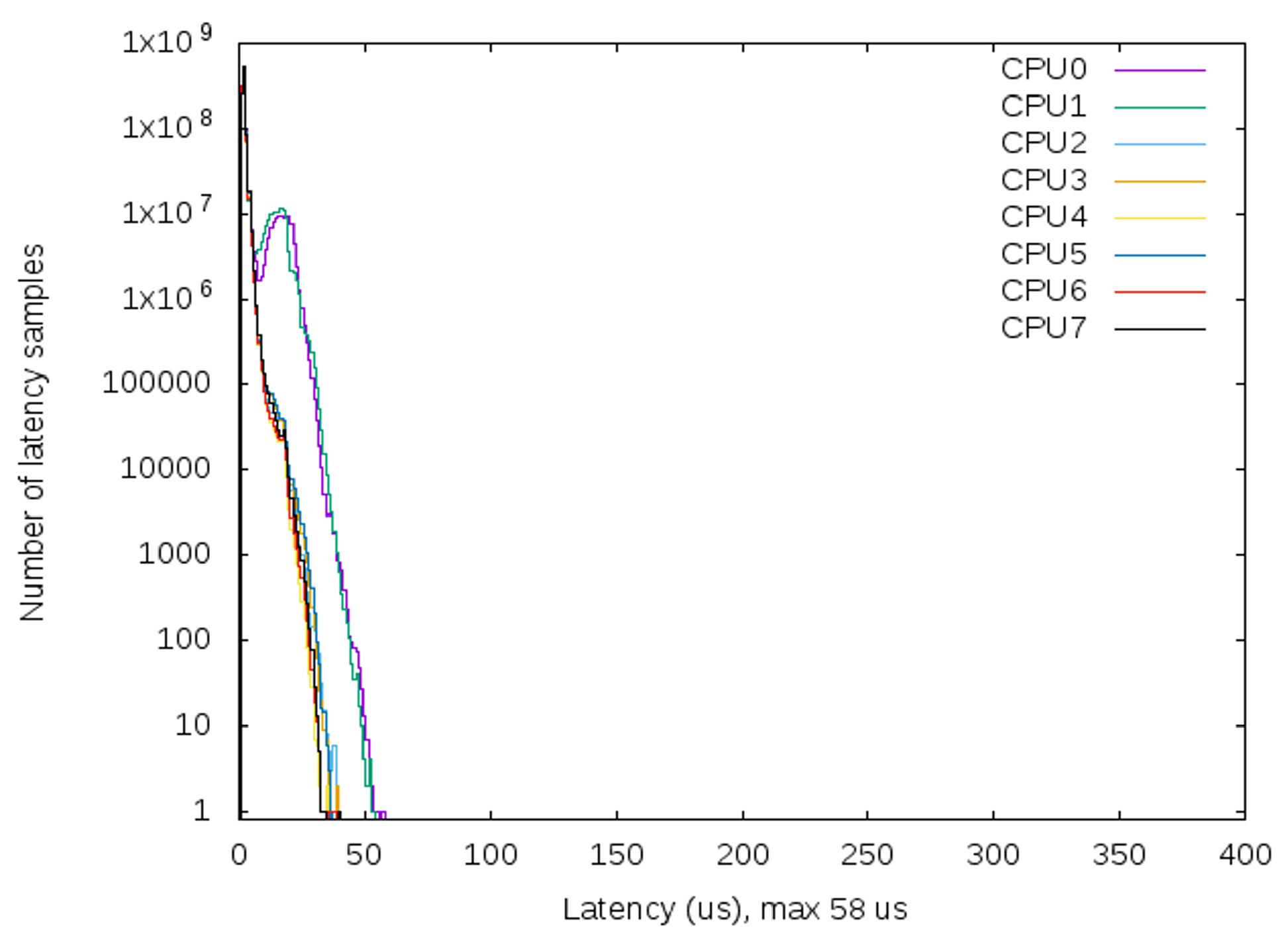
6.1. Joint Controller Performance
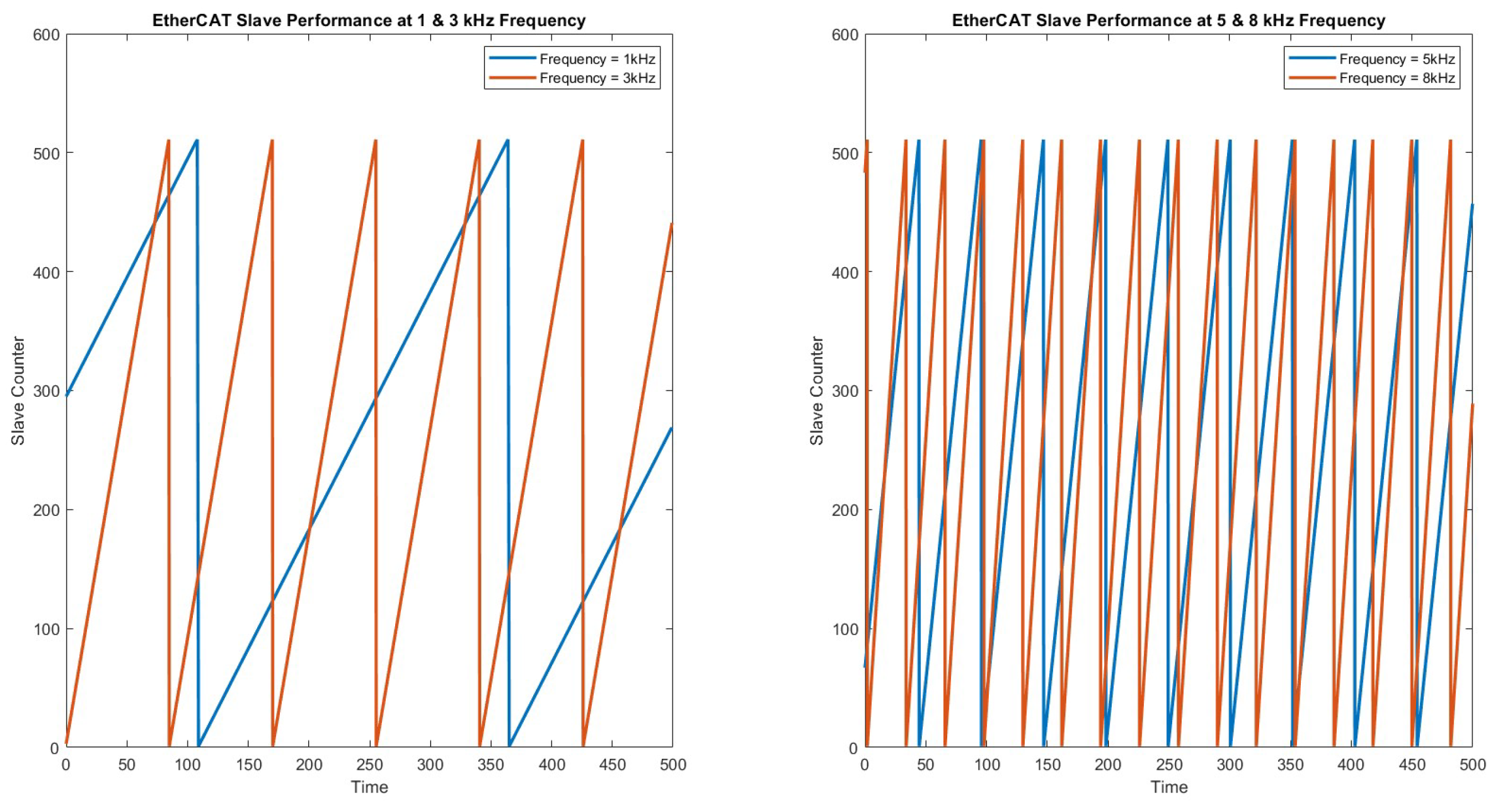
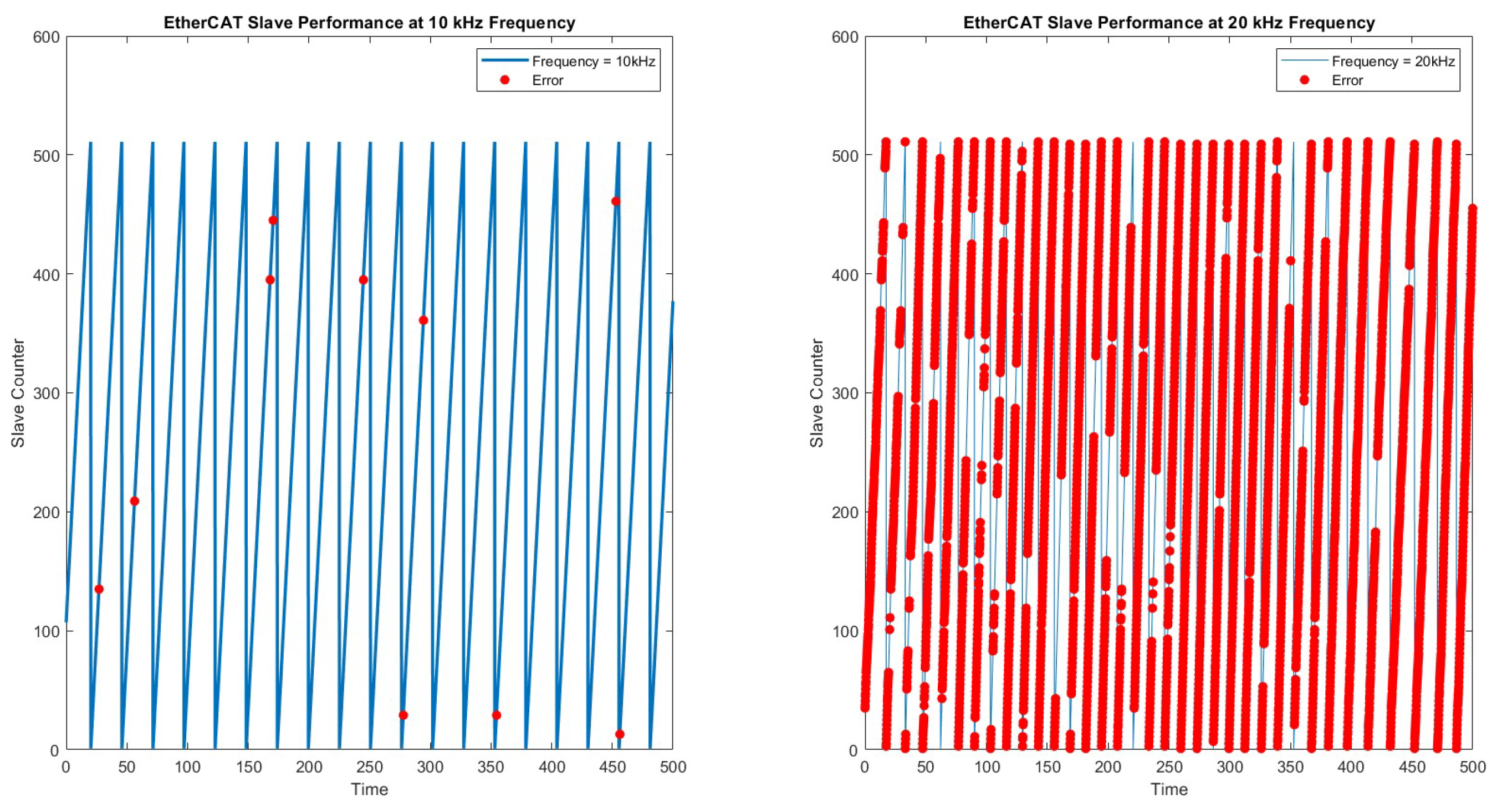
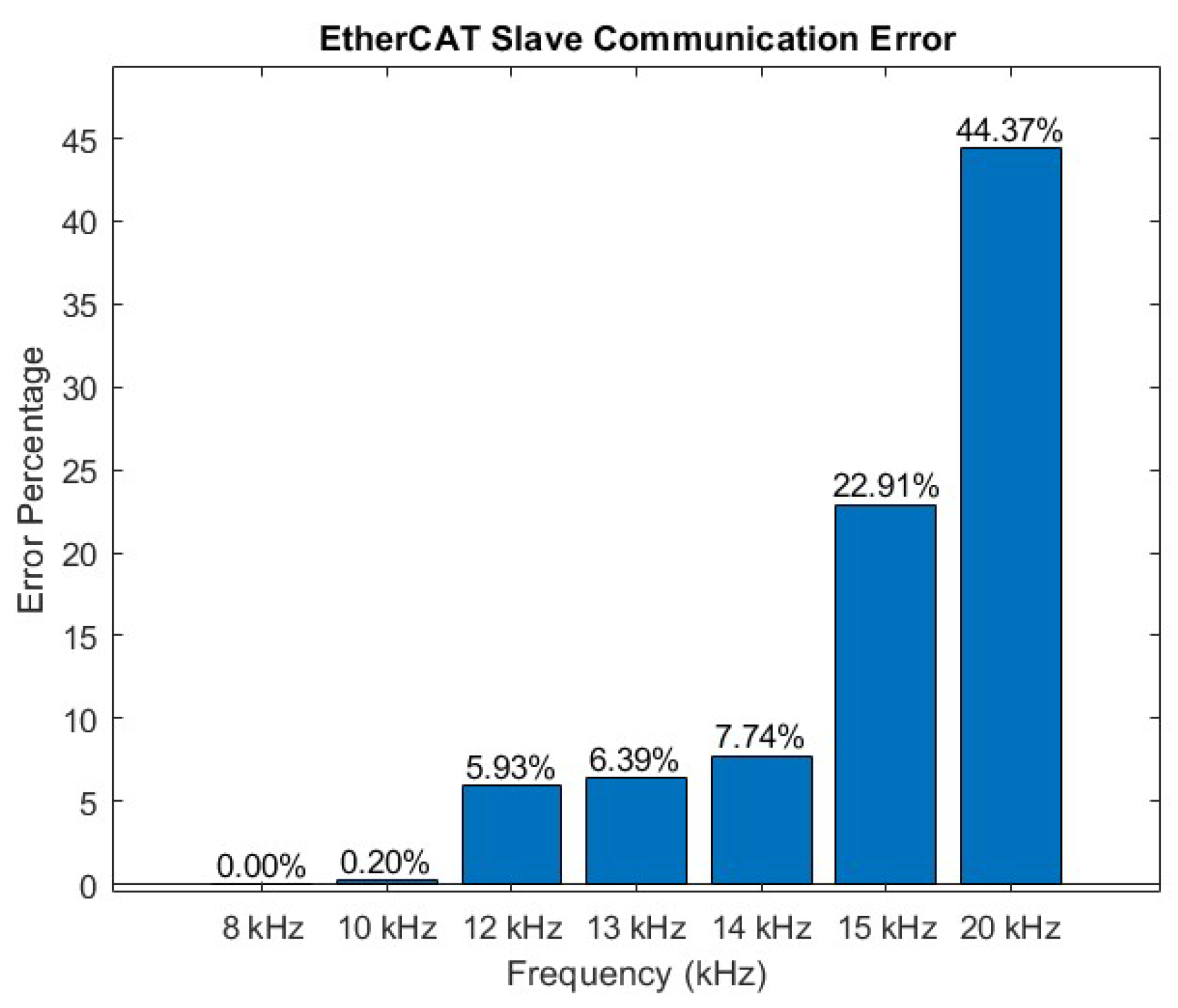
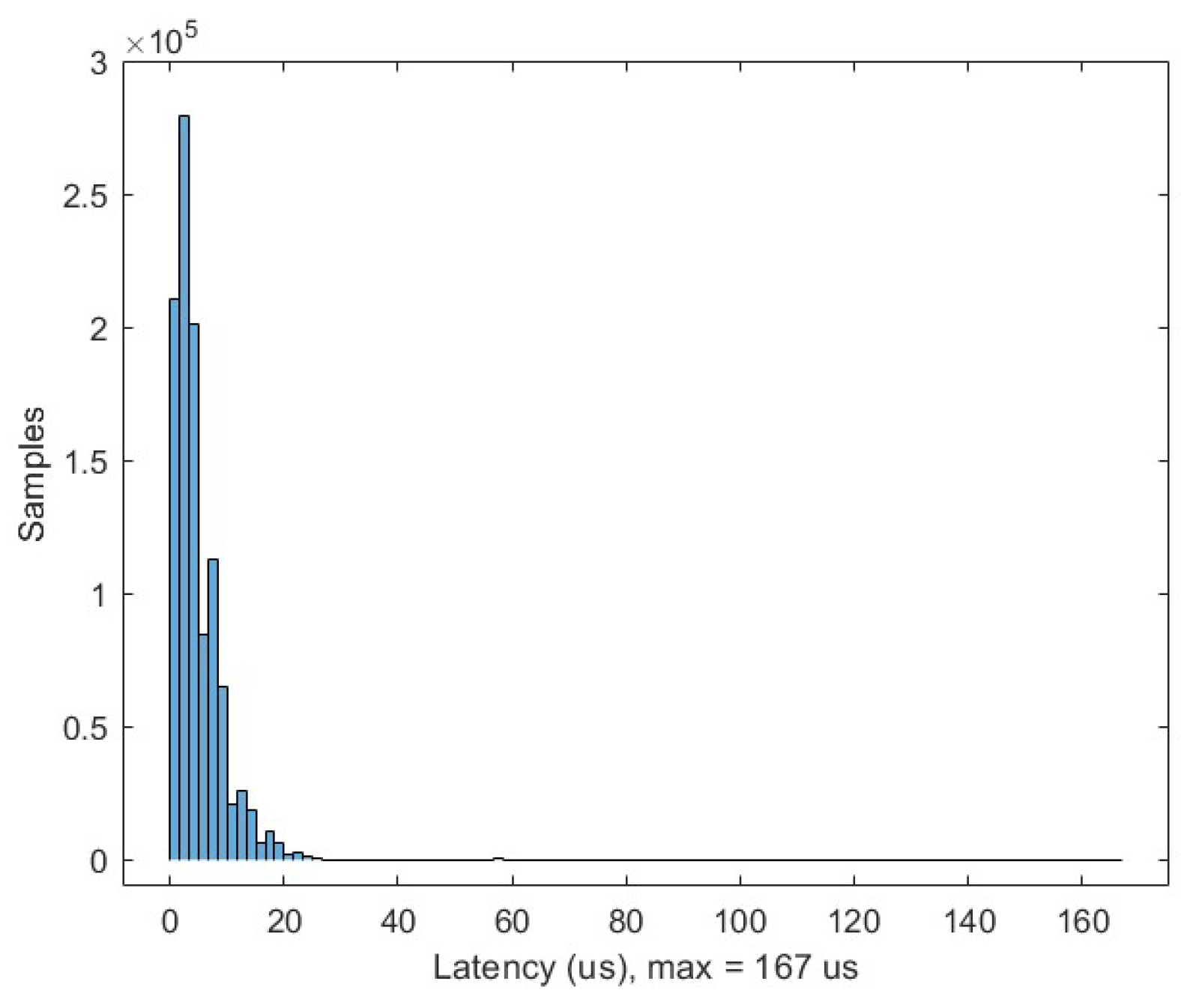
6.2. EtherCAT Bus Performance
6.3. Software Performance
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Calculation of IKM
References
- Ibrahim, A.A.H.; Ammounah, A.; Alfayad, S.; Tliba, S.; Ouezdou, F.B.; Delaplace, S. Hydraulic Robotic Leg for HYDROïD Robot: Modeling and Control. J. Robot. Mechatron. 2022, 34, 576–587. [Google Scholar] [CrossRef]
- Alfayad, S.; Kardofaki, M.; Sleiman, M. Hydraulic Actuator with Overpressure Compensation. WO Patent WO2020173933A1, 3 September 2020. [Google Scholar]
- Fischmeister, S.; Lam, P. Time-Aware Instrumentation of Embedded Software. IEEE Trans. Ind. Inform. 2010, 6, 652–663. [Google Scholar] [CrossRef]
- Gouaillier, D.; Hugel, V.; Blazevic, P.; Kilner, C.; Monceaux, J.; Lafourcade, P.; Marnier, B.; Serre, J.; Maisonnier, B. Mechatronic design of NAO humanoid. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 769–774. [Google Scholar] [CrossRef]
- Kaneko, K.; Kaminaga, H.; Sakaguchi, T.; Kajita, S.; Morisawa, M.; Kumagai, I.; Kanehiro, F. Humanoid Robot HRP-5P: An Electrically Actuated Humanoid Robot with High-Power and Wide-Range Joints. IEEE Robot. Autom. Lett. 2019, 4, 1431–1438. [Google Scholar] [CrossRef]
- Nelson, G.; Saunders, A.; Neville, N.; Swilling, B.; Bondaryk, J.; Billings, D.; Lee, C.; Playter, R.; Raibert, M. PETMAN: A Humanoid Robot for Testing Chemical Protective Clothing. J. Robot. Soc. Jpn. 2012, 30, 372–377. [Google Scholar] [CrossRef]
- Radford, N.A.; Strawser, P.; Hambuchen, K.; Mehling, J.S.; Verdeyen, W.K.; Donnan, A.S.; Holley, J.; Sanchez, J.; Nguyen, V.; Bridgwater, L.; et al. Valkyrie: NASA’s First Bipedal Humanoid Robot. J. Field Robot. 2015, 32, 397–419. [Google Scholar] [CrossRef]
- Sygulla, F.; Wittmann, R.; Seiwald, P.; Berninger, T.; Hildebrandt, A.; Wahrmann, D.; Rixen, D. An EtherCAT-Based Real-Time Control System Architecture for Humanoid Robots. In Proceedings of the 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE), Munich, Germany, 20–24 August 2018; pp. 483–490. [Google Scholar] [CrossRef]
- Akachi, K.; Kaneko, K.; Kanehira, N.; Ota, S.; Miyamori, G.; Hirata, M.; Kajita, S.; Kanehiro, F. Development of humanoid robot HRP-3P. In Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots, San Diego, CA, USA, 5–7 December 2005; pp. 50–55. [Google Scholar] [CrossRef]
- Cereia, M.; Bertolotti, I.C.; Scanzio, S. Performance of a Real-Time EtherCAT Master Under Linux. IEEE Trans. Ind. Inform. 2011, 7, 679–687. [Google Scholar] [CrossRef]
- Park, I.W.; Kim, J.Y.; Lee, J.; Oh, J.H. Mechanical design of humanoid robot platform KHR-3 (KAIST Humanoid Robot 3: HUBO). In Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots, Tsukuba, Japan, 5 December 2005; pp. 321–326. [Google Scholar] [CrossRef]
- Park, I.W.; Kim, J.Y.; Park, S.W.; Oh, J.H. Development of humanoid robot platform KHR-2 (KAIST humanoid robot-2). In Proceedings of the 4th IEEE/RAS International Conference on Humanoid Robots, Santa Monica, CA, USA, 10–12 November 2004; Volume 1, pp. 292–310. [Google Scholar] [CrossRef]
- Cena, G.; Seno, L.; Valenzano, A.; Vitturi, S. Performance analysis of Ethernet Powerlink networks for distributed control and automation systems. Comput. Standards Interfaces 2009, 31, 566–572. [Google Scholar] [CrossRef]
- Jansen, D.; Buttner, H. Real-time Ethernet: The EtherCAT solution. Comput. Control Eng. 2004, 15, 16–21. [Google Scholar] [CrossRef]
- Nelson, G.; Saunders, A.; Playter, R. The PETMAN and Atlas Robots at Boston Dynamics. In Humanoid Robotics: A Reference; Springer: Dordrecht, The Netherlands, 2019; pp. 169–186. [Google Scholar] [CrossRef]
- Stasse, O.; Flayols, T.; Budhiraja, R.; Giraud-Esclasse, K.; Carpentier, J.; Mirabel, J.; Del Prete, A.; Souères, P.; Mansard, N.; Lamiraux, F.; et al. TALOS: A new humanoid research platform targeted for industrial applications. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 689–695. [Google Scholar] [CrossRef]
- Kaminaga, H.; Ko, T.; Masumura, R.; Komagata, M.; Sato, S.; Yorita, S.; Nakamura, Y. Mechanism and Control of Whole-Body Electro-Hydrostatic Actuator Driven Humanoid Robot Hydra. In Proceedings of the 2016 International Symposium on Experimental Robotics, Nagasaki, Japan, 3–8 October 2016; Kulić, D., Nakamura, Y., Khatib, O., Venture, G., Eds.; Springer: Cham, Switzerland, 2017; pp. 656–665. [Google Scholar] [CrossRef]
- Ahn, J.; Park, S.; Sim, J.; Park, J. Dual-Channel EtherCAT Control System for 33-DOF Humanoid Robot TOCABI. IEEE Access 2023, 11, 44278–44286. [Google Scholar] [CrossRef]
- Ferrati, M.; Settimi, A.; Muratore, L.; Cardellino, A.; Rocchi, A.; Mingo Hoffman, E.; Pavan, C.; Kanoulas, D.; Tsagarakis, N.G.; Natale, L.; et al. The Walk-Man Robot Software Architecture. Front. Robot. AI 2016, 3, 25. [Google Scholar] [CrossRef]
- Nori, F.; Traversaro, S.; Eljaik, J.; Romano, F.; Del Prete, A.; Pucci, D. iCub Whole-Body Control through Force Regulation on Rigid Non-Coplanar Contacts. Front. Robot. AI 2015, 2, 6. [Google Scholar] [CrossRef]
- Stasse, O.; Flayols, T. An Overview of Humanoid Robots Technologies. In Biomechanics of Anthropomorphic Systems; Venture, G., Laumond, J.P., Watier, B., Eds.; Springer Tracts in Advanced Robotics; Springer International Publishing: Cham, Switzerland, 2019; Volume 124, pp. 281–310. [Google Scholar] [CrossRef]
- Karumanchi, S.; Edelberg, K.; Baldwin, I.; Nash, J.; Reid, J.; Bergh, C.; Leichty, J.; Carpenter, K.; Shekels, M.; Gildner, M.; et al. Team RoboSimian: Semi-autonomous Mobile Manipulation at the 2015 DARPA Robotics Challenge Finals. J. Field Robot. 2017, 34, 305–332. [Google Scholar] [CrossRef]
- Asfour, T.; Waechter, M.; Kaul, L.; Rader, S.; Weiner, P.; Ottenhaus, S.; Grimm, R.; Zhou, Y.; Grotz, M.; Paus, F. ARMAR-6: A High-Performance Humanoid for Human-Robot Collaboration in Real-World Scenarios. IEEE Robot. Autom. Mag. 2019, 26, 108–121. [Google Scholar] [CrossRef]
- Ammounah, A. Architecture de Contrôle pour un robot Humanoïde à Actionnement Hydraulique. Ph.D. Thesis, Université Paris-Saclay, Paris, France, 2021. [Google Scholar]
- Alfayad, S.; Tayba, A.M.; Ouezdou, F.B.; Namoun, F. Kinematic Synthesis and Modeling of a Three Degrees-of-Freedom Hybrid Mechanism for Shoulder and Hip Modules of Humanoid Robots. J. Mech. Robot. 2016, 8, 041017. [Google Scholar] [CrossRef]
- Abdellatif Hamed Ibrahim, A.; Alfayad, S.; Hildebrandt, A.C.; Ouezdou, F.; Mechbal, N.; Zweiri, Y. Development of a New Hydraulic Ankle for HYDROïD Humanoid Robot. J. Intell. Robot. Syst. 2018, 92, 293–308. [Google Scholar] [CrossRef]
- Alfayad, S.; Kardofaki, M.; Sleiman, M.; Arlot, R. Verin a Capteur de Position Integre. WO Patent WO2023088972A1, 25 May 2023. [Google Scholar]
- Robert, J.; Georges, J.P.; Rondeau, E.; Divoux, T. Minimum Cycle Time Analysis of Ethernet-Based Real-Time Protocols. Int. J. Comput. Commun. Control 2012, 7, 743–757. [Google Scholar] [CrossRef]
- Elkady, A.; Sobh, T. Robotics Middleware: A Comprehensive Literature Survey and Attribute-Based Bibliography. J. Robot. 2012, 2012, 959013. [Google Scholar] [CrossRef]
- Bruyninckx, H. Open robot control software: The OROCOS project. In Proceedings of the 2001 ICRA—IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 3, pp. 2523–2528. [Google Scholar] [CrossRef]
- Quigley, M.; Gerkey, B.; Conley, K.; Faust, J.; Foote, T.; Leibs, J.; Berger, E.; Wheeler, R.; Ng, A. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Puck, L.; Keller, P.; Schnell, T.; Plasberg, C.; Tanev, A.; Heppner, G.; Roennau, A.; Dillmann, R. Performance Evaluation of Real-Time ROS2 Robotic Control in a Time-Synchronized Distributed Network. In Proceedings of the 2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), Lyon, France, 23–27 August 2021; pp. 1670–1676. [Google Scholar] [CrossRef]
- Macenski, S.; Foote, T.; Gerkey, B.; Lalancette, C.; Woodall, W. Robot Operating System 2: Design, Architecture, and Uses in the Wild. Sci. Robot. 2022, 7, eabm6074. [Google Scholar] [CrossRef] [PubMed]






| Mechanism | DoF/Mechanism | Quantity | Total DoF |
|---|---|---|---|
| Toe | 1 | 2 | 2 |
| Ankle | 3 | 2 | 6 |
| Knee | 1 | 2 | 2 |
| Hip | 3 | 2 | 6 |
| Torso | 4 | 1 | 4 |
| Shoulder | 4 | 2 | 8 |
| Elbow | 1 | 2 | 2 |
| Wrist | 3 | 2 | 6 |
| 36 |
| Terms | Notation | Units |
|---|---|---|
| Geometric capacity of engine | cm3 | |
| Gradient of flow losses proportional to the pressure in the engine | cm5/daNs | |
| Reduced moment of inertia at the shaft of rotating hydraulic motor | daNcms2/rad | |
| Moment of inertia at the motor | daNcms2/rad | |
| Moment of inertia at the stator | daNcms2/rad | |
| Resisting moment | daNcm | |
| Moment of friction | daNcms | |
| Gradient of moment losses proportional to angular velocity | daNcms/rad | |
| Dry friction coefficient | - | |
| Angular speed of the rotating hydraulic motor shaft | rad/s | |
| Modulus of elasticity of oil | E | daN/cm2 |
| Damping factor | - | |
| Natural pulsation | rad/s | |
| Current output flow from servo valve | cm3/s | |
| Angular acceleration | rad/s2 | |
| Angular space | rad | |
| Active moment | daNcm | |
| Active power | N | W |
| Active pressure | daN/cm2 | |
| Pressure on discharge path | daN/cm2 |
| Algorithm | Number of Operations | Execution Time (ms) |
|---|---|---|
| IGM | 52 | 5.3 |
| IKM | 150 | 15.4 |
| PID | 15 | 4.6 |
| PDO | Object | Data Type | Index |
|---|---|---|---|
| RxPDO | Index | Uint32 | 0x1600 |
| Data1 | Uint32 | 0x1600 | |
| Data2 | Uint32 | 0x1600 | |
| Total bits | 96 bits | ||
| TxPDO | Valve Current | Uint32 | 0x1A00 |
| Temperature | Uint32 | 0x1A00 | |
| Position | Uint32 | 0x1A00 | |
| Force | Uint32 | 0x1A00 | |
| System State | Uint16 | 0x1A00 | |
| Total bits | 144 bits |
| Terms | Notation | Units |
|---|---|---|
| Minimum cycle time | s | |
| Transmission delay | s | |
| Network device latency | ℓ | s |
| Propagation delay | s | |
| Link capacity | C | bits/s |
| Payload | x | bytes |
| Number of network devices (slaves) | n |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghandour, M.; Jleilaty, S.; Ait Oufroukh, N.; Olaru, S.; Alfayad, S. Real-Time EtherCAT-Based Control Architecture for Electro-Hydraulic Humanoid. Mathematics 2024, 12, 1405. https://doi.org/10.3390/math12091405
Ghandour M, Jleilaty S, Ait Oufroukh N, Olaru S, Alfayad S. Real-Time EtherCAT-Based Control Architecture for Electro-Hydraulic Humanoid. Mathematics. 2024; 12(9):1405. https://doi.org/10.3390/math12091405
Chicago/Turabian StyleGhandour, Maysoon, Subhi Jleilaty, Naima Ait Oufroukh, Serban Olaru, and Samer Alfayad. 2024. "Real-Time EtherCAT-Based Control Architecture for Electro-Hydraulic Humanoid" Mathematics 12, no. 9: 1405. https://doi.org/10.3390/math12091405
APA StyleGhandour, M., Jleilaty, S., Ait Oufroukh, N., Olaru, S., & Alfayad, S. (2024). Real-Time EtherCAT-Based Control Architecture for Electro-Hydraulic Humanoid. Mathematics, 12(9), 1405. https://doi.org/10.3390/math12091405






