On Angles and Pseudo-Angles in Minkowskian Planes

Abstract

The main purpose of the present paper is to well define Minkowskian angles and pseudo-angles between the two null directions and between a null direction and any non-null direction, respectively. Moreover, in a kind of way that will be tried to be made clear at the end of the paper, these new sorts of angles and pseudo-angles can similarly to the previously known angles be seen as (combinations of) Minkowskian lengths of arcs on a Minkowskian unit circle together with Minkowskian pseudo-lengths of parts of the straight null lines.

1. Introduction

In his 1908 lecture “Raum und Zeit" (cfr. Figure 1), Hermann Minkowski presented his indefinite geometry, which made possible the development of Lorentzian geometry and, more generally, of pseudo-Euclidean geometry and of pseudo-Riemannian geometry; (for references on these geometries, see e.g., [1,2,3,4,5,6,7,8,9] and the references in these books and chapters of books and articles).

In the course of time, in Minkowskian planes, proper definitions have been given for the angles between any two spacelike directions and for the angles between any two timelike directions (which two cases geometrically are the same, of course) and for the angle between any spacelike direction and any timelike direction. A notion of such angles as equivalence classes under Minkowskian rotations, and their therefrom coming measure of angles has proper meaning only for two spacelike directions and equivalently for two timelike directions which direct to one and the same branch of a Minkowskian circle, or, still, to one and the same branch of a Euclidean orthogonal hyperbola with the two null directions of the Minkowskian plane as asymptotic directions, centered at the center of such rotations. And the measures of such angles then in fact are given by the Minkowskian lengths of the corresponding arcs on the concerned branches of this unit Minkowskian circle, in a perfect double analogy with the Euclidean angles between any two directions and their measure as central angles on a unit Euclidean circle. For the other above-mentioned Minkowskian angles then, the term angle essentially refers just to a measure of angle in some generalised above sense whereby trying to deal a bit cautiously with positive and negative arcs on Minkowskian circles. And further on, geometrically, the terms Minkowskian angles between any spacelike and any timelike directions—angles involving directions of one or both causal characters alike—will always refer to this common interpretation as central Minkowskian angles.

The main purpose of the present paper is to moreover well define Minkowskian angles and pseudo-angles between the two null directions and between a null direction and any non-null direction, respectively. Moreover, in a kind of way that will be tried to be made clear at the end of the paper, these new sorts of angles and pseudo-angles can similarly to the previously known angles be seen as (combinations of) Minkowskian lengths of arcs on a Minkowskian unit circle together with Minkowskian pseudo-lengths of parts of the straight null lines.

While all above central Minkowskian angles are invariant under Minkowskian rotations, the central Minkowskian pseudo-angles are not. However, in all cases—at least in the author’s opinion—all of these Minkowskian angles and pseudo-angles may turn out not to be without some uses in geometry and in applications of geometry. In this respect, for instance: (i) they may give some geometrical interpretations of the so far merely algebraical or analytical conditions that did occur in some articles on geometry and its applications; (ii) they may lead to extensions of several theories about Riemannian submanifolds in which Euclidean angles play a role to corresponding theories in pseudo-Riemannian geometry; (iii) they may be studied by working out a corresponding trigonometry; (iv) they may be extended to suitable notions for angles and pseudo-angles between higher-dimensional linear subspaces of various causal natures in general pseudo-Euclidean spaces; etcetera.

For related literature on geometry and its applications, see, e.g., also [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].

The point of departure of this paper is the definition of the pseudo-angles or “angles" between any two vectors in a Minkowskian plane as given by Garry Helzer in his relativistic version of the formula of Gauss-Bonnet [27].

In the present paper, like in several of his other recent papers, when it seems to the author of real importance for a better understanding of the text, he included a number of handmade figures. In his experience, so much more than artificially made illustrations, such figures do essentially contribute to the readability of the paper. This is very related to the real value of the drawings made on blackboards during proper lectures on mathematics and on the exact sciences. The author is very grateful for the editors of the journal Mathematics having been so kind to include the scans of ten handmade figures in the present paper.

2. The Pseudo-Angles of Helzer

Let $E_1^2$ be the Minkowskian plane$(R^2,g)$ fixed by the $(+,-)$ metric

$$g(\overrightarrow{v},\overrightarrow{w})=v_1{w}_1-v_2{w}_2$$

(1)

on the standard two-dimensional real vector space $R^2$, whereby $\overrightarrow{v}=(v_1,v_2)$ and $\overrightarrow{w}=(w_1,w_2)$ here denote arbitrary vectors in $R^2$ expanded with respect to the standard oriented orthonormal basis $B=\{\overrightarrow{e_1},\overrightarrow{e_2}\}$. Next, let ${\phi }_B$ be the real valued function which is defined on the set S of the unit vectors and of the null vectors in $E_1^2$, that is, on the set of the vectors $\overrightarrow{z}=z_1\overrightarrow{e_1}+z_2\overrightarrow{e_2}$ for which $z_1^2-z_2^2=\pm 1$ (i.e., on the two Euclidean unit orthogonal hyperbola’s $H_1:z_1^2-z_2^2=1$ and $H_2:z_1^2-z_2^2=-1$) and on the vectors $\overrightarrow{z}=z_1\overrightarrow{e_1}+z_2\overrightarrow{e_2}\ne \overrightarrow{o}$ for which $z_1^2-z_2^2=0$ (i.e., on the first and second diagonals or Euclidean bisectrices $D_1:z_1-z_2=0$ and $D_2:z_1+z_2=0$, "minus" the origin O), by

$${\phi }_{\mathit{B}}\left(\overrightarrow{z}\right)=\left\{\begin{array}{cc}\hfill ln|z_1+z_2|,& when{z}_1+z_2\ne 0,\hfill \\ \hfill -ln|z_1-z_2|,& when{z}_1+z_2=0.\hfill \end{array}\right.$$

(2)

And finally, let ${\psi }_B$ be the real valued function which is defined on the pairs of vectors from S, say $\overrightarrow{v}$ and $\overrightarrow{w}$, by

$${\psi }_B(\overrightarrow{v},\overrightarrow{w})={\phi }_B\left(\overrightarrow{w}\right)-{\phi }_B\left(\overrightarrow{v}\right).$$

(3)

when similarly defining functions ${\phi }_{B^{\prime }}$ and ${\psi }_{B^{\prime }}$ corresponding to any other ordered orthonormal basis $B^{\prime }$ of $E_1^2$, then ${\psi }_{B^{\prime }}={\psi }_B$ or ${\psi }_{B^{\prime }}=-{\psi }_B$, depending on $B^{\prime }$ and B having the same or opposite orientations, respectively; (as a kind of intermediate step in this having ${\phi }_{B^{\prime }}\left(\overrightarrow{z}\right)={\phi }_B\left(\overrightarrow{z}\right)+{\phi }_{B^{\prime }}\left({\overrightarrow{e}}_1\right)$ and ${\phi }_{B^{\prime }}\left(\overrightarrow{z}\right)=-{\phi }_B\left(\overrightarrow{z}\right)+{\phi }_{B^{\prime }}\left({\overrightarrow{e}}_1\right)$, respectively).

Therefore, the following makes good sense indeed: the oriented pseudo-angle $\psi (\overrightarrow{v},\overrightarrow{w})$ of Helzer [27] from $\overrightarrow{v}$ to $\overrightarrow{w}$, ($\overrightarrow{v},\overrightarrow{w}\in S$), is defined by

$$\psi (\overrightarrow{v},\overrightarrow{w})={\psi }_B(\overrightarrow{v},\overrightarrow{w}).$$

(4)

According to this definition, clearly

$$\psi (\overrightarrow{v},\overrightarrow{w})=\psi (-\overrightarrow{v},\overrightarrow{w})=\psi (\overrightarrow{v},-\overrightarrow{w})=\psi (-\overrightarrow{v},-\overrightarrow{w}).$$

(5)

And for any number k of unit or null vectors $\overrightarrow{v_1},\overrightarrow{v_2},\cdots ,\overrightarrow{v_k}$ in $E_1^2$, one has

$$\psi (\overrightarrow{v_1},\overrightarrow{v_2})+\psi (\overrightarrow{v_2},\overrightarrow{v_3})+\cdots +\psi ({\overrightarrow{v}}_{k-1},\overrightarrow{v_k})+\psi (\overrightarrow{v_k},\overrightarrow{v_1})=0.$$

(6)

3. The Minkowskian Angles between Spacelike and Timelike Directions

The following result shows that for unit spacelike or timelike vectors $\overrightarrow{v}$ and $\overrightarrow{w}$ in a Minkowskian plane $E_1^2$ the oriented pseudo-angle $\psi (\overrightarrow{v},\overrightarrow{w})$ of Helzer is equal to what O’Neill in [5] called the oriented Lorentz angle between two spacelike unit vectors $\overrightarrow{v}$ and $\overrightarrow{w}$, or is equal to what Birman and Nomizu in [28,29] simply called the oriented angle between two timelike unit vectors $\overrightarrow{v}$ and $\overrightarrow{w}$, or is equal to what in [30,31] was called the oriented hyperbolic angle between a spacelike unit vector $\overrightarrow{v}$ and a timelike unit vector $\overrightarrow{w}$, depending on the causal characters of $\overrightarrow{v}$ and $\overrightarrow{w}$.

Before giving the formulation and a proof of this result, I would like to make the following proposal concerning terminology: let us use the term “Minkowskian angles” when dealing with the above kind of angles between unit vectors, and also between their directions in a Minkowskian plane, (rather than just “angles”, since angles as such are commonly used for the common angles of Euclidean geometry, and rather than “Lorentzian angles”, since also on Lorentzian surfaces the angles are essentially defined in the tangent planes to such surfaces and these are Minkowskian planes, and also rather than “hyperbolic angles”, which seem better to be reserved for use in the geometry of Lobachevsky-Bolyai; see also Section 7 concerning this matter).

Theorem 1.

Let $\overrightarrow{v}$ and $\overrightarrow{w}$ be unit vectors in a Minkowskian plane $E_1^2$ and let $\psi (\overrightarrow{v},\overrightarrow{w})$ be the oriented pseudo-angle of Helzer from $\overrightarrow{v}$ to $\overrightarrow{w}$. Then, when $(v_1,v_2)$ and $(w_1,w_2)$ are the co-ordinates of $\overrightarrow{v}$ and $\overrightarrow{w}$ with respect to the standard basis B in $E_1^2$ and when D is the Euclidean reflection in the first diagonal of B, in terms of the hyperbolic functions cosh and sinh, this pseudo-angle ψ is related to the Minkowskian metric g in the following way:

(i) if $\overrightarrow{v}$ and $\overrightarrow{w}$ are both spacelike,

$$cosh\psi (\overrightarrow{v},\overrightarrow{w})=\left\{\begin{array}{cc}\hfill -g(\overrightarrow{v},\overrightarrow{w})& whensgn{v}_1\ne sgn{w}_1\hfill \\ \hfill g(\overrightarrow{v},\overrightarrow{w})& whensgn{v}_1=sgn{w}_1,\hfill \end{array}\right.$$

(7)

$$sinh\psi (\overrightarrow{v},\overrightarrow{w})=\left\{\begin{array}{cc}\hfill -g(\overrightarrow{v},D\overrightarrow{w})& whensgn{v}_1\ne sgn{w}_1\hfill \\ \hfill g(\overrightarrow{v},D\overrightarrow{w})& whensgn{v}_1=sgn{w}_1;\hfill \end{array}\right.$$

(8)

(ii) if $\overrightarrow{v}$ and $\overrightarrow{w}$ are both timelike,

$$cosh\psi (\overrightarrow{v},\overrightarrow{w})=\left\{\begin{array}{cc}\hfill g(\overrightarrow{v},\overrightarrow{w})& whensgn{v}_2\ne sgn{w}_2\hfill \\ \hfill -g(\overrightarrow{v},\overrightarrow{w})& whensgn{v}_2=sgn{w}_2,\hfill \end{array}\right.$$

(9)

$$sinh\psi (\overrightarrow{v},\overrightarrow{w})=\left\{\begin{array}{cc}\hfill g(\overrightarrow{v},D\overrightarrow{w})& whensgn{v}_2\ne sgn{w}_2,\hfill \\ \hfill -g(\overrightarrow{v},D\overrightarrow{w})& whensgn{v}_2=sgn{w}_2;\hfill \end{array}\right.$$

(10)

(iii) if $\overrightarrow{v}$ is spacelike and $\overrightarrow{w}$ is timelike,

$$cosh\psi (\overrightarrow{v},\overrightarrow{w})=\left\{\begin{array}{cc}\hfill -g(\overrightarrow{v},D\overrightarrow{w})& whensgn{v}_1\ne sgn{w}_2\hfill \\ \hfill g(\overrightarrow{v},D\overrightarrow{w})& whensgn{v}_1=sgn{w}_2,\hfill \end{array}\right.$$

(11)

$$sinh\psi (\overrightarrow{v},\overrightarrow{w})=\left\{\begin{array}{cc}\hfill -g(\overrightarrow{v},\overrightarrow{w})& whensgn{v}_1\ne sgn{w}_2\hfill \\ \hfill g(\overrightarrow{v},\overrightarrow{w})& whensgn{v}_1=sgn{w}_2.\hfill \end{array}\right.$$

(12)

Proof. 

For any pair of unit vectors $\overrightarrow{v}=(v_1,v_2)$ and $\overrightarrow{w}=(w_1,w_2)$ according to (1)–(4),

$$\begin{array}{ccc}\psi (\overrightarrow{v},\overrightarrow{w})\hfill & =& ln|w_1+w_2|-ln|v_1+v_2|\hfill \\ & =& ln|\frac{w_1+w_2}{v_1+v_2}|\hfill \\ & =& ln|\frac{(w_1+w_2)(v_1-v_2)}{v_1^2-v_2^2}|\hfill \\ & =& ln|(w_1+w_2)(v_1-v_2)|\hfill \\ & =& ln|v_1{w}_1-v_2{w}_2+v_1{w}_2-v_2{w}_1|,\hfill \end{array}$$

and, so, since $D\overrightarrow{w}=D(w_1,w_2)=(w_2,w_1)$,

$$\psi (\overrightarrow{v},\overrightarrow{w})=ln|g(\overrightarrow{v},\overrightarrow{w})+g(\overrightarrow{v},D\overrightarrow{w})|.$$

(13)

Hence, by the very definitions of the functions cosinushyperbolicus and sinushyperbolicus,

$$cosh\psi (\overrightarrow{v},\overrightarrow{w})=\frac{{[g(\overrightarrow{v},\overrightarrow{w})+g(\overrightarrow{v},D\overrightarrow{w})]}^2+1}{2|g(\overrightarrow{v},\overrightarrow{w})+g(\overrightarrow{v},D\overrightarrow{w})|}$$

(14)

and

$$sinh\psi (\overrightarrow{v},\overrightarrow{w})=\frac{{[g(\overrightarrow{v},\overrightarrow{w})+g(\overrightarrow{v},D\overrightarrow{w})]}^2-1}{2|g(\overrightarrow{v},\overrightarrow{w})+g(\overrightarrow{v},D\overrightarrow{w})|}.$$

(15)

In the cases (i) and (ii), i.e., if $\overrightarrow{v}$ and $\overrightarrow{w}$ either are both spacelike (i) or are both timelike (ii),

$$g{(\overrightarrow{v},\overrightarrow{w})}^2-g{(\overrightarrow{v},D\overrightarrow{w})}^2=1,$$

(16)

which combined with (14) and (15), yields

$$cosh\psi (\overrightarrow{v},\overrightarrow{w})=ϵg(\overrightarrow{v},\overrightarrow{w})$$

(17)

and

$$sinh\psi (\overrightarrow{v},\overrightarrow{w})=ϵg(\overrightarrow{v},D\overrightarrow{w}),$$

(18)

whereby $ϵ=sgn[g(\overrightarrow{v},\overrightarrow{w})+g(\overrightarrow{v},D\overrightarrow{w})]$. In addition, then formulae (7) and (8) and formulae (9) and (10) follow from formulae (17) and (18) since, when $\overrightarrow{v}$ and $\overrightarrow{w}$ are both spacelike, $ϵ=1$ when $sgn{v}_1=sgn{w}_1$ and $ϵ=-1$ when $sgn{v}_1\ne sgn{w}_1$, and when $\overrightarrow{v}$ and $\overrightarrow{w}$ are both timelike, $ϵ=1$ when $sgn{v}_2\ne sgn{w}_2$ and $ϵ=-1$ when $sgn{v}_2=sgn{w}_2$.

Finally, in case (iii), i.e., if $\overrightarrow{v}$ and $\overrightarrow{w}$ do have different causal characters, say if $\overrightarrow{v}$ is spacelike and $\overrightarrow{w}$ is timelike,

$$g{(\overrightarrow{v},\overrightarrow{w})}^2-g{(\overrightarrow{v},D\overrightarrow{w})}^2=-1,$$

(19)

which, combined with (14) and (15), now yields

$$cosh\psi (\overrightarrow{v},\overrightarrow{w})=ϵg(\overrightarrow{v},D\overrightarrow{w})$$

(20)

and

$$sinh\psi (\overrightarrow{v},\overrightarrow{w})=ϵg(\overrightarrow{v},\overrightarrow{w}).$$

(21)

In addition, then formulae (11) and (12) follow from formulae (20) and (21) since, for a spacelike unit vector $\overrightarrow{v}$ and a timelike unit vector $\overrightarrow{w}$, $ϵ=-1$ when $sgn{v}_1\ne sgn{w}_2$ and $ϵ=1$ when $sgn{v}_1=sgn{w}_2$. ☐

From here on, we agree to systematically use the notation $\theta (\overrightarrow{v},\overrightarrow{w})$ for the oriented Minkowskian angles between unit vectors $\overrightarrow{v}$ and $\overrightarrow{w}$ for any causal characters, (rather than the former $\psi (\overrightarrow{v},\overrightarrow{w})$, keeping on the use of $\psi$ though for the pseudo-angles of Helzer in general, cfr. definition (3)).

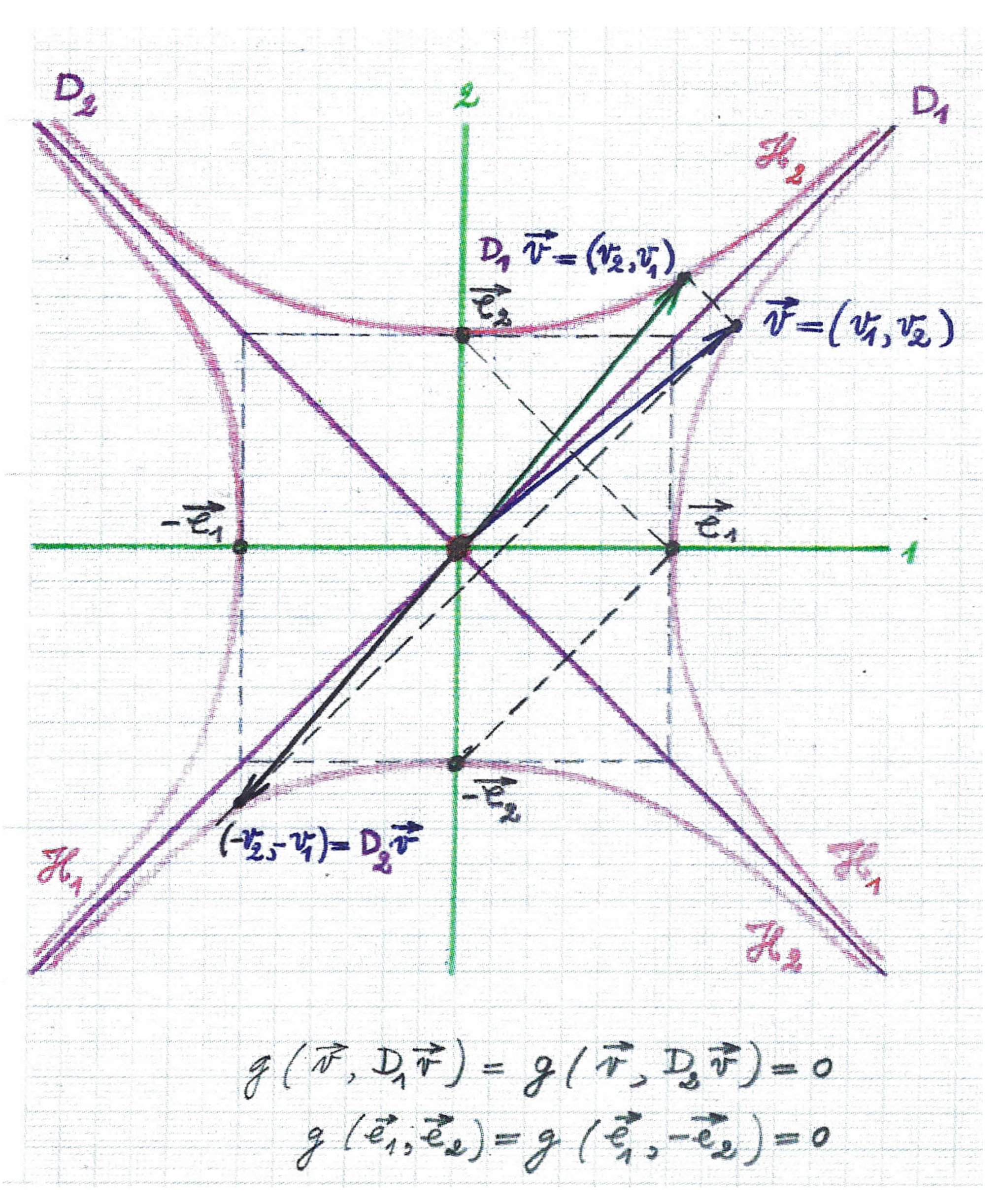
In the Minkowskian geometry on a plane, unit vectors $\overrightarrow{v}$ and $\overrightarrow{w}$ for which $g(\overrightarrow{v},\overrightarrow{w})=0$, apart from pairs of vectors $\pm \overrightarrow{e_1}$ and $\pm \overrightarrow{e_2}$, are not at all orthogonal or perpendicular to each other in accordance with our common visual senses, or, still, in accordance with the Euclidean geometry on this plane. However, such unit vectors in a Minkowskian plane, i.e., unit vectors in $E_1^2$ with vanishing Minkowskian scalar product, nevertheless, conventionally often remain said to be mutually orthogonal. All in all, this terminology may not be so recommendable (but, unfortunately, it is to be expected that this terminology will continue to be used, like; for instance, one has been going on to speak of “the orthogonal group” when speaking of “the orthonormal group”...). Actually, such vectors are each other’s Euclidean reflections in the first or second diagonals $D=D_1$ and $D_2$ of the standard orthonormal basis $B=\{\overrightarrow{e_1},\overrightarrow{e_2}\}$, or, put otherwise, such vectors are pairs of vectors lying on the Euclidean orthogonal hyperbola’s $H:u_1^2-u_2^2=\pm 1$ with Euclidean unit axes and which are bisected either by the first or second diagonals or bisectrices $D_1$ and $D_2$ (cfr. Figure 2). It could be observed here in passing, and it will become more clear later on, that the just used expressions that refer to bisecting, however, do enjoy their proper meanings in the sense of the angles in the geometries of Euclid and of Minkowski alike. In any case, based on Theorem 1, one has the following.

Corollary 1.

While in a Minkowskian plane any two unit vectors with the same causal character can never be mutually orthogonal, a timelike and a spacelike unit vector are mutually orthogonal if and only if their oriented Minkowskian angle is zero.

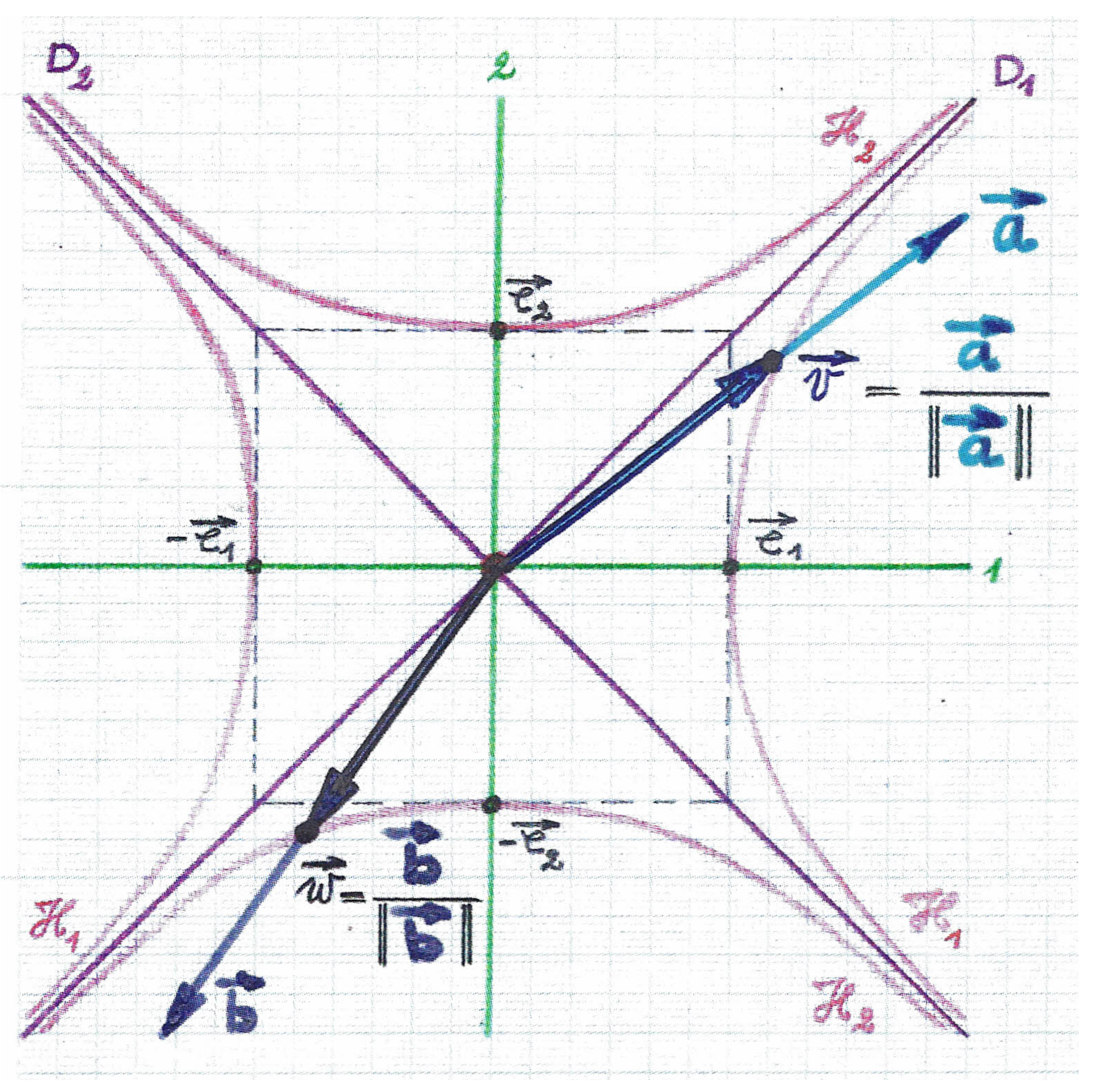
For two arbitrary (non-null) vectors $\overrightarrow{a}=(a_1,a_2)$ and $\overrightarrow{b}=(b_1,b_2)$ of Minkowskian lengths $\left|\right|\overrightarrow{a}\left|\right|=|g(\overrightarrow{a},\overrightarrow{a}){|}^{\frac{1}{2}}(\ne 0)$ and $\left|\right|\overrightarrow{b}\left|\right|=|g(\overrightarrow{b},\overrightarrow{b}){|}^{\frac{1}{2}}(\ne 0)$, from $\overrightarrow{a}$ to $\overrightarrow{b}$ the oriented Minkowskian angle $\theta (\overrightarrow{a},\overrightarrow{b})$ is defined as the oriented Minkowskian angle of their normalised corresponding unit vectors $\overrightarrow{v}=\overrightarrow{a}/\left|\right|\overrightarrow{a}\left|\right|$ and $\overrightarrow{w}=\overrightarrow{b}/\left|\right|\overrightarrow{b}\left|\right|$; $\theta (\overrightarrow{a},\overrightarrow{b})=\theta (\overrightarrow{v},\overrightarrow{w})$ , (cfr. Figure 3). Thus, according to (13), in terms of the Minkowskian scalar product:

$$\theta (\overrightarrow{a},\overrightarrow{b})=ln|\frac{g(\overrightarrow{a},\overrightarrow{b})+g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}|.$$

(22)

Further, based on relations (1)–(6), for all pairs of arbitrary non-null vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ we recover the following formulae which relate these oriented Minkowskian angles $\theta (\overrightarrow{a},\overrightarrow{b})$ to the Minkowskian metric by means of the hyperbolic functions, (cfr. [28]).

Theorem 2.

(i) If $\overrightarrow{a}$ and $\overrightarrow{b}$ are both spacelike,

$$cosh\theta (\overrightarrow{a},\overrightarrow{b})=\left\{\begin{array}{cc}\hfill {\displaystyle -\frac{g(\overrightarrow{a},\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1\ne sgn{b}_1\hfill \\ \hfill {\displaystyle \frac{g(\overrightarrow{a},\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1=sgn{b}_1,\hfill \end{array}\right.$$

(23)

$$sinh\theta (\overrightarrow{a},\overrightarrow{b})=\left\{\begin{array}{cc}\hfill {\displaystyle -\frac{g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1\ne sgn{b}_1\hfill \\ \hfill {\displaystyle \frac{g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1=sgn{b}_1;\hfill \end{array}\right.$$

(24)

(ii) if $\overrightarrow{a}$ and $\overrightarrow{b}$ are both timelike,

$$cosh\theta (\overrightarrow{a},\overrightarrow{b})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{g(\overrightarrow{a},\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_2\ne sgn{b}_2\hfill \\ \hfill {\displaystyle -\frac{g(\overrightarrow{a},\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_2=sgn{b}_2,\hfill \end{array}\right.$$

(25)

$$sinh\theta (\overrightarrow{a},\overrightarrow{b})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_2\ne sgn{b}_2\hfill \\ \hfill {\displaystyle -\frac{g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_2=sgn{b}_2;\hfill \end{array}\right.$$

(26)

(iii) if $\overrightarrow{a}$ is spacelike and $\overrightarrow{b}$ is timelike,

$$cosh\theta (\overrightarrow{a},\overrightarrow{b})=\left\{\begin{array}{cc}\hfill {\displaystyle -\frac{g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1\ne sgn{b}_2\hfill \\ \hfill {\displaystyle \frac{g(\overrightarrow{a},D\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1=sgn{b}_2,\hfill \end{array}\right.$$

(27)

$$sinh\theta (\overrightarrow{a},\overrightarrow{b})=\left\{\begin{array}{cc}\hfill {\displaystyle -\frac{g(\overrightarrow{a},\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1\ne sgn{b}_2\hfill \\ \hfill {\displaystyle \frac{g(\overrightarrow{a},\overrightarrow{b})}{\left|\right|\overrightarrow{a}\left|\right|·\left|\right|\overrightarrow{b}\left|\right|}}& whensgn{a}_1=sgn{b}_2.\hfill \end{array}\right.$$

(28)

Based on the definitions given above for the oriented Minkowskian angles between any two spacelike or timelike vectors, and also in view of (5), the oriented Minkowskian angle $\theta (L_1,L_2)$ between any two non-null directions or between any non-null lines $L_1$ and $L_2$ passing through the origin of a Minkowskian plane $E_1^2$ may be well defined as the oriented Minkowskian angle $\theta (\overrightarrow{l_1},\overrightarrow{l_2})$ between a unit vector $\overrightarrow{l_1}$ on the line $L_1$ and a unit vector $\overrightarrow{l_2}$ on the line $L_2$; $\theta (L_1,L_2)=\theta (\overrightarrow{l_1},\overrightarrow{l_2})$.

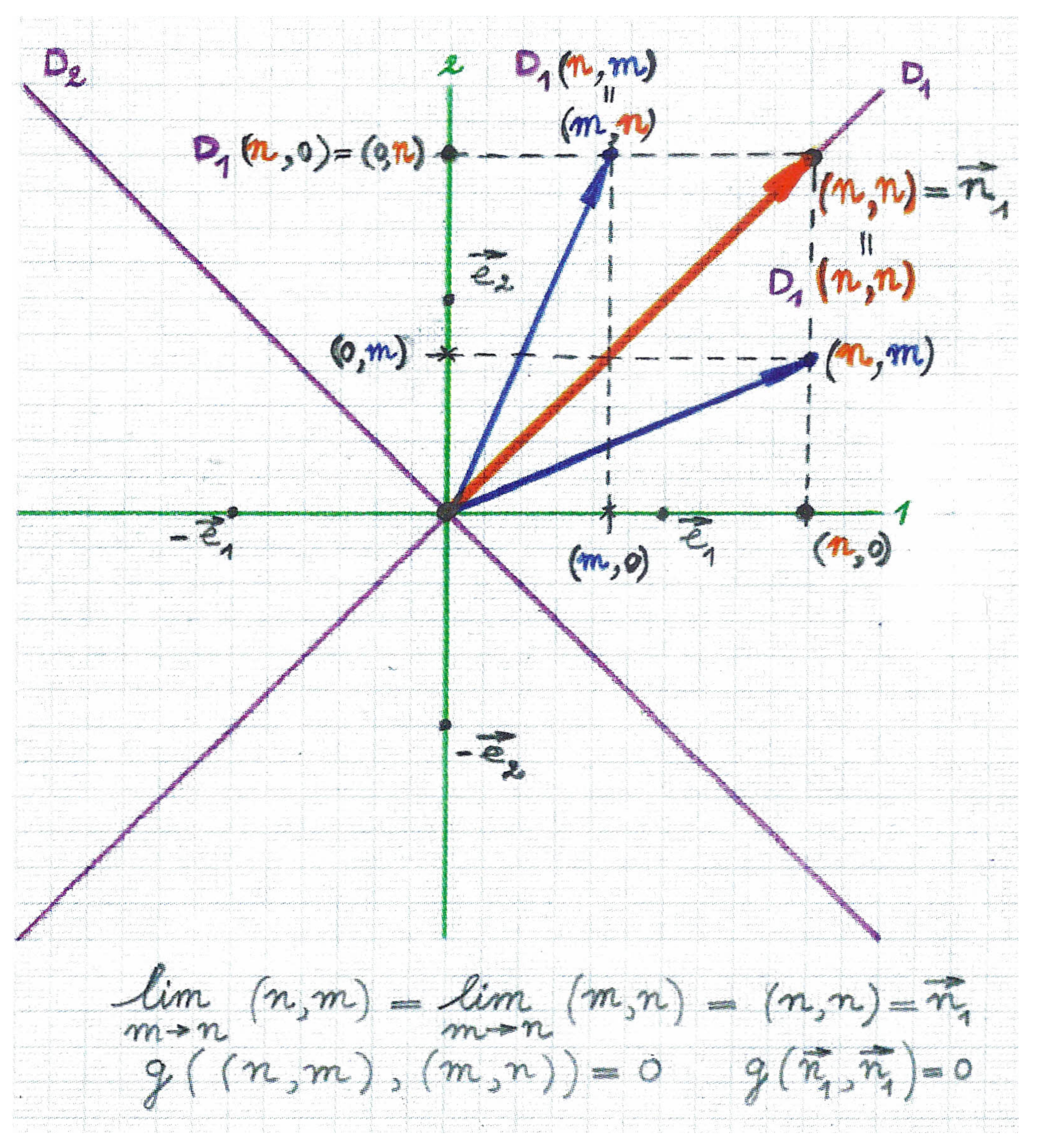
As a kind of transition to the definition of Minkowskian angles involving one or two null vectors and also in a way continuing the former comment on perpendicular vectors in a Minkowskian plane, now, (hereby somewhat following O’Neill [5], p. 48, Figure 3), one may visualise, for instance, the following pair of vectors that are mutually orthogonal in $E_1^2$: $\{(n,m),D(n,m)=(m,n)|n\in R_0^{+},m\in ]0,n\left[\right\}$. A null vector like $\overrightarrow{v}=(n,n)$ may thus be seen to originate as the limit of the pair of the mutually orthogonal vectors formed by the spacelike vector $(n,m)$ and the timelike vector $(m,n)$ for m going to n: $(n,n)=li{m}_{m\to n}(n,m)=li{m}_{m\to n}(m,n)$, this limit thus yielding a non-trivial vector $\overrightarrow{n}$ that is perpendicular to itself; (cfr. Figure 4). And of course, similarly one may think of the null vectors of the second diagonal too as non-trivial auto-orthogonal vectors.

4. The Minkowskian Pseudo-Angles between A Null Direction and Any Spacelike or Timelike Direction

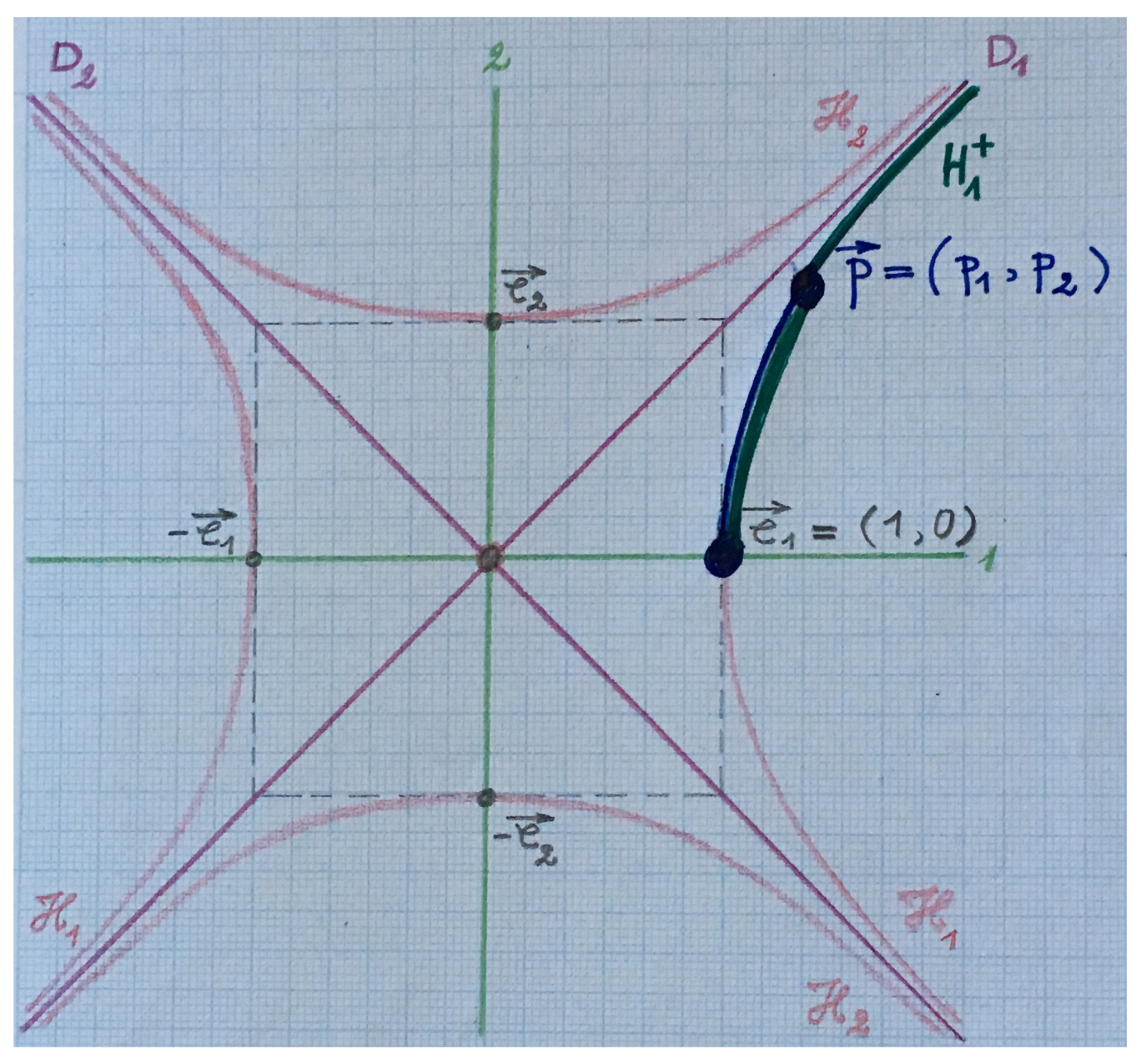
Any spacelike or timelike vector $\overrightarrow{a}=(a_1,a_2)$ has a well determined Minkowskian length or norm $\left|\right|\overrightarrow{a}\left|\right|=|a_1^2-a_2^2{|}^{\frac{1}{2}}$ which is essentially non-zero and thus such a vector can be normalised to the corresponding unit spacelike or timelike vector$\overrightarrow{v}=\overrightarrow{a}/\left|\right|\overrightarrow{a}\left|\right|$. For null vectors $\overrightarrow{n_1}=(n,n)$ of $D_1$ and $\overrightarrow{n_2}=(-n,n)$ of $D_2$, ($n\in R_0$), this kind of normalisation of course is not possible, since actually $\left|\right|\overrightarrow{n_1}{\left|\right|}^2=\left|\right|\overrightarrow{n_2}{\left|\right|}^2=|n^2-n^2|=0$. 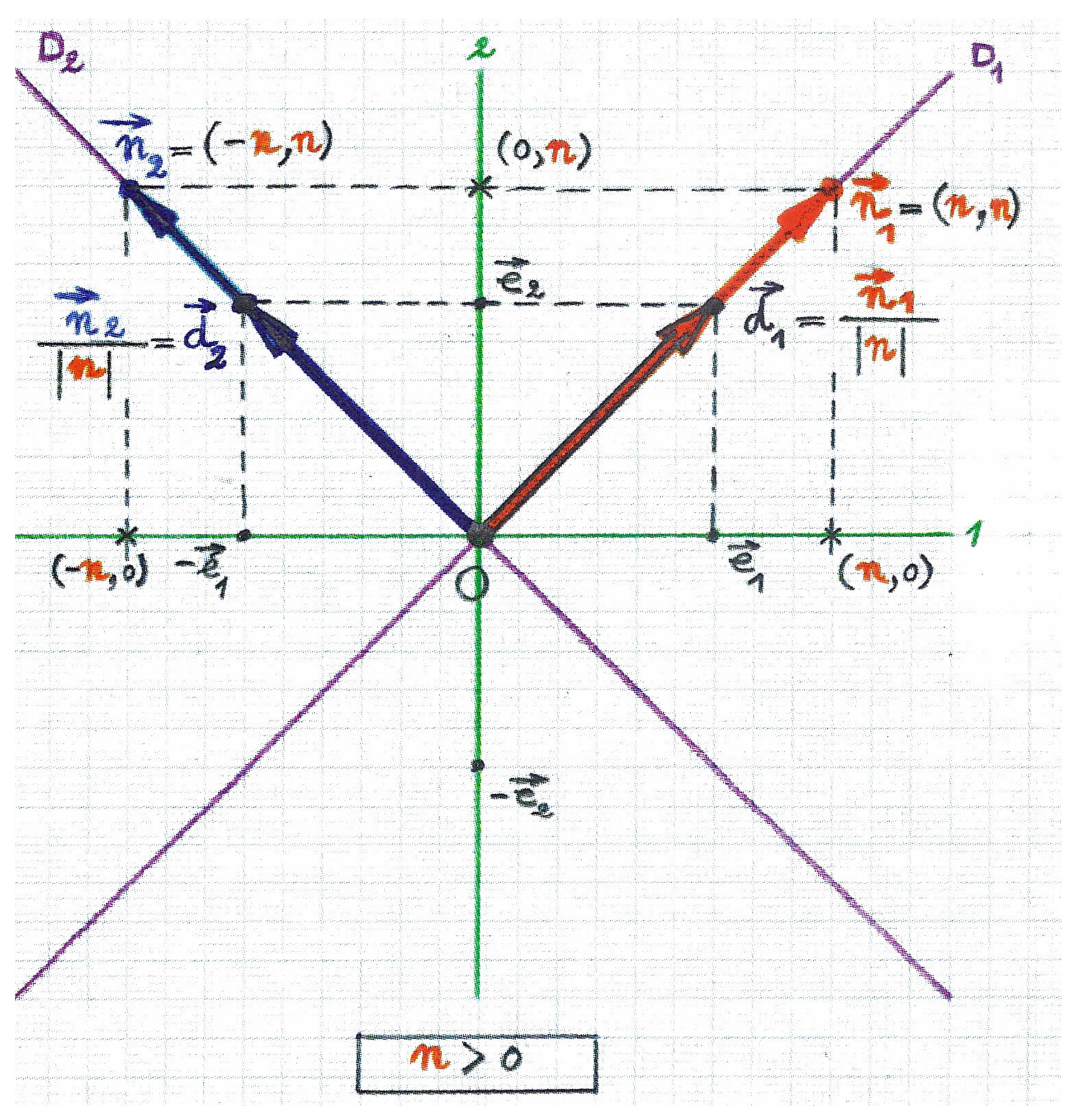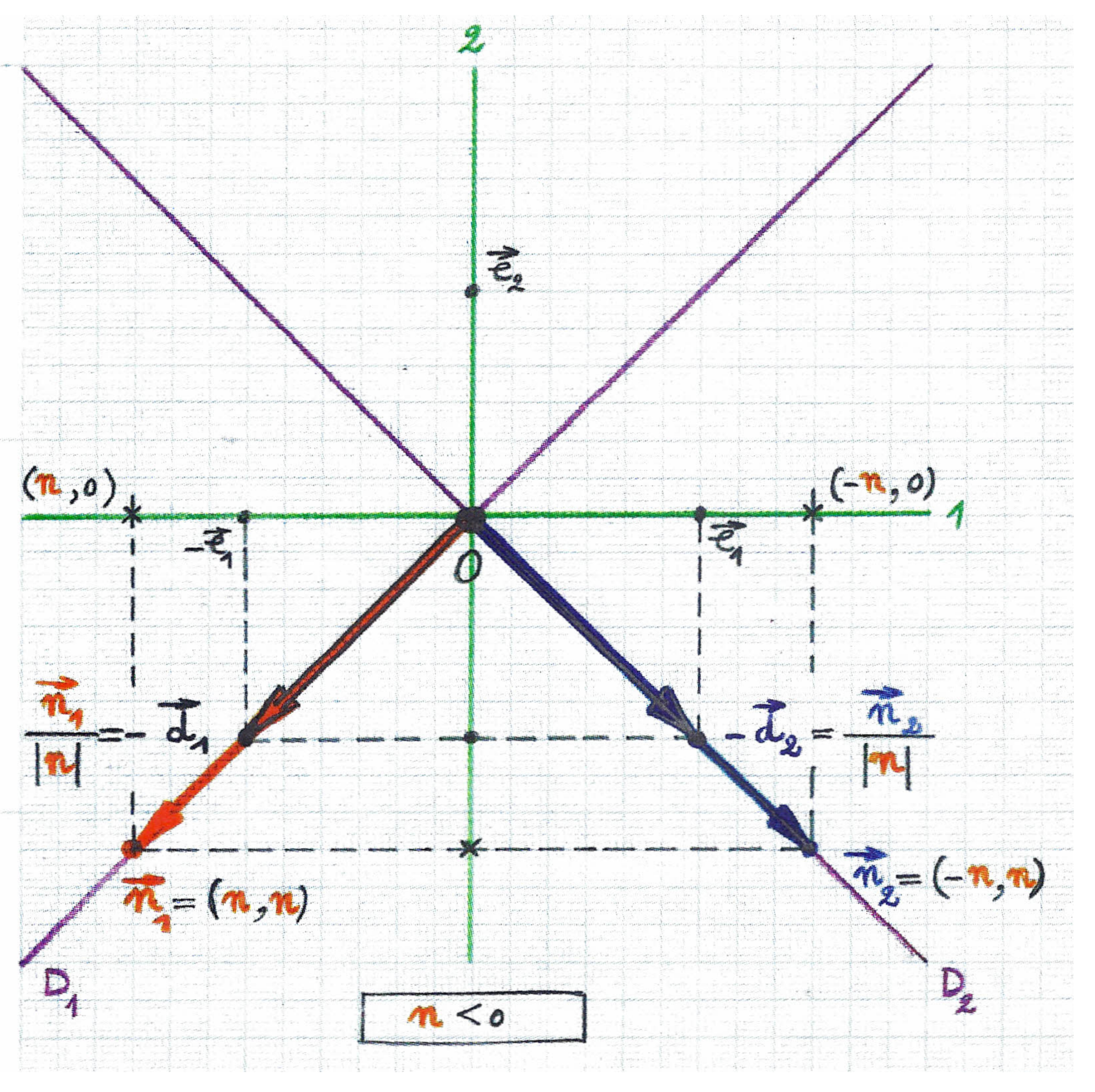Then, for null vectors in a Minkowskian plane choosing as a way of standardi-sation the individual normalisation of their two components, from now on, we propose to consider, respectively $\overrightarrow{d_1}=(1,1)=\overrightarrow{n_1}/\left|n\right|$ in case $n>0$ and $-\overrightarrow{d_1}=(-1,-1)=\overrightarrow{n_1}/\left|n\right|$ in case $n<0$, and $\overrightarrow{d_2}=(-1,1)=\overrightarrow{n_2}/\left|n\right|$ in case $n>0$ and $-\overrightarrow{d_2}=(1,-1)=\overrightarrow{n_1}/\left|n\right|$ in case $n<0$, as the normalised null vectors corresponding to given null vectors $\overrightarrow{n_1}$ and $\overrightarrow{n_2}$; (cfr. Figure 5 and Figure 6). And while for spacelike and timelike vectors$\overrightarrow{a}=(a_1,a_2)$ their norm equals their length $\left|\right|\overrightarrow{a}\left|\right|$, for null vectors $\overrightarrow{n_1}=(n,n)$ and $\overrightarrow{n_2}=(-n,n)$, $n\in R_0$, their lengths $\left|\right|\overrightarrow{n_1}\left|\right|$ and $\left|\right|\overrightarrow{n_2}\left|\right|$ being zero, we propose to define their pseudo-norms $|\overrightarrow{n_1}|$ and $|\overrightarrow{n_2}|$ to be equal to the absolute value $\left|n\right|=|-n|\ne 0$ of their co-ordinates: $|\overrightarrow{n_1}|=|\overrightarrow{n_2}|=|n|$. Thus, we have the normalisations $\overrightarrow{d_i}=\pm \overrightarrow{n_i}/\left|\overrightarrow{n_i}\right|$, + or − depending on n being positive or negative, respectively.

The oriented Minkowskian pseudo-angles θ between unit spacelike or timelike vectors$\overrightarrow{u}=(u_1,u_2)$, ($u_1^2-u_2^2=\pm 1$), and normalised null vectors $\pm \overrightarrow{d_1}$ or $\pm \overrightarrow{d_2}$ are defined to be given by their pseudo-angles ψ of Helzer. In order to establish the formulae for these angles in terms of the hyperbolic functions, next the angles $\theta (\overrightarrow{u},\overrightarrow{d_1})$ and $\theta (\overrightarrow{d_2},\overrightarrow{u})$ will be dealt with explicitly; (thereby, in view of (5) and (6), essentially all possibilities are taken care of). The oriented Minkowskian pseudo-angle $\theta (\overrightarrow{u},\overrightarrow{d_1})$ from $\overrightarrow{u}$ to $\overrightarrow{d_1}$ is defined to be given by the pseudo-angle $\psi (\overrightarrow{u},\overrightarrow{d_1})$ from $\overrightarrow{u}$ to $\overrightarrow{d_1}$ such that according to (1)–(4),

$$\begin{array}{ccc}\theta (\overrightarrow{u},\overrightarrow{d_1})\hfill & =\hfill & ln2-ln|u_1+u_2|\hfill \\ & =\hfill & ln|\frac{2}{u_1+u_2}|\hfill \\ & =\hfill & ln|\frac{2(u_1-u_2)}{u_1^2-u_2^2}|\hfill \\ & =\hfill & ln\left|2\right(u_1-u_2\left)\right|\hfill \\ & =\hfill & ln\left|2g\right(\overrightarrow{u},\overrightarrow{d_1}\left)\right|\hfill \\ & (=\hfill & ln|g(\overrightarrow{u},\overrightarrow{d_1})+g(\overrightarrow{u},D\overrightarrow{d_1})\left|\right).\hfill \end{array}$$

(29)

And, the oriented Minkowskian pseudo-angle $\theta (\overrightarrow{d_2},\overrightarrow{u})$ from $\overrightarrow{d_2}$ to $\overrightarrow{u}$ is defined to be given by the pseudo-angle $\psi (\overrightarrow{d_2},\overrightarrow{u})$ from $\overrightarrow{d_2}$ to $\overrightarrow{u}$ such that, according to (1)–(4),

$$\begin{array}{ccc}\theta (\overrightarrow{d_2},\overrightarrow{u})\hfill & =\hfill & ln|u_1+u_2|+ln2\hfill \\ & =\hfill & ln\left|2\right(u_1+u_2\left)\right|\hfill \\ & =\hfill & ln\left|2g\right(\overrightarrow{d_2},\overrightarrow{u}\left)\right|\hfill \\ & (=\hfill & ln|g(\overrightarrow{d_2},\overrightarrow{u})+g(\overrightarrow{d_2},D\overrightarrow{u})\left|\right).\hfill \end{array}$$

(30)

Hence, in analogy with Theorem 1, from (29) and (30), one has the following.

Theorem 3.

Let $\theta (\overrightarrow{u},\overrightarrow{d_1})$ and $\theta (\overrightarrow{d_2},\overrightarrow{u})$ be the oriented Minkowskian pseudo-angles from a unit vector $\overrightarrow{u}$ to the normalised null vector $\overrightarrow{d_1}$ and from the normalised null vector $\overrightarrow{d_2}$ to a unit vector $\overrightarrow{u},$ respectively. Then,

$$cosh\theta (\overrightarrow{u},\overrightarrow{d_1})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{1+4g{(\overrightarrow{u},\overrightarrow{d_1})}^2}{4g(\overrightarrow{u},\overrightarrow{d_1})}}& when{u}_1-u_2>0\hfill \\ \hfill {\displaystyle -\frac{1+4g{(\overrightarrow{u},\overrightarrow{d_1})}^2}{4g(\overrightarrow{u},\overrightarrow{d_1})}}& when{u}_1-u_2<0,\hfill \end{array}\right.$$

(31)

$$sinh\theta (\overrightarrow{u},\overrightarrow{d_1})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{1-4g{(\overrightarrow{u},\overrightarrow{d_1})}^2}{4g(\overrightarrow{u},\overrightarrow{d_1})}}& when{u}_1-u_2<0\hfill \\ \hfill {\displaystyle -\frac{1-4g{(\overrightarrow{u},\overrightarrow{d_1})}^2}{4g(\overrightarrow{u},\overrightarrow{d_1})}}& when{u}_1-u_2>0;\hfill \end{array}\right.$$

(32)

$$cosh\theta (\overrightarrow{d_2},\overrightarrow{u})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{1+4g{(\overrightarrow{d_2},\overrightarrow{u})}^2}{4g(\overrightarrow{d_2},\overrightarrow{u})}}& when{u}_1+u_2>0\hfill \\ \hfill {\displaystyle -\frac{1+4g{(\overrightarrow{d_2},\overrightarrow{u})}^2}{4g(\overrightarrow{d_2},\overrightarrow{u})}}& when{u}_1+u_2<0,\hfill \end{array}\right.$$

(33)

$$sinh\theta (\overrightarrow{d_2},\overrightarrow{u})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{1-4g{(\overrightarrow{d_2},\overrightarrow{u})}^2}{4g(\overrightarrow{d_2},\overrightarrow{u})}}& when{u}_1+u_2<0\hfill \\ \hfill {\displaystyle -\frac{1-4g{(\overrightarrow{d_2},\overrightarrow{u})}^2}{4g(\overrightarrow{d_2},\overrightarrow{u})}}& when{u}_1+u_2>0.\hfill \end{array}\right.$$

(34)

In connection with a general comment made in the Introduction concerning potential applications of the contents of this paper in semi-Riemannian geometry, based on Theorems 1 and 3, it may be good to explicitly formulate the following.

Corollary 2.

For any two different normalised spacelike, timelike or null vector fields, their Minkowskian scalar product is constant if and only if their Minkowskian angle or pseudo-angle is constant.

For any spacelike or timelike vector $\overrightarrow{a}$ of Minkowskian length $\left|\right|\overrightarrow{a}\left|\right|$, $\overrightarrow{u}=\overrightarrow{a}/\left|\right|\overrightarrow{a}\left|\right|$ is the corresponding normalised spacelike or timelike vector, and for any null vector $\overrightarrow{n_1}=(n,n)$ or ${\overrightarrow{n}}_2=(-n,n)$, $(n\in R_0)$, $\pm \overrightarrow{d_1}=\overrightarrow{n_1}/\left|\overrightarrow{n_1}\right|$ or $\pm \overrightarrow{d_2}=\overrightarrow{n_2}/\left|\overrightarrow{n_2}\right|$, (+ when $n>0$ and − when $n<0$) is the corresponding normalised null vector, and the oriented Minkowskian pseudo-angles between such vectors$\overrightarrow{a}$ and $\overrightarrow{n_i}$, ($i=1,2$), are defined as the oriented Minkowskian pseudo-angles between their corresponding normalised vectors $\overrightarrow{u}$ and $\pm \overrightarrow{d_i}$; $\theta (\overrightarrow{a},\overrightarrow{n_i})=\theta (\overrightarrow{u},\pm \overrightarrow{d_i})$. In addition, following this definition, the above expressions (31)–(34) may readily be adapted to corresponding formulae involving the Minkowskian scalar products $g(\overrightarrow{a},\overrightarrow{n_i})$ as follows.

Theorem 4.

Let $\theta (\overrightarrow{a},\overrightarrow{n_1})$ and $\theta (\overrightarrow{n_2},\overrightarrow{a})$ be the oriented Minkowskian pseudo-angles from a non-null vector $\overrightarrow{a}=(a_1,a_2)$ of arbitrary length $\left|\right|\overrightarrow{a}\left|\right|\ne 0$ to an arbitrary null vector $\overrightarrow{n_1}=(n,n)$, $n\in R_0$ and from an arbitrary null vector $\overrightarrow{n_2}=(-n,n)$ to a non-null vector $\overrightarrow{a}$, respectively. Then,

$$cosh\theta (\overrightarrow{a},\overrightarrow{n_1})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2+4g{(\overrightarrow{a},\overrightarrow{n_1})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_1})}}& whenn(a_1-a_2)>0\hfill \\ \hfill {\displaystyle -\frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2+4g{(\overrightarrow{a},\overrightarrow{n_1})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_1})}}& whenn(a_1-a_2)<0,\hfill \end{array}\right.$$

(35)

$$sinh\theta (\overrightarrow{a},\overrightarrow{n_1})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2-4g{(\overrightarrow{a},\overrightarrow{n_1})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_1})}}& whenn(a_1-a_2)<0\hfill \\ \hfill {\displaystyle -\frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2-4g{(\overrightarrow{a},\overrightarrow{n_1})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_1})}}& whenn(a_1-a_2)>0;\hfill \end{array}\right.$$

(36)

$$cosh\theta (\overrightarrow{n_2},\overrightarrow{a})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2+4g{(\overrightarrow{a},\overrightarrow{n_2})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_2})}}& whenn(a_1+a_2)>0\hfill \\ \hfill {\displaystyle -\frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2+4g{(\overrightarrow{a},\overrightarrow{n_2})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_2})}}& whenn(a_1+a_2)<0,\hfill \end{array}\right.$$

(37)

$$sinh\theta (\overrightarrow{n_2},\overrightarrow{a})=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2-4g{(\overrightarrow{a},\overrightarrow{n_2})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_2})}}& whenn(a_1+a_2)<0\hfill \\ \hfill {\displaystyle -\frac{{\left|n\right|}^2\left|\right|\overrightarrow{a}{\left|\right|}^2-4g{(\overrightarrow{a},\overrightarrow{n_2})}^2}{4\left|n\right|\left|\right|\overrightarrow{a}\left|\right|g(\overrightarrow{a},\overrightarrow{n_2})}}& whenn(a_1+a_2)>0.\hfill \end{array}\right.$$

(38)

Based on the definitions given above for the oriented Minkowskian pseudo-angles between any null vector and any spacelike or timelike vector, and also in view of (5), the oriented Minkowskian pseudo-angle $\theta (D_i,L)$ between a null direction and any spacelike or timelike direction or between one of the null lines $D_1,D_2$ and any non-null line L passing through the origin of a Minkowskian plane $E_1^2$, may be well defined as the oriented Minkowskian pseudo-angle $\theta ({\overrightarrow{d}}_i,\overrightarrow{l}),$ whereby $\overrightarrow{l}$ is a unit vector on the line L; $\theta (D_i,L)=\theta ({\overrightarrow{d}}_i,\overrightarrow{l})$.

5. The Minkowskian Angles between Null Directions

Finally, to deal with the situation involving two null vectors, of course, two cases are to be considered: (i) the null vectors are co-linear and (ii) they are not. To begin with, for the normalised null vectors $\pm {\overrightarrow{d}}_i$, the oriented Minkowskian angles $\theta (\pm {\overrightarrow{d}}_i,\pm {\overrightarrow{d}}_j)$, $(i,j\in \{1,2\left\}\right)$, are defined to be given by their pseudo-angles $\psi (\pm {\overrightarrow{d}}_i,\pm {\overrightarrow{d}}_j)$ of Helzer. In addition, based on (5) and (6), it then suffices to look at the angles $\theta ({\overrightarrow{d}}_1,{\overrightarrow{d}}_1),\theta ({\overrightarrow{d}}_2,{\overrightarrow{d}}_2)$ and $\theta ({\overrightarrow{d}}_2,{\overrightarrow{d}}_1)$. (i) In the case of normalised null vectors on the same diagonal, since $\psi (\overrightarrow{v},\overrightarrow{v})=0$ for all $\overrightarrow{v}\ne \overrightarrow{o}$,

$$\theta ({\overrightarrow{d}}_1,{\overrightarrow{d}}_1)=\theta ({\overrightarrow{d}}_2,{\overrightarrow{d}}_2)=0.$$

(39)

(ii) In the case of normalised null vectors on different diagonals,

$$\theta ({\overrightarrow{d}}_2,{\overrightarrow{d}}_1)=ln2+ln2=2ln2.$$

(40)

In case (i), matters are well in agreement with what we commonly expect to be natural enough the way it is, while, later on, there will follow some geometrical comments that may make the value $2ln2$ occurring in case (ii) not to appear as too unnatural after all. For the time being and for the sake of more easy reference, (39) and (40) will be put together in the following.

Theorem 5.

For the normalised null vectors $\overrightarrow{d_1}=(1,1)$ and $\overrightarrow{d_2}=(-1,1)$ their oriented Minkowskian angles are given by $\theta (\overrightarrow{d_1},\overrightarrow{d_1})=\theta (\overrightarrow{d_2},\overrightarrow{d_2})=0$ and $\theta (\overrightarrow{d_2},\overrightarrow{d_1})=2ln2$.

At this stage, without further expanding on it, since (29) and (30) in particular imply that

$$\theta (\pm \overrightarrow{d_i},\pm \overrightarrow{e_i})=\pm ln2,$$

(41)

we may conclude the following.

Proposition 1.

In a Minkowskian plane $E_1^2$ the standard basic vectors $\{\pm \overrightarrow{e_1},\pm \overrightarrow{e_2}\}$ are the only unit vectors which bisect the null vectors $\{\pm \overrightarrow{d_1},\pm \overrightarrow{d_2}\}$.

Next, for an arbitrary pair of null vectors, their oriented Minkowskian angle is defined as to be given by the oriented Minkowskian angle between their normalised null vectors. In addition, for any pair of null directions or diagonals $D_i$ and $D_j$, their Minkowskian angle is defined to be the Minkowskian angle between their normalised vectors ${\overrightarrow{d}}_i$ and ${\overrightarrow{d}}_j$; $\theta (D_i,D_j)=\theta (\overrightarrow{d_i},\overrightarrow{d_j})$.

6. The Unoriented Minkowskian Angles and Pseudo-Angles

For two vectors $\overrightarrow{v}$ and $\overrightarrow{w}$ of any causal characters each and in whatever combination together, let $\theta (\overrightarrow{v},\overrightarrow{w})$ be their oriented Minkowskian angle when both $\overrightarrow{v}$ and $\overrightarrow{w}$ are non-null vectors or when both are null vectors (cfr. Section 3 and Section 5) or their oriented Minkowskian pseudo-angle when one of the vectors $\overrightarrow{v}$ and $\overrightarrow{w}$ is null and the other one is non-null (cfr. Section 4). In any case, from (6), it follows that $\theta (\overrightarrow{w},\overrightarrow{v})=-\theta (\overrightarrow{v},\overrightarrow{w})$, so that it makes sense to define $\overline{\theta }(\overrightarrow{v},\overrightarrow{w})=|\theta (\overrightarrow{v},\overrightarrow{w})|=|\theta (\overrightarrow{w},\overrightarrow{v})|$ as the unoriented or absolute Minkowskian angle or Minkowskian pseudo-angle between these vectors. And, the unoriented or absolute Minkowskian angles between two non-null directions and between two null directions and the unoriented or absolute Minkowskian pseudo-angles between one null and one non-null direction are likewise defined.

In a Minkowskian plane $E_1^2$, geometrically, the two most distinguished directions may very well be the null directions $D_1$ and $D_2$; their absolute Minkowskian angle is given by $\overline{\theta }(D_1,D_2)=2ln2$. The absolute Minkowskian pseudo-angles between the co-ordinate axes $A_1$ and $A_2$ (spanned respectively by the standard unit vectors $\pm \overrightarrow{e_1}$ and $\pm \overrightarrow{e_2}$) and the null diagonals $D_1$ and $D_2$ (spanned by $\pm \overrightarrow{d_1}$ and $\pm \overrightarrow{d_2}$) being given by $\overline{\theta }(A_i,D_j)=ln2$, ($i,j\in \{1,2\}$), and, further also taking into account (29) and (30), in a way, Proposition 1 may be reformulated as follows.

Proposition 2.

In a Minkowskian plane $E_1^2,$ the co-ordinate axes $A_1$ and $A_2$ are geometrically characterised as the only two bisectrices of the null lines $D_1$ and $D_2$.

7. A Geometrical Meaning of the Minkowskian Angles and Pseudo-Angles

Let us recall that the Minkowskian arclengths L on the unit Minkowskian circle $H:z_1^2-z_2^2=\pm 1$, say, for simplicity, from $e_1=(1,0)$ to the points $\overrightarrow{p}=(p_1,p_2)$ on its upper branch $H_2^{+}:z_2={(z_1^2-1)}^{\frac{1}{2}},z_1\ge 1$, are given by

$$\begin{array}{ccc}L({\overrightarrow{e}}_1,\overrightarrow{p})\hfill & =\hfill & {\int }_1^{p_1}{|1-{(d{z}_2/d{z}_1)}^2|}^{-1/2}d{z}_1\hfill \\ & =\hfill & {\int }_1^{p_1}{(z_1^2-1)}^{-1/2}d{z}_1\hfill \\ & =\hfill & ln\{z_1+{(z_1^2-1)}^{1/2}\}{|}_1^{p_1}\hfill \\ & =\hfill & ln(p_1+p_2),\hfill \end{array}$$

(42)

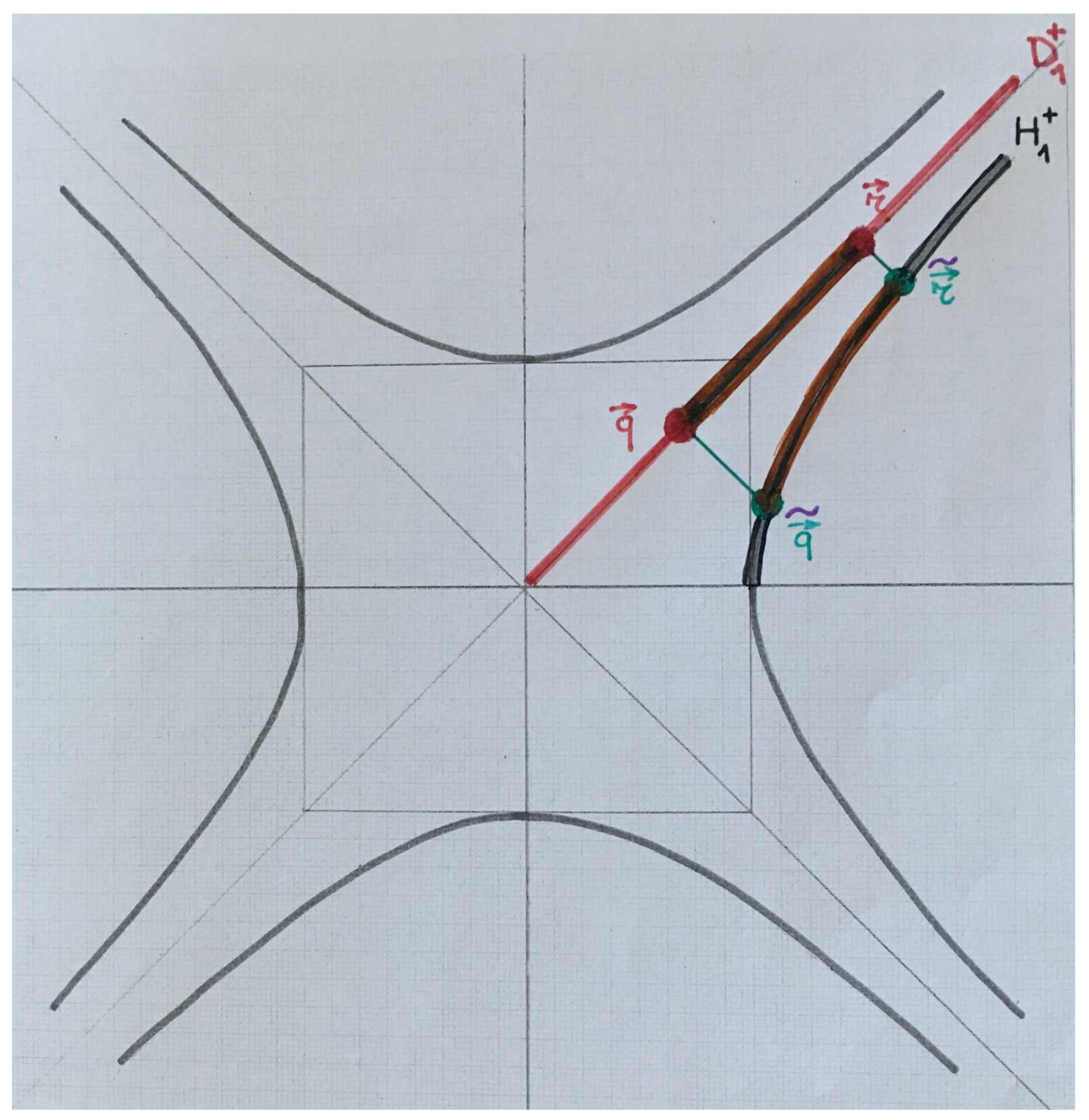
cfr. Figure 7; (the readers likely will have thought about this already when observing the former formulae (2) and (3), from Helzer). And for geometrical interpretations of oriented Minkowskian angles and pseudo-angles, it is good “to count" Minkowskian lengths on and of arcs on the Euclidean hyperbola’s H taking into account their orientations as indicated in Figure 8.

Next, Minkowskian pseudo-distances $\tilde{d}$ between two points on the same half straight null line $z_2=\pm z_1,z_1>0$ or $z_1<0$, and the Minkowskian pseudo-lengths of the corresponding parts on the diagonals $D_1$ and $D_2$ are defined by the Minkowskian lengths of arcs on H that are determined thereupon by the Euclidean orthogonal projections of these points on $D_1$ or $D_2$. To be more concrete, say, for points $\overrightarrow{q}=(q,q)$ and $\overrightarrow{r}=(r,r),(q,r\in R_0^{+}$), on $D_1:z_2=z_1,z_1>0$, their Minkowskian pseudo-distance $\tilde{d}(\overrightarrow{q},\overrightarrow{r})$ is defined by the Minkowskian arclength $L(\tilde{\overrightarrow{q}},\tilde{\overrightarrow{r}})$ on $H_1^{+}$ between the Euclidean projections $\tilde{\overrightarrow{q}}$ and $\tilde{\overrightarrow{r}}$ on $H_1^{+}$ of the points $\overrightarrow{q}$ and $\overrightarrow{r}$ of $D_1$ orthogonal in the Euclidean sense to $D_1$, cfr. Figure 9:

$$\begin{array}{ccc}\tilde{d}(\overrightarrow{q},\overrightarrow{r})\hfill & =\hfill & L(\tilde{\overrightarrow{q}},\tilde{\overrightarrow{r}})\hfill \\ & =\hfill & \overline{\theta }(\tilde{\overrightarrow{q}},\tilde{\overrightarrow{r}}).\hfill \end{array}$$

(43)

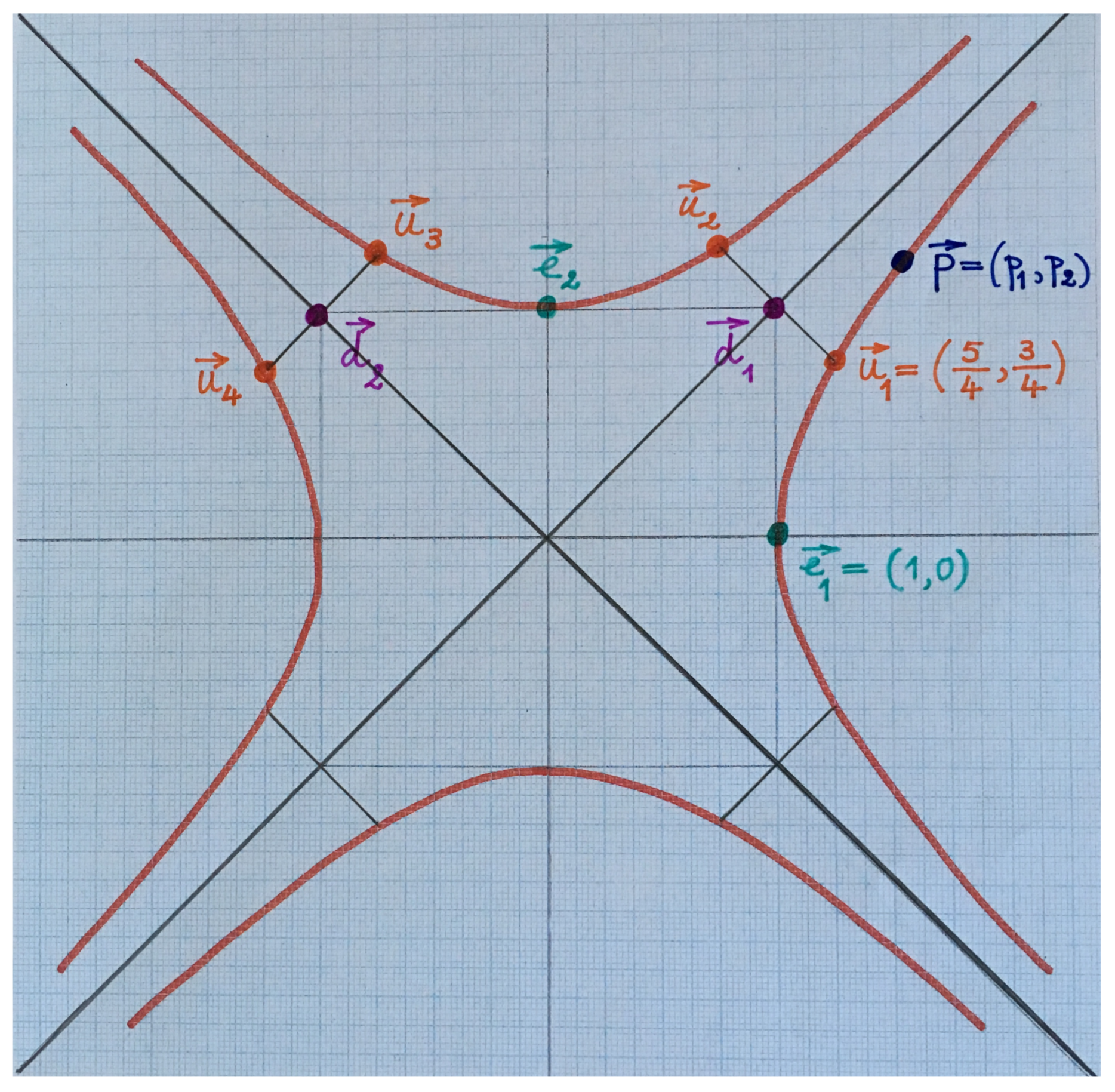
And, finally, let us—in maybe too primitive a way—think $\mathcal{C}$ $=H\cup \{\pm {\overrightarrow{d}}_1,\pm {\overrightarrow{d}}_2\}$ as a closed central curve, centered at the origin O of the Minkowskian plane $E_1^2$, having precisely one point in each radial direction going out of O. Then, any pair of directions in this plane well determines a pair of points on $\mathcal{C}$. In addition, the oriented Minkowskian angles or pseudo-angles between these directions then correspond to the oriented arclengths on H and the oriented pseudo-lengths of parts of the null lines $D_1$ and $D_2$, whereby these pseudo-lengths come about in an oriented way as suggested in Figure 10. By way of examples, here are the Minkowskian angles or pseudo-angles $\theta$ between some unit spacelike or timelike vectors and some normalised null vectors as well, whereby ${\overrightarrow{u}}_1=(\frac{5}{4},\frac{3}{4})$, ${\overrightarrow{u}}_2=(\frac{3}{4},\frac{5}{4})$, ${\overrightarrow{u}}_3=(\frac{-3}{4},\frac{5}{4})$ and ${\overrightarrow{u}}_4=(\frac{-5}{4},\frac{3}{4}):\theta ({\overrightarrow{e}}_1,{\overrightarrow{d}}_1)=ln2,\theta ({\overrightarrow{u}}_1,{\overrightarrow{d}}_1)=0,\theta ({\overrightarrow{d}}_1,{\overrightarrow{d}}_2)=-2ln2,\theta ({\overrightarrow{e}}_1,{\overrightarrow{u}}_2)=ln2,\theta ({\overrightarrow{e}}_1,{\overrightarrow{e}}_2)=0,\theta ({\overrightarrow{e}}_1,{\overrightarrow{u}}_3)=-ln2,\theta ({\overrightarrow{d}}_1,{\overrightarrow{u}}_2)=0,\theta ({\overrightarrow{d}}_1,{\overrightarrow{u}}_3)=-2ln2,\theta ({\overrightarrow{e}}_1,{\overrightarrow{u}}_4)=-ln2,\theta ({\overrightarrow{e}}_1,\overrightarrow{p})=ln(p_1+p_2),\theta ({\overrightarrow{e}}_1,{\overrightarrow{u}}_1)=ln2,\theta ({\overrightarrow{u}}_1,{\overrightarrow{p}}_1)=ln(p_1+p_2)-ln2$ ; (cfr. Figure 11).

8. Conclusions

The 4D physical space-time of Minkowski with co-ordinates $(x,y,z;t)$ is the 4D pseudo-Euclidean geometrical space that is the product of a negative definite Euclidean line $(R,-d{t}^2)$ and a positive definite 3D Euclidean space $(R^3,d{x}^2+d{y}^2+d{z}^2)$, whereby the time-space scaling “i seconds = 300 000 kilometers” is taken into account. At any given moment of time t, the angles between any two directions in the physical 3D Euclidean $(x,y,z)$ space at that moment are their standard original Euclidean angles; they are algebraically determined in terms of the group of the Euclidean rotations in a plane around a same point in this plane and they are geometrically measured by the Euclidean lengths of corresponding arcs on a Euclidean unit circle. From a natural scientific point of view there has been no immediate need to be occupied with looking for meaningful angles between two directions with arbitrary causal characters in planes of Minkowski. However, for two spacelike directions and geometrically equivalently for two timelike directions in a Minkowskian plane that belong to a same branch of the Minkowskian unit circle -an Euclidean orthogonal hyperbola-, their Minkowskian angles classically have been determined algebraically and measured geometrically by the straightforward adaptation of the traditional Euclidean approaches, now making use of the Minkowskian rotations with a same center and with Minkowskian lengths of corresponding arcs on a Minkowskian unit circle.

On the other hand, the algebraical definition in Minkowskian geometry of a proper notion of angle in the Euclidean way fails for directions that from a center point toward different branches of a Minkowskian unit circle with this center and also fails when null directions are involved. In the present paper, a geometrical generalisation of the Euclidean measure of angles between any two directions as the Euclidean lengths of corresponding arcs on a Euclidean unit circle is given for any two directions with arbitrary causal characters in a Minkowskian plane, by a well-defined notion of the Minkowskian angles or pseudo-angles of these two directions. This notion bases on the measurements of Minkowskian lengths and pseudo-lengths of corresponding parts of a Minkowskian unit circle and of parts of the asymptotes of this Euclidean orthogonal hyperbola. However imperfect that this extension of Euclidean angles to Minkowskian angles and pseudo-angles cannot help to be, it does have qualities of generality and of geometrical naturalness (up to an eventual change of calibration related to the choice of normalisation of the null vectors). And, of course, the classical Minkowskian angles between any two spacelike directions and between any two timelike directions within a same branch of the Minkowskian unit circle do properly fit in well into the above given notion of central Minkowskian angles and pseudo-angles.