Insights into the Stability of Mixed Convective Darcy–Forchheimer Flows of Cross Liquids from a Vertical Plate with Consideration of the Significant Impact of Velocity and Thermal Slip Conditions

Abstract

This paper reflects the effects of velocity and thermal slip conditions on the stagnation-point mixed convective flow of Cross liquid moving over a vertical plate entrenched in a Darcy–Forchheimer porous medium. A Cross liquid is a type of non-Newtonian liquid whose viscosity depends on the shear rate. The leading partial differential equations (PDEs) are altered to nonlinear ordinary differential equations (ODEs) via feasible similarity transformations. These transmuted equations are computed numerically through the bvp4c solver. The authority of sundry parameters on the temperature and velocity distributions is examined graphically. In addition, the characteristics of heat transfer are analyzed in the presence of the impact of drag forces. The outcomes reveal that the permeability parameter decelerates the drag forces and declines the rate of heat transfer in both forms of solutions. Moreover, it is found that the drag forces decline with the growing value of the Weissenberg parameter in the upper branch solutions, while a reverse trend is revealed in the lower branch solutions. However, the rate of heat transfer shows a diminishing behavior with an increasing value of the Weissenberg parameter.

1. Introduction

Many liquids such as detergents, printer ink, animal blood, foodstuff, paints, polymer fluids, etc., transform their properties of flow subjected to operating shear stress, and thus diverge from viscous fluids. These fluids are identified as non-Newtonian substances. Numerous researchers have reported different non-Newtonian fluid models and a few of them are micropolar, Casson, Burgers, Sisko, Maxwell, Oldroyd-B, generalized Burgers, and Cross models, etc. In this paper, we report the Cross liquid [1] model, which states features of stress. In addition, this model sufficiently distinguishes the flow in the region of the power law and high, as well as low, regions of shear rates. In this study, unlike the fluid of power law, first, we achieve a finite viscosity as the rate of shear disappears which also involves a time constant owing to the importance of this model in numerous industrial and engineering computations. Utilization of Cross fluid in industries comprises the polymer latex of the aqueous solution and blood, as well as solutions of synthesis polymeric. Khan et al. [2] inspected the flow of Cross liquid through heat transfer from a planar stretched sheet and found the numerical solution through the shooting technique. The impact of electric field with the characteristic of heat transfer involving Cross liquid from a stretched sheet was scrutinized by Hayat et al. [3] who found that the liquid velocity grew with a rising Weissenberg parameter while temperature distribution decayed due to the Pr. Khan et al. [4] scrutinized the axisymmetric flow and the characteristic of heat transfer containing Cross liquid using a radial stretched sheet and observed that the power-law index raised the structure of the velocity boundary layer. Ijaz Khan et al. [5] scanned the activation energy impact on the magnetic flow of Cross liquid from a stretched surface. Another study, by Ijaz Khan et al. [6], surveyed the magnetic influence on mixed convective flow involving Cross nanofluid with activation energy. Recently, Azam et al. [7] applied the concept of solar energy on time-dependent flow in the presence of Cross nanofluid from a stretched sheet with nonlinear radiation.

The impact of non-Newtonian liquids in the porous media is significant in the fields of engineering and industries due to its numerous applications such as mud injections, cement or slurry grouts to strengthen soils, blood circulation through the kidney, insulation of fibrous, electrochemistry, and drilling liquid injection in rocks for ornamental oil recovery, or for the fortification of the well, etc. Bejan et al. [8], Vafai [9], and Vadasz [10] discussed further applications in their books. Darcy’s law has been utilized generally to inspect the behavior of flow in a porous medium. However, the connection between the velocity of flow and pressure gradient at rates of high flow cannot be modeled through Darcy’s law (Spivey et al. [11]). There is further indication that at a high rate of flow, the non-Darcy involve several subsurface systems of biological porous and engineering porous flow [12,13,14]. Forchheimer [15] included a term of velocity squared in the Darcy to analyze the boundary and inertia aspects. This term is constantly applied to larger Reynolds numbers. Rashidi et al. [16] discovered the influence of electric field on fluid flow with the characteristic of heat transfer in a Darcy–Brinkman–Forchheimer medium. The impact of variable thermal conductivity of Darcy–Forchheimer flow in the presence of Cattaneo–Christov heat-flux was considered by Hayat et al. [17]. In another paper, Hayat et al. [18] examined the non-Newtonian viscoelastic fluid involving nanoliquid through nonlinear stretched surface engrossed in the Darcy–Forchheimer porous medium. Kang et al. [19] employed finite difference technique to discuss the Neumann condition for the general Darcy–Forchheimer problem. Hayat et al. [20] explored the homogenous-heterogeneous reaction of viscous liquid in a Darcy–Forchheimer porous medium through a curved stretched surface. They scrutinized that the porosity and inertia parameters produce larger temperature. Recently, Rasool [21] considered the Darcy–Forchheimer flow to investigate electric field containing nanoparticle through a nonlinear stretched surface. They observed that the mass and heat flux decline due to porosity while drag force is enhanced. A few other similar studies are given in [22,23,24].

As mentioned above, the present literature is packed with works comprising the heat transfer characteristics of boundary-layer flow involving Newtonian and non-Newtonian liquids. In addition, the research regarding the Darcy–Forchheimer flow through heat transport comprising Cross liquid has disclosed a vital pledge in industrial and environmental systems, such as the process of fermentation, petroleum resources, usage of geothermal energy, production of crude oil, grain storage, etc. However, the review of literature revealed that no one has considered the impact of slip effects on mixed convection flow of Cross liquid in the porous media. Therefore, in this research, we focus our attention to the Darcy–Forchheimer flows involving non-Newtonian Cross liquids from a vertical plate with mixed convection and slip effects. Similarity variables are employed to metamorphose the PDEs into nonlinear ODE’s. The metamorphosed system is then exercised through bvp4c solver. The dual nature of solutions is acquired in opposing flow. The vital constraints in the flow field are discussed via graphical portraits.

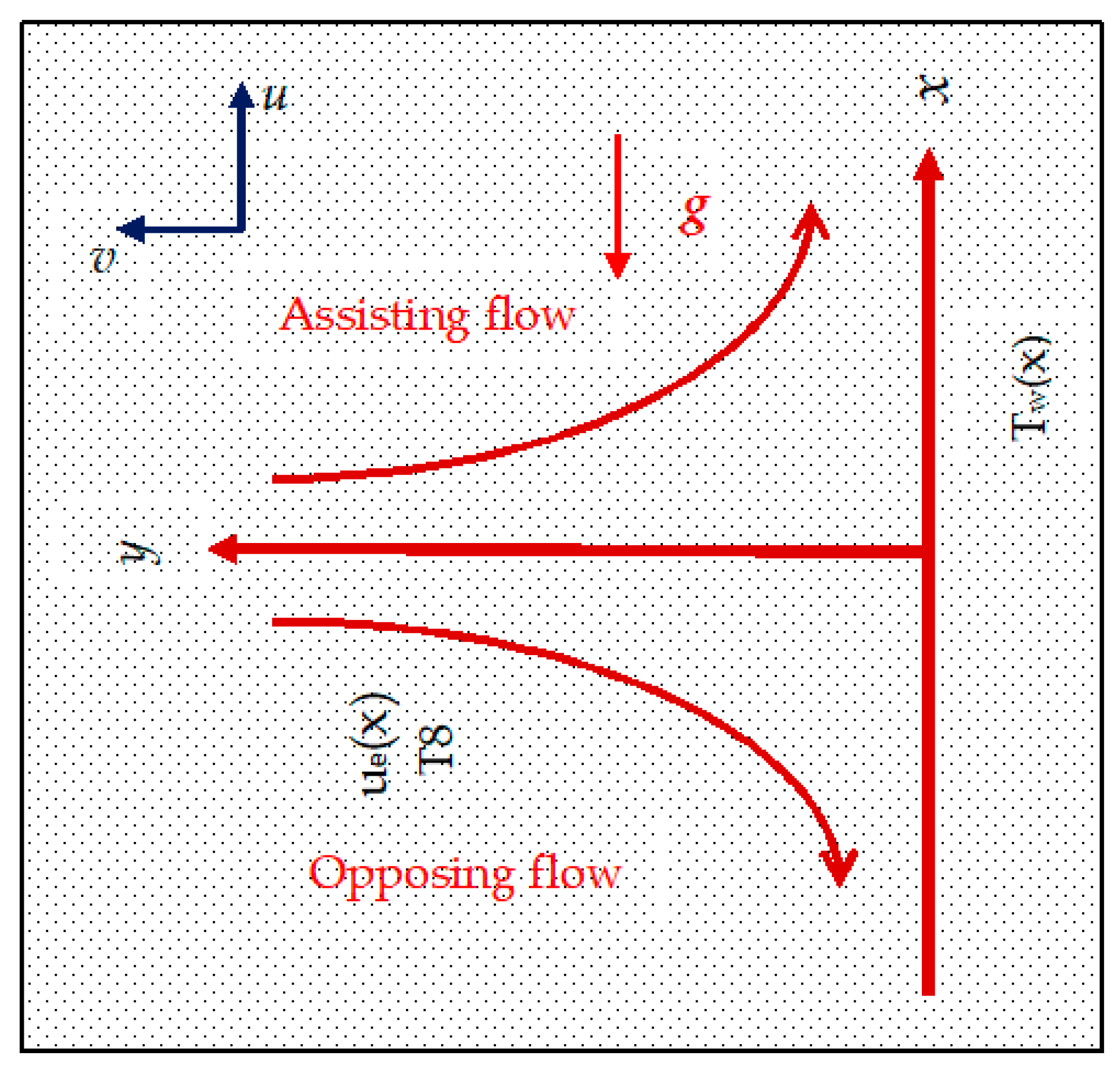
2. Formulation of the Problem

Consider a steady incompressible flow of Cross liquid past a vertical plate in a porous medium with slip impacts. The x-axis is taking along the plate and the y-axis perpendicular to it, as illustrated in Figure 1.

It is presumed that the free stream velocity $u_e(x)=bx$ and the wall temperature $T_w(x)=T_{\infty }+cx$ vary linearly, where $b$ and $c$ are two constants and $T_{\infty }$ is the temperature away from the plate. We utilize the Darcy–Forchheimer model in which the square of the velocity factor is included. In addition, the rheology equations of Cross liquid in term of viscosity are

$$\{\begin{array}{l}\tau =-\stackrel{⌣}{p}\mathrm{I}+{\mathrm{A}}_1\stackrel{⌣}{\mu }\left(\dot{\gamma }\right),\\ \stackrel{⌣}{\mu }-{\stackrel{⌣}{\mu }}_{\infty }=\frac{{\stackrel{⌣}{\mu }}_0-{\stackrel{⌣}{\mu }}_{\infty }}{1+{\left(\stackrel{⌣}{\Gamma }\dot{\gamma }\right)}^n},\end{array}$$

(1)

Here, $n$ the power-law index, $\stackrel{⌣}{\Gamma }$ the time constant, ${\mathrm{A}}_1$ the first tensor of Rivlin–Ericksen and defined as ${\mathrm{A}}_1=\left(\mathrm{grad}\mathrm{V}\right)+{\left(\mathrm{grad}\mathrm{V}\right)}^T$, $\stackrel{⌣}{p}$ the pressure, $\mathrm{I}$ the identity vector, $\dot{\gamma }$ the rate of shear for the current model is taken as

$$\dot{\gamma }={\left[4{\left(\frac{\partial u}{\partial x}\right)}^2+\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right]}^{1/2},$$

(2)

whereas ${\stackrel{⌣}{\mu }}_0$ and ${\stackrel{⌣}{\mu }}_{\infty }$ represent the zero and infinite shear rates, respectively. In the present study, ${\stackrel{⌣}{\mu }}_{\infty }$ is considered to be zero. Therefore, Equation (1) can be written as

$$\stackrel{⌣}{\mu }=\frac{{\stackrel{⌣}{\mu }}_0}{1+{\left(\stackrel{⌣}{\Gamma }\dot{\gamma }\right)}^n}.$$

(3)

Keeping in mind that the temperature and velocity of the two-dimensional (2D) fluid flow are considered in the forms $T=T(x,t)$ and $\mathrm{V}=\left[u\left(x,y\right),v\left(x,y\right),0\right]$, then the governing equations become

$$\frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}=0$$

(4)

$$\frac{1}{{\epsilon }^2}\left(u\frac{\partial u}{\partial x}-u_e\frac{d{u}_e}{dx}+v\frac{\partial u}{\partial y}\right)={\nu }_{eff}\frac{\partial }{\partial y}\left(\frac{\frac{\partial u}{\partial y}}{1+{\left\{\Gamma \frac{\partial u}{\partial y}\right\}}^{1-n}}\right)-\frac{\nu \left(u-u_e\right)}{K_1}-\frac{C_F\left(u^2-u_e^2\right)}{K^{1/2}}+g{\beta }_T\left(T-T_{\infty }\right)$$

(5)

$${\alpha }_m\frac{{\partial }^{2}T}{\partial y^2}-u\frac{\partial T}{\partial x}-v\frac{\partial T}{\partial y}=0$$

(6)

The physical boundary conditions are

$$\begin{gathered} u=L_1\frac{\partial u}{\partial y},v=0,T=T_w(x)+S_1\frac{\partial T}{\partial y}\mathrm{at}y=0, \\ u\to u_e(x),T\to T_{\infty }\mathrm{as}y\to \infty . \end{gathered}$$

(7)

Here, $\left(v,u\right)$ signify, respectively, the velocity components in $x$- and $y$-directions, ${\mu }_{eff}$ the effective (or “apparent”) viscosity, ${\nu }_{eff}={\mu }_{eff}/\rho$ the effective kinematic viscosity, $\rho$ the density, $\epsilon$ the porosity parameter, $K_1$ the porous medium permeability, $k$ the thermal conductivity of fluid, $C_F$ drag coefficient, ${\alpha }_m$ the thermal diffusivity, $T$ the temperature, $L_1$ length of slip, and $S_1$ proportionality constant.

Following Rosali et al. [22], we set up the similarity transformation

$$\eta =y\sqrt{\frac{b}{{\alpha }_m}},\psi =\sqrt{b{\alpha }_m}xf(\eta ),\theta (\eta )=\frac{T-T_{\infty }}{T_w-T_{\infty }}.$$

(8)

Using the similarity transformation in the above PDEs we obtain

$${\epsilon }_{1}f‴\left(1+n{\left(Wef″\right)}^{1-n}\right)+\left(\begin{array}{l}1+ff″-{\left(f\prime \right)}^2+K\left(1-f\prime \right)+\\ B\left(1-{\left(f\prime \right)}^2\right)+\lambda K\theta \end{array}\right){\left(1+{\left(Wef″\right)}^{1-n}\right)}^2=0,$$

(9)

$$\theta ″+\theta \prime f-\theta f\prime =0.$$

(10)

The physical boundary conditions are

$$\begin{gathered} f\prime (0)={\gamma }_{1}f″\left(0\right),f(0)=0,\theta \left(0\right)=1+{\gamma }_2\theta \prime \left(0\right)\mathrm{at}\eta =0, \\ f\prime (\eta )\to 1,\theta \left(\eta \right)\to 0\mathrm{as}\eta \to \infty . \end{gathered}$$

(11)

Here, the parameters are used in the above ODE’s are modified porosity, dimensionless permeability, mixed convection, inertia coefficient, velocity slip, and thermal slip. These are defined as ${\epsilon }_1=\frac{{\epsilon }^2{\nu }_{eff}}{{\alpha }_m}={\epsilon }^2\mathrm{Pr},K=\frac{{\epsilon }^2\nu }{K_{1}b},\lambda =\frac{{\epsilon }^{2}g{\beta }_{T}c}{b^2}=\frac{R{a}_x}{P{e}_x^2}\mathrm{Pr},B=\frac{{\epsilon }^2{u}_e{C}_F}{b\sqrt{K}}$, ${\gamma }_1=L_1\sqrt{\frac{b}{{\alpha }_m}},{\gamma }_2=\sqrt{\frac{b}{{\alpha }_m}}{S}_1$.

Here, $R{a}_x=\frac{{\epsilon }^{2}g{\beta }_T\left(T_w-T_{\infty }\right)x^3}{{\nu }_{eff}{\alpha }_m}$ is the Rayleigh number and $P{e}_x=\frac{x{u}_e}{{\alpha }_m}$ is the Peclet number.

3. Skin Friction and Nusselt Number

The coefficients of skin friction $C_f$ and Nusselt number $N{u}_x$ are identified as

$$C_f=\frac{2{\tau }_w}{\rho u_e{}^2}\mathrm{and}N{u}_x=\frac{x{q}_w}{k\left(T_w-T_{\infty }\right)},$$

(12)

where $q_w$ and ${\tau }_w$ are identified as the heat flux and the shear stress, respectively, which are specified as

$$q_w={-k\frac{\partial T}{\partial y}|}_{y=0}\mathrm{and}{\tau }_w={\left[\frac{\mu \frac{\partial u}{\partial y}}{\left(1+{\left(\Gamma \frac{\partial u}{\partial y}\right)}^{1-n}\right)}\right]}_{y=0}.$$

(13)

Utilizing Equation (8), we have

$$\frac{1}{2}\sqrt{\frac{{\mathrm{Re}}_x}{\mathrm{Pr}}}{C}_f=\frac{f″(0)}{\left(1+{(Wef″(0))}^{1-n}\right)}\mathrm{and}-\theta \prime \left(0\right)=\frac{N{u}_x}{\sqrt{P{e}_x}}.$$

(14)

4. Numerical Procedure

The nonlinear coupled ODEs (9) and (10) with boundary constraint (11) through the bvp4c by converting the leading ODEs to an initial value problem (IVP). In this method, it is further helpful to provide a fixed value to $\eta \to \infty$, say ${\eta }_{\infty }$. The above-mentioned higher order equations are converted into a first-order system as follows:

$$f\prime =p,$$

(15)

$$p\prime =q,$$

(16)

$$q\prime =\frac{{\left(1+{\left(Wef″\right)}^{1-n}\right)}^2}{{\epsilon }_1\left(1+n{\left(Wef″\right)}^{1-n}\right)}\left[p^2-fq-1+K\left(1-p\right)-B\left(1-p^2\right)-\lambda \theta \right],$$

(17)

$${\theta }^{\prime }=z,$$

(18)

$$z\prime =p\theta -fz,$$

(19)

with

$$f(0)=0,p(0)={\gamma }_{1}q\left(0\right),\theta (0)=1+{\gamma }_{2}z\left(0\right).$$

(20)

Numerically grip the system of Equations (15)–(20) as an IVP, we require that the values for $q\left(0\right)$ and $\theta (0)$ are needed, however these values are not mentioned. The initial estimated values for $q\left(0\right)$ and $\theta (0)$ are conjectured and bvp4c is pertained on MATLAB software to achieve accurate results. It is also noted that the multiple solutions are attained by setting different guesses. After that, the considered values of $\theta (\eta )$ and $f\prime (\eta )$ at (${\eta }_{\infty }$ = 8) are evaluated with the boundary conditions $\theta ({\eta }_{\infty })=0$ and $f\prime ({\eta }_{\infty })=1$, in which the predictable values of $q\left(0\right)$ and $\theta (0)$ are prescribed by the Secant method to achieve a better guess for the solutions. The step size is considered as $\Delta \eta =0.01$. The procedure is iteratively repeated until required solutions with an acceptable level of accuracy (i.e., up to 10⁻⁵) to fulfill the criterion of convergence.

5. Physical Explanation

In this study, the dimensionless parameters that were appearing in the momentum and the energy equations and the value of these parameters were taken to be fixed for the computational purpose are given as $\lambda =-3.5$, $n=0.5$, $We=0.5$, ${\gamma }_1={\gamma }_2=0.5$, ${\epsilon }_1=0.5$, $B=0.1$. The graphical features of the embedded flow of fluids were captured in Figures 2–21 on the velocity, temperature profiles, the skin friction, and the local Nusselt number against the enormous distinct parameters. The numerical results with accessible conclusions are referenced in

Table 1. Comparison of the values of $f″\left(0\right)$ for distinct values of ${\epsilon }_1$ and $\lambda$ when $K=1$ and rest of variables are absent.

${\mathit{\epsilon }}_1$	$\mathit{\lambda }$	Rosali et al. [22]	Present Results
0.1	−0.5	4.1508	4.1389
	1	6.4874	6.4864
	2	7.7611	7.7614
0.5	−0.5	1.8821	1.8838
	1	2.8597	2.8453
	2	3.3944	3.3944
0.7	−0.5	1.5967	1.6008
	1	2.4074	2.4124
	2	2.8514	2.8499
1	−0.5	1.3418	1.3438
	1	2.0050	2.0050
	2	2.3690	2.3620

, which shows the authenticity of our problem by comparing the results with the available results in the literature. Additionally, the green lines throughout the study demonstrate the first solution, which is also called the upper branch solution while the red lines exhibit the second solution called the lower branch in all the invoked figures.

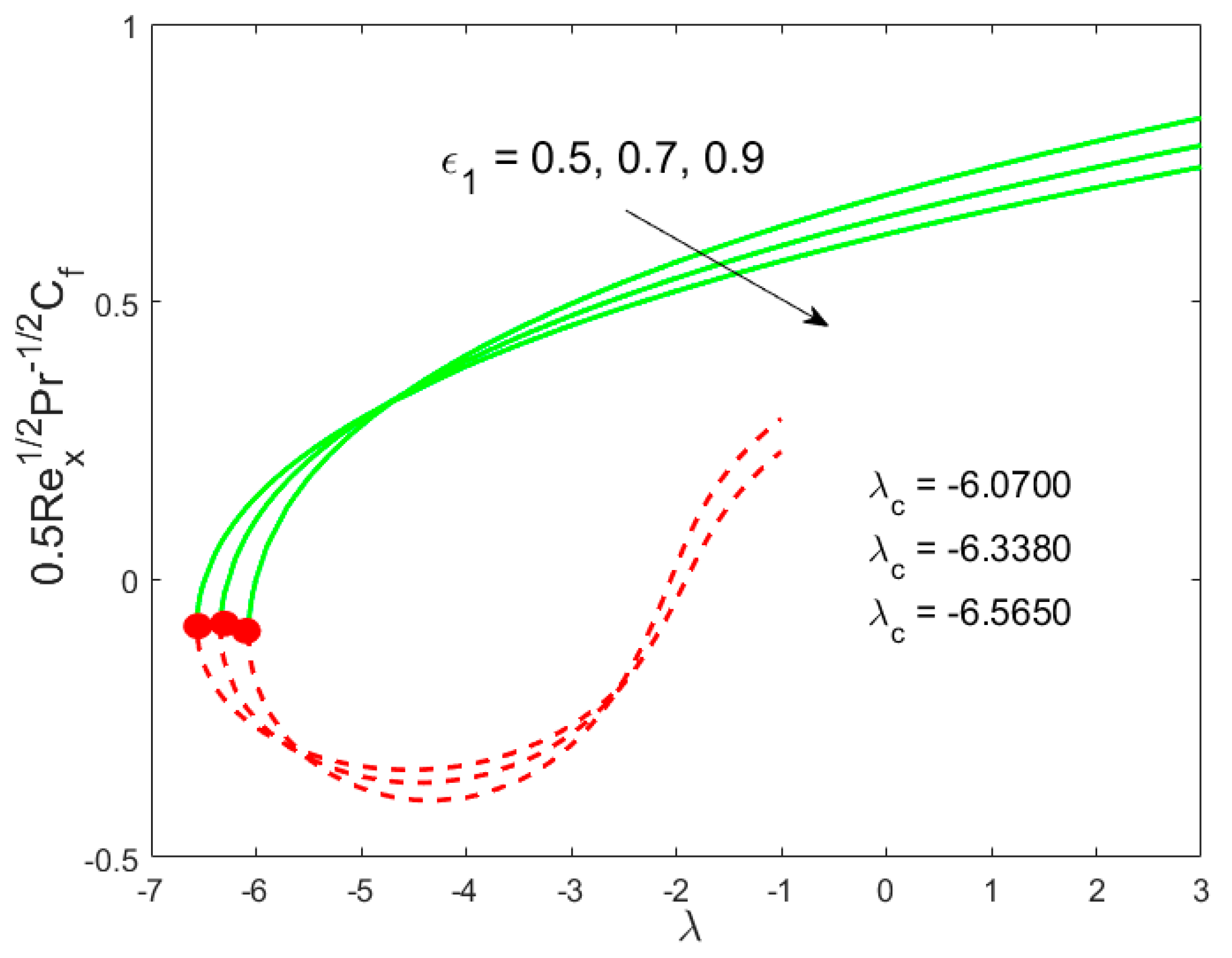
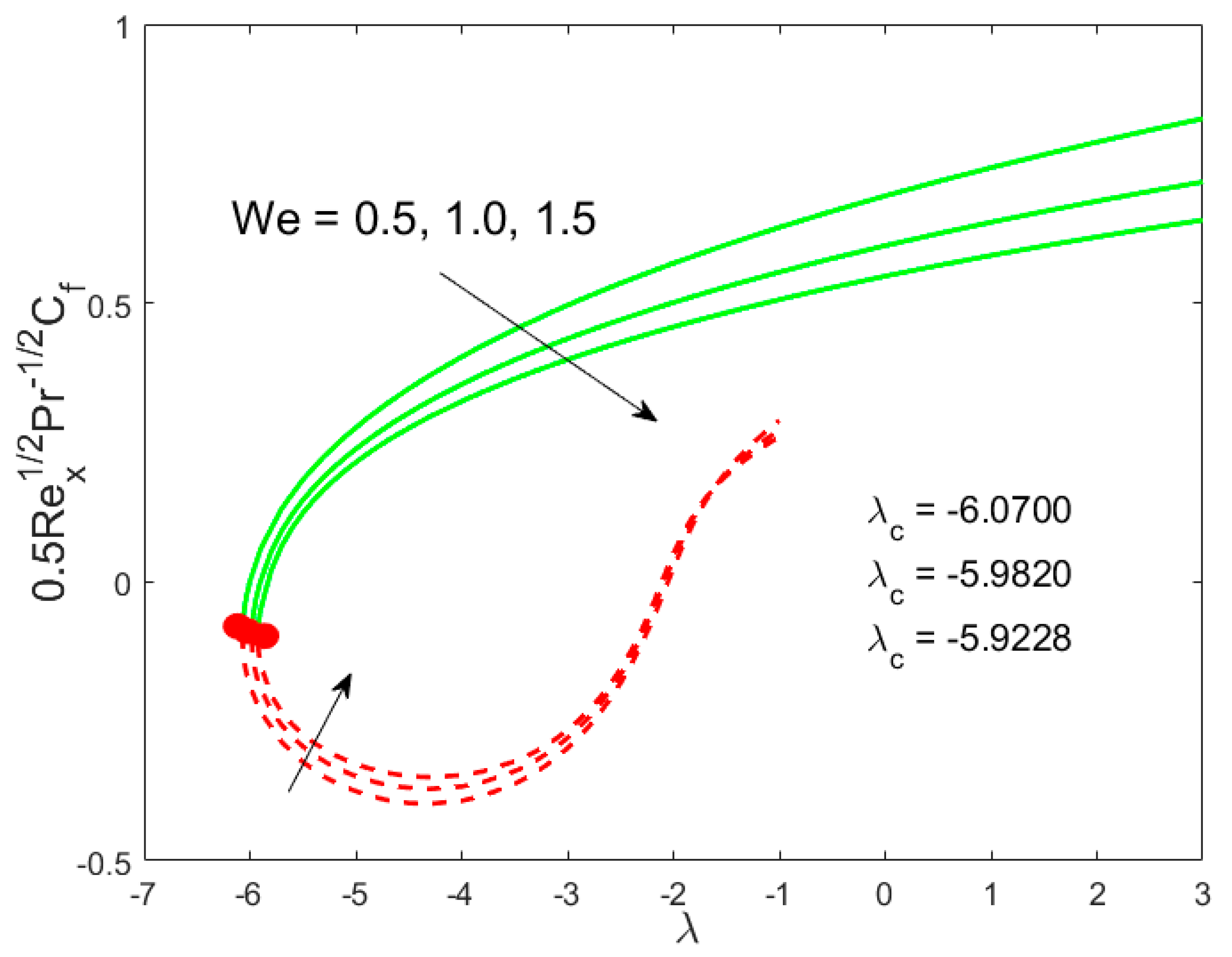
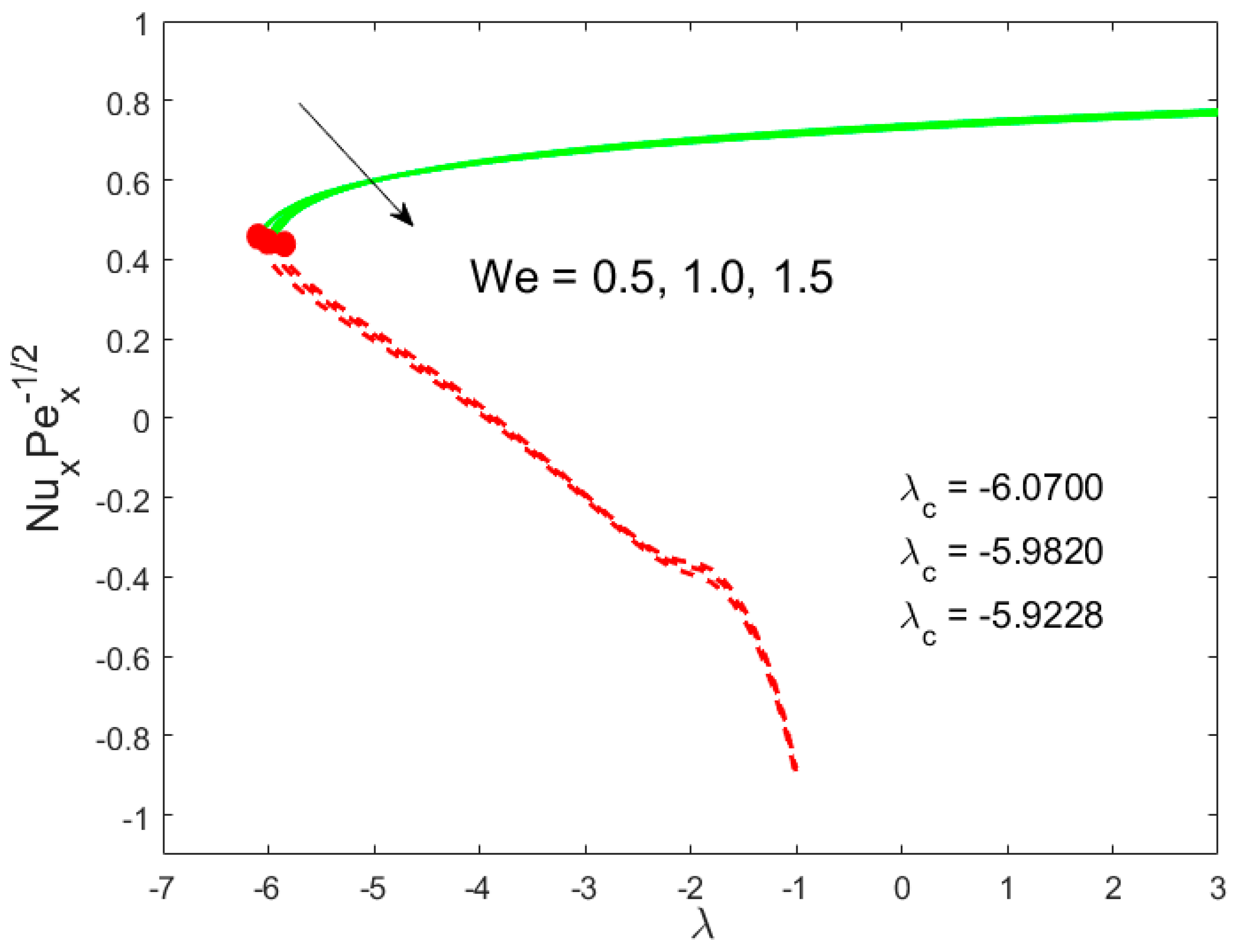
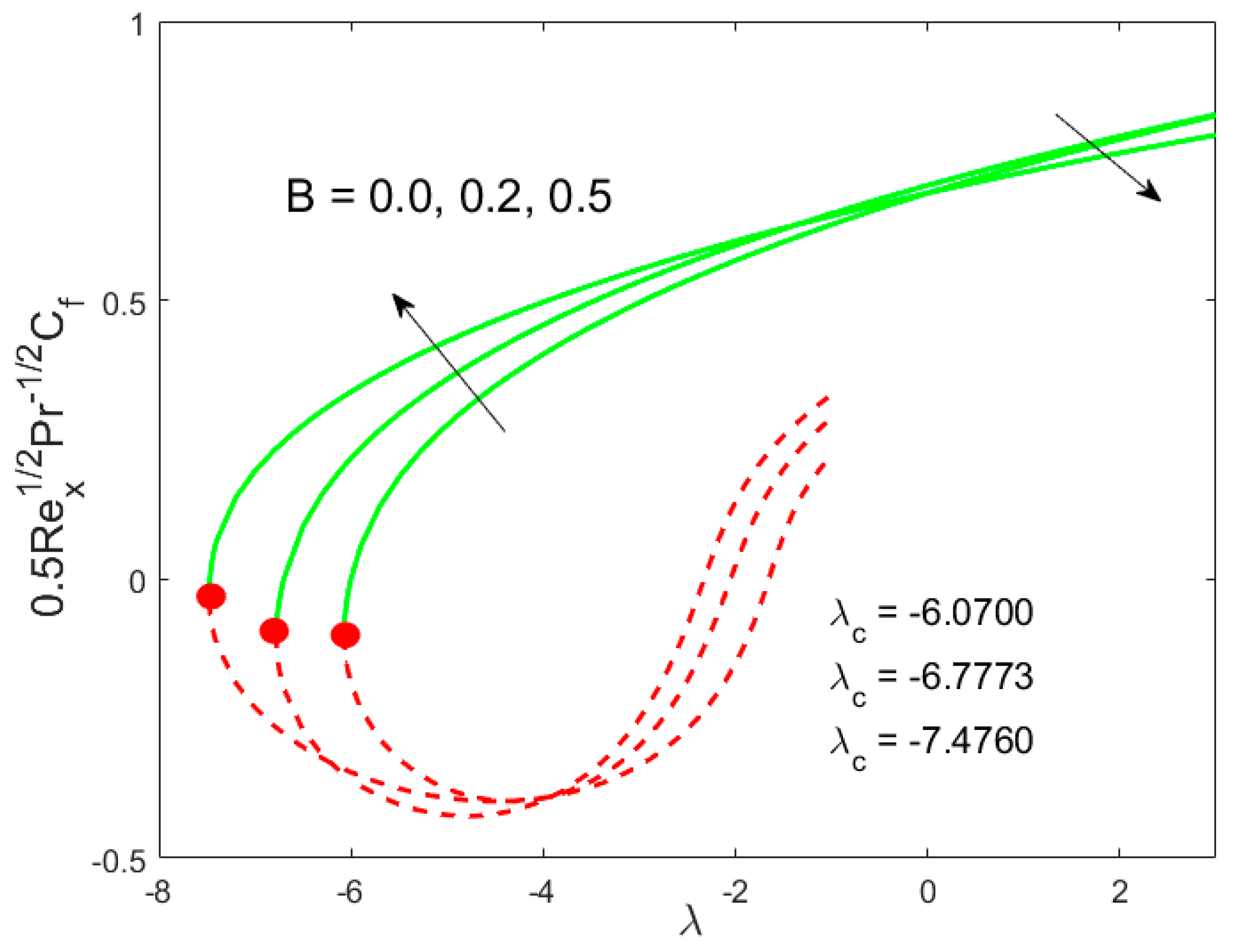
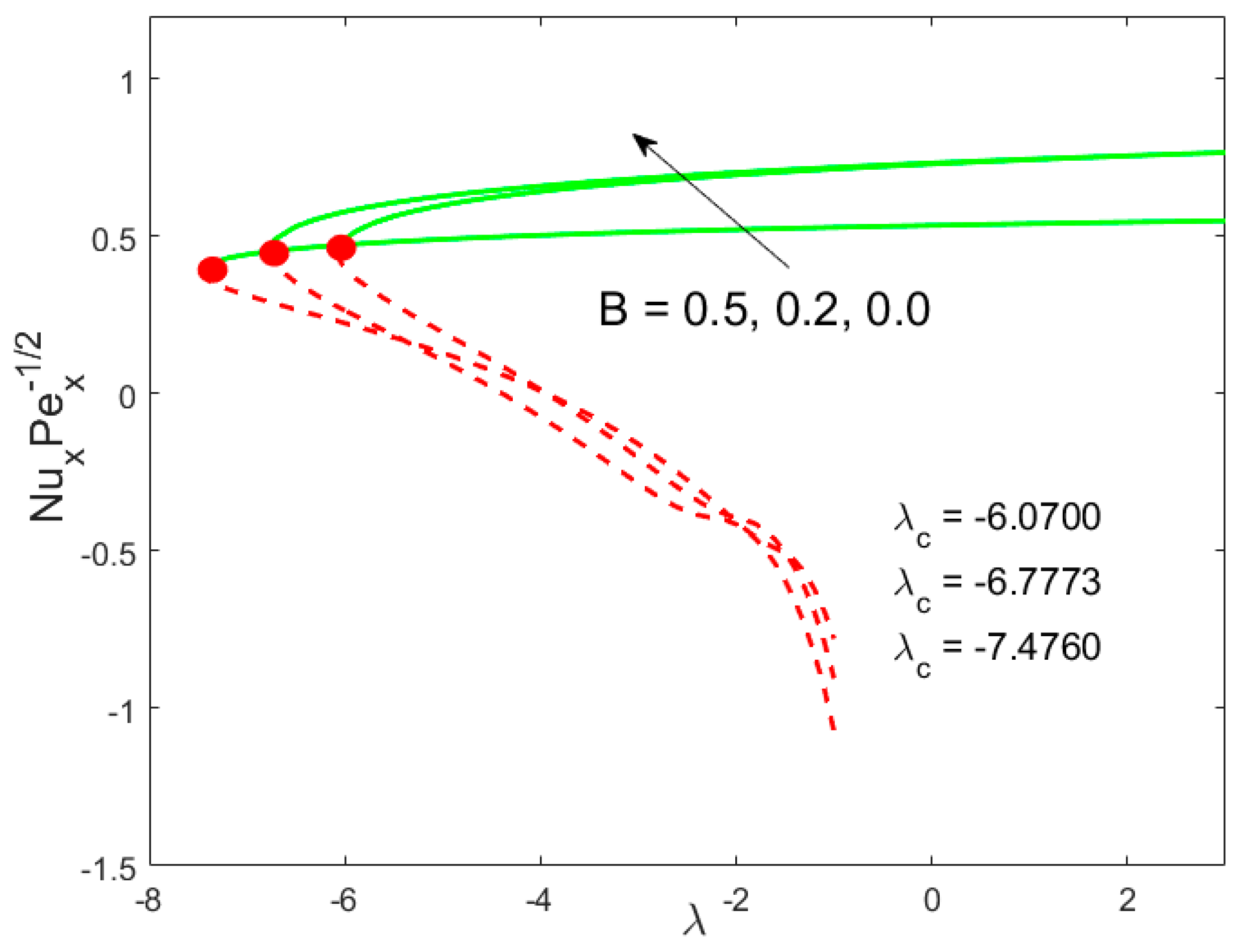
6. Deviation of the Skin Coefficient and the Local Nusselt Number

The graphical behavior of our solutions for the skin friction coefficient $0.5{\left({\mathrm{Re}}_x\right)}^{\frac{1}{2}}{\left(\mathrm{Pr}\right)}^{\frac{-1}{2}}{C}_f$ and the local Nusselt number $N{u}_x{\left(P{e}_x\right)}^{\frac{-1}{2}}$ by exercising the different parameters against the mixed convection parameter $\lambda$ are shown in all invoked Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. The existing of dual solutions is marked in all the aforementioned figures in the case of mixed convection opposing flow $\left(\lambda <0\right)$ while the outcome is unique for the phenomenon of mixed convection assisting flow $\left(\lambda >0\right)$. The influence of the modified porosity parameter ${\epsilon }_1$ on the skin friction and the local Nusselt number versus $\lambda$ is depicted in Figure 2 and Figure 3, respectively. Figure 2 shows that the values of the skin friction decelerate in the first solution with enhancing ${\epsilon }_1$ in the range of $\left(-4\le \lambda \right)$, while the reverse trend is seen in the range of $\left(\lambda <-4\right)$. Figure 3 scrutinizes that the values of the Nusselt number accelerate due to ${\epsilon }_1$. It is also observed from these sketches that the physical realizable solution is represented by the green solid lines and the decline of the unstable solution is displayed by the red dotted lines. The critical values $\left|\lambda \right|$ enhance as ${\epsilon }_1$ augments, suggesting that the modified porosity parameter delays the boundary-layer separation. In addition, it can be clearly observed from these figures that the skin friction as well as the Nusselt number augments as $\lambda$ increases in the assisting flow, while the contrary behavior is observed in the opposing flow. Physically, in the assisting flow case, the favorable pressure gradient produces which augments the motion of liquid, which consequently raises the shear stress and heat transfer rate. In contrast, opposing flow guides to an adverse pressure gradient that delays the motion of liquid. The impacts of the Weissenberg number $We$ and the inertia parameter $B$ against $\lambda$ on $\left(0.5{\left({\mathrm{Re}}_x\right)}^{\frac{1}{2}}{\left(\mathrm{Pr}\right)}^{\frac{-1}{2}}{C}_f\right)$ and $\left(N{u}_x{\left(P{e}_x\right)}^{\frac{-1}{2}}\right)$ are depicted in Figure 4, Figure 5, Figure 6 and Figure 7. For the upper branch solution, both the momentum boundary layer and the thermal boundary layer become lower by changing the value of $We$, while the opposite behavior is marked for the lower branch solution as shown in Figure 4 and Figure 5. Figure 6 and Figure 7 suggest that the fall trend with augmenting $B$ in the lower branch solution, while the upper branch solution is enhanced for the similar choice of $B$.

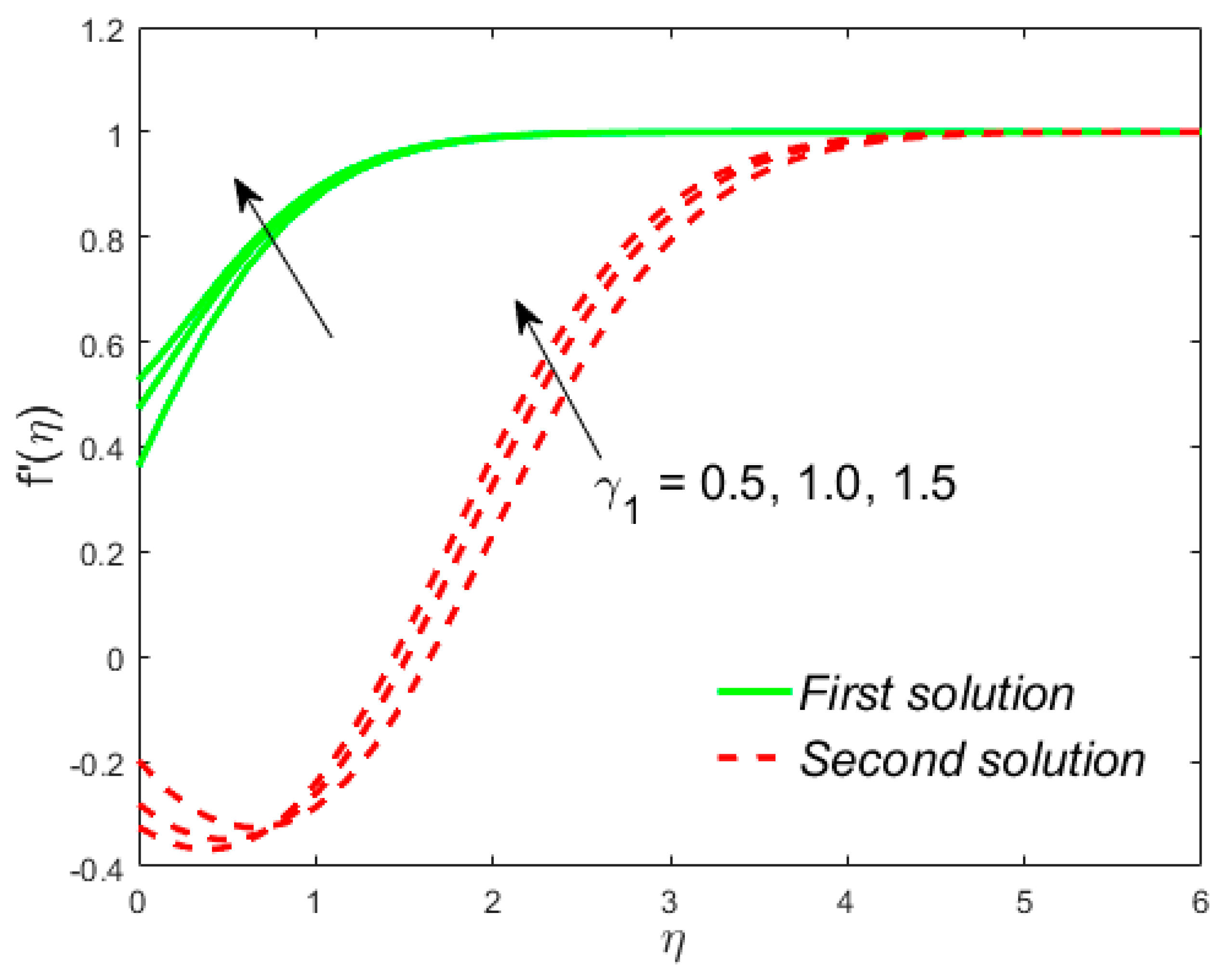
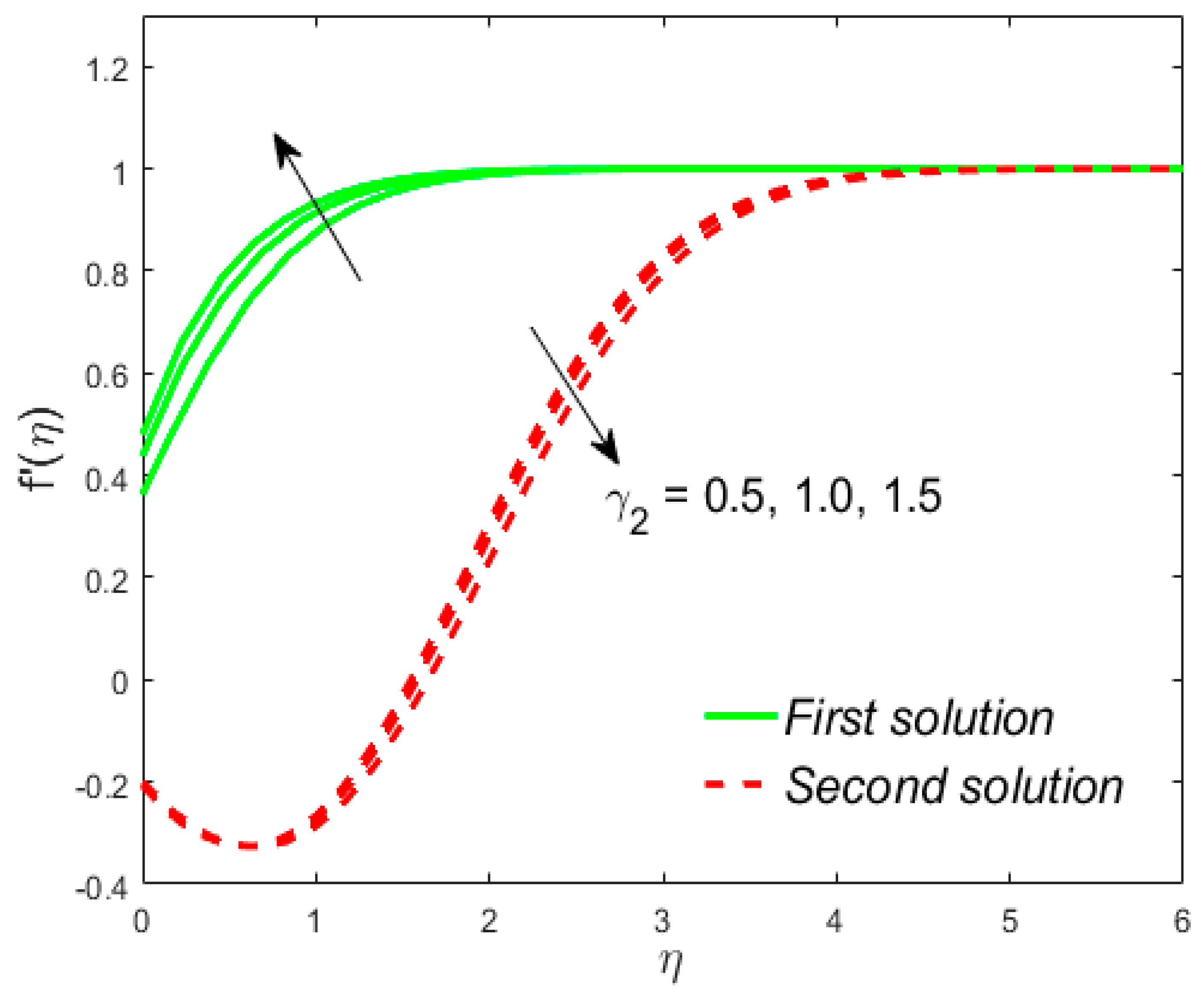
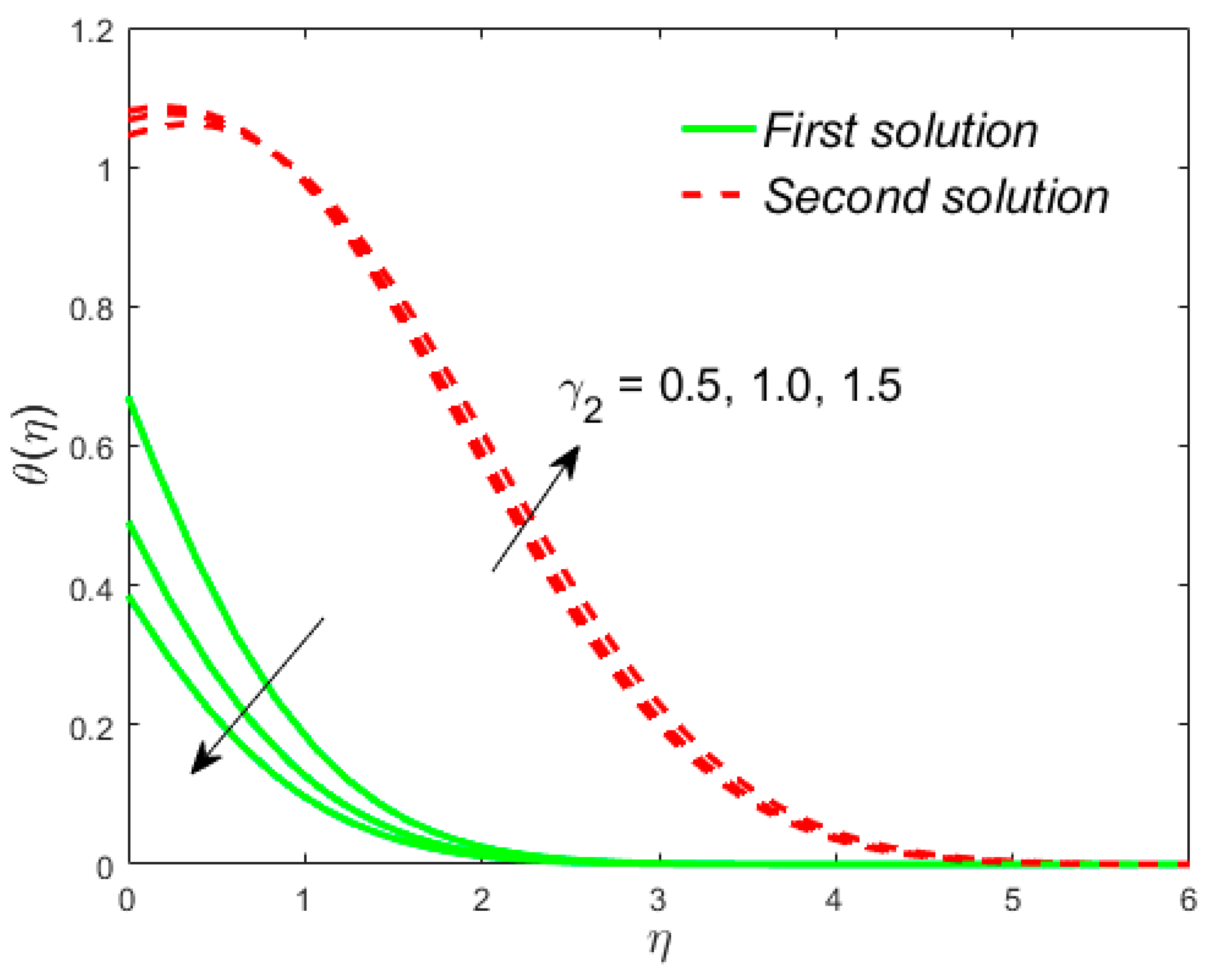
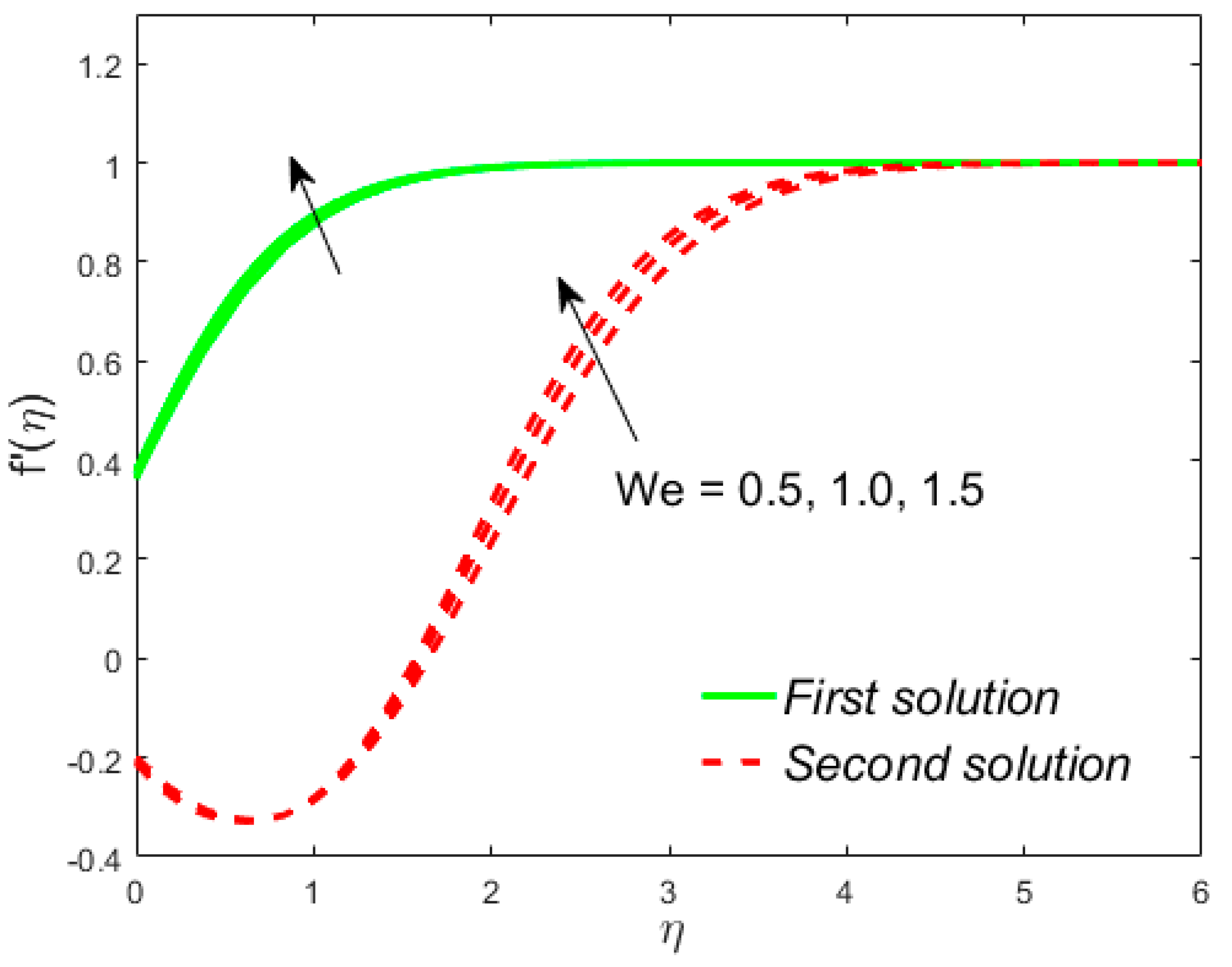
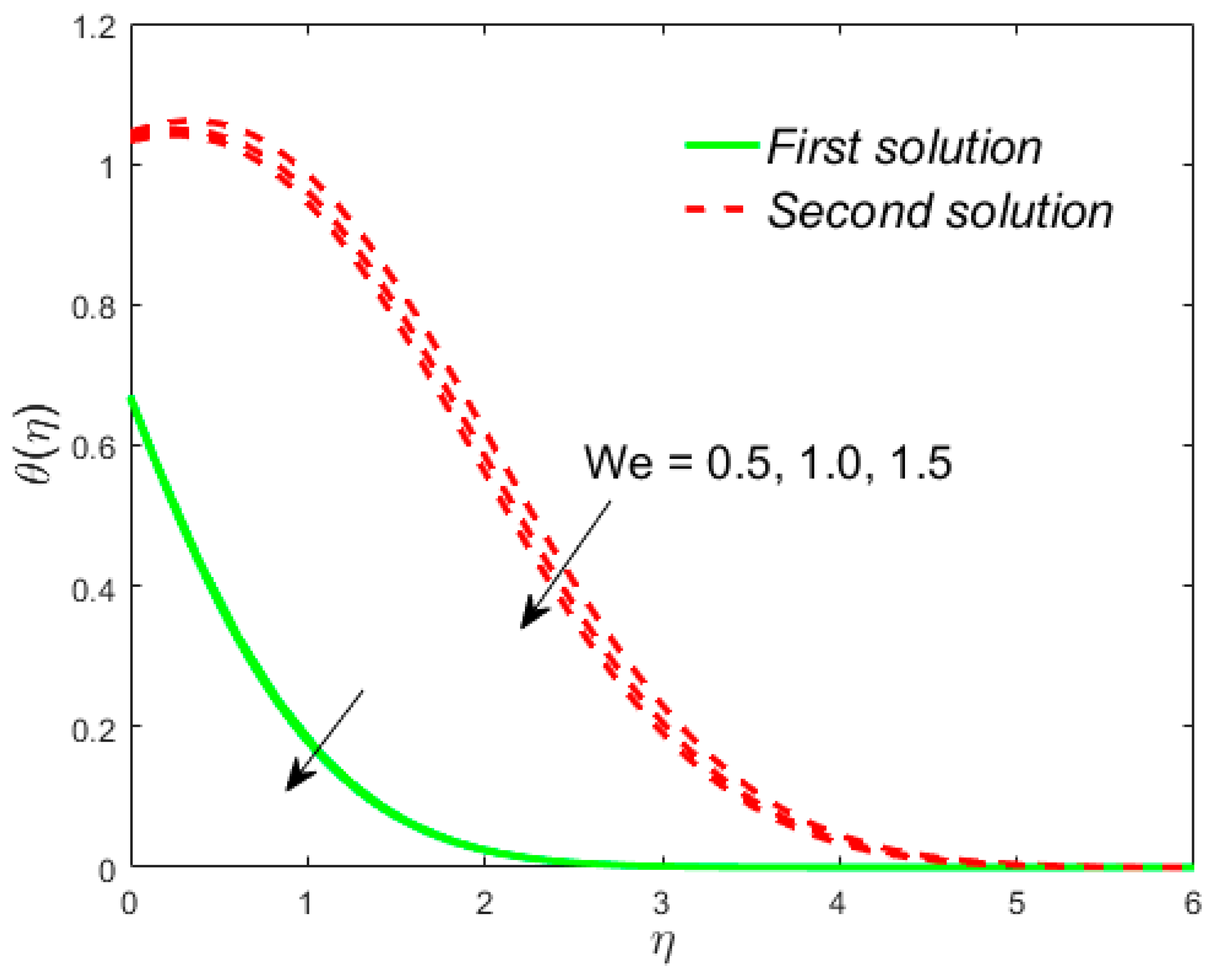
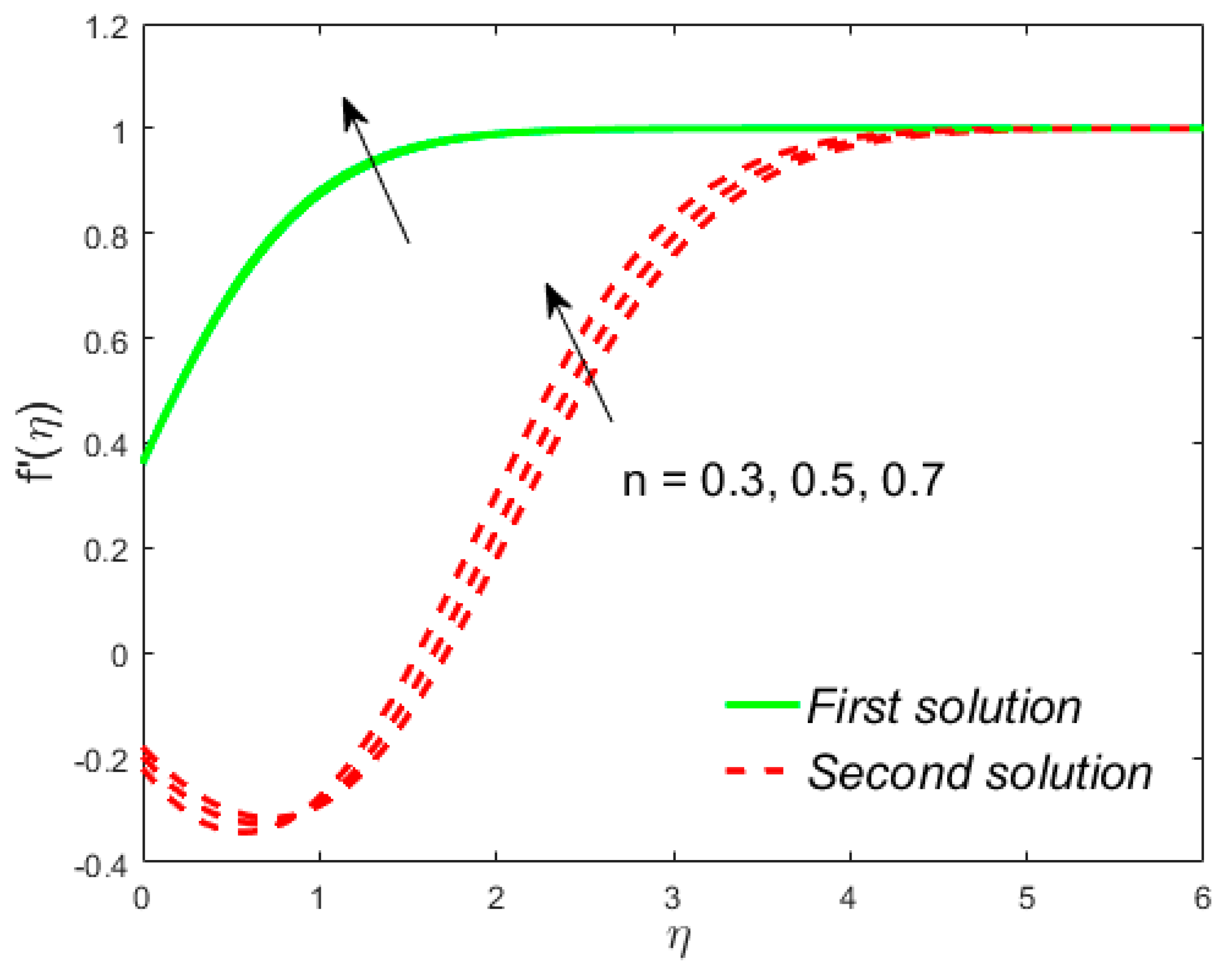
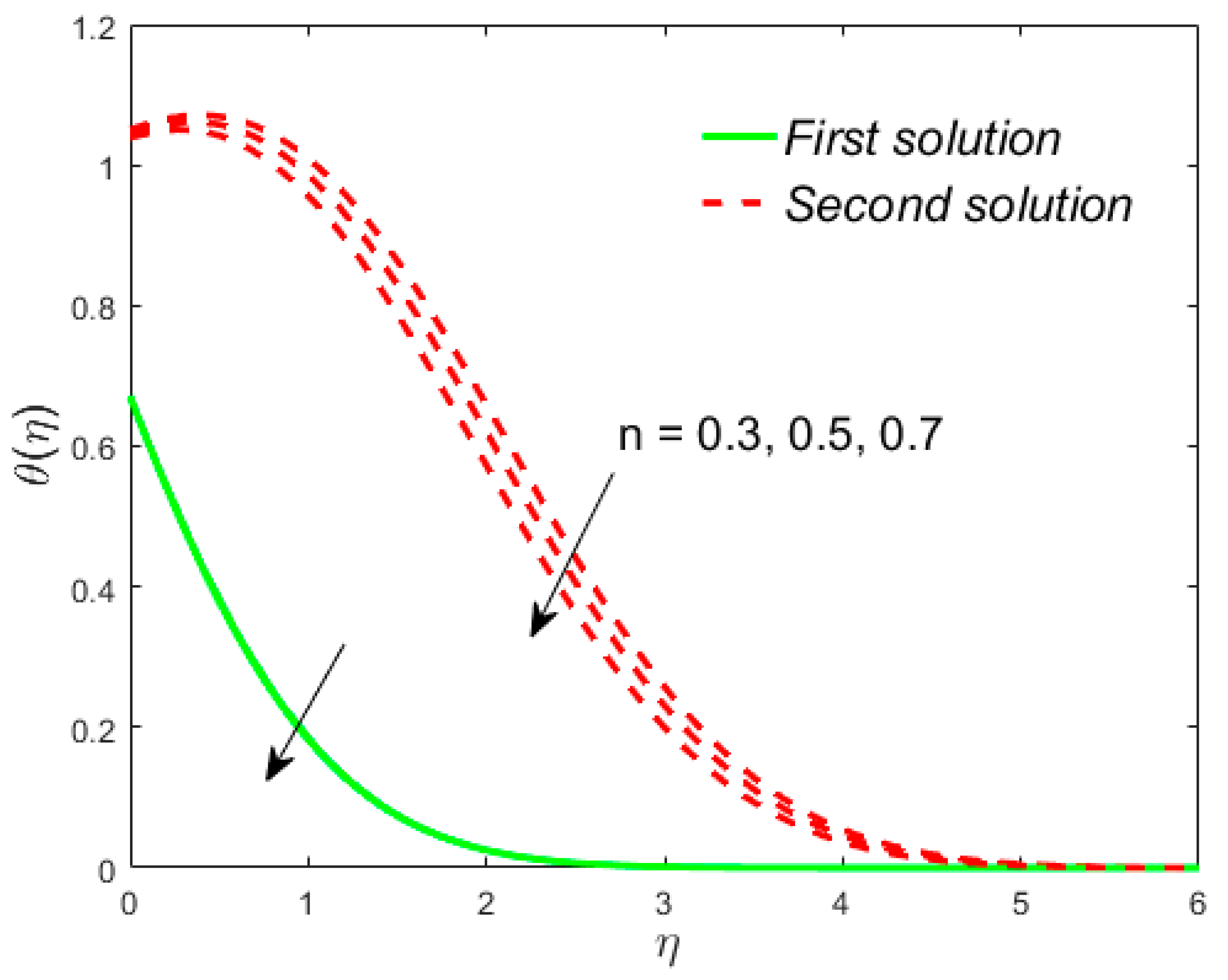
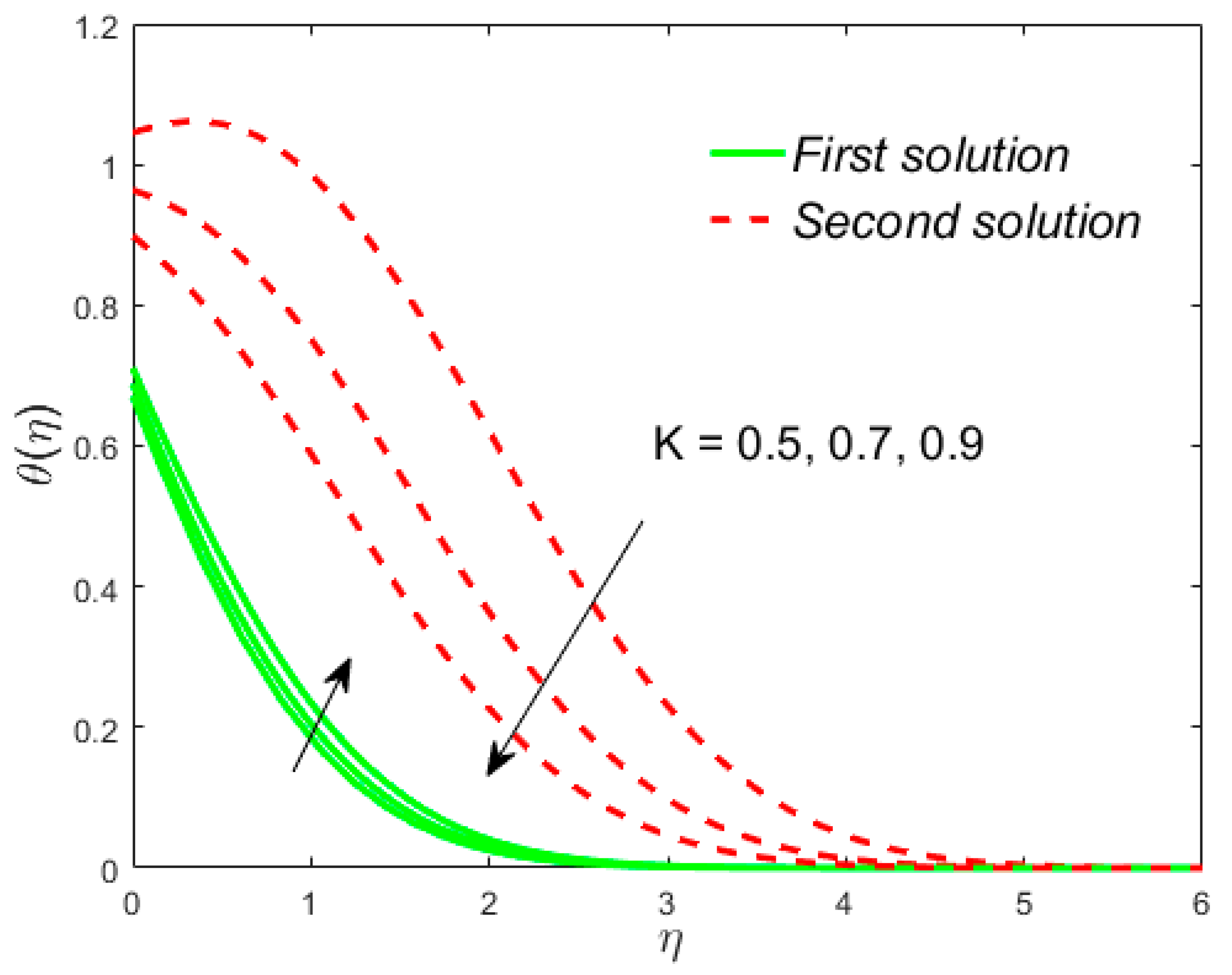
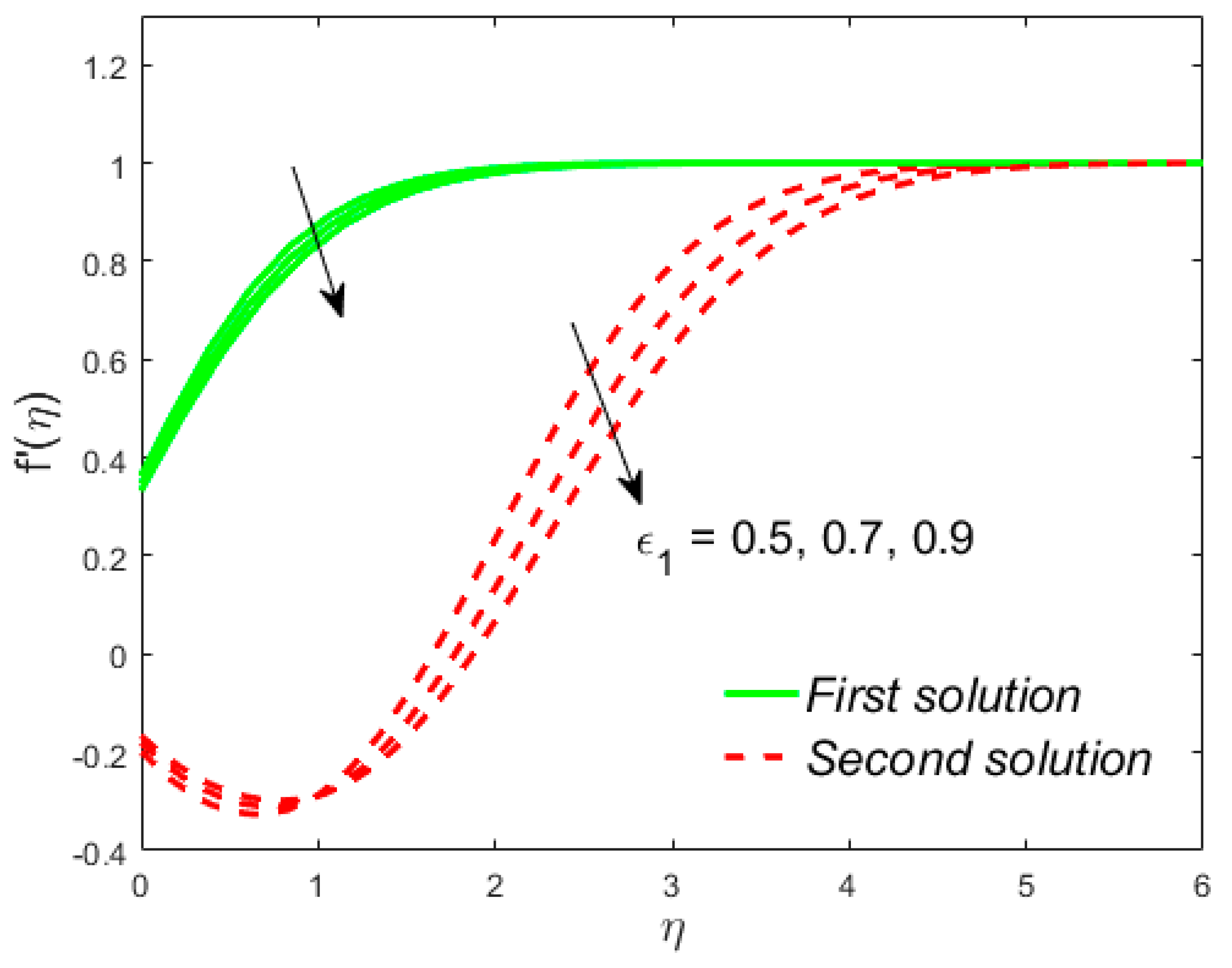
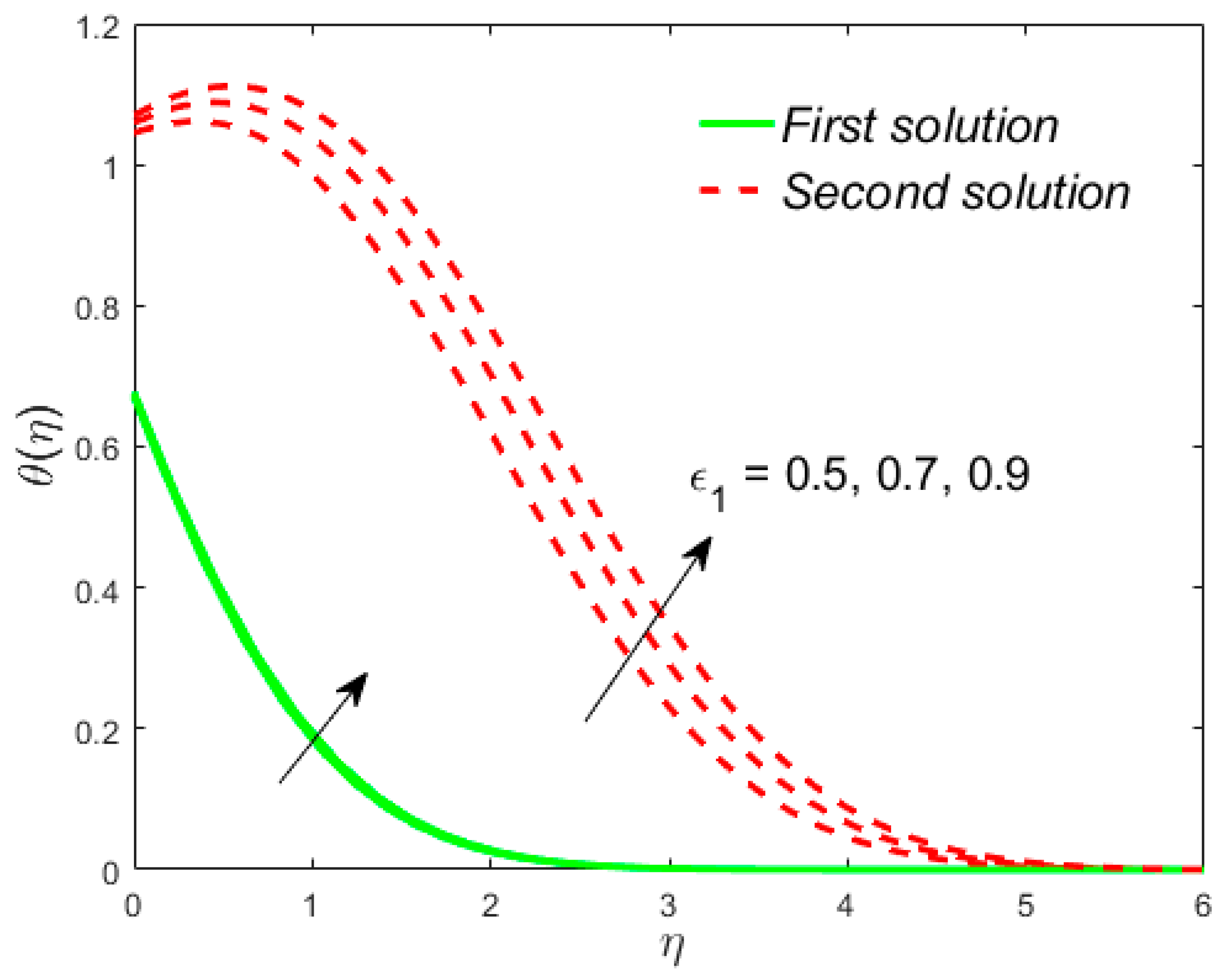
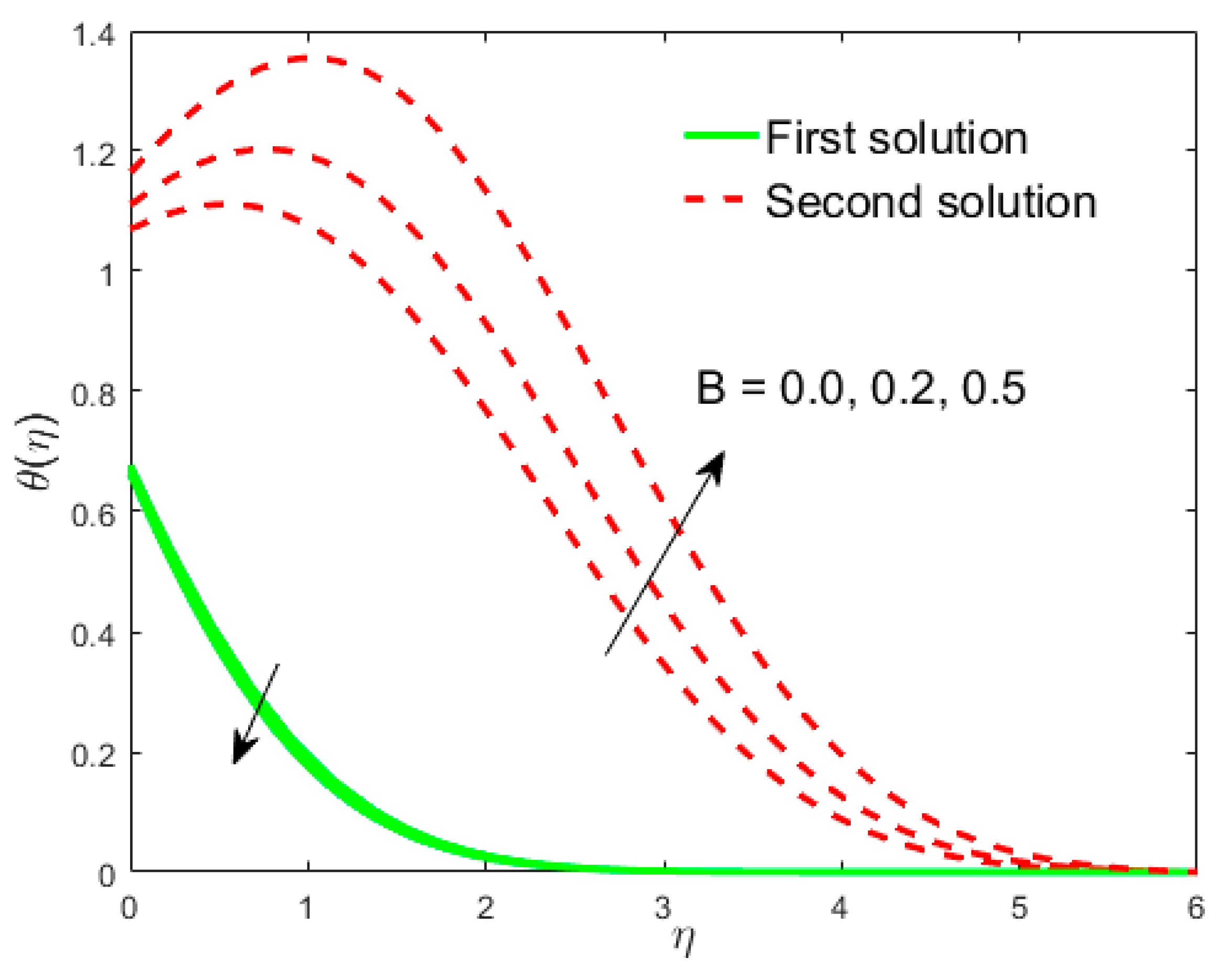
7. Deviation of the Velocity and Temperature Fields

The analyses and the behavior are captured in Figure 8 and Figure 9, respectively, showing the tasters of the $f\prime (\eta )$ and $\theta \left(\eta \right)$ profiles for the distinct values of the slip parameter ${\gamma }_1$ for both branches of the solutions, while the effects of the thermal slip parameter ${\gamma }_2$ on the velocity and temperature for various selected values are portrayed in Figure 10 and Figure 11, respectively. Physically, when augmenting the values of ${\gamma }_1$, the wall shear stress insignificant and as a result, the momentum boundary layer (Figure 8) becomes larger and larger for both the upper branch and lower branch solutions, while the reverse trend is scrutinized for the temperature profile (Figure 9) due to escalating the ${\gamma }_1$. Figure 10 shows that the velocity of fluid rises with ${\gamma }_2$ in the first solution and declines in the second solution, while the opposite behavior is observed in the sketch of temperature, as shown in Figure 11. This is due to fact that the extra flow penetrates through the thermal boundary layer which consequently transmitted the additional heat and this guides in the decline of temperature distribution. Thus, for the authenticity of our solutions, it is clearly visible from behavior of momentum and temperature profiles in Figure 8, Figure 9, Figure 10 and Figure 11 that these solutions satisfied the boundary conditions asymptotically. As shown in Figure 12, Figure 13, Figure 14 and Figure 15, the behavior of the fluid flow is explored by exercising the dimensionless parameters $We$ and $n$ on $f\prime (\eta )$ and $\theta \left(\eta \right)$, respectively. The increment in the local Weissenberg number $We$ and power-law index $n$, both the green solid lines, as well as the red dotted lines (first and second solution) are rising in Figure 12 and Figure 13, while the contrary flow of fluid motion is noticeable corresponding to these parameters in Figure 13 and Figure 15, respectively. From the physical view, the additional relaxation time is needed when the values of $We$ increases and as a result, the velocity boundary layer and the fluid temperature was shrunk and declined in Figure 12 and Figure 13, respectively. Figure 14 exhibits that the velocity profile increases due to the augmenting values of $n$ in case of shear thinning and vice versa for the temperature profile which is invoked in Figure 15. Figure 16 shows the behavior of the permeability parameter $K$ on $f\prime (\eta )$ as we enhance the parameter $K$, the upper solution is decelerated while the lower solution shows increasing behavior, whereas for the same parameter, the reverse behavior is noted in the temperature profile, as presented in Figure 17. Figure 18 illustrates that the liquid velocity enhances in both upper and lower solutions by changing the values of the modified porosity parameter ${\epsilon }_1$, while the temperature profile behavior is shown in Figure 19, which decelerates in both branches of solutions as we boost up the value of ${\epsilon }_1$. In Figure 20, we plotted the velocity profile for various values of inertia coefficient $B$, which shows that the first solution is enhanced and the second solution is declined. The temperature profile declines in the upper branch solution and rises in the second branch solution as the value of $B$ augments and this behavior is captured in Figure 21. The cause for this trend is that the inertia of the porous medium offers an extra confrontation to the mechanism of the liquid flow, which grounds the liquid to progress at a retarded rate with reduced temperature.

8. Closing Remarks

The impact of slip factors on the mixed convective flow of Cross liquid has been examined from a vertical plate immersed in Darcy–Forchheimer porous medium. The similarity variables are adopted to convert the PDEs to nonlinear ODEs. The transmuted system is numerically deciphered through the bvp4c solver. Core verdicts of the current research are stated as follows:

• Permeability parameter decelerates the drag force, as well as the rate of heat transfer in both forms of solutions;
• Due to the porosity parameter, the drag force slows down in upper and lower branch solutions, while the rate of heat transfer accelerates;
• The drag forces decline with the growing values of the Weissenberg parameter in the upper branch solutions, while a reverse trend is observed in the lower branch solutions. However, the rate of heat transfer is diminished with the Weissenberg parameter;
• The drag forces are declined initially and then enhance due to the inertia coefficient, while the rate of heat transfer increases in both solutions;
• Liquid velocity increases due to ${\gamma }_1$ in both solutions, while the temperature distribution behaves in a contrary direction;
• The temperature of the liquid is decreased due to ${\gamma }_2$ in the upper branch solutions and augmented in the lower branch solutions. The repeal tendency is scrutinized for the velocity;
• The velocity of the liquid has an enhancing behavior with the increasing values of $We$ in both solutions, while the temperature is a declining function of $We$;
• The power-law index accelerates the velocity and reduces the temperature of the liquid in both solutions.

It is expected that the current numerical results provide significant knowledge for computer routines for further complex problems involving mixed convection of non-Newtonian fluids in porous media and stimulate curiosity for experimental work. In addition, the influence of slip effects in Darcy–Forchheimer flow with mixed convection has been of great interest especially in the utilization of geothermal energy and petroleum reservoir, etc.