Impact of Material Stiffness and Anisotropy on Coaptation Characteristics for Aortic Valve Cusps Reconstructed from Pericardium
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometry of Leaflet Design
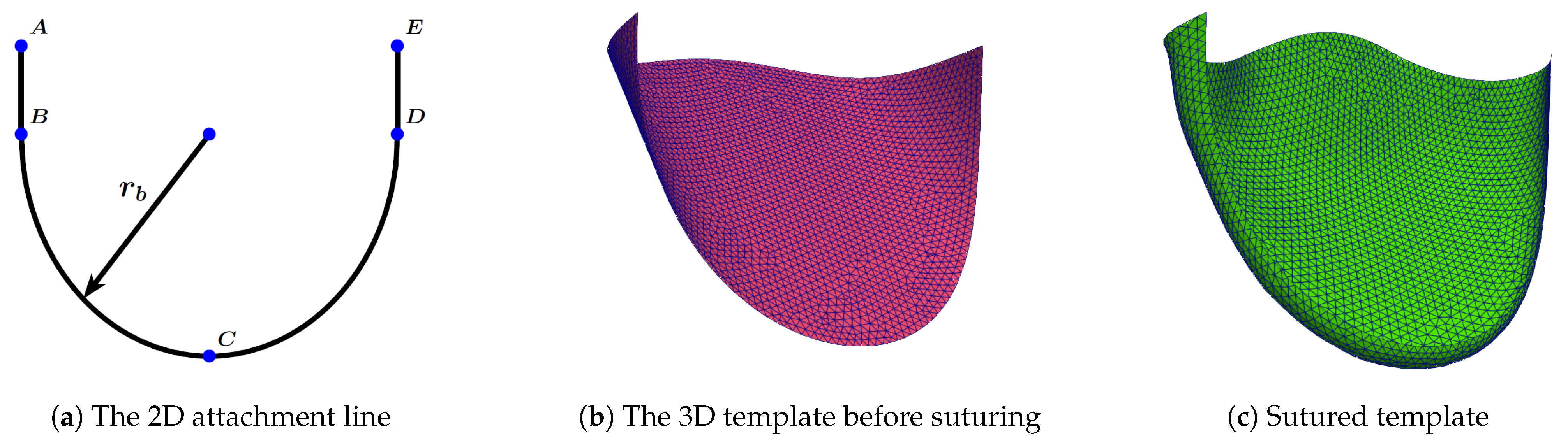
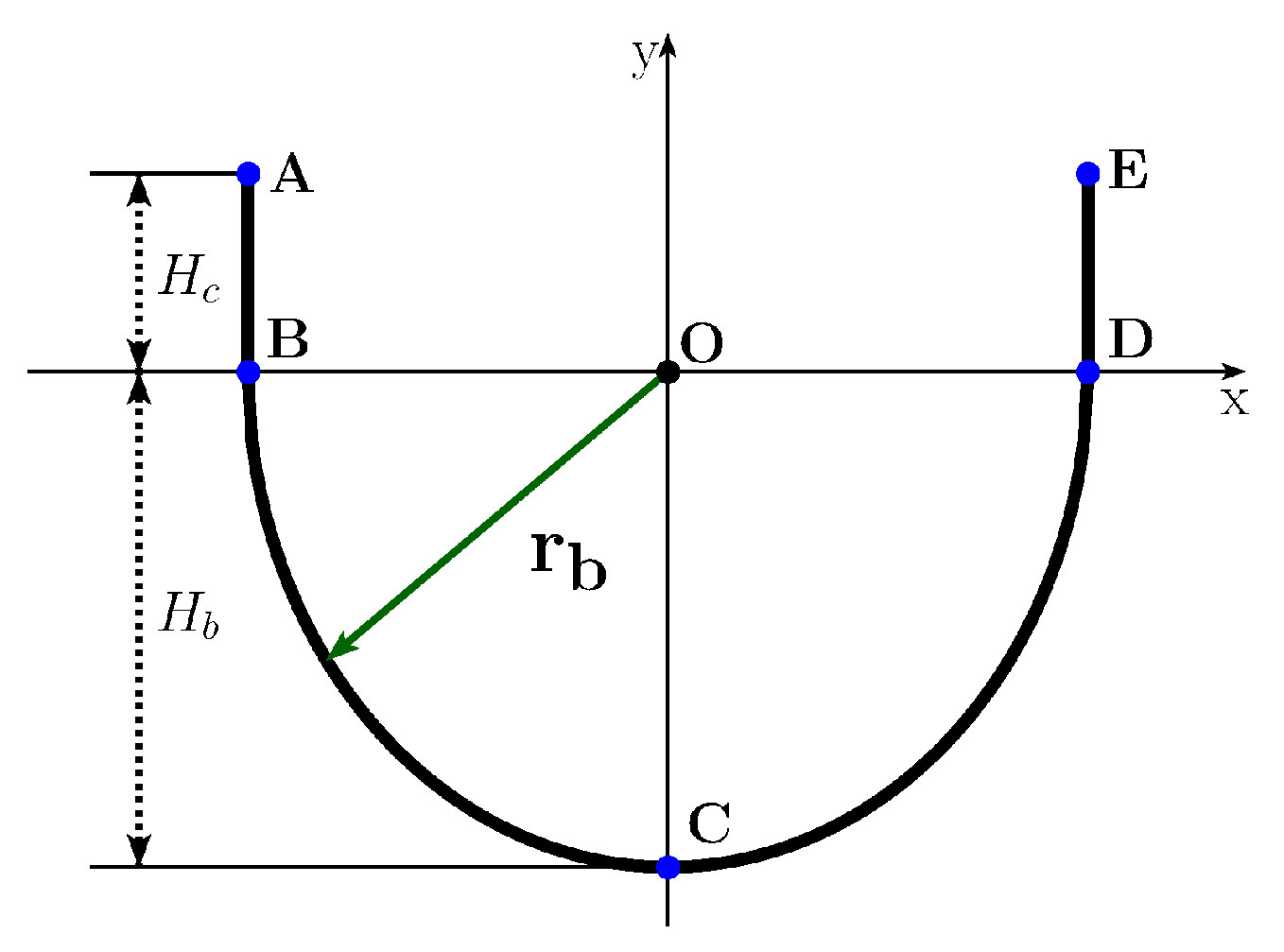
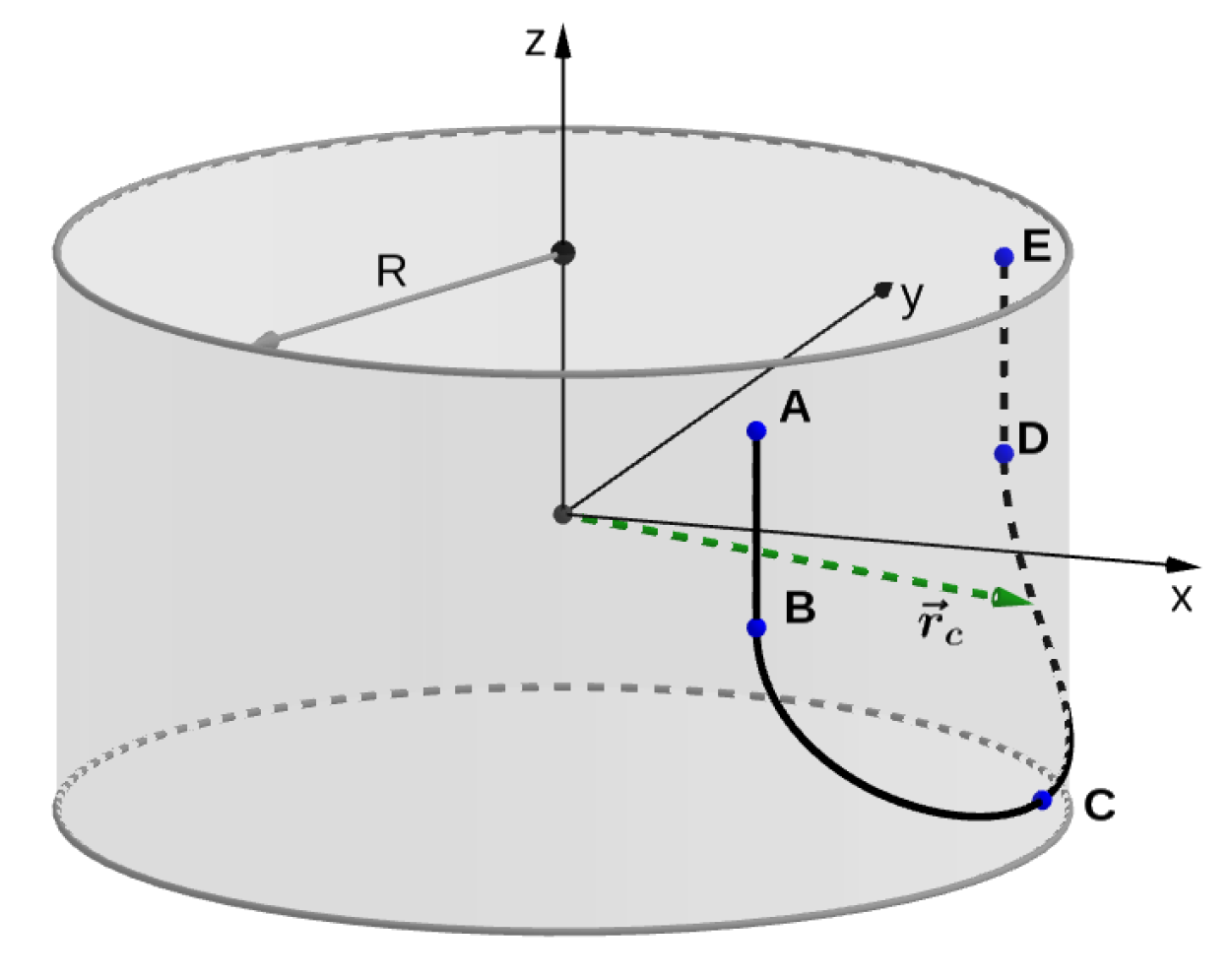
- We define the leaflet attachment line as a curve on a plane, using four geometric parameters R, , , (Figure 2), where is the height of the comissures, is the leaflet height, R is the radius of the base and the comissures (cylinder), and characterizes the angle between the surfaces of the two neighboring leaflets.The line is defined by the following function:where . Thus, the attachment line on a plane consists of two straight line segments and of length and a part of ellipse .
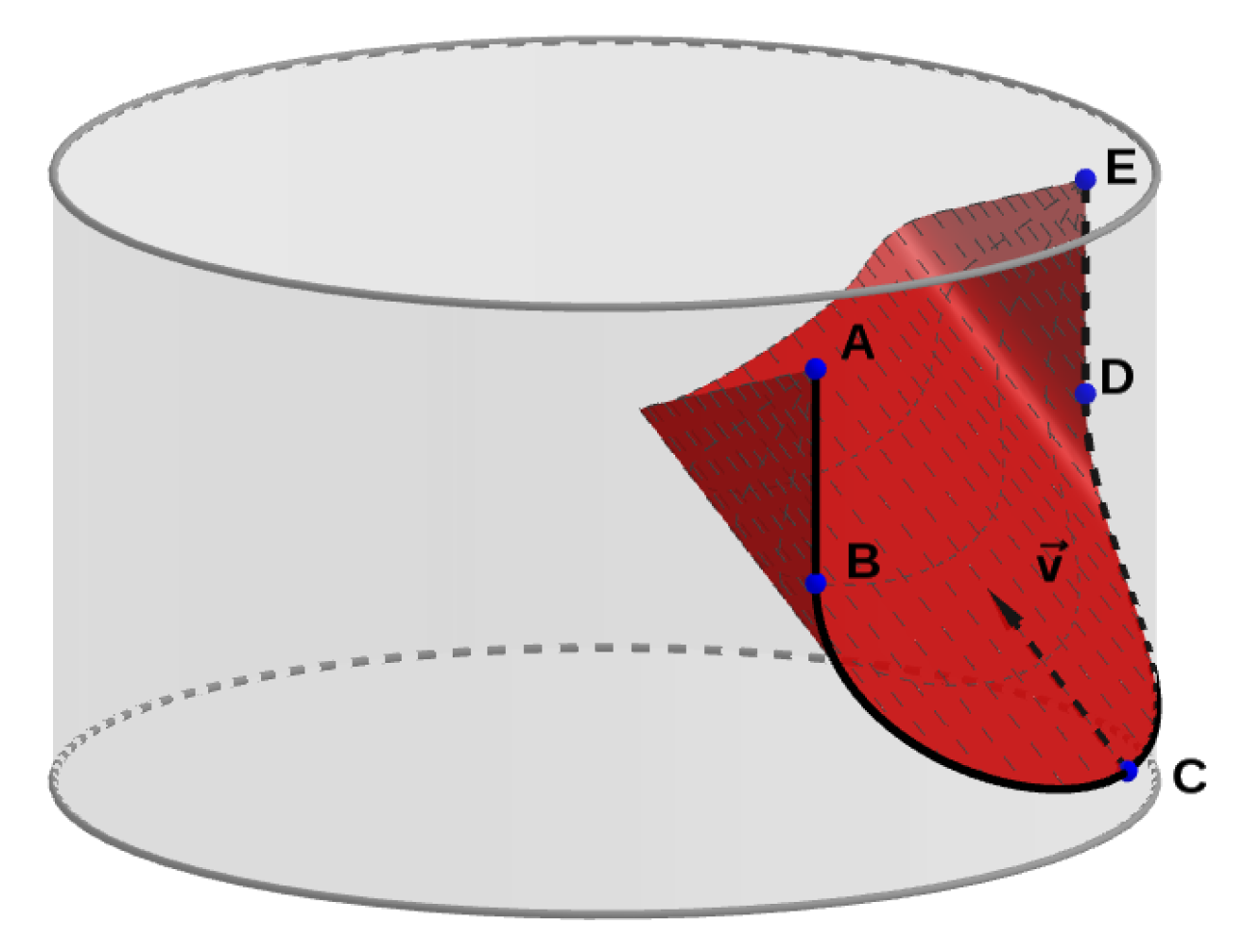
- We form the 3D leaflet template by extruding a vector along the 3D attachment line (Figure 4). The direction of the vector is given by an angle , . The template surface is the union of line segments started at points (2) with lengthThus each point of may be associated with two parameters: .In order to define fiber directions on the leaflet, we map the 3D surface to the unfolded template on the plane passing through the point with normal . Any point with parameters is mapped to with coordinates .
- We suture the 3D template and obtain its more realistic initial configuration by solving an auxiliary problem on the leaflet deformation (Figure 1c). For details, we refer to Section 3.1. The initial configuration mimics the sutured leaflets during neocuspidization procedure.
2.2. Kinematics of Shell
2.3. Hyperelasticity
2.4. Weak Formulation
2.5. Discretization
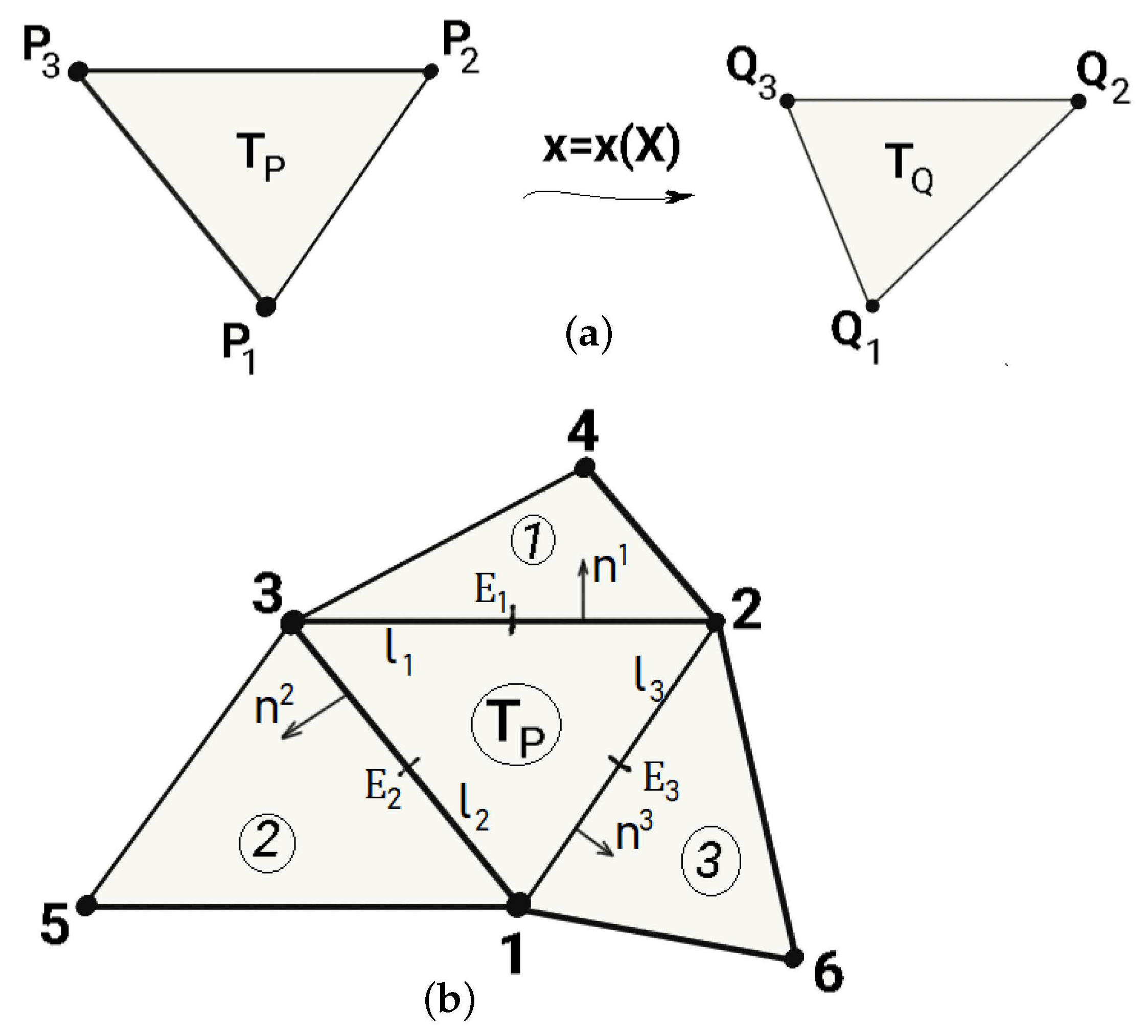
2.5.1. Discretization of the Membrane Part
2.5.2. Discretization of Bending Part
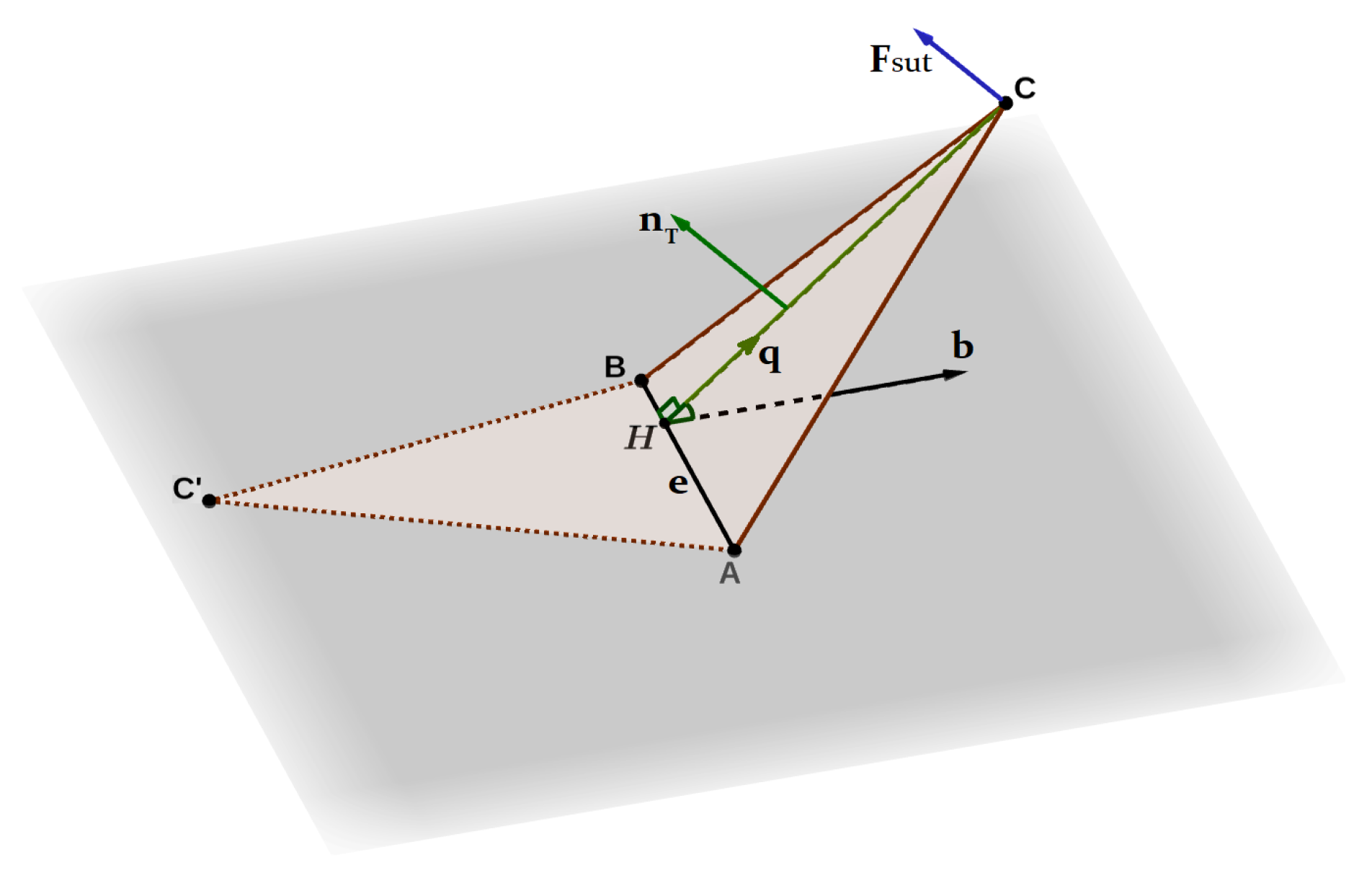
2.5.3. External Forces
2.5.4. Discretized Equilibrium Equations
2.5.5. Computational Algorithms
| Algorithm 1 Algorithm of suturing leaflet |
|
| Algorithm 2 Combined Newton and relaxation methods |
|
| Algorithm 3 Algorithm of relaxation method |
|
3. Test Problems and Results
3.1. Setting the Problems
- Plane : , , mmHg, ;
- Plane : , , mmHg, ;
- Plane : , , mmHg, .
- Left: , , mmHg, ;
- Right: , , mmHg, .
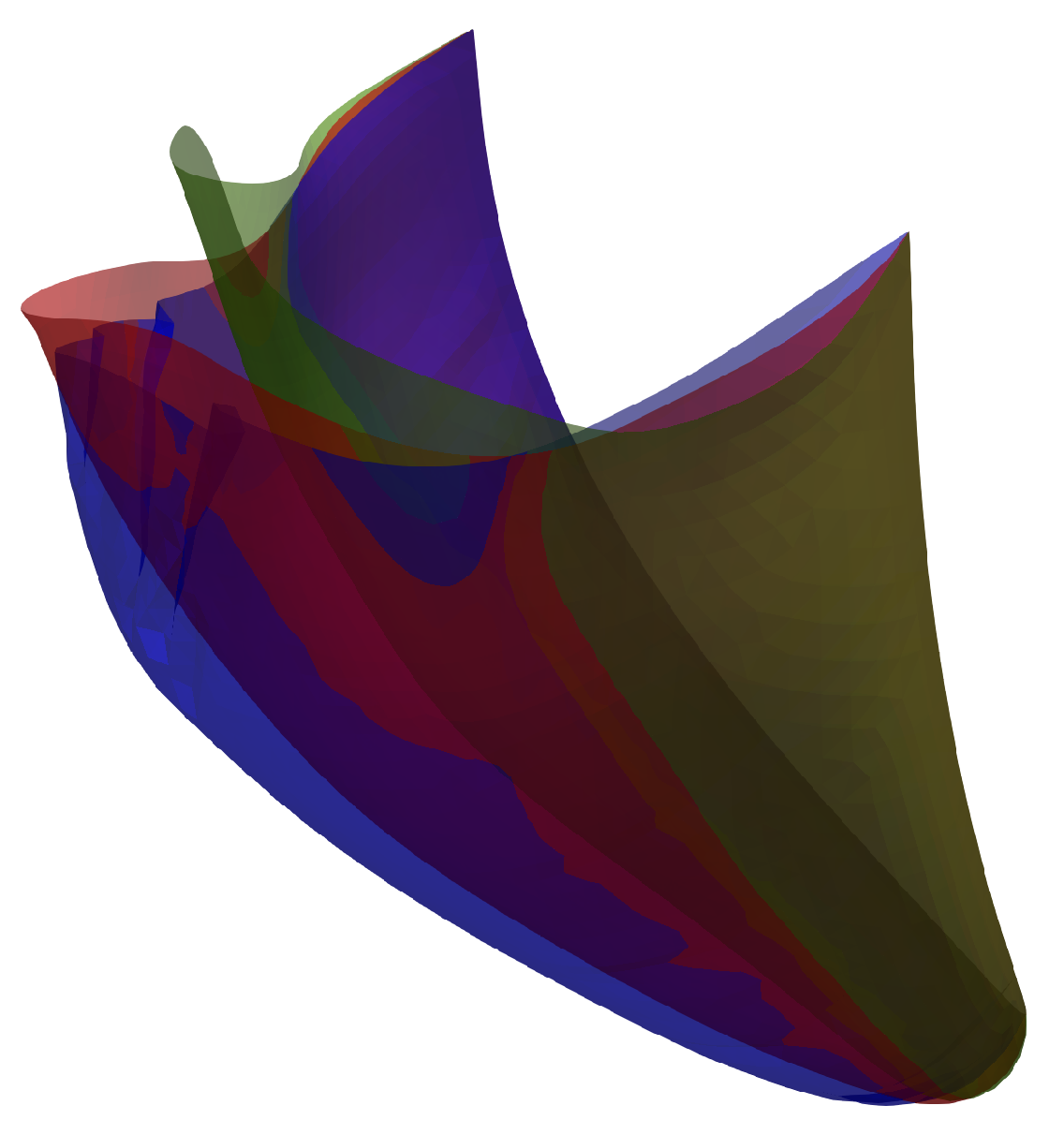
3.2. Configuration of the Closed Valve
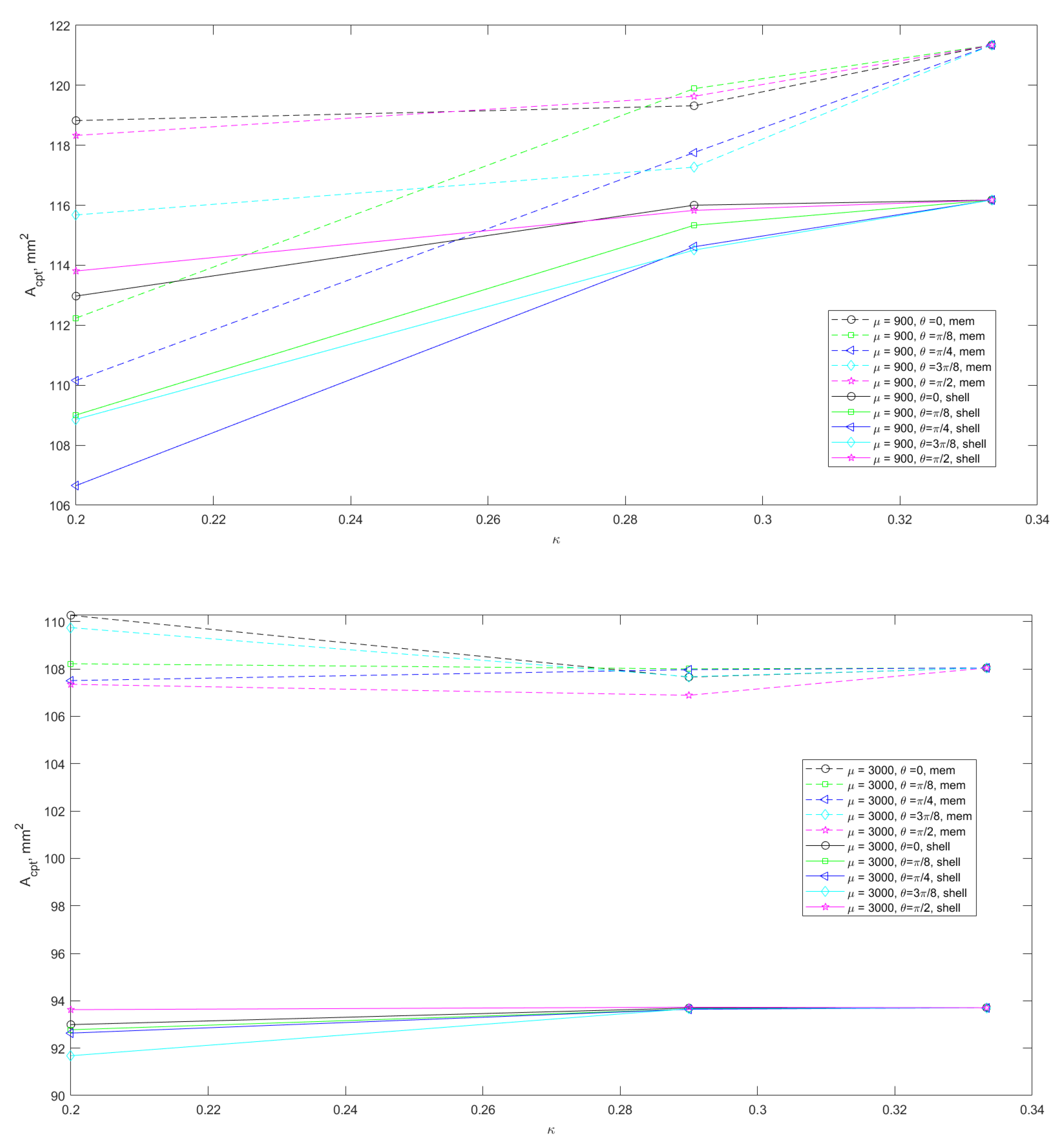
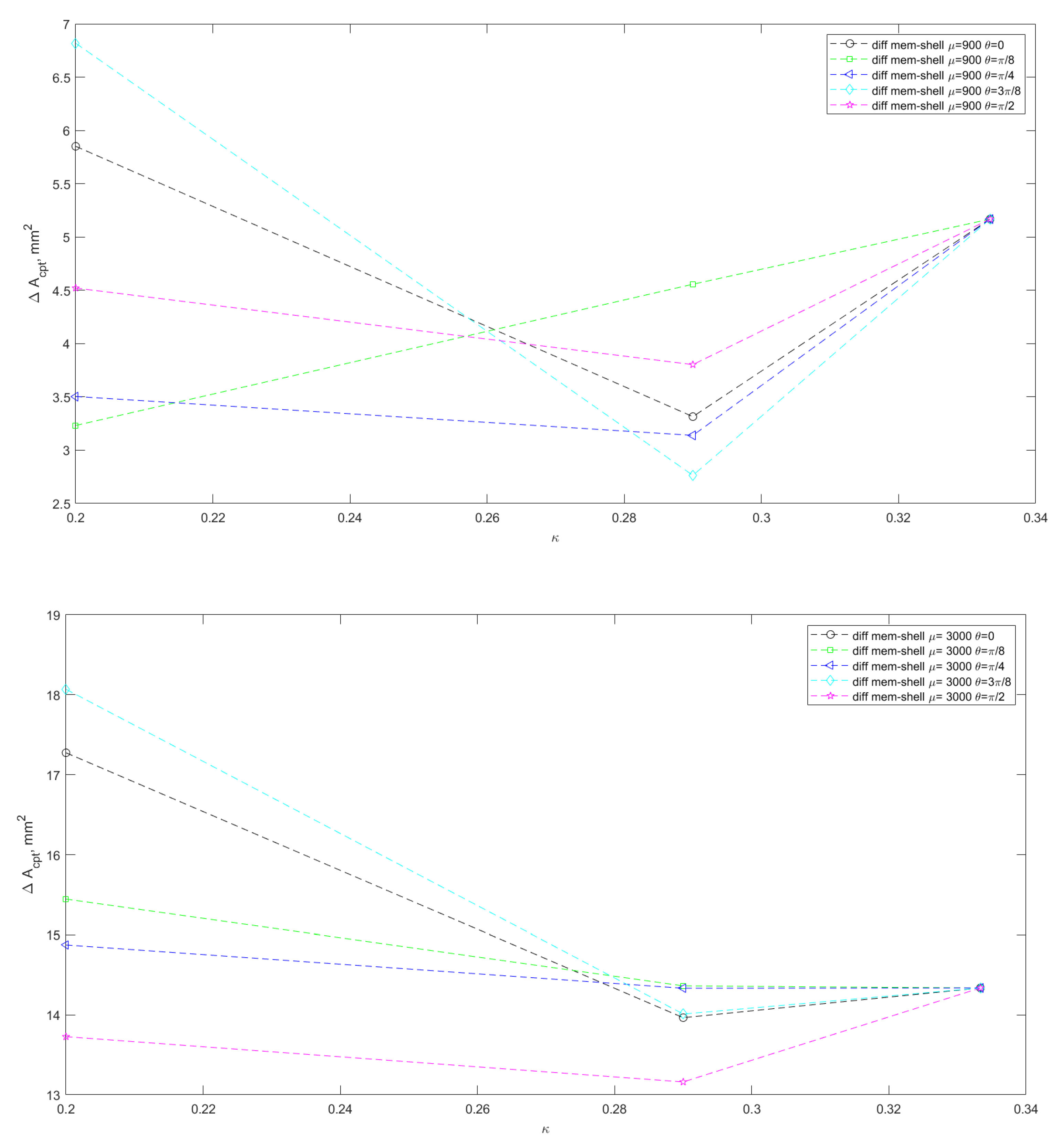
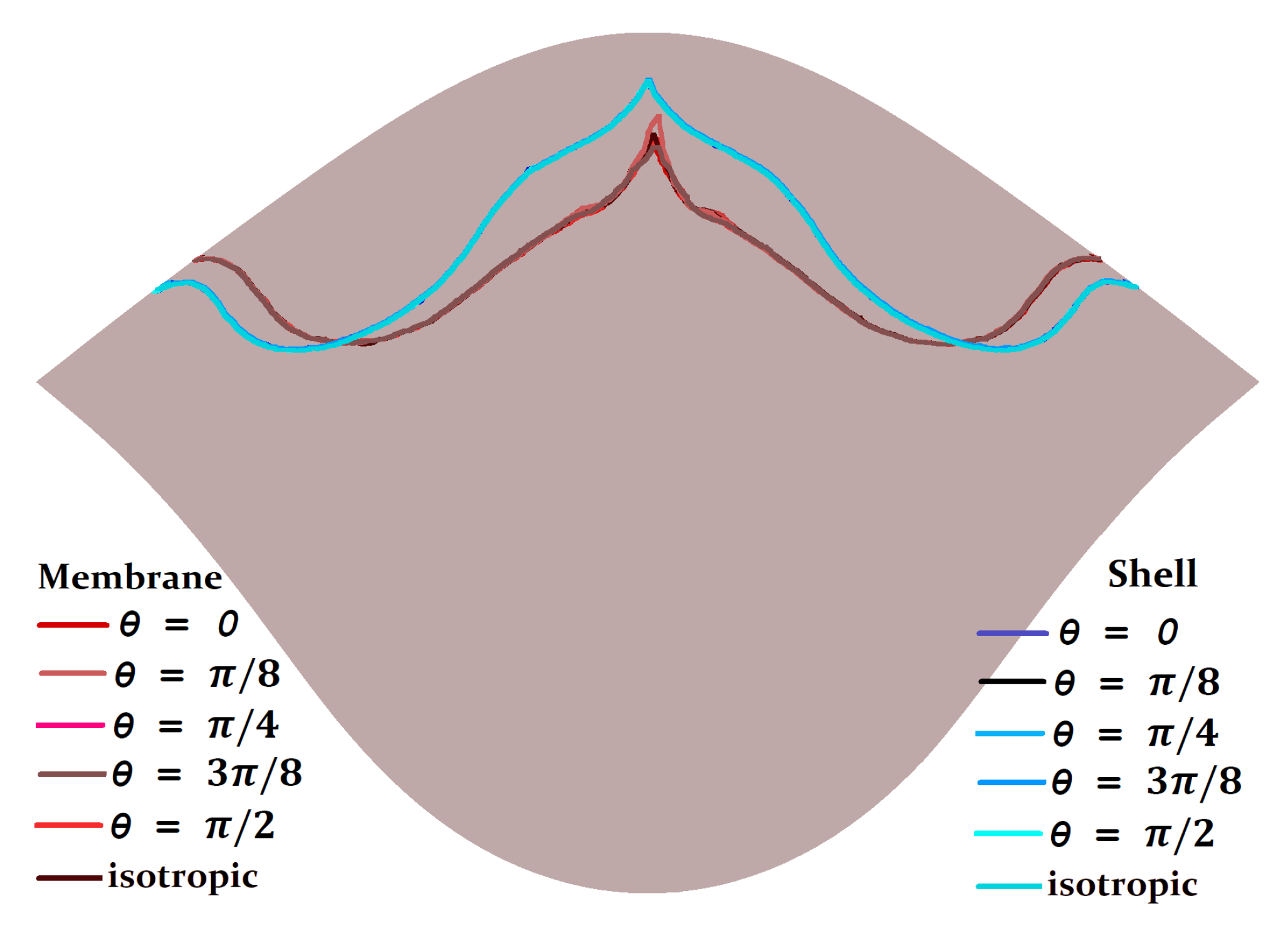
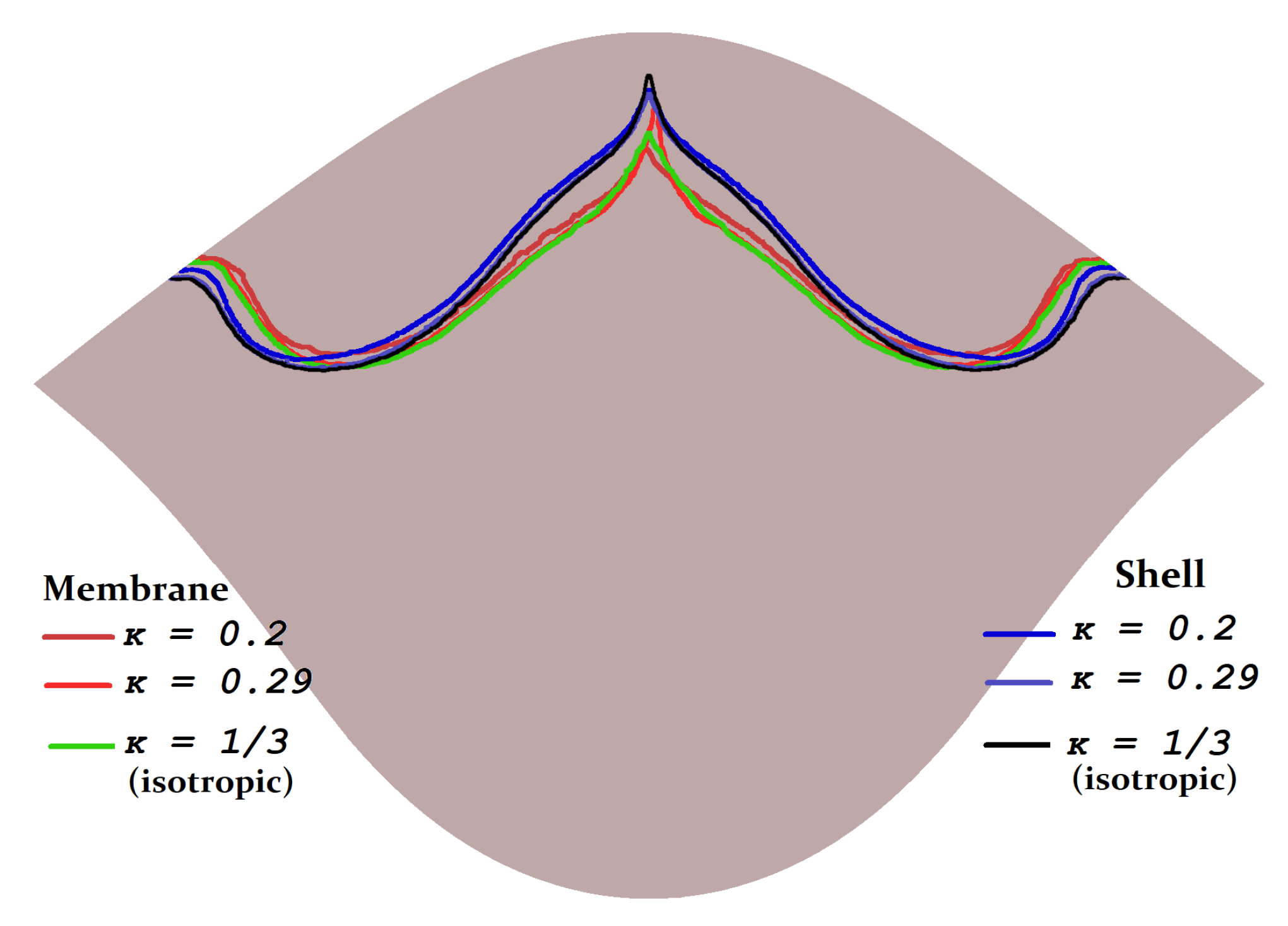
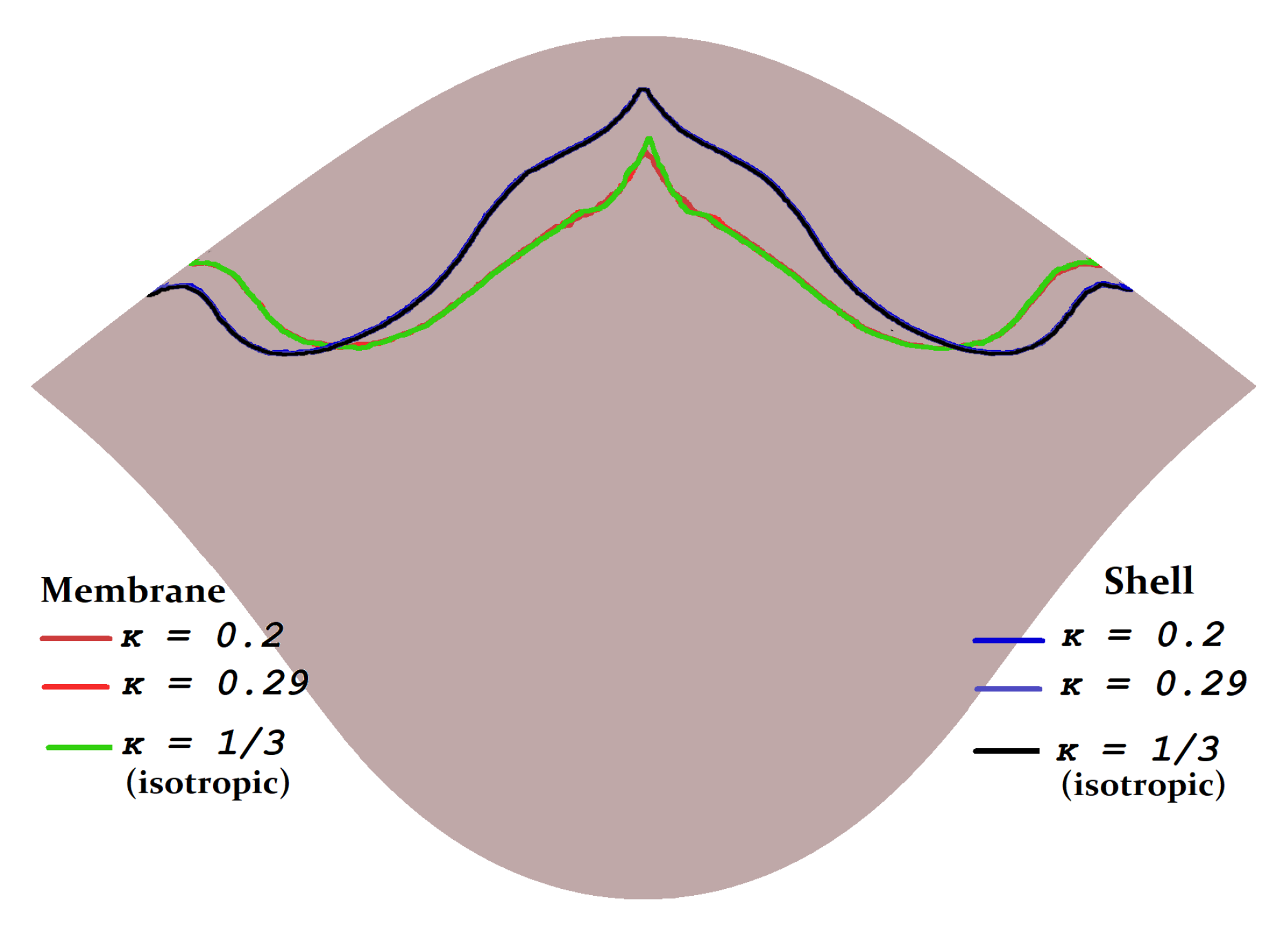
3.3. Coaptation Profiles and Coaptation Characteristics
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osnabrugge, R.L.J.; Mylotte, D.; Head, S.J.; Van Mieghem, N.M.; Nkomo, V.T.; LeReun, C.M.; Bogers, A.J.J.C.; Piazza, N.; Kappetein, A.P. Aortic stenosis in the elderly: Disease prevalence and number of candidates for transcatheter aortic valve replacement: A meta-analysis and modeling study. J. Am. Coll. Cardiol. 2013, 62, 1002–1012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, Y.; Gössl, M.; Garcia, S.; Enriquez-Sarano, M.; Cavalcante, J.L.; Bae, R.; Hashimoto, G.; Fukui, M.; Lopes, B.; Ahmed, A.; et al. Natural history observations in moderate aortic stenosis. BMC Cardiovasc. Disord. 2021, 21, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lowenstern, A.; Sheridan, P.; Wang, T.Y.; Boero, I.; Vemulapalli, S.; Thourani, V.H.; Leon, M.B.; Peterson, E.D.; Brennan, J.M. Sex disparities in patients with symptomatic severe aortic stenosis. Am. Heart J. 2021, 237, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Ando, T.; Onishi, T.; Kuno, T.; Briasoulis, A.; Takagi, H.; Grines, C.L.; Hatori, K.; Tobaru, T.; Malik, A.H.; Ahmad, H. Transcatheter versus surgical aortic valve replacement in the United States (from the Nationwide Readmission Database). Am. J. Cardiol. 2021, 148, 110–115. [Google Scholar] [CrossRef]
- Head, S.J.; Çelik, M.; Kappetein, A.P. Mechanical versus bioprosthetic aortic valve replacement. Eur. Heart J. 2017, 38, 2183–2191. [Google Scholar] [CrossRef]
- Kiyose, A.T.; Suzumura, E.A.; Laranjeira, L.; Buehler, A.M.; Santo, J.A.E.; Berwanger, O.; de Camargo Carvalho, A.C.; de Paola, A.A.; Moises, V.A.; Cavalcanti, A.B. Comparison of biological and mechanical prostheses for heart valve surgery: A systematic review of randomized controlled trials. Arq. Bras. Cardiol. 2019, 112, 292–301. [Google Scholar] [CrossRef]
- Korteland, N.M.; Etnel, J.R.G.; Arabkhani, B.; Mokhles, M.M.; Mohamad, A.; Roos-Hesselink, J.W.; Bogers, A.J.J.C.; Takkenberg, J.J.M. Mechanical aortic valve replacement in non-elderly adults: Meta-analysis and microsimulation. Eur. Heart J. 2017, 38, 3370–3377. [Google Scholar] [CrossRef]
- Rodríguez-Caulo, E.A.; Blanco-Herrera, O.R.; Berastegui, E.; Arias-Dachary, J.; Souaf-Khalafi, S.; Parody-Cuerda, G.; Laguna, G. Biological versus mechanical prostheses for aortic valve replacement. J. Thorac. Cardiovasc. Surg. 2021. Epub ahead of print. [Google Scholar] [CrossRef]
- Diaz, R.; Hernandez-Vaquero, D.; Alvarez-Cabo, R.; Avanzas, P.; Silva, J.; Moris, C.; Pascual, I. Long-term outcomes of mechanical versus biological aortic valve prosthesis: Systematic review and meta-analysis. J. Thorac. Cardiovasc. Surg. 2019, 158, 706–714. [Google Scholar] [CrossRef]
- Zhao, D.F.; Seco, M.; Wu, J.J.; Edelman, J.J.; Wilson, M.K.; Vallely, M.P.; Byrom, M.J.; Bannon, P.G. Mechanical versus bioprosthetic aortic valve replacement in middle-aged adults: A systematic review and meta-analysis. Ann. Thorac. Surg. 2016, 102, 315–327. [Google Scholar] [CrossRef] [Green Version]
- Björk, V.O.; Hultquist, G. Teflon and pericardial aortic valve prosthesis. J. Thorac. Cardiovasc. Surg. 1964, 47, 693–701. [Google Scholar] [CrossRef]
- Love, J.W.; Calvin, J.H.; Phelan, R.F.; Love, C.S. Rapid intraoperative fabrication of an autologous tissue heart valve: A new technique. In Proceedings of the Third International Symposium on Cardiac Bioprostheses, London, UK, 21–23 May 1985; Bodnar, E., Yacoub, M.H., Eds.; Yorke Medical Books: New York, NY, USA, 1986; pp. 691–698. [Google Scholar]
- Ozaki, S.; Kawase, I.; Yamashita, H.; Uchida, S.; Nozawa, Y.; Matsuyama, T.; Takatoh, M.; Hagiwara, S. Aortic valve reconstruction using self-developed aortic valve plasty system in aortic valve disease. Interact. Cardiovasc. Thorac. Surg. 2011, 12, 550–553. [Google Scholar] [CrossRef] [Green Version]
- Benedetto, U.; Sinha, S.; Dimagli, A.; Dixon, L.; Stoica, S.; Cocomello, L.; Quarto, C.; Angelini, G.D.; Dandekar, U.; Caputo, M. Aortic valve neocuspidization with autologous pericardium in adult patients: UK experience and meta-analytic comparison with other aortic valve substitutes. Eur. J. -Cardio-Thorac. Surg. 2021, 60, 34–46. [Google Scholar] [CrossRef] [PubMed]
- Thakeb, Y.M.; Sakr, S.; El Sarawy, E.; Salem, A.M. Short-term competency of aortic valve repair in Egyptian patients. J. Card. Surg. 2020, 35, 598–602. [Google Scholar] [CrossRef] [PubMed]
- Iida, Y.; Akiyama, S.; Shimura, K.; Fujii, S.; Hashimoto, C.; Mizuuchi, S.; Arizuka, Y.; Nishioka, M.; Shimura, N.; Moriyama, S.; et al. Comparison of aortic annulus dimensions after aortic valve neocuspidization with those of normal aortic valve using transthoracic echocardiography. Eur. J. -Cardio-Thorac. Surg. 2018, 54, 1081–1084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siondalski, P.; Wilczynski, L.; Rogowski, J.; Zembala, M. Human aortic bioprosthesis. Eur. J. -Cardio-Thorac. Surg. 2008, 6, 1268. [Google Scholar] [CrossRef] [PubMed]
- Muller, W.H.J.; Warren, W.D.; Dammann, J.F.J.; Beckwith, J.R.; Wood, J.E., Jr. Surgical relief of aortic insufficiency by direct operation on the aortic valve. Circulation 1960, 21, 587–597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tada, N.; Tanaka, N.; Abe, K.; Hata, M. Transcatheter aortic valve implantation after aortic valve neocuspidization using autologous pericardium: A case report. Eur. Heart-J.-Case Rep. 2019, 3, ytz105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hayama, H.; Suzuki, M.; Hashimoto, G.; Makino, K.; Isekame, Y.; Yamashita, H.; Ono, T.; Iijima, R.; Hara, H.; Moroi, M.; et al. Early detection of possible leaflet thrombosis after aortic valve neo-cuspidization surgery using autologous pericardium. J. Am. Soc. Echocardiogr. 2018, 31, B62. [Google Scholar]
- Le Polain De Waroux, J.B.; Pouleur, A.C.; Robert, A.; Pasquet, A.; Gerber, B.L.; Noirhomme, P.; Khoury, G.E.; Vanoverschelde, J.-L.J. Mechanisms of recurrent aortic regurgitation after aortic valve repair: Predictive value of intraoperative transesophageal echocardiography. JACC Cardiovasc. Imaging 2009, 2, 931–939. [Google Scholar] [CrossRef] [Green Version]
- Kunihara, T.; Aicher, D.; Rodionycheva, S.; Groesdonk, H.V.; Langer, F.; Sata, F.; Schäfers, H.J. Preoperative aortic root geometry and postoperative cusp configuration primarily determine long-term outcome after valve-preserving aortic root repair. J. Thorac. Cardiovasc. Surg. 2012, 143, 1389–1395. [Google Scholar] [CrossRef] [Green Version]
- Miyahara, S.; Omura, A.; Sakamoto, T.; Nomura, Y.; Inoue, T.; Minami, H.; Okada, K.; Okita, Y. Impact of postoperative cusp configuration on midterm durability after aortic root reimplantation. J. Heart Valve Dis. 2013, 22, 509–516. [Google Scholar]
- Ridley, C.; Sohmer, B.; Vallabhajosyula, P.; Augoustides, J.G.T. Aortic leaflet billowing as a risk factor for repair failure after aortic valve repair. J. Cardiothorac. Vasc. Anesth. 2017, 31, 1001–1006. [Google Scholar] [CrossRef]
- Schäfers, H.-J.; Bierbach, B.; Aicher, D. A new approach to the assessment of aortic cusp geometry. J. Thorac. Cardiovasc. Surg. 2006, 132, 436–438. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Sun, W. Simulated transcatheter aortic valve deformation: A parametric study on the impact of leaflet geometry on valve peak stress. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e02814. [Google Scholar] [CrossRef] [Green Version]
- Travaglino, S.; Murdock, K.; Tran, A.; Martin, C.; Liang, L.; Wang, Y.; Sun, W. Computational optimization study of transcatheter aortic valve leaflet design using porcine and bovine leaflets. J. Biomech. Eng. 2020, 142, 011007. [Google Scholar] [CrossRef]
- Loerakker, S.; Argento, G.; Oomens, C.W.; Baaijens, F.P. Effects of valve geometry and tissue anisotropy on the radial stretch and coaptation area of tissue-engineered heart valves. J. Biomech. 2013, 46, 1792–1800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hammer, P.E.; Chen, P.C.; Pedro, J.; Howe, R.D. Computational model of aortic valve surgical repair using grafted pericardium. J. Biomech. 2012, 45, 1199–1204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zakerzadeh, R.; Hsu, M.C.; Sacks, M.S. Computational methods for the aortic heart valve and its replacements. Expert Rev. Med. Devices 2017, 14, 849–866. [Google Scholar] [CrossRef]
- Auricchio, F.; Conti, M.; Ferrara, A.; Morganti, S.; Reali, A. Patient-specific simulation of a stentless aortic valve implant: The impact of fibres on leaflet performance. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 277–285. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Abad, A.; Sacks, M.S. Simulated bioprosthetic heart valve deformation under quasi-static loading. J. Biomech. Eng. 2005, 127, 905–914. [Google Scholar] [CrossRef]
- Kim, H.; Lu, J.; Sacks, M.S.; Chandran, K.B. Dynamic simulation of bioprosthetic heart valves using a stress resultant shell model. Ann. Biomed. Eng. 2008, 36, 262–275. [Google Scholar] [CrossRef] [PubMed]
- Smuts, A.N.; Blaine, D.C.; Scheffer, C.; Weich, H.; Doubell, A.F.; Dellimore, K.H. Application of finite element analysis to the design of tissue leaflets for a percutaneous aortic valve. J. Mech. Behav. Biomed. Mater. 2011, 4, 85–98. [Google Scholar] [CrossRef] [PubMed]
- Morganti, S.; Auricchio, F.; Benson, D.J.; Gambarin, F.I.; Hartmann, S.; Hughes, T.J.R.; Reali, A. Patient-specific isogeometric structural analysis of aortic valve closure. Comput. Methods Appl. Mech. Eng. 2015, 284, 508–520. [Google Scholar] [CrossRef]
- Vassilevski, Y.; Liogky, A.; Salamatova, V. Application of Hyperelastic Nodal Force Method to Evaluation of Aortic Valve Cusps Coaptation: Thin Shell vs. Membrane Formulations. Mathematics 2021, 9, 1450. [Google Scholar] [CrossRef]
- Fan, R.; Bayoumi, A.S.; Chen, P.; Hobson, C.M.; Wagner, W.R.; Mayer, J.E., Jr.; Sacks, M.S. Optimal elastomeric scaffold leaflet shape for pulmonary heart valve leaflet replacement. J. Biomech. 2013, 46, 662–669. [Google Scholar] [CrossRef] [Green Version]
- Hofferberth, S.C.; Baird, C.W.; Hoganson, D.M.; Quinonez, L.G.; Emani, S.M.; Pedro, J.; Hammer, P.E. Mechanical properties of autologous pericardium change with fixation time: Implications for valve reconstruction. Semin. Thorac. Cardiovasc. Surg. 2019, 31, 852–854. [Google Scholar] [CrossRef]
- Aguiari, P.; Fiorese, M.; Iop, L.; Gerosa, G.; Bagno, A. Mechanical testing of pericardium for manufacturing prosthetic heart valves. Interact. Cardiovasc. Thorac. Surg. 2016, 22, 72–84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ozolins, V.; Ozolanta, I.; Smits, L.; Lacis, A.; Kasyanov, V. Biomechanical Properties of Glutaraldehyde Treated Human Pericadium. In IFMBE Proceedings, Volume 20, Proceedings of the 14th Nordic-Baltic Conference on Biomedical Engineering and Medical Physics, Riga, Latvia, 16–20 June 2008; Katashev, A., Dekhtyar, Y., Spigulis, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 143–145. [Google Scholar]
- Zigras, T.C. Biomechanics of Human Pericardium: A Comparative Study of Fresh and Fixed Tissue. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2007. [Google Scholar]
- Salamatova, V.Y.; Liogky, A.A. Method of Hyperelastic Nodal Forces for Deformation of Nonlinear Membranes. Differ. Equ. 2020, 56, 950–958. [Google Scholar] [CrossRef]
- Pavan, P.G.; Pachera, P.; Tiengo, C.; Natali, A.N. Biomechanical behavior of pericardial human tissue: A constitutive formulation. Proc. Inst. Mech. Eng. Part J. Eng. Med. 2014, 228, 926–934. [Google Scholar] [CrossRef]
- Abbasi, M.; Barakat, M.S.; Dvir, D.; Azadani, A.N. A non-invasive material characterization framework for bioprosthetic heart valves. Ann. Biomed. Eng. 2019, 47, 97–112. [Google Scholar] [CrossRef]
- Tepole, A.B.; Kabaria, H.; Bletzinger, K.U.; Kuhl, E. Isogeometric Kirchhoff—Love shell formulations for biological membranes. Comput. Methods Appl. Mech. Eng. 2015, 293, 328–347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oñate, E.; Flores, F.G. Advances in the formulation of the rotation-free basic shell triangle. Comput. Methods Appl. Mech. Eng. 2005, 194, 2406–2443. [Google Scholar] [CrossRef]
- Holzapfel, G. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science; John Wiley & Sons Ltd.: Chichester, UK, 2000; p. 470. [Google Scholar]
- Holzapfel, G.A.; Ogden, R.W.; Sherifova, S. On fibre dispersion modelling of soft biological tissues: A review. Proc. R. Soc. A 2019, 475, 20180736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, J.; Zhou, X.; Raghavan, M.L. Inverse method of stress analysis for cerebral aneurysms. Biomech. Model. Mechanobiol. 2008, 7, 477–486. [Google Scholar] [CrossRef] [PubMed]
- Roohbakhshan, F.; Duong, T.X.; Sauer, R.A. A projection method to extract biological membrane models from 3D material models. J. Mech. Behav. Biomed. Mater. 2016, 58, 90–104. [Google Scholar] [CrossRef] [PubMed]
- Ciarlet, P.G. Mathematical Elasticity. Volume I: Three-Dimensional Elasticity; Publishing House: Amsterdam, The Netherlands, 1988; p. 451. [Google Scholar]
- User Documentation for KINSOL v5.7.0 (SUNDIALS v5.7.0). Available online: https://computing.llnl.gov/sites/default/files/kin_guide.pdf (accessed on 7 September 2021).
- Terekhov, K.M.; Konshin, I.N.; Vassilevski, Y.V.; Danilov, A.A. Parallel software platform INMOST: A framework for numerical modeling. Supercomput. Front. Innov. 2016, 2, 55–66. [Google Scholar]
- Baird, C.W.; Marathe, S.P.; Pedro, J. Aortic valve neo-cuspidation using the Ozaki technique for acquired and congenital disease: Where does this procedure currently stand? Indian J. Thorac. Cardiovasc. Surg. 2020, 36, 113–122. [Google Scholar] [CrossRef]

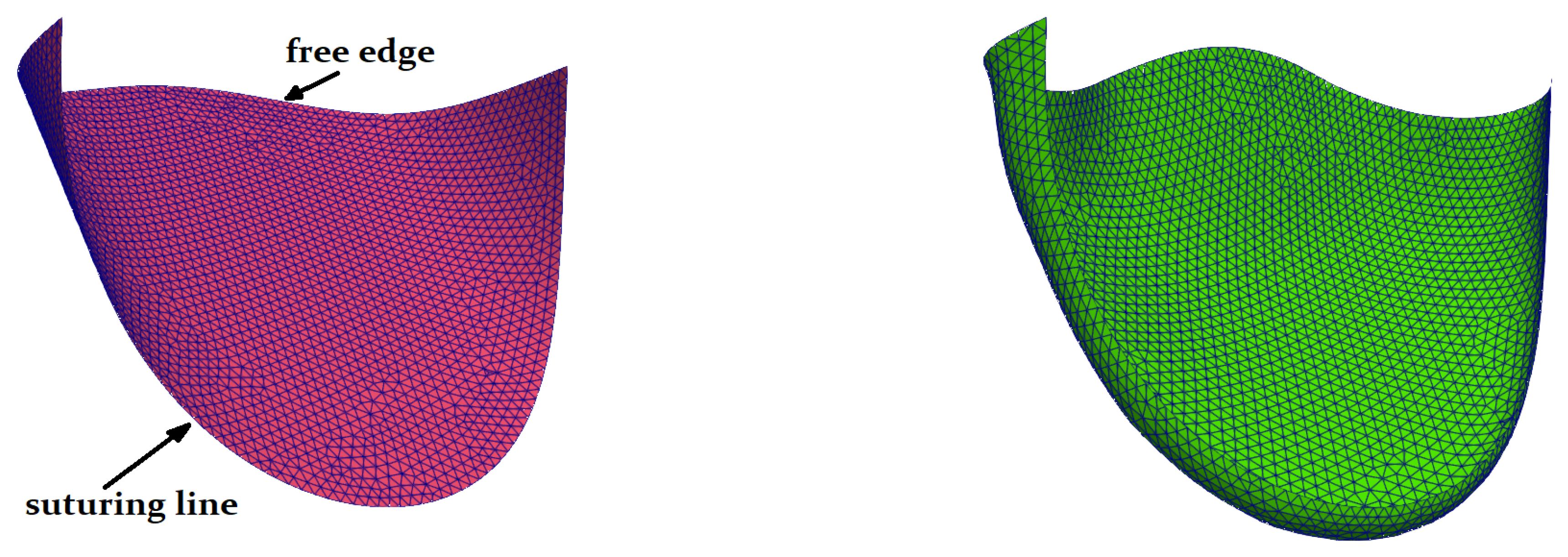





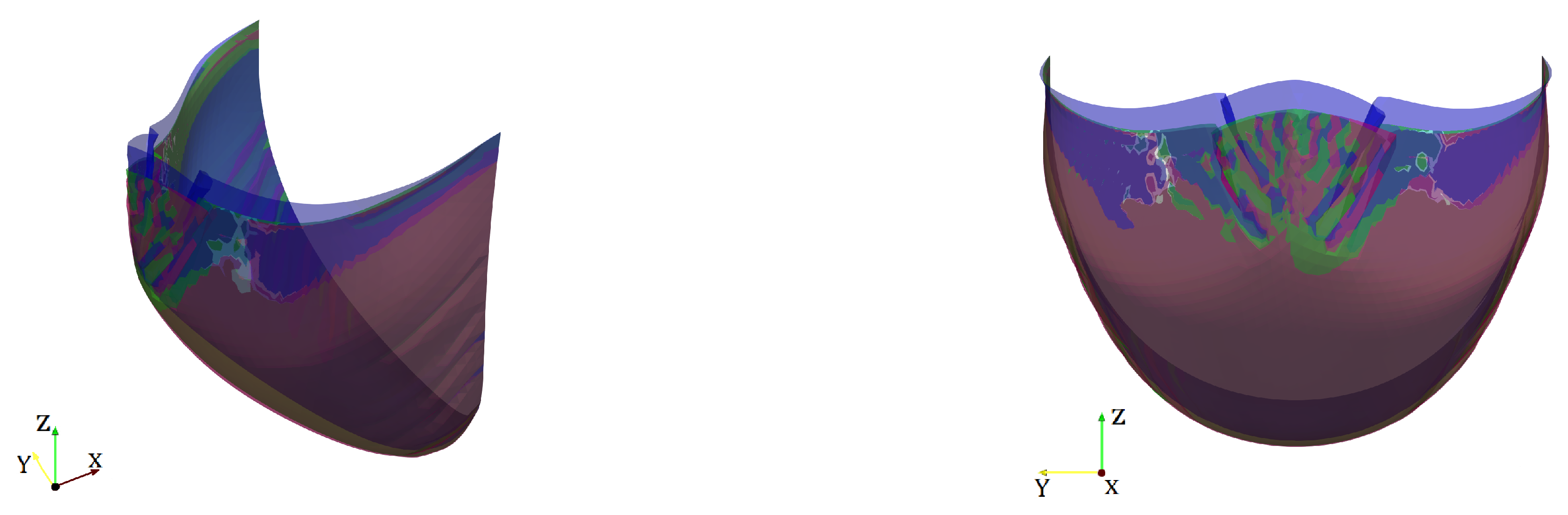

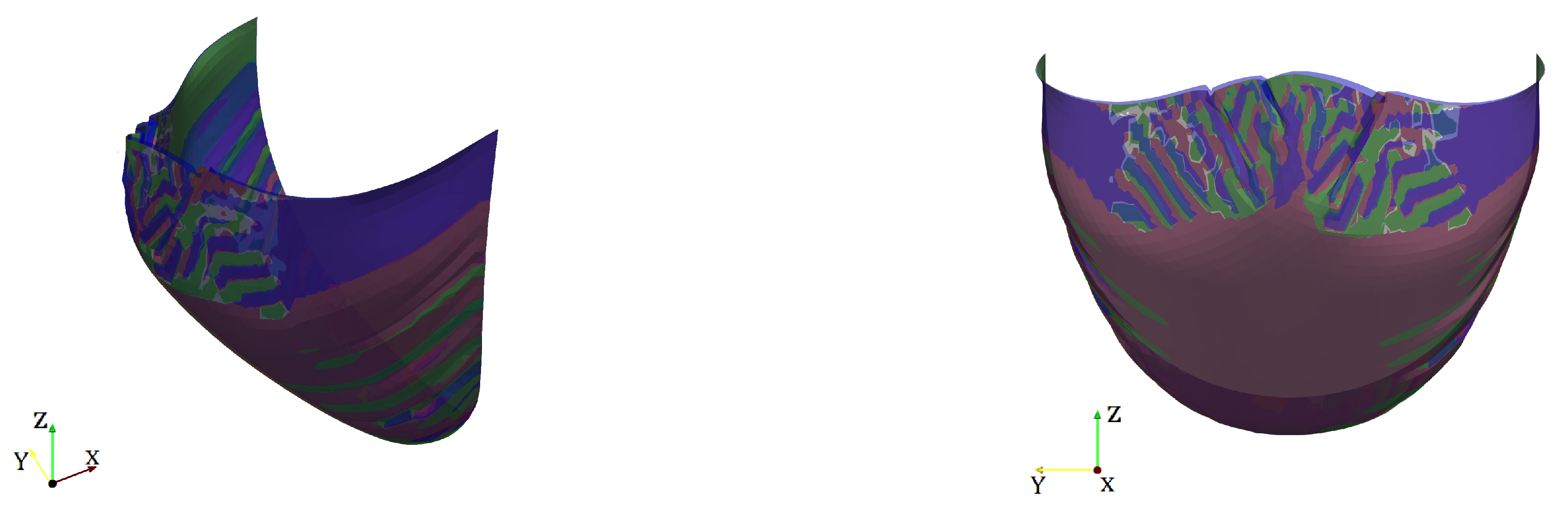
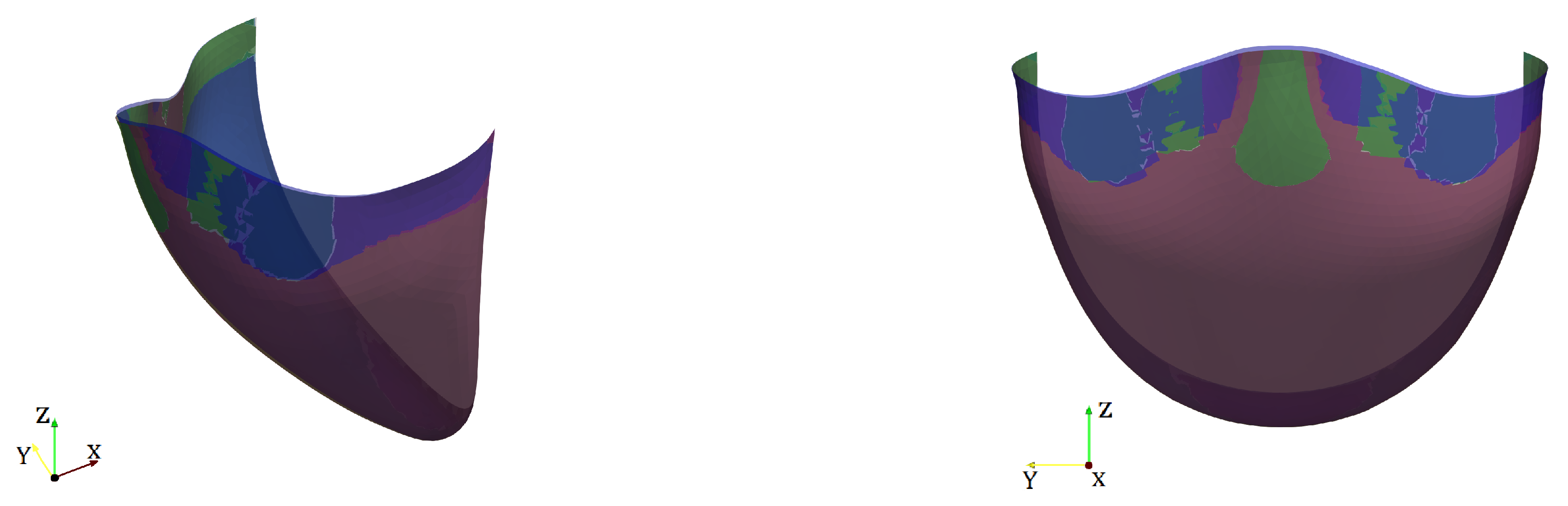

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liogky, A.; Karavaikin, P.; Salamatova, V. Impact of Material Stiffness and Anisotropy on Coaptation Characteristics for Aortic Valve Cusps Reconstructed from Pericardium. Mathematics 2021, 9, 2193. https://doi.org/10.3390/math9182193
Liogky A, Karavaikin P, Salamatova V. Impact of Material Stiffness and Anisotropy on Coaptation Characteristics for Aortic Valve Cusps Reconstructed from Pericardium. Mathematics. 2021; 9(18):2193. https://doi.org/10.3390/math9182193
Chicago/Turabian StyleLiogky, Alexey, Pavel Karavaikin, and Victoria Salamatova. 2021. "Impact of Material Stiffness and Anisotropy on Coaptation Characteristics for Aortic Valve Cusps Reconstructed from Pericardium" Mathematics 9, no. 18: 2193. https://doi.org/10.3390/math9182193





