Energy Based Calculation of the Second-Order Levitation in Magnetic Fluid
Abstract
:1. Introduction
2. Materials and Methods
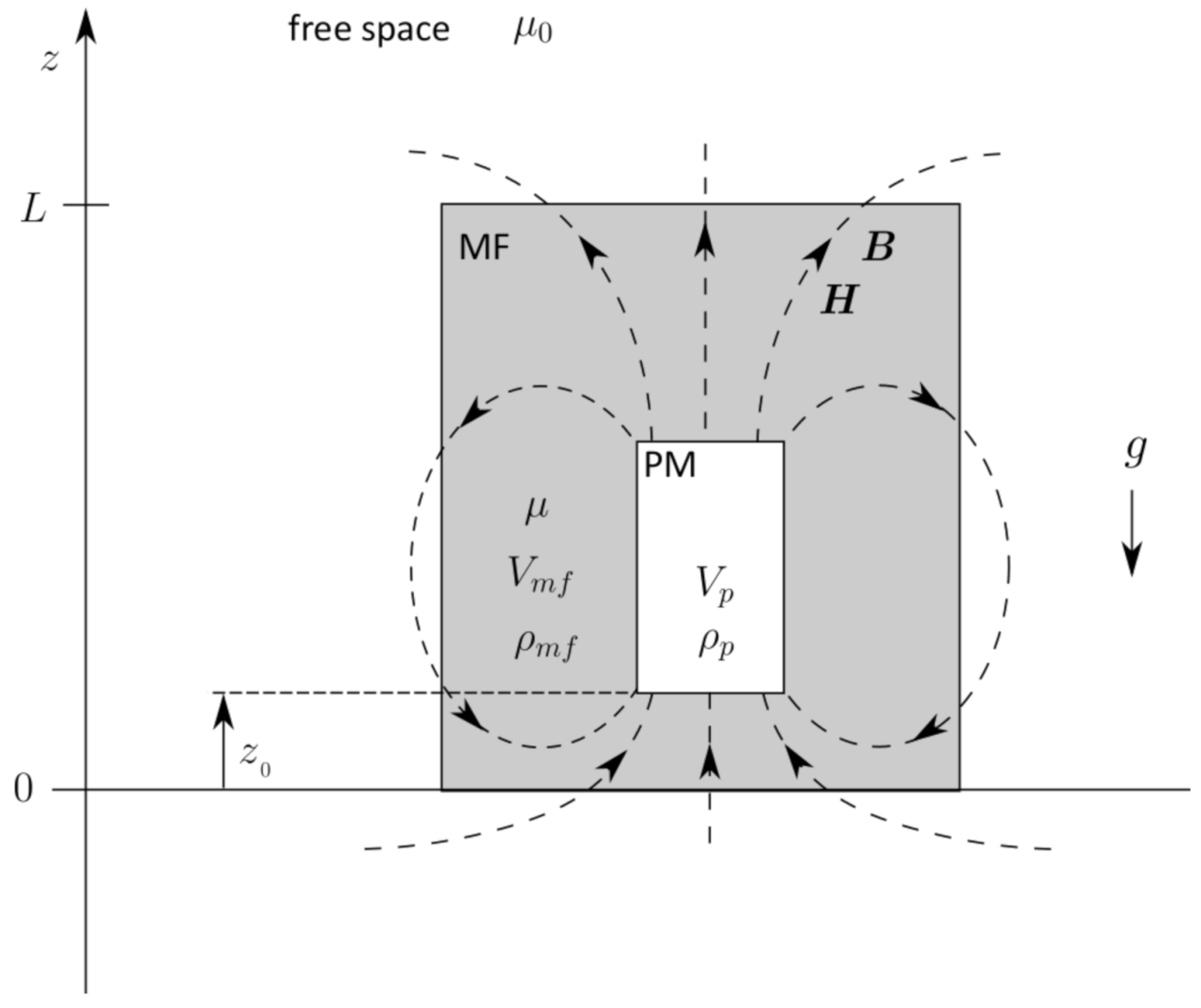
2.1. Problem Definition
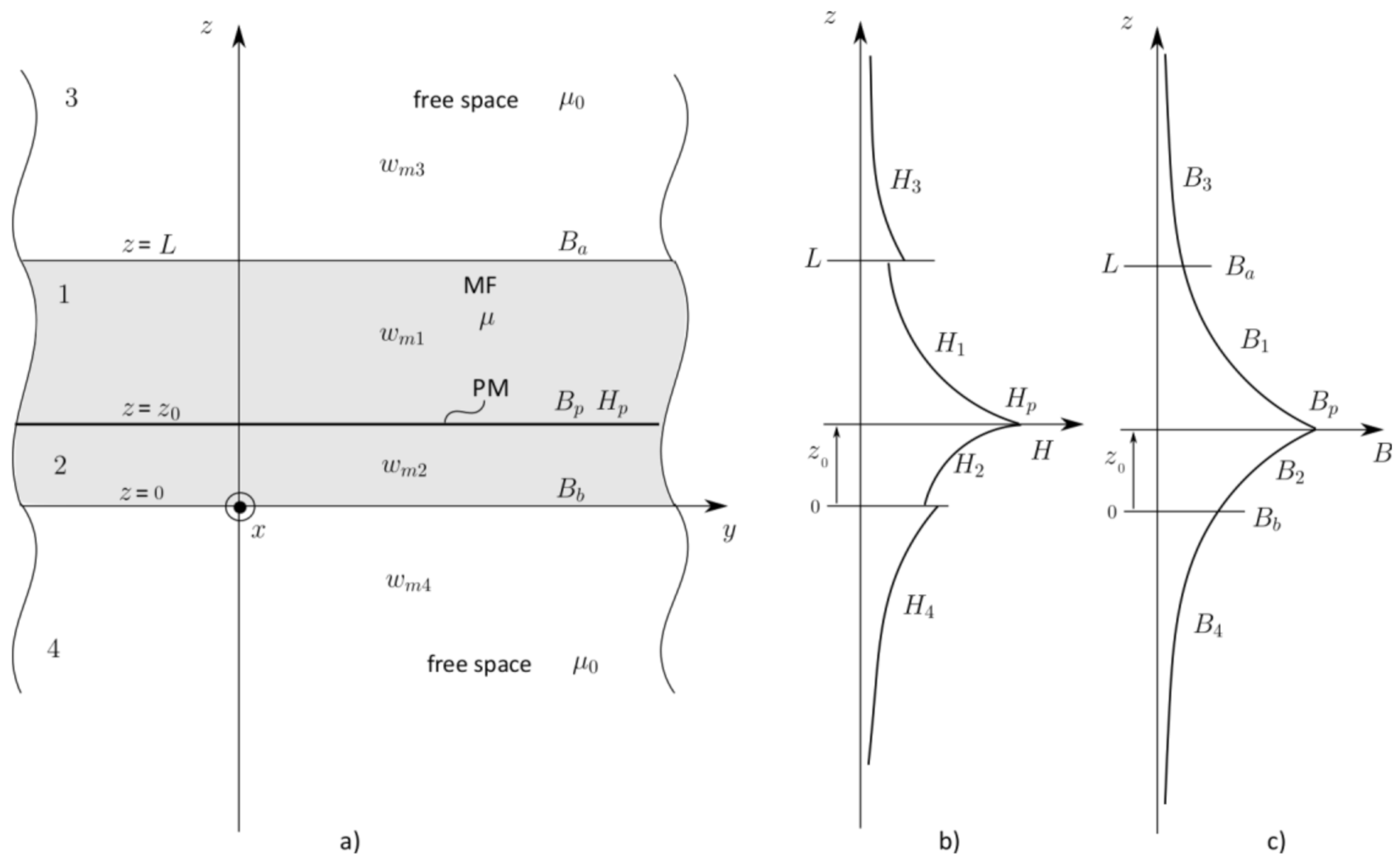
2.2. Surface Integral Method (SIM)
2.3. Energy Method
2.4. Simulation Setup
3. Results and Discussion
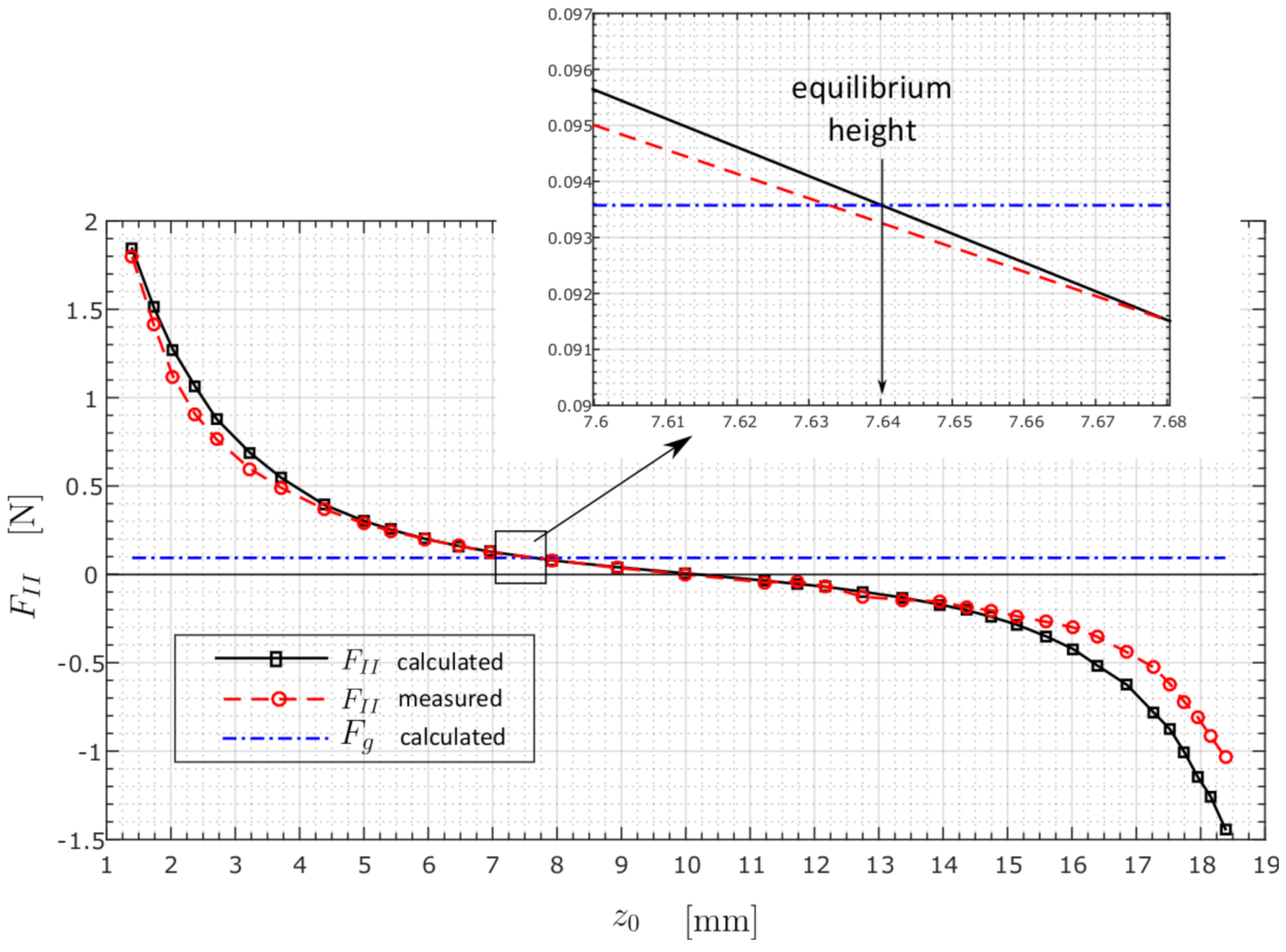
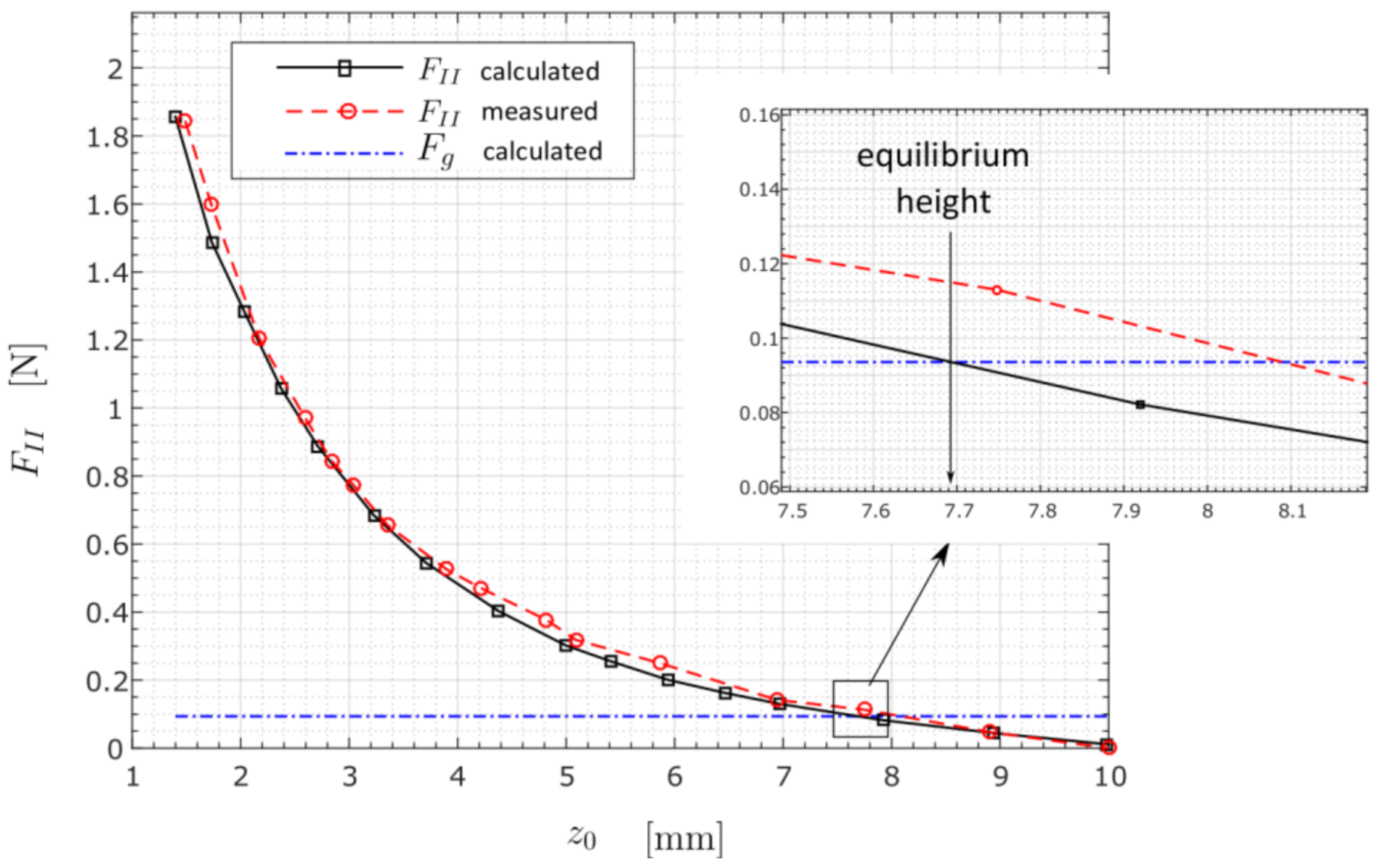
3.1. Calculations Based on the Surface Integral Method (SIM)
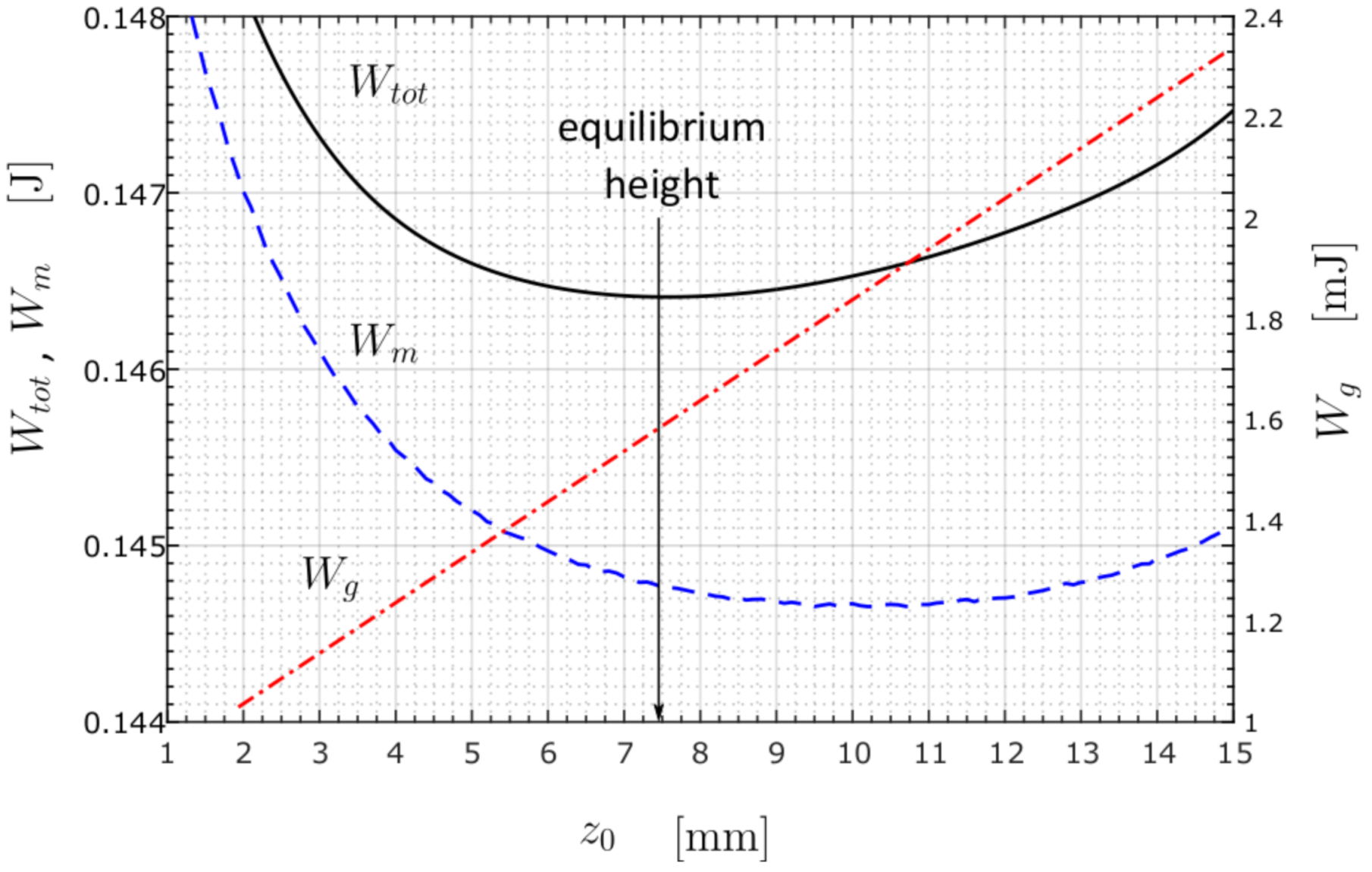
3.2. Calculations Based on the Energy Method (EM)
3.3. Parametric Analysis
- the radius of the rod ()
- relative permeability of the MF ()
- the remanent flux density of the PM (
- the ratio between the PM’s diameter and height at constant volume (/)
- the ratio between the container’s diameter and height at constant volume (/)
3.3.1. Case A (Variation of the Rod’s Radius—)
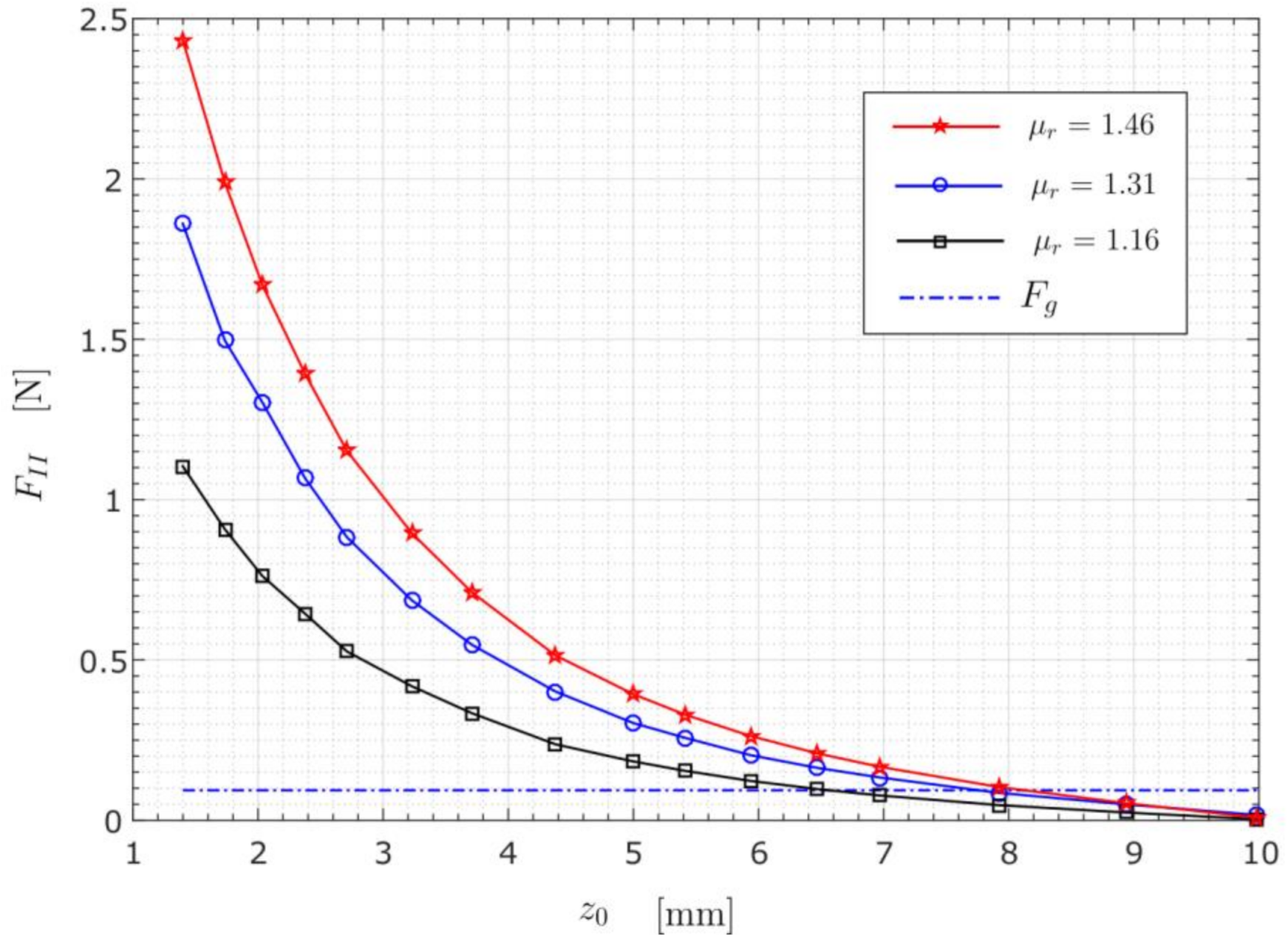
3.3.2. Case B (Variation of the MF’s Relative Permeability—)
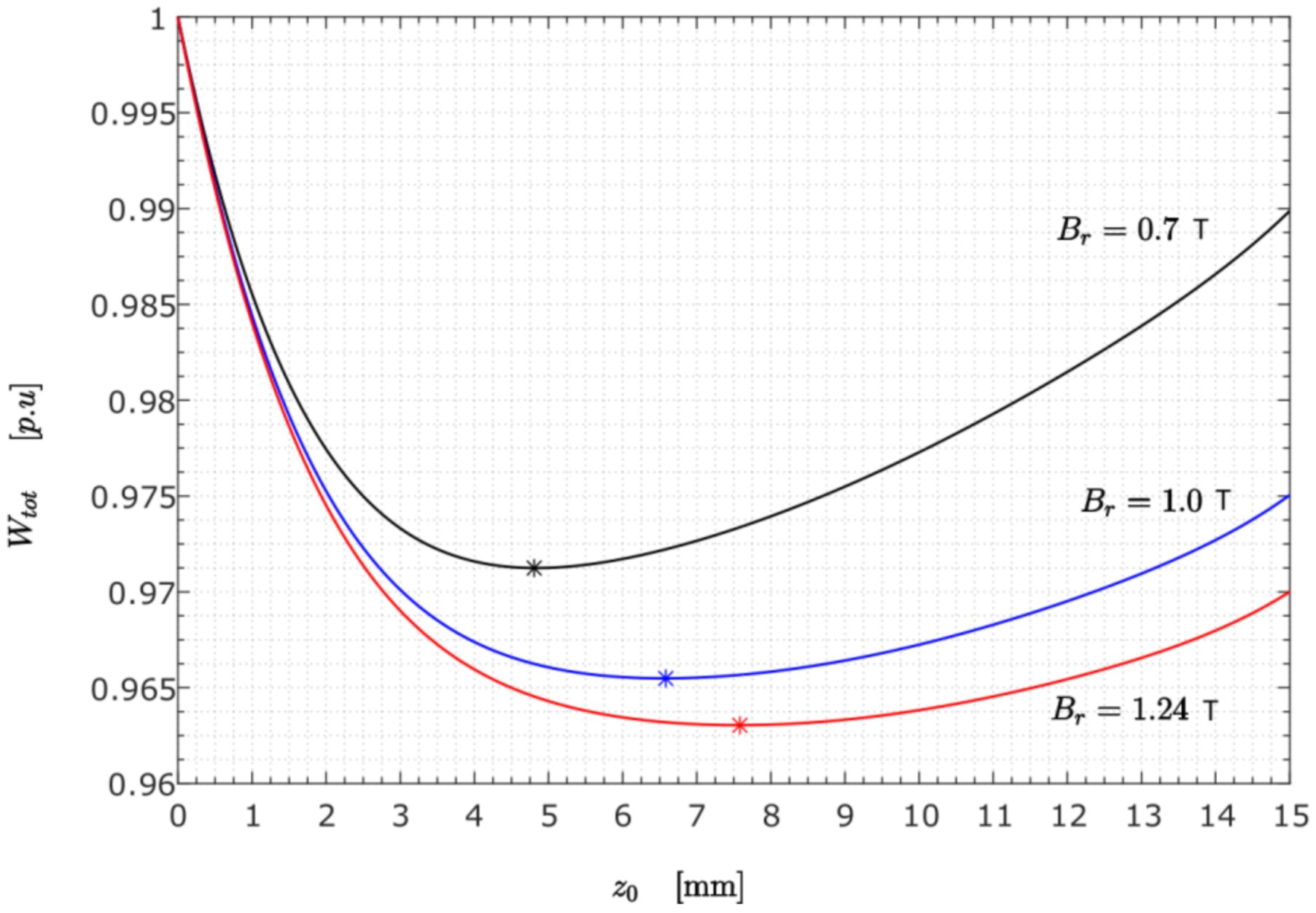
3.3.3. Case C (Variation of the PM’s Remanence flux Density—)
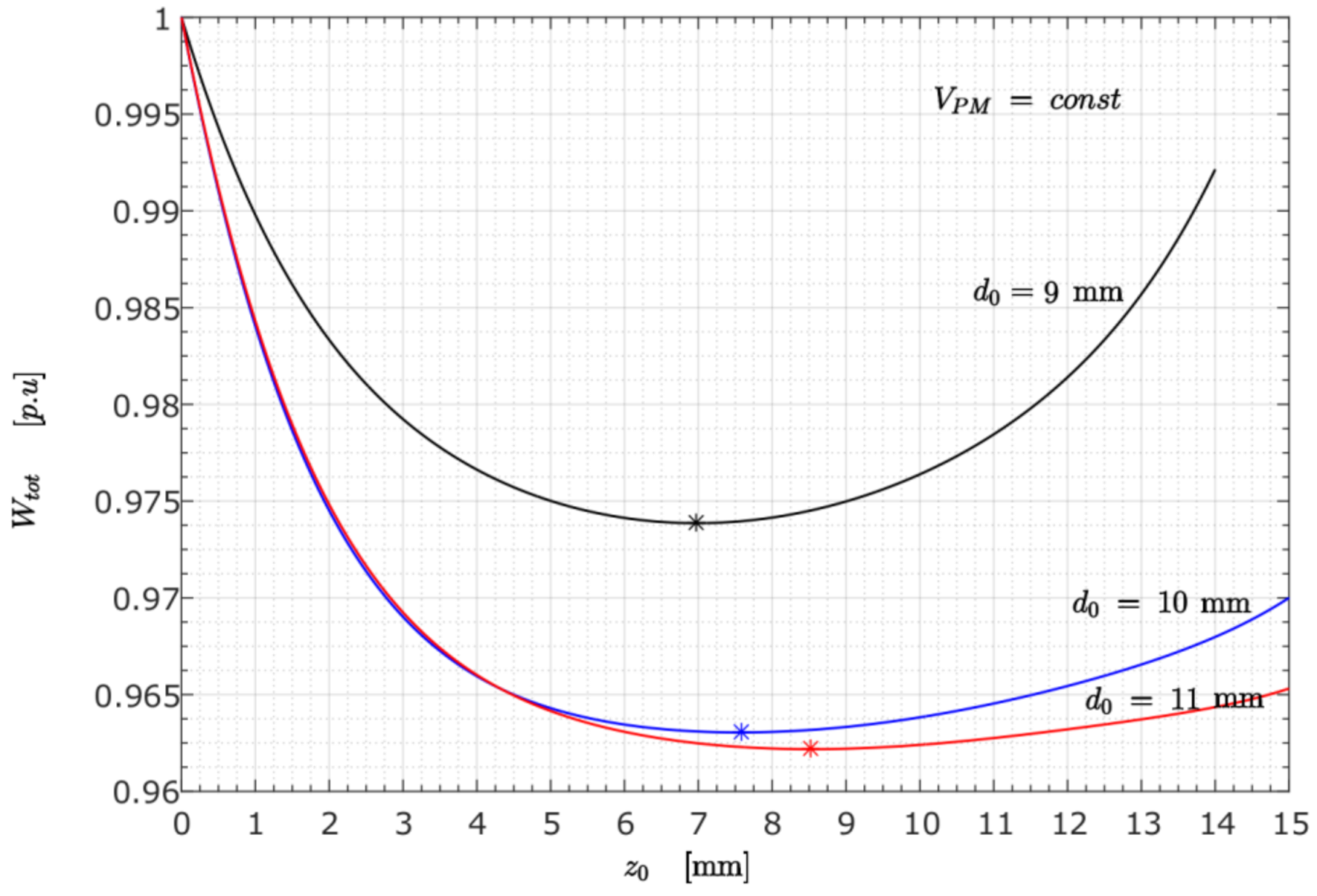
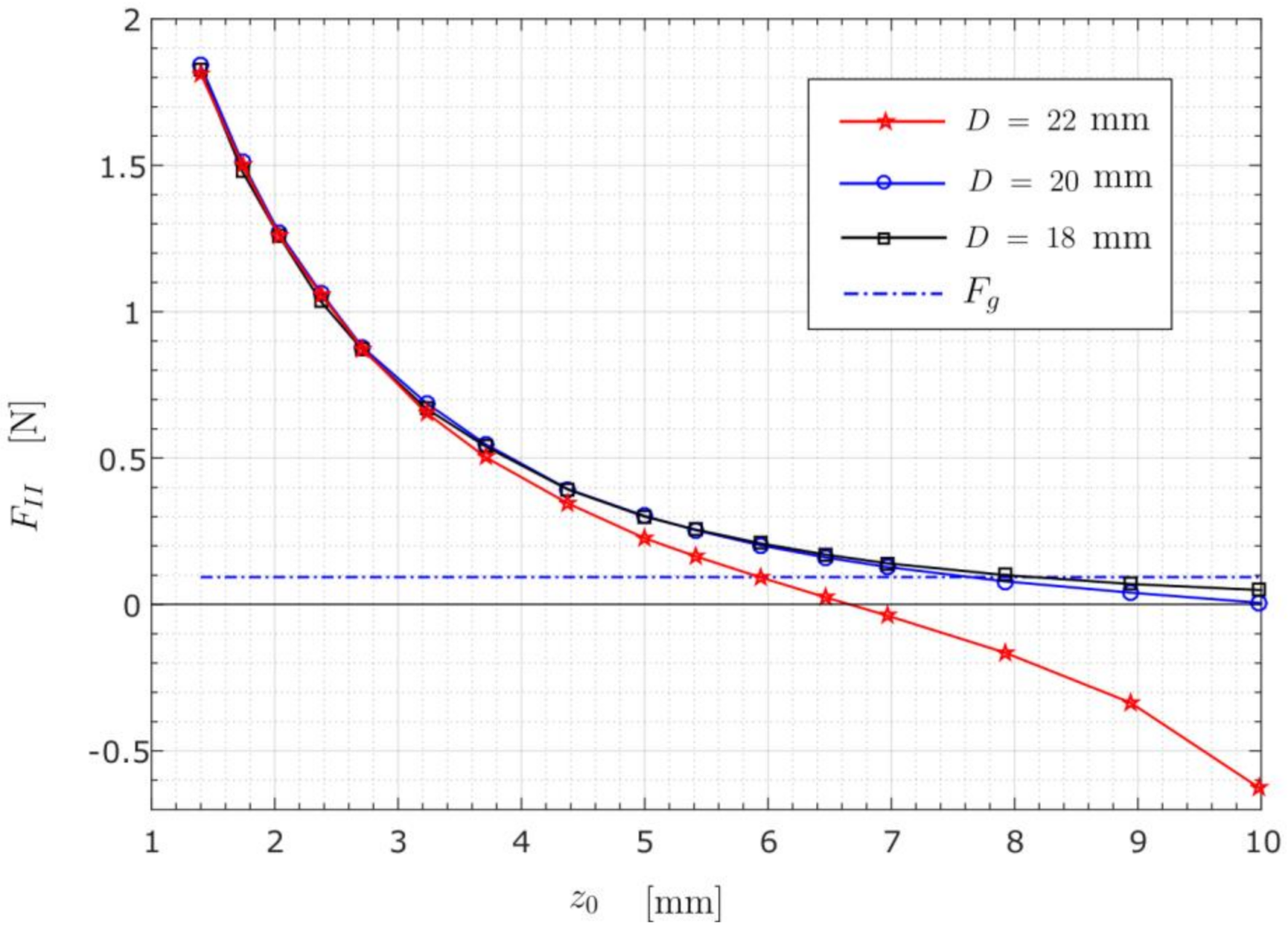
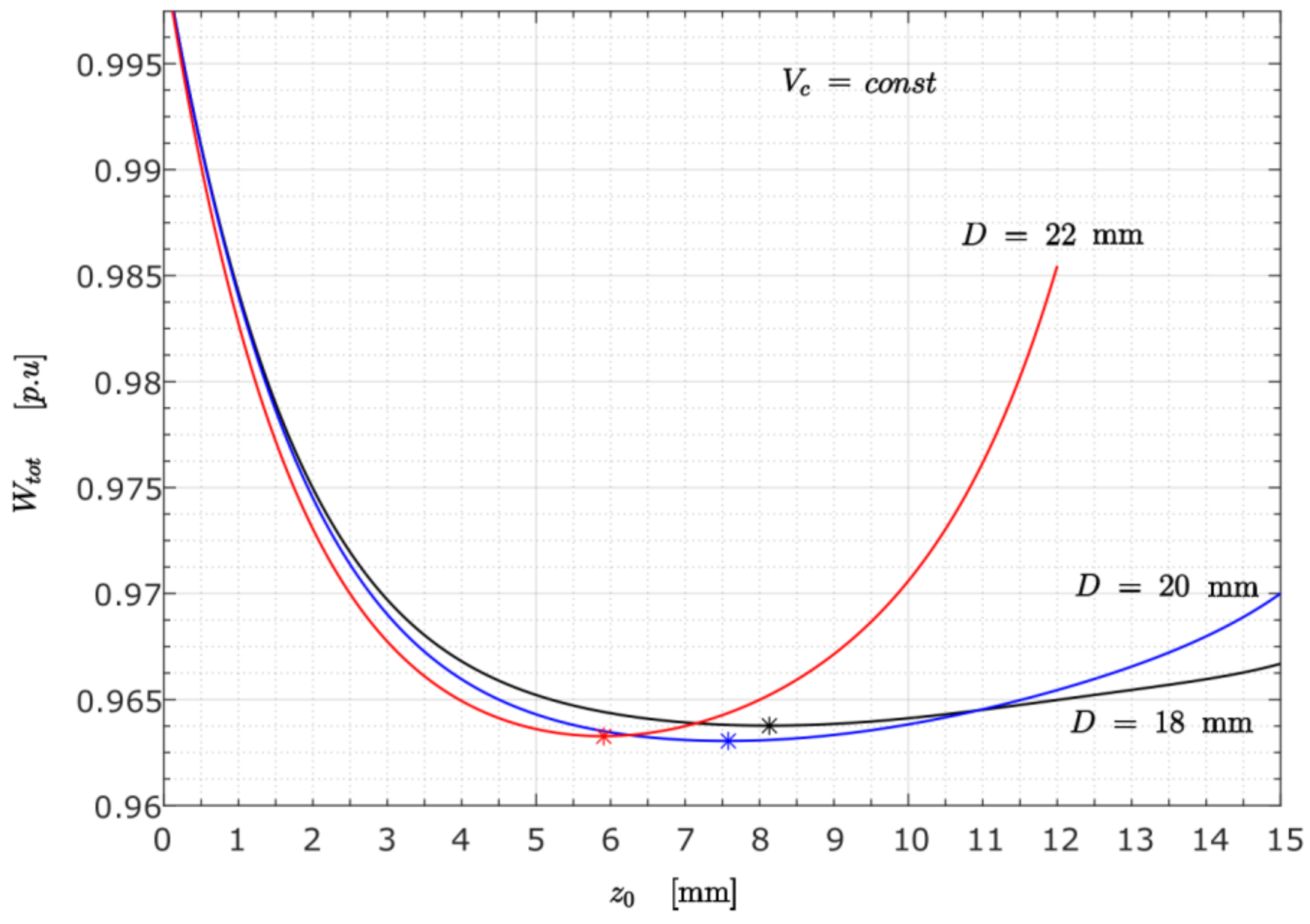
3.3.4. Case D (Variation of the PM’s Diameter at Constant PM Volume)
3.3.5. Case E (Variation of the Container’s Diameter at Constant Container’s Volume)
4. Conclusions
- By increasing the radius of the measuring rod (), the PM’s levitation height will tend to reach a higher level. The reason is evident; while the rod usually consists of non-magnetic material, the fluid-magnetic pressure at the PM’s top face is going to produce a lower force than at the PM’s bottom face. The difference in this pressure acts upward, hence, the magnet will levitate at a higher level. For this case, the error between SIM and EM was less than 1%.
- The magnetic properties of the MF are reflected in the value of relative permeability which is, here, assumed as a constant. Truly speaking, this is only a rough approximation. Namely, in real magnetic fluids, the magnetizing characteristic are non-linear, and the concentration of the particles also decreases with the distance from the magnet. However, even with this simplification, the conclusion can be declared that the PM immersed in a magnetic fluid with lower permeability will experience a weaker magnetic buoyancy force. Consequently, the levitation height will be lower to some extent.
- The same can be derived by considering the problem in the light of the energy. In highly permeable MF, the PM would rather be centered in the fluid, because its magnetostatic energy is minimal there. By decreasing the MF’s permeability the magnetostatic energy increases and its variation with respect to the levitation height becomes smaller, thus, the influence of the gravitational energy comes to the fore, and moves the minimum of the total energy curve towards a lower value. The results’ comparison obtained by the SIM and EM for the case shows that the error between the methods is less than 4%. The results fit better at higher values of the MF’s permeabilities.
- A remanent magnetic flux density is a property of a PM, and from the presented results, it is evident that higher leads to a higher levitation height. The remanence is related to the origin of the magnetic force in the MF, and, therefore, it is reasonable to expect such an effect. Again, a good agreement was achieved between the methods. The maximum error value was about 5%.
- Variation in the PM’s geometry shows that the levitation height is proportional to the PM’s diameter defining the top and the bottom surface area. The theoretical explanation is straightforward. The magnetic levitation force appears mainly as a consequence of a fluid-magnetic pressure acting on those surfaces. An increase in the surface area will result in a rise in the magnetic levitation force. The numerical results attained by the SIM and EM showed the same tendency, with the maximum error of 12.2%.
- Change in the container’s geometry acts oppositely to the change in the PM’s geometry as discussed previously. Namely, in this case, the magnetic force acting on the PM reduces proportionally to the ratio of the diameters of the PM and container. The error in the analysis between the methods was less than 1%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosensweig, R.E. Fluidmagnetic Buoyancy. AIAA J. 1966, 4, 1751–1758. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Buoyancy and Stable Levitation of a Magnetic Body immersed in a Magnetizable Fluid. Nature 1966, 210, 613–614. [Google Scholar] [CrossRef]
- Moskowitz, R.; Stahl, P.; Reed, W.R. Inertia Damper Using Ferrofluid. US Patent 4123675, 31 October 1978. [Google Scholar]
- Miller, D.L. Magnetic Viscous Damper. US Patent 4200003, 29 April 1980. [Google Scholar]
- Kogure, T. Damper Device for a Motor. US Patent 5191811, 9 March 1993. [Google Scholar]
- Bashtovoi, V.G.; Kabachikov, D.N.; Kolobov, A.Y.; Samoylov, V.B.; Vikoulenkov, A.V. Research of the dynamics of a magnetic fluid dynamic absorber. J. Magn. Magn. Mater. 2002, 252, 312–314. [Google Scholar] [CrossRef]
- Wang, Z.; Bossis, G.; Volkova, O.; Bashtovoi, V.; Krakov, M.S. Active Control of Rod Using Magnetic Fluids. J. Intell. Mater. Syst. Struct. 2003, 14, 93–97. [Google Scholar] [CrossRef]
- Yang, W. Magnetic levitation force exerted on the cylindrical magnet in a ferrofluid damper. J. Vib. Control 2015, 23, 2345–2354. [Google Scholar] [CrossRef]
- Yao, J.; Chang, J.; Li, D.; Yang, X. The dynamics analysis of a ferrofluid shock absorber. J. Magn. Magn. Mater. 2016, 402, 28–33. [Google Scholar] [CrossRef]
- Piso, M.I. Applications of magnetic fluids for inertial sensors. J. Magn. Magn. Mater. 1999, 201, 380–384. [Google Scholar] [CrossRef]
- Qian, L.; Li, D.; Yu, J. Study of the Second-Order Levitation Force in the Magnetic Fluid Accelerometer. IEEE Sens. J. 2015, 15, 6805–6810. [Google Scholar] [CrossRef]
- Yu, J.; He, X.; Li, D.; Li, W. Effective and Practical Methods to Calculate the Second-Order Buoyancy in Magnetic Fluid Acceleration Sensor. IEEE Sens. J. 2018, 18, 2278–2284. [Google Scholar] [CrossRef]
- Yang, W.; Li, D.; He, X.; Li, Q. Calculation of magnetic levitation force exerted on the cylindrical magnets immersed in ferrofluid. Int. J. Appl. Electromagn. Mech. 2012, 40, 37–49. [Google Scholar] [CrossRef]
- Yang, W.; Wang, P.; Hao, R.; Ma, B. Experimental verification of radial magnetic levitation force on the cylindrical magnets in ferrofluid dampers. J. Magn. Magn. Mater. 2017, 426, 334–339. [Google Scholar] [CrossRef]
- Yu, J.; Chen, J.; Li, D. Experimental error analysis of measuring the magnetic self-levitation force experienced by a permanent magnet suspended in magnetic fluid with a nonmagnetic rod. J. Magn. Magn. Mater. 2019, 469, 323–328. [Google Scholar] [CrossRef]
- Yu, J.; Chen, D.; Cai, Z.; Li, D.; Cao, Q.; Qian, L. Research on the magnetic fluid levitation force received by a permanent magnet suspended in magnetic fluid: Consideration a surface instability. J. Magn. Magn. Mater. 2019, 492, 165678. [Google Scholar] [CrossRef]
- Sudo, S.; Takaki, Y.; Hashiguchi, Y.; Nishiyama, H. Magnetic Fluid Devices for Driving Micro Machines. JSME Int. J. 2005, 48, 464–470. [Google Scholar] [CrossRef] [Green Version]
- Imai, S.; Tsukioka, T. A magnetic MEMS actuator using a permanent magnet and magnetic fluid enclosed in a cavity sandwiched by polymer diaphragms. Precis. Eng. 2014, 38, 548–554. [Google Scholar] [CrossRef]
- Yu, J.; He, X.; Li, D.; Li, W. Boundary interface condition of magnetic fluid determines the magnetic levitation force experienced by a permanent magnet suspended in the magnetic fluid. Phys. Fluids 2018, 30, 092004. [Google Scholar] [CrossRef]
- Meeker, D. Finite Element Method Magnetics—User’s Manual. Verison 4.2. 2007, pp. 44–46. Available online: https://www.femm.info/Archives/doc/manual42.pdf (accessed on 31 August 2021).
- Bastos, J.P.A.; Sadowski, N. Electromagnetic Modeling by Finite Element Methods, 1st ed.; Marcel Dekker Inc.: New York, NY, USA, 2003; pp. 381–383. [Google Scholar]
- Rosensweig, R.E. Ferrohydrodynamics, 1st ed.; Dover Publications, Inc.: New York, NY, USA, 2014. [Google Scholar]
- Trbušić, M.; Beković, M.; Trlep, M.; Hamler, A. Nonlinear analysis of magnetic liquid free surface deformation in a 3D space. J. Magn. Magn. Mater. 2019, 482, 364–369. [Google Scholar] [CrossRef]













| Permanent Magnet (PM) | Magnetic Fluid (MF) | Rod | Free Space | |
|---|---|---|---|---|
| material | NdFeB (N38) | - | copper | Air |
| 𝜌 [kgm−3] | 7450 | 1377.6 | 8900 | 1.2 |
| 1 | 1.31 | 1 | 1 | |
| [T] | 1.24 | - | - | - |
| [kAm−1] | 986.7 | - | - | - |
| 0 | 0.31 | 0 | 0 | |
| Max. mesh size in material [mm] | 0.25 | 0.25 | 0.5 | 10 |
| Max. mesh size at boundary [mm] | 0.05 | 0.05 | - | - |
| Levitation Height 1 | Magnetic Levitation Force—Calculated | Magnetic Levitation Force—Measured 1 | Error |
|---|---|---|---|
| 1.40 | 1.84 | 1.80 | 2.2 |
| 1.73 | 1.51 | 1.41 | 6.6 |
| 2.03 | 1.27 | 1.12 | 11.8 |
| 2.37 | 1.07 | 0.91 | 15.0 |
| 2.71 | 0.88 | 0.76 | 13.6 |
| 3.23 | 0.69 | 0.60 | 13.0 |
| 3.71 | 0.55 | 0.49 | 10.9 |
| 4.38 | 0.39 | 0.37 | 5.1 |
| 5.00 | 0.30 | 0.29 | 3.3 |
| 5.41 | 0.25 | 0.25 | 0.0 |
| 5.94 | 0.20 | 0.20 | 0.0 |
| 6.47 | 0.16 | 0.16 | 0.0 |
| 6.97 | 0.13 | 0.12 | 7.7000 |
| 7.92 | 0.08 | 0.08 | 0.0 |
| 8.94 | 0.04 | 0.04 | 0.0 |
| 9.98 | 0.01 | 0.00 | - |
| 11.23 | −0.04 | −0.05 | −25.0 |
| 11.74 | −0.05 | −0.04 | 20.0 |
| 12.16 | −0.07 | −0.07 | 0.00 |
| 12.76 | −0.10 | −0.13 | −30.0 |
| 13.37 | −0.13 | −0.14 | −7.7 |
| 13.95 | −0.17 | −0.15 | 11.8 |
| 14.35 | −0.20 | −0.19 | 5.0 |
| 14.75 | −0.24 | −0.20 | 16.7 |
| 15.15 | −0.29 | −0.24 | 17.2 |
| 15.60 | −0.35 | −0.27 | 22.9 |
| 16.02 | −0.42 | −0.30 | 28.6 |
| 16.39 | −0.51 | −0.35 | 31.4 |
| 16.85 | −0.62 | −0.44 | 29.0 |
| 17.27 | −0.78 | −0.53 | 32.1 |
| 17.53 | −0.88 | −0.62 | 29.5 |
| 17.75 | −1.01 | −0.72 | 28.7 |
| 17.95 | −1.14 | −0.81 | 28.9 |
| 18.15 | −1.26 | −0.92 | 27.0 |
| 18.39 | −1.44 | −1.04 | 27.8 |
| Method | |||
|---|---|---|---|
| SIM | 7.59 | 7.64 | 7.69 |
| EM | 7.53 | 7.58 | 7.63 |
| Experiment 1 | 8.20 | 7.63 | 8.09 |
| Error ∆𝜖 | 0.8% | 0.8% | 0.8% |
| Method | |||
|---|---|---|---|
| SIM | 6.56 | 7.64 | 8.13 |
| EM | 6.32 | 7.58 | 8.08 |
| Error | 3.6% | 0.8% | 0.6% |
| Method | |||
|---|---|---|---|
| SIM | 5.08 | 6.73 | 7.64 |
| EM | 4.82 | 6.57 | 7.58 |
| [%] | 5.1% | 2.4% | 0.8% |
| Method | |||
|---|---|---|---|
| SIM | 6.22 | 7.64 | 8.66 |
| EM | 6.98 | 7.58 | 8.53 |
| [%] | −12.2% | 0.8% | 1.5% |
| Method | |||
|---|---|---|---|
| SIM | 8.15 | 7.64 | 5.93 |
| EM | 8.13 | 7.58 | 5.90 |
| [%] | 0.2% | 0.8% | 0.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trbušić, M.; Jesenik, M.; Trlep, M.; Hamler, A. Energy Based Calculation of the Second-Order Levitation in Magnetic Fluid. Mathematics 2021, 9, 2507. https://doi.org/10.3390/math9192507
Trbušić M, Jesenik M, Trlep M, Hamler A. Energy Based Calculation of the Second-Order Levitation in Magnetic Fluid. Mathematics. 2021; 9(19):2507. https://doi.org/10.3390/math9192507
Chicago/Turabian StyleTrbušić, Mislav, Marko Jesenik, Mladen Trlep, and Anton Hamler. 2021. "Energy Based Calculation of the Second-Order Levitation in Magnetic Fluid" Mathematics 9, no. 19: 2507. https://doi.org/10.3390/math9192507







