Study on Enhanced Heat Transfer of the Convex Columns in the Cooling Channel of Motorized Spindle Based on Field Synergy
Abstract
:1. Introduction
2. Cooling Channel Model and Field Synergy Principle
2.1. Cooling Channel Model of Motorized Spindle
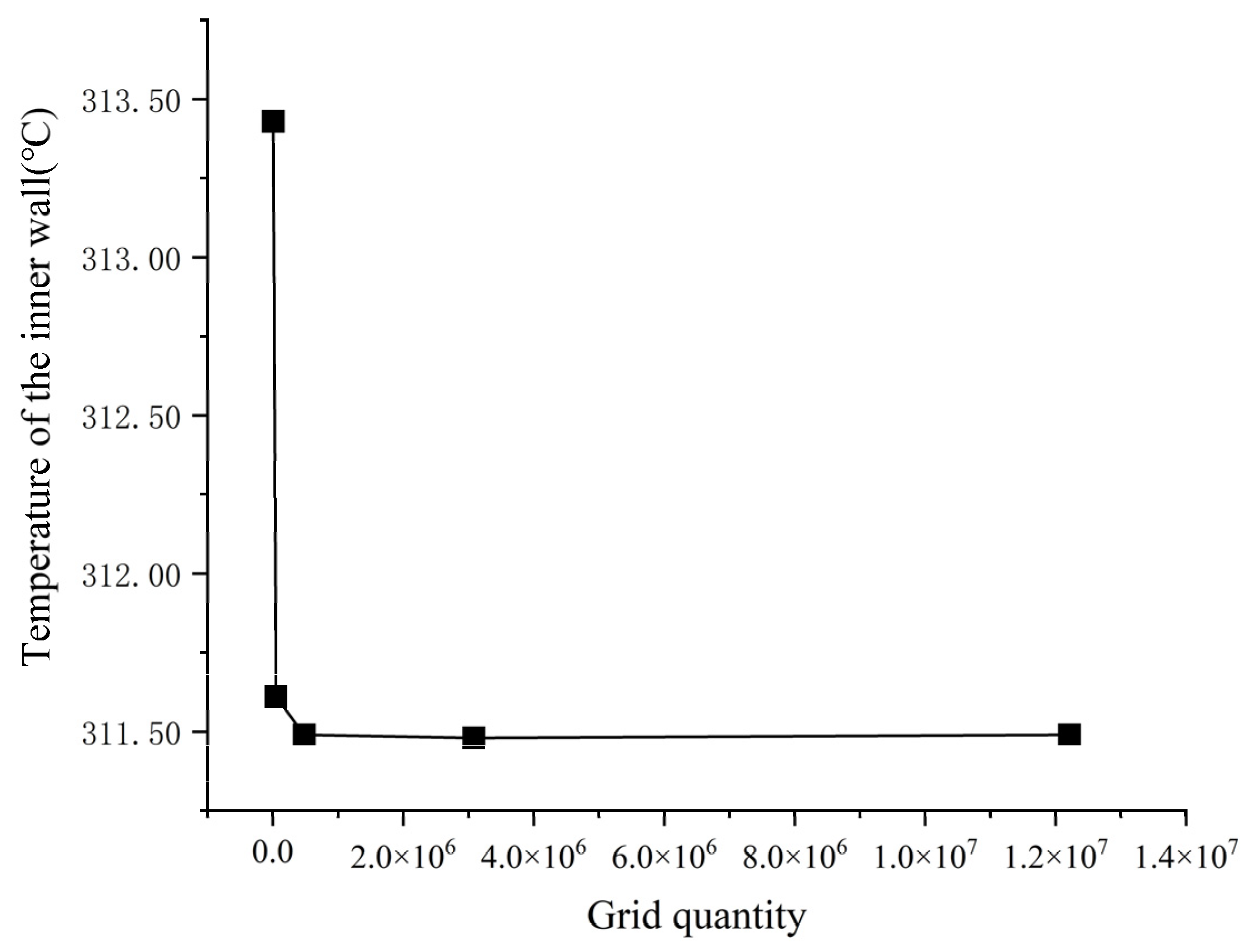
2.2. Boundary Conditions and Grid Division
- A heat flux of 30,000 W/m2, which is calculated according to a reference, is transferred from the heat source.
- The heat is dissipated by the forced convection of the cooling water in the cooling channel and natural convection with the surrounding air.
- The radiation is ignored.
- The air temperature is set at 25 °C, and the natural convection coefficient with the outer wall of the model is set at 9.7 W/(m2·K).
2.3. Field Synergy Principle
3. Results and Analysis of Heat Transfer Simulation
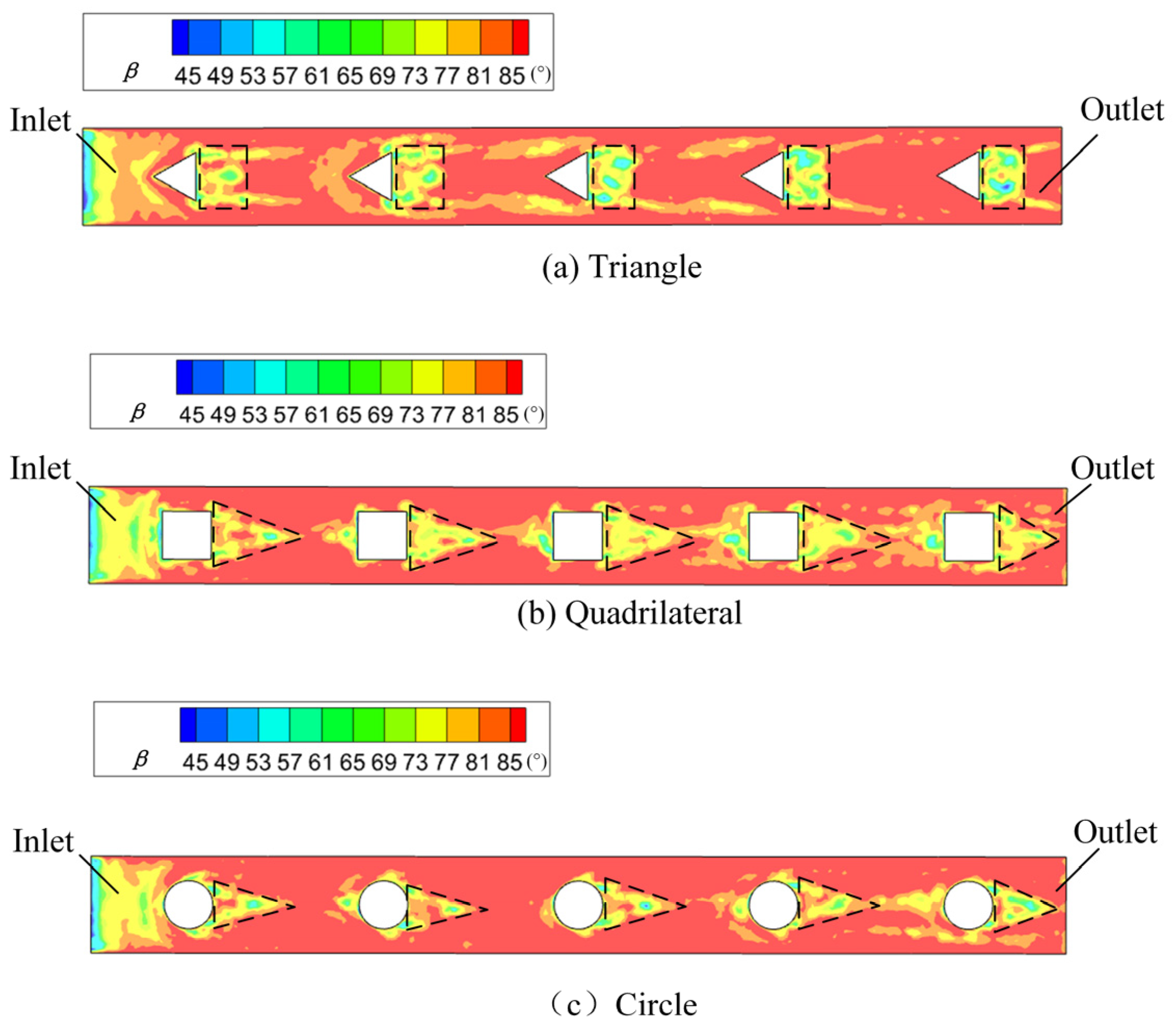
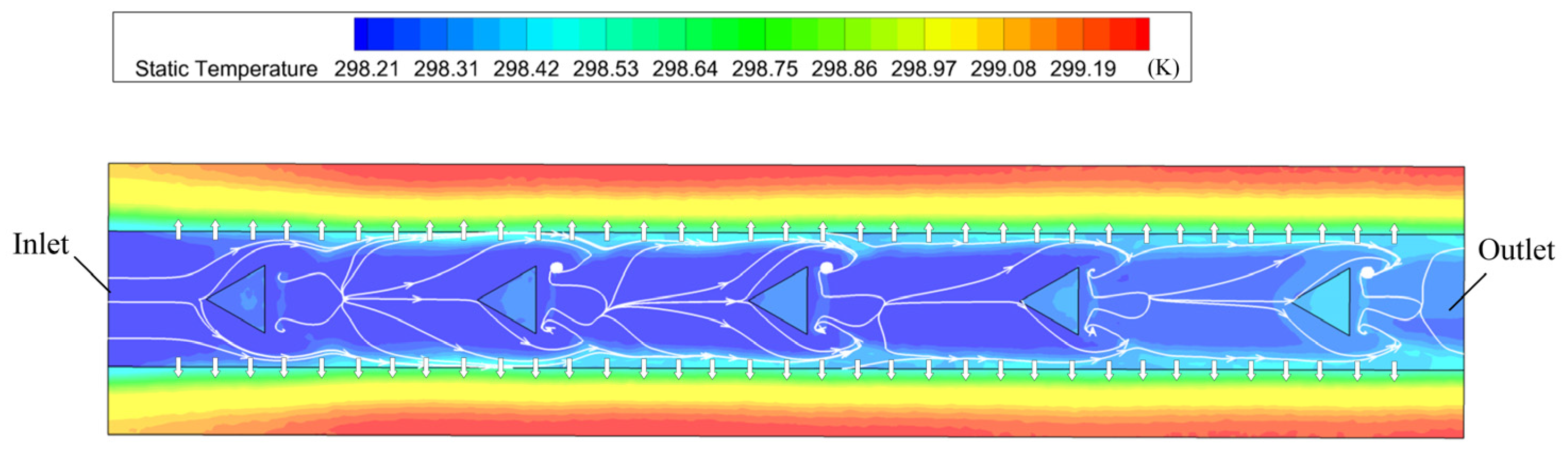
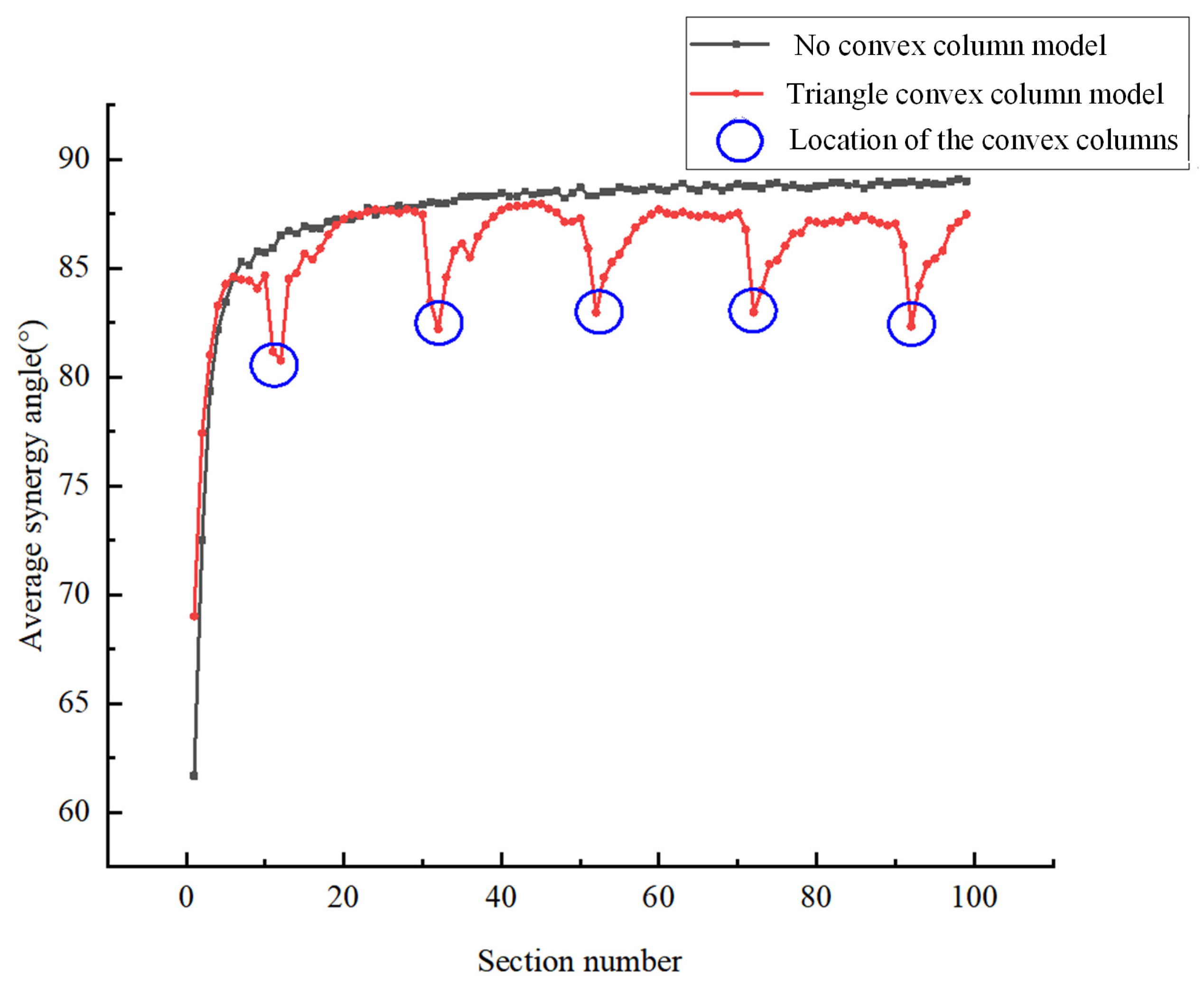
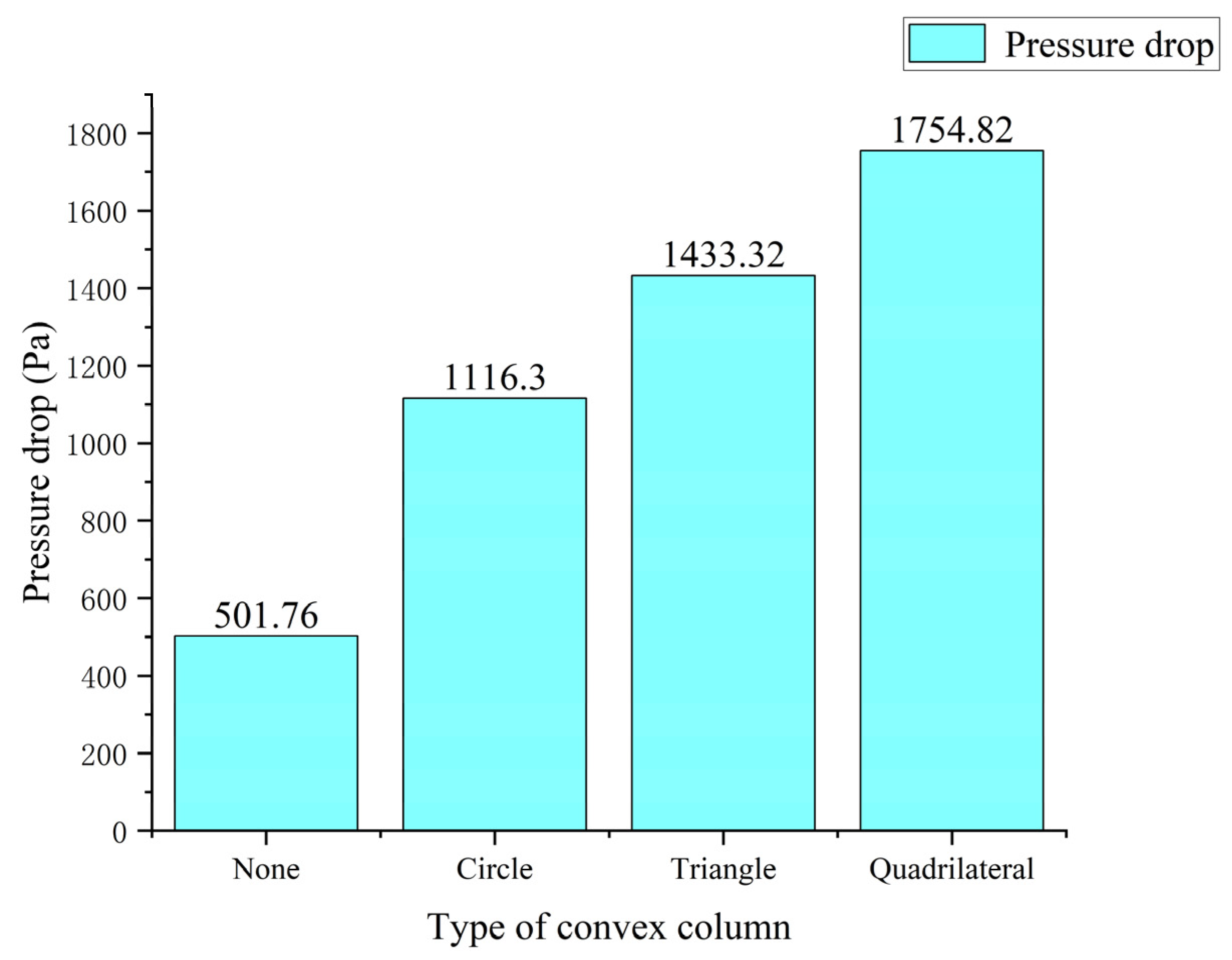
3.1. Analysis of the Field Synergy for Different Shapes of Convex Columns
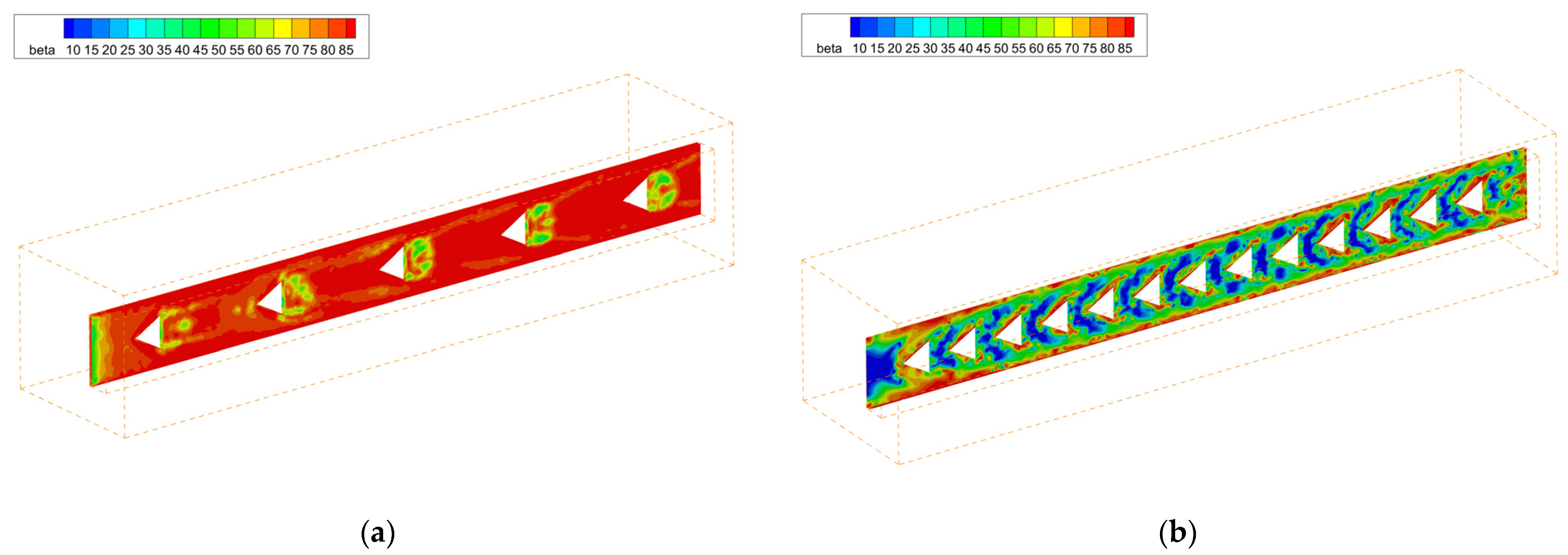
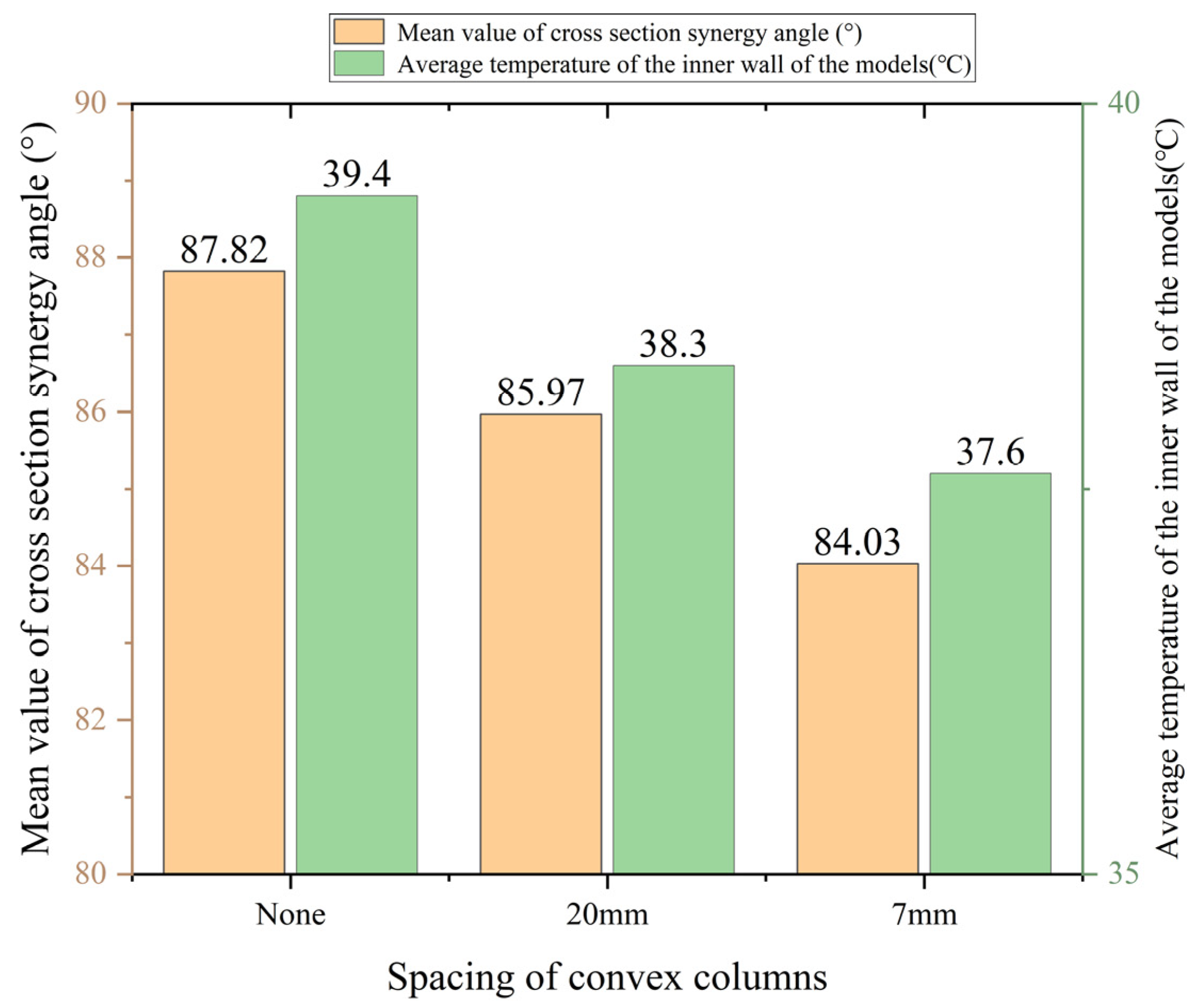
3.2. Optimization of the Intervals between Convex Columns
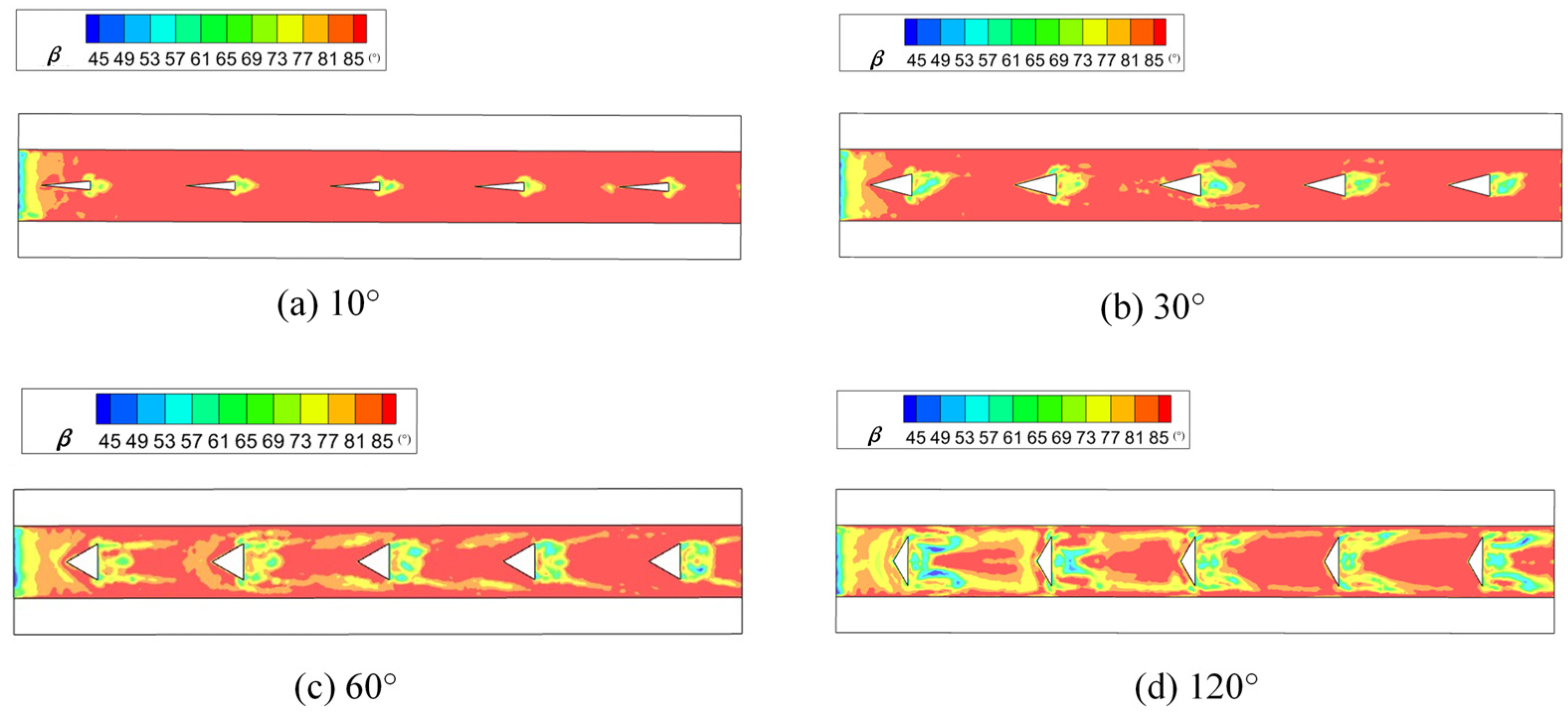
3.3. Angle Optimization of Triangular Convex Column
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bryan, J.B. International Status of Thermal Error Research (1990). CIRP Ann. 1990, 39, 645–656. [Google Scholar] [CrossRef]
- Jiao, Y. Study on Thermal Characteristics of New Laminated Cooling Water Jacket for High-Speed Motorized Spindle. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
- Li, Y.; Zhao, W.; Lan, S.; Ni, J.; Wu, W.; Lu, B. A review on spindle thermal error compensation in machine tools. Int. J. Mach. Tools Manuf. 2015, 95, 20–38. [Google Scholar] [CrossRef]
- Li, F.; Gao, J.; Shi, X.; Liang, F.; Zhu, K. Experimental investigation of single loop thermosyphons utilized in motorized spindle shaft cooling. Appl. Therm. Eng. 2018, 134, 229–237. [Google Scholar] [CrossRef]
- Liang, F.; Gao, J.; Xu, L. Investigation on a grinding motorized spindle with miniature-revolving-heat-pipes central cooling structure. Int. Commun. Heat Mass Transf. 2020, 112, 104502. [Google Scholar] [CrossRef]
- Maurya, S.N.; Li, K.-Y.; Luo, W.-J.; Kao, S.-Y. Effect of Coolant Temperature on the Thermal Compensation of a Machine Tool. Machines 2022, 10, 1201. [Google Scholar] [CrossRef]
- Chien, C.H.; Jang, J.Y. 3-D numerical and experimental analysis of a built-in motorized high-speed spindle with helical water cooling channel. Appl. Therm. Eng. 2008, 28, 2327–2336. [Google Scholar] [CrossRef]
- Li, K.-Y.; Luo, W.-J.; Hong, X.-H.; Wei, S.-J.; Tsai, P.-H. Enhancement of Machining Accuracy Utilizing Varied Cooling Oil Volume for Machine Tool Spindle. IEEE Access 2020, 8, 28988–29003. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, T.; Li, C. Research on the Effects of Cooling Water Velocity on Temperature Rise of the Water-cooled Motor in Motorized Spindle. Modul. Mach. Tool Autom. Manuf. Tech. 2015, 25, 583–589. [Google Scholar]
- Wegener, K.; Mayr, J.; Merklein, M.; Behrens, B.A.; Aoyama, T.; Sulitka, M.; Fleischer, J.; Groche, P.; Kaftanoglu, B.; Jochum, N.; et al. Fluid elements in machine tools. CIRP Ann. 2017, 66, 611–634. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, X.; Zhang, G.; Jiang, W.; Li, B. Study and Application of Cooling Technology for High Speed Motorized Spindle. J. Harbin Univ. Sci. Technol. 2022, 27, 1–12. [Google Scholar]
- Li, K.-Y.; Luo, W.-J.; Wei, S.-J. Machining Accuracy Enhancement of a Machine Tool by a Cooling Channel Design for a Built-in Spindle. Appl. Sci. 2020, 10, 3991. [Google Scholar] [CrossRef]
- Xia, C. Research on Fast Identification Method for Machine Tool Spindle Temperature Rise Characteristics and a Novel Cooling Structure Design. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2015. [Google Scholar]
- Deng, X.L.; Pang, S.J.; Li, R.Q.; Zhou, Y.B.; Wang, J.C.; Fu, J.Z. Fluid-Structure Interaction Thermal Design of Cooling Structure for Spindle System Based on Comby Bionic Channel. Comput. Simul. 2020, 37, 183–188. [Google Scholar]
- Deng, X.L.; Pang, S.J.; Li, R.Q.; Zhou, Y.B.; Wang, J.C.; Fu, J.Z. Thermal design of cooling structure for CNC machine tool spindle system based on insect wing vein bionic channel. Chin. J. Eng. Des. 2018, 25, 583–589. [Google Scholar]
- Sleiti, A.K. Heat transfer and pressure drop through rectangular helical ducts. J. Renew. Sustain. Energy 2011, 3, 043119. [Google Scholar] [CrossRef]
- Tang, Y.; Jing, X.; Li, W.; He, Y.; Yao, J. Analysis of influence of different convex structures on cooling effect of rectangular water channel of motorized spindle. Appl. Therm. Eng. 2021, 198, 117478. [Google Scholar] [CrossRef]
- Weber, J.; Shabi, L.; Weber, J. State of the art and optimization of the energy flow in cooling systems of motorized high-speed spindles in machine tools. Procedia CIRP 2018, 67, 81–86. [Google Scholar] [CrossRef]
- Wang, J.; Yu, K.; Ye, M.; Wang, E.; Wang, W.; Sundén, B. Effects of pin fins and vortex generators on thermal performance in a microchannel with Al2O3 nanofluids. Energy 2022, 239, 122606. [Google Scholar] [CrossRef]
- Li, F.; Zhu, W.; He, H. Field synergy analysis on flow and heat transfer characteristics of nanofluid in microchannel with non-uniform cavities configuration. Int. J. Heat Mass Transf. 2019, 144, 118617. [Google Scholar] [CrossRef]
- Yan, Y.; Zhao, T.; He, Z.; Yang, Z.Q.; Zhang, L. Numerical investigation on the characteristics of flow and heat transfer enhancement by micro pin-fin array heat sink with fin-shaped strips. Chem. Eng. Process. Process Intensif. 2021, 160, 108273. [Google Scholar] [CrossRef]
- Bossmanns, B.; Tu, J.F. A thermal model for high speed motorized spindles. Int. J. Mach. Tools Manuf. 1999, 39, 1345–1366. [Google Scholar] [CrossRef]
- Guo, Z. Mechanism and control of convective heat transfer: Coordination of velocity and heat flow fields. Chin. Sci. Bull. 2001, 46, 596–599. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Tao, W.Q.; Shah, R.K. The field synergy (coordination) principle and its applications in enhancing single phase convective heat transfer. Int. J. Heat Mass Transf. 2005, 48, 1797–1807. [Google Scholar] [CrossRef]
- Leng, X.; Zhang, G.; Tian, M.; Cheng, L. Application method of field synergy principle in convective heat transfer. J. Eng. Therm. Energy Power 2009, 24, 352–354. [Google Scholar]


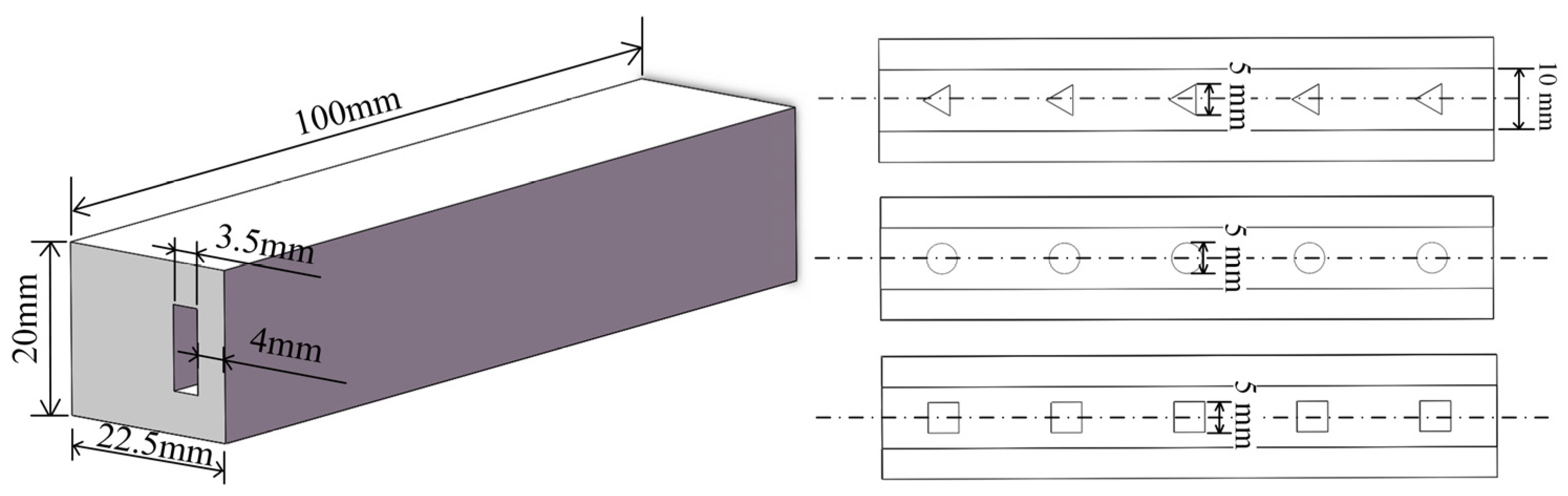







| Channel Parameters | Values |
|---|---|
| Length of the model | 100 mm |
| Width of the model | 22.5 mm |
| Height of the model | 20 mm |
| Distance between the channel and inner wall | 4 mm |
| convex column spacing | 20 mm |
| Width of cooling channel | 3.5 mm |
| Height of cooling channel | 10 mm |
| Height of convex columns | 1.5 mm |
| Length/Diameter of the side of the convex column | 5 mm |
| Number of convex columns | 5 |
| Parameters of Steel | Values |
|---|---|
| density | 8030 kg/m3 |
| specific heat capacity | 502.48 J/(kg·K) |
| heat conductivity | 16.27 W/(m·K) |
| Main Parameters | Values |
|---|---|
| inlet velocity | 1 m/s |
| inlet temperature | 298.15 K (25 °C) |
| outlet pressure | 0 Pa (Gage pressure) |
| environment temperature | 298.15 K (25 °C) |
| inner surface heat flux | 30,000 W/m2 |
| natural convection heat transfer | 9.7 W/(m2·K) |
| Shape of the Convex Column | Increased Heat Transfer Area (mm2) |
|---|---|
| triangle | 112.5 |
| quadrilateral | 150 |
| circle | 117.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Nie, Z.; Su, D.; Tian, J.; He, W.; Zhao, W. Study on Enhanced Heat Transfer of the Convex Columns in the Cooling Channel of Motorized Spindle Based on Field Synergy. Processes 2023, 11, 2431. https://doi.org/10.3390/pr11082431
Li Y, Nie Z, Su D, Tian J, He W, Zhao W. Study on Enhanced Heat Transfer of the Convex Columns in the Cooling Channel of Motorized Spindle Based on Field Synergy. Processes. 2023; 11(8):2431. https://doi.org/10.3390/pr11082431
Chicago/Turabian StyleLi, Yang, Zhe Nie, Dongxu Su, Jingyao Tian, Wenlei He, and Wanhua Zhao. 2023. "Study on Enhanced Heat Transfer of the Convex Columns in the Cooling Channel of Motorized Spindle Based on Field Synergy" Processes 11, no. 8: 2431. https://doi.org/10.3390/pr11082431





