Comparison of Polymer Networks Synthesized by Conventional Free Radical and RAFT Copolymerization Processes in Supercritical Carbon Dioxide
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents
2.2. Polymerization System
2.3. Polymer Network Characterization
2.4. Estimation of Mc from the Flory–Rehner Equation
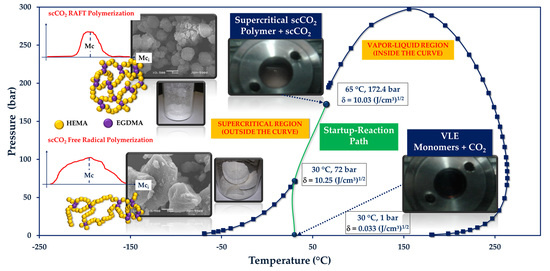
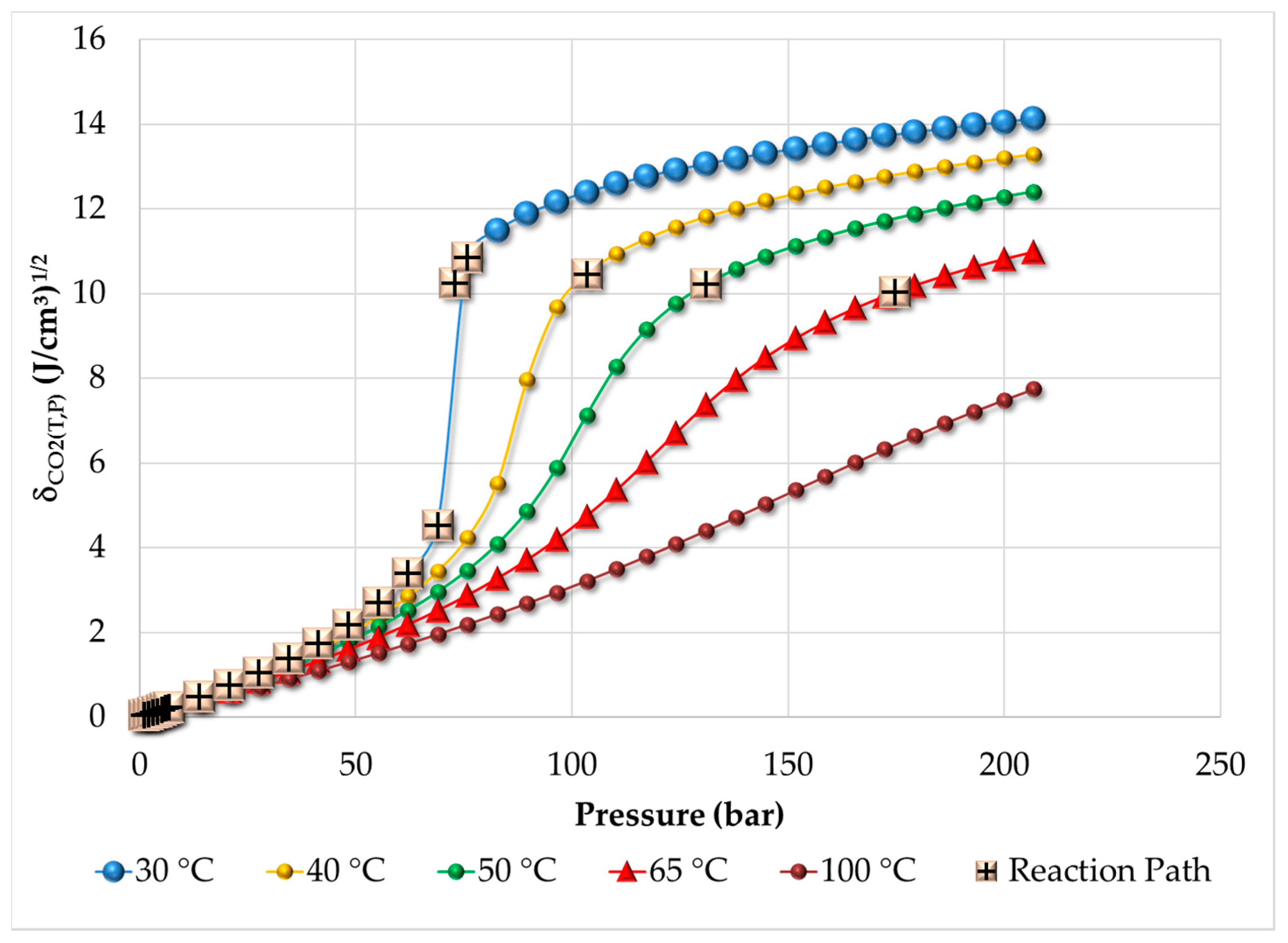
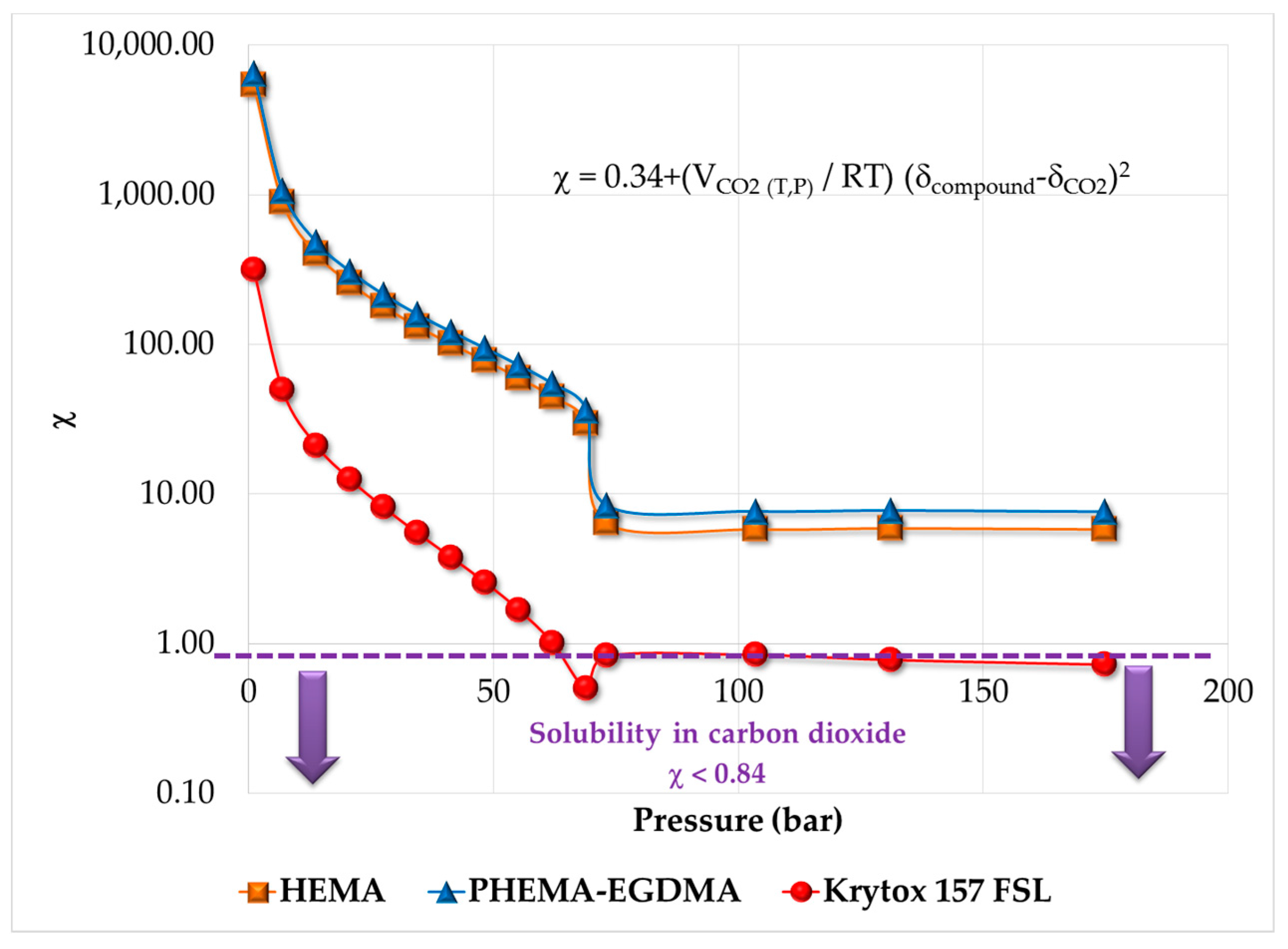
2.5. Thermodynamic Analysis, Estimation of Solubility Parameters of Components and Solubility in Supercritical CO2
3. Results and Discussion
3.1. Thermodynamic Behavior of the Reacting Mixture
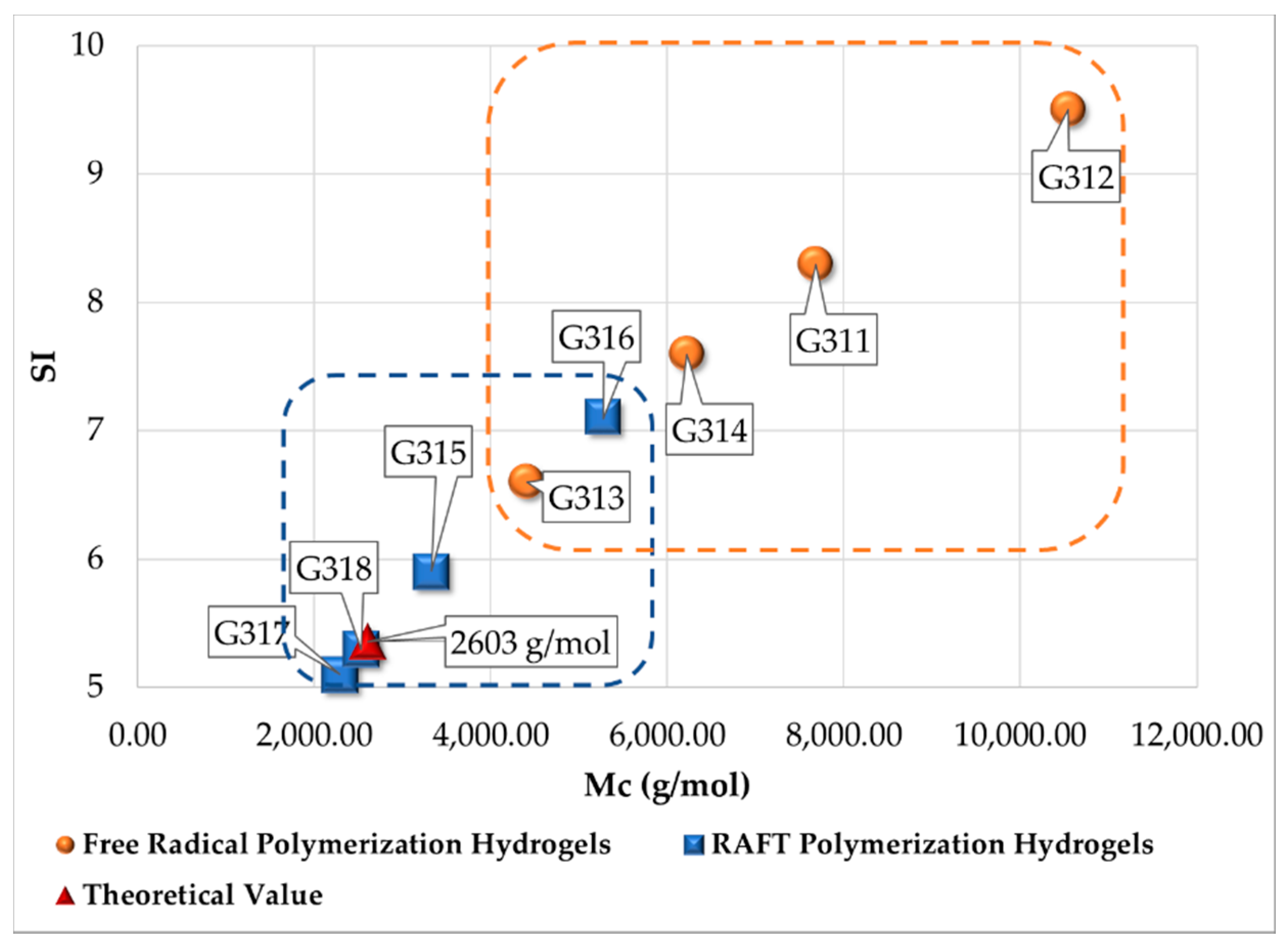
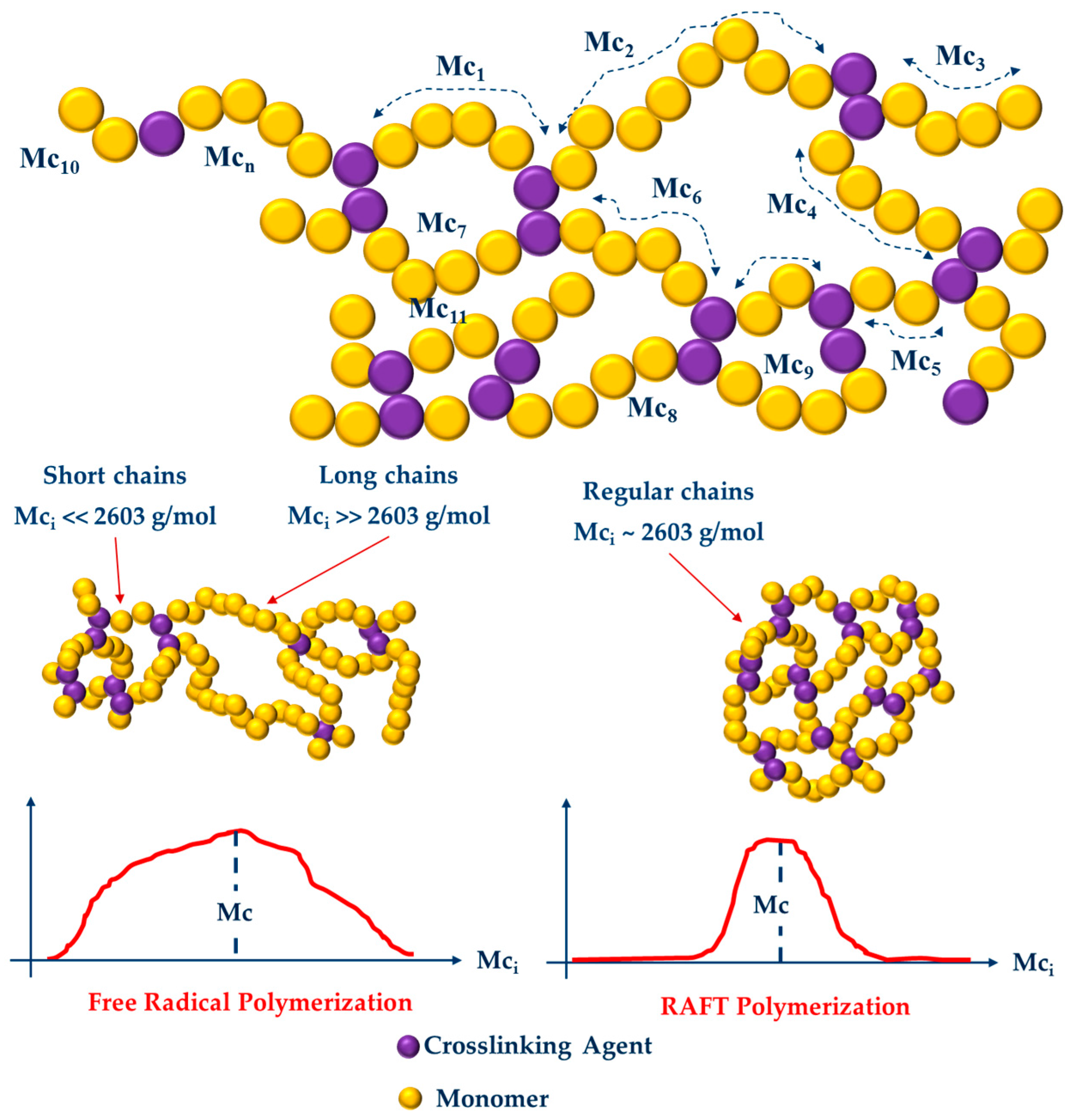
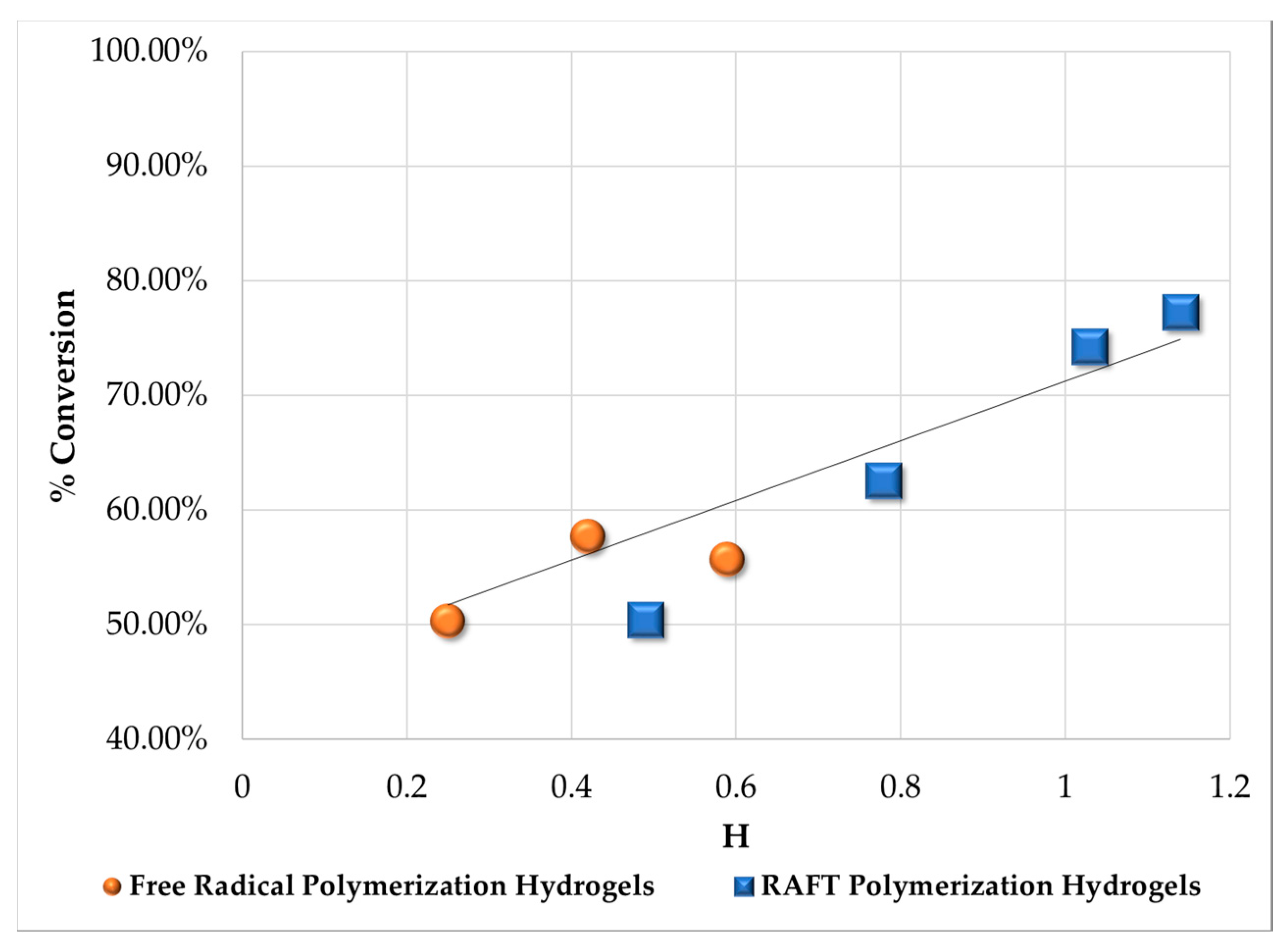
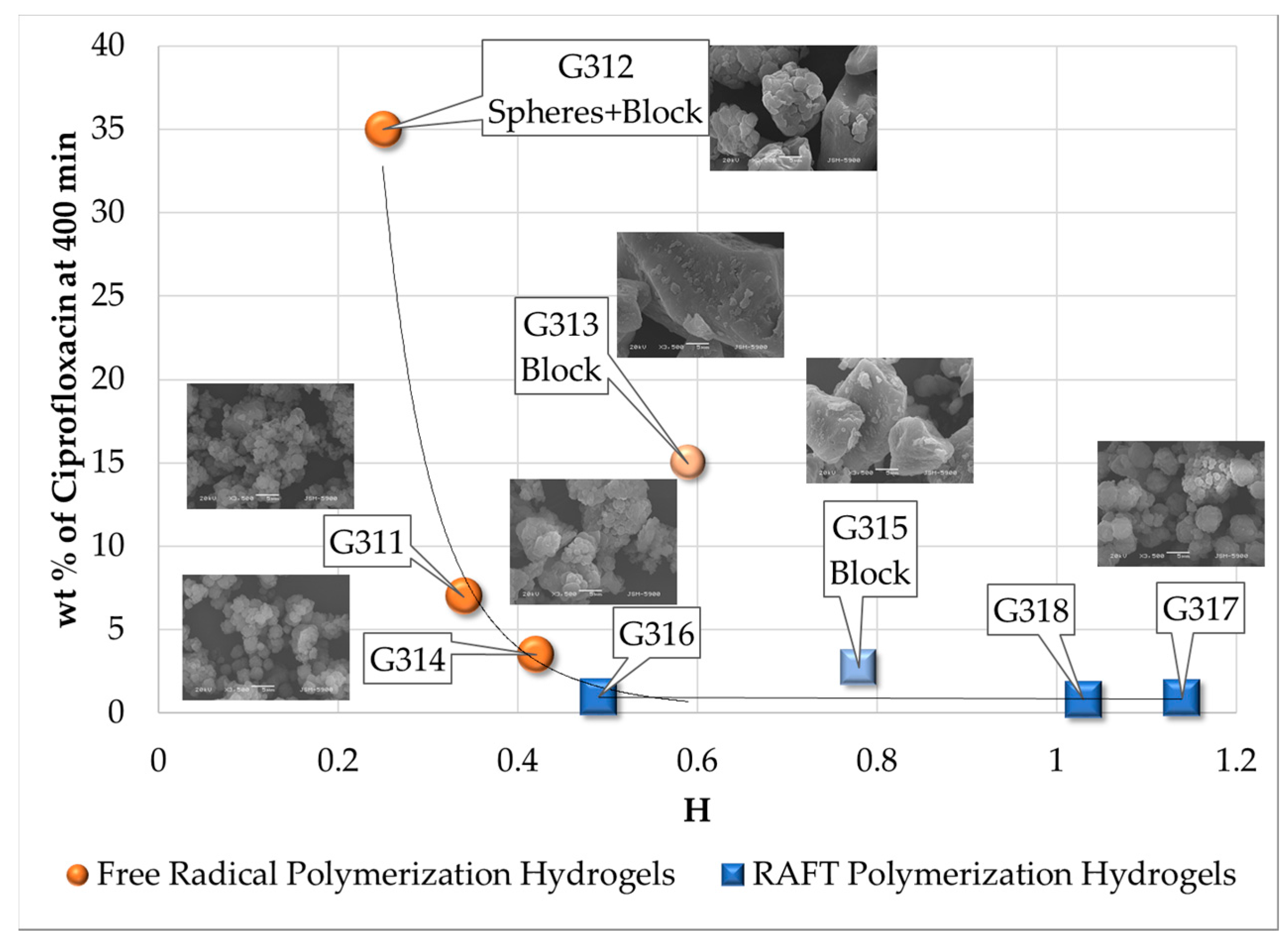
3.2. Swelling Index, Gel Content and Homogeneity Parameter
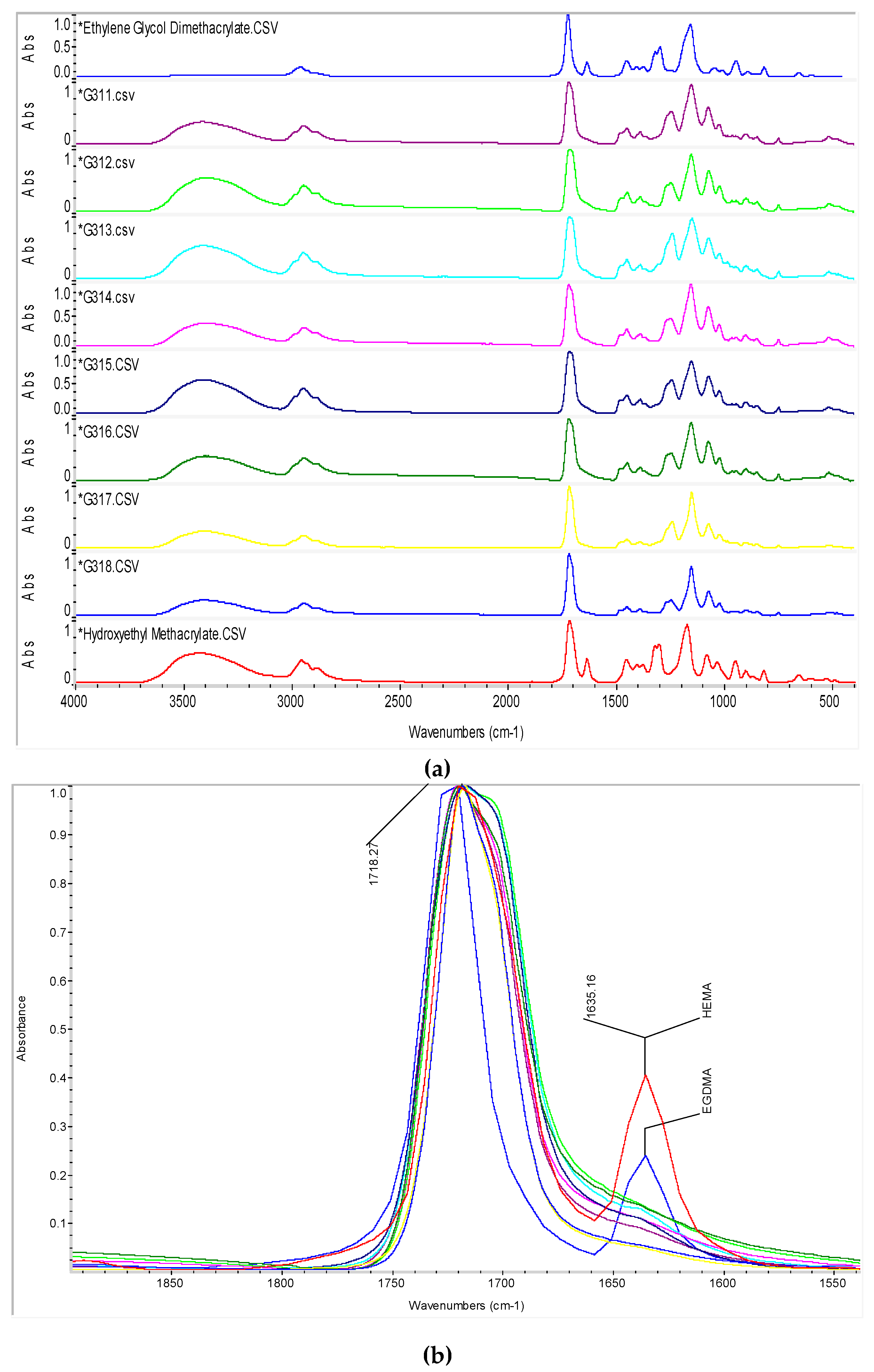
3.3. Unreacted Pendant Double Bonds from FTIR
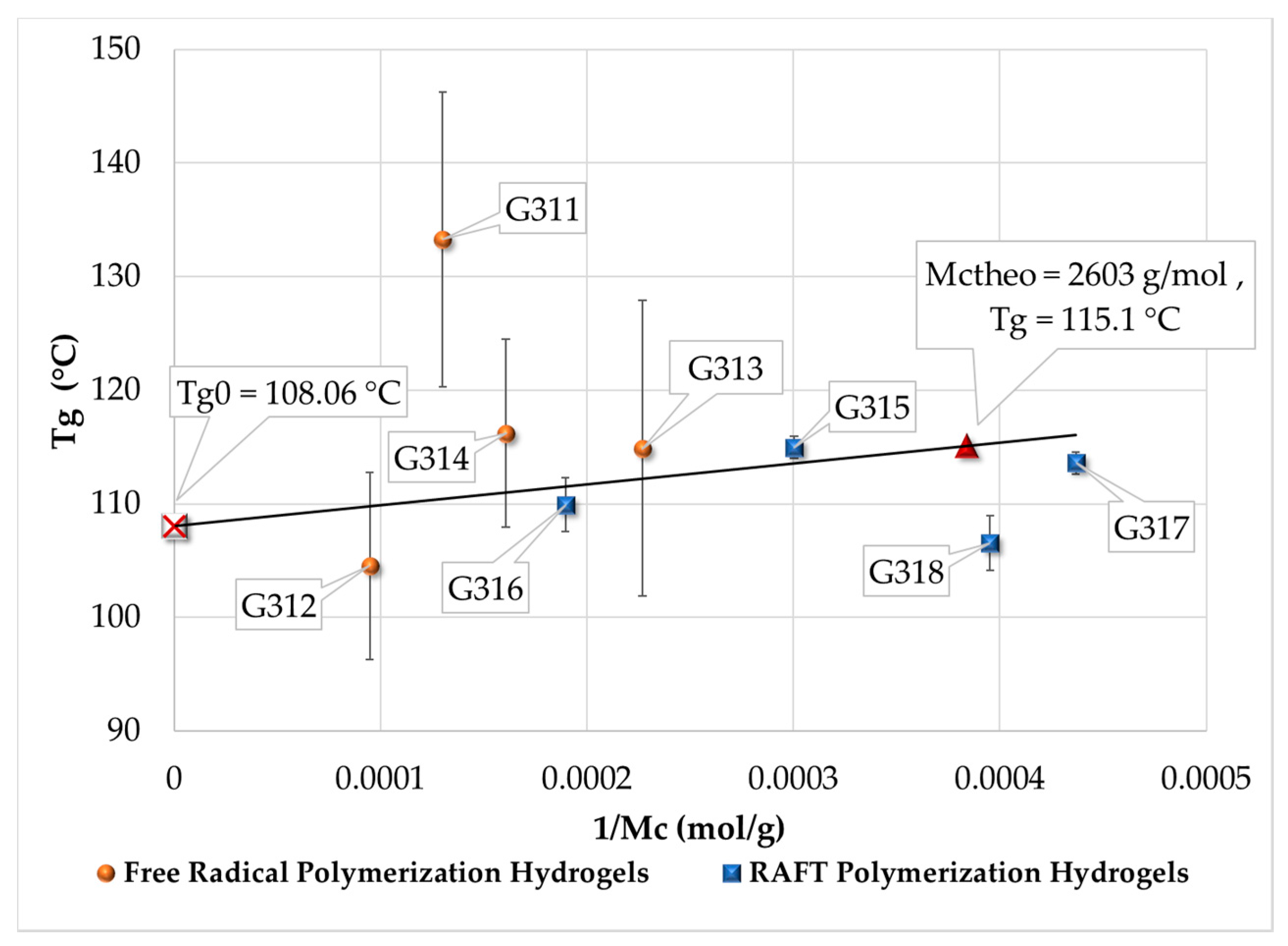
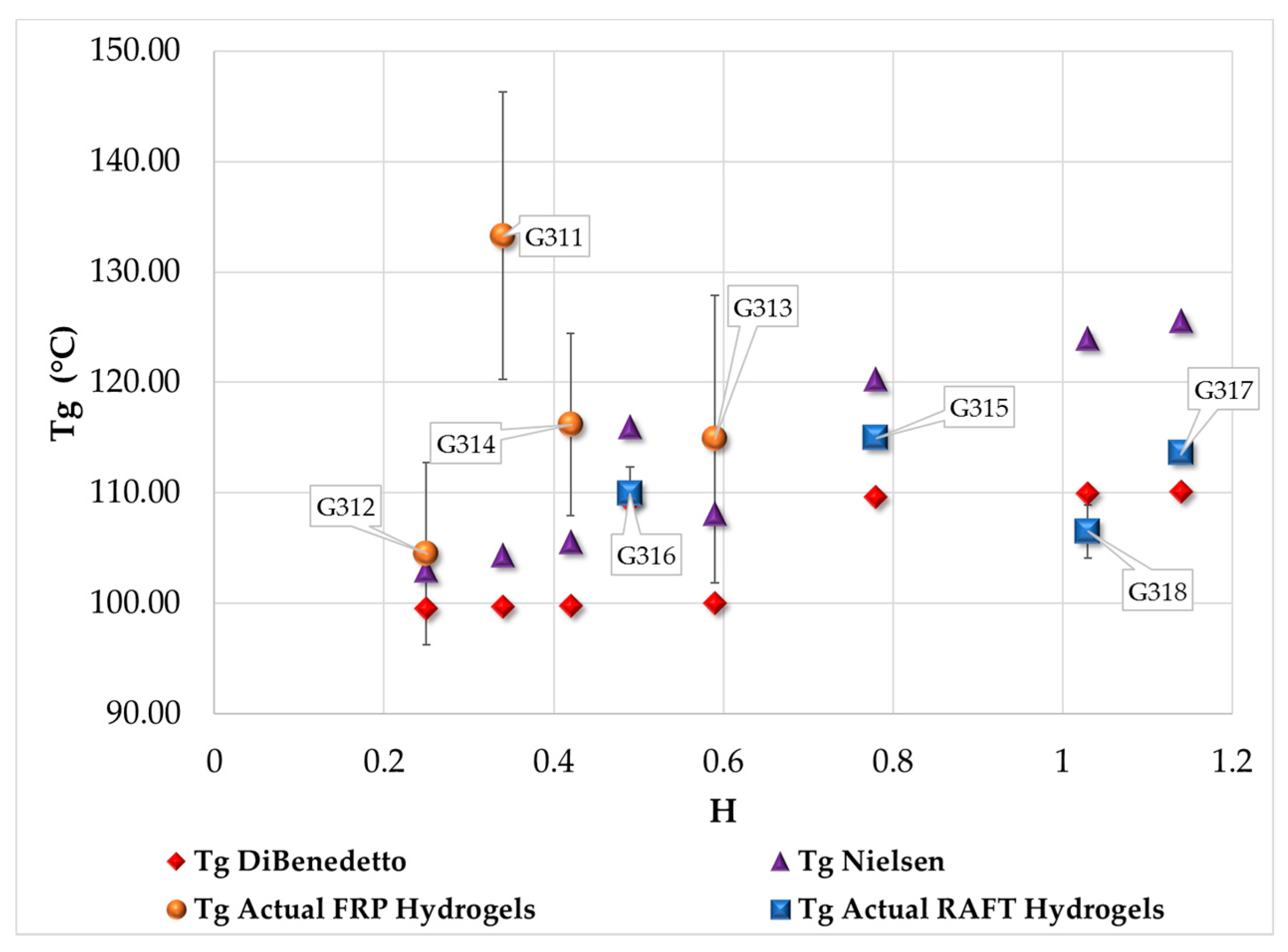
3.4. Measurement of Tg by DSC
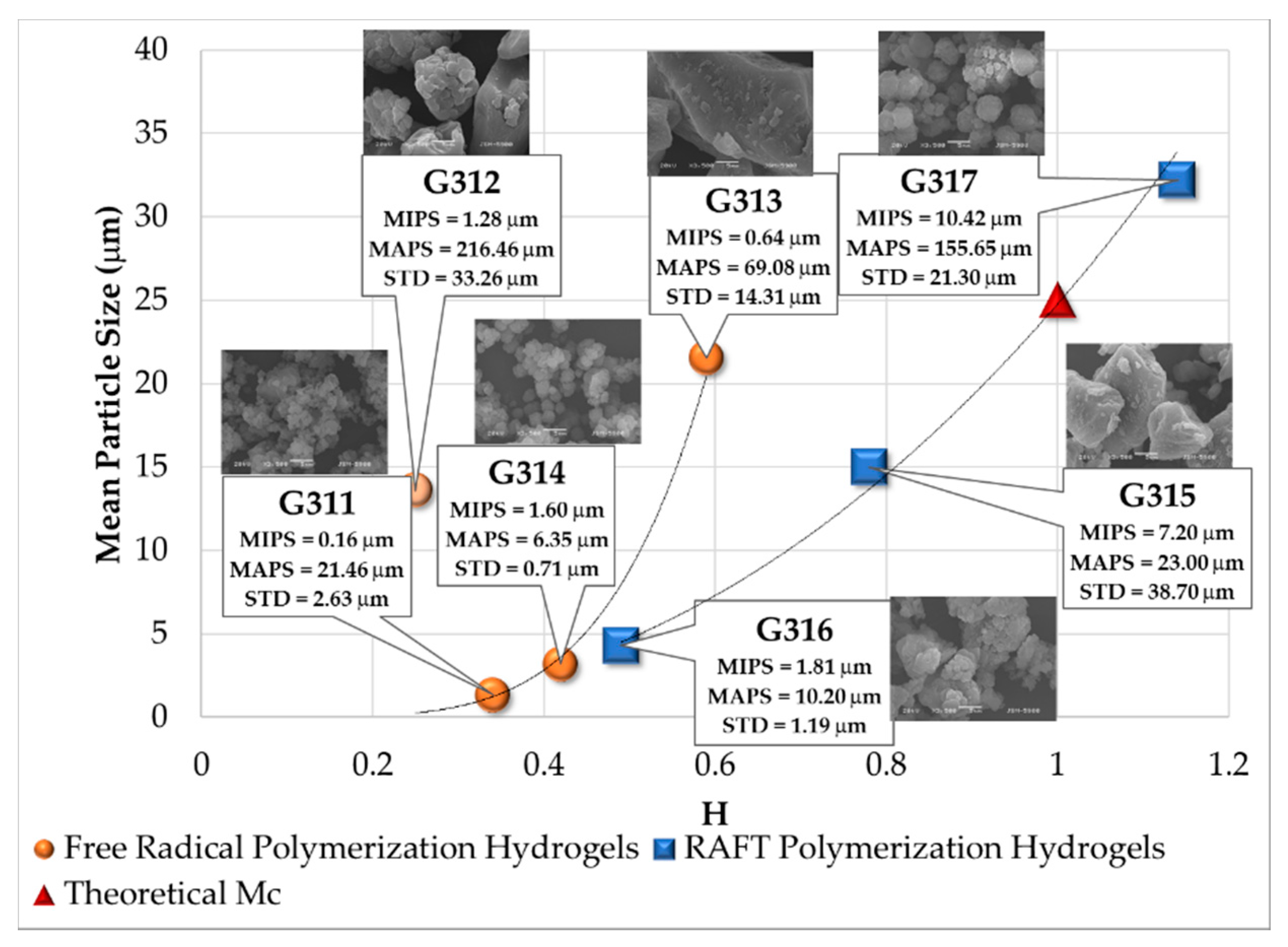
3.5. Analysis of SEM Images
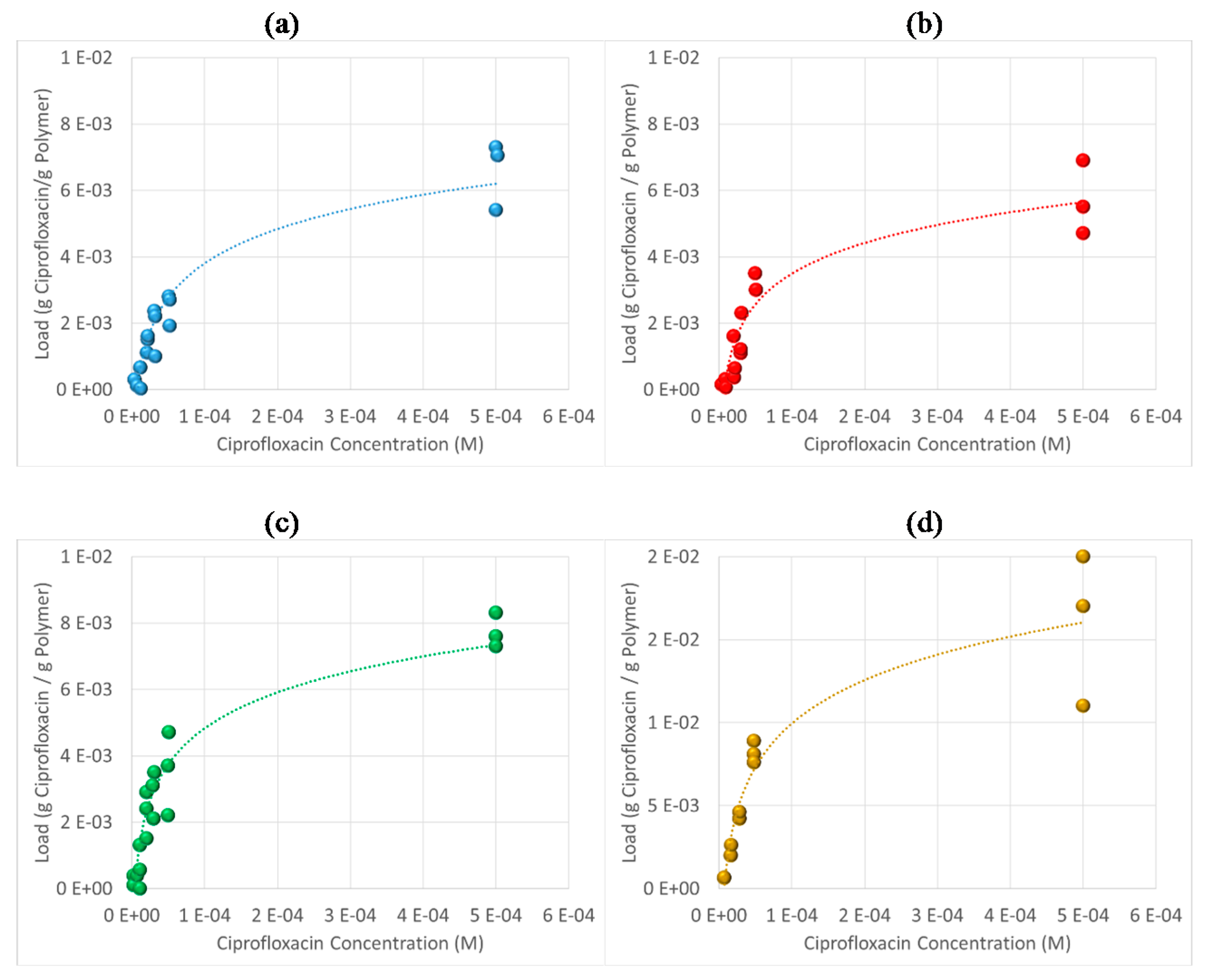
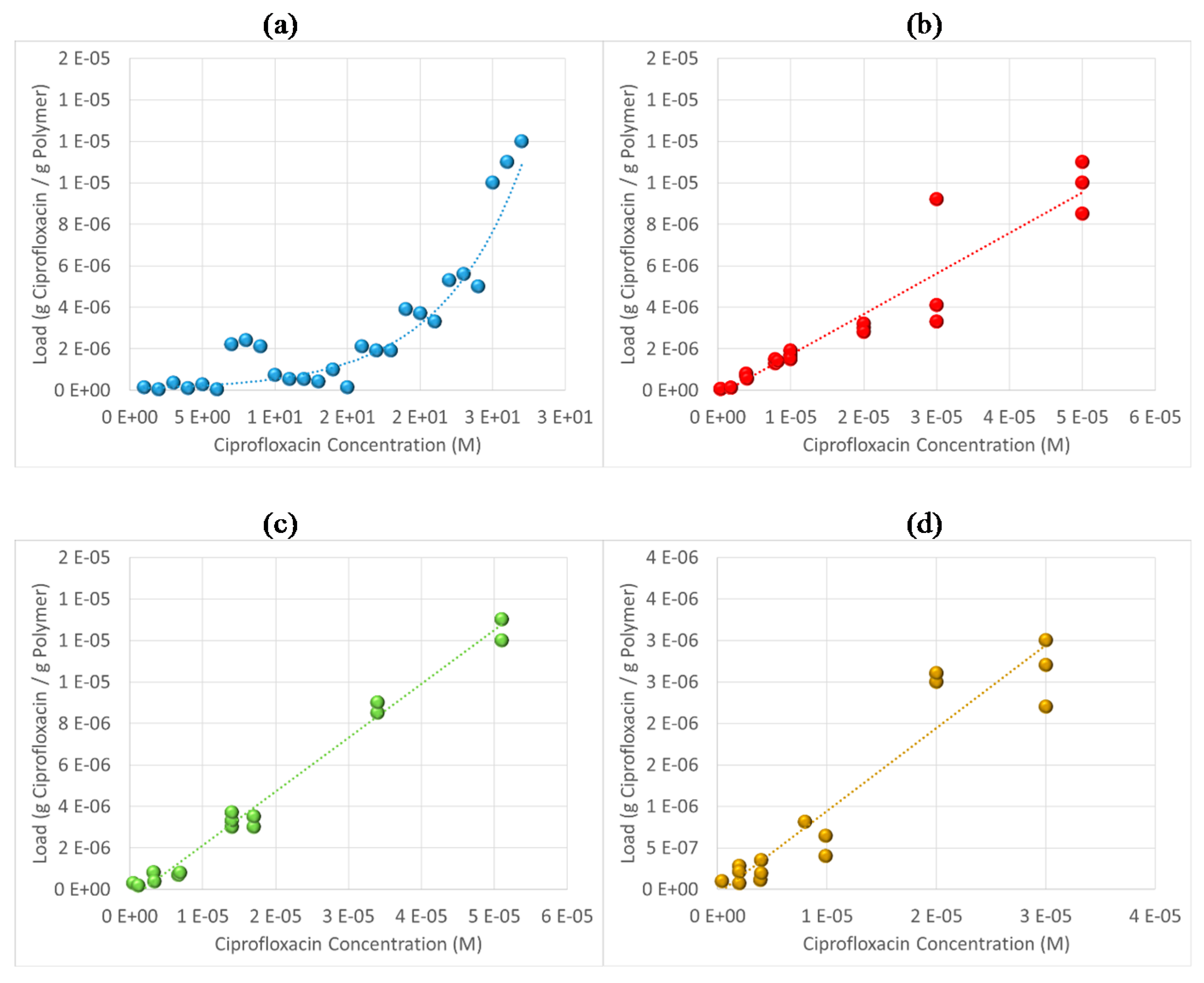
3.6. Antibiotic Loading, Adsorption and Release Studies
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bhattacharya, A.; Rawlins, J.W.; Ray, P. Polymer Grafting and Crosslinking, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 1–100, 145–319. [Google Scholar]
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008; pp. 95–122. [Google Scholar]
- Seidel, A. Characterization Analysis of Polymers, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 2008; pp. 649–675. [Google Scholar]
- Wunderlich, B. Thermal Analysis of Polymeric Materials, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 597–609. [Google Scholar]
- Espinosa-Pérez, L.; Hernández-Ortiz, J.C.; López-Domínguez, P.; Jaramillo-Soto, G.; Vivaldo-Lima, E.; Péerez-Salinas, P.; Rosas-Aburto, A.; Licea-Claverie, Á.; Vázquez-Torres, H.; Bernad-Bernad, M.J. Modeling of the Production of Hydrogels from Hydroxyethyl Methacrylate and (Di) Ethylene Glycol Dimethacrylate in the Presence of RAFT Agents. Macromol. React. Eng. 2014, 8, 564–579. [Google Scholar] [CrossRef]
- Scherf, R.; Müller, L.S.; Grosch, D.; Hübner, E.G.; Oppermann, W. Investigation on the homogeneity of PMMA gels synthesized via RAFT polymerization. Polymer 2015, 58, 36–42. [Google Scholar] [CrossRef]
- Moad, G. RAFT (Reversible Addition-Fragmentation Chain Transfer) Crosslinking (Co)polymerization of Multi-Olefinic Monomers to Form Polymer Networks. Polym. Int. 2015, 64, 15–24. [Google Scholar] [CrossRef]
- Matyjaszewski, K. Atom Transfer Radical Polymerization (ATRP): Current Status and Future Perspectives. Macromolecules 2016, 45, 4015–4039. [Google Scholar] [CrossRef]
- Chatgilialoglu, C.; Ferreri, C.; Matyjaszewski, K. Radicals and Dormant Species in Biology and Polymer Chemistry. ChemPlusChem 2016, 81, 11–29. [Google Scholar] [CrossRef]
- Jaramillo-Soto, G.; Vivaldo-Lima, E. RAFT Copolymerization of Styrene/Divinylbenzene in Supercritical Carbon Dioxide. Aust. J. Chem. 2012, 65, 1177–1185. [Google Scholar] [CrossRef]
- García-Morán, P.R.; Jaramillo-Soto, G.; Albores-Velasco, M.E.; Vivaldo-Lima, E. An Experimental Study on the Free-Radical Copolymerization Kinetics with Crosslinking of Styrene and Divinylbenzene in Supercritical Carbon Dioxide. Macromol. React. Eng. 2009, 3, 58–70. [Google Scholar] [CrossRef]
- Kiran, E. Supercritical Fluids and Polymers—The Year in Review—2014. J. Supercrit. Fluids 2016, 110, 126–153. [Google Scholar] [CrossRef]
- Boyère, C.; Jérôme, C.; Debuigne, A. Input of Supercritical Carbon dioxide to Polymer Synthesis: An Overview. Eur. Polym. J. 2014, 61, 45–63. [Google Scholar] [CrossRef]
- Kemmere, M.F. Supercritical Carbon Dioxide in Polymer Reaction Engineering, 1st ed.; Kemmere, M.F., Meyer, T., Eds.; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2005; pp. 15–34. [Google Scholar]
- Gupta, R.B.; Shim, J.J. Solubility in Supercritical Carbon Dioxide, 1st ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2007; pp. 1–18. [Google Scholar]
- Khansary, M.A.; Amiri, F.; Hosseini, A.; Sani, A.H.; Shahbeig, H. Representing Solute Solubility in Supercitical Carbon Dioxide: A Novel Empirical Model. Chem. Eng. Res. Des. 2015, 93, 355–365. [Google Scholar] [CrossRef]
- Brown, R. Physical Testing of Rubber, 4th ed.; Springer: New York, NY, USA, 2006; pp. 316–326. [Google Scholar]
- Flory, P.J.; Rehner, J. Statistical Mechanics of Crosslinked Polymer Networks. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Swelling of Network Structures. J. Chem. Phys. 1950, 18, 108–111. [Google Scholar] [CrossRef]
- Yang, Y. Fluorous Membrane-Based Separations and Reactions. Ph.D. Thesis, University of Pittsburg, Pittsburgh, PA, USA, 22 February 2011. [Google Scholar]
- Bush, D. Equation of State for Windows 95 Software, version 1.0.14; Georgia Institute of Technology: Atlanta, GA, USA, 2005.
- Ely, J.F.; Haynes, W.M.; Bain, B.C. Isochoric (p, Vm, T) measurements on CO2 and on (0.982CO2 + 0.018N2) from 250 to 330 K at pressures to 35 MPa. J. Chem. Thermodyn. 1989, 21, 879–894. [Google Scholar] [CrossRef]
- Mark, J.E. Physical Properties of Polymers Handbook, 2nd ed.; Springer: New York, NY, USA, 2007; pp. 289–303. [Google Scholar]
- Van Krevelen, D.W.; Tenijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Oxford UK, 2009; pp. 129–225. [Google Scholar]
- Aspen Technology Inc. Aspen Plus Software, version 8.8; Aspen Technology, Inc.: Bedford, MA, USA, 2016.
- Pérez-Salinas, P.; Rosas-Aburto, A.; Antonio-Hernández, C.H.; Jaramillo-Soto, G.; Vivaldo-Lima, E.; Licea-Claverie, Á.; Castro-Ceseña, A.B.; Vázquez-Torres, H. Controlled Release of Vitamin B-12 Using Hydogels Synthesized by Free Radical and RAFT Copolymerization in scCO2. Macromol. Symp. 2016, 360, 69–77. [Google Scholar] [CrossRef]






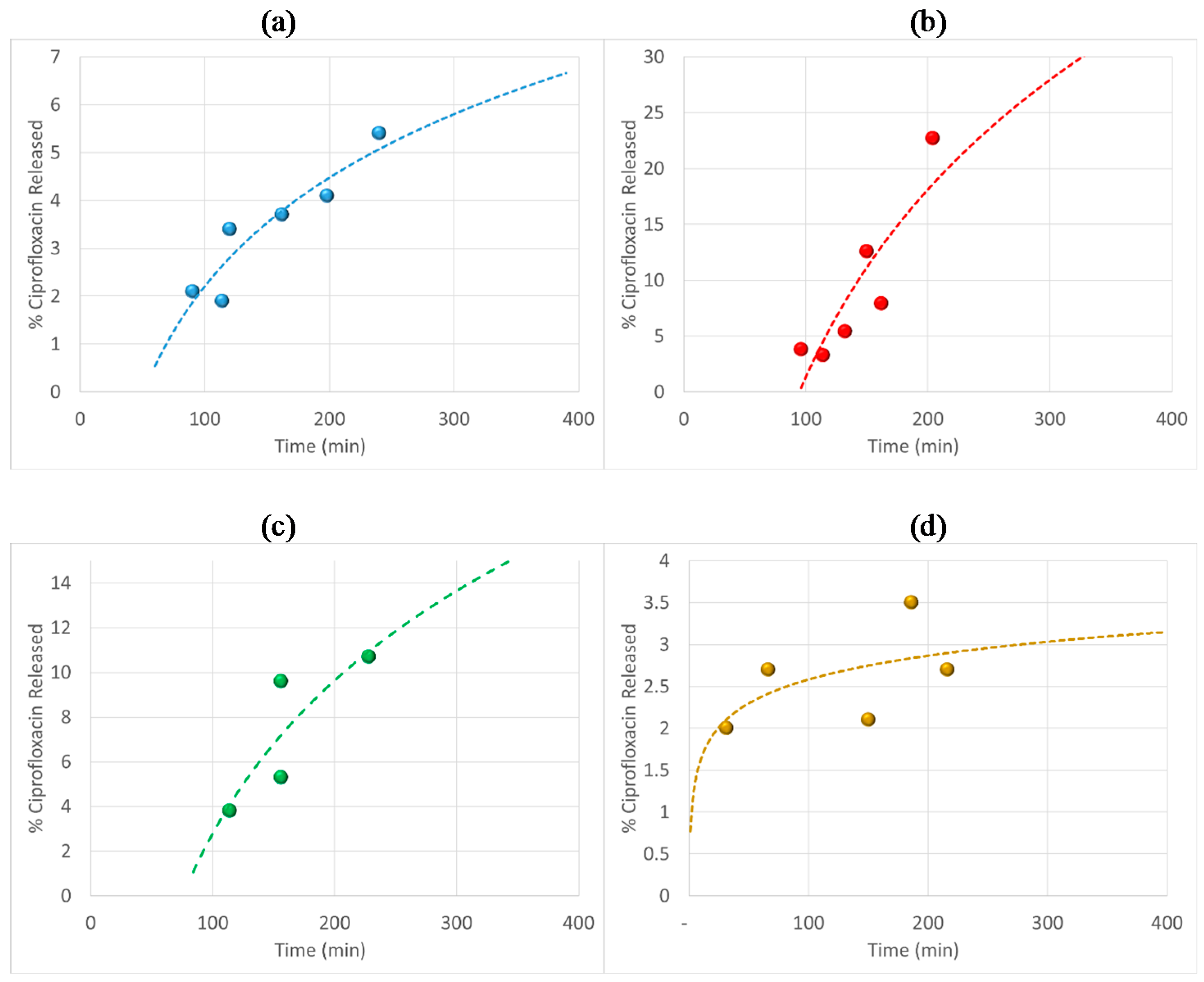
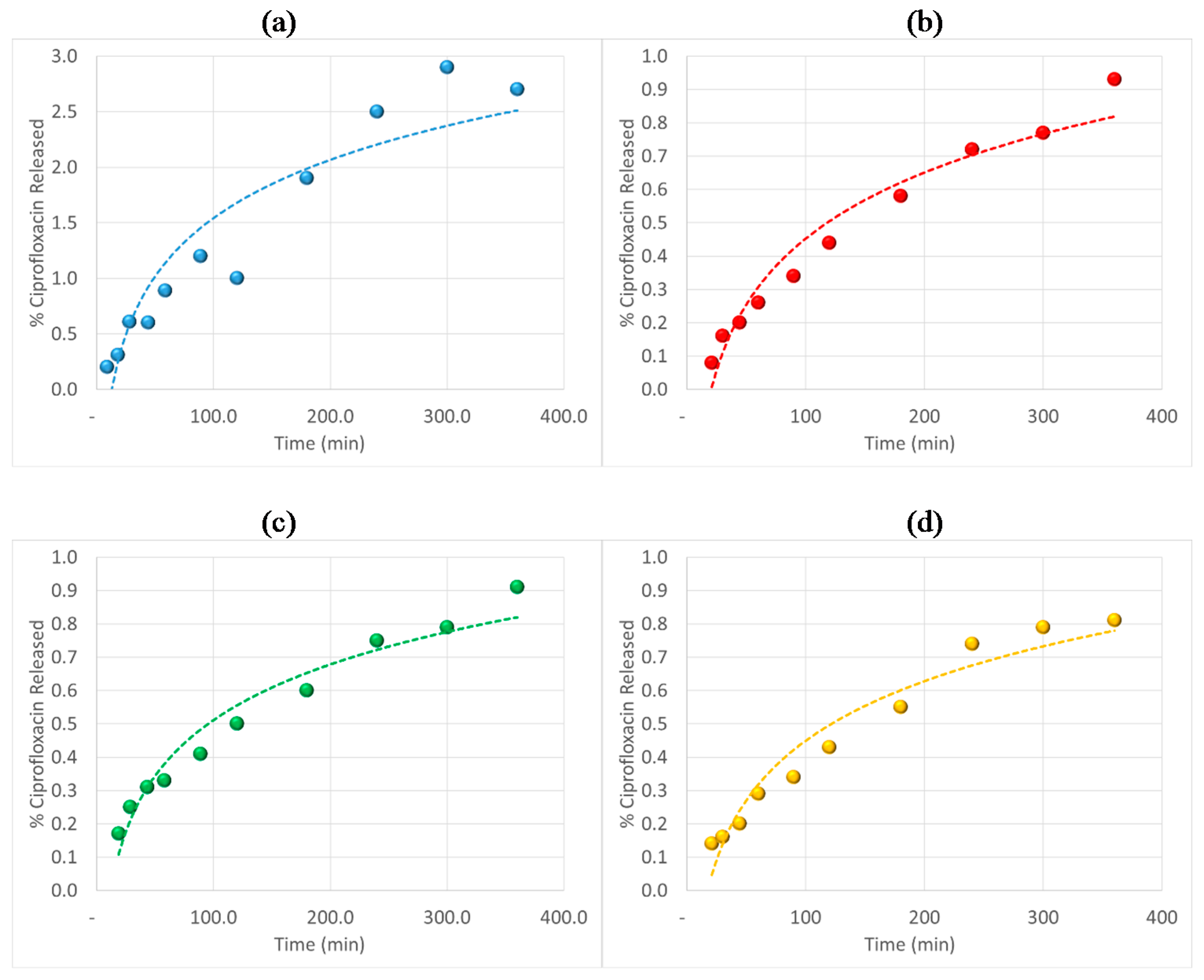
| Sample | HEMA (mmol) | EGDMA (mmol) | AIBN (mmol) | RAFT Agent (mmol) | Krytox (mmol) |
|---|---|---|---|---|---|
| G311 | 25 | 1.25 | 0.1 | 0 | 5 wt%/HEMA |
| G312 | 25 | 1.25 | 0.1 | 0 | 0 |
| G313 | 25 | 1.25 | 0.1 | 0 | 5 wt%/HEMA |
| G314 | 25 | 1.25 | 0.1 | 0 | 0 |
| G315 | 25 | 1.25 | 0.1 | 0.05 | 5 wt%/HEMA |
| G316 | 25 | 1.25 | 0.1 | 0.05 | 0 |
| G317 | 25 | 1.25 | 0.1 | 0.05 | 5 wt%/HEMA |
| G318 | 25 | 1.25 | 0.1 | 0.05 | 0 |
| Molecule | Contribution Groups | Contribution Value for Ecoh (J/mol) | Contribution Value for Vnetwork (cm3/mol) | Frequency |
|---|---|---|---|---|
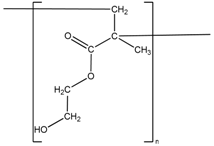 | –CH3 | 4710 | 33.5 | 1 |
| –CH2– | 4940 | 16.1 | 3 | |
| >C< | 1470 | −19.2 | 1 | |
| –CO2– | 18,000 | 18 | 1 | |
| –OH | 29,800 | 10 | 1 | |
 | –CH3 | 4710 | 33.5 | 2 |
| –CH2– | 4940 | 16.1 | 4 | |
| >C< | 1470 | −19.2 | 2 | |
| –CO2– | 18,000 | 18 | 2 |
| Polymerization Process | Sample | Swell Index | Mc Experimental (g/mol) | Mc Theoretical (g/mol) | Polymer Network Homogeneity H ≈ 1.0 | Krytox Content |
|---|---|---|---|---|---|---|
| Free Radical Polymerization | G311 | 8.3 | 7,681 | 2,603; this value was calculated as the HEMA to EGDMA molar ratio | 0.34 | Yes |
| G312 | 9.5 | 10,541 | 0.25 | No | ||
| G313 | 6.6 | 4,407 | 0.59 | Yes | ||
| G314 | 7.6 | 6,221 | 0.42 | No | ||
| RAFT Polymerization | G315 | 5.9 | 3,329 | 0.78 | Yes | |
| G316 | 7.1 | 5,274 | 0.49 | No | ||
| G317 | 5.1 | 2,289 | 1.14 | Yes | ||
| G318 | 5.3 | 2,530 | 1.03 | No |
| Band (cm−1) | Functional Group |
|---|---|
| 3,420 | –OH from HEMA |
| 2,990 | –CH from HEMA and EGDMA in polymer |
| 2,950 | –CH2 from HEMA and EGDMA structures |
| 1,717 | –C=O from HEMA and EGDMA structures |
| 1,635 | –C=CH2 remaining from HEMA and EGDMA monomers |
| 1,450 | –CH from HEMA and EGDMA in polymer |
| 1,320 to 1,300 | –C–O– ester from HEMA and EGDMA |
| 1,170 | –C–O– carboxylic derivate |
| 1,080 to 1,030 | –C–O– from the –OH of HEMA |
| 950 | remaining –C=CH2 from HEMA and EGDMA monomers |
| 900 | remaining –C=CH2 from HEMA and EGDMA monomers |
| Sample | Area Measured for Total C=O | Area Measured for Total C=C | Area Ratio between C=C/C=O | % Conversion Total C=C | Mean % Conversion Total C=C |
|---|---|---|---|---|---|
| G311 | 48.662 | 4.251 | 0.0873 | 64.88% | Hydrogels synthesized by FRP 56.98% |
| G312 | 51.952 | 6.425 | 0.1236 | 50.28% | |
| G313 | 53.434 | 5.890 | 0.1102 | 55.68% | |
| G314 | 47.482 | 4.999 | 0.1052 | 57.67% | |
| G315 | 53.029 | 4.944 | 0.0932 | 62.52% | Hydrogels synthesized by RAFT 66.10% |
| G316 | 49.214 | 6.066 | 0.1232 | 50.44% | |
| G317 | 39.497 | 2.235 | 0.0565 | 77.25% | |
| G318 | 39.128 | 2.511 | 0.0641 | 74.20% | |
| HEMA | 46.718 | 11.620 | 0.2487 | - | - |
| EGDMA | 35.502 | 5.721 | 0.1611 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Salinas, P.; Jaramillo-Soto, G.; Rosas-Aburto, A.; Vázquez-Torres, H.; Bernad-Bernad, M.J.; Licea-Claverie, Á.; Vivaldo-Lima, E. Comparison of Polymer Networks Synthesized by Conventional Free Radical and RAFT Copolymerization Processes in Supercritical Carbon Dioxide. Processes 2017, 5, 26. https://doi.org/10.3390/pr5020026
Pérez-Salinas P, Jaramillo-Soto G, Rosas-Aburto A, Vázquez-Torres H, Bernad-Bernad MJ, Licea-Claverie Á, Vivaldo-Lima E. Comparison of Polymer Networks Synthesized by Conventional Free Radical and RAFT Copolymerization Processes in Supercritical Carbon Dioxide. Processes. 2017; 5(2):26. https://doi.org/10.3390/pr5020026
Chicago/Turabian StylePérez-Salinas, Patricia, Gabriel Jaramillo-Soto, Alberto Rosas-Aburto, Humberto Vázquez-Torres, María Josefa Bernad-Bernad, Ángel Licea-Claverie, and Eduardo Vivaldo-Lima. 2017. "Comparison of Polymer Networks Synthesized by Conventional Free Radical and RAFT Copolymerization Processes in Supercritical Carbon Dioxide" Processes 5, no. 2: 26. https://doi.org/10.3390/pr5020026
APA StylePérez-Salinas, P., Jaramillo-Soto, G., Rosas-Aburto, A., Vázquez-Torres, H., Bernad-Bernad, M. J., Licea-Claverie, Á., & Vivaldo-Lima, E. (2017). Comparison of Polymer Networks Synthesized by Conventional Free Radical and RAFT Copolymerization Processes in Supercritical Carbon Dioxide. Processes, 5(2), 26. https://doi.org/10.3390/pr5020026