Development of 3D Finite Element Method for Non-Aqueous Phase Liquid Transport in Groundwater as Well as Verification
Abstract
:1. Introduction
1.1. Numerical Developing Status on NAPL Contaminant Analysis
2. Fundamental Theory of Two-Phase Flow in Porous Media
2.1. Governing Equations
2.2. Finite Differential Discretization in Time
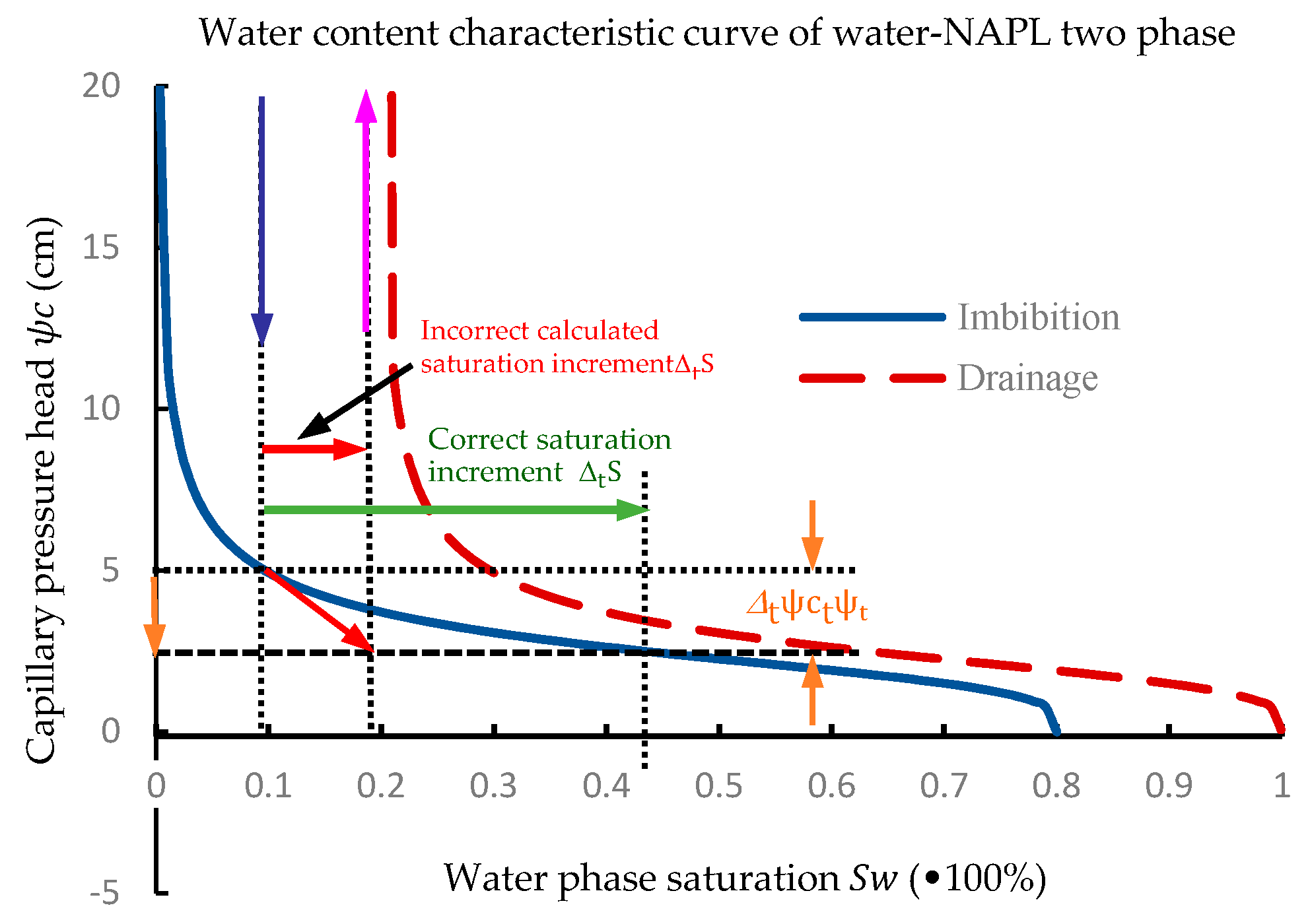
2.3. Mixed-Form Formulation Adopted in FEM Program Development
3. Numerical Discretization Formulations Using the Finite Element Method
4. Verifying the Numerical Solution with Two Examples
4.1. Water Flooding Oil in the Pillar Rock Sample (LNAPL)
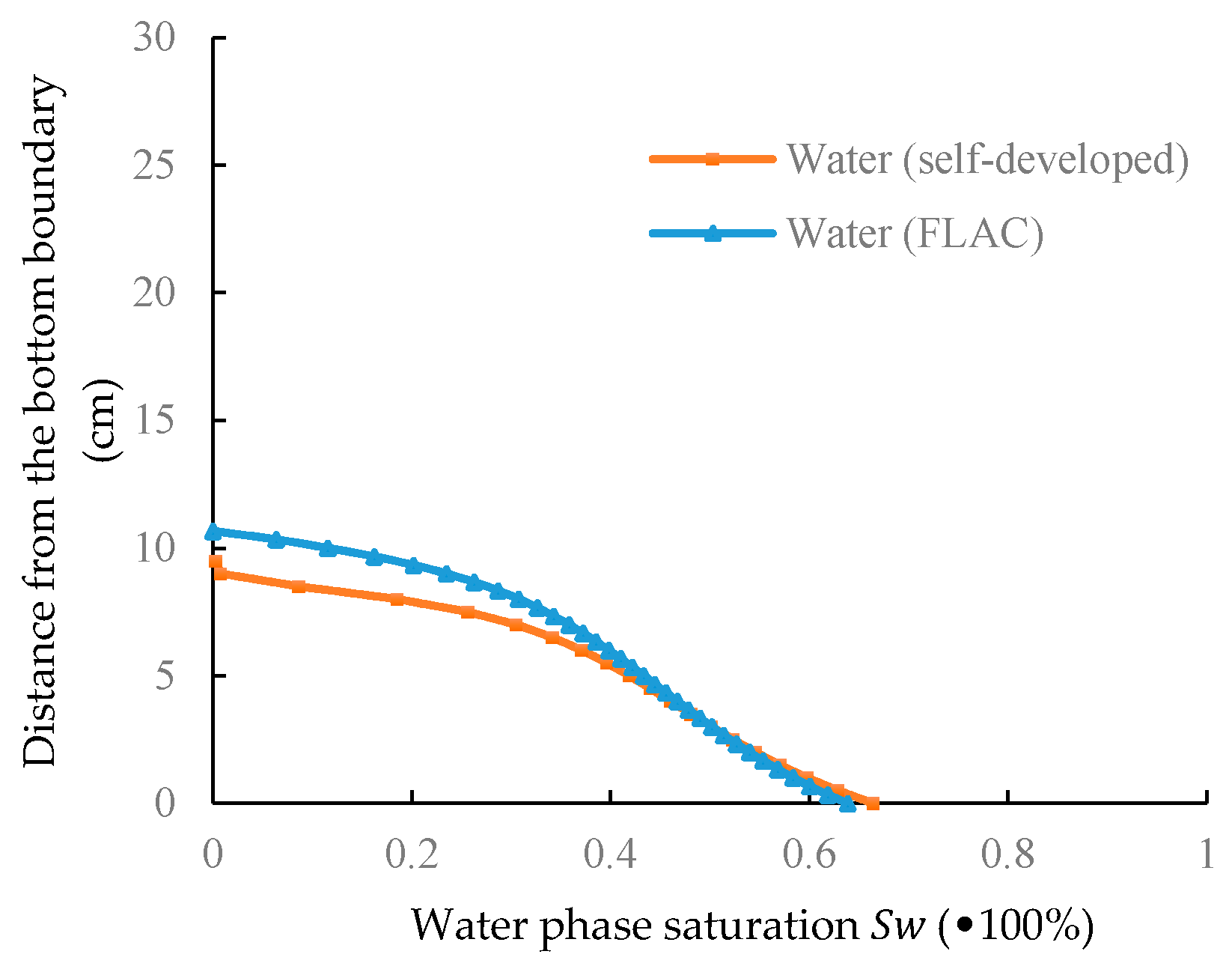
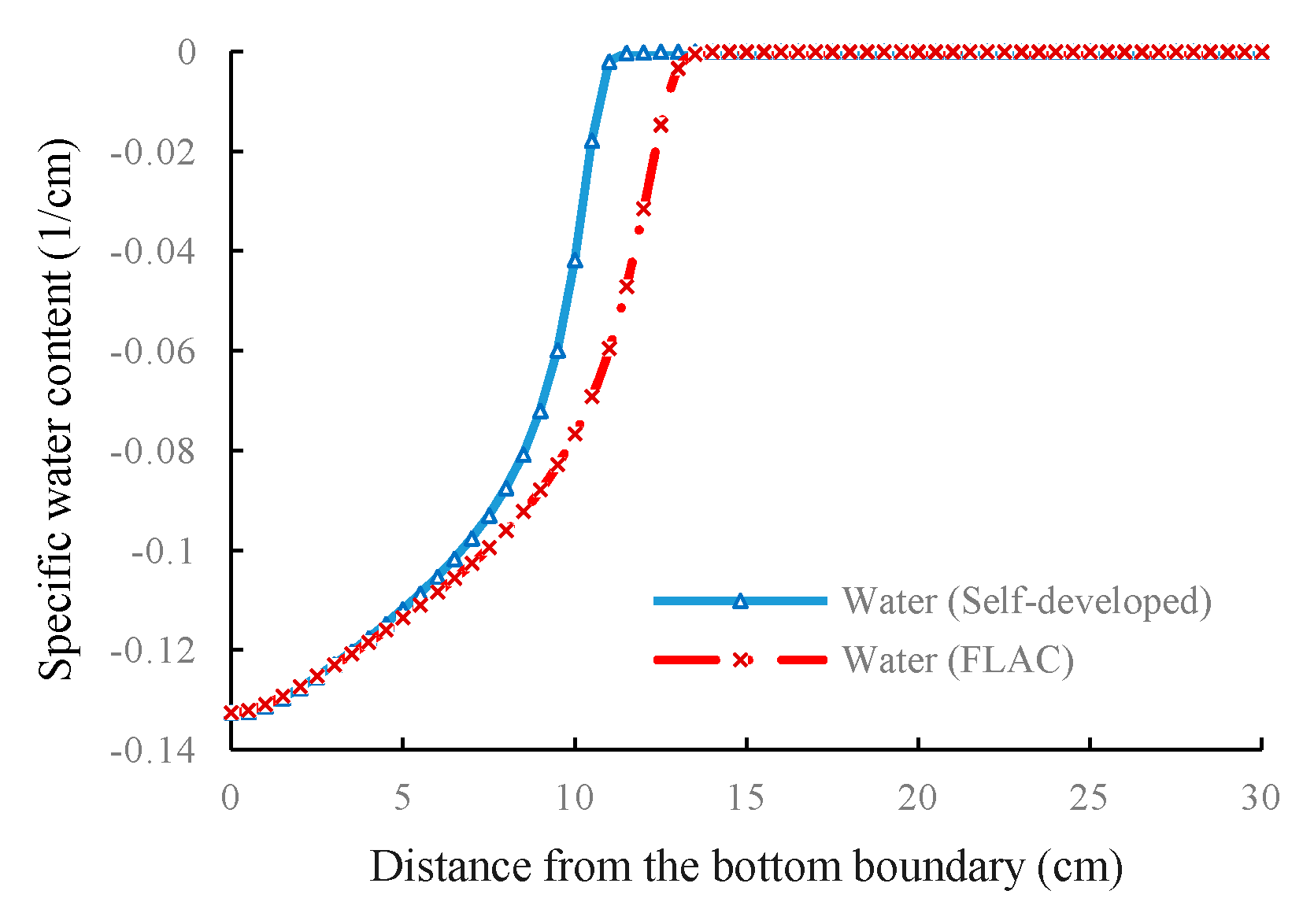
4.2. Simulation of Trichloroethylene Transport in the Aquifer (DNAPL)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FLAC | Fast Lagrangian Analysis of Continua |
| () | Flow rate flowing into (out of) the infinitesimal element |
| Cumulative storage amount in the infinitesimal element () | |
| Water volumetric flow rate | |
| NAPL volumetric flow rate | |
| Mass density of water | |
| Mass density of NAPL | |
| Volume of the porous media | |
| The fluid volume | |
| Volume of the pores contained in the porous media | |
| Porosity ( | |
| Water saturation | |
| NAPL saturation | |
| The relative permeability coefficient of water | |
| The relative permeability coefficient of NAPL | |
| Absolutely permeability tensor | |
| Pore pressure of water phase | |
| NAPL pressure of NAPL phase | |
| g | Gravitational acceleration |
| Relative density of NAPL to water () | |
| Signs of Kronecker delta | |
| κ | Intrinsic or absolute permeability |
| Dynamic viscosity of flow phase | |
| Dynamic viscosity of water | |
| Dynamic viscosity of NAPL | |
| Relative viscosity of NAPL to water () | |
| Hydraulic conductivity | |
| Pressure in water head of water () | |
| Pressure in water head of NAPL ( ) | |
| Capillary pressure in water head () | |
| C | Specific water content |
| Effective water saturation | |
| Residual saturations of water | |
| Residual saturations of NAPL | |
| Undrained coefficient | |
| Water bulk modulus | |
| NAPL bulk modulus |
References
- Bernaus, A.; Gaona, X.; Ree, D.V.; Valiente, M. Determination of mercury in polluted soils surrounding a chlor-alkali plant: Direct speciation by X-ray absorption spectroscopy techniques and preliminary geochemical characterisation of the area. Anal. Chim. Acta 2006, 565, 73–80. [Google Scholar] [CrossRef]
- Bollen, A.; Wenke, A.; Biester, H. Mercury speciation analyses in HgCl2-contaminated soils and groundwater—Implications for risk assessment and remediation strategies. Water Res. 2008, 42, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Arbestain, M.C.; Rodriguez-Lado, L.; Bao, M.; Macías, F. Assessment of Mercury-Polluted Soils Adjacent to an Old Mercury-Fulminate Production Plant. Appl. Environ. Soil Sci. 2009, 2009. [Google Scholar] [CrossRef]
- Lynge, E.; Tinnerberg, H.; Rylander, L.; Romundstad, P.; Johansen, K.; Lindbohm, ML.; Heikkilä, P.; Westberg, H.; Clausen, L.B.; Piombino, A.; et al. Exposure to tetrachloroethylene in dry cleaning shops in the Nordic countries. Ann. Occup. Hyg. 2011, 55, 387–396. [Google Scholar] [PubMed]
- Kvenvolden, K.; Cooper, C. Natural seepage of crude oil into the marine environment. Geo-Mar. Lett. 2003, 23, 140–146. [Google Scholar] [CrossRef]
- Das, N.; Chandran, P. Microbial degradation of petroleum hydrocarbon contaminants: An overview. Biotechnol. Res. Int. 2011, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Bear, J. Dynamics of Fluids in Porous Media; Li, J.S., Chen, C.X., Eds.; China Architecture and Building Press: Beijing, China, 1983. (In Chinese) [Google Scholar]
- Abriolal, M.; Pinder, G.F. A multiphase approach to the modeling of porous media contamination by organic compounds 1. Equation development. Water Resour. Res. 1985, 21, 11–18. [Google Scholar] [CrossRef]
- Abriolal, M.; Pinder, G.F. A multiphase approach to the modeling of porous media contamination by organic compounds 2. Numerical simulation. Water Resour. Res. 1985, 21, 19–26. [Google Scholar] [CrossRef]
- Lenhard, R.J.; Oostrom, M.; Dane, J.H. A constitutive model for air-NAPL-water flow in the vadose zone accounting for immobile, non-occluded (residual) NAPL in strongly water-wet porous media (Journal of Contaminant Hydrology (2004) 71 (261-282) doi:10.1016/j.jconhyd.2003.10.014). J. Contam. Hydrol. 2004, 73, 281. [Google Scholar]
- White, M.D.; Oostrom, M.; Lenhard, R.J. A practical model for mobile, residual, and entrapped NAPL in water-wet porous media. Ground Water 2004, 42, 734–746. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.; Liang, B.; Liu, X.L. Study on environmental prediction model of organic contaminants transport in soil-water environment. J. Hydraul. Eng. 2003, 6, 48–55. (In Chinese) [Google Scholar]
- Wu, D.Y.; Wang, C. Analysis of the Relationship Between the Oil Holdup Measured by Coaxial Conductivity Sensor and the Oil Volume Fraction. J. Tianjin Univ. 2013, 46, 276–280. (In Chinese) [Google Scholar]
- Chen, J.J.; Yang, J.; Tian, L. Advances in NAPLs transport experiment in porous media based on pore network model. Adv. Earth Sci. 2007, 22, 997–1004. (In Chinese) [Google Scholar]
- Kleinknecht, S.M.; Class, H.; Braun, J. Density-driven migration of heavy NAPL vapor in the unsaturated zone. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
- Kikumoto, M.; Nakamura, K. Simulation of seepage flow of non-aqueous phase liquid in vadose zone. Environ. Geotech. 2017, 4, 171–183. [Google Scholar] [CrossRef]
- Javanbakht, G.; Arshadi, M.; Qin, T.; Goual, L. Micro-scale Displacement of NAPL by Surfactant and Microemulsion in Heterogeneous Porous Media. Adv. Water Resour. 2017, 105, 173–187. [Google Scholar] [CrossRef]
- Joun, W.; Lee, S.-S.; Koh, Y.E.; Lee, K.-K. Impact of water table fluctuations on the concentration of borehole gas from NAPL sources in the vadose zone. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Xie, B.; Kong, D.; Kong, L.; Kong, W.; Li, L. Analysis of vertical upward oil-gas-water three-phase flow based on multi-scale time irreversibility. Flow Meas. Instrum. 2018, 62, 9–18. [Google Scholar] [CrossRef]
- Tan, C.; Li, P.; Dai, W.; Dong, F. Characterization of oil-water two-phase pipe flow with a combined conductivity/capacitance sensor and wavelet analysis. Chem. Eng. Sci. 2015, 134, 153–168. [Google Scholar] [CrossRef]
- Picchi, D.; Battiato, I. The Impact of Pore-Scale Flow Regimes on Upscaling of Immiscible Two-Phase Flow in Porous Media. Water Resour. Res. 2018, 54, 6683–6707. [Google Scholar] [CrossRef]
- Balasuriya, S. Transport between two fluids across their mutual flow interface: The Streakline Approach. SIAM J. Appl. Dyn. Syst. 2017, 16, 1015–1044. [Google Scholar] [CrossRef]
- Li, Y.; Gao, J.; Liu, X.; Xie, R. Energy demodulation algorithm for flow velocity measurement of oil-gas-water three-phase flow. Math. Probl. Eng. 2014, 5, 1–13. [Google Scholar] [CrossRef]
- Kacem, M.; Benadda, B. Mathematical Model for Multiphase Extraction Simulation. J. Environ. Eng. USA 2018, 144. [Google Scholar] [CrossRef]
- Bear, J.; Cheng, H.D. Modeling Groundwater Flow and Contaminant Transport; Springer: Berlin, Germany, 2010. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier: Amsterdam, The Netherlands, 1972; Volume 764. [Google Scholar]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Van Genucheten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multiphase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J. A model for hysteretic constitutive relations governing multiphase flow: 1. Saturation–pressure relations. Water Resour. Res. 1987, 23, 2187–2196. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J. A model for hysteretic constitutive relations governing multiphase flow: 2. Permeability–saturation relations. Water Resour. Res. 1987, 23, 2197–2206. [Google Scholar] [CrossRef]
- Nikolaevskii, V.N. Mechanics of Porous and Fractured Media; World Scientific: Singapore, 1990. [Google Scholar]








| Density/g· | Dynamic Viscosity/cp | Sample | |||
|---|---|---|---|---|---|
| Water | Oil | Water | Oil | Porosity | Saturated permeability coefficient/ |
| 1.00 | 0.86 | 0.914 | 38.560 | 0.37 | |
| Media | Density | Dynamic Viscosity | Surface Tension | |
|---|---|---|---|---|
| Water NAPL Aquifer | 999.1 1462.0 | 0.914 0.55 | 0.0728 0.0293 | |
| Media | Porosity | Hydraulic Conductivity | Van Genuchten Parameters | |
| Water | ||||
| NAPL | ||||
| Aquifer | 0.35 | 10 | 2 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Li, H. Development of 3D Finite Element Method for Non-Aqueous Phase Liquid Transport in Groundwater as Well as Verification. Processes 2019, 7, 116. https://doi.org/10.3390/pr7020116
Yu W, Li H. Development of 3D Finite Element Method for Non-Aqueous Phase Liquid Transport in Groundwater as Well as Verification. Processes. 2019; 7(2):116. https://doi.org/10.3390/pr7020116
Chicago/Turabian StyleYu, Wei, and Hong Li. 2019. "Development of 3D Finite Element Method for Non-Aqueous Phase Liquid Transport in Groundwater as Well as Verification" Processes 7, no. 2: 116. https://doi.org/10.3390/pr7020116





