Development of a Microwave Irradiation Probe for a Cylindrical Applicator
Abstract
:1. Introduction
2. Materials and Methods
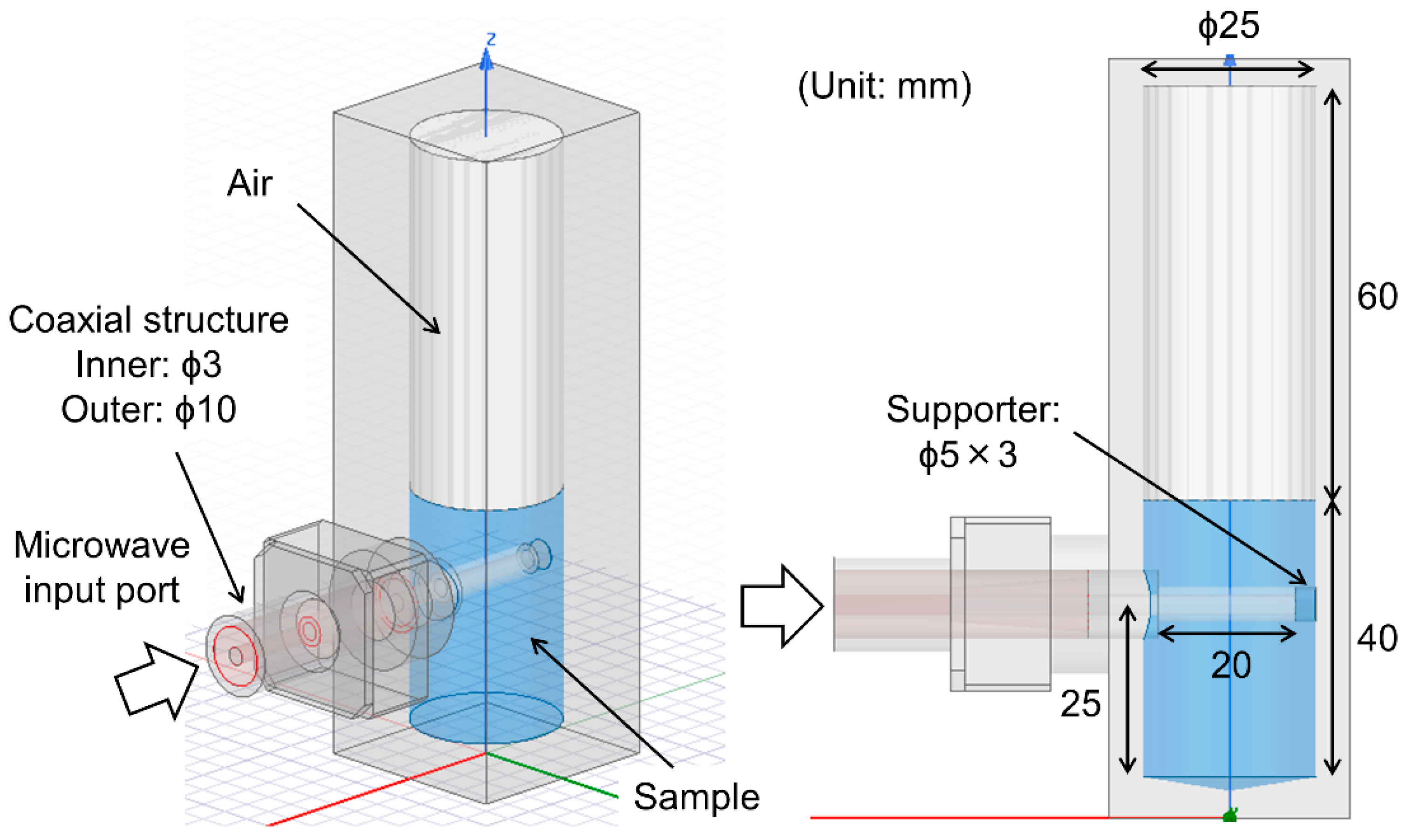
2.1. Overview of the Proposed Microwave Irradiation Probe and Cylindrical Applicator
2.2. Liquid Samples and Permittivity Measurements
2.3. Design of the Proposed Microwave Irradiation Probe and Cylindrical Applicator
2.4. Microwave Reflection Measurements for the Cylindrical Applicator
2.5. Microwave Heating Tests
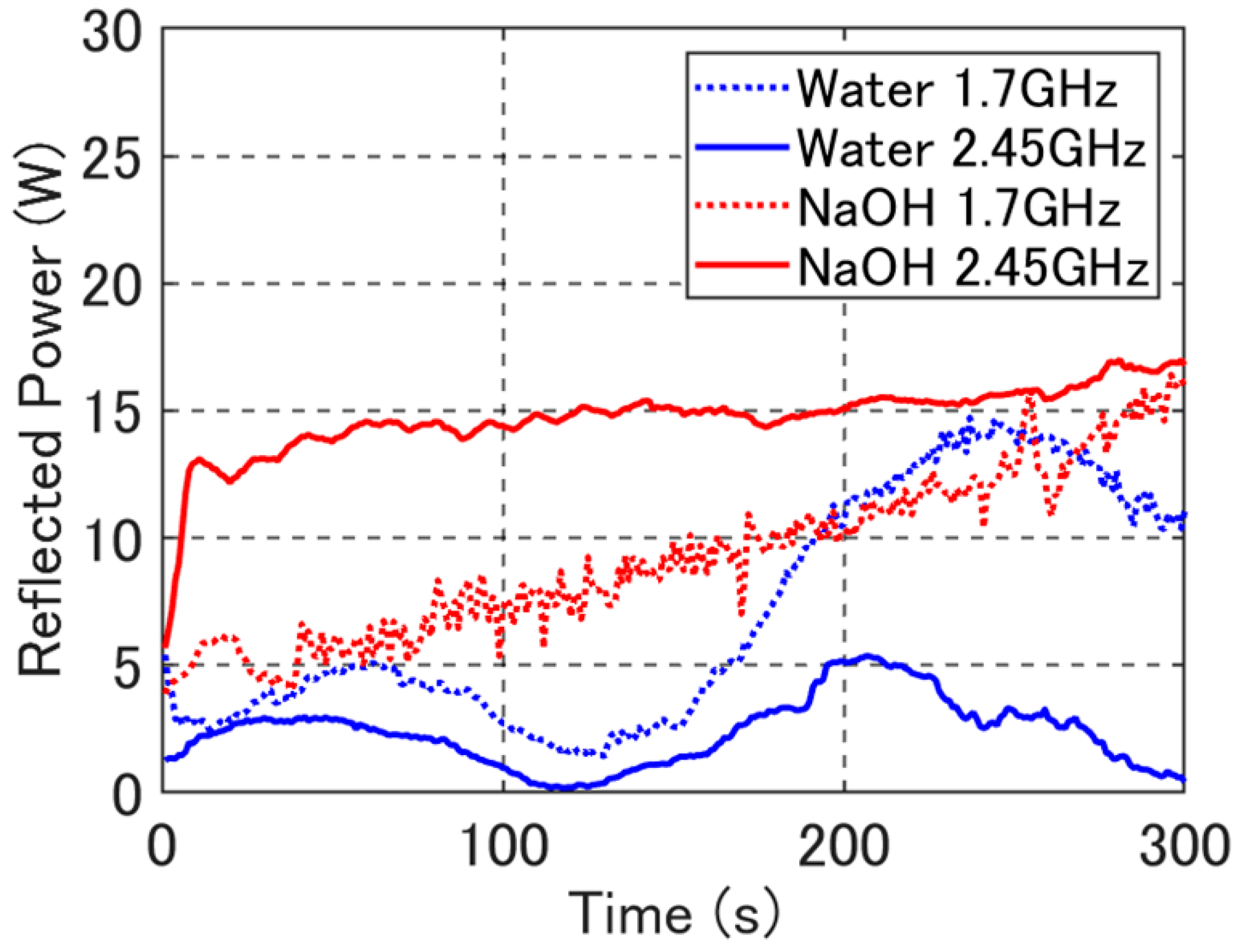
3. Results
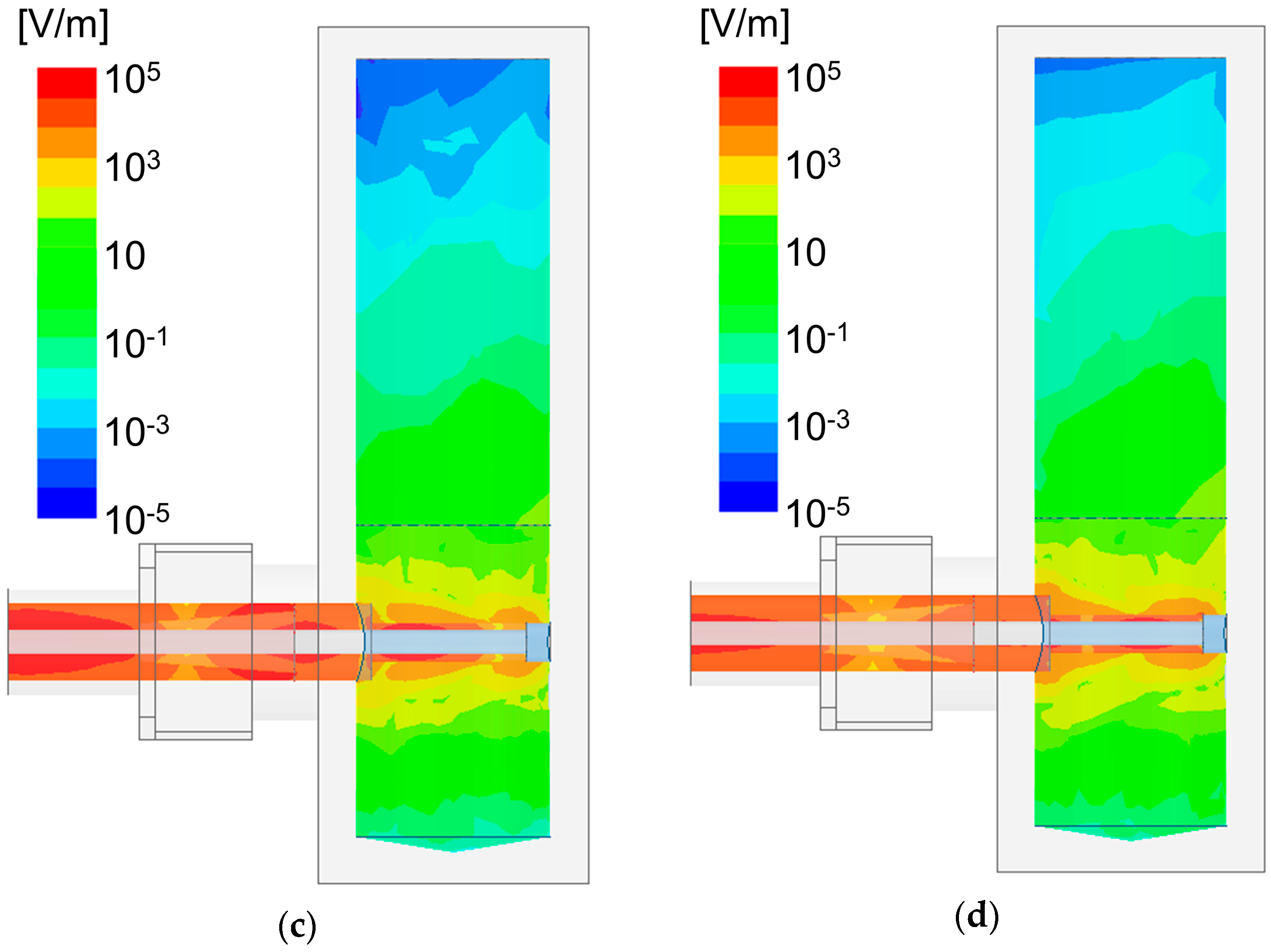
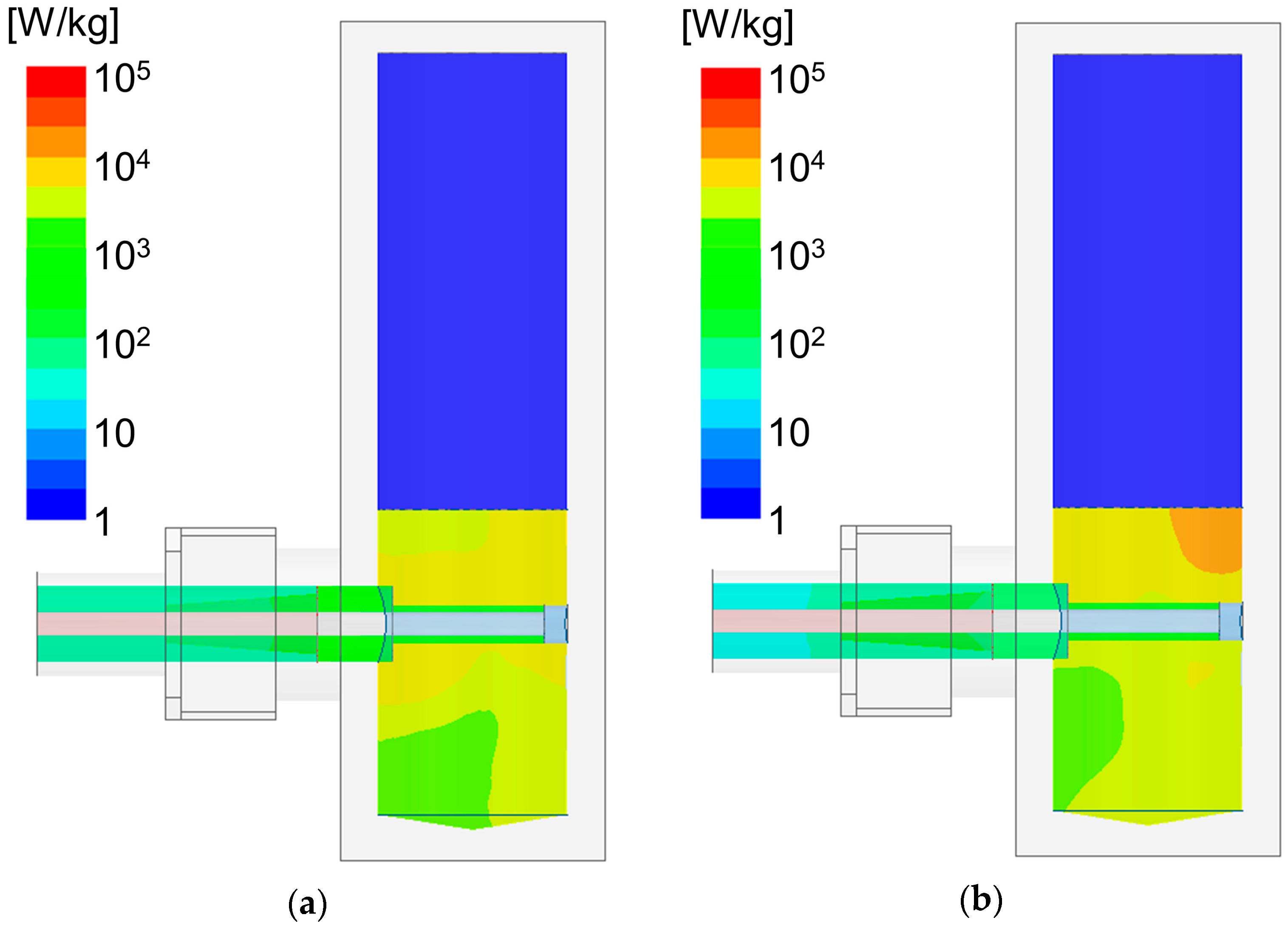
4. Discussion
4.1. Estimation of the Conductivity and Permittivity
4.2. Reflection Ratio and Heating Rate of the Developed Applicator
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Estel, L.; Poux, M.; Benamara, N.; Polaert, I. Continuous flow-microwave reator: Where are we? Chem. Eng. Process. Process Intensif. 2017, 113, 56–64. [Google Scholar] [CrossRef]
- Tung, T.T.; Alotaibi, F.; Nine, M.J.; Silva, R.; Tran, D.N.H.; Janowska, I.; Losic, D. Engineering of highly conductive and ultra-thin nitrogen-doped graphene films by combined methods of microwave irradiation, ultrasonic spraying and thermal annealing. Chem. Eng. J. 2018, 338, 764–773. [Google Scholar] [CrossRef]
- Beneroso, D.; Monti, T.; Kostas, E.T.; Robinson, J. Microwave pyrolysis of biomass for bio-oil production: Scalable processing concepts. Chem. Eng. J. 2017, 316, 481–498. [Google Scholar] [CrossRef] [Green Version]
- Aguilar-Reynosa, A.; Romaní, A.; Rodríguez-Jasso, R.M.; Aguilar, C.N.; Garrote, G.; Ruiz, H.A. Microwave heating processing as alternative of pretreatment in second-generation biorefinery: An overview. Energy Convers. Manag. 2017, 136, 50–65. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Qu, Y.; Yang, Y.; Chang, S.; Xu, J. Microwave irradiation—A green and efficient way to pretreat biomass. Bioresour. Technol. 2017, 122, 53–73. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Sun, D.; Cheng, J.; Han, Z. Microwave processing techniques and their recent applications in the food industry. Trends Food Sci. Technol. 2017, 67, 236–247. [Google Scholar] [CrossRef]
- McKinstry, C.; Cussen, E.J.; Fletcher, A.J.; Patwardhan, S.V.; Sefcik, J. Scalable continuous production of high quality HKUST-1 via conventional and microwave heating. Chem. Eng. J. 2017, 326, 570–577. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Wang, P. Study and application status of microwave in organic wastewater treatment—A review. Chem. Eng. J. 2016, 283, 193–214. [Google Scholar] [CrossRef]
- Rybakov, K.I.; Olevsky, E.A.; Krikun, E.V. Microwave sintering: Fundamentals and modeling. J. Am. Ceram. Sci. 2013, 96, 1003–1020. [Google Scholar] [CrossRef]
- Yin, S.; Chen, K.; Srinivasakannan, C.; Guo, S.; Li, S.; Peng, J.; Zhang, L. Enhancing recovery of ammonia from rare earth wastewater by air stripping combination of microwave heating and high gravity technology. Chem. Eng. J. 2018, 337, 515–521. [Google Scholar] [CrossRef]
- He, W.; Fang, Z.; Zhang, K.; Tu, T.; Lv, N.; Qiu, C.; Guo, K. A novel micro-flow system under microwave irradiation for continuous synthesis of 1,4-dihydropyridines in the absence of solvents via Hantzsch reaction. Chem. Eng. J. 2018, 331, 161–168. [Google Scholar] [CrossRef]
- Garagalza, O.; Petit, C.; Mignard, E.; Sarrazin, F.; Reynaud, S.; Grassl, B. Droplet-based millifluidic device under microwave irradiation: Temperature measurement and polymer particle synthesis. Chem. Eng. J. 2017, 308, 1105–1111. [Google Scholar] [CrossRef]
- Sturm, G.S.J.; Verweij, M.D.; Stankiewicz, A.I.; Stefanidis, G.D. Microwaves and microreactors: Design challenges and remedies. Chem. Eng. J. 2014, 243, 147–158. [Google Scholar] [CrossRef] [Green Version]
- Sivan, L. Magnetron—Detailed principle of operation. In Microwave Tube Transmitters; Chapman & Hall: London, UK, 1994; pp. 155–193. [Google Scholar]
- Williams, R.; Lindseth, B. Compact 1 kW 2.45 GHz solid-state source for in industrial applications. In Proceedings of the 50th Annual Microwave Power Symposium, Orlando, FL, USA, 21–23 June 2016; pp. 39–41. [Google Scholar]
- Bartola, B.; Kaplan, K.; Williams, R. 64 kW microwave generator using LDMOS power amplifiers for industrial heating applications. In Proceedings of the 50th Annual Microwave Power Symposium, Orlando, FL, USA, 21–23 June 2016; pp. 37–38. [Google Scholar]
- Wang, K.; Dimistrakis, G.; Irvine, D.J. Exemplification of catalyst design for microwave selective heating and its application to efficient in situ catalyst synthesis. Chem. Eng. Process. Process Intensif. 2017, 122, 389–396. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, C.; Bonato, P.; Dughiero, F.; Canu, P. Enhanced power density uniformity for microwave catalytic reactions adopting solid-state generators: Comparison with magnetron technology. Chem. Eng. Process. Process Intensif. 2017, 120, 286–300. [Google Scholar] [CrossRef]
- Kapranov, S.V.; Kouzaev, G.A. Models of water, methanol, and ethanol and their applications in the design of miniature microwave heating reactors. Int. J. Therm. Sci. 2017, 122, 53–73. [Google Scholar] [CrossRef]
- Sumi, T.; Horikoshi, S. Microwave selective heating for size effect of water droplet in W/O emulsion with sorbitan fatty acid monostearate surfactant. Radiat. Phys. Chem. 2015, 114, 31–37. [Google Scholar] [CrossRef]
- Mitani, T.; Hasegawa, N.; Nakajima, R.; Shinohara, N.; Nozaki, Y.; Chikata, T.; Watanabe, T. Development of a wideband microwave reactor with a coaxial cable structure. Chem. Eng. J. 2016, 299, 209–216. [Google Scholar] [CrossRef] [Green Version]
- Yokozawa, S.; Ohneda, N.; Muramatsu, K.; Okamoto, T.; Odajima, H.; Ikawa, T.; Sugiyama, J.; Fujita, M.; Sawairi, T.; Egami, H.; et al. Development of a highly efficient single-mode microwave reacttor with a resonant cavity and its application to continuous flow syntheses. RSC Adv. 2015, 5, 10204–10210. [Google Scholar] [CrossRef]
- Nishioka, M.; Miyakawa, M.; Kataoka, H.; Koda, H.; Sato, K.; Suzuki, T.M. Continuous synthesis of monodispersed silver nanoparticles using a homogeneous heating microwave reactor system. Nanoscale 2011, 3, 2621–2626. [Google Scholar] [CrossRef] [PubMed]
- Arshanista, A.; Akishin, Y.; Zile, E.; Dizhbite, T.; Solovnik, V.; Telysheva, G. Microwave treatment combined with conventional heating of plant biomass pellets in a rotated reactor as a high rate process for solid biofuel manufacture. Renew. Energy 2016, 91, 386–396. [Google Scholar] [CrossRef]
- Hong, Y.; Lin, B.; Li, H.; Dai, H.; Zhu, C.; Yao, H. Three-dimensional simulation of microwave heating coal sample with varying parameters. Appl. Therm. Eng. 2016, 93, 1145–1154. [Google Scholar] [CrossRef]
- Blackham, D.V.; Pollard, R.D. An improved technique for permittivity measurements using a coaxial probe. IEEE Trans. Instrum. Meas. 1997, 46, 1093–1099. [Google Scholar] [CrossRef]
- Kremer, F.; Schönhals, A. Analysis of Dielectric Spectra. In Broadband Dielectric Spectroscopy; Springer: Heidelberg, Germany, 2003; pp. 59–98. [Google Scholar]
- Kaatze, U. Complex permittivity of water as a function of frequency and temperature. J. Chem. Eng. Data 1989, 34, 371–374. [Google Scholar] [CrossRef]
- Pozer, D.M. Microwave network analysis. In Microwave Engineering, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2012; pp. 165–227. [Google Scholar]
- Qu, C.; Kaneko, M.; Kashimura, K.; Tanaka, K.; Ozawa, S.; Watanabe, T. Direct production of vanillin from wood particles by copper oxide-peroxide reaction promoted by electric and magnetic fields of microwaves. ACS Sustain. Chem. Eng. 2017, 5, 11551–11557. [Google Scholar] [CrossRef]










| Parameters | Values |
|---|---|
| Target frequency | 2.45 GHz |
| Start frequency | 80 MHz |
| Stop frequency | 2.7 GHz |
| Input power | 100 W |
| Number of mesh | 19,236 (water), 15,674 (NaOH solution) |
| Permittivity of PTFE | 2.08–j 0.00208 |
| Permittivity of alumina | 9.4–j 0.0564 |
| Conductivity of SUS 316L | 1.1 × 106 S/m |
| Sample | Relative Permittivity | Conductivity (S/m) |
|---|---|---|
| Water | 74.0–j 9.4 | 0 |
| Water (Debye, 25 °C) [28] | 77.2–j 9.2 | 0 |
| NaOH solution | 22.5–j 2.2 | 34.7 |
| Frequency (GHz) | Temperature (°C) | Simulation (W) | Measurement (W) |
|---|---|---|---|
| 1.7 | 30 | 2.2 | 3.9 |
| 40 | 8.7 | 3.8 | |
| 50 | 16.5 | 4.4 | |
| 60 | 17.9 | 1.9 | |
| 2.45 | 30 | 2.2 | 1.3 |
| 40 | 4.0 | 2.7 | |
| 50 | 5.1 | 2.6 | |
| 60 | 8.6 | 0.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitani, T.; Nakajima, R.; Shinohara, N.; Nozaki, Y.; Chikata, T.; Watanabe, T. Development of a Microwave Irradiation Probe for a Cylindrical Applicator. Processes 2019, 7, 143. https://doi.org/10.3390/pr7030143
Mitani T, Nakajima R, Shinohara N, Nozaki Y, Chikata T, Watanabe T. Development of a Microwave Irradiation Probe for a Cylindrical Applicator. Processes. 2019; 7(3):143. https://doi.org/10.3390/pr7030143
Chicago/Turabian StyleMitani, Tomohiko, Ryo Nakajima, Naoki Shinohara, Yoshihiro Nozaki, Tsukasa Chikata, and Takashi Watanabe. 2019. "Development of a Microwave Irradiation Probe for a Cylindrical Applicator" Processes 7, no. 3: 143. https://doi.org/10.3390/pr7030143
APA StyleMitani, T., Nakajima, R., Shinohara, N., Nozaki, Y., Chikata, T., & Watanabe, T. (2019). Development of a Microwave Irradiation Probe for a Cylindrical Applicator. Processes, 7(3), 143. https://doi.org/10.3390/pr7030143






