Nonlocal FEM Formulation for Vibration Analysis of Nanowires on Elastic Matrix with Different Materials

Abstract

In this study, free vibration behaviors of various embedded nanowires made of different materials are investigated by using Eringen’s nonlocal elasticity theory. Silicon carbide nanowire (SiCNW), silver nanowire (AgNW), and gold nanowire (AuNW) are modeled as Euler–Bernoulli nanobeams with various boundary conditions such as simply supported (S-S), clamped simply supported (C-S), clamped–clamped (C-C), and clamped-free (C-F). The interactions between nanowires and medium are simulated by the Winkler elastic foundation model. The Galerkin weighted residual method is applied to the governing equations to gain stiffness and mass matrices. The results are given by tables and graphs. The effects of small-scale parameters, boundary conditions, and foundation parameters on frequencies are examined in detail. In addition, the influence of temperature change on the vibrational responses of the nanowires are also pursued as a case study.

1. Introduction

Nanoscale structures/materials have very different characteristics. Nanostructures/nanomaterials have attracted great attention because their extraordinary features, such as high strength, low density, high elasticity modulus, and high hardness [1,2,3,4], have become the focus of researchers. The aforementioned unique properties of such structures, materials, and rapid developments in nanotechnology has led to use of these structural elements in designing micro- and nanoelectro mechanical systems (MEMS and NEMS) such as resonators, atomic force microscopes, switches, actuators, and sensors.

Some experimental studies have revealed the deformation behaviors of micro-/nanosized structures [5,6]. However, experiments are very difficult and quite expensive on these scales because high precision test devices are needed. On the other hand, atomistic modeling such as molecular dynamic simulations is computationally expensive and requires a long period of time. Consequently, this option is limited to structures that have only a few atoms [7].

To understand and accurately interpret the mechanical properties and behaviors of nanoscale structures, use of models based on continuum mechanics may be a better alternative than experiments and atomistic modelling. Unfortunately, classical continuum theories are not sufficient to predict and estimate size dependency because they lack internal/additional material length scale parameters. In ultrasmall scales (micrometer dimension, nanometer dimension) interactions between atoms and molecules have increasing importance and cannot be neglected. Therefore, the solution to classical continuum theories, which does not take into account size effects, does not give accurate results. In order to obtain more accurate results, higher-order continuum theories such as couple stress theory [8,9,10], modified couple stress theory [11], strain gradient theory [12], modified strain gradient theory [13], and nonlocal elasticity theory [14] have been developed and contain various length scale parameters. These theories were used by many researchers for various analyses such as buckling [15], bending [16,17], free vibration [18,19], forced vibration [20], and nonlinear vibration [21].

Rahmanian et al. [22] presented free vibrations of single-walled carbon nanotubes (SWCNT) on a Winkler elastic foundation via nonlocal elasticity theory. In this study, SWCNT was modeled as both beam and shell structures. Demir and Civalek [23] reported thermal vibration formulation of a nonlocal Euler–Bernoulli beam embedded in an elastic matrix. Finite element formulation for Eringen’s nonlocal elasticity theory was employed via Hermitian cubic shape functions. Thermal vibrational behaviors of silicon carbide nanowire on an elastic matrix were investigated for simply supported (S-S) and clamped–clamped (C-C) boundary conditions. Finite element formulations of nonlocal elastic Euler–Bernoulli and Timoshenko beam theories were achieved by Pradhan [24]. Vibration, buckling, and bending analyses of carbon nanotubes with four different boundary conditions were performed by the Galerkin finite element technique. Rajasekaran and Bakhshi Khaniki [25] reported static deformation, stability, and free vibration responses of small-scale beams. A finite element model of axial, functionally graded, nonuniform small-scale beams was investigated by using nonlocal strain gradient theory. Eltaher et al. [26] pursued free vibration analysis of functionally graded Euler–Bernoulli nanobeams by using Eringen’s nonlocal elasticity theory. Finite element results were given for a dynamic analysis of the nanobeam. Nejad and Hadi [27] studied bending analysis of non-homogeneous nanobeams. Eringen’s nonlocal elasticity theory was utilized in Euler–Bernoulli nanobeams made of bi-directional, functionally graded material. Murmu and Pradhan [28] studied the thermo-mechanical vibration response of embedded carbon nanotubes surrounded by an elastic matrix based on nonlocal elasticity theory. Reddy [29] developed nonlocal beam models based on four different beam theories. Static bending, free vibration, and buckling analyses of nanobeams are performed in this study. Tornabene et al. [30] presented a multiscale approach for three-phase carbon nanotube (CNT)/polymer/fiber-laminated nanocomposite structures. Detailed formulations can be found in the literature [31,32,33,34,35] about CNT-reinforcement or the finite element method (FEM). More recently, Uzun et al. [36] investigated the free vibration responses of carbon nanotubes and boron nitride nanotubes based on nonlocal elasticity theory. Nonlocal natural frequencies are obtained for various cross-section geometries.

In the present study, free vibration analysis of three kinds of nanowires resting on a Winkler elastic foundation with various boundary conditions are performed. Simply supported (S-S), clamped simply supported (C-S), clamped–clamped (C-C), and clamped-free (C-F) boundary conditions are selected. Silicon carbide nanowire (SiCNW), silver nanowire (AgNW), and gold nanowire (AuNW) are modeled as nonlocal Euler–Bernoulli beams, and their vibration behaviors are investigated using the finite element method (FEM). A Galerkin weighted residual method is utilized to govern equations and matrices, and the Winkler foundation parameter and small-scale parameter are gained. Effects of boundary conditions, temperature rise, and small-scale and Winkler foundation parameters of frequency values are investigated and compared for three kinds of nanowires.

2. Euler–Bernoulli Nanobeam Resting on a Winkler Elastic Foundation

The nonlocal stress tensor ${\sigma }_{ij}$ at point x is expressed as follows [14]:

$${\sigma }_{ij,j}=0,$$

(1)

$${\sigma }_{ij}(x)={\displaystyle {\int }_{\mathsf{\Omega }}K(|x^{\prime }}-x|),\tau )C_{ijkl}{\epsilon }_{kl}d\mathsf{\Omega }(x^{\prime }),$$

(2)

where $K(|x^{\prime }-x|,\tau )$ is the Kernel function, $|x^{\prime }-x|$ is the distance in the Euclidean form, $\tau =e_{0}a/l$ is a material constant that depends upon the internal characteristic lengths ($a$) and external characteristic length ($l$), and $e_0$ is a material constant that is determined experimentally. $C_{ijkl}$ and ${\epsilon }_{kl}$ represent the fourth-order elasticity and the strain tensors, respectively, and $\mathsf{\Omega }$ is the region occupied by the body.

The nonlocal constitutive formulation is [28]:

$$[1-{\tau }^2{l}^2{\nabla }^2]{\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl}.$$

(3)

x, y, z depict length, width, and height of the beam, respectively and u₁, u₂, u₃ are the displacements in the x, y, z directions. The displacements for a Bernoulli–Euler beam can be written as below [17]:

$$u_1(x,z,t)=-z\frac{\partial w(x,t)}{\partial x},u_2(x,z,t)=0,u_3(x,z,t)=w(x,t).$$

(4)

${\epsilon }_{ij}$ is the strain tensor, expressed as:

$${\epsilon }_{ij}=0.5(\partial u_{i,j}+\partial u_{j,i}).$$

(5)

From Equation (5) we find the strains of the Euler–Bernoulli beam as follows:

$${\epsilon }_{xx}=-z\frac{{\partial }^{2}w(x,t)}{\partial x^2},{\epsilon }_{xy}={\epsilon }_{yx}={\epsilon }_{xz}={\epsilon }_{zx}={\epsilon }_{yy}={\epsilon }_{yz}={\epsilon }_{zy}={\epsilon }_{zz}=0.$$

(6)

Stress $\sigma$ for the linear elastic materials is expressed as follows:

$$\sigma =E\epsilon ,$$

(7)

where E is the elastic modulus of the material. If ${\epsilon }_{xx}$, the only nonzero component of strain, is written in Equation (7), ${\sigma }_{xx}$ is obtained as:

$${\sigma }_{xx}=-Ez\frac{{\partial }^{2}w(x,t)}{\partial x^2}.$$

(8)

Moment (M) and the moment of inertia (I) are given by:

$$M={\displaystyle \underset{A}{\int }z{\sigma }_{xx}}dA,I={\displaystyle \underset{A}{\int }{z}^2}dA,$$

(9)

where A represents the cross-section area.

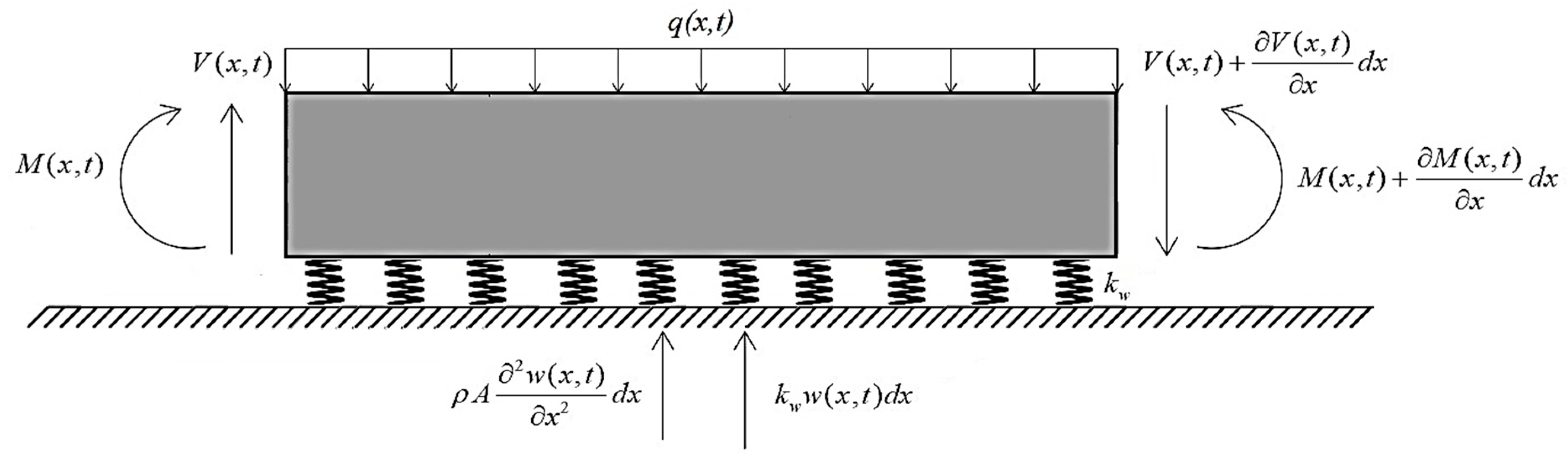
For the transverse vibration of an Euler–Bernoulli beam (shown in Figure 1) resting on a Winkler elastic foundation, the equilibrium conditions are:

$$\frac{\partial V(x,t)}{\partial x}=-q(x,t)+\rho A\frac{{\partial }^{2}w(x,t)}{\partial x^2}+k_{w}w(x,t),$$

(10)

$$V(x,t)=\frac{\partial M(x,t)}{\partial x},$$

(11)

$$\frac{{\partial }^{2}M(x,t)}{\partial x^2}=-q(x,t)+\rho A\frac{{\partial }^{2}w(x,t)}{\partial x^2}+k_{w}w(x,t),$$

(12)

where ρ, q(x,t), and k_w are the mass density, distributed load, and Winkler foundation parameter, respectively.

Figure 1. Euler–Bernoulli beam resting on a Winkler foundation.

The nonlocal constitutive relations can be simplified in the following form for a one-dimensional case [14,29]:

$${\sigma }_{xx}-{(e_{0}a)}^2\frac{{\partial }^2{\sigma }_{xx}}{\partial x^2}=E{\epsilon }_{xx}.$$

(13)

By multiplying z on both sides of Equation (13) and integrating the cross-sectional area of the beam, we obtain:

$${\displaystyle {\int }_{A}z}\sigma dA-{(e_{0}a)}^2{\displaystyle \underset{A}{\int }z}\frac{{\partial }^2\sigma }{\partial x^2}dA={\displaystyle \underset{A}{\int }z}E\epsilon dA=0.$$

(14)

Substituting Equations (6) and (9) into (14), we get:

$$M(x,t)-{(e_{0}a)}^2\frac{{\partial }^{2}M(x,t)}{\partial x^2}=-EI\frac{{\partial }^{2}w(x,t)}{\partial x^2}.$$

(15)

By differentiating Equation (15) twice with respect to variable x and substituting Equation (12) into Equation (15), we obtain the governing equation for the vibration of an Euler–Bernoulli nanobeam resting on a Winkler elastic foundation, as below:

$$EI\frac{{\partial }^{4}w(x,t)}{\partial x^4}+\rho A\frac{\partial w^2(x,t)}{\partial t^2}+k_{w}w-{(e_{0}a)}^2\frac{{\partial }^2}{\partial x^2}\left[\rho A\frac{{\partial }^{2}w(x,t)}{\partial t^2}+k_{w}w\right]=0.$$

(16)

3. Solution to the Vibration Problem

3.1. Galerkin Weighted Residual Method

The shape function for beam $\phi$ is as follows [37,38]:

$$\phi =\left\{\begin{array}{c}{\phi }_1\\ {\phi }_2\\ {\phi }_3\\ {\phi }_4\end{array}\right\}=\left\{\begin{array}{c}1-3{\xi }^2+2{\xi }^3\\ L\left(\xi -2{\xi }^2+{\xi }^3\right)\\ 3{\xi }^2-2{\xi }^3\\ L\left(-{\xi }^2+{\xi }^3\right)\end{array}\right\},$$

(17)

where ξ = x/L is a non-dimensional local coordinate. In order to obtain the weak form of the governing equation of an Euler–Bernoulli nanobeam resting on a Winkler elastic foundation, the residue can be expressed as:

$$\left[EI\frac{{\partial }^{4}w(x,t)}{\partial x^4}+\rho A\frac{\partial w^2(x,t)}{\partial t^2}+k_{w}w-{(e_{0}a)}^2\frac{{\partial }^2}{\partial x^2}\left(\rho A\frac{{\partial }^{2}w(x,t)}{\partial t^2}+k_{w}w\right)\right]=residue.$$

(18)

To determine the weighted residue, Equation (18) is multiplied by a weighting function $\phi$. When the weighted residual is integrated over the length:

$${\displaystyle {\int }_0^L\left[\phi EI\frac{{\partial }^{4}w(x,t)}{\partial x^4}+\phi \rho A\frac{\partial w^2(x,t)}{\partial t^2}+\phi k_{w}w-\phi {(e_{0}a)}^2\frac{{\partial }^2}{\partial x^2}\left(\rho A\frac{{\partial }^{2}w(x,t)}{\partial t^2}+k_{w}w\right)\right]}dx=0.$$

(19)

Equation (19) is integrated by parts. According to the chain rule, in the general form:

$${{\displaystyle \int }}_0^L\left[EI\frac{{\partial }^2\phi }{\partial x^2}\frac{{\partial }^2{\phi }^T}{\partial x^2}+\rho A\phi {\phi }^T\ddot{w}+k_w\phi {\phi }^T-{\left(e_{0}a\right)}^2\rho A\frac{\partial \phi }{\partial x}\frac{\partial {\phi }^T}{\partial x}\ddot{w}-{\left(e_{0}a\right)}^2{k}_w\frac{\partial \phi }{\partial x}\frac{\partial {\phi }^T}{\partial x}\right]dx=0.$$

(20)

By using the shape function in Equation (17) and the non-dimensional local coordinate, bending stiffness matrix K^b, Winkler foundation stiffness matrix K^w, and the mass matrix M, the following are obtained:

$$K^b=EI{\displaystyle \underset{0}{\overset{L}{\int }}\left\{\begin{array}{c}{\phi }_1^{″}\\ {\phi }_2^{″}\\ {\phi }_3^{″}\\ {\phi }_4^{″}\end{array}\right\}}\left\{\begin{array}{ccc}\begin{array}{cc}{\phi }_1^{″}& {\phi }_2^{″}\end{array}& {\phi }_3^{″}& {\phi }_4^{″}\end{array}\right\}dx;$$

(21a)

$$K^b=\frac{EI}{L^3}\left[\begin{array}{cccc}12& 6L& -12& 6L\\ 6L& 4L^2& -6L& 2L^2\\ -12& -6L& 12& -6L\\ 6L& 2L^2& -6L& 4L^2\end{array}\right];$$

(21b)

$$K^{w1}=k_w{\displaystyle \underset{0}{\overset{L}{\int }}\left\{\begin{array}{c}{\phi }_1\\ {\phi }_2\\ {\phi }_3\\ {\phi }_4\end{array}\right\}}\left\{\begin{array}{ccc}\begin{array}{cc}{\phi }_1& {\phi }_2\end{array}& {\phi }_3& {\phi }_4\end{array}\right\}dx;$$

(22a)

$$K^{w1}=\frac{k_w}{420}\left[\begin{array}{cccc}156L& 22L^2& 54L& -13L^2\\ 22L^2& 4L^3& 13L^2& -3L^3\\ 54L& 13L^2& 156L& -22L^2\\ -13L^2& -3L^3& -22L^2& 4L^3\end{array}\right];$$

(22b)

$$K^{w2}={(e_{0}a)}^2{k}_w{\displaystyle \underset{0}{\overset{L}{\int }}\left\{\begin{array}{c}{\phi }_1^{\prime }\\ {\phi }_2^{\prime }\\ {\phi }_3^{\prime }\\ {\phi }_4^{\prime }\end{array}\right\}}\left\{\begin{array}{ccc}\begin{array}{cc}{\phi }_1^{\prime }& {\phi }_2^{\prime }\end{array}& {\phi }_3^{\prime }& {\phi }_4^{\prime }\end{array}\right\}dx;$$

(23a)

$$K^{w2}=\frac{{(e_{0}a)}^2{k}_w}{30L}\left[\begin{array}{cccc}36& 3L& -36& 3L\\ 3L& 4L^2& -3L& -L^2\\ -36& -3L& 36& -3L\\ 3L& -L^2& -3L& 4L^2\end{array}\right];$$

(23b)

$$M^1=\rho A{\displaystyle \underset{0}{\overset{L}{\int }}\left\{\begin{array}{c}{\phi }_1\\ {\phi }_2\\ {\phi }_3\\ {\phi }_4\end{array}\right\}}\left\{\begin{array}{ccc}\begin{array}{cc}{\phi }_1& {\phi }_2\end{array}& {\phi }_3& {\phi }_4\end{array}\right\}dx;$$

(24a)

$$M^1=\frac{\rho A}{420}\left[\begin{array}{cccc}156L& 22L& 54L& -13L^2\\ 22L^2& 4L^3& 13L^2& -3L^3\\ 54L& 13L^2& 156L& -22L^2\\ -13L^2& -3L^3& -22L^2& 4L^3\end{array}\right];$$

(24b)

$$M^2={(e_{0}a)}^2\rho A{\displaystyle \underset{0}{\overset{L}{\int }}\left\{\begin{array}{c}{\phi }_1^{\prime }\\ {\phi }_2^{\prime }\\ {\phi }_3^{\prime }\\ {\phi }_4^{\prime }\end{array}\right\}}\left\{\begin{array}{ccc}\begin{array}{cc}{\phi }_1^{\prime }& {\phi }_2^{\prime }\end{array}& {\phi }_3^{\prime }& {\phi }_4^{\prime }\end{array}\right\}dx;$$

(25a)

$$M^2=\frac{{(e_{0}a)}^2\rho A}{30L}\left[\begin{array}{cccc}36& 3L& -36& 3L\\ 3L& 4L^2& -3L& -L^2\\ -36& -3L& 36& -3L\\ 3L& -L^2& -3L& 4L^2\end{array}\right].$$

(25b)

The vibration of the Euler–Bernoulli beam is found as follows:

$$|K-{\omega }^{2}M|=0,$$

(26)

where K = K^b + K^w1 + K^w2, M = M¹ + M², and $\omega$ is frequency.

3.2. Thermal Effect on the Vibrational Response of Embedded Nanowires

Here, the effect of temperature change on the natural frequencies of embedded nanowires in a thermal environment is investigated. Equation (16) can be rewritten in the presence of thermal loading as:

$$(EI-N^T{(e_{0}a)}^2)\frac{{\partial }^{4}w}{\partial x^4}+k_{w}w+(N^T-k_w{(e_{0}a)}^2)\frac{{\partial }^{2}w}{\partial x^2}+\rho A\frac{{\partial }^{2}w}{\partial t^2}-\rho A{\left(e_{0}a\right)}^2\frac{{\partial }^{4}w}{\partial x^2\partial t^2}=0,$$

(27)

where the additional term $N^T$ is the axial load resulting from the temperature change and can be defined as [28]:

$$N^T=\frac{EA}{1-2v}\alpha \Delta T,$$

(28)

in which $\alpha$ is the thermal expansion coefficient in the axial direction, $\Delta T$ is the temperature change, and $v$ is Poisson’s ratio. It is notable that only an axial load resulting from temperature change exists for the nanowires in this study [28].

The following Navier’s solution procedure is applied to achieve simply supported (S-S) nanowires as an illustrative example:

$$w\left(x,t\right)={{\displaystyle \sum }}_{n=1}^{\infty }{W}_n\sin \beta e^{i{\omega }_{n}t},$$

(29)

where $n$ is the mode number, $W_n$ is the unknown Fourier coefficient, and $\beta =\frac{n\pi x}{L}$. Using Equation (29) in Equation (27) yields the following relation for small-scale-dependent natural frequencies of embedded S-S nanowires that includes the thermal effect:

$${\omega }_n=\sqrt{\frac{{\beta }^4\left(EI-N^T{\left(e_{0}a\right)}^2\right)+k_w-{\beta }^2\left(N^T-k_w{\left(e_{0}a\right)}^2\right)}{\rho A\left(1+{\beta }^2{\left(e_{0}a\right)}^2\right)}}.$$

(30)

4. Results and Discussion

In this section, frequency values of nanowires were obtained with various non-dimensional small-scale parameters (e₀a/L), different non-dimensional Winkler foundation parameters (K_W), different boundary conditions, and different number of elements (N). The material properties for the three nanowires are listed in Table 1. The results obtained were shown in tables and graphs. The dimensionless Winkler parameter used for the results is expressed as the formula below:

$$K_W=\frac{k_w{L}^4}{EI}.$$

(31)

Table 1. Material properties of the nanowires.

Material Properties	SiCNW	AuNW	AgNW
$E\left(\mathrm{GPa}\right)$	524.8	79	82.7
$v$	0.14	0.42	0.37
$\rho \left(\mathrm{kg}/{\mathrm{m}}^3\right)$	3100	19,320	10,490
$\alpha \left(1/℃\right)$	3.7 $\times {10}^{-6}$	14.2 $\times {10}^{-6}$	19.68 $\times {10}^{-6}$

Table 2 presents the natural frequencies of nanowires with C-C, C-S, S-S, and C-F boundary conditions. Finite element solutions for the three nanowires were compared with each other. It was clearly observed from the table that the highest frequency value occurred for both SiCNW and the C-C boundary condition, while the lowest value was seen in both AuNW and C-F boundary conditions.

Table 2. The first three natural frequencies (GHz) of isolated nanowires for four different boundary conditions (K_W = 0, e₀a/L = 0.1).

Mode Number	SiCNW
	C-C	C-S	S-S	C-F
1	21.8286	15.0969	9.7369	3.5540
2	52.7211	43.2195	34.5672	19.7887
3	88.6384	77.4034	66.8450	48.0785
Mode Number	AuNW
	C-C	C-S	S-S	C-F
1	3.3525	2.3186	1.4954	0.5458
2	8.0970	6.6378	5.3089	3.0392
3	13.6133	11.8878	10.2662	7.3840
Mode Number	AgNW
	C-C	C-S	S-S	C-F
1	4.6550	3.2195	2.0764	0.7579
2	11.2430	9.2167	7.3716	4.2200
3	18.9025	16.5066	14.2550	10.2529

Table 3, Table 4, Table 5 and Table 6 show natural frequencies of embedded simply supported nanowires for K_W = 1, K_W = 10, K_W = 100, and K_W = 1000, respectively, with different e₀a/L values. It was found from these tables that frequency values increased as K_W values increased, but frequencies decreased by increasing e₀a/L. Moreover, it was evident that small-scale effects became more considerable for higher modes.

Table 3. The first three natural frequencies (GHz) of embedded nanowires corresponding to various values of e₀a/L (K_W = 1).

Mode Number	SiCNW
	e0a/L
	0.0	0.1	0.2	0.3
1	10.2583	9.7916	8.7034	7.4989
2	40.8373	34.5827	25.4413	19.1602
3	91.8603	66.8530	43.0600	30.6452
Mode Number	AuNW
	e0a/L
	0.0	0.1	0.2	0.3
1	1.5755	1.5038	1.3367	1.1517
2	6.2719	5.3113	3.9073	2.9427
3	14.1081	10.2675	6.6133	4.7066
Mode Number	AgNW
	e0a/L
	0.0	0.1	0.2	0.3
1	2.1876	2.0881	1.8560	1.5992
2	8.7087	7.3749	5.4255	4.0860
3	19.5896	14.2567	9.1827	6.5352

Table 4. The first three natural frequencies (GHz) of embedded nanowires for various values of e₀a/L (K_W = 10).

Mode Number	SiCNW
	e0a/L
	0.0	0.1	0.2	0.3
1	10.7171	10.2713	9.2398	8.1152
2	40.9550	34.7215	25.6298	19.4097
3	91.9126	66.9249	43.1716	30.8018
Mode Number	AuNW
	e0a/L
	0.0	0.1	0.2	0.3
1	1.6460	1.5775	1.4191	1.2464
2	6.2900	5.3326	3.9363	2.9810
3	14.1162	10.2785	6.6304	4.7306
Mode Number	AgNW
	e0a/L
	0.0	0.1	0.2	0.3
1	2.2855	2.1904	1.9704	1.7306
2	8.7338	7.4045	5.4656	4.1392
3	19.6007	14.2720	9.2065	6.5686

Table 5. The first three natural frequencies (GHz) of embedded nanowires with respect to various values of e₀a/L (K_W = 100).

Mode Number	SiCNW
	e0a/L
	0.0	0.1	0.2	0.3
1	14.5292	14.2035	13.4764	12.7318
2	42.1135	36.0808	27.4431	21.7480
3	92.4347	67.6401	44.2722	32.3263
Mode Number	AuNW
	e0a/L
	0.0	0.1	0.2	0.3
1	2.2314	2.1814	2.0697	1.9554
2	6.4679	5.5414	4.2148	3.3401
3	14.1964	10.3883	6.7994	4.9648
Mode Number	AgNW
	e0a/L
	0.0	0.1	0.2	0.3
1	3.0984	3.0290	2.8739	2.7151
2	8.9809	7.6944	5.8524	4.6379
3	19.7121	14.4245	9.4412	6.8937

Table 6. The first three natural frequencies (GHz) of embedded nanowires against various values of e₀a/L (K_W = 1000).

Mode Number	SiCNW
	e0a/L
	0.0	0.1	0.2	0.3
1	34.2564	34.1196	33.8234	33.5336
2	52.3064	47.5839	41.4190	37.8864
3	97.5017	74.4150	54.0595	44.8040
Mode Number	AuNW
	e0a/L
	0.0	0.1	0.2	0.3
1	5.2612	5.2402	5.1947	5.1502
2	8.0333	7.3081	6.3612	5.8187
3	14.9746	11.4288	8.3026	6.8811
Mode Number	AgNW
	e0a/L
	0.0	0.1	0.2	0.3
1	7.3053	7.2761	7.2130	7.1512
2	11.1545	10.1475	8.8328	8.0794
3	20.7926	15.8693	11.5284	9.5546

In Table 7, the frequency values of C-C nanowires are given by analytical and finite element solutions for e₀a/L = 0.2. For the finite element solution, as the element number increased, the results approached the real value.

Table 7. Convergence of the present results with the analytical results of different element numbers.

Mode Number	SiCNW
	N = 4	N = 5	N = 6	N = 7	N = 8	N = 9	N = 10	Analytical
1	18.9418	18.9252	18.9189	18.9162	18.9148	18.9141	18.9137	18.9129
2	38.0339	37.8398	37.7549	37.7155	37.6955	37.6845	37.6781	37.6656
3	56.8236	57.2104	56.8478	56.6515	56.5467	56.4878	56.4529	56.3826
Mode Number	AuNW
	N = 4	N = 5	N = 6	N = 7	N = 8	N = 9	N = 10	Analytical
1	2.9091	2.9066	2.9056	2.9052	2.9050	2.9049	2.9048	2.9047
2	5.8413	5.8115	5.7985	5.7924	5.7894	5.7877	5.7867	5.7848
3	8.7271	8.7865	8.7308	8.7007	8.6846	8.6755	8.6702	8.6594
Mode Number	AgNW
	N = 4	N = 5	N = 6	N = 7	N = 8	N = 9	N = 10	Analytical
1	4.0394	4.0359	4.0345	4.0340	4.0337	4.0335	4.0334	4.0332
2	8.1109	8.0695	8.0514	8.0430	8.0387	8.0364	8.0350	8.0323
3	12.1179	12.2003	12.1230	12.0811	12.059	12.0462	12.0388	12.0238

Effects of both temperature rise and the Winkler parameter on the first three natural frequencies of nanowires are revealed in Table 8. It is apparent from the table that an increase temperature rise led to a decrease in frequency, contrary to the Winkler parameter. Also, it can be emphasized that the frequencies of AuNW were more affected than the other nanowires because of their related material properties, given in Table 1. Moreover, it can be observed that the influence of temperature rise was more prominent for lower modes and smaller Winkler parameters.

Table 8. The first three small-scale-dependent natural frequencies (GHz) of embedded nanowires for different Winkler parameters and temperature changes (e₀a/L = 0.1, d = 1 nm, and L = 20 d).

Mode Number	SiCNW
	$\Delta \mathit{T}=0$			$\Delta \mathit{T}=30 ℃$
	Kw = 100	Kw = 500	Kw = 1000	Kw = 100	Kw = 500	Kw = 1000
1	17.7768	31.4013	42.7034	17.3120	31.1405	42.5119
2	45.1580	52.0507	59.5551	44.4297	51.4201	59.0047
3	84.6569	88.5259	93.1362	83.7854	87.6928	92.3448
Mode Number	AuNW
	$\Delta \mathit{T}=0$			$\Delta \mathit{T}=30 ℃$
	Kw = 100	Kw = 500	Kw = 1000	Kw = 100	Kw = 500	Kw = 1000
1	2.7628	4.8802	6.6368	0.9103	4.1246	6.1026
2	7.0182	8.0895	9.2558	4.6945	6.1824	7.6454
3	13.157	13.7583	14.4748	10.5767	11.3159	12.177
Mode Number	AgNW
	$\Delta \mathit{T}=0$			$\Delta \mathit{T}=30 ℃$
	Kw = 100	Kw = 500	Kw = 1000	Kw = 100	Kw = 500	Kw = 1000
1	3.8362	6.7764	9.2153	1.8782	5.8932	8.5868
2	9.7450	11.2325	12.8519	7.0859	9.0229	10.9734
3	18.2689	19.1038	20.0987	15.2661	16.2559	17.4143

Effects of nanoscale and foundation parameters on the first five natural frequencies are respectively depicted in Figure 2 and Figure 3. It can be concluded from these figures that size dependency was more pronounced for higher modes, while the natural frequencies in lower modes were more affected from foundation parameters. As stated before, it was clear that the natural frequencies decreased and increased by increasing e₀a/L and K_W, respectively.

Figure 2. Variation of the first five natural frequencies of nanowires with respect to e₀a/L.

Figure 3. Effect of the Winkler parameter on the first five natural frequencies of nanowires.

Figure 4 displays the variation of fundamental frequencies of the three embedded nanowires with respect to temperature rise for various small-scale parameter values. It can be recognized from the figure that the effect of e₀a/L was more prominent for SiCNW than the other ones. On the other hand, the influence of temperature rise was more significant for gold and silver nanowires than the silicon carbide nanowire.

Figure 4. Variation of the fundamental frequency for several e₀a/L against temperature rise (L = 30 d, K_w = 1000).

5. Conclusions

Three types of nanowires, SiCNW, AgNW, and AuNW, are modeled as nonlocal Euler–Bernoulli nanobeams resting on a Winkler elastic foundation. Frequency values of these nanowires are obtained via a finite element solution, and results are given by tables and graphs. The effect of temperature change on the vibrational responses of simply supported nanowires is also examined as a case study. It can be concluded from the results that among all boundary conditions, C-C has the highest frequency values and C-F has the lowest ones. Also, it can be emphasized that by increasing the Winkler parameter value, frequency values increase, while by increasing non-dimensional small-scale parameter (e₀a/L), frequency value decreases. When we compare the frequency values of nanowires, SiCNW has the highest frequency values, while AuNW has the lowest frequency values because of its different material properties. Additionally, it is revealed that the effects of temperature change and small-scale parameters on the frequencies of nanowires are both considerable and negligible depending on the values of the involved material properties.