The Unit Teissier Distribution and Its Applications
Abstract
:1. Introduction
2. The Unit Teissier Distribution
2.1. Presentation
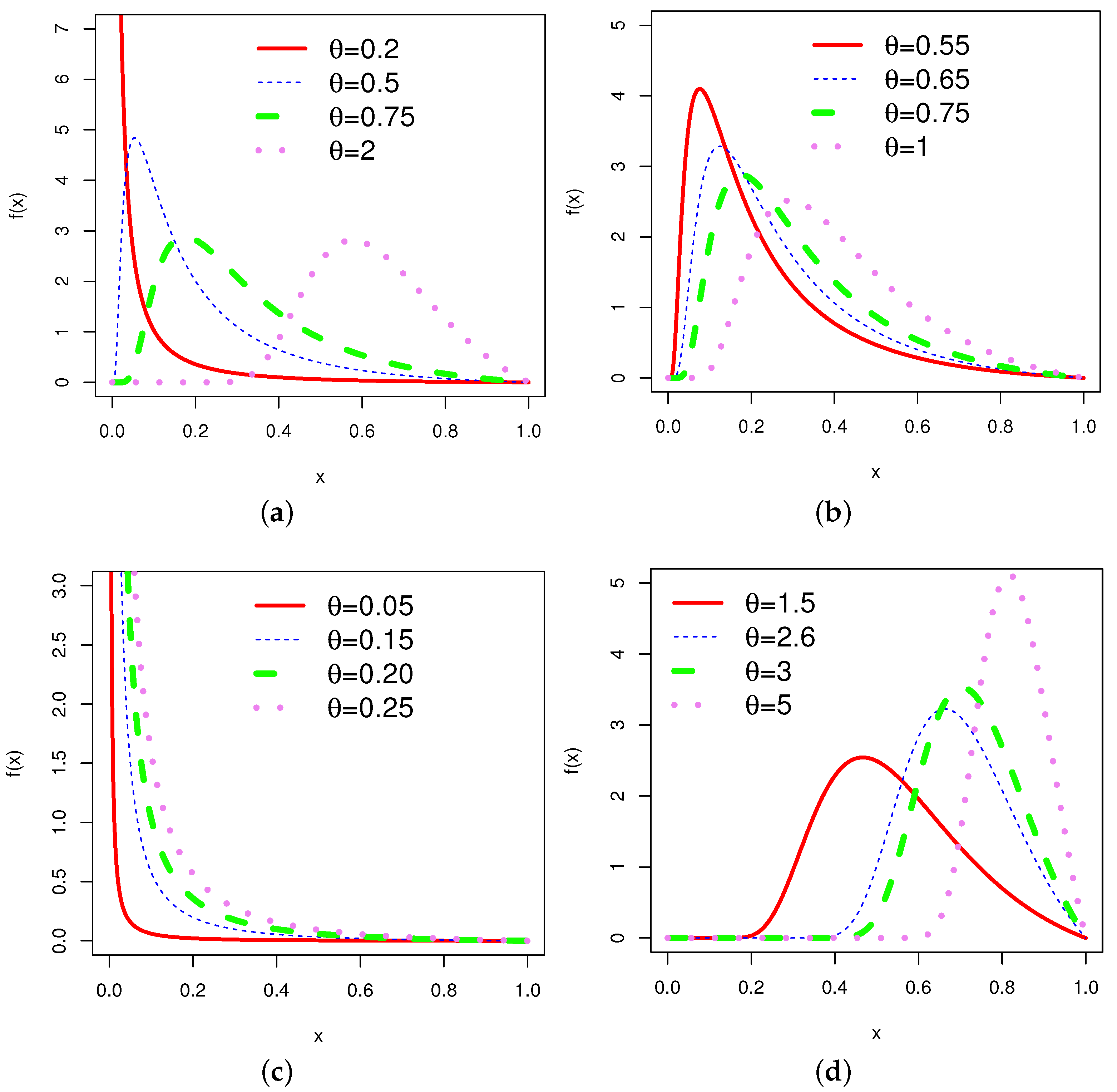
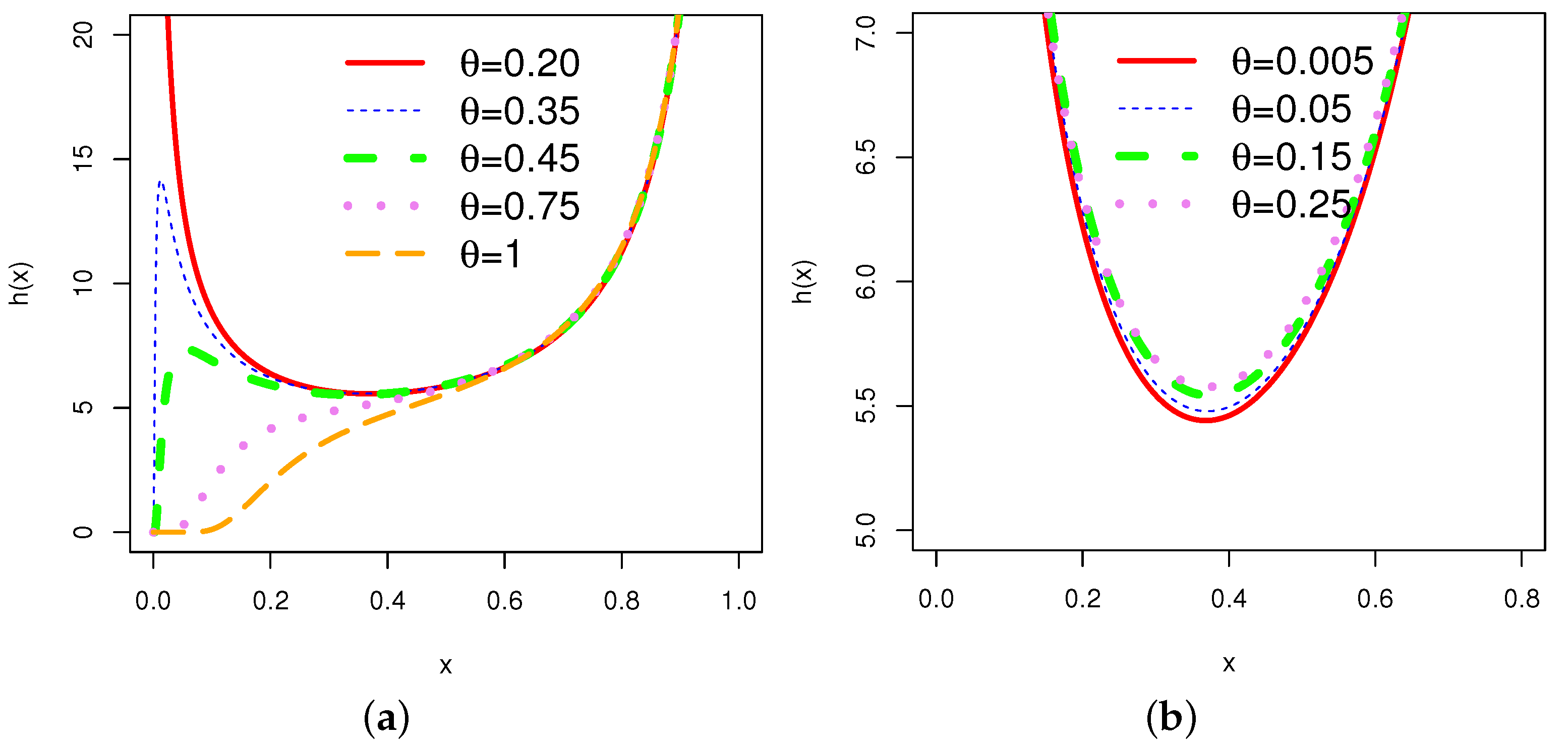
2.2. Shapes of the pdf and hrf
2.3. Moments
2.4. Incomplete Moments
2.5. Probability-Weighted Moments
2.6. Mean Residual Life Function
2.7. Quantile Function
- the median given as ;
- the Galton coefficient of skewness specified by
- the Moors coefficient of kurtosis (with correction) defined by
3. Shannon Entropy and Extropy
3.1. Shannon Entropy
- The upper incomplete gamma function already introduced;
- The derivative of the gamma function given as ;
- The derivative of the incomplete gamma function given as ;
- The exponential integral defined by
3.2. Extropy
4. Estimation and Inference
4.1. Maximum Likelihood Estimation
Fisher Information Matrix and Asymptotic Confidence Interval
4.2. Ordinary and Weighted Least-Squares Estimation
4.3. Bayesian Estimation
- Case 1:, then the posterior pdf is given by
- Case 2:, then the posterior pdf is given bywhere is derived from (12).
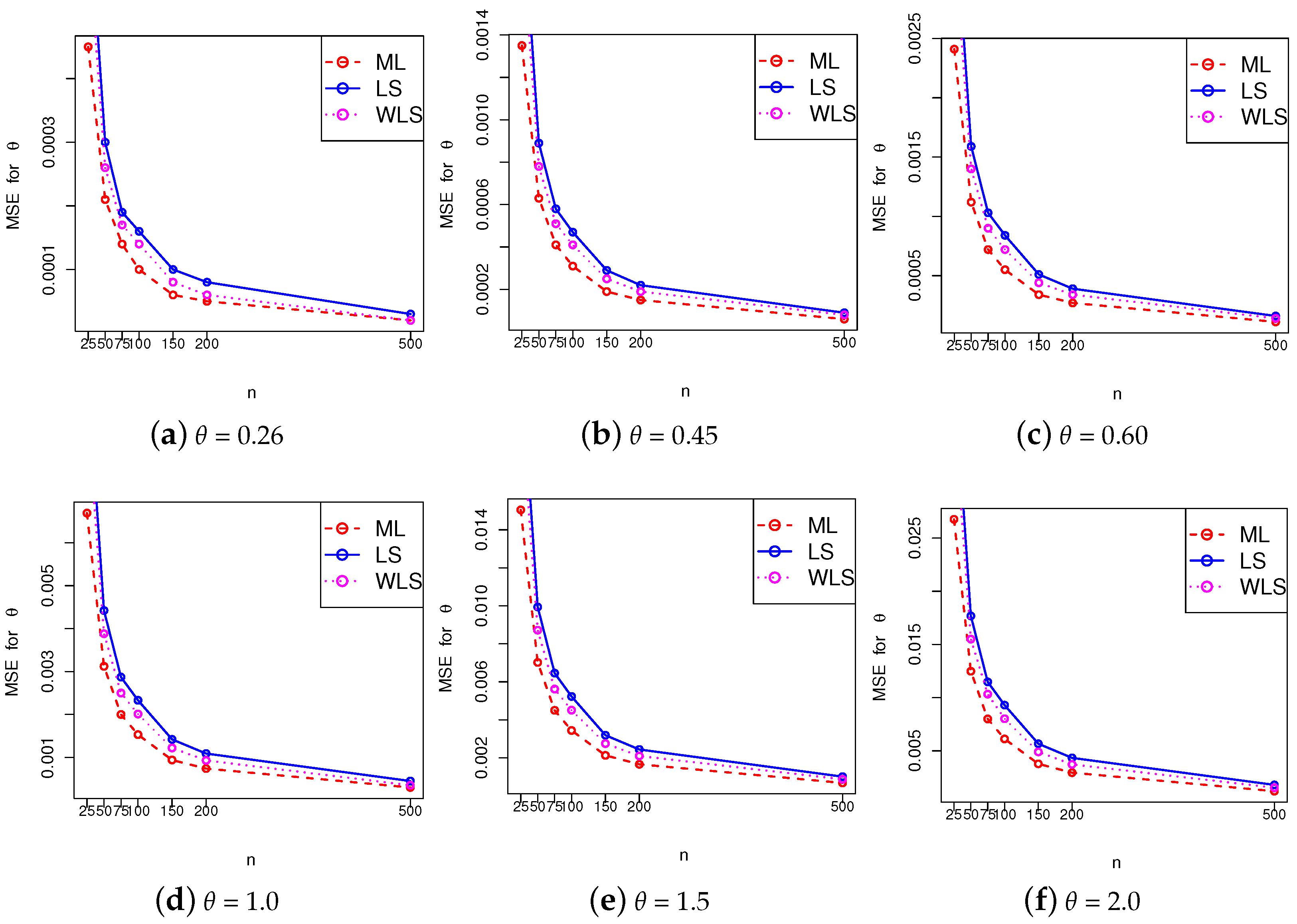
5. Simulation Study
5.1. Simulation for ML, LS, and WLS Estimates
- Mean of the estimates: Mean;
- Average bias of the estimates: Bias;
- Mean square error (MSE) of the estimates: MSE
5.2. Simulation for Bayesian Estimates
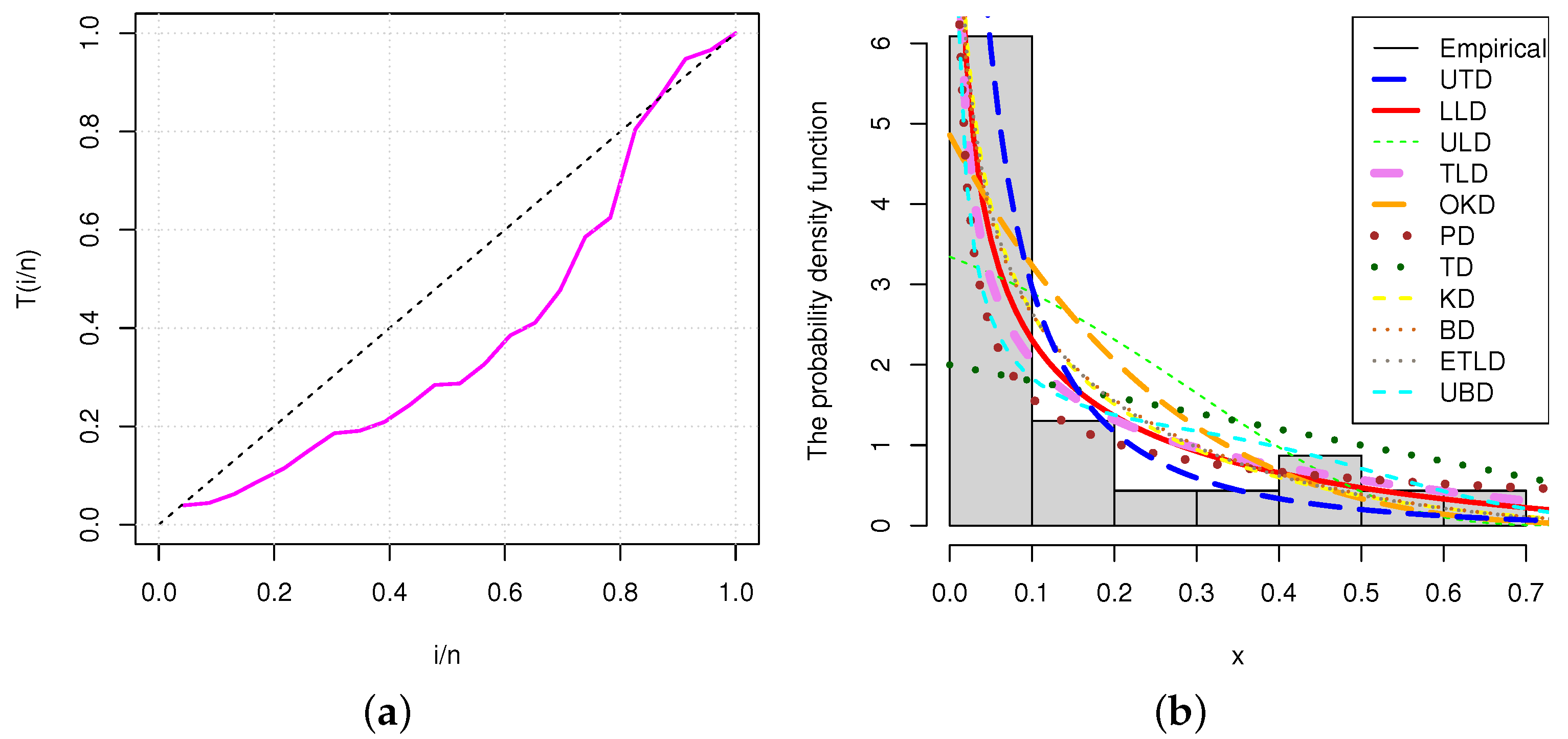
6. Application
6.1. Methodology
- Akaike information criterion defined by ;
- Akaike information criterion corrected given as ;
- Consistent Akaike information criterion specified by ;
- Bayesian information criterion defined by
6.2. Flood Level Data
6.3. Times between Failures of Secondary Reactor Pumps Data
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lemonte, A.J.; Bazán, J.L. New class of Johnson distributions and its associated regression model for rates and proportions. Biom. J. 2016, 58, 727–746. [Google Scholar] [CrossRef]
- Smithson, M.; Shou, Y. CDF-quantile distributions for modelling random variables on the unit interval. Br. J. Math. Stat. Psychol. 2017, 70, 412–438. [Google Scholar] [CrossRef] [PubMed]
- Topp, C.W.; Leone, F.C. A family of J-shaped frequency functions. J. Am. Stat. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Jorgensen, B. The Theory of Dispersion Models. CRC Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Gómez-Déniz, E.; Sordo, M.A.; Calderin-Ojeda, E. The Log–Lindley distribution as an alternative to the beta regression model with applications in insurance. Insur. Math. Econ. 2014, 54, 49–57. [Google Scholar] [CrossRef]
- Pourdarvish, A.; Mirmostafaee, S.M.T.K.; Naderi, K. The exponentiated Topp–Leone distribution: Properties and application. J. Appl. Environ. Biol. Sci. 2015, 5, 251–256. [Google Scholar]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The unit-inverse Gaussian distribution: A new alternative to two-parameter distributions on the unit interval. Commun. Stat. Theory Methods 2019, 48, 3423–3438. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the one parameter unit-Lindley distribution and its associated regression model for proportion data. J. Appl. Stat. 2019, 46, 700–714. [Google Scholar] [CrossRef] [Green Version]
- Mazucheli, J.; Menezes, A.F.B.; Fernandes, L.B.; de Oliveira, R.P.; Ghitany, M.E. The unit-Weibull distribution as an alternative to the Kumaraswamy distribution for the modeling of quantiles conditional on covariates. J. Appl. Stat. 2020, 47, 954–974. [Google Scholar] [CrossRef]
- Modi, K.; Gill, V. Unit Burr-III distribution with application. J. Stat. Manag. Syst. 2020, 23, 579–592. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Nik, A.S.; Asgharzadeh, A.; Salinas, H.S. A flexible probability model for proportion data: Unit-half-normal distribution. Commun. Stat. Case Stud. Data Anal. Appl. 2021, 7, 1–18. [Google Scholar] [CrossRef]
- Teissier, G. Recherches sur le vieillissement et sur les lois de la mortalité. Ann. Physiol. Physicochim. Biol. 1934, 10, 237–284. [Google Scholar]
- Laurent, A.G. Failure and mortality from wear and ageing. The Teissier model. In A Modern Course on Statistical Distributions in Scientific Work; Patil, G.P., Kotz, S., Ord, J.K., Eds.; ASIC; Springer: Berlin/Heidelberg, Germany, 1975; Volume 17, pp. 301–320. [Google Scholar]
- Muth, E.J. Reliability models with positive memory derived from the mean residual life function. Theory Appl. Reliab. 1977, 2, 401–436. [Google Scholar]
- Rinne, H. Estimating the lifetime distribution of private motor-cars using prices of used cars: The Teissier model. In Statistiks Zwischen Theorie und Praxis; Vandenhoeck & Ruprecht: Göttingen, Germany, 1985; pp. 172–184. [Google Scholar]
- Leemis, L.M.; McQueston, J.T. Univariate distribution relationships. Am. Stat. 2008, 62, 45–53. [Google Scholar] [CrossRef]
- Jodrá, P.; Jiménez-Gamero, M.D.; Alba-Fernandez, M.V. On the Muth distribution. Math. Model. Anal. 2015, 20, 291–310. [Google Scholar] [CrossRef]
- Jodrá, P.; Gómez, H.W.; Jiménez-Gamero, M.D.; Alba-Fernández, M.V. The power Muth distribution. Math. Model. Anal. 2017, 22, 186–201. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Elbatal, I.; Chesneau, C.; Jamal, F. The transmuted Muth generated class of distributions with applications. Symmetry 2020, 12, 1677. [Google Scholar] [CrossRef]
- Biçer, C.; Bakouch, H.S.; Biçer, H.D. Inference on parameters of a geometric process with scaled Muth distribution. Fluct. Noise Lett. 2021, 20, 2150006. [Google Scholar] [CrossRef]
- Irshad, M.R.; Maya, R.; Arun, S.P. Muth distribution and estimation of a parameter using order statistics. Statistica 2021, 81, 93–119. [Google Scholar]
- Irshad, M.R.; Maya, R.; Krishna, A. Exponentiated power Muth distribution and associated inference. J. Indian Soc. Probab. Stat. 2021, 22, 265–302. [Google Scholar] [CrossRef]
- Abd EL-Baset, A.A.; Ghazal, M.G.M. Exponentiated additive Weibull distribution. Reliab. Eng. Syst. Saf. 2020, 193, 106663. [Google Scholar]
- Alamgir Khalil, M.I.; Ali, K.; Mashwani, W.K.; Shafiq, M.; Kumam, P.; Kumam, W. A novel flexible additive Weibull distribution with real-life applications. Commun. Stat. Theory Methods 2021, 50, 1557–1572. [Google Scholar] [CrossRef]
- Irshad, M.R.; Shibu, D.S.; Maya, R.; D’cruz, V. Binominal mixture Lindley distribution: Properties and Applications. J. Indian Soc. Probab. Stat. 2020, 21, 437–469. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç. A new heavy-tailed distribution defined on the bounded interval: The logit slash distribution and its application. J. Appl. Stat. 2020, 47, 2097–2119. [Google Scholar] [CrossRef]
- Haq, M.A.U.; Hashmi, S.; Aidi, K.; Ramos, P.L.; Louzada, F. Unit modified Burr-III distribution: Estimation, characterizations and validation test. Ann. Data Sci. 2020, 1–26. [Google Scholar] [CrossRef]
- Bebbington, M.; Lai, C.D.; Murthy, D.N.P.; Zitikis, R. Modelling N-and W-shaped hazard rate functions without mixing distributions. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2009, 223, 59–69. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: http://www.R-project.org/ (accessed on 28 December 2021).
- Swain, J.J.; Venkatraman, S.; Wilson, J.R. Least-squares estimation of distribution functions in Johnson’s translation system. J. Stat. Comput. Simul. 1988, 29, 271–297. [Google Scholar] [CrossRef]
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Dumonceaux, R.; Antle, C.E. Discrimination between the log-normal and the Weibull distributions. Technometrics 1973, 15, 923–926. [Google Scholar] [CrossRef]
- Suprawhardana, M.S.; Prayoto, S. Total time on test plot analysis for mechanical components of the RSG-GAS reactor. At. Indones. 1999, 25, 81–90. [Google Scholar]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. On the arcsecant hyperbolic normal distribution. Properties, quantile regression modeling and applications. Symmetry 2021, 13, 117. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C. On the unit Burr-XII distribution with the quantile regression modeling and applications. Comput. Appl. Math. 2021, 40, 29. [Google Scholar] [CrossRef]



| n | Bias() | MSE() | Bias() | MSE() | Bias() | MSE() | |||
| 25 | 0.26352 | 0.00352 | 0.00045 | 0.45610 | 0.00610 | 0.00135 | 0.60813 | 0.00813 | 0.00241 |
| 50 | 0.26164 | 0.00164 | 0.00021 | 0.45284 | 0.00284 | 0.00063 | 0.60379 | 0.00379 | 0.00112 |
| 75 | 0.26116 | 0.00116 | 0.00014 | 0.45200 | 0.00200 | 0.00041 | 0.60267 | 0.00267 | 0.00072 |
| 100 | 0.26074 | 0.00074 | 0.00010 | 0.45129 | 0.00129 | 0.00031 | 0.60172 | 0.00172 | 0.00055 |
| 150 | 0.26042 | 0.00042 | 0.00006 | 0.45074 | 0.00074 | 0.00019 | 0.60098 | 0.00098 | 0.00034 |
| 200 | 0.26028 | 0.00028 | 0.00005 | 0.45049 | 0.00049 | 0.00015 | 0.60065 | 0.00065 | 0.00027 |
| 500 | 0.26011 | 0.00011 | 0.00002 | 0.45019 | 0.00019 | 0.00006 | 0.60025 | 0.00025 | 0.00011 |
| n | Bias() | MSE() | Bias() | MSE() | Bias() | MSE() | |||
| 25 | 1.01355 | 0.01355 | 0.00669 | 1.52033 | 0.02033 | 0.01505 | 2.02711 | 0.02711 | 0.02676 |
| 50 | 1.00632 | 0.00632 | 0.00312 | 1.50948 | 0.00948 | 0.00702 | 2.01264 | 0.01264 | 0.01248 |
| 75 | 1.00446 | 0.00446 | 0.00200 | 1.50668 | 0.00668 | 0.00450 | 2.00891 | 0.00891 | 0.00800 |
| 100 | 1.00286 | 0.00286 | 0.00153 | 1.50429 | 0.00429 | 0.00344 | 2.00572 | 0.00572 | 0.00612 |
| 150 | 1.00163 | 0.00163 | 0.00094 | 1.50245 | 0.00245 | 0.00213 | 2.00327 | 0.00327 | 0.00378 |
| 200 | 1.00109 | 0.00109 | 0.00074 | 1.50164 | 0.00164 | 0.00166 | 2.00218 | 0.00218 | 0.00295 |
| 500 | 1.00041 | 0.00041 | 0.00030 | 1.50062 | 0.00062 | 0.00068 | 2.00082 | 0.00082 | 0.00121 |
| n | Bias() | MSE() | Bias() | MSE() | Bias() | MSE() | |||
| 25 | 0.26122 | 0.00122 | 0.00069 | 0.45210 | 0.00210 | 0.00207 | 0.60280 | 0.00280 | 0.00368 |
| 50 | 0.25998 | −0.00002 | 0.00030 | 0.44997 | −0.00003 | 0.00089 | 0.59996 | −0.00004 | 0.00159 |
| 75 | 0.25997 | −0.00003 | 0.00019 | 0.44994 | −0.00006 | 0.00058 | 0.59992 | −0.00008 | 0.00103 |
| 100 | 0.25990 | −0.00010 | 0.00016 | 0.44983 | −0.00017 | 0.00047 | 0.59977 | −0.00023 | 0.00084 |
| 150 | 0.25954 | −0.00046 | 0.00010 | 0.44920 | −0.00080 | 0.00029 | 0.59893 | −0.00107 | 0.00051 |
| 200 | 0.26057 | 0.00057 | 0.00008 | 0.44914 | −0.00086 | 0.00022 | 0.59886 | −0.00114 | 0.00039 |
| 500 | 0.25980 | −0.00020 | 0.00003 | 0.44964 | −0.00036 | 0.00009 | 0.59953 | −0.00047 | 0.00016 |
| n | Bias() | MSE() | Bias() | MSE() | Bias() | MSE() | |||
| 25 | 1.00467 | 0.00467 | 0.01021 | 1.50701 | 0.00701 | 0.02297 | 2.00935 | 0.00935 | 0.04083 |
| 50 | 0.99993 | −0.00007 | 0.00442 | 1.49990 | −0.00010 | 0.00994 | 1.99986 | −0.00014 | 0.01768 |
| 75 | 0.99986 | −0.00014 | 0.00287 | 1.49979 | −0.00021 | 0.00646 | 1.99972 | −0.00028 | 0.01148 |
| 100 | 0.99961 | −0.00039 | 0.00233 | 1.49942 | −0.00058 | 0.00523 | 1.99923 | −0.00077 | 0.00930 |
| 150 | 0.99821 | −0.00179 | 0.00142 | 1.49732 | −0.00268 | 0.00319 | 1.99643 | −0.00357 | 0.00567 |
| 200 | 0.99809 | −0.00191 | 0.00109 | 1.49714 | −0.00286 | 0.00244 | 1.99619 | −0.00381 | 0.00434 |
| 500 | 0.99921 | −0.00079 | 0.00045 | 1.49881 | −0.00119 | 0.00101 | 1.99842 | −0.00158 | 0.00180 |
| n | Bias() | MSE() | Bias() | MSE() | Bias() | MSE() | |||
| 25 | 0.26141 | 0.00141 | 0.00062 | 0.45243 | 0.00243 | 0.00186 | 0.60324 | 0.00324 | 0.00330 |
| 50 | 0.26024 | 0.00024 | 0.00026 | 0.45041 | 0.00041 | 0.00078 | 0.60055 | 0.00055 | 0.00140 |
| 75 | 0.26018 | 0.00018 | 0.00017 | 0.45030 | 0.00030 | 0.00051 | 0.60041 | 0.00041 | 0.00090 |
| 100 | 0.26007 | 0.00007 | 0.00014 | 0.45012 | 0.00012 | 0.00041 | 0.60016 | 0.00016 | 0.00072 |
| 150 | 0.25971 | −0.00029 | 0.00008 | 0.44950 | −0.00050 | 0.00025 | 0.59934 | −0.00066 | 0.00044 |
| 200 | 0.25968 | −0.00032 | 0.00006 | 0.44944 | −0.00056 | 0.00019 | 0.59925 | −0.00075 | 0.00034 |
| 500 | 0.25986 | 0.00014 | 0.00001 | 0.44976 | −0.00024 | 0.00008 | 0.59968 | −0.00032 | 0.00014 |
| n | Bias() | MSE() | Bias() | MSE() | Bias() | MSE() | |||
| 25 | 1.00540 | 0.00540 | 0.00917 | 1.50809 | 0.00809 | 0.02063 | 2.01079 | 0.01079 | 0.03668 |
| 50 | 1.00091 | 0.00091 | 0.00388 | 1.50137 | 0.00137 | 0.00872 | 2.00182 | 0.00182 | 0.01550 |
| 75 | 1.00067 | 0.00067 | 0.00250 | 1.50101 | 0.00101 | 0.00562 | 2.00135 | 0.00135 | 0.00999 |
| 100 | 1.00026 | 0.00026 | 0.00201 | 1.50039 | 0.00039 | 0.00451 | 2.00052 | 0.00052 | 0.00802 |
| 150 | 0.99889 | −0.00111 | 0.00122 | 1.49834 | −0.00166 | 0.00275 | 1.99778 | −0.00222 | 0.00490 |
| 200 | 0.99876 | −0.00124 | 0.00093 | 1.49813 | −0.00187 | 0.00210 | 1.99751 | −0.00249 | 0.00373 |
| 500 | 0.99946 | −0.00054 | 0.00038 | 1.49919 | −0.00081 | 0.00087 | 1.99892 | −0.00108 | 0.00154 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 0.26217 | 0.01971 | 0.00300 | 0.22331 | 0.28030 | 0.26770 |
| 50 | 0.26834 | 0.01649 | 0.00213 | 0.24361 | 0.29064 | 0.26831 |
| 75 | 0.27247 | 0.01599 | 0.00206 | 0.25154 | 0.29064 | 0.27118 |
| 100 | 0.26770 | 0.01057 | 0.00175 | 0.25917 | 0.28695 | 0.26957 |
| 150 | 0.27098 | 0.00938 | 0.00154 | 0.25339 | 0.28218 | 0.26928 |
| 200 | 0.26300 | 0.00638 | 0.00123 | 0.25714 | 0.26781 | 0.26407 |
| 500 | 0.27236 | 0.00264 | 0.00109 | 0.26706 | 0.27597 | 0.27425 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 0.45493 | 0.04530 | 0.00889 | 0.36841 | 0.52298 | 0.45676 |
| 50 | 0.47560 | 0.02125 | 0.00716 | 0.43660 | 0.51318 | 0.46884 |
| 75 | 0.46305 | 0.02069 | 0.00598 | 0.41964 | 0.50306 | 0.46555 |
| 100 | 0.47071 | 0.01648 | 0.00517 | 0.42378 | 0.49429 | 0.47592 |
| 150 | 0.46769 | 0.01489 | 0.00393 | 0.42507 | 0.49429 | 0.46646 |
| 200 | 0.45651 | 0.00991 | 0.00262 | 0.44271 | 0.47886 | 0.45687 |
| 500 | 0.46907 | 0.00830 | 0.00231 | 0.44839 | 0.48607 | 0.46841 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 0.62836 | 0.05583 | 0.01269 | 0.51515 | 0.69347 | 0.65291 |
| 50 | 0.63488 | 0.03203 | 0.00815 | 0.55716 | 0.68275 | 0.63661 |
| 75 | 0.63130 | 0.02958 | 0.00740 | 0.54930 | 0.68275 | 0.63682 |
| 100 | 0.64362 | 0.02506 | 0.00657 | 0.59327 | 0.68275 | 0.65125 |
| 150 | 0.61670 | 0.02001 | 0.00473 | 0.59286 | 0.65175 | 0.60516 |
| 200 | 0.58433 | 0.01135 | 0.00361 | 0.56540 | 0.60849 | 0.58477 |
| 500 | 0.61527 | 0.00864 | 0.00333 | 0.60791 | 0.63575 | 0.61179 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 1.02150 | 0.08400 | 0.01689 | 0.84895 | 1.13786 | 1.02060 |
| 50 | 1.02859 | 0.08394 | 0.01243 | 0.94449 | 1.15295 | 1.02883 |
| 75 | 1.04385 | 0.04133 | 0.01163 | 0.92371 | 1.09369 | 1.04292 |
| 100 | 1.06278 | 0.04029 | 0.01001 | 1.02172 | 1.22162 | 1.05589 |
| 150 | 1.03099 | 0.03427 | 0.00846 | 0.98819 | 1.07907 | 1.03083 |
| 200 | 1.02172 | 0.02549 | 0.00573 | 0.99575 | 1.05466 | 1.02620 |
| 500 | 0.97150 | 0.01249 | 0.00484 | 0.94968 | 0.98967 | 0.97079 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 1.52918 | 0.14300 | 0.04025 | 1.31918 | 1.78305 | 1.50069 |
| 50 | 1.51870 | 0.11159 | 0.03641 | 1.17142 | 1.67897 | 1.55316 |
| 75 | 1.40491 | 0.09922 | 0.03165 | 1.20423 | 1.52690 | 1.42708 |
| 100 | 1.56450 | 0.07915 | 0.02093 | 1.25097 | 1.64389 | 1.57598 |
| 150 | 1.54486 | 0.05005 | 0.01196 | 1.47530 | 1.61097 | 1.55532 |
| 200 | 1.52040 | 0.02288 | 0.00591 | 1.50104 | 1.56919 | 1.52027 |
| 500 | 1.55005 | 0.02201 | 0.00390 | 1.52843 | 1.58571 | 1.55540 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 2.06736 | 0.15240 | 0.03757 | 1.74925 | 2.30008 | 2.13126 |
| 50 | 2.07023 | 0.14915 | 0.02789 | 1.75671 | 2.29423 | 2.09929 |
| 75 | 2.07862 | 0.11586 | 0.02615 | 1.92777 | 2.22704 | 2.06513 |
| 100 | 2.09001 | 0.07422 | 0.02596 | 1.99647 | 2.20813 | 2.07646 |
| 150 | 2.03891 | 0.07322 | 0.02149 | 1.75963 | 2.14525 | 2.06189 |
| 200 | 2.06265 | 0.05250 | 0.01654 | 1.99405 | 2.26134 | 2.05505 |
| 500 | 2.09538 | 0.04211 | 0.01636 | 2.06500 | 2.21627 | 2.06596 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 0.25141 | 0.05134 | 0.01312 | 0.04355 | 0.30548 | 0.26122 |
| 50 | 0.25790 | 0.04318 | 0.01151 | 0.15933 | 0.29794 | 0.26140 |
| 75 | 0.26324 | 0.03247 | 0.00592 | 0.24319 | 0.28917 | 0.26559 |
| 100 | 0.27617 | 0.01091 | 0.00322 | 0.25228 | 0.29550 | 0.27556 |
| 150 | 0.24699 | 0.01081 | 0.00208 | 0.23512 | 0.26737 | 0.24183 |
| 200 | 0.26654 | 0.01409 | 0.00285 | 0.25307 | 0.30800 | 0.26631 |
| 500 | 0.26818 | 0.01401 | 0.00159 | 0.26320 | 0.28228 | 0.26949 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 0.44924 | 0.04779 | 0.01029 | 0.37730 | 0.52804 | 0.44985 |
| 50 | 0.46277 | 0.03141 | 0.00797 | 0.41231 | 0.51942 | 0.46657 |
| 75 | 0.46092 | 0.02074 | 0.00545 | 0.41995 | 0.49405 | 0.45864 |
| 100 | 0.47382 | 0.01515 | 0.00498 | 0.44194 | 0.50921 | 0.47630 |
| 150 | 0.43418 | 0.01103 | 0.00326 | 0.41547 | 0.44902 | 0.43349 |
| 200 | 0.46069 | 0.01011 | 0.00263 | 0.44098 | 0.48238 | 0.46259 |
| 500 | 0.46553 | 0.00599 | 0.00182 | 0.45494 | 0.47738 | 0.46694 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 0.60442 | 0.05548 | 0.01444 | 0.49541 | 0.71972 | 0.60913 |
| 50 | 0.54888 | 0.03104 | 0.01281 | 0.49527 | 0.62074 | 0.55447 |
| 75 | 0.61557 | 0.02836 | 0.00759 | 0.57167 | 0.65640 | 0.61174 |
| 100 | 0.62561 | 0.01481 | 0.00538 | 0.60462 | 0.65368 | 0.62487 |
| 150 | 0.58561 | 0.01322 | 0.00402 | 0.55367 | 0.60185 | 0.58913 |
| 200 | 0.59753 | 0.01138 | 0.00449 | 0.58214 | 0.61691 | 0.59483 |
| 500 | 0.61042 | 0.01113 | 0.00361 | 0.59462 | 0.63647 | 0.61434 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 1.02150 | 0.08400 | 0.01689 | 0.84895 | 1.13786 | 1.02060 |
| 50 | 1.03794 | 0.06691 | 0.01658 | 0.89983 | 1.14142 | 1.04985 |
| 75 | 1.04394 | 0.05572 | 0.01330 | 0.90487 | 1.14142 | 1.04432 |
| 100 | 1.04440 | 0.04849 | 0.01302 | 0.92824 | 1.14142 | 1.03943 |
| 150 | 1.05009 | 0.04125 | 0.01278 | 0.98320 | 1.13767 | 1.05431 |
| 200 | 1.00869 | 0.07225 | 0.01869 | 0.90478 | 1.07876 | 1.01865 |
| 500 | 1.01614 | 0.06391 | 0.00458 | 1.00317 | 1.04602 | 1.01625 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 1.52918 | 0.14300 | 0.04025 | 1.31918 | 1.78305 | 1.50069 |
| 50 | 1.54627 | 0.07872 | 0.02170 | 1.38232 | 1.64742 | 1.55280 |
| 75 | 1.55881 | 0.06692 | 0.01959 | 1.44383 | 1.66958 | 1.55559 |
| 100 | 1.55876 | 0.04834 | 0.01311 | 1.45950 | 1.62751 | 1.55994 |
| 150 | 1.55805 | 0.03772 | 0.01221 | 1.48935 | 1.63206 | 1.55871 |
| 200 | 1.52328 | 0.10483 | 0.00849 | 1.45942 | 1.66891 | 1.52085 |
| 500 | 1.53107 | 0.09938 | 0.00683 | 1.51895 | 1.62075 | 1.51895 |
| n | Mean | SD | MCE | LB | UB | Median |
| 25 | 1.93826 | 0.19074 | 0.03847 | 1.58829 | 2.30034 | 1.93391 |
| 50 | 2.06358 | 0.14649 | 0.03532 | 1.62112 | 2.28823 | 2.10545 |
| 75 | 2.02426 | 0.13764 | 0.02461 | 1.86401 | 2.29424 | 2.01176 |
| 100 | 2.11171 | 0.10124 | 0.02076 | 1.85800 | 2.22242 | 2.11979 |
| 150 | 2.05937 | 0.10096 | 0.01815 | 1.97012 | 2.21942 | 2.07596 |
| 200 | 2.03326 | 0.10071 | 0.01678 | 1.94723 | 2.23003 | 2.03772 |
| 500 | 2.05469 | 0.06821 | 0.01188 | 1.98674 | 2.26369 | 2.06343 |
| 0.654 | 0.613 | 0.315 | 0.449 | 0.297 | 0.402 | 0.379 | 0.423 |
| 0.379 | 0.324 | 0.269 | 0.740 | 0.418 | 0.412 | 0.494 | 0.416 |
| 0.338 | 0.392 | 0.484 | 0.265 |
| Distribution | MLE of the Parameters (Standard Error) | KS | p-Value |
|---|---|---|---|
| 0.2527 | 0.1555 | ||
| , | 0.3157 | 0.0372 | |
| 0.3182 | 0.0349 | ||
| 0.3352 | 0.0223 | ||
| 0.4128 | 0.0022 | ||
| 0.3941 | 0.0040 | ||
| 0.4598 | 0.0004 |
| Distribution | Log-Likelihood | AIC | AICc | CAIC | BIC |
|---|---|---|---|---|---|
| 13.5818 | −25.1635 | −24.9414 | −23.1679 | −24.1678 | |
| 6.6716 | −9.3431 | −8.6373 | −5.3517 | −7.3517 | |
| 7.1410 | −12.2821 | −12.0598 | −10.2863 | −11.2864 | |
| 7.3682 | −12.7365 | −12.5142 | −10.7407 | −11.7407 | |
| 2.5110 | −3.0220 | −2.7998 | −1.0263 | −2.0263 | |
| 0.1124 | 1.7751 | 1.9974 | 3.7709 | 2.7708 | |
| 2.2856 | −2.5713 | −2.3489 | −0.5755 | −1.5756 |
| Median of Estimates | Lower Limit | Upper Limit |
|---|---|---|
| 1.0815 | 1.4176 |
| 0.2160 | 0.0150 | 0.4082 | 0.0746 | 0.0358 | 0.0199 | 0.0402 | 0.0101 |
| 0.0605 | 0.0954 | 0.1359 | 0.0273 | 0.0491 | 0.3465 | 0.0070 | 0.6560 |
| 0.1060 | 0.0062 | 0.4992 | 0.0614 | 0.5320 | 0.0347 | 0.1921 |
| Distribution | MLE of the Parameters (Standard Error) | KS | p-Value |
|---|---|---|---|
| 0.1366 | 0.7341 | ||
| , | 0.1584 | 0.5573 | |
| 0.3274 | 0.0107 | ||
| 0.1962 | 0.2982 | ||
| 0.2568 | 0.0796 | ||
| 0.2247 | 0.1678 | ||
| 0.4514 | 0.00008 | ||
| , | 0.1393 | 0.7123 | |
| , | 0.1542 | 0.5919 | |
| , | 0.1465 | 0.6536 | |
| , | 0.2243 | 0.1688 |
| Distribution | Log-Likelihood | AIC | AICc | CAIC | BIC |
|---|---|---|---|---|---|
| 21.7499 | −41.4998 | −41.3093 | −39.3643 | −40.3643 | |
| 20.0761 | −36.1522 | −35.5522 | −31.8812 | −33.8812 | |
| 14.5035 | −27.0070 | −26.8165 | −24.8715 | −25.8715 | |
| 18.7827 | −35.5653 | −35.3749 | −33.4299 | −34.4298 | |
| 18.0840 | −34.1679 | −33.9775 | −32.0325 | −33.0324 | |
| 15.5307 | −29.0615 | −28.8709 | −26.9259 | −27.9259 | |
| 11.2067 | −20.2229 | −20.2229 | −18.2779 | −19.2778 | |
| 20.3296 | −36.6592 | −36.0592 | −32.3882 | −34.3883 | |
| 20.0285 | −36.0571 | −35.4570 | −31.7860 | −33.7861 | |
| 20.1709 | −36.3418 | −35.7418 | −32.0708 | −34.0708 | |
| 17.5294 | −31.0588 | −30.4588 | −26.7878 | −28.7878 |
| Median of Estimates | Lower Limit | Upper Limit |
|---|---|---|
| 0.3154 | 0.4216 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishna, A.; Maya, R.; Chesneau, C.; Irshad, M.R. The Unit Teissier Distribution and Its Applications. Math. Comput. Appl. 2022, 27, 12. https://doi.org/10.3390/mca27010012
Krishna A, Maya R, Chesneau C, Irshad MR. The Unit Teissier Distribution and Its Applications. Mathematical and Computational Applications. 2022; 27(1):12. https://doi.org/10.3390/mca27010012
Chicago/Turabian StyleKrishna, Anuresha, Radhakumari Maya, Christophe Chesneau, and Muhammed Rasheed Irshad. 2022. "The Unit Teissier Distribution and Its Applications" Mathematical and Computational Applications 27, no. 1: 12. https://doi.org/10.3390/mca27010012







