An Analysis of Trabecular Bone Structure Based on Principal Stress Trajectory
Abstract
:1. Introduction
2. Materials and Methods
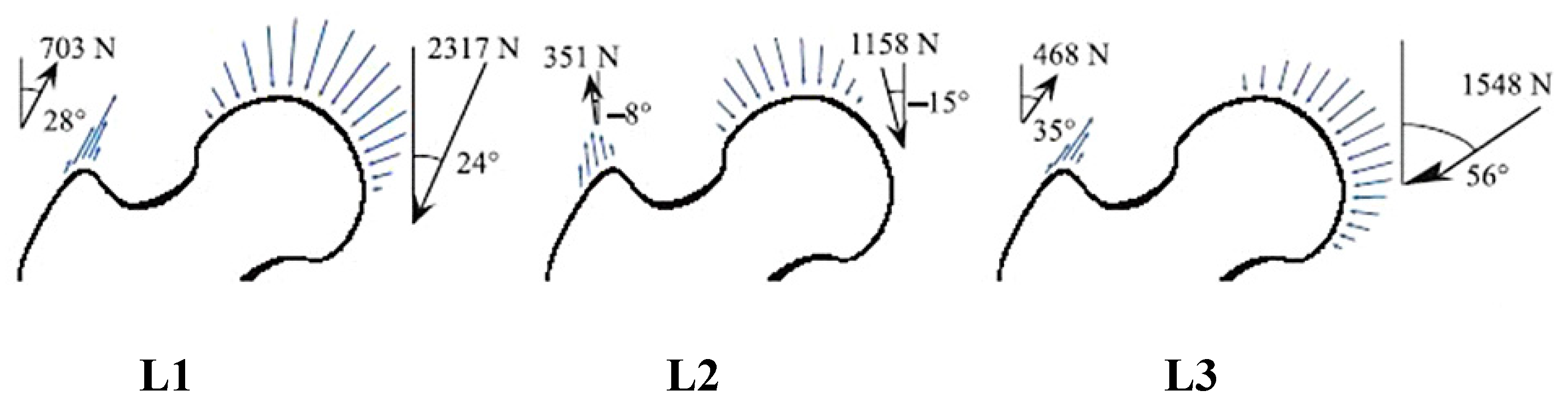
2.1. Modeling and Simulation Conditions
2.2. Visualization Method
2.3. Equivalent Principal Stress Trajectory Distribution
3. Results
3.1. Stress Distribution
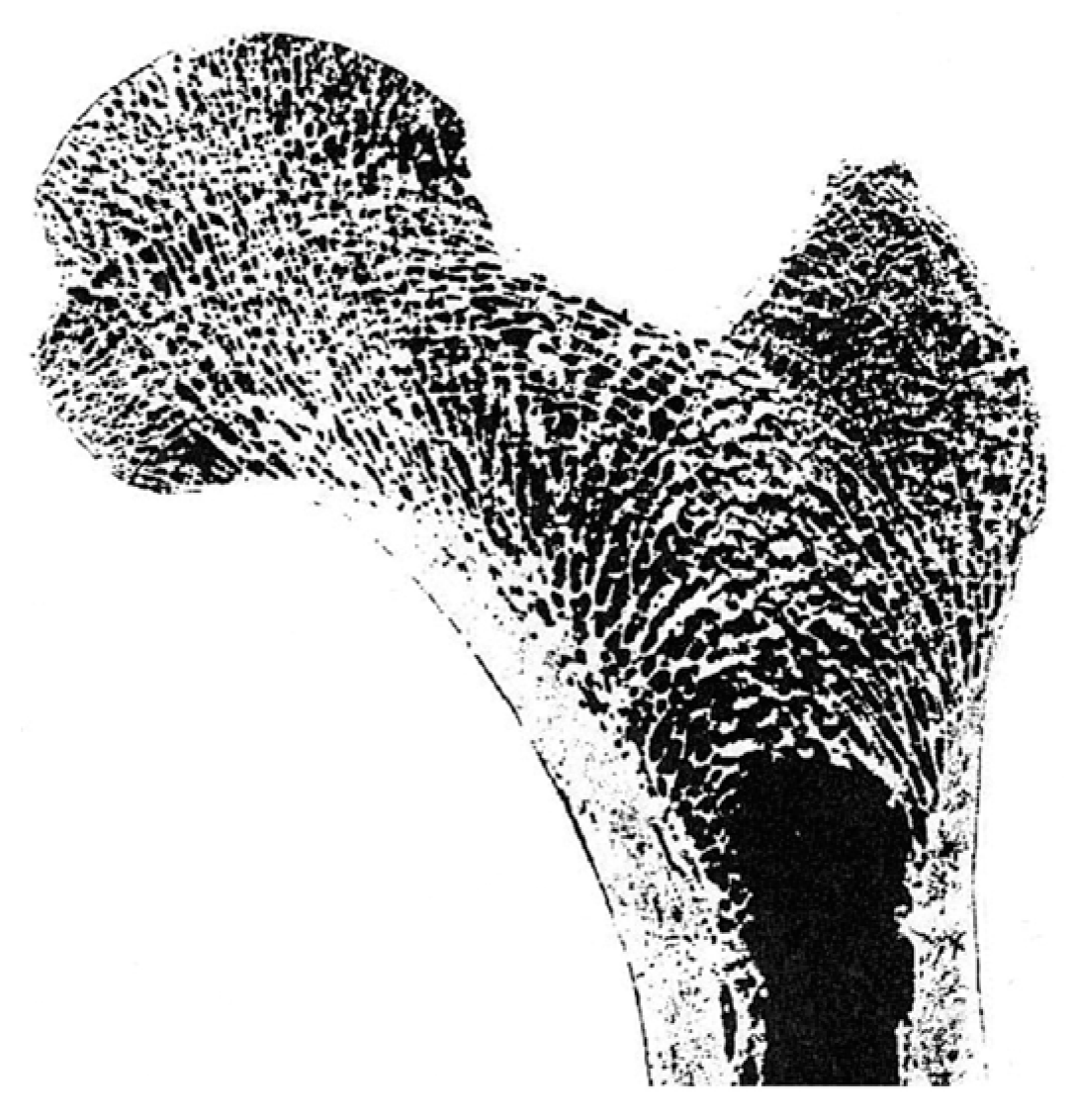
3.2. 2D Principal Stress Trajectory Distribution
3.3. Three-Dimensional Principal Stress Trajectory Distribution
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
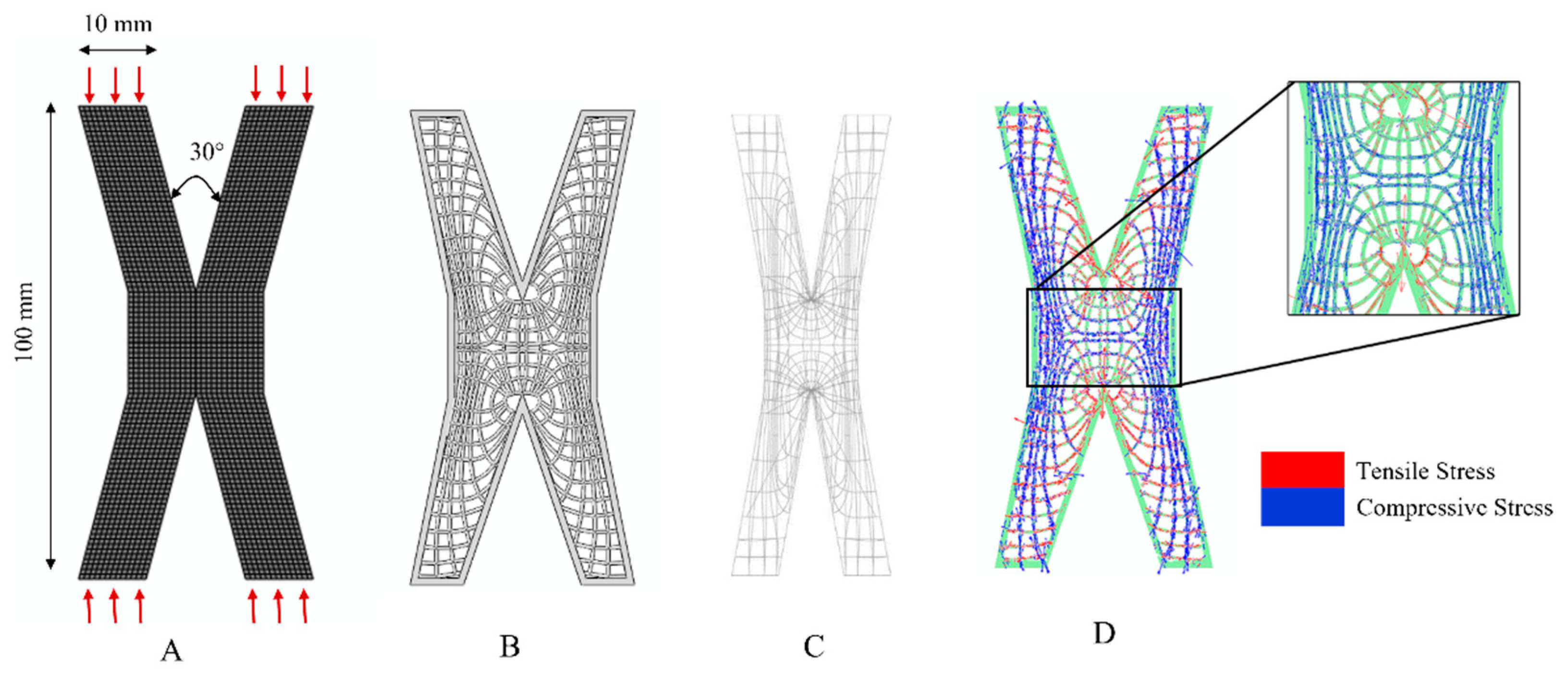
Appendix A.1. Cantilever Beam Structure

Appendix A.2. X-Shaped Structure
References
- Mirzaali, M.J.; Schwiedrzik, J.J.; Thaiwichai, S.; Best, J.P.; Michler, J.; Zysset, P.K.; Wolfram, U. Mechanical properties of cortical bone and their relationships with age, gender, composition and microindentation properties in the elderly. Bone 2016, 93, 196–211. [Google Scholar] [CrossRef] [PubMed]
- Keaveny, T.M.; Wachtel, E.F.; Guo, X.E.; Hayes, W.C. Mechanical behavior of damaged trabecular bone. J. Biomech. 1994, 27, 1309–1318. [Google Scholar] [CrossRef]
- Eswaran, S.K.; Gupta, A.; Adams, M.F.; Keaveny, T.M. Cortical and trabecular load sharing in the human vertebral body. J. Bone Miner. Res. 2006, 21, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Wolff, J. Das gesetz der transformation der knochen. DMW-Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef]
- Wolff, J. The Law of Bone Remodelling; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar] [CrossRef]
- Barak, M.M.; Lieberman, D.E.; Hublin, J.J. A Wolff in sheep’s clothing: Trabecular bone adaptation in response to changes in joint loading orientation. Bone 2011, 49, 1141–1151. [Google Scholar] [CrossRef]
- Young, D.G. The Gram Stain in Tissue: Increasing the Clarity and Contrast Between Gram-Negative Bacteria and Other Cell Components. J. Histotechnol. 2013, 26, 37–39. [Google Scholar] [CrossRef]
- Smith, M.A.; Dyson, S.J.; Murray, R.C. Reliability of high-and low-field magnetic resonance imaging systems for detection of cartilage and bone lesions in the equine cadaver fetlock. Equine Vet. J. 2012, 44, 684–691. [Google Scholar] [CrossRef]
- Dias, D.R.; Leles, C.R.; Batista, A.C.; Lindh, C.; Ribeiro-Rotta, R.F. Agreement between Histomorphometry and Microcomputed Tomography to Assess Bone Microarchitecture of Dental Implant Sites. Clin. Implant. Dent. Relat. Res. 2015, 17, 732–741. [Google Scholar] [CrossRef]
- Dalle, C.L.; Ballanti, P.; Bertoldo, F.; Valenti, M.T.; Giovanazzi, B.; Giannini, S.; Realdi, G.; Cascio, V.L. Trabecular bone microarchitecture in mild primary hyperparathyroidism. J. Endocrinol. Investig. 2008, 31, 525–530. [Google Scholar] [CrossRef]
- Burr, D.B. The use of finite element analysis to estimate the changing strength of bone following treatment for osteoporosis. Osteoporos. Int. 2016, 27, 2651–2654. [Google Scholar] [CrossRef]
- Engelke, K.; Rietbergen, B.; Zysset, P. FEA to Measure Bone Strength: A Review. Clin. Rev. Bone Miner. Metab. 2016, 14, 26–37. [Google Scholar] [CrossRef]
- Boyle, C.; Kim, I.Y. Three-dimensional micro-level computational study of Wolff’s law via trabecular bone remodeling in the human proximal femur using design space topology optimization. J. Biomech. 2011, 44, 935–942. [Google Scholar] [CrossRef] [PubMed]
- Adachi, T.; Suzuki, Y.; Tsubota, K.; Tsubota, K.I.; Masaki, H. Computer simulation of trabecular remodeling in human proximal femur using large-scale voxel FE models. J. Biomech. 2008, 42, S124. [Google Scholar] [CrossRef]
- Hammond, M.A.; Wallace, J.M.; Allen, M.R.; Siegmund, T. Incorporating tissue anisotropy and heterogeneity in finite element models of trabecular bone altered predicted local stress distributions. Biomech. Model. Mechanobiol. 2018, 17, 605–614. [Google Scholar] [CrossRef] [PubMed]
- Hollister, S.J.; Brennan, J.M.; Kikuchi, N. A homogenization sampling procedure for calculating trabecular bone effective stiffness and tissue level stress. J. Biomech. 1994, 27, 433–444. [Google Scholar] [CrossRef]
- Rietbergen, B.V.; Weinans, H.; Huiskes, R.; Odgaard, A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite-element models. J. Biomech. 1995, 28, 69–81. [Google Scholar] [CrossRef]
- Kim, J.J.; Nam, J.; Jang, I.G. Computational study of estimating 3D trabecular bone microstructure for the volume of interest from CT scan data. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2950. [Google Scholar] [CrossRef]
- Christen, P.; Ito, K.; Ellouz, R.; Boutroy, S.; Sornay-Rendu, E.; Chapurlat, R.D.; Van Rietbergen, B. Bone remodelling in humans is load-driven but not lazy. Nat. Commun. 2014, 5, 4855. [Google Scholar] [CrossRef]
- Huo, M.; He, S.; Zhang, Y.; Feng, Y.; Lu, J. Simulation on bone remodeling with stochastic nature of adult and elderly using topology optimization algorithm. J. Biomech. 2022, 136, 111078. [Google Scholar] [CrossRef]
- Goda, I.; Ganghoffer, J.F.; Czarnecki, S.; Czubacki, R.; Wawruch, P. Topology optimization of bone using cubic material design and evolutionary methods based on internal remodeling. Mech. Res. Commun. 2019, 95, 52–60. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.J. Topology Optimization-Based Localized Bone Microstructure Reconstruction for Image Resolution Enhancement: Accuracy and Efficiency. Bioengineering 2022, 9, 644. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Chun, B.J.; Kim, J.J. Quantitative Load Dependency Analysis of Local Trabecular Bone Microstructure to Understand the Spatial Characteristics in the Synthetic Proximal Femur. Biology 2023, 12, 170. [Google Scholar] [CrossRef] [PubMed]
- Jang, I.G.; Kim, I.Y. Computational simulation of trabecular adaptation progress in human proximal femur during growth. J. Biomech. 2009, 42, 573–580. [Google Scholar] [CrossRef] [PubMed]
- Viceconti, M.; Casali, M.; Massari, B.; Cristofolini, L.; Bassini, S.; Toni, A. The ‘standardized femur program’ proposal for a reference geometry to be used for the creation of finite element models of the femur. J. Biomech. 1996, 29, 1241. [Google Scholar] [CrossRef]
- Peng, L.; Bai, J.; Zeng, X.; Zhou, Y. Comparison of isotropic and orthotropic material property assignments on femoral finite element models under two loading conditions. Med. Eng. Phys. 2006, 28, 227–233. [Google Scholar] [CrossRef]
- Sarathi Kopparti, P.; Lewis, G. Influence of three variables on the stresses in a three-dimensional model of a proximal tibia-total knee implant construct. Bio-Med. Mater. Eng. 2007, 17, 19–28. [Google Scholar] [CrossRef]
- Tsubota, K.; Adachi, T.; Tomita, Y. Functional adaptation of cancellous bone in human proximal femur predicted by trabecular surface remodeling simulation toward uniform stress state. J. Biomech. 2002, 35, 1541–1551. [Google Scholar] [CrossRef]
- Liu, Z.; Moorhead, R.; Groner, J. An Advanced Evenly-Spaced Streamline Placement Algorithm. IEEE Trans. Vis. Comput. Graph. 2006, 12, 965–972. [Google Scholar] [CrossRef]
- Stalling, D.; Hege, H. Fast and resolution independent line integral convolution. In Proceedings of the ACM Siggraph, Los Angeles, CA, USA, 6–11 August 1995; pp. 249–256. [Google Scholar]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An approach for time-dependent bone modeling and remodeling—Application: A preliminary remodeling simulation. J. Orthop. Res. 1990, 8, 662–670. [Google Scholar] [CrossRef]
- Kahla, R.B.; Barkaoui, A.; Merzouki, T. Age-related mechanical strength evolution of trabecular bone under fatigue damage for both genders: Fracture risk evaluation. J. Mech. Behav. Biomed. Mater. 2018, 84, 64–73. [Google Scholar] [CrossRef]
- Roux, W. Beitrage zur Morphologie der funktionellen Anpassung. Arch. Anat. Physiol. Anat. Abt. 1885, 9, 120–185. [Google Scholar]
- Cowin, S.C. Bone Mechanics Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2001; Chapter 30; pp. 13–14. [Google Scholar] [CrossRef]





| Model | Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| Cortical bone | 10,500 | 0.3 |
| Cancellous bone | 150 | 0.3 |
| Elements | Nodes | |
|---|---|---|
| Cortical bone | 2313 | 454 |
| Cancellous bone | 1553 | 490 |
| L1 | L2 | L3 | |
|---|---|---|---|
| Cortical bone | 183.45 | 152.60 | 74.75 |
| Cancellous bone | 24.40 | 8.35 | 4.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, H.; Zhou, Y.; Chen, S.; Rong, Q. An Analysis of Trabecular Bone Structure Based on Principal Stress Trajectory. Bioengineering 2023, 10, 1224. https://doi.org/10.3390/bioengineering10101224
Zhang J, Li H, Zhou Y, Chen S, Rong Q. An Analysis of Trabecular Bone Structure Based on Principal Stress Trajectory. Bioengineering. 2023; 10(10):1224. https://doi.org/10.3390/bioengineering10101224
Chicago/Turabian StyleZhang, Jiwu, Haoran Li, Yuqing Zhou, Songhao Chen, and Qiguo Rong. 2023. "An Analysis of Trabecular Bone Structure Based on Principal Stress Trajectory" Bioengineering 10, no. 10: 1224. https://doi.org/10.3390/bioengineering10101224






