Hydrodynamics of Highly Viscous Flow past a Compound Particle: Analytical Solution
Abstract
:1. Introduction
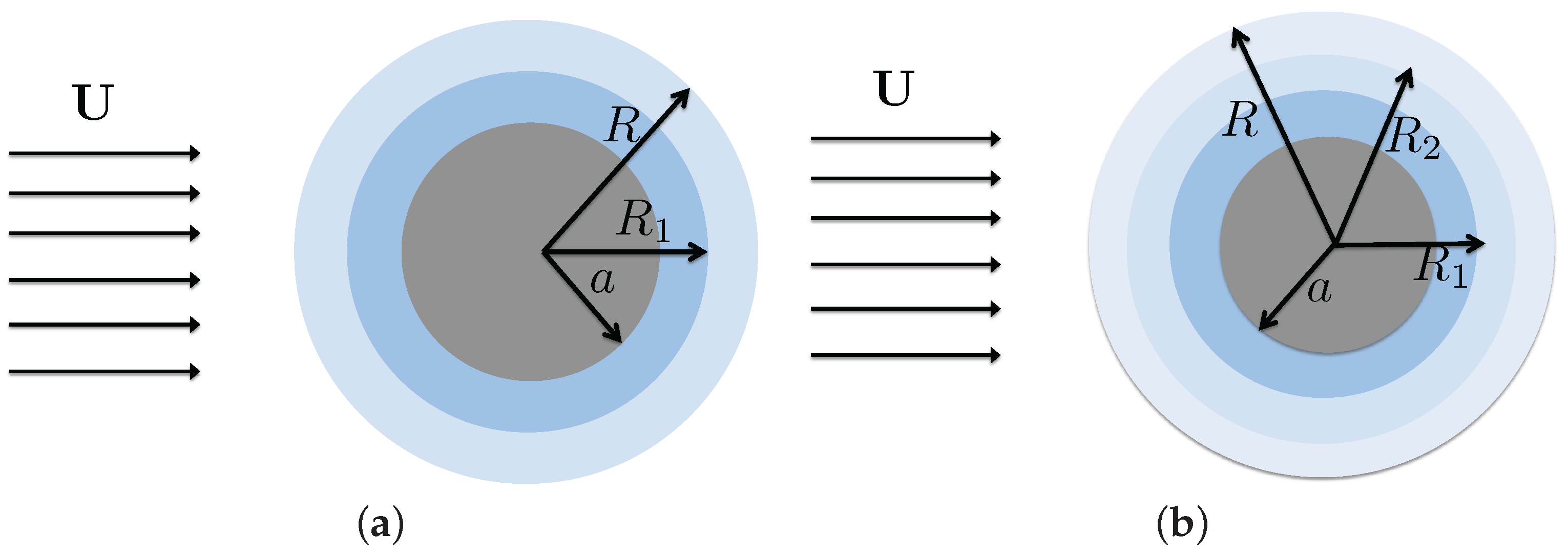
2. Formulation of Problem
3. Analytical Solution for Uniform Flow past Spherical Objects
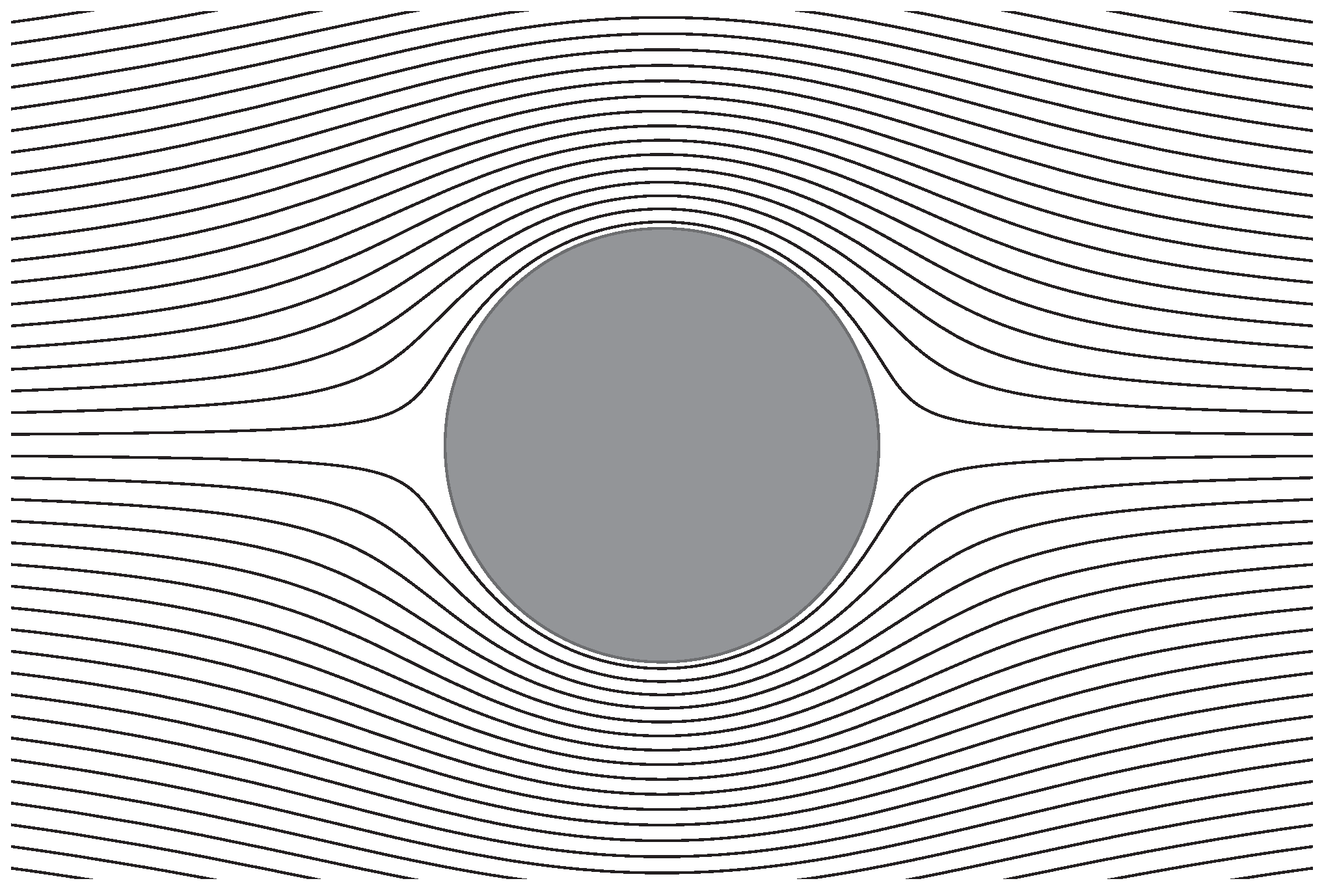
3.1. Uniform Flow past a Rigid Sphere
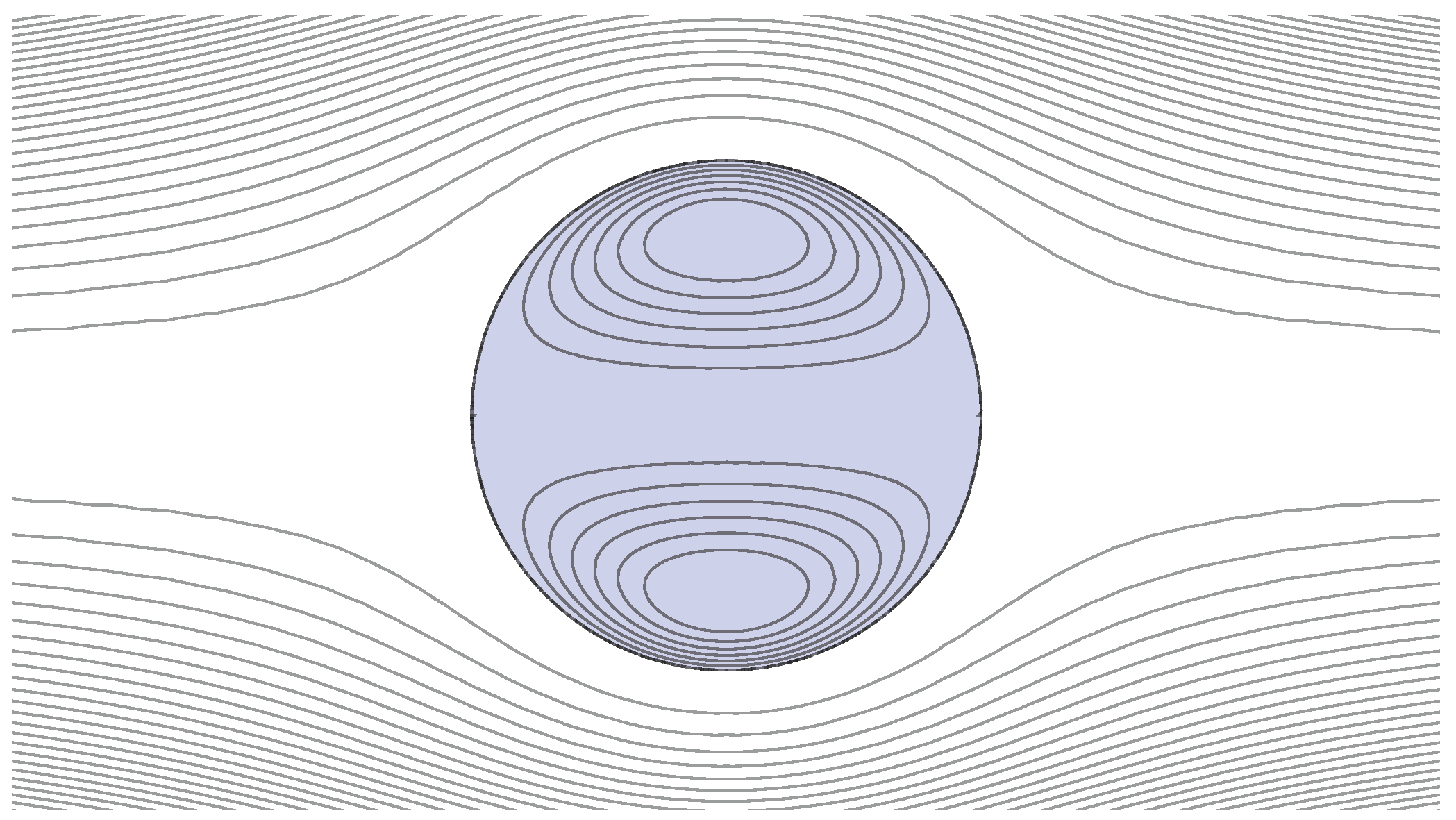
3.2. Uniform Flow past a Fluid Drop
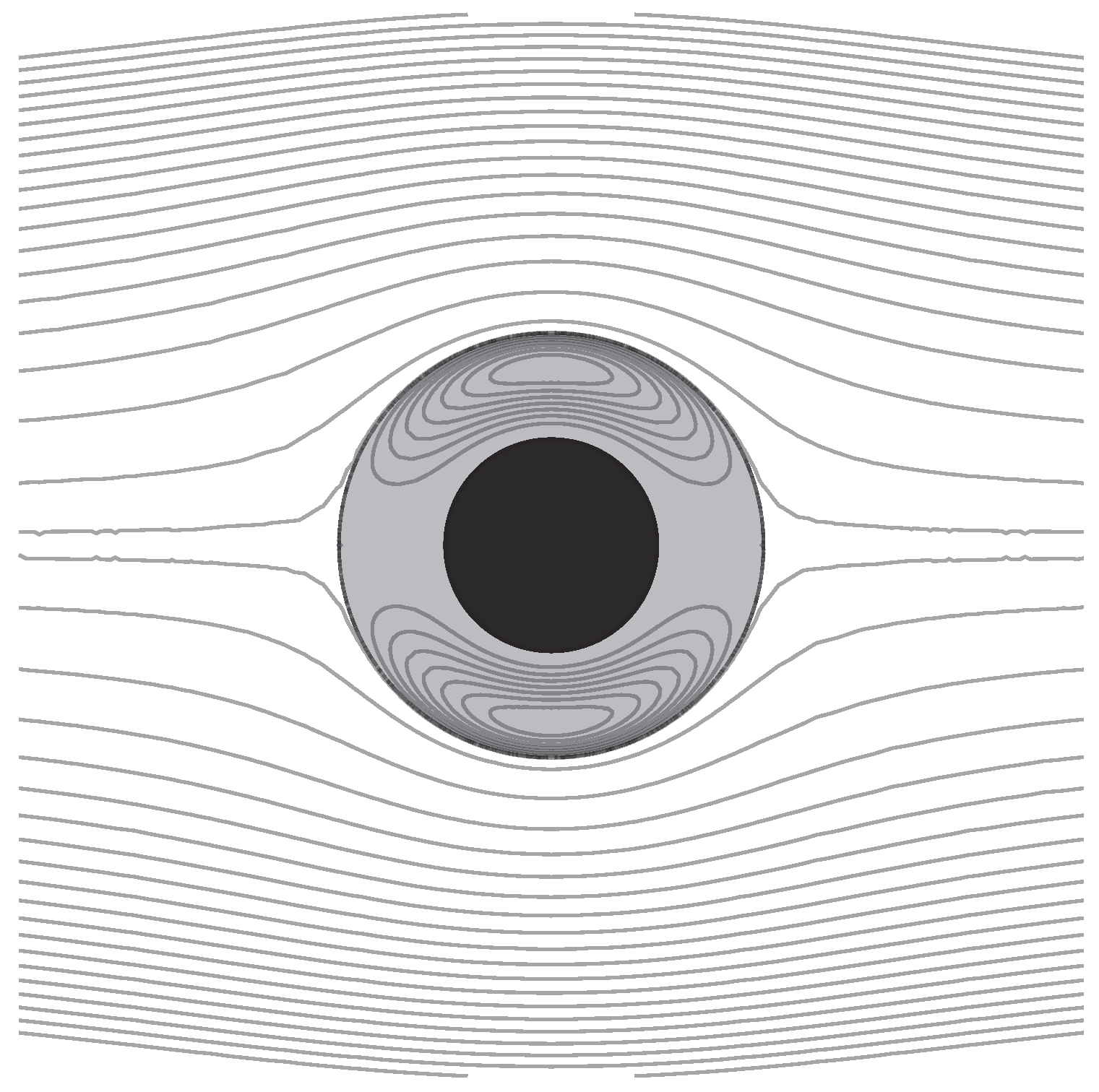
3.3. Uniform Flow past a Rigid-Kernel Sphere with a Fluid Coating
- The boundary condition at infinity implies
- The zero normal velocity at the interface of fluids sets
- With the continuity of tangential velocity at the interface of fluids, the following equation is satisfied
- The no-slip boundary condition at requires
- Continuity of tangential stress at the interface of the fluids implies
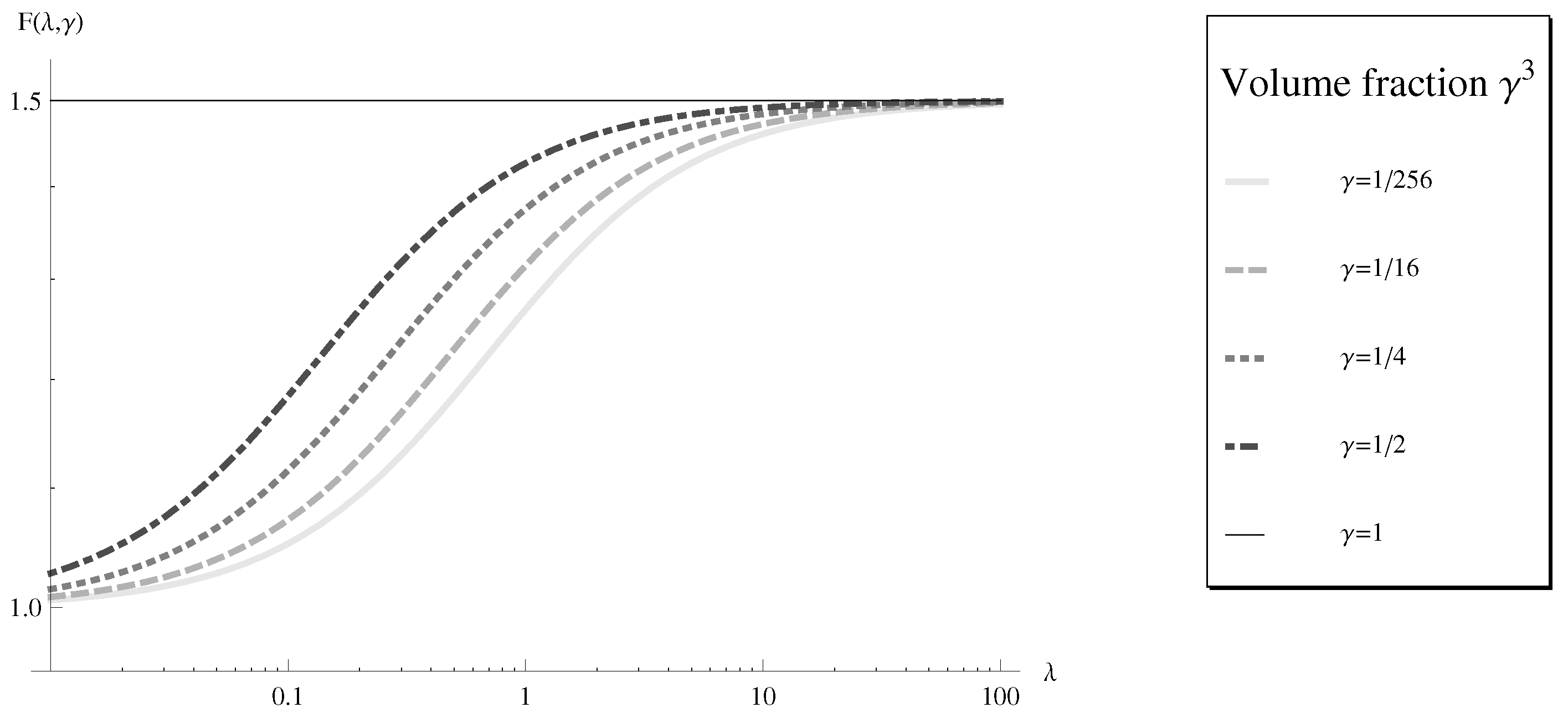
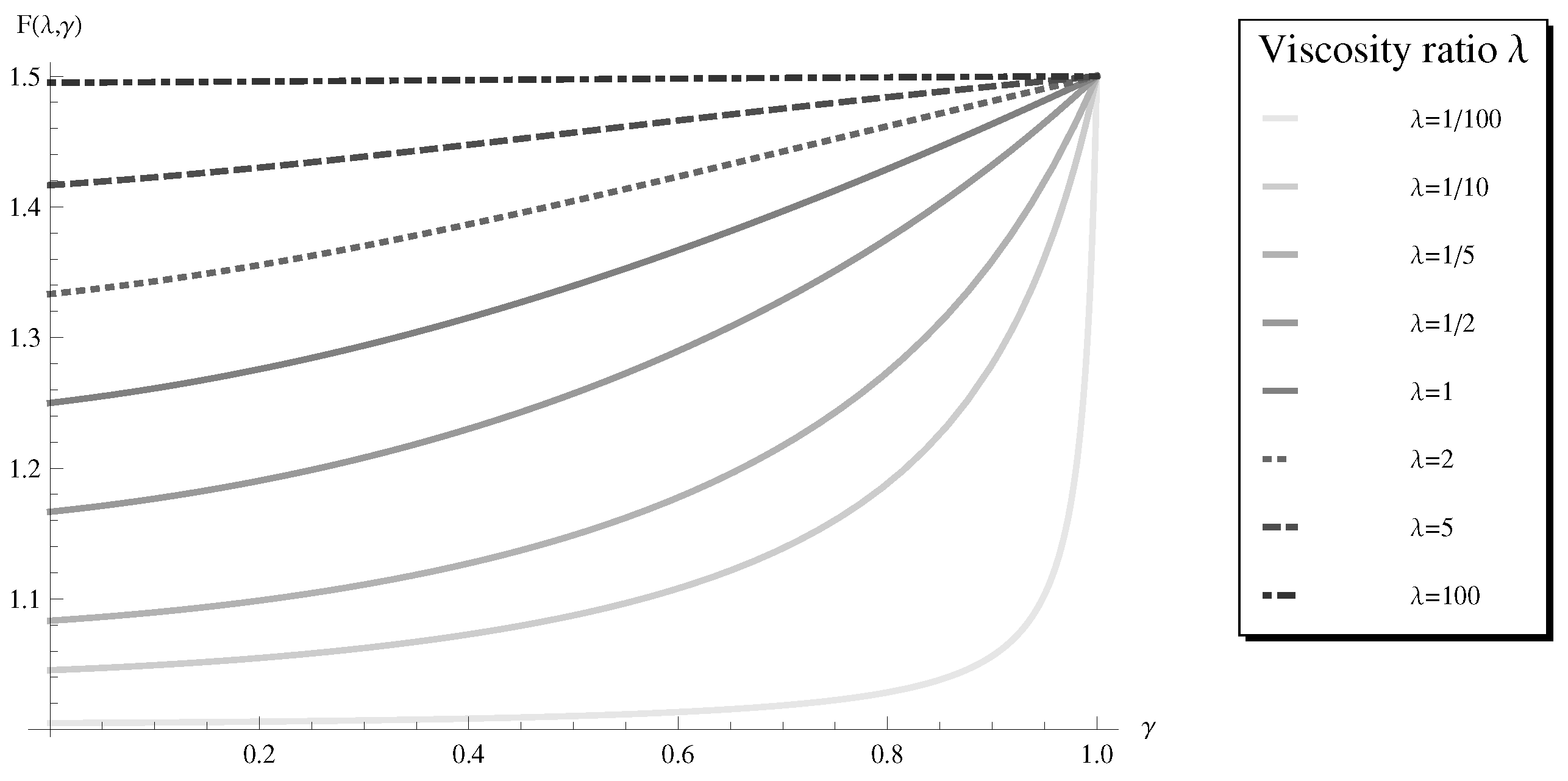
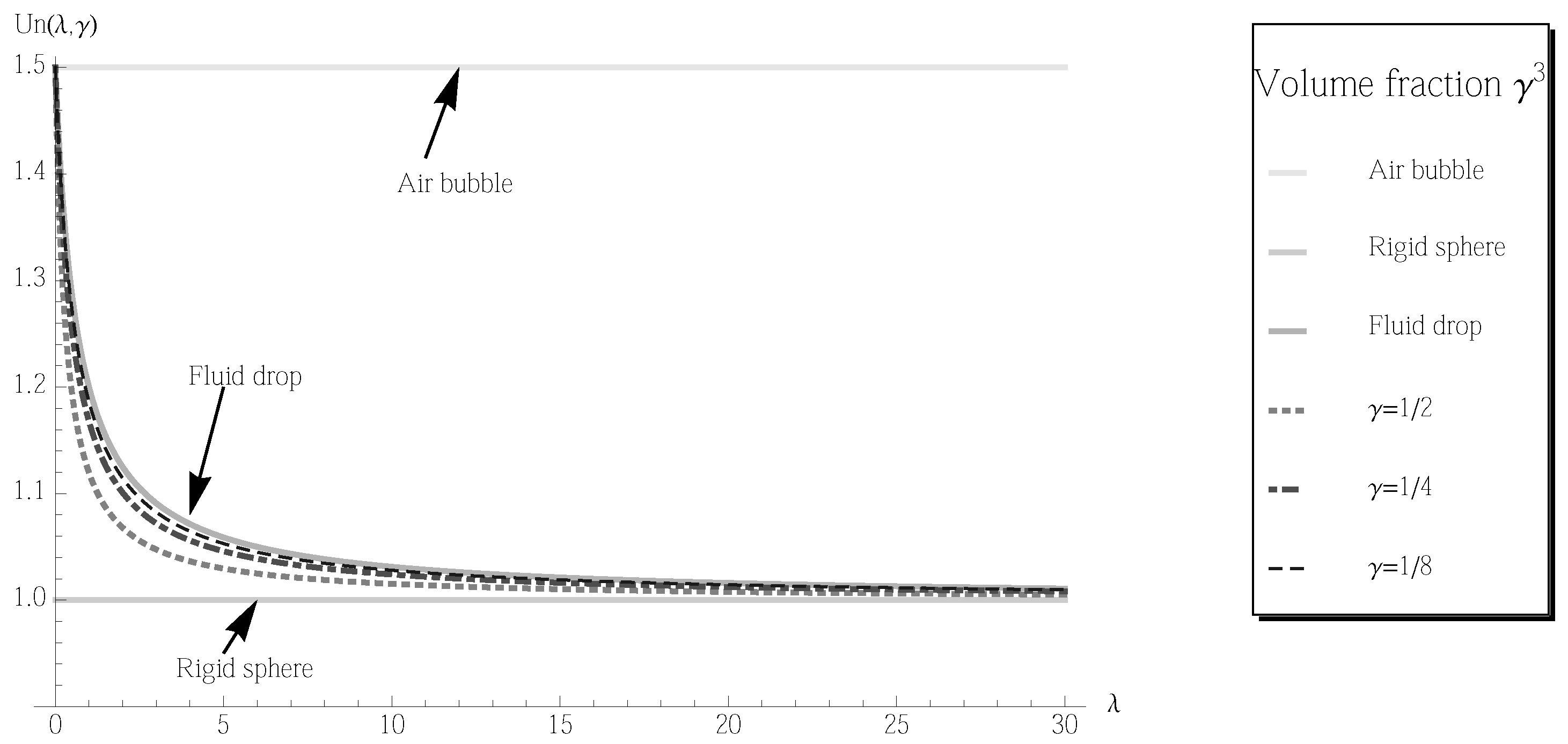
3.4. Hydrodynamic Drag Force and Terminal Velocity
3.5. Multiple-Layer Fluid Coating


4. Summary and Future Directions
Conflicts of Interest
References
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation-dissipation: Response theory in statistical physics. Phys. Rep. 2008, 461, 111–195. [Google Scholar] [CrossRef]
- Millikan, R.A. On the elementary electrical charge and the avogadro constant. Phys. Rev. 1913, 2, 109–143. [Google Scholar] [CrossRef]
- Schirber, M. Landmarks. Physics 2012, 5, 9. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- McBain, S.C.; Yiu, H.H.; Dobson, J. Magnetic nanoparticles for gene and drug delivery. Int. J. Nanomed. 2008, 3, 169–180. [Google Scholar]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Philos. Soc. 1851, 9, 8. [Google Scholar]
- Brenner, H. The Stokes resistance of an arbitrary particle-IV Arbitrary fields of flow. Chem. Eng. Sci. 1964, 19, 703–727. [Google Scholar] [CrossRef]
- Hetsroni, G.; Haber, S. The flow in and around a droplet or bubble submerged in an unbound arbitrary velocity field. Rheol. Acta 1970, 9, 488–496. [Google Scholar] [CrossRef]
- Proudman, I.; Pearson, J.R.A. Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 1957, 2, 237–262. [Google Scholar] [CrossRef]
- Jeffery, G.B. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 1922, 102, 161–179. [Google Scholar] [CrossRef]
- Wang, K.C.; Zhou, H.C.; Hu, C.H.; Harrington, S. Three-dimensional separated flow structure over prolate spheroids. Proc. R. Soc. Lond. A 1990, 421, 73–91. [Google Scholar] [CrossRef]
- Chwang, A.T.; Wu, T.Y. Hydromechanics of low-Reynolds-number flow. Part 2. Singularity method for Stokes flows. J. Fluid Mech. 1975, 67, 787–815. [Google Scholar] [CrossRef]
- Chwang, A.T. Hydromechanics of low-Reynolds-number flow. Part 3. Motion of a spheroidal particle in quadratic flows. J. Fluid Mech. 1975, 72, 17–34. [Google Scholar] [CrossRef]
- Zhao, L. Fluid-structure interaction in viscous dominated flows. Ph.D. Thesis, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, 2011. [Google Scholar]
- Camassa, R.; McLaughlin, R.M.; Zhao, L. Lagrangian blocking in highly viscous shear flows past a sphere. J. Fluid Mech. 2011, 669, 120–166. [Google Scholar] [CrossRef]
- Leal, L.G. Laminar Flow and Convective Transport Processes; Butterworth-Heinemann: Oxford, UK, 1992. [Google Scholar]
- Pozrikidis, C. Introduction to Theoretical and Computational Fluid Dynamics; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Mori, Y.H. Configurations of gas-liquid two-phase bubbles in immiscible liquid media. Int. J. Multiph. Flow 1978, 4, 383–396. [Google Scholar] [CrossRef]
- Johnson, R.E. Stokes flow past a sphere coated with a thin fluid film. J. Fluid Mech. 1981, 110, 217–238. [Google Scholar] [CrossRef]
- Harper, J.F. Surface activity and bubble motion. Appl. Sci. Res. 1982, 38, 343–352. [Google Scholar] [CrossRef]
- Sadhal, S.; Ayyaswamy, P.; Chung, J. Compound drops and bubbles. In Transport Phenomena with Drops and Bubbles; Springer: New York, NY, USA, 1997; pp. 403–442. [Google Scholar]
- Kawano, S.; Hashimoto, H. A numerical study on motion of a sphere coated with a thin liquid film at intermediate reynolds numbers. J. Fluids Eng. 1997, 119, 397–403. [Google Scholar] [CrossRef]
- Sagis, L.M.C.; Öttinger, H.C. Dynamics of multiphase systems with complex microstructure. i. development of the governing equations through nonequilibrium thermodynamics. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Sadhal, S.S.; Johnson, R.E. Stokes flow past bubbles and drops partially coated with thin films. Part 1. stagnant cap of surfactant film- exact solution. J. Fluid Mech. 1983, 126, 237–250. [Google Scholar] [CrossRef]
- Johnson, R.E.; Sadhal, S.S. Stokes flow past bubbles and drops partially coated with thin films. Part 2. thin films with internal circulation-a perturbation solution. J. Fluid Mech. 1983, 132, 295–318. [Google Scholar] [CrossRef]
- Gupta, B.R.; Deo, S. Axisymmetric creeping flow of a micropolar fluid over a sphere coated with a thin fluid film. J. Appl. Fluid Mech. 2013, 6, 149–155. [Google Scholar]
- Rushton, E.; Davies, G.A. Settling of encapsulated droplets at low Reynolds numbers. Int. J. Multiph. Flow 1983, 9, 337–342. [Google Scholar] [CrossRef]
- Li, X.; Pozrikidis, C. The effect of surfactants on drop deformation and on the rheology of dilute emulsions in Stokes flow. J. Fluid Mech. 1997, 341, 165–194. [Google Scholar] [CrossRef]
- Blawzdziewics, J.; Wajnryb, E.; Loewenberg, M. Hydrodynamic interactions and collision efficiencies of spherical drops covered with an incompressible surfactant film. J. Fluid Mech. 1999, 395, 29–59. [Google Scholar] [CrossRef]
- Datta, S.; Raturi, S. Cell model for slow viscous flow past spherical particles with surfactant layer coating. J. Appl. Fluid Mech. 2014, 7, 263–273. [Google Scholar]
- Fung, Y.-C. Biomechanics: Circulation; Springer Science & Business Media: New York, NY, USA, 1997. [Google Scholar]
- Somersalo, E.; Occhipinti, R.; Boron, W.F.; Calvetti, D. A reaction-diffusion model of co2 influx into an oocyte. J. Theor. Biol. 2012, 309, 185–203. [Google Scholar] [CrossRef] [PubMed]
- Klein, C.A. Cancer. The metastasis cascade. Science 2008, 321, 1785–1787. [Google Scholar] [CrossRef] [PubMed]
- Gusenbauer, M.; Kovacs, A.; Reichel, F.; Exl, L.; Bance, S.; Özelt, H.; Schrefl, T. Self-organizing magnetic beads for biomedical applications. J. Magn. Magn. Mater. 2012, 324, 977–982. [Google Scholar] [CrossRef]
- Nakhoul, N.L.; Davis, B.A.; Romero, M.F.; Boron, W.F. Effect of expressing the water channel aquaporin-1 on the co2 permeability of xenopus oocytes. Am. J. Physiol. Cell Physiol. 1998, 274, C543–C548. [Google Scholar]
- Batchelor, G.K. Slender-body theory for particles of arbitrary cross-section in stokes flow. J. Fluid Mech. 1970, 44, 419–440. [Google Scholar] [CrossRef]
- Rivkind, V.Y.; Ryskin, G.M. Flow structure in motion of a spherical drop in a fluid medium at intermediate reynolds numbers. Fluid Dyn. 1976, 11, 5–12. [Google Scholar] [CrossRef]
- Oliver, D.L.R.; Chung, J.N. Steady flows inside and around a fluid sphere at low Reynolds numbers. J. Fluid Mech. 1985, 154, 215–230. [Google Scholar] [CrossRef]
- Pozrikidis, C. Introduction to Theoretical and Computational Fluid Dynamics; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L. Hydrodynamics of Highly Viscous Flow past a Compound Particle: Analytical Solution. Fluids 2016, 1, 36. https://doi.org/10.3390/fluids1040036
Zhao L. Hydrodynamics of Highly Viscous Flow past a Compound Particle: Analytical Solution. Fluids. 2016; 1(4):36. https://doi.org/10.3390/fluids1040036
Chicago/Turabian StyleZhao, Longhua. 2016. "Hydrodynamics of Highly Viscous Flow past a Compound Particle: Analytical Solution" Fluids 1, no. 4: 36. https://doi.org/10.3390/fluids1040036
APA StyleZhao, L. (2016). Hydrodynamics of Highly Viscous Flow past a Compound Particle: Analytical Solution. Fluids, 1(4), 36. https://doi.org/10.3390/fluids1040036




