Riblet Drag Reduction Modeling and Simulation
Abstract
:1. Introduction
2. Drag Reduction Modeling
2.1. Governing Equations
2.2. Turbulence Model Based Boundary Condition
2.3. Slip Length Based Boundary Condition
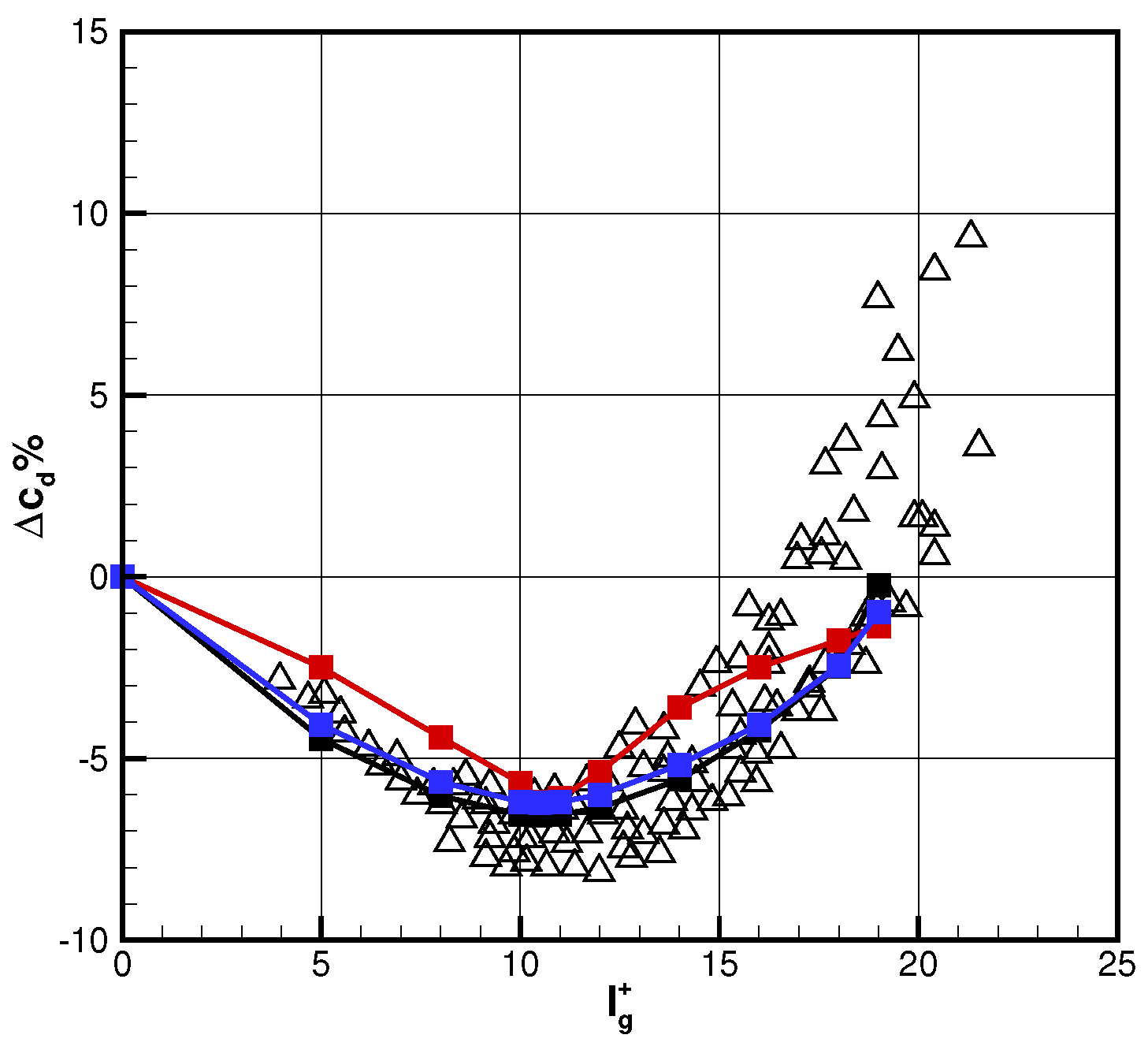
2.4. Performance Comparison
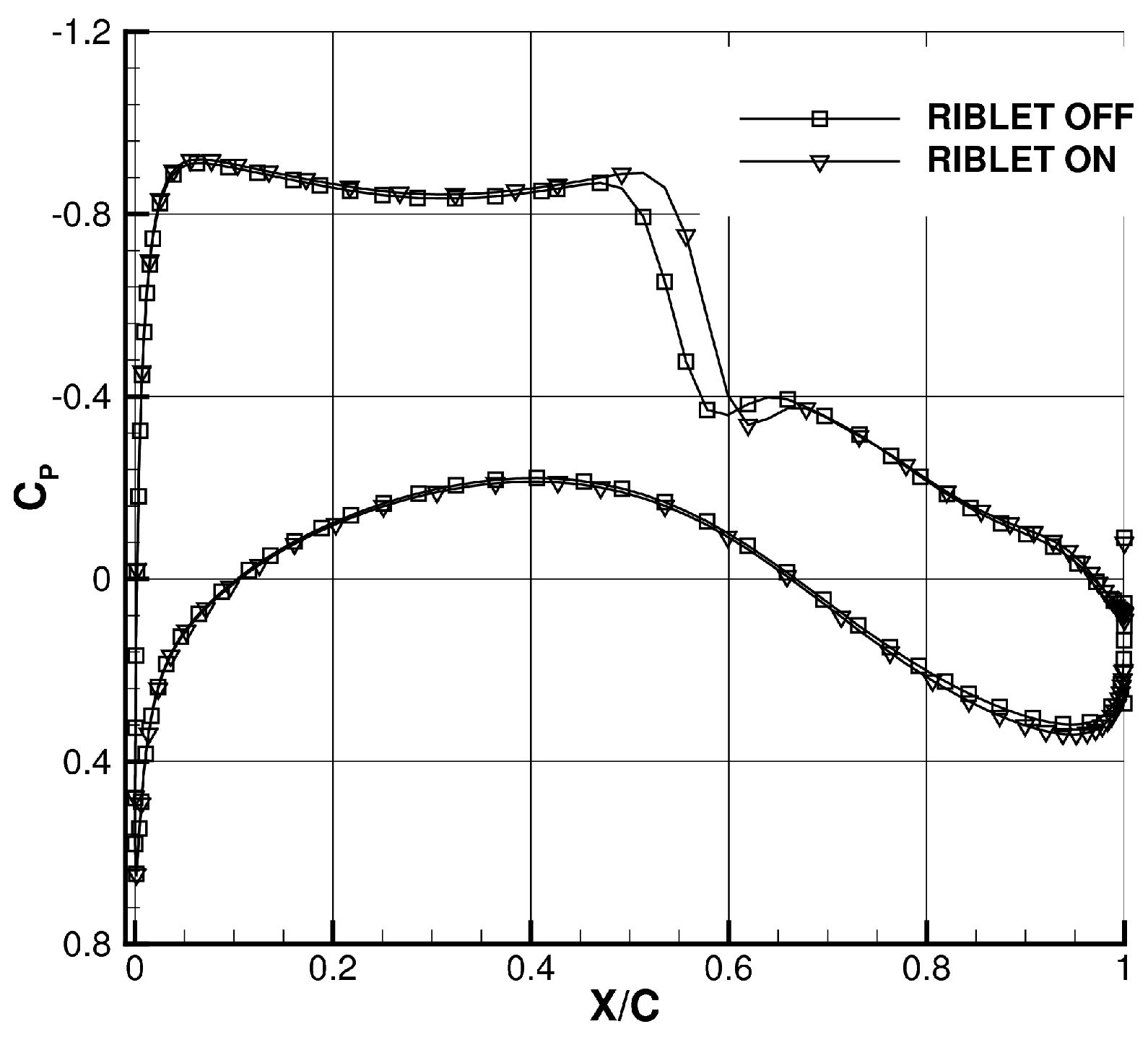
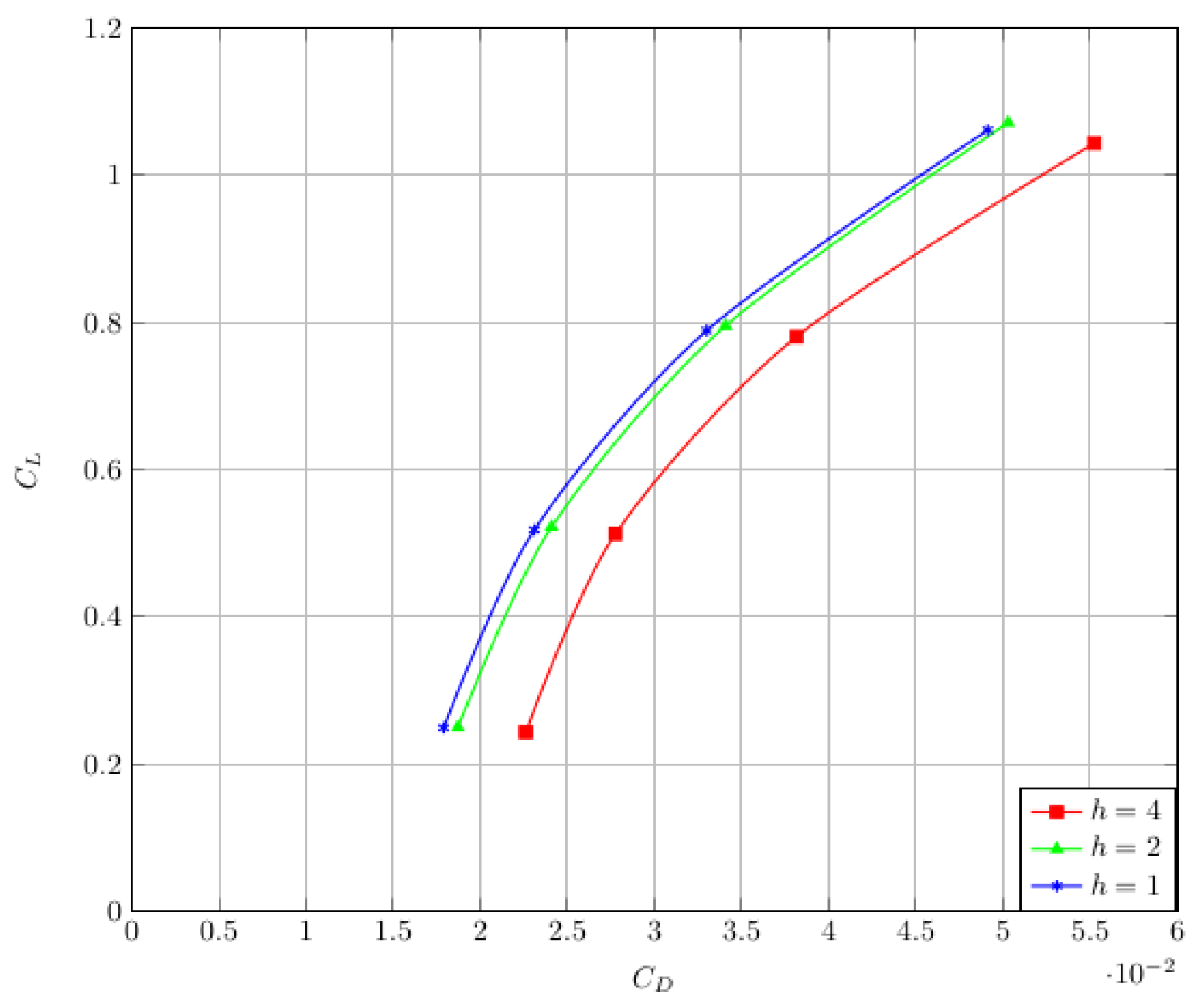
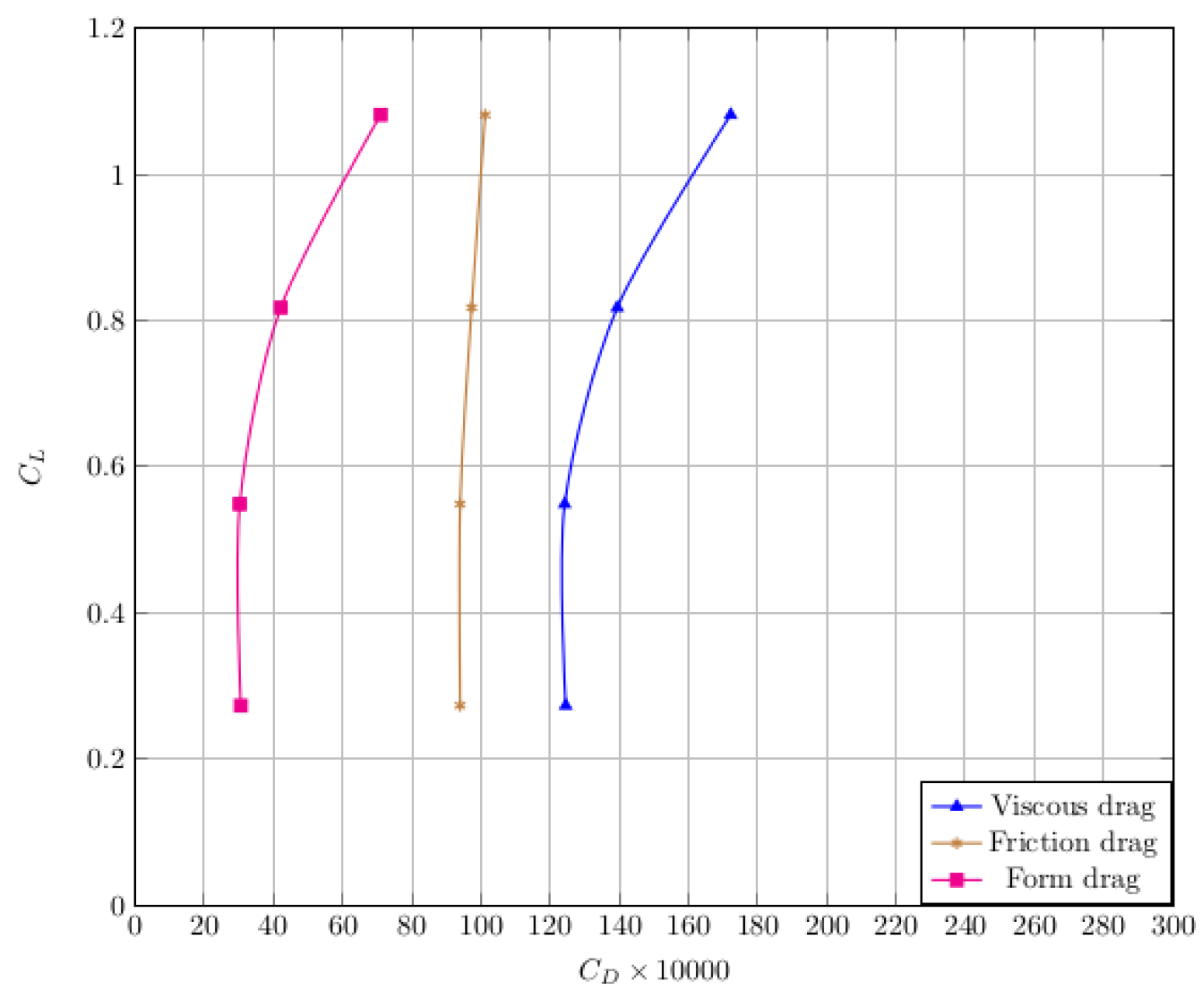
3. Effect of Riblets on Form Drag and Shock Wave
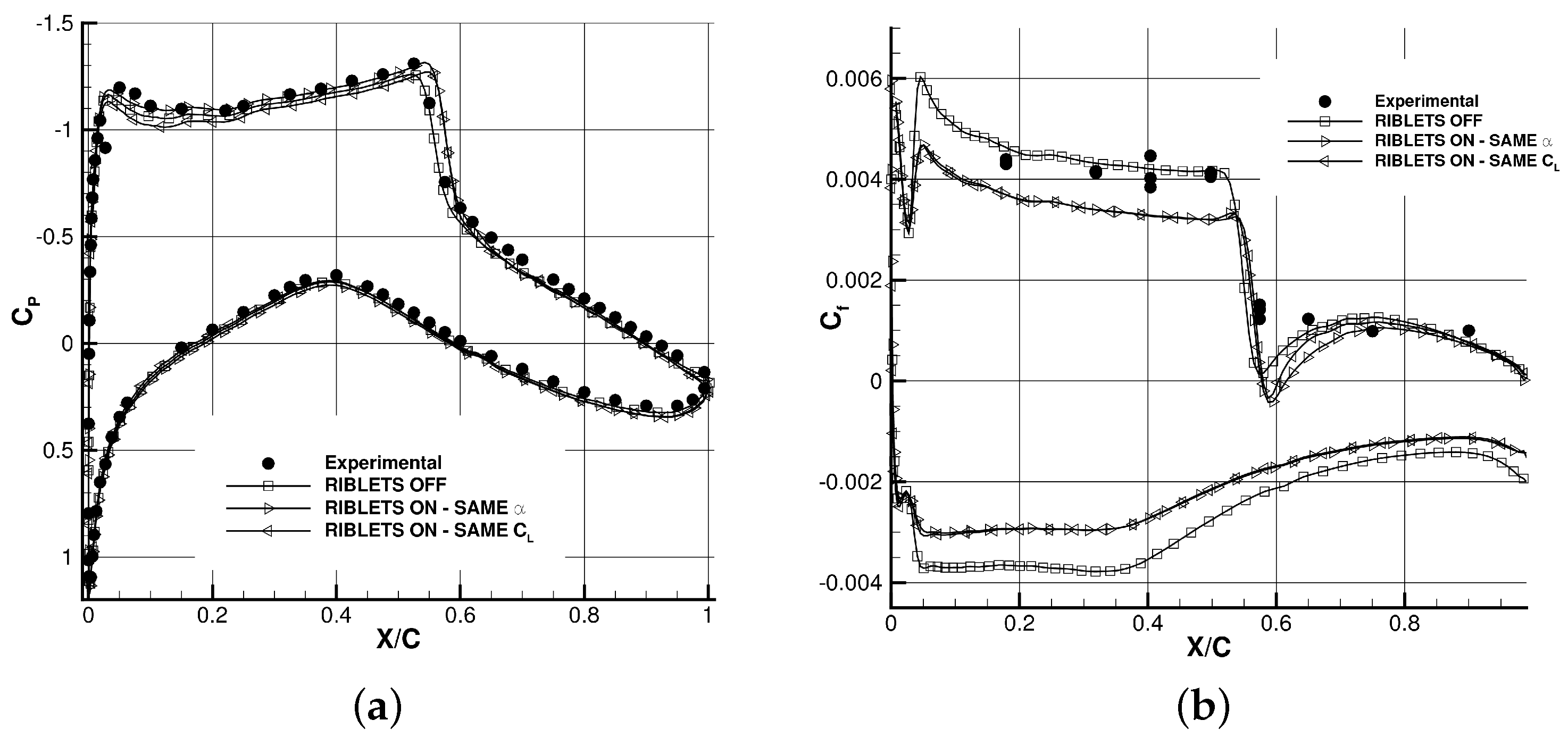
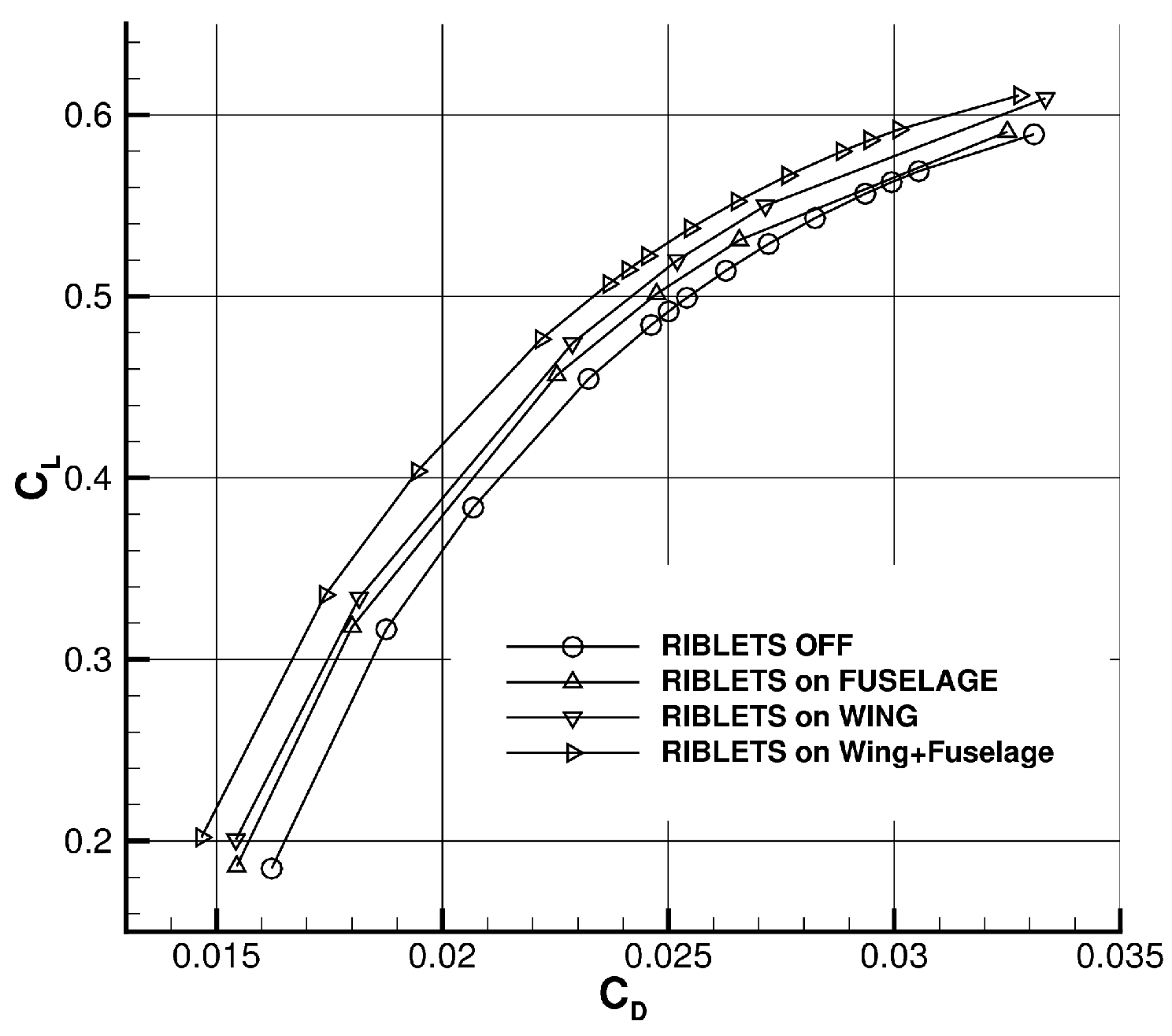
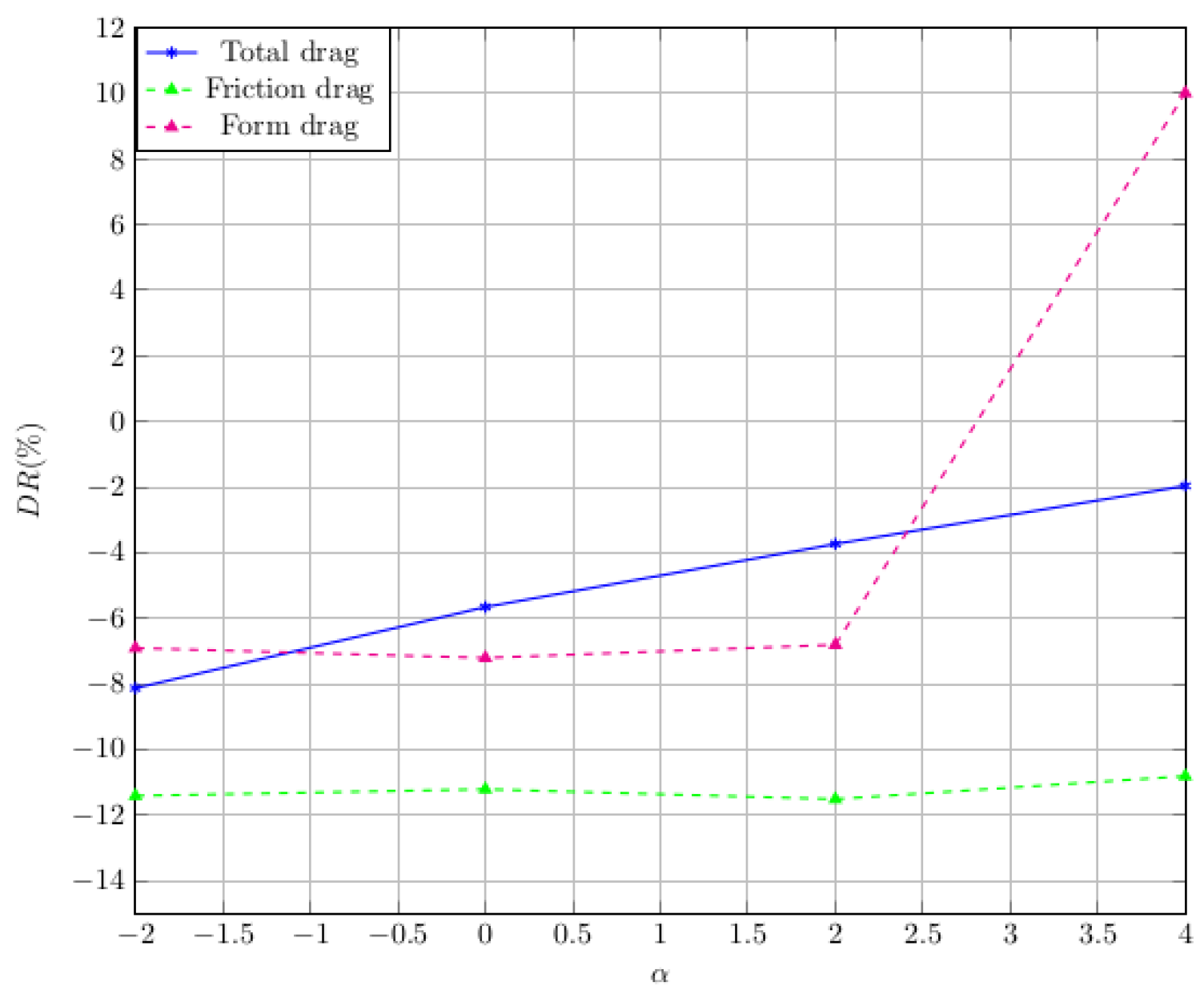
4. Modeling the Riblet Effect on Aircraft Configuration
5. Conclusions
Funding
Conflicts of Interest
References
- Spalart, P.R.; McLean, J.D. Drag reduction: Enticing turbulence, and then an industry. Philos. Trans. R. Soc. A 2011, 369, 1556–1569. [Google Scholar] [CrossRef] [Green Version]
- Martin, S.; Bhushan, B. Modeling and optimization of shark-inspired riblet geometries for low drag applications. J. Colloid Interface Sci. 2016, 474, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, H.; Fu, S.; Dong, W. Numerical study of an airfoil with riblets installed based on large eddy simulation. Aerosp. Sci. Technol. 2018, 78, 661–670. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P.; Kim, J. Direct Numerical Simulation of Turbulent Flow over Riblets. J. Fluid Mech. 1993, 255, 503–539. [Google Scholar] [CrossRef]
- El-Samni, O.; Chun, H.; Yoon, H. Drag reduction of turbulent flow over thin rectangular riblets. Int. J. Eng. Sci. 2007, 45, 436–454. [Google Scholar] [CrossRef]
- Walsh, M.J. Drag Characteristics of V-groove and Transverse Curvature Riblets. Prog. Astronaut. Aeronaut. 1980, 72, 168–184. [Google Scholar]
- Bechert, D.; Bruse, M.; Hage, W.; van der Hoeven, J.; Hoppe, G. Experiments on Drag-reducing Surfaces and their Optimization with an Adjustable Geometry. JFM 1997, 338, 59–87. [Google Scholar] [CrossRef]
- Choi, K. Near-wall structure of a turbulent boundary layer with riblets. J. Fluid Mech. 1989, 208, 417–458. [Google Scholar] [CrossRef]
- Lee, S.J.; Jang, Y. Control of Flow around a NACA 0012 Airfoil with a Micro-Riblet Film. J. Fluids Struct. 2005, 20, 659–672. [Google Scholar] [CrossRef]
- Hou, J.; Hokmabad, B.; Ghaemi, S. Three-dimensional measurement of turbulent flow over a riblet surface. Exp. Therm. Fluid Sci. 2017, 85, 229–239. [Google Scholar] [CrossRef]
- Luchini, P.; Manzo, F.; Pozzi, A. Resistance of Grooved Surface to Parallel Flow and Cross-flow. J. Fluid Mech. 1991, 228, 87–109. [Google Scholar] [CrossRef]
- Aupoix, B.; Pailhas, G.; Houdeville, R. Towards a General Strategy to Model Riblet Effects. AIAA J. 2012, 50, 708–716. [Google Scholar] [CrossRef]
- Koepplin, V.; Herbst, F.; Seume, J.R. Correlation-based riblet model for turbomachinery applications. J. Turbomach. 2017, 139. [Google Scholar] [CrossRef]
- Mele, B.; Tognaccini, R. Numerical simulation of riblets on airfoils and wings. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA 2012-0861, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Jiménez, J. Turbulent Flows over Rough Walls. Annu. Rev. Fluid Mech. 2004, 36, 173–196. [Google Scholar] [CrossRef]
- Mele, B.; Tognaccini, R.; Catalano, P. Performance assessment of a transonic wing-body configuration with riblets installed. J. Aircr. 2016, 53, 129–140. [Google Scholar] [CrossRef] [Green Version]
- Mele, B.; Russo, L.; Tognaccini, R. Drag bookkeeping on an aircraft with riblets and NLF control. Aerosp. Sci. Technol. 2020, 98, 105714. [Google Scholar] [CrossRef]
- Catalano, P.; de Rosa, D.; Mele, B.; Tognaccini, R.; Moens, F. Performance Improvements of a Regional Aircraft by Riblets and Natural Laminar Flow. J. Aircr. 2020, 57, 29–40. [Google Scholar] [CrossRef]
- Jiahe, L.; Yanming, L.; Jiang, W. Evaluation method of riblets effects and application on a missile surface. Aerosp. Sci. Technol. 2019, 95, 105418. [Google Scholar]
- Ran, W.; Zare, A.; Jovanovic, M. Model-based design of riblets for turbulent drag reduction. J. Fluid Mech. 2020, 906, 1–37. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Wang, S.; Sun, G.; You, B.; Hu, Y. A novel ANN-Based boundary strategy for modeling micro/nanopatterns on airfoil with improved aerodynamic performances. Aerosp. Sci. Technol. 2022, 121, 107347. [Google Scholar] [CrossRef]
- Mele, B.; Tognaccini, R. Slip length based boundary condition for modeling drag reduction devices. AIAA J. 2018, 56, 3478–3490. [Google Scholar] [CrossRef]
- Min, T.; Kim, J. Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 2004, 16, L55. [Google Scholar] [CrossRef]
- Rastegari, A.; Akhavan, R. The common mechanism of turbulent skin-friction drag reduction with superhydrophobic longitudinal microgrooves and riblets. J. Fluid Mech. 2018, 838, 68–104. [Google Scholar] [CrossRef]
- Alinovi, E.; Bottaro, A. Apparent slip and drag reduction for the flow over superhydrophobic and lubricant-impregnated surfaces. Phys. Rev. Fluids 2018, 3, 124002. [Google Scholar] [CrossRef]
- Bottaro, A.; Naqvi, S. Effective boundary conditions at a rough wall: A high-order homogenization approach. Meccanica 2020, 55, 1781–1800. [Google Scholar] [CrossRef]
- Chang, J.; Jung, T.; Choi, H.; Kim, J. Predictions of the effective slip length and drag reduction with a lubricated micro-groove surface in a turbulent channel flow. J. Fluid Mech. 2019, 874, 797–820. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, N.; Cai, C.; Kang, K. A General Model for the Riblet Simulation in Turbulent Flows. Int. J. Comput. Fluid Dyn. 2020, 34, 333–345. [Google Scholar] [CrossRef]
- Luchini, P. Linearized no-slip boundary conditions at a rough surface. J. Fluid Mech. 2013, 737, 349–367. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Turbulence Modeling for CFD-II Edition; DCW Industries: San Bernardino, CA, USA, 1998. [Google Scholar]
- Menter, F.R.; Egorov, Y. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Hirsch, C. The Numerical Computation of Internal and External Flows, Volumes 1, 2; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- García-Mayoral, R.; Jiménez, J. Hydrodynamic Stability and Breakdown of the Viscous Regime over Riblets. J. Fluid Mech. 2011, 678, 317–347. [Google Scholar] [CrossRef]
- Saffman, P. A Model for Inhomogeneous Turbulent Flow. Proc. R. Soc. Lond. A 1970, 317, 417–433. [Google Scholar] [CrossRef]
- Mele, B.; Tognaccini, R.; Catalano, P.; de Rosa, D. Effect of body shape on riblets performance. Phys. Rev. Fluids 2020, 5, 124609. [Google Scholar] [CrossRef]
- Debisschop, J.; Nieuwstadt, F. Turbulent Boundary Layer in an Adverse Pressure Gradient: Effectiveness of Riblets. AIAA J. 1996, 34, 932–937. [Google Scholar] [CrossRef]
- Boomsma, A.; Sotiropoulos, F. Riblet drag reduction in mild adverse pressure gradient: A numerical investigation. Int. J. Heat Fluid Flow 2015, 56, 251–260. [Google Scholar] [CrossRef]
- Stroh, A.; Hasegawa, Y.; Schlatter, P.; Frohnapfel, B. Global effect of local skin friction drag reduction in spatially developing turbulent boundary layer. J. Fluid Mech. 2016, 805, 303–321. [Google Scholar] [CrossRef] [Green Version]
- Banchetti, J.; Luchini, P.; Quadrio, M. Turbulent Drag Reduction Over Curved Walls. J. Fluid Mech. 2020, 896, A10. [Google Scholar] [CrossRef]
- Mollicone, J.; Battista, F.; Gualtieri, P.; Casciola, C. Superhydrophobic surfaces to reduce form drag in turbulent separated flows. AIP Adv. 2022, 12, 075003. [Google Scholar] [CrossRef]
- Quadrio, M.; Chiarini, A.; Banchetti, J.; Gatti, D.; Memmolo, A.; Pirozzoli, S. Drag reduction on a transonic airfoil. J. Fluid Mech. 2022, 942, R2. [Google Scholar] [CrossRef]
- Catalano, P.; Mele, B.; Tognaccini, R. On the implementation of a turbulence model for low Reynolds number flows. Comput. Fluids 2015, 109, 67–71. [Google Scholar] [CrossRef]
- Paparone, L.; Tognaccini, R. Computational Fluid Dynamics-based drag prediction and decomposition. AIAA J. 2003, 41, 1647–1657. [Google Scholar] [CrossRef] [Green Version]
- Lanzetta, M.; Mele, B.; Tognaccini, R. Advances in aerodynamic drag extraction by far field methods. J. Aircr. 2015, 52, 1873–1886. [Google Scholar] [CrossRef]
 : riblets off,
: riblets off,  : riblets on.
: riblets on.
 : riblets off,
: riblets off,  : riblets on.
: riblets on.
 : riblets off,
: riblets off,  : riblets on.
: riblets on.
 : riblets off,
: riblets off,  : riblets on.
: riblets on.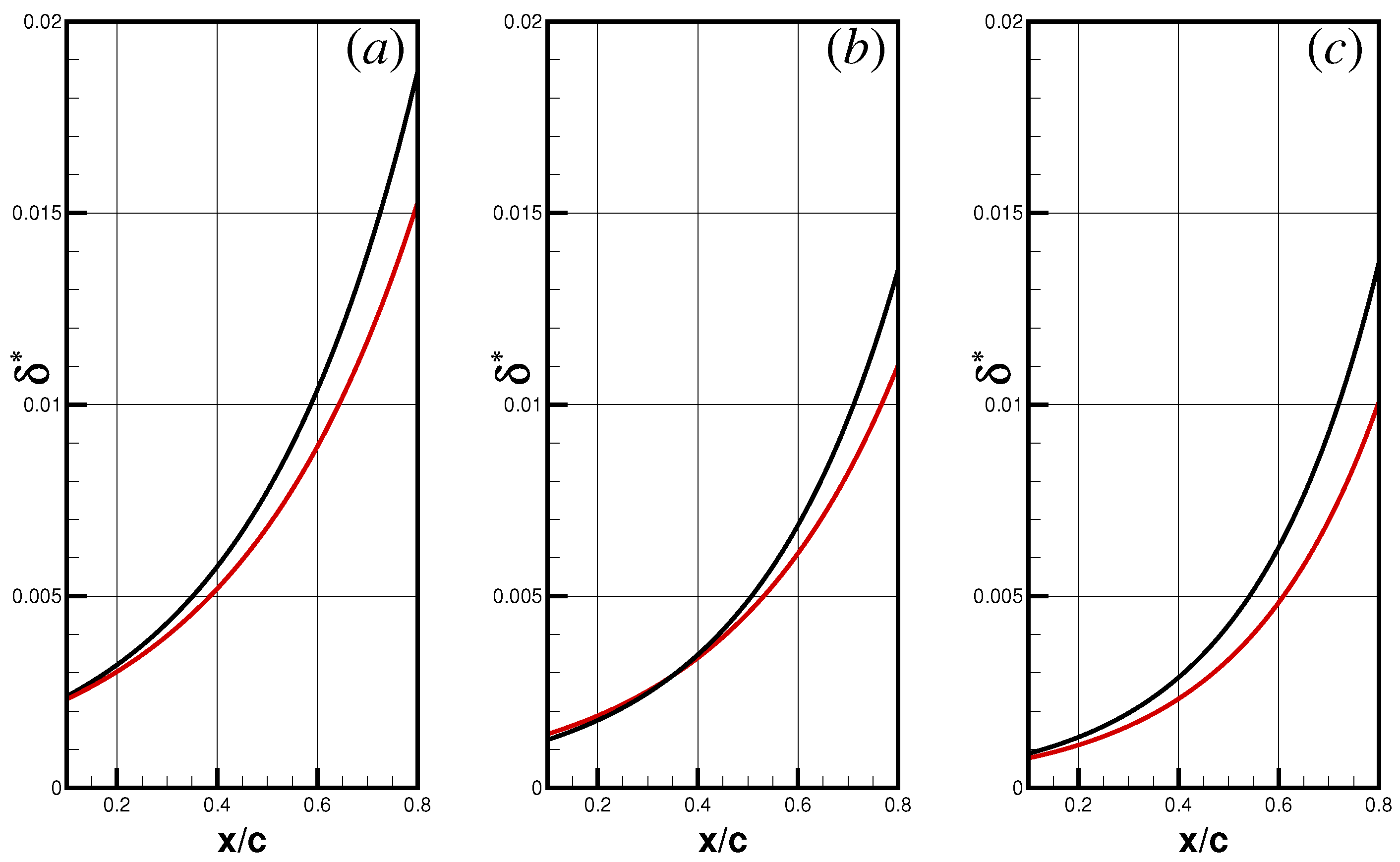




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mele, B. Riblet Drag Reduction Modeling and Simulation. Fluids 2022, 7, 249. https://doi.org/10.3390/fluids7070249
Mele B. Riblet Drag Reduction Modeling and Simulation. Fluids. 2022; 7(7):249. https://doi.org/10.3390/fluids7070249
Chicago/Turabian StyleMele, Benedetto. 2022. "Riblet Drag Reduction Modeling and Simulation" Fluids 7, no. 7: 249. https://doi.org/10.3390/fluids7070249









