A Fast-Tracking-Particle-Inspired Flow-Aided Control Approach for Air Vehicles in Turbulent Flow
Abstract
:1. Introduction
2. Background on Transport Theory and the Fast-Tracking Effect
2.1. Fast-Tracking Effect
2.2. Cellular Flow Fields
3. Problem Formulation and Assumptions
4. FTC Control Design via Implicit Model Following (IMF)
4.1. Ideal Fast-Tracking Particle Model
4.2. Fast-Tracking Controller (FTC) Design
5. Minimum-Energy Solutions and Results
5.1. Comparison with Linear Quadratic Regulator (LQR)
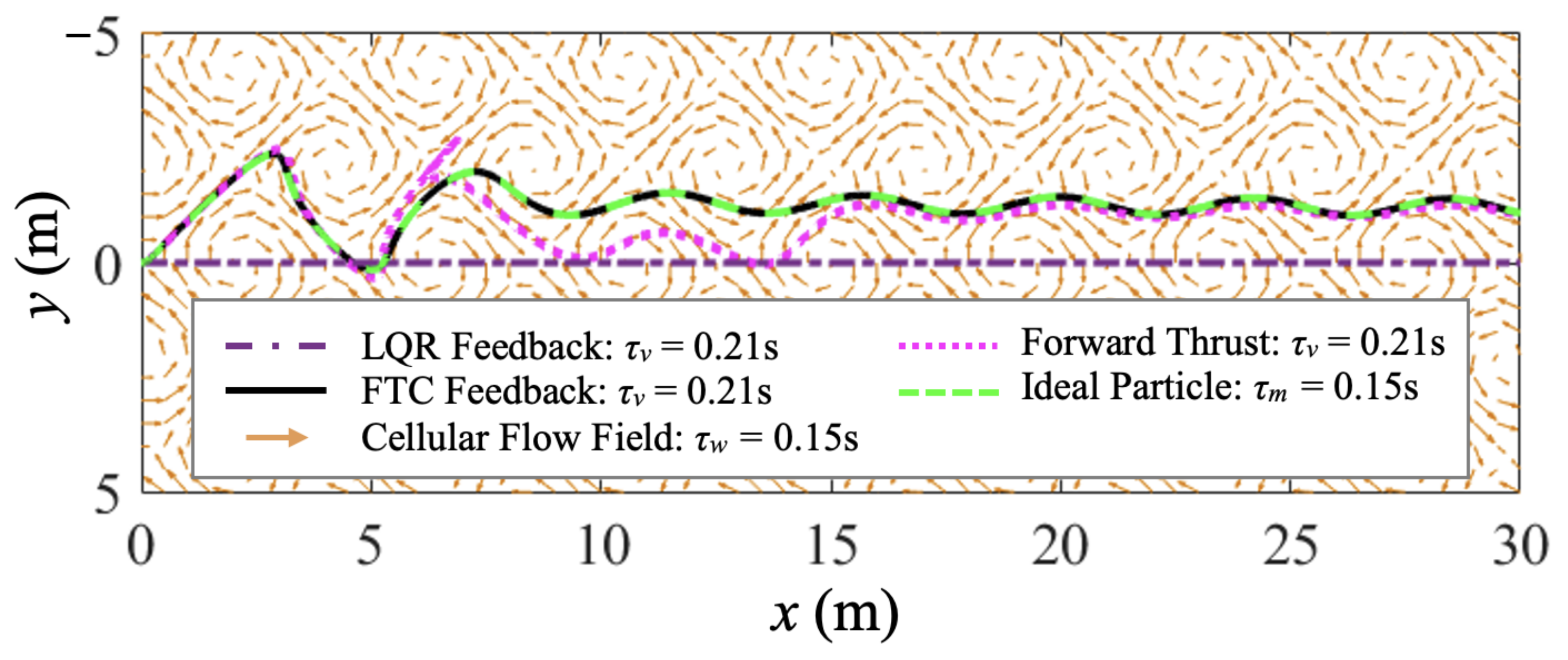
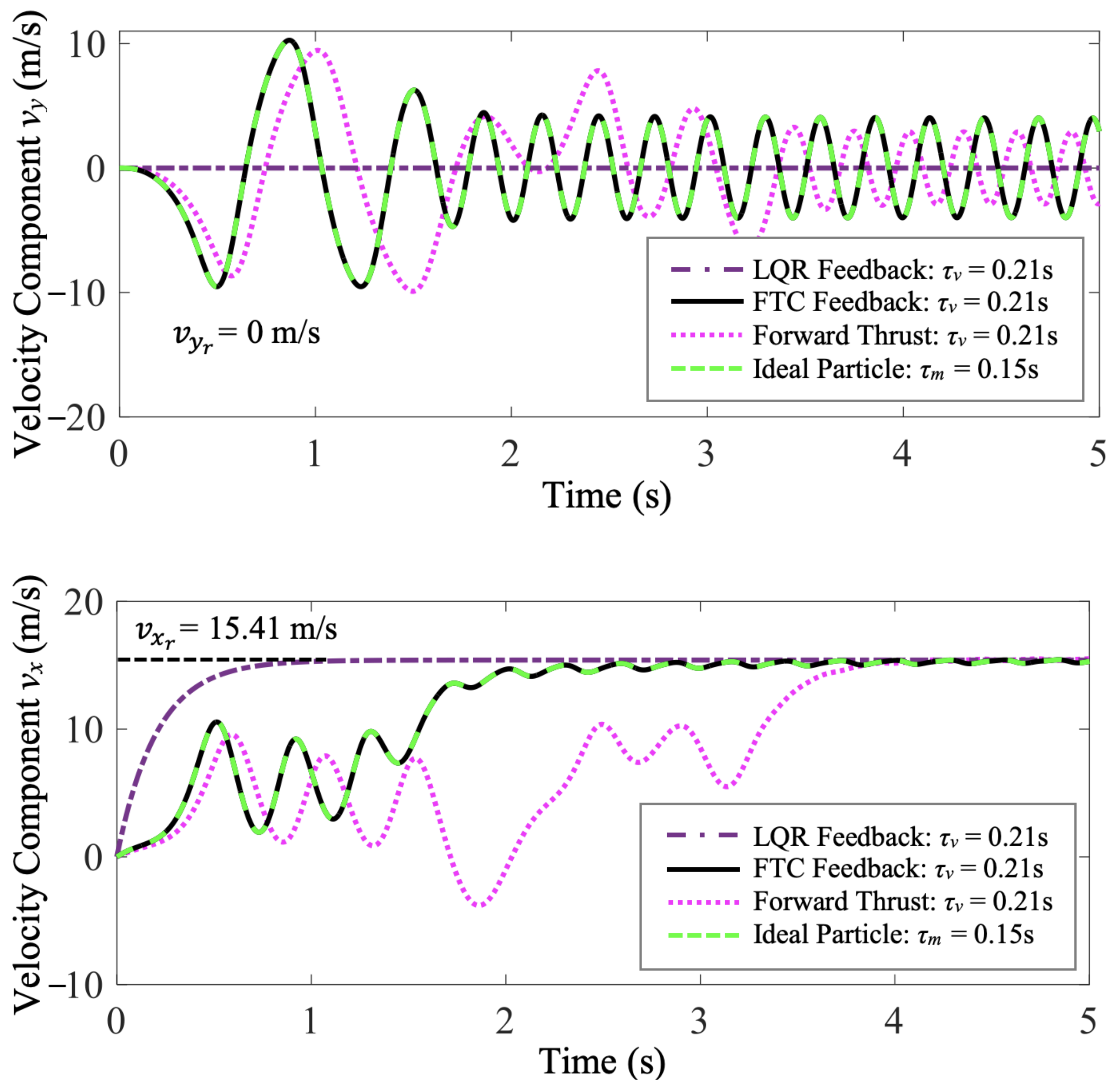
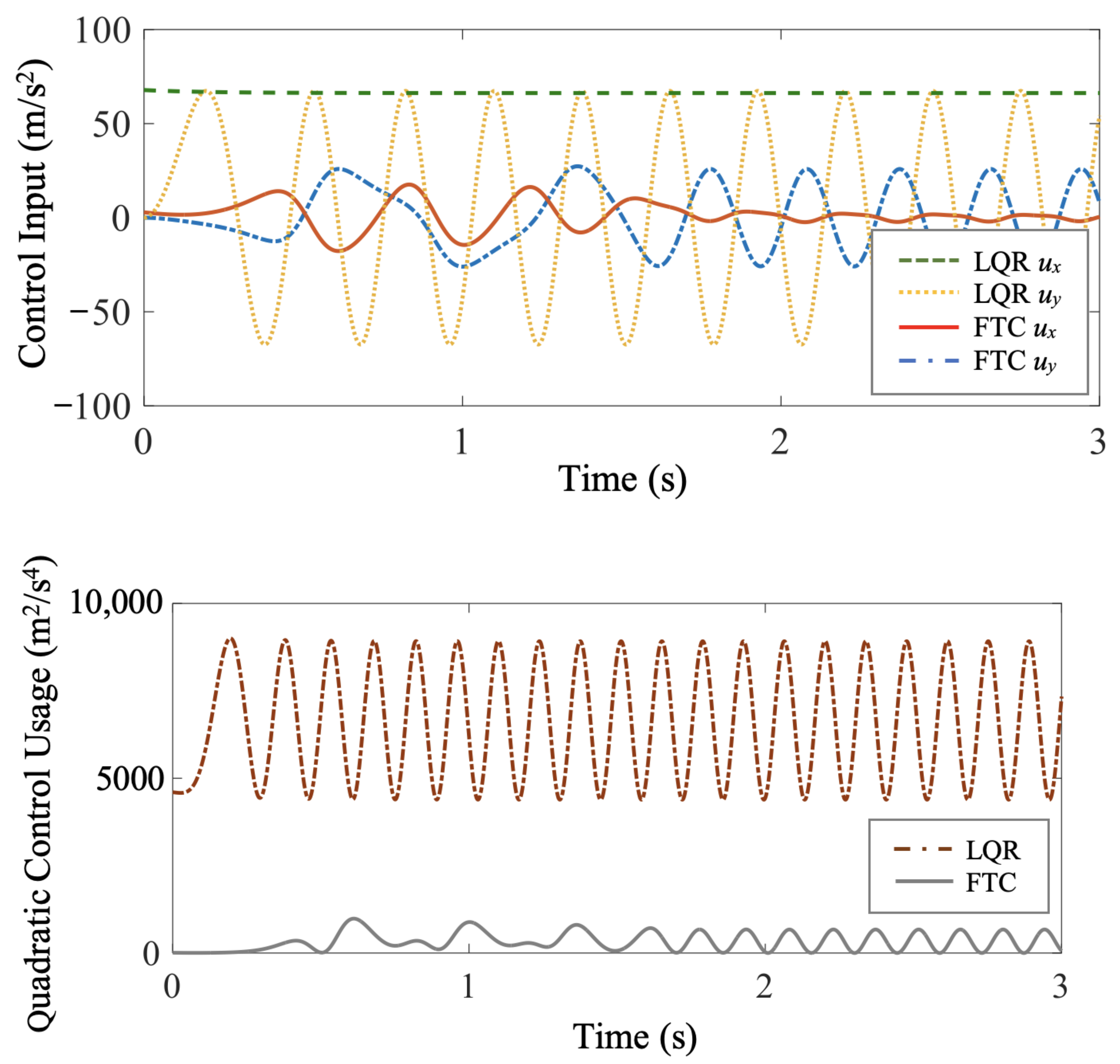
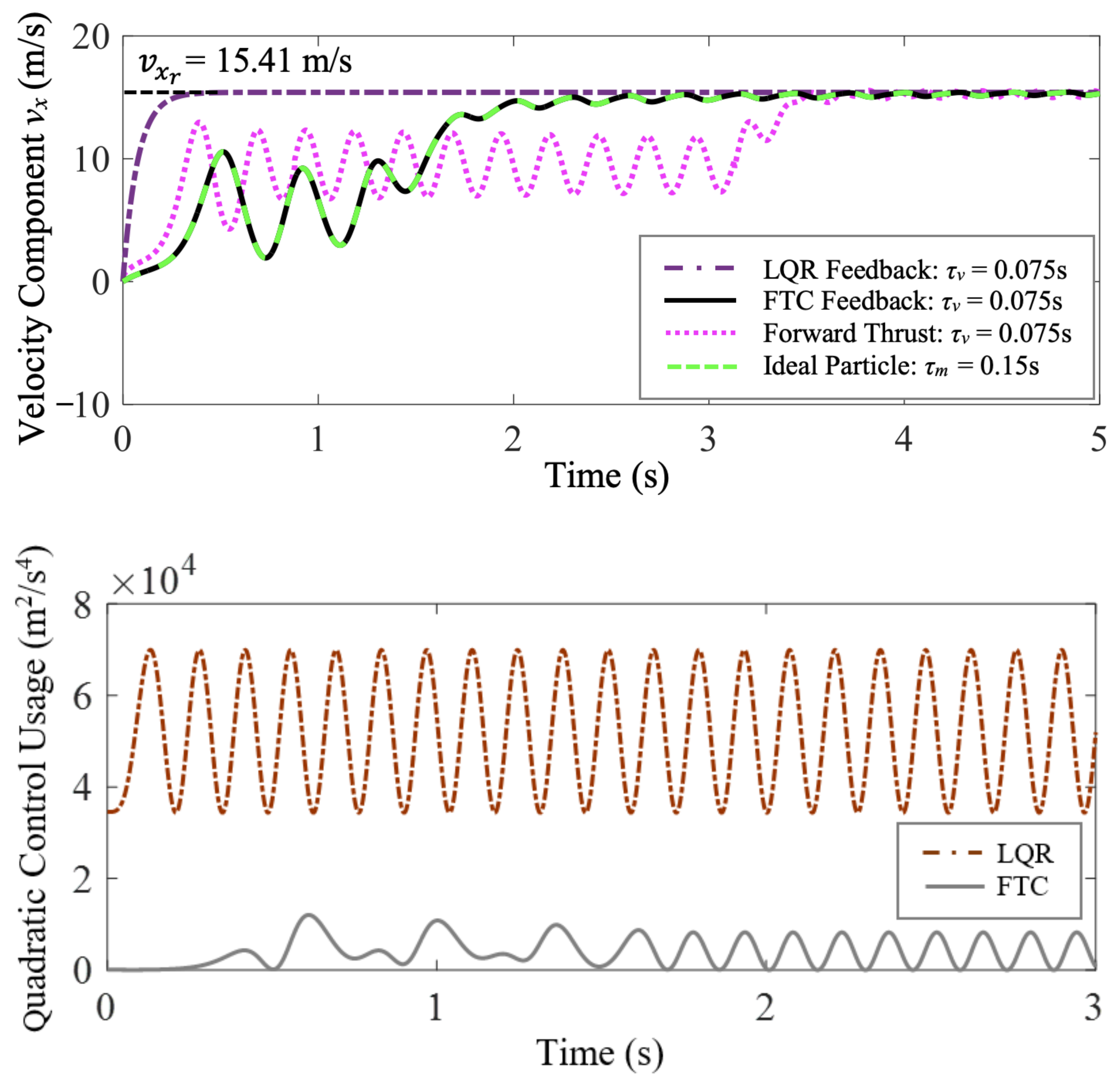
5.2. FTC Minimum-Energy Case Study 1
5.3. FTC Minimum-Energy Case Study 2
6. Minimum-Time Solutions and Results
6.1. Comparison with Bang-Bang Controller (BBC)
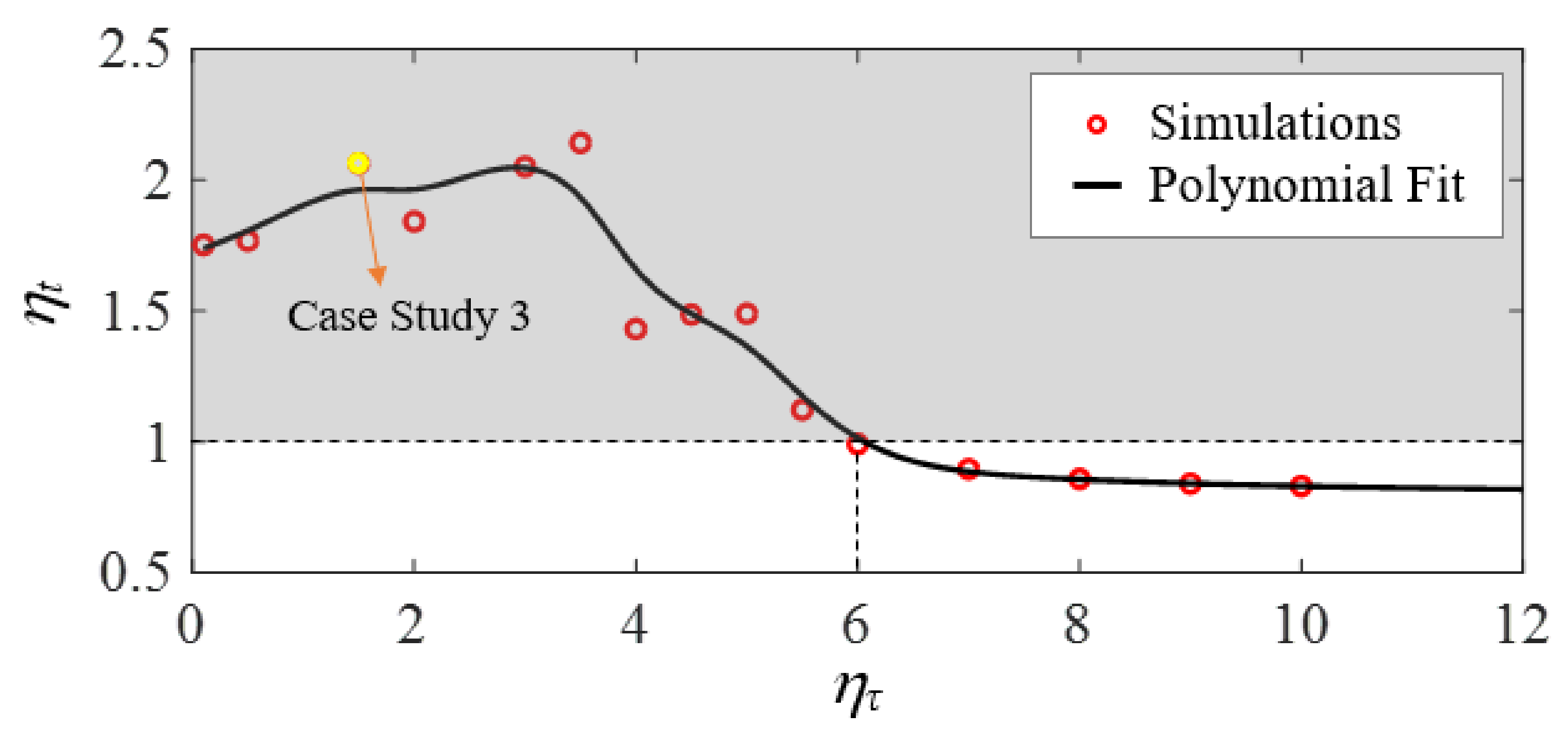
6.2. FTC Minimum-Time Case Study 3
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ákos, Z.; Nagy, M.; Leven, S.; Vicsek, T. Thermal soaring flight of birds and unmanned aerial vehicles. Bioinspir. Biomim. 2010, 5, 045003. [Google Scholar] [CrossRef] [PubMed]
- Pennycuick, C.J. Thermal soaring compared in three dissimilar tropical bird species, Fregata magnificens, Pelecanus occidentals and Coragyps atratus. J. Exp. Biol. 1983, 102, 307–325. [Google Scholar] [CrossRef]
- Poessel, S.A.; Brandt, J.; Miller, T.A.; Katzner, T.E. Meteorological and environmental variables affect flight behaviour and decision-making of an obligate soaring bird, the California Condor Gymnogyps californianus. IBIS 2018, 160, 36–53. [Google Scholar] [CrossRef]
- Deittert, M.; Richards, A.; Toomer, C.; Pipe, A. Dynamic soaring flight in turbulence. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6012. [Google Scholar] [CrossRef]
- Panta, K.; Gramignano, J.; Moser, T.; Cheng, B.; Eslam-Panah, A. The Interaction Between a Plunging Wing and Gusty Environment. In Proceedings of the 74th Annual Meeting of the APS Division of Fluid Dynamics, Phoenix, AZ, USA, 21–23 November 2021; p. E25.004. [Google Scholar]
- Song, J.; Tobalske, B.W.; Powers, D.R.; Hedrick, T.L.; Luo, H. Three-dimensional simulation for fast forward flight of a calliope hummingbird. R. Soc. Open Sci. 2016, 3, 160230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grönroos, J.; Green, M.; Alerstam, T. To fly or not to fly depending on winds: Shorebird migration in different seasonal wind regimes. Anim. Behav. 2012, 83, 1449–1457. [Google Scholar] [CrossRef]
- Airy, H. The soaring of birds. Nature 1883, 28, 103. [Google Scholar] [CrossRef]
- Garstang, M.; Greco, S.; Emmitt, G.D.; Miller, T.A.; Lanzone, M. An Instrumented Golden Eagle’s (Aquila chrysaetos) Long-Distance Flight Behavior. Animals 2022, 12, 1470. [Google Scholar] [CrossRef]
- Drake, V.; Farrow, R. The influence of atmospheric structure and motions on insect migration. Annu. Rev. Entomol. 1988, 33, 183–210. [Google Scholar] [CrossRef]
- Mikkola, K. Direction of insect migrations in relation to the wind. In Insect Flight; Springer: Berlin/Heidelberg, Germany, 1986; pp. 152–171. [Google Scholar]
- El Jundi, B.; Dacke, M. Insect orientation: The Drosophila wind compass pathway. Curr. Biol. 2021, 31, R83–R85. [Google Scholar] [CrossRef]
- Cheng, B. Flying of Insects. In Bioinspired Structures and Design; Cambridge University Press: Cambridge, UK, 2020; pp. 271–299. [Google Scholar]
- Jiao, Y.; Ling, F.; Heydari, S.; Heess, N.; Merel, J.; Kanso, E. Learning to swim in potential flow. Phys. Rev. Fluids 2021, 6, 050505. [Google Scholar] [CrossRef]
- Castro-Santos, T. Optimal swim speeds for traversing velocity barriers: An analysis of volitional high-speed swimming behavior of migratory fishes. J. Exp. Biol. 2005, 208, 421–432. [Google Scholar] [CrossRef] [Green Version]
- Bleckmann, H.; Zelick, R. Lateral line system of fish. Integr. Zool. 2009, 4, 13–25. [Google Scholar] [CrossRef]
- Song, J.; Zhong, Y.; Luo, H.; Ding, Y.; Du, R. Hydrodynamics of larval fish quick turning: A computational study. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2515–2523. [Google Scholar] [CrossRef]
- Maxey, M.; Corrsin, S. Gravitational settling of aerosol particles in randomly oriented cellular flow fields. J. Atmos. Sci. 1986, 43, 1112–1134. [Google Scholar] [CrossRef]
- Nielsen, P. Turbulence effects on the settling of suspended particles. J. Sediment. Res. 1993, 63, 835–838. [Google Scholar] [CrossRef]
- Laurent, K.M.; Fogg, B.; Ginsburg, T.; Halverson, C.; Lanzone, M.J.; Miller, T.A.; Winkler, D.W.; Bewley, G.P. Turbulence explains the accelerations of an eagle in natural flight. Proc. Natl. Acad. Sci. USA 2021, 118, e2102588118. [Google Scholar] [CrossRef]
- Bollt, S.A.; Bewley, G.P. How to extract energy from turbulence in flight by fast tracking. J. Fluid Mech. 2021, 921, A18. [Google Scholar] [CrossRef]
- McGee, T.G.; Hedrick, J.K. Path planning and control for multiple point surveillance by an unmanned aircraft in wind. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 4261–4266. [Google Scholar] [CrossRef]
- Tran, N.K.; Bulka, E.; Nahon, M. Quadrotor control in a wind field. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 320–328. [Google Scholar] [CrossRef]
- Sydney, N.; Smyth, B.; Paley, D.A. Dynamic control of autonomous quadrotor flight in an estimated wind field. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 3609–3616. [Google Scholar] [CrossRef] [Green Version]
- Reddy, G.; Wong-Ng, J.; Celani, A.; Sejnowski, T.J.; Vergassola, M. Glider soaring via reinforcement learning in the field. Nature 2018, 562, 236. [Google Scholar] [CrossRef]
- Koehl, M.; Cooper, T. Swimming in an unsteady world. Integr. Comp. Biol. 2015, 55, 683–697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ristevski, S.; Koru, A.T.; Yucelen, T.; Dogan, K.M.; Muse, J.A. Experimental results of a quadrotor UAV with a model reference adaptive controller in the presence of unmodeled dynamic. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1381. [Google Scholar] [CrossRef]
- Arabi, E.; Gruenwald, B.C.; Yucelen, T.; Nguyen, N.T. A set-theoretic model reference adaptive control architecture for disturbance rejection and uncertainty suppression with strict performance guarantees. Int. J. Control 2018, 91, 1195–1208. [Google Scholar] [CrossRef]
- Woodbury, T.D.; Dunn, C.; Valasek, J. Autonomous soaring using reinforcement learning for trajectory generation. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0990. [Google Scholar] [CrossRef] [Green Version]
- Reddy, G.; Celani, A.; Sejnowski, T.J.; Vergassola, M. Learning to soar in turbulent environments. Proc. Natl. Acad. Sci. USA 2016, 113, E4877–E4884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biferale, L.; Bonaccorso, F.; Buzzicotti, M.; Clark Di Leoni, P.; Gustavsson, K. Zermelo’s problem: Optimal point-to-point navigation in 2D turbulent flows using reinforcement learning. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 103138. [Google Scholar] [CrossRef]
- Gunnarson, P.; Mandralis, I.; Novati, G.; Koumoutsakos, P.; Dabiri, J.O. Learning efficient navigation in vortical flow fields. Nat. Commun. 2021, 12, 7143. [Google Scholar] [CrossRef]
- Baumgartner, K.A.; Ferrari, S.; Rao, A.V. Optimal control of an underwater sensor network for cooperative target tracking. IEEE J. Ocean. Eng. 2009, 34, 678–697. [Google Scholar] [CrossRef]
- Ferrari, S.; Foderaro, G. A potential field approach to finding minimum-exposure paths in wireless sensor networks. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 335–341. [Google Scholar] [CrossRef]
- Zadeh, S.M.; Powers, D.M.; Yazdani, A.M.; Sammut, K.; Atyabi, A. Differential evolution for efficient AUV path planning in time variant uncertain underwater environment. arXiv 2016, arXiv:1604.02523. [Google Scholar]
- Robinson, A.R. Forecasting and simulating coastal ocean processes and variabilities with the Harvard Ocean Prediction System. In Coastal Ocean Prediction; AGU Coastal and Estuarine Studies Series; American Geophysical Union: Washington, DC, USA, 1999; pp. 77–100. [Google Scholar]
- Robinson, A. Physical processes, field estimation and an approach to interdisciplinary ocean modeling. Earth-Sci. Rev. 1996, 40, 3–54. [Google Scholar] [CrossRef]
- Robinson, A.R.; Arango, H.G.; Warn-Varnas, A.; Leslie, W.G.; Miller, A.J.; Haley, P.J.; Lozano, C.J. Real-time regional forecasting. Elsevier Oceanogr. Ser. 1996, 61, 377–410. [Google Scholar] [CrossRef]
- Hollinger, G.A.; Pereira, A.A.; Binney, J.; Somers, T.; Sukhatme, G.S. Learning uncertainty in ocean current predictions for safe and reliable navigation of underwater vehicles. J. Field Robot. 2016, 33, 47–66. [Google Scholar] [CrossRef]
- Smith, R.N.; Chao, Y.; Li, P.P.; Caron, D.A.; Jones, B.H.; Sukhatme, G.S. Planning and implementing trajectories for autonomous underwater vehicles to track evolving ocean processes based on predictions from a regional ocean model. Int. J. Robot. Res. 2010, 29, 1475–1497. [Google Scholar] [CrossRef] [Green Version]
- Burnett, W.; Harper, S.; Preller, R.; Jacobs, G.; LaCroix, K. Overview of operational ocean forecasting in the US Navy: Past, present, and future. Oceanography 2014, 27, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Langelaan, J.W. Gust energy extraction for mini and micro uninhabited aerial vehicles. J. Guid. Control Dyn. 2009, 32, 464–473. [Google Scholar] [CrossRef]
- Andersson, K.; Kaminer, I.; Dobrokhodov, V.; Cichella, V. Thermal centering control for autonomous soaring: Stability analysis and flight test results. J. Guid. Control Dyn. 2012, 35, 963–975. [Google Scholar] [CrossRef]
- Gavrilovic, N.; Benard, E.; Pastor, P.; Moschetta, J.M. Performance improvement of small unmanned aerial vehicles through gust energy harvesting. J. Aircr. 2018, 55, 741–754. [Google Scholar] [CrossRef] [Green Version]
- Kawanisi, K.; Shiozaki, R. Turbulent effects on the settling velocity of suspended sediment. J. Hydraul. Eng. 2008, 134, 261–266. [Google Scholar] [CrossRef]
- Janhäll, S. Review on urban vegetation and particle air pollution–Deposition and dispersion. Atmos. Environ. 2015, 105, 130–137. [Google Scholar] [CrossRef]
- Kronenburg, A.; Bilger, R.; Kent, J. Modeling soot formation in turbulent methane—Air jet diffusion flames. Combust. Flame 2000, 121, 24–40. [Google Scholar] [CrossRef]
- Aliseda, A.; Cartellier, A.; Hainaux, F.; Lasheras, J.C. Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 2002, 468, 77–105. [Google Scholar] [CrossRef] [Green Version]
- Good, G.; Ireland, P.; Bewley, G.; Bodenschatz, E.; Collins, L.; Warhaft, Z. Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 2014, 759, R3. [Google Scholar] [CrossRef]
- Maxey, M. The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 1987, 174, 441–465. [Google Scholar] [CrossRef]
- Wang, L.P.; Maxey, M.R. Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 1993, 256, 27–68. [Google Scholar] [CrossRef] [Green Version]
- Nogar, S.M.; Serrani, A.; Gogulapati, A.; McNamara, J.J.; Oppenheimer, M.W.; Doman, D.B. Design and evaluation of a model-based controller for flapping-wing micro air vehicles. J. Guid. Control Dyn. 2018, 41, 2513–2528. [Google Scholar] [CrossRef]
- Sigthorsson, D.; Oppenheimer, M.; Doman, D. Insect sized flapping wing vehicles versus rotorcrafts, a comparative study. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 28. [Google Scholar] [CrossRef]
- Townsend, A. The Structure of Turbulent Shear Flow; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Yang, H.; Jing, D.; Tarokh, V.; Bewley, G.; Ferrari, S. Flow parameter estimation based on on-board measurements of air vehicle traversing turbulent flows. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021; p. 0380. [Google Scholar] [CrossRef]
- Tom, J.; Bragg, A.D. Multiscale preferential sweeping of particles settling in turbulence. J. Fluid Mech. 2019, 871, 244–270. [Google Scholar] [CrossRef]
- Stommel, H. Trajectories of small bodies sinking slowly through convection cells. J. Mar. Res. 1949, 8, 24–29. [Google Scholar]
- Langmuir, I. Surface motion of water induced by wind. Science 1938, 87, 119–123. [Google Scholar] [CrossRef]
- Maxey, M. The motion of small spherical particles in a cellular flow field. Phys. Fluids 1987, 30, 1915–1928. [Google Scholar] [CrossRef]
- Riazi, A.; Türker, U. The drag coefficient and settling velocity of natural sediment particles. Comput. Part. Mech. 2019, 6, 427–437. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Fiorelli, E.; Leonard, N.E.; Bhatta, P.; Paley, D.A.; Bachmayer, R.; Fratantoni, D.M. Multi-AUV control and adaptive sampling in Monterey Bay. IEEE J. Ocean. Eng. 2006, 31, 935–948. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Zhong, Y.D.; Leonard, N.E. Multi-robot task allocation games in dynamically changing environments. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8678–8684. [Google Scholar] [CrossRef]
- Wangermann, J.P.; Stengel, R.F. Optimization and coordination of multiagent systems using principled negotiation. J. Guid. Control Dyn. 1999, 22, 43–50. [Google Scholar] [CrossRef]
- Chung, T.H.; Clement, M.R.; Day, M.A.; Jones, K.D.; Davis, D.; Jones, M. Live-fly, large-scale field experimentation for large numbers of fixed-wing UAVs. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Hauert, S.; Leven, S.; Varga, M.; Ruini, F.; Cangelosi, A.; Zufferey, J.C.; Floreano, D. Reynolds flocking in reality with fixed-wing robots: Communication range vs. maximum turning rate. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 5015–5020. [Google Scholar] [CrossRef] [Green Version]
- Preiss, J.A.; Honig, W.; Sukhatme, G.S.; Ayanian, N. Crazyswarm: A large nano-quadcopter swarm. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3299–3304. [Google Scholar] [CrossRef]
- Preiss, J.A.; Hönig, W.; Ayanian, N.; Sukhatme, G.S. Downwash-aware trajectory planning for large quadrotor teams. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 250–257. [Google Scholar] [CrossRef] [Green Version]
- Yang, H. Particles in Cellular Flow. Available online: https://youtu.be/o2OF5Et1opA (accessed on 4 August 2021).
- Wen, L.; Tao, G.; Yang, H.; Yang, Y. Aircraft turbulence compensation using adaptive multivariable disturbance rejection techniques. J. Guid. Control Dyn. 2015, 38, 954–963. [Google Scholar] [CrossRef]
- Iliff, K.W. Identification and stochastic control of an aircraft flying in turbulence. J. Guid. Control 1978, 1, 101–108. [Google Scholar] [CrossRef]
- Abdulrahim, M.; Mohamed, A.; Watkins, S. Control strategies for flight in extreme turbulence. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; p. 1909. [Google Scholar] [CrossRef]
- Foster, N.; Postlethwaite, I.; Walker, D. Rotorcraft control system design for rejection of atmospheric turbulence. In Proceedings of the IEE Colloquium on Multivariable Methods for Flight Control Applications, London, UK, 25 May 1994; pp. 6/1–6/4. [Google Scholar]
- Psiaki, M.L.; Stengel, R.F. Analysis of aircraft control strategies for microburst encounter. J. Guid. Control Dyn. 1985, 8, 553–559. [Google Scholar] [CrossRef]
- Psiaki, M.L.; Stengel, R.F. Optimal flight paths through microburst wind profiles. J. Aircr. 1986, 23, 629–635. [Google Scholar] [CrossRef]
- Stratton, D.; Stengel, R. Real-time decision aiding: Aircraft guidance for wind shear avoidance. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 117–124. [Google Scholar] [CrossRef]
- Elmeseiry, N.; Alshaer, N.; Ismail, T. A detailed survey and future directions of unmanned aerial vehicles (uavs) with potential applications. Aerospace 2021, 8, 363. [Google Scholar] [CrossRef]
- PS, R.; Jeyan, M.L. Mini Unmanned Aerial Systems (UAV)-A Review of the Parameters for Classification of a Mini UAV. Int. J. Aviat. Aeronaut. Aerosp. 2020, 7, 5. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Cambridge Philos. Soc. 1901, 9, 1–141. [Google Scholar]
- Solberg, J. Susceptibility of Quadcopter Flight to Turbulence. Master’s Thesis, Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY, USA, 2018. [Google Scholar]
- Hull, D.G. Fundamentals of Airplane Flight Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 19. [Google Scholar] [CrossRef]
- Seddon, J.M.; Newman, S. Basic Helicopter Aerodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ferrari, S.; Stengel, R.F. Online adaptive critic flight control. J. Guid. Control Dyn. 2004, 27, 777–786. [Google Scholar] [CrossRef] [Green Version]
- Stengel, R.F. Optimal Control and Estimation; Courier Corporation: North Chelmsford, MA, USA, 1994. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 1. [Google Scholar]
- Pruppacher, H.R.; Klett, J.D. Microstructure of atmospheric clouds and precipitation. In Microphysics of Clouds and Precipitation; Springer: Berlin/Heidelberg, Germany, 1978; pp. 9–55. [Google Scholar] [CrossRef]
- Watanabe, H.; Kurose, R.; Komori, S.; Pitsch, H. Effects of radiation on spray flame characteristics and soot formation. Combust. Flame 2008, 152, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, S. Multiobjective algebraic synthesis of neural control systems by implicit model following. IEEE Trans. Neural Netw. 2009, 20, 406–419. [Google Scholar] [CrossRef] [PubMed]
- Wood, R.J. Design, fabrication, and analysis of a 3DOF, 3cm flapping-wing MAV. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1576–1581. [Google Scholar] [CrossRef]
- Galkin, B.; Kibilda, J.; DaSilva, L.A. UAVs as mobile infrastructure: Addressing battery lifetime. IEEE Commun. Mag. 2019, 57, 132–137. [Google Scholar] [CrossRef] [Green Version]
- Murray, R.M. Optimization-Based Control; California Institute of Technology: Pasadena, CA, USA, 2009; pp. 111–128. [Google Scholar]
- Chabot, D. Trends in drone research and applications as the Journal of Unmanned Vehicle Systems turns five. J. Unmanned Veh. Syst. 2018, 6, 6–15. [Google Scholar] [CrossRef] [Green Version]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned aerial vehicles (UAVs): A survey on civil applications and key research challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Wonham, W.M.; Johnson, C.D. Optimal bang-bang control with quadratic performance index. J. Basic Eng. 1964, 86, 107–115. [Google Scholar] [CrossRef]



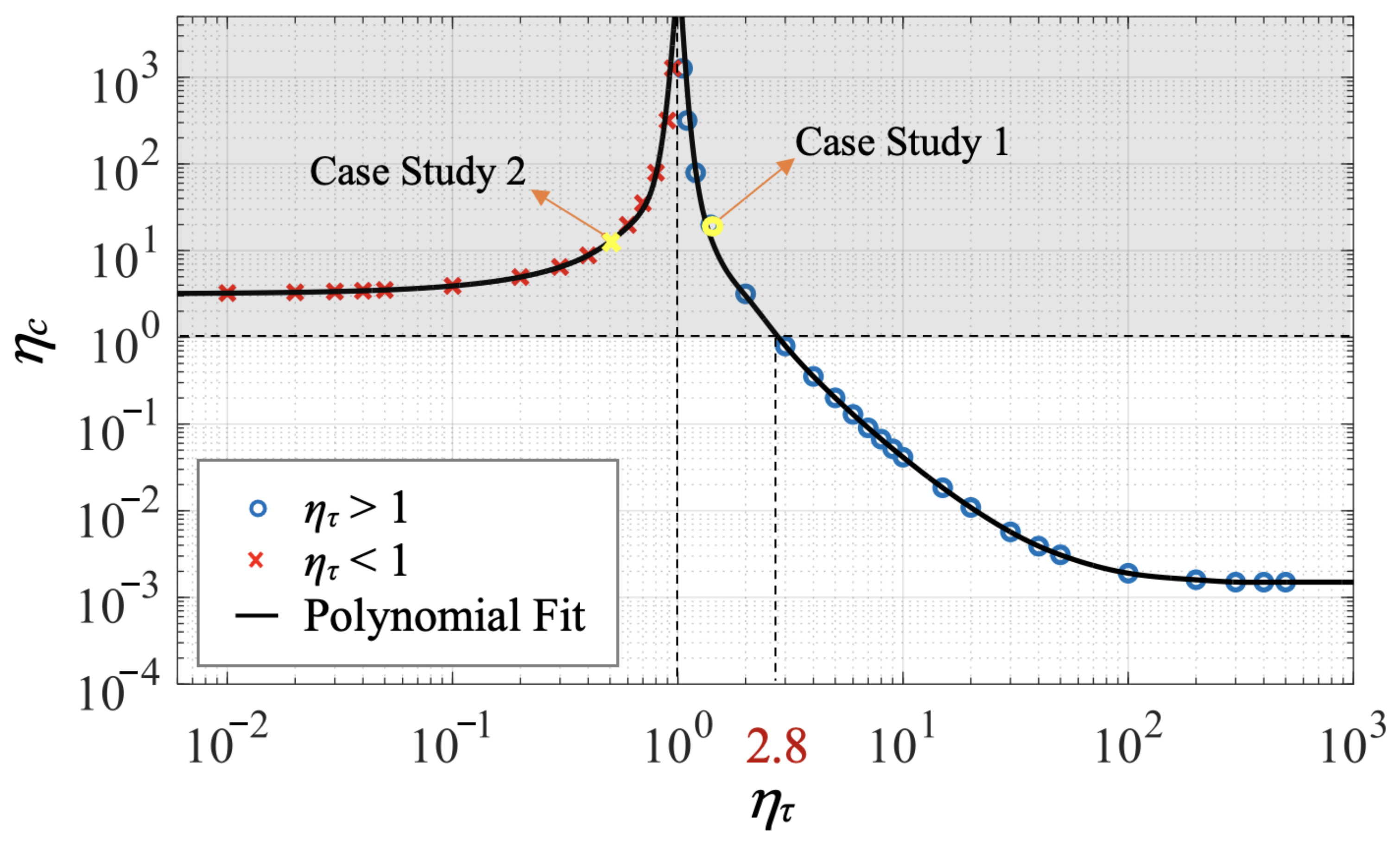
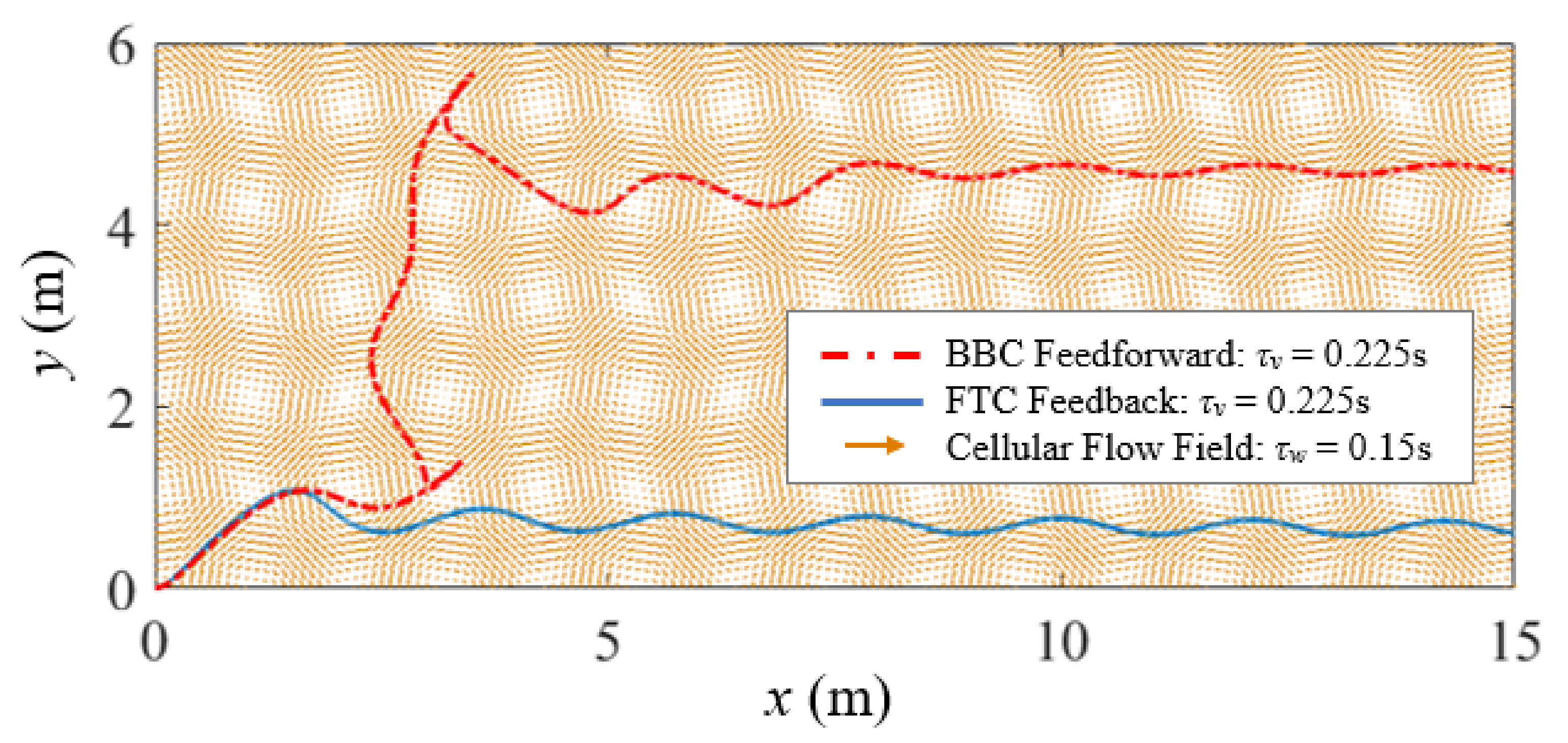
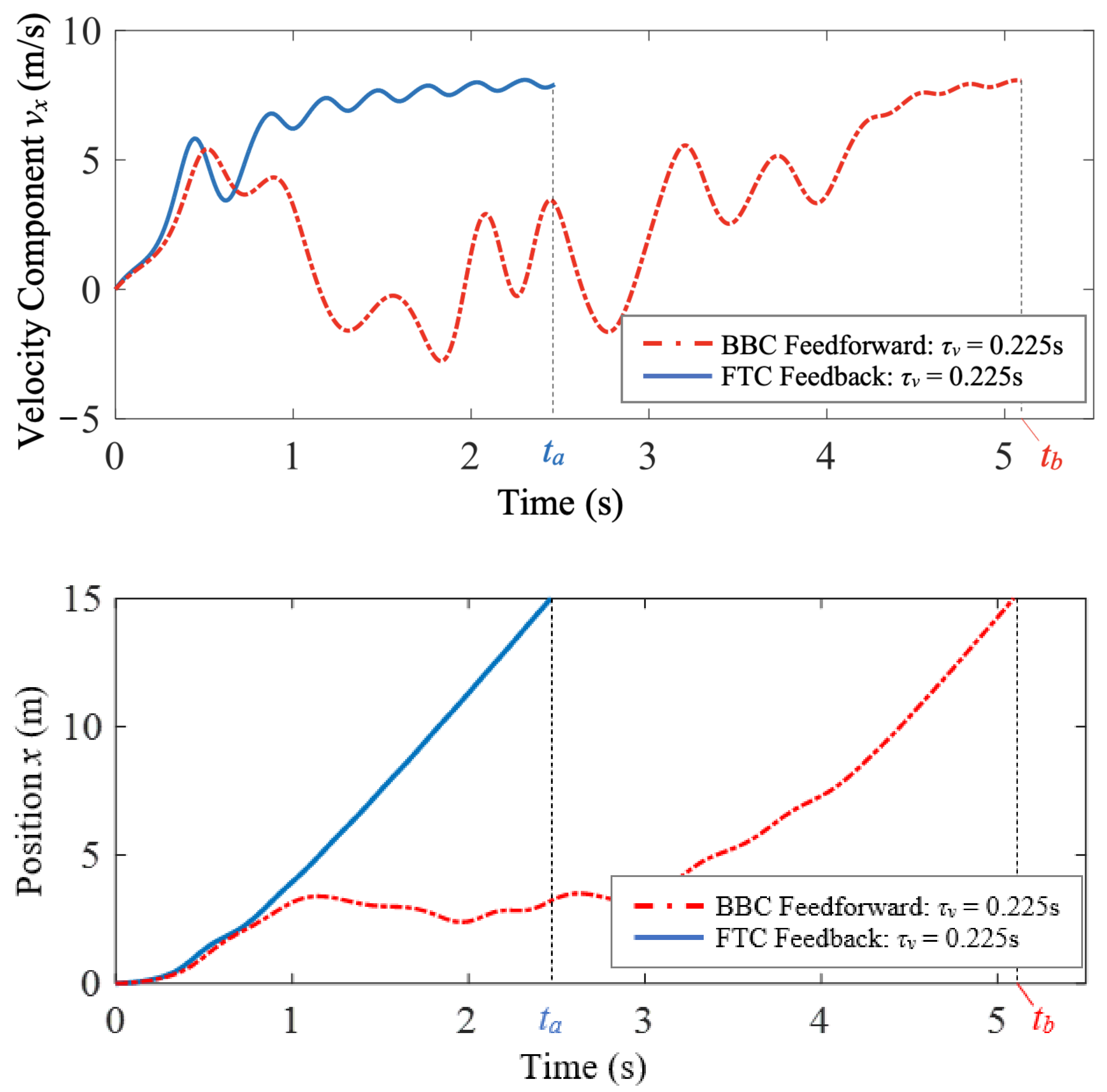
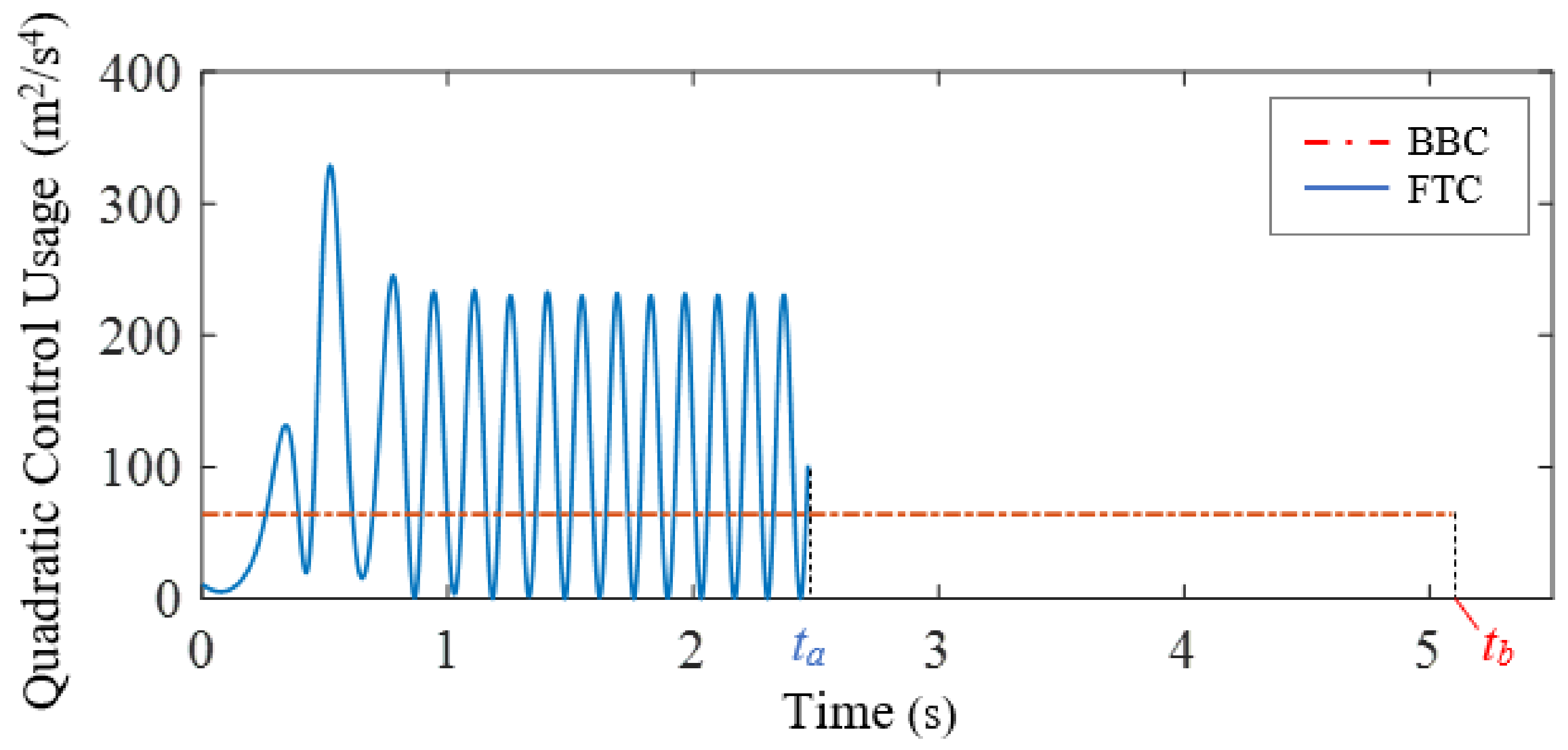
| Controller | (s) | (m) | C (m2/s3) |
|---|---|---|---|
| FTC | 2.47 | 15.00 | 266.73 |
| BBC | 5.09 | 15.00 | 325.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Bewley, G.P.; Ferrari, S. A Fast-Tracking-Particle-Inspired Flow-Aided Control Approach for Air Vehicles in Turbulent Flow. Biomimetics 2022, 7, 192. https://doi.org/10.3390/biomimetics7040192
Yang H, Bewley GP, Ferrari S. A Fast-Tracking-Particle-Inspired Flow-Aided Control Approach for Air Vehicles in Turbulent Flow. Biomimetics. 2022; 7(4):192. https://doi.org/10.3390/biomimetics7040192
Chicago/Turabian StyleYang, Hengye, Gregory P. Bewley, and Silvia Ferrari. 2022. "A Fast-Tracking-Particle-Inspired Flow-Aided Control Approach for Air Vehicles in Turbulent Flow" Biomimetics 7, no. 4: 192. https://doi.org/10.3390/biomimetics7040192





