Crossover Induced Electron Pairing and Superconductivity by Kinetic Renormalization in Correlated Electron Systems
Abstract
:1. Introduction
2. Model Hamiltonians
3. Optimization Variational Monte Carlo Method
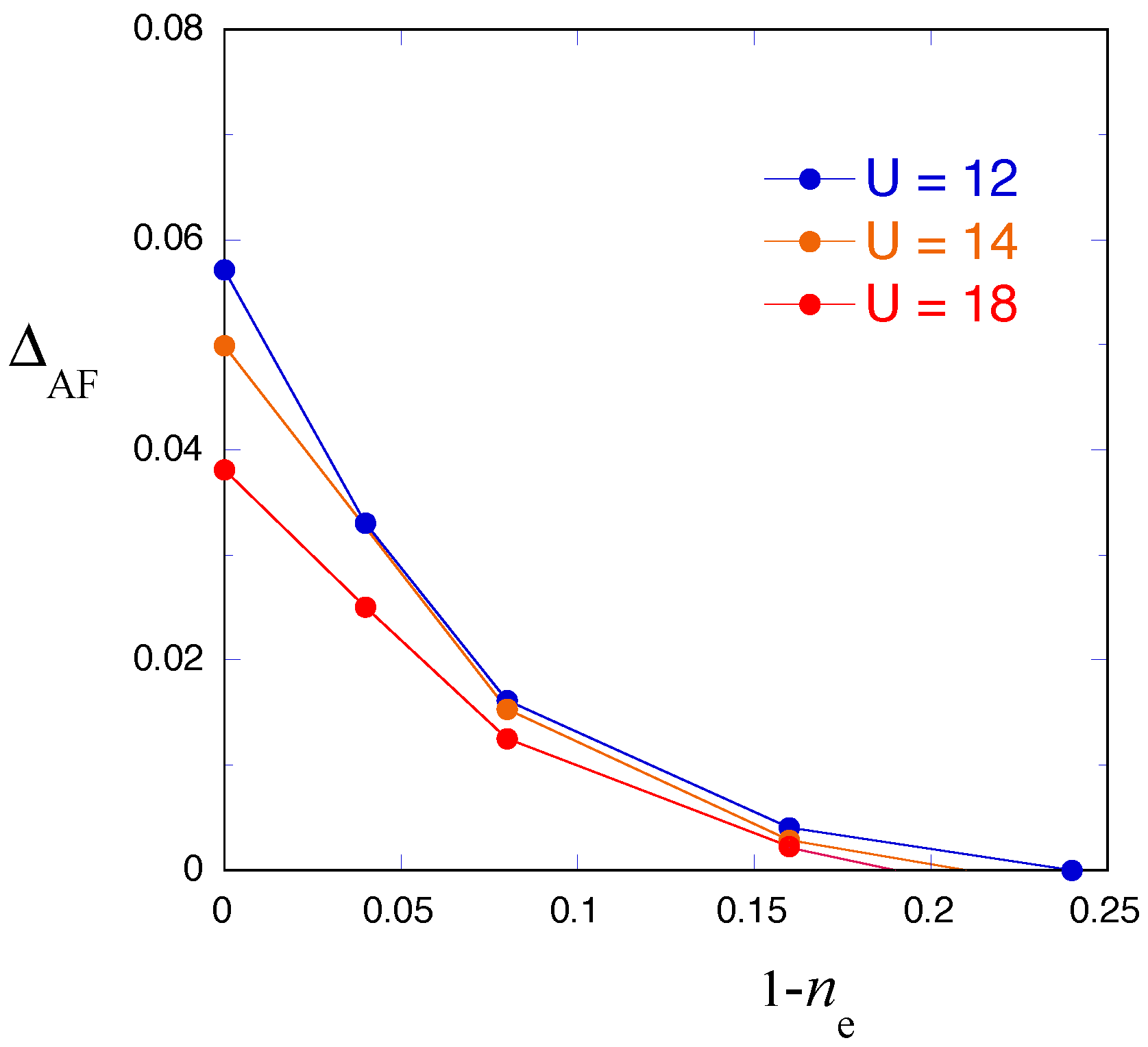
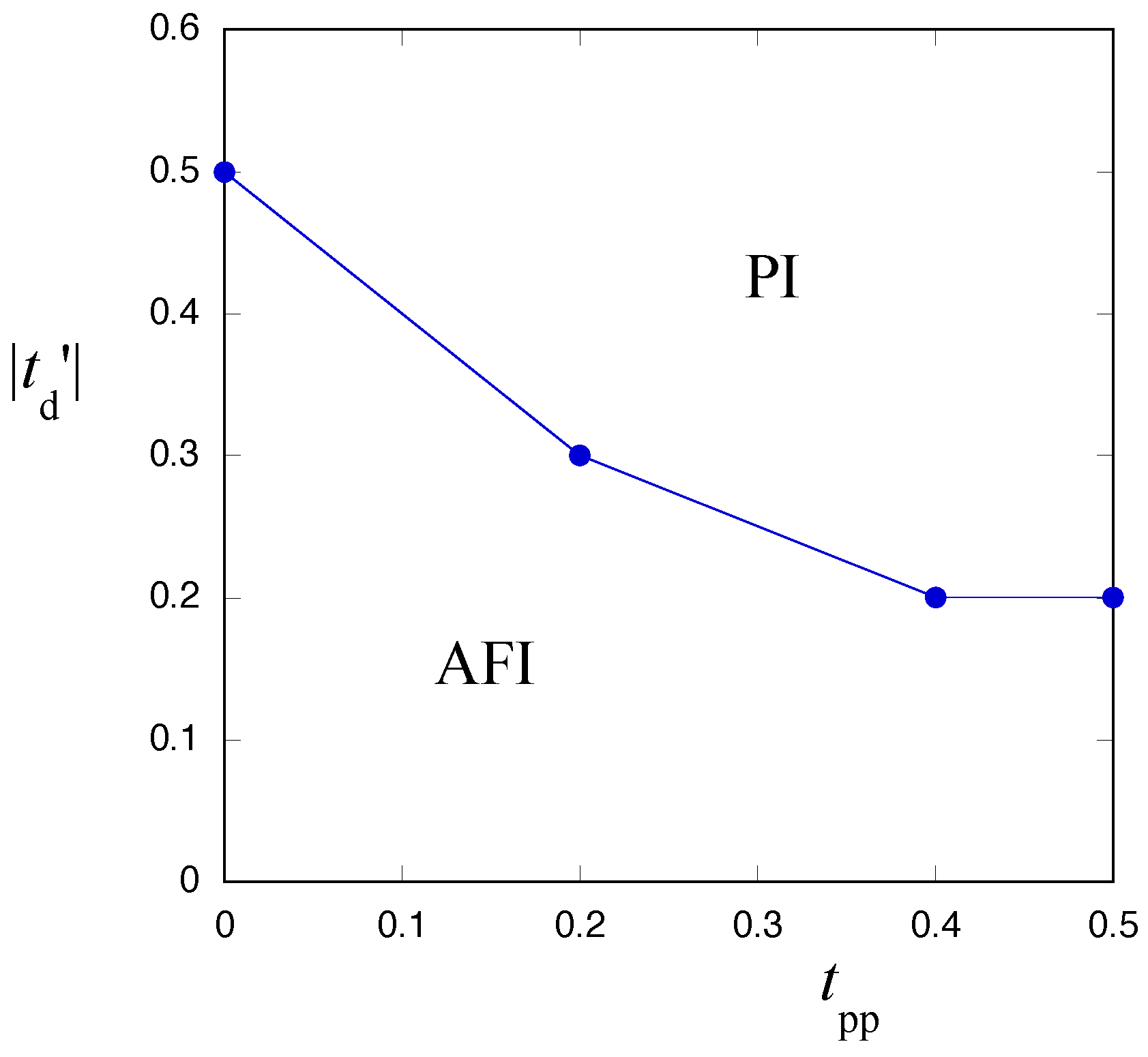
4. Antiferromagnetic Crossover
5. Correlated Superconductivity
6. Phase Separation
7. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| VMC | variational Monte Carlo method |
| AF | antiferromagnetic |
| SC | superconductivity or superconducting |
| 2D | two-dimensional |
| AFI | antiferromagnetic insulator |
| PI | paramagnetic insulator |
References
- Bednorz, J.B.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. 1986, B64, 189–193. [Google Scholar] [CrossRef]
- Emery, V.J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 1987, 58, 2794. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, J.E.; Loh, E.Y.; Scalapinom, D.J.; Tang, S. Pairing interaction in CuO clusters. Phys. Rev. B 1989, B39, 243. [Google Scholar] [CrossRef]
- Scalettar, R.T.; Scalapino, D.J.; Sugar, R.L.; White, S.R. Antiferromagnetic, charge-transfer, and pairing correlations in the three-band Hubbard model. Phys. Rev. B 1991, B44, 770. [Google Scholar] [CrossRef]
- Oguri, A.; Asahatam, T.; Maekawa, S. Gutzwiller wave function in the three-band Hubarf model: A variational Monte Carlo study. Phys. Rev. B 1994, B49, 6880. [Google Scholar] [CrossRef]
- Koikegami, S.; Yamada, K. Antiferromagnetic and superconducting correlations on the d-p model. J. Phys. Soc. Jpn. 2000, 69, 768–776. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Ground state of the three-band Hubbard model. Phys. Rev. B 2001, B64, 184509. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconducting gap of the two-dimensional d-p model with small Ud. J. Phys. Soc. Jpn. 2001, 70, 3499–3502. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Lattice distortions, incommensurability, and stripes in the electronic model for high-Tc cuprates. Phys. Rev. B 2003, B67, 132408. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconductivity in Sr2RuO4 mediated by Coulomb scattering. Phys. Rev. B 2003, B67, 134517. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconductivity in multilayer perovskite. J. Phys. Soc. Jpn. 2006, 75, 034715. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional d-p model. J. Phys. Soc. 2009, 78, 031706. [Google Scholar] [CrossRef]
- Weber, C.; Lauchi, A.; Mila, F.; Giamarchi, T. Orbital currents in extended Hubbard model of High-Tc cuprate superconductors. Phys. Rev. Lett. 2009, 102, 017005. [Google Scholar] [CrossRef] [PubMed]
- Lau, B.; Berciu, M.; Sawatzky, G.A. High spin polaron in lightly doped CuO2 planes. Phys. Rev. Lett. 2011, 106, 036401. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.; Giamarchi, T.; Varma, C.M. Phase diagram of a three-orbital model for high-Tc cuprate superconductors. Phys. Rev. Lett. 2014, 112, 117001. [Google Scholar] [CrossRef] [PubMed]
- Avella, A.; Mancini, F.; Paolo, F.; Plekhanov, E. Emery vs Hubbard model for cuprate superconductors: A composite operator method study. Eur. Phys. J. 2013, B86, 265. [Google Scholar] [CrossRef]
- Ebrahimnejad, H.; Sawatzky, G.A.; Berciu, M. Differences between the insulating limit quasiparticles of one-band and three-band cuprate models. J. Phys. Cond. Matter 2016, 28, 105603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tamura, S.; Yokoyama, H. Variational study of magnetic ordered state in d-p model. Phys. Procedia 2016, 81, 5. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. Roy. Soc. Lond. 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands III. Proc. Roy. Soc. Lond. 1964, 281, 401–419. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 1963, 10, 159. [Google Scholar] [CrossRef]
- Zhang, S.; Carlson, J.; Gubernatis, J.E. Constrained path Monte Carlo method for fermion ground states. Phys. Rev. B 1997, B55, 7464. [Google Scholar] [CrossRef]
- Zhang, S.; Carlson, J.; Gubernatis, J.E. Pairing correlation in the two-dimensional Hubbard model. Phys. Rev. Lett. 1997, 78, 4486. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y. Exact results in strongly correlated electrons. Int. J. Mod. Phys. 1996, B10, 3383. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y. Ground state of the Kondo-Hubbard model at half-filling. Phys. Rev. Lett. 1995, 74, 4939. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, T.; Yamaji, K.; Yanagisawa, T. Variational Monte Carlo indications of d-wave superconductivity in the two-dimensional Hubbard model. J. Phys. Soc. Jpn. 1997, 66, 294–297. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Nakanishi, T.; Koike, S. Variational Monte Carlo study on the superconductivity in the two-dimensional Hubbard model. Physica 1998, C304, 225–238. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Koike, S. Bulk limit of superconducting condensation energy in 2D Hubbard model. Physica 2000, 284, 415–416. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Miyazaki, M.; Kadono, R. Superconducting condensation energy of the two-dimensional Hubbard model in the large-negative-t’ region. J. Phys. Soc. Jpn. 2011, 80, 083702. [Google Scholar] [CrossRef]
- Hardy, T.M.; Hague, P.; Samson, J.H.; Alexandrov, A.S. Superconductivity in a Hubbard-Fröhlich model in cuprates. Phys. Rev. B 2009, B79, 212501. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Correlated-electron systems and high-temperature superconductivity. J. Mod. Phys. 2013, 4, 33. [Google Scholar] [CrossRef]
- Bulut, N. dx2−y2 superconductivity and the Hubbard model. Adv. Phys. 2002, 51, 1587–1667. [Google Scholar] [CrossRef]
- Yokoyama, H.; Tanaka, Y.; Ogata, M.; Tsuchiura, H. Crossover of superconducting properties and kinetic-energy gain in two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2004, 73, 1119–1122. [Google Scholar] [CrossRef]
- Aimi, T.; Imada, M. Does simple two-dimensional Hubbard model account for high-Tc superconductivity in copper oxides? J. Phys. Soc. Jpn. 2007, 76, 113708. [Google Scholar] [CrossRef]
- Miyazaki, M.; Yanagisawa, T.; Yamaji, K. Diagonal stripe states in th elight-doping region in the two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2004, 73, 1643–1646. [Google Scholar] [CrossRef]
- Yanagisawa, T. Phase diagram of the t-U2 Hamiltonian of the weak coupling Hubbard model. N. J. Phys. 2008, 10, 023014. [Google Scholar] [CrossRef]
- Yanagisawa, T. Enhanced pair correlation functions in the two-dimensional Hubbard model. N. J. Phys. 2013, 15, 033012. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T. Crossover from wealy to strongly correlated regions in the two-dimensional Hubbard model—Off-diagonal Monte Carlo studies of Hubbard model II. J. Phys. Soc. Jpn. 2016, 85, 114707. [Google Scholar] [CrossRef]
- Noack, R.M.; White, S.R.; Scalapino, D.J. The doped two-chain Hubbard model. Europhys. Lett. 1995, 30, 163. [Google Scholar] [CrossRef]
- Noack, R.M.; Bulut, N.; Scalapino, D.J.; Zacher, M.J. Enhanced dx2−y2 pairing correlations in the two-leg Hubbard ladder. Phys. Rev. B 1997, B56, 7162. [Google Scholar] [CrossRef]
- Yamaji, K.; Shimoi, Y.; Yanagisawa, T. Superconductivity indications of the two-chain Hubbard model due to the two-band effect. Physica 1994, C235, 2221–2222. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y.; Yamaji, K. Superconducting phase of a two-chain Hubbard model. Phys. Rev. B 1995, B52, R3860. [Google Scholar] [CrossRef]
- Nakano, T.; Kuroki, K.; Onari, S. Superconductivity due to spin fluctuations originating from multiple Fermi surfaces in the double chain superconductor Pr2Ba4Cu7O15−δ. Phys. Rev. B 2007, B76, 014515. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transitions; Taylor and Francis Ltd.: London, UK, 1974. [Google Scholar]
- Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism; Springer-Verlag: Berlin, Germany, 1985. [Google Scholar]
- Yosida, K. Theory of Magnetism; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Tranquada, J.M.; Axe, J.D.; Ichikawa, N.; Nakamura, Y.; Uchida, S.; Nachumi, B. Neutron-scattering study of stripe-phase order of holes and spins in La1.48Nd0.4Sr0.12CuO4. Phys. Rev. B 1996, B54, 7489. [Google Scholar] [CrossRef]
- Suzuki, T.; Goto, T.; Chiba, K.; Shinoda, T.; Fukase, T.; Kimura, H.; Yamada, K.; Ohashi, M.; Yamaguchi, Y. Observation of modulated magnetic long-range order in La1.88Sr0.12CuO4. Phys. Rev. B 1998, B57, R3229. [Google Scholar] [CrossRef]
- Yamada, K.; Lee, C.H.; Kurahashi, K.; Wada, J.; Wakimoto, S.; Ueki, S.; Kimura, H.; Endoh, Y.; Hosoya, S.; Shirane, G.; et al. Doping dependence of the spatially modulated dynamical spin correlations and the superconducting-transition temperature in La2−xSrxCuO4. Phys. Rev. B 1998, B57, 6165. [Google Scholar] [CrossRef]
- Arai, M.; Nishijima, T.; Endoh, Y.; Egami, T.; Tajima, S.; Tomimoto, K.; Shiohara, Y.; Takahashi, M.; Garrett, A.; Bennington, S.M. Incommensurate spin dynamics of underdoped superconductor YBa2Cu3Y6.7. Phys. Rev. Lett. 1999, 83, 608. [Google Scholar] [CrossRef]
- Mook, H.A.; Dai, P.; Dogan, F.; Hunt, R.D. One-dimensional nature of the magnetic fluctuations in YBa2Cu3O6.6. Nature 2000, 404, 729. [Google Scholar] [CrossRef] [PubMed]
- Wakimoto, S.; Birgeneau, R.J.; Kastner, M.A.; Lee, Y.S.; Erwin, R.; Gehring, P.M.; Lee, S.H.; Fujita, M.; Yamada, K.; Endoh, Y.; et al. Direct observation of a one-dimensional static spin modulation in insulating La1.95Sr0.05CuO4. Phys. Rev. B 2000, B61, 3699. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the local lattice distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A. Quantum materials: shape resonances in superstripes. Nat. Phys. 2013, 9, 536. [Google Scholar] [CrossRef]
- Hoffman, J.E.; McElroy, K.; Lee, D.H.; Lang, K.M.; Eisaki, H.; Uchida, S.; Davis, J.C. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ. Science 2002, 295, 466. [Google Scholar] [CrossRef] [PubMed]
- Wise, W.D.; Boyer, M.C.; Chatterjee, K.; Kondo, T.; Takeuchi, T.; Ikuta, H.; Wang, Y.; Hudson, E.W. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 2008, 4, 696. [Google Scholar] [CrossRef]
- Hanaguri, T.; Lupien, C.; Kohsaka, Y.; Lee, D.H.; Azuma, M.; Takano, M.; Takagi, H.; Davis, J.C. A checkerboard electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2. Nature 2004, 430, 1001. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, M.; Yanagisawa, T.; Yamaji, K. Checkerboard states in the two-dimensional Hubbard model with the Bi2212-type band. J. Phys. Soc. Jpn. 2009, 78, 043706. [Google Scholar] [CrossRef]
- Koike, S.; Yamaji, K.; Yanagisawa, T. Effect of the medium-range transfer energies to the superconductivity in the two-chain Hubbard model. J. Phys. Soc. Jpn. 1999, 68, 1657–1663. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Off-diagonal wave function Monte Carlo Studies of Hubbard model I. J. Phys. Soc. Jpn. 1998, 67, 3867–3874. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M. Mott transition in cuprate high-temperature superconductors. Eur. Phys. Lett. 2014, 107, 27004. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Optimized wave funtion by kinetic renormalization effect in strongly correlated region of the three-band Hubbard model. J. Phys. Conf. Ser. 2018, 1054, 012017. [Google Scholar] [CrossRef]
- McElroy, K.; Simmonds, R.W.; Hoffman, J.E.; Lee, D.H.; Orenstein, J.; Eisaki, H.; Uchida, S.; Davis, J.C. Relating atomic-scale electronic phenomena to wave-like quasiparticle states in superconducting Bi2Sr2CaCu2O8+δ. Nature 2003, 422, 592. [Google Scholar] [CrossRef] [PubMed]
- Hussey, N.E.; Abdel-Jawad, M.; Carrington, A.; Mackenzie, A.P.; Balicas, L. A coherent three-dimensional Fermi surface in a high-transition-temperature superconductor. Nature 2003, 425, 814. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.; Haule, K.; Kotliar, G. Critical weights and waterfalls in doped charge-transfer insulators. Phys. Rev. B 2008, B78, 134519. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Schlüter, M.; Christensen, N.E. Calculation of Coulomb-interaction parameter for La2CuO4 using a constrained-density-functional approach. Phys. Rev. B 1989, B39, 9028. [Google Scholar] [CrossRef]
- Eskes, H.; Sawatzky, G.A.; Feiner, L.F. Effective transfer for singlets formed by hole doping in the high-Tc superconductors. Physica 1989, C160, 424–430. [Google Scholar] [CrossRef]
- McMahan, A.K.; Annett, J.F.; Martin, R.M. Cuprate parameters from numerical Wannier functions. Phys. Rev. B 1990, B42, 6268. [Google Scholar] [CrossRef]
- Eskes, H.; Sawatzky, G. Single-, triple-, or multiplel-band Hubbard models. Phys. Rev. B 1991, B43, 119. [Google Scholar] [CrossRef]
- Otsuka, H. Variational Monte Carlo studies of the Hubbard model in one- and two-dimensions. J. Phys. Soc. Jpn. 1992, 61, 1645–1656. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. d-wave state with multiplicative correlation factors for the Hubbard model. J. Phys. Soc. Jpn. 1999, 68, 3608–3614. [Google Scholar] [CrossRef]
- Eichenberger, D.; Baeriswyl, D. Superconductivity and antiferromagnetism in the-dimensional Hubbard model: A variational study. Phys. Rev. B 2007, B76, 180504. [Google Scholar] [CrossRef]
- Baeriswyl, D.; Eichenberger, D.; Menteshashvii, M. Variational ground states of the two-dimensional Hubbard model. N. J. Phys. 2009, 11, 075010. [Google Scholar] [CrossRef] [Green Version]
- Baeriswyl, D. Superconductivity in the repulsive Hubbards model. J. Supercond. Novel Magn. 2011, 24, 1157–1159. [Google Scholar] [CrossRef]
- Yanagisawa, T. Quantum Monte Carlo diagonalization for many-fermion systems. Phys. Rev. B 2007, B75, 224503. [Google Scholar] [CrossRef]
- Misawa, T.; Imada, M. Origin of high-Tc superconductivity in doped Hubbard models and their extensions: Roles of uniform charge fluctuations. Phys. Rev. B 2014, B90, 115137. [Google Scholar] [CrossRef]
- Kondo, J. The Physics of Dilute Magnetic Alloys; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Yuval, G.; Anderson, P.W. Exact results for the Kondo problem: one-body theory and extension to finite temperature. Phys. Rev. B 1970, B1, 1522. [Google Scholar] [CrossRef]
- Wilson, K.G. The renormalization group: Critical phenomena and the Kondo problem. Rev. Mod. Phys. 1975, 47, 773. [Google Scholar] [CrossRef]
- Nagaoka, Y. Self-consistent treatment of Kondo’s effect in dilute alloys. Phys. Rev. B 1965, 138, A1112. [Google Scholar] [CrossRef]
- Zittartz, J.; Müller-Hartmann, E. Green’s function theory of the Kondo effect in dilute magnetic alloys. Z. Phys. 1968, 212, 380–407. [Google Scholar] [CrossRef]
- Anderson, P.W.; Yuval, G.; Hamann, D.R. Exact results in the Kondo problem II. Scaling theory, qualitatively correct solution, ans some new results on one-dimensional classical statistical models. Phys. Rev. B 1970, B1, 4464. [Google Scholar] [CrossRef]
- Yanagisawa, T. Kondo effect in the presence of spin-orbit coupling. J. Phys. Soc. Jpn. 2012, 81, 094713. [Google Scholar] [CrossRef]
- Yanagisawa, T. Kondo effect in Dirac systems. J. Phys. Soc. Jpn. 2015, 84, 074705. [Google Scholar] [CrossRef]
- Yanagisawa, T. Dirac fermions and Kondo effect. J. Phys. Conf. Ser. 2015, 603, 012014. [Google Scholar] [CrossRef] [Green Version]
- Jayaprakash, C.; Krishna-murthy, H.R.; Wilkins, J.W. Two-impurity Kondo problem. Phys. Rev. Lett. 1981, 47, 737. [Google Scholar] [CrossRef]
- Jones, B.A.; Varma, C.M. Critical point in the solution of the two-impurity Kondo problem. Phys. Rev. B 1989, B40, 324. [Google Scholar] [CrossRef]
- Yanagisawa, T. Ground state and staggered susceptibility of the two-impurity Kondo problem. J. Phys. Soc. Jpn. 1989, 60, 29–32. [Google Scholar] [CrossRef]
- Ellis, R.K.; Stirling, W.J.; Webber, B.R. QCD and Collider Physics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Nozieres, P.; Schmitt-Rink, S. Bose condensation in an attractive fermi gas: From weak to strong coupling superconductivity. J. Low Temp. Phys. 1985, 59, 195–211. [Google Scholar] [CrossRef]
- Rajaraman, R. Solitons and Instantons; North-Holland: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Solyom, J. The Fermi gas model of one-dimensional conductors. Adv. Phys. 1979, 28, 201–303. [Google Scholar] [CrossRef]
- Yanagisawa, T. Chiral sine-Gordon model. Eur. Lett. 2016, 113, 41001. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T. Nambu-Goldstone bosons characterized by the order parameters in spontaneous symmetry breaking. J. Phys. Soc. Jpn. 2017, 86, 104711. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Crossover Induced Electron Pairing and Superconductivity by Kinetic Renormalization in Correlated Electron Systems. Condens. Matter 2018, 3, 26. https://doi.org/10.3390/condmat3030026
Yanagisawa T, Miyazaki M, Yamaji K. Crossover Induced Electron Pairing and Superconductivity by Kinetic Renormalization in Correlated Electron Systems. Condensed Matter. 2018; 3(3):26. https://doi.org/10.3390/condmat3030026
Chicago/Turabian StyleYanagisawa, Takashi, Mitake Miyazaki, and Kunihiko Yamaji. 2018. "Crossover Induced Electron Pairing and Superconductivity by Kinetic Renormalization in Correlated Electron Systems" Condensed Matter 3, no. 3: 26. https://doi.org/10.3390/condmat3030026
APA StyleYanagisawa, T., Miyazaki, M., & Yamaji, K. (2018). Crossover Induced Electron Pairing and Superconductivity by Kinetic Renormalization in Correlated Electron Systems. Condensed Matter, 3(3), 26. https://doi.org/10.3390/condmat3030026



