Spectral Function of a Boson Ladder in an Artificial Gauge Field
Abstract
:1. Introduction
2. Model
3. Spectral Function in the Meissner Phase for Weak Interchain Hopping
4. Spectral Function in the Vortex Phase for Weak Interchain Hopping
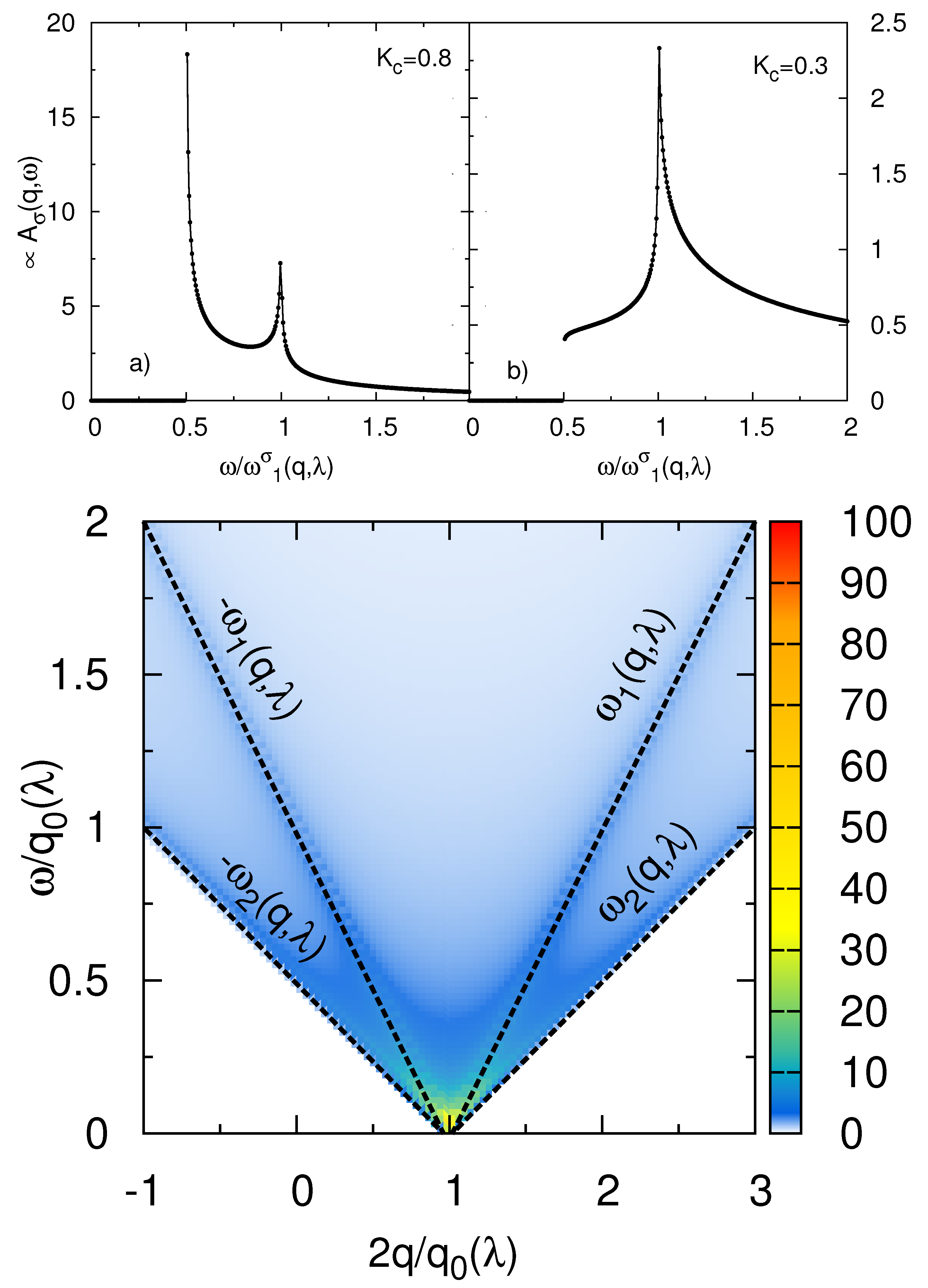
5. Spectral Functions in the Weakly Interacting Regime From Bosonization
6. Spectral Function in the Bogoliubov Theory
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kardar, M. Josephson-junction ladders and quantum fluctuations. Phys. Rev. B 1986, 33, 3125. [Google Scholar] [CrossRef] [PubMed]
- Orignac, E.; Giamarchi, T. Meissner effect in a bosonic ladder. Phys. Rev. B 2001, 64, 144515. [Google Scholar] [CrossRef] [Green Version]
- Cha, M.C.; Shin, J.G. Two peaks in the momentum distribution of bosons in a weakly frustrated two-leg optical ladder. Phys. Rev. A 2011, 83, 055602. [Google Scholar] [CrossRef]
- Tokuno, A.; Georges, A. Ground States of a Bose-Hubbard Ladder in an Artificial Magnetic Field: Field-Theoretical Approach. New J. Phys. 2014, 16, 073005. [Google Scholar] [CrossRef] [Green Version]
- Richaud, A.; Penna, V. Quantum dynamics of bosons in a two-ring ladder: Dynamical algebra, vortexlike excitations, and currents. Phys. Rev. A 2017, 96, 013620. [Google Scholar] [CrossRef] [Green Version]
- Japaridze, G.I.; Nersesyan, A.A. Magnetic-field phase transition in a one-dimensional system of electrons with attraction. JETP Lett. 1978, 27, 334. [Google Scholar]
- Pokrovsky, V.L.; Talapov, A.L. Ground State, Spectrum, and Phase Diagram of Two-Dimensional Incommensurate Crystals. Phys. Rev. Lett. 1979, 42, 65. [Google Scholar] [CrossRef]
- Schulz, H.J. Critical behavior of commensurate-incommensurate phase transitions in two dimensions. Phys. Rev. B 1980, 22, 5274. [Google Scholar] [CrossRef]
- Jaksch, D.; Zoller, P. The cold atom Hubbard toolbox. Ann. Phys. 2005, 315, 52. [Google Scholar] [CrossRef] [Green Version]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V.; Damski, B.; Sen De, A.; Sen, U. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond. Ann. Phys. 2007, 56, 243. [Google Scholar] [CrossRef] [Green Version]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef] [Green Version]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Cole, W.S.; Paramekanti, A.; Trivedi, N. Spin-Orbit Coupling In Optical Lattices. In Annual Review of Cold Atoms and Molecules; Madison, K.W., Bongs, K., Carr, L.D., Rey, A.M., Zhai, H., Eds.; World Scientific: Singapore, 2015; Volume 3, Chapter 3; p. 135. [Google Scholar] [CrossRef] [Green Version]
- Barbarino, S.; Taddia, L.; Rossini, D.; Mazza, L.; Fazio, R. Synthetic gauge fields in synthetic dimensions: interactions and chiral edge modes. New J. Phys. 2016, 18, 035010. [Google Scholar] [CrossRef] [Green Version]
- Osterloh, K.; Baig, M.; Santos, L.; Zoller, P.; Lewenstein, M. Cold Atoms in Non-Abelian Gauge Potentials: From the Hofstadter “Moth” to Lattice Gauge Theory. Phys. Rev. Lett. 2005, 95, 010403. [Google Scholar] [CrossRef] [Green Version]
- Ruseckas, J.; Juzeliūnas, G.; Öhberg, P.; Fleischhauer, M. Non-Abelian Gauge Potentials for Ultracold Atoms with Degenerate Dark States. Phys. Rev. Lett. 2005, 95, 010404. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Jimenez-Garcia, K.; Spielman, I.B. Spin-orbit-coupled Bose-Einstein condensates. Nature 2011, 471, 83. [Google Scholar] [CrossRef]
- Piraud, M.; Cai, Z.; McCulloch, I.P.; Schollwöck, U. Quantum magnetism of bosons with synthetic gauge fields in one-dimensional optical lattices: A Density Matrix Renormalization Group study. Phys. Rev. A 2014, 89, 063618. [Google Scholar] [CrossRef] [Green Version]
- Piraud, M.; Heidrich-Meisner, F.; McCulloch, I.P.; Greschner, S.; Vekua, T.; Schollwöck, U. Vortex and Meissner phases of strongly interacting bosons on a two-leg ladder. Phys. Rev. B 2015, 91, 140406. [Google Scholar] [CrossRef] [Green Version]
- Orignac, E.; Citro, R.; Di Dio, M.; De Palo, S.; Chiofalo, M.L. Incommensurate phases of a bosonic two-leg ladder under a flux. New J. Phys. 2016, 18, 055017. [Google Scholar] [CrossRef] [Green Version]
- Giamarchi, T. Quantum Physics in One Dimension; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Cazalilla, M.A.; Citro, R.; Giamarchi, T.; Orignac, E.; Rigol, M. One dimensional Bosons: From Condensed Matter Systems to Ultracold Gases. Rev. Mod. Phys. 2011, 83, 1405. [Google Scholar] [CrossRef] [Green Version]
- Kleine, A.; Kollath, C.; McCulloch, I.; Giamarchi, T.; Schollwoeck, U. Spin-charge separation in two-component Bose gases. Phys. Rev. A 2008, 77, 013607. [Google Scholar] [CrossRef] [Green Version]
- Dhar, A.; Maji, M.; Mishra, T.; Pai, R.V.; Mukerjee, S.; Paramekanti, A. Bose-Hubbard model in a strong effective magnetic field: Emergence of a chiral Mott insulator ground state. Phys. Rev. A 2012, 85, 041602. [Google Scholar] [CrossRef] [Green Version]
- Dhar, A.; Mishra, T.; Maji, M.; Pai, R.V.; Mukerjee, S.; Paramekanti, A. Chiral Mott insulator with staggered loop currents in the fully frustrated Bose-Hubbard model. Phys. Rev. B 2013, 87, 174501. [Google Scholar] [CrossRef] [Green Version]
- Petrescu, A.; Le Hur, K. Bosonic Mott Insulator with Meissner Currents. Phys. Rev. Lett. 2013, 111, 150601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petrescu, A.; Le Hur, K. Chiral Mott insulators, Meissner effect, and Laughlin states in quantum ladders. Phys. Rev. B 2015, 91, 054520. [Google Scholar] [CrossRef] [Green Version]
- Victorin, N.; Pedri, P.; Minguzzi, A. Excitation spectrum and supersolidity of a two-leg bosonic ring ladder. Phys. Rev. A 2020, arXiv:1910.06410. [Google Scholar]
- Iucci, A.; Fiete, G.A.; Giamarchi, T. Fourier transform of the 2kF Luttinger liquid density correlation function with different spin and charge velocities. Phys. Rev. B 2007, 75, 205116. [Google Scholar] [CrossRef] [Green Version]
- Fabbri, N.; Panfil, M.; Clément, D.; Fallani, L.; Inguscio, M.; Fort, C.; Caux, J.S. Dynamical structure factor of one-dimensional Bose gases: Experimental signatures of beyond-Luttinger-liquid physics. Phys. Rev. A 2015, 91, 043617. [Google Scholar] [CrossRef] [Green Version]
- Dao, T.L.; Georges, A.; Dalibard, J.; Salomon, C.; Carusotto, I. Measuring the One-Particle Excitations of Ultracold Fermionic Atoms by Stimulated Raman Spectroscopy. Phys. Rev. Lett. 2007, 98, 240402. [Google Scholar] [CrossRef] [Green Version]
- Stewart, J.T.; Gaebler, J.P.; Jin, D.S. Using photoemission spectroscopy to probe a strongly interacting Fermi gas. Nature 2008, 454, 744. [Google Scholar] [CrossRef] [Green Version]
- Strinati, M.C.; Cornfeld, E.; Rossini, D.; Barbarino, S.; Dalmonte, M.; Fazio, R.; Sela, E.; Mazza, L. Laughlin-like states in bosonic and fermionic atomic synthetic ladders. Phys. Rev. X 2017, 7, 021033. [Google Scholar]
- Celi, A.; Massignan, P.; Ruseckas, J.; Goldman, N.; Spielman, I.B.; Juzeliūnas, G.; Lewenstein, M. Synthetic Gauge Fields in Synthetic Dimensions. Phys. Rev. Lett. 2014, 112, 043001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saito, T.Y.; Furukawa, S. Devil’s staircases in synthetic dimensions and gauge fields. Phys. Rev. A 2017, 95, 043613. [Google Scholar] [CrossRef] [Green Version]
- Livi, L.F.; Cappellini, G.; Diem, M.; Franchi, L.; Clivati, C.; Frittelli, M.; Levi, F.; Calonico, D.; Catani, J.; Inguscio, M.; et al. Synthetic Dimensions and Spin-Orbit Coupling with an Optical Clock Transition. Phys. Rev. Lett. 2016, 117, 220401. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M. Effective Harmonic-Fluid Approach to Low-Energy Properties of One-Dimensional Quantum Fluids. Phys. Rev. Lett. 1981, 47, 1840. [Google Scholar] [CrossRef]
- Citro, R.; Palo, S.D.; Dio, M.D.; Orignac, E. Quantum phase transitions of a two-leg bosonic ladder in an artificial gauge field. Phys. Rev. B 2018, 97, 174523. [Google Scholar] [CrossRef] [Green Version]
- Karowski, M.; Wiesz, P. Exact form factors in (1+1)Dimensional Field theoretic models with soliton behavior. Nucl. Phys. B 1978, 139, 455. [Google Scholar] [CrossRef]
- Smirnov, F.A. Form Factors in Completely Integrable Models of Quantum Field Theory; World Scientific: Singapore, 1992. [Google Scholar]
- Babujian, H.; Fring, A.; Karowski, M.; Zapletal, A. Exact Form Factors in Integrable Quantum Field Theories: the Sine-Gordon Model. Nucl. Phys. B 1999, 538, 535. [Google Scholar] [CrossRef] [Green Version]
- Babujian, H.; Karowski, M. Exact form factors in integrable quantum field theories: the sine-Gordon model (II). Nucl. Phys. B 2002, 620, 407. [Google Scholar] [CrossRef] [Green Version]
- Essler, F.H.; Konik, R.M. Applications of Massive Integrable Quantum Field Theories to Problems in Condensed Matter Physics. From Fields Strings Circumnavigat. Theoret. Phys. 2005, 684–830. [Google Scholar] [CrossRef] [Green Version]
- José, J.V.; Kadanoff, L.P.; Kirkpatrick, S.; Nelson, D.R. Renormalization, vortices, and symmetry-breaking perturbations in the two-dimensional planar model. Phys. Rev. B 1977, 16, 1217. [Google Scholar] [CrossRef]
- Zuber, J.B.; Itzykson, C. Quantum field theory and the two-dimensional Ising model. Phys. Rev. D 1977, 15, 2875. [Google Scholar] [CrossRef]
- Schroer, B.; Truong, T.T. The order/disorder quantum field operators associated with the two-dimewnsional Ising model in the continuum limit. Nucl. Phys. B 1978, 144, 80. [Google Scholar] [CrossRef]
- Ogilvie, M. Spin waves, vortices, Fermions and duality in the Ising and Baxter models. Ann. Phys. 1981, 136, 273. [Google Scholar] [CrossRef]
- Boyanovsky, D. Field theory of the two-dimensional Ising model: Conformal invariance, order and disorder, and bosonization. Phys. Rev. B 1989, 39, 6744. [Google Scholar] [CrossRef] [PubMed]
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sachdev, S.; Senthil, T.; Shankar, R. Finite-temperature properties of quantum antiferromagnets in a uniform magnetic field in one and two dimensions. Phys. Rev. B 1994, 50, 258. [Google Scholar] [CrossRef] [Green Version]
- Barthel, T.; Schollwöck, U.; Sachdev, S. Scaling of the thermal spectral function for quantum critical bosons in one dimension. arXiv 2012, arXiv:1212.3570. [Google Scholar]
- Blosser, D.; Bhartiya, V.K.; Voneshen, D.J.; Zheludev, A. $z=2$ Quantum Critical Dynamics in a Spin Ladder. Phys. Rev. Lett. 2018, 121, 247201. [Google Scholar] [CrossRef] [Green Version]
- Orignac, E.; Citro, R.; Di Dio, M.; De Palo, S. Vortex lattice melting in a boson-ladder in artificial gauge f ield. Phys. Rev. B 2017, 96, 014518. [Google Scholar] [CrossRef] [Green Version]
- Di Dio, M.; De Palo, S.; Orignac, E.; Citro, R.; Chiofalo, M.L. Persisting Meissner state and incommensurate phases of hard-core boson ladders in a flux. Phys. Rev. B 2015, 92, 060506. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Citro, R.; De Palo, S.; Victorin, N.; Minguzzi, A.; Orignac, E. Spectral Function of a Boson Ladder in an Artificial Gauge Field. Condens. Matter 2020, 5, 15. https://doi.org/10.3390/condmat5010015
Citro R, De Palo S, Victorin N, Minguzzi A, Orignac E. Spectral Function of a Boson Ladder in an Artificial Gauge Field. Condensed Matter. 2020; 5(1):15. https://doi.org/10.3390/condmat5010015
Chicago/Turabian StyleCitro, Roberta, Stefania De Palo, Nicolas Victorin, Anna Minguzzi, and Edmond Orignac. 2020. "Spectral Function of a Boson Ladder in an Artificial Gauge Field" Condensed Matter 5, no. 1: 15. https://doi.org/10.3390/condmat5010015
APA StyleCitro, R., De Palo, S., Victorin, N., Minguzzi, A., & Orignac, E. (2020). Spectral Function of a Boson Ladder in an Artificial Gauge Field. Condensed Matter, 5(1), 15. https://doi.org/10.3390/condmat5010015




