An Extended Dissipative Analysis of Fractional-Order Fuzzy Networked Control Systems
Abstract
:1. Introduction
- In this paper, the extended dissipativity and control synthesis is concerned for FFONCSs with time-varying delay. Up to now, there has been no result on these problems since solving their needs not only to deal with the extended dissipative performance for the underlying FFONCS but also to handle the Lyapunov-Krasovskii functional (LKF) theory.
- In this study, NCSs with time-varying delays, which takes place in the sensor-to-controller and controller-to-actuator channels are investigated.
- For the stabilization analysis of the proposed system model, novel LKF based on fractional order derivative is constructed, which can fully take more information about the sampling interval, using novel integral inequality and some new adequate conditions to ensure the asymptotic stability of FFONCS which are derived with respect to linear matrix inequalities (LMI).
- Finally, numerical simulations are proposed to illustrate the effectiveness and applicability of the suggested theories.
2. Problem Formulation and Preliminaries
3. Main Results
4. Robust Stabilisation for Extended Dissipative Criteria
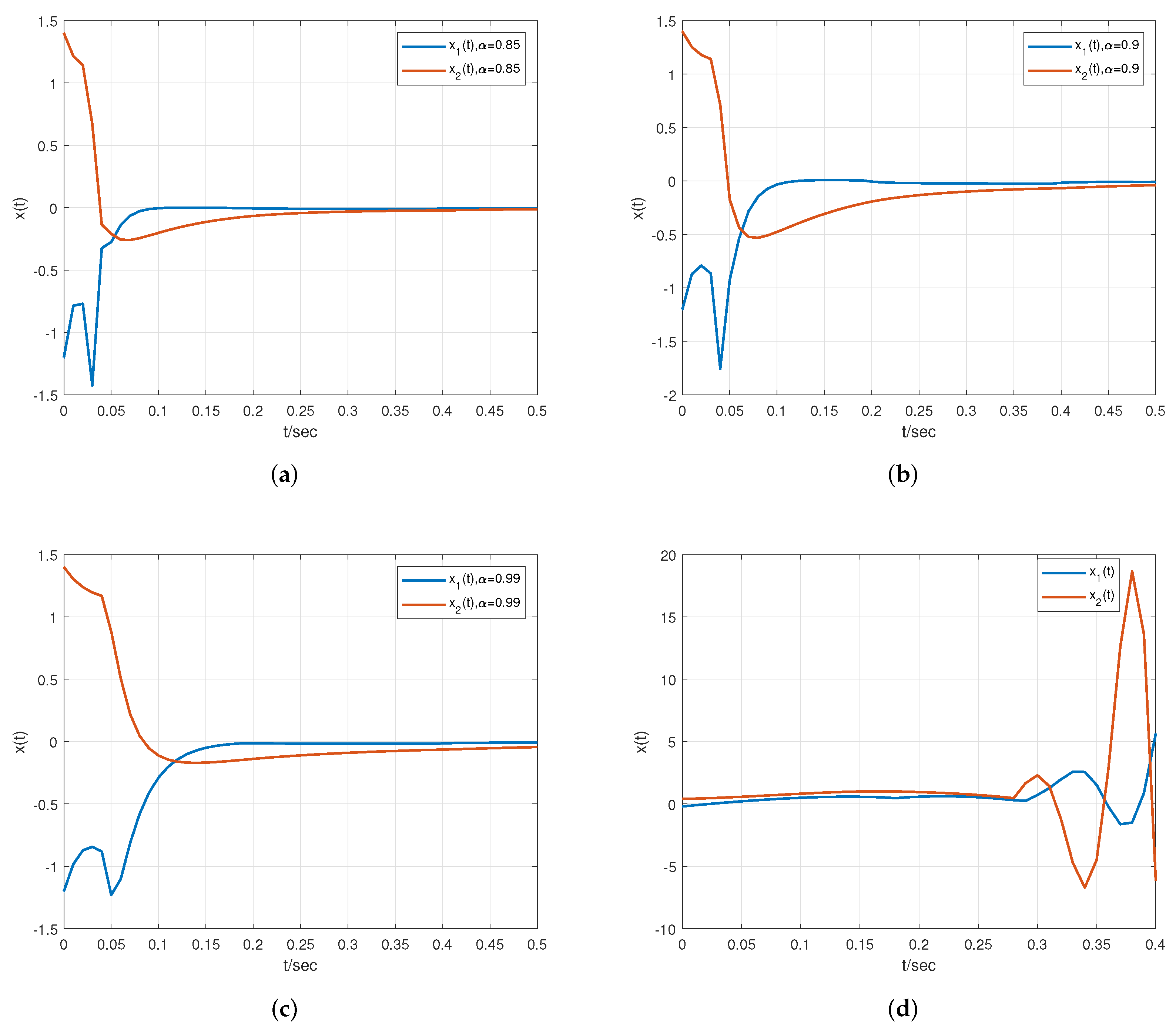
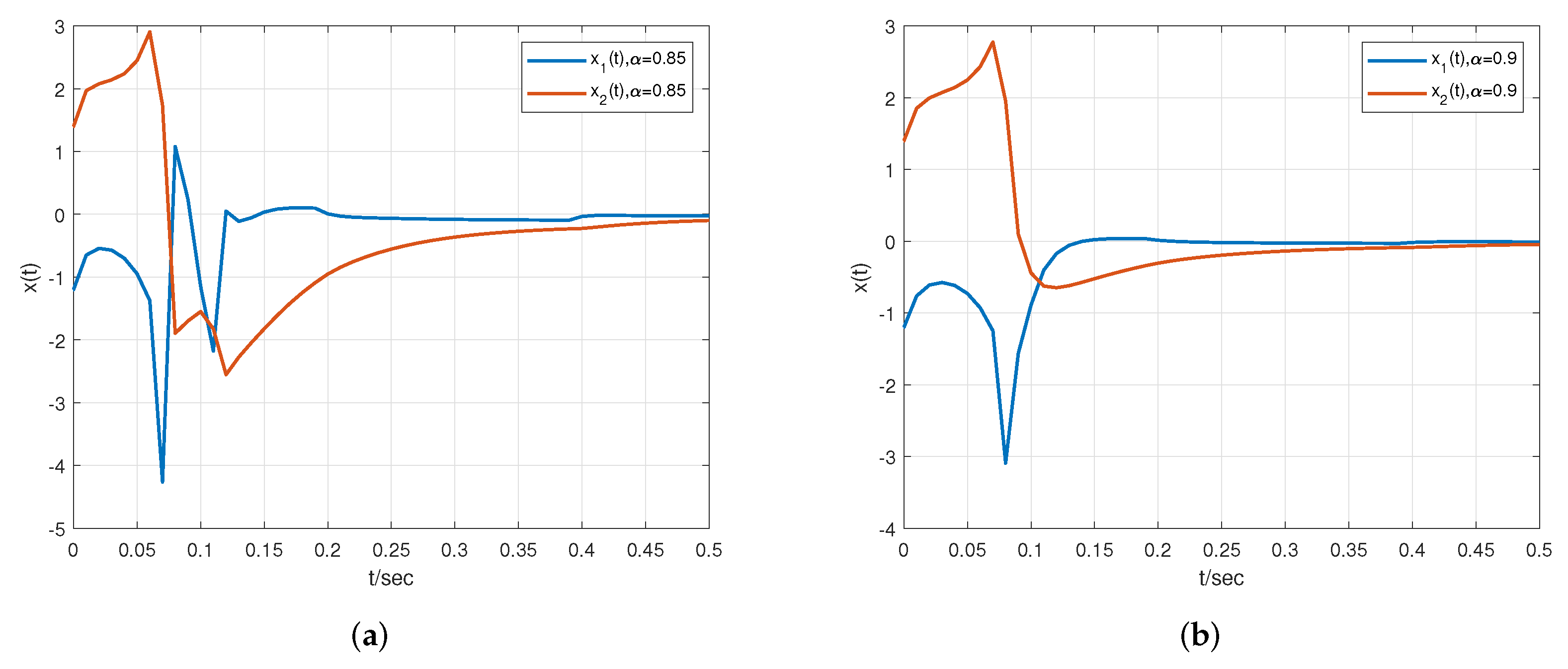
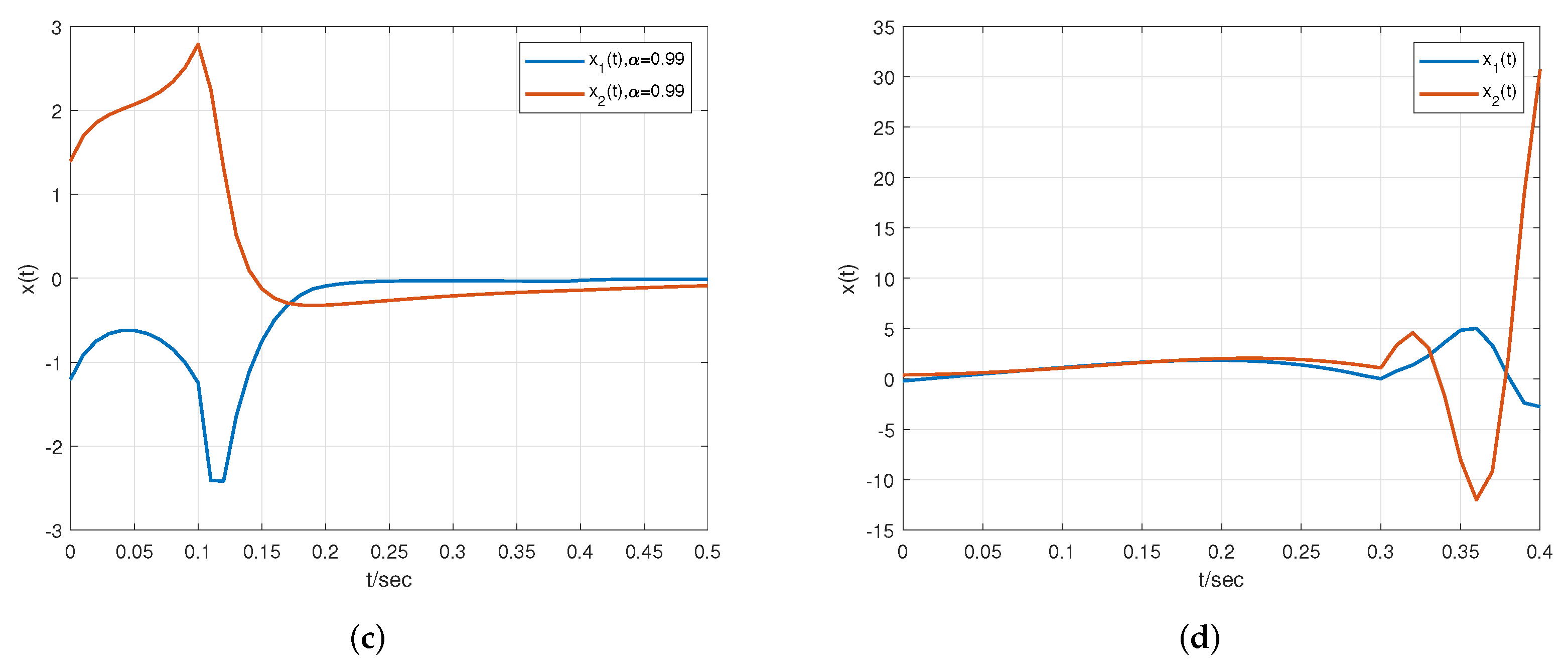
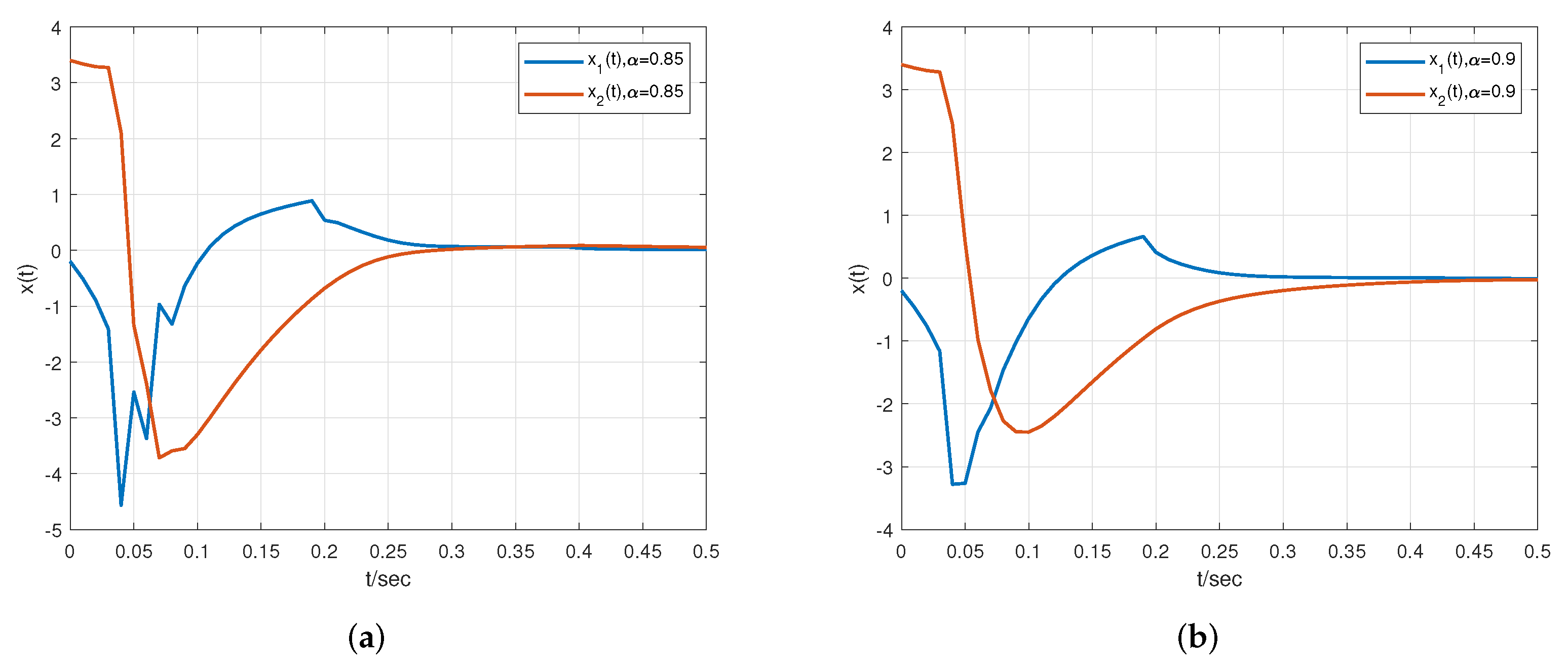
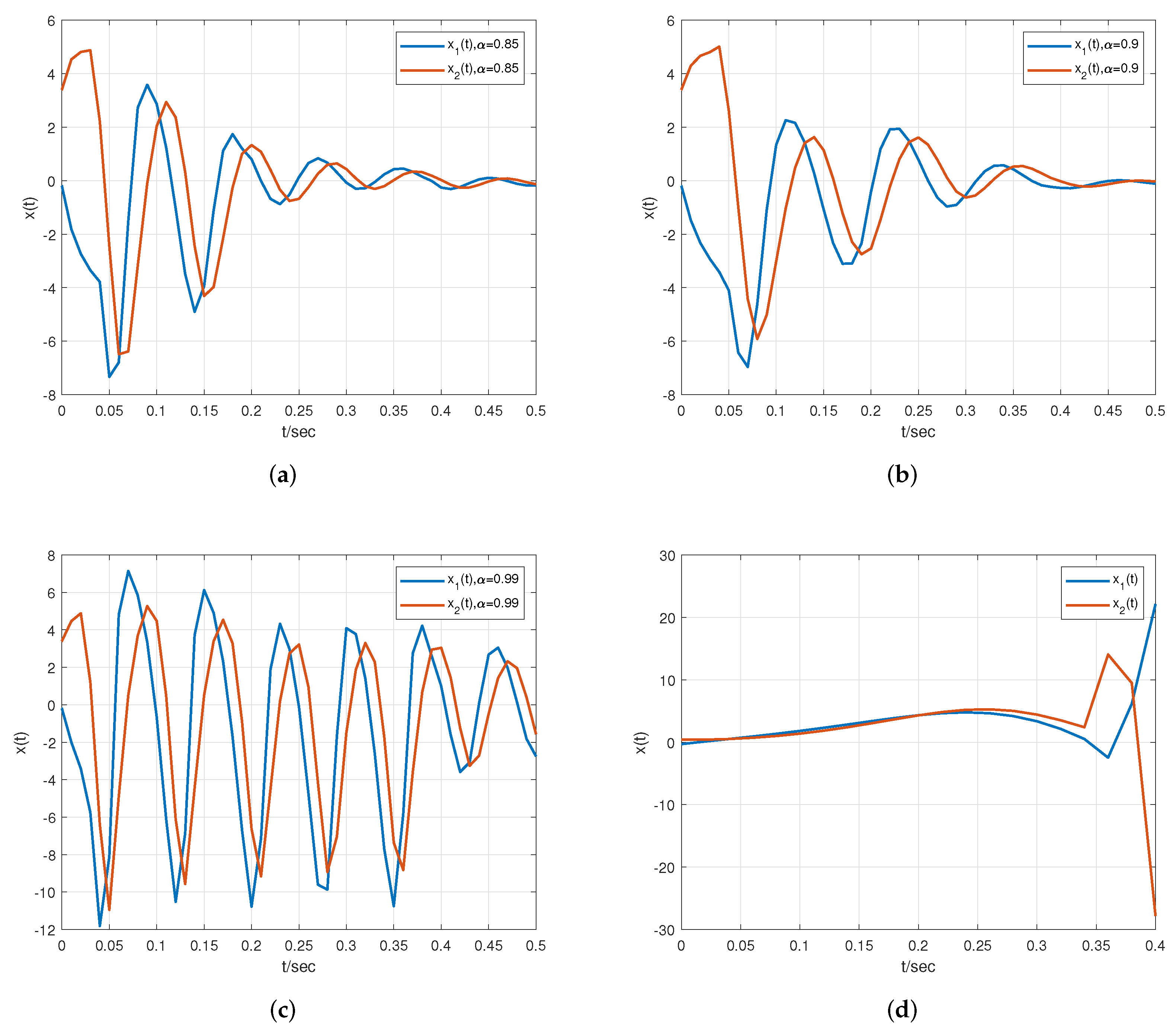
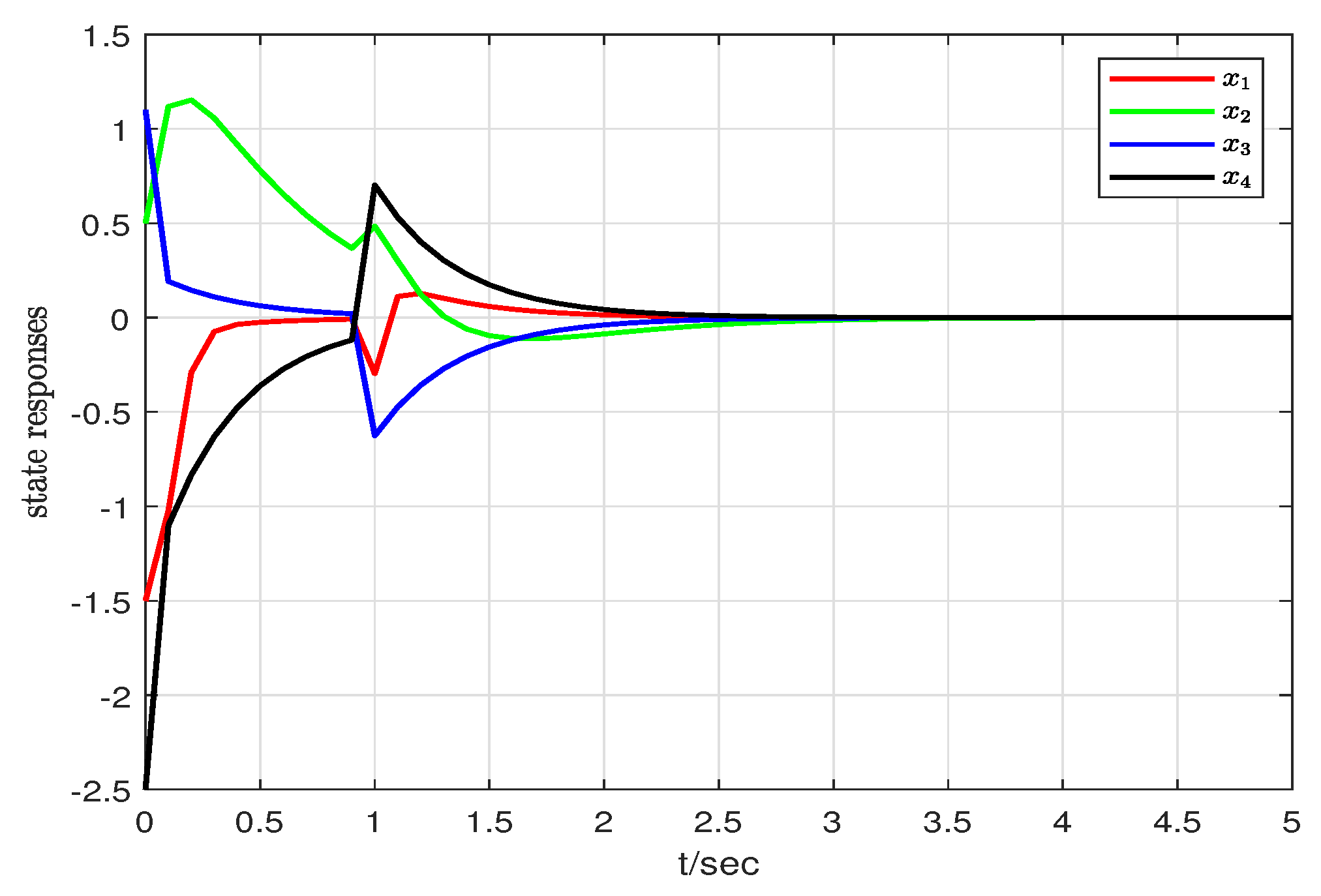
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, J.; Lam, J. Stability and performance analysis for positive fractional-order systems with time-varying delays. IEEE Trans. Autom. Control 2015, 61, 2676–2681. [Google Scholar] [CrossRef]
- Manigandan, M.; Muthaiah, S.; Nandhagopal, T.; Vadivel, R.; Unyong, B.; Gunasekaran, N. Existence results for coupled system of nonlinear differential equations and inclusions involving sequential derivatives of fractional order. AIMS Math. 2022, 7, 723–755. [Google Scholar] [CrossRef]
- Phat, V.; Niamsup, P.; Thuan, M.V. A new design method for observer-based control of nonlinear fractional-order systems with time-variable delay. Eur. J. Control 2020, 56, 124–131. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Ghaemi, S. Robust synchronization of uncertain fractional-order chaotic systems with time-varying delay. Nonlinear Dyn. 2018, 93, 1809–1821. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N. Improved approach for finite-time stability of nonlinear fractional-order systems with interval time-varying delay. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 1356–1360. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, M.; Cao, J.; Alsaedi, A. Synchronization control of Riemann-Liouville fractional competitive network systems with time-varying delay and different time scales. Int. J. Control Autom. Syst. 2018, 16, 1404–1414. [Google Scholar] [CrossRef]
- Liu, C.; Gong, Z.; Teo, K.L.; Wang, S. Optimal control of nonlinear fractional-order systems with multiple time-varying delays. J. Optim. Theory Appl. 2022, 193, 856–876. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Tenreiro Machado, J. Stability analysis of fractional order neutral-type systems considering time varying delays, nonlinear perturbations, and input saturation. Math. Methods Appl. Sci. 2020, 43, 10332–10345. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, H.; Cao, J.; Li, S. Composite learning fuzzy synchronization for incommensurate fractional-order chaotic systems with time-varying delays. Int. J. Adapt. Control Signal Process. 2019, 33, 1739–1758. [Google Scholar] [CrossRef]
- Mahmoudabadi, P.; Tavakoli-Kakhki, M. Improved stability criteria for nonlinear fractional order fuzzy systems with time-varying delay. Soft Comput. 2022, 26, 4215–4226. [Google Scholar] [CrossRef]
- Song, S.; Park, J.H.; Zhang, B.; Song, X. Observer-based adaptive hybrid fuzzy resilient control for fractional-order nonlinear systems with time-varying delays and actuator failures. IEEE Trans. Fuzzy Syst. 2019, 29, 471–485. [Google Scholar] [CrossRef]
- Karthick, S.; Sakthivel, R.; Ma, Y.K.; Mohanapriya, S.; Leelamani, A. Disturbance rejection of fractional-order TS fuzzy neural networks based on quantized dynamic output feedback controller. Appl. Math. Comput. 2019, 361, 846–857. [Google Scholar]
- Du, F.; Lu, J.G. Finite-time stability of fractional-order fuzzy cellular neural networks with time delays. Fuzzy Sets Syst. 2022, 438, 107–120. [Google Scholar] [CrossRef]
- Zhang, B.; Zhuang, J.; Liu, H.; Cao, J.; Xia, Y. Master–slave synchronization of a class of fractional-order Takagi–Sugeno fuzzy neural networks. Adv. Differ. Equ. 2018, 2018, 473. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Zhang, X. TS Fuzzy Control of Uncertain Fractional-Order Systems with Time Delay. J. Math. 2021, 2021, 6636882. [Google Scholar] [CrossRef]
- Sweetha, S.; Sakthivel, R.; Almakhles, D.; Priyanka, S. Non-Fragile Fault-Tolerant Control Design for Fractional-Order Nonlinear Systems with Distributed Delays and Fractional Parametric Uncertainties. IEEE Access 2022, 10, 19997–20007. [Google Scholar] [CrossRef]
- Hua, C.; Zhang, T.; Li, Y.; Guan, X. Robust output feedback control for fractional order nonlinear systems with time-varying delays. IEEE/CAA J. Autom. Sin. 2016, 3, 477–482. [Google Scholar]
- Liu, H.; Xie, G.; Gao, Y. Containment control of fractional-order multi-agent systems with time-varying delays. J. Frankl. Inst. 2019, 356, 9992–10014. [Google Scholar] [CrossRef]
- Chen, L.; Wu, R.; Yuan, L.; Yin, L.; Chen, Y.; Xu, S. Guaranteed cost control of fractional-order linear uncertain systems with time-varying delay. Optim. Control Appl. Methods 2021, 42, 1102–1118. [Google Scholar] [CrossRef]
- Hespanha, J.P.; Naghshtabrizi, P.; Xu, Y. A survey of recent results in networked control systems. Proc. IEEE 2007, 95, 138–162. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.A.; Yu, L. A robust control approach to stabilization of networked control systems with time-varying delays. Automatica 2009, 45, 2440–2445. [Google Scholar] [CrossRef]
- Peng, C.; Tian, Y.C.; Tade, M.O. State feedback controller design of networked control systems with interval time-varying delay and nonlinearity. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2008, 18, 1285–1301. [Google Scholar] [CrossRef]
- Song, X.; Tejado, I.; Chen, Y. Stabilization for fractional-order networked control systems with input time-varying delays. In Proceedings of the 2011 International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 11–13 August 2011; pp. 39–42. [Google Scholar]
- Zhang, B.; Zheng, W.X.; Xu, S. Filtering of Markovian jump delay systems based on a new performance index. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1250–1263. [Google Scholar] [CrossRef]
- Ali, M.S.; Vadivel, R.; Alsaedi, A.; Ahmad, B. Extended dissipativity and event-triggered synchronization for T–S fuzzy Markovian jumping delayed stochastic neural networks with leakage delays via fault-tolerant control. Soft Comput. 2020, 24, 3675–3694. [Google Scholar] [CrossRef]
- Vadivel, R.; Hammachukiattikul, P.; Gunasekaran, N.; Saravanakumar, R.; Dutta, H. Strict dissipativity synchronization for delayed static neural networks: An event-triggered scheme. Chaos Solitons Fractals 2021, 150, 111212. [Google Scholar] [CrossRef]
- Anbuvithya, R.; Sri, S.D.; Vadivel, R.; Gunasekaran, N.; Hammachukiattikul, P. Extended dissipativity and non-fragile synchronization for recurrent neural networks with multiple time-varying delays via sampled-data control. IEEE Access 2021, 9, 31454–31466. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Wang, L.; Lam, H.K. A new approach to stability and stabilization analysis for continuous-time Takagi–Sugeno fuzzy systems with time delay. IEEE Trans. Fuzzy Syst. 2017, 26, 2460–2465. [Google Scholar] [CrossRef] [Green Version]
- Gu, K.; Chen, J.; Kharitonov, V.L. Stability of Time-Delay Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Ali, M.S.; Narayanan, G.; Nahavandi, S.; Wang, J.L.; Cao, J. Global dissipativity analysis and stability analysis for fractional-order quaternion-valued neural networks with time delays. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4046–4056. [Google Scholar] [CrossRef]
- Shafiya, M.; Nagamani, G. Extended dissipativity criterion for fractional-order neural networks with time-varying parameter and interval uncertainties. Comput. Appl. Math. 2022, 41, 95. [Google Scholar] [CrossRef]
- Thi Hong, D.; Huu Sau, N.; Viet Thuan, M. Output feedback finite-time dissipative control for uncertain nonlinear fractional-order systems. Asian J. Control 2021, 24, 2284–2293. [Google Scholar] [CrossRef]
- Ji, Y.; Su, L.; Qiu, J. Design of fuzzy output feedback stabilization for uncertain fractional-order systems. Neurocomputing 2016, 173, 1683–1693. [Google Scholar] [CrossRef]
- Lin, C.; Chen, B.; Wang, Q.G. Static output feedback stabilization for fractional-order systems in T-S fuzzy models. Neurocomputing 2016, 218, 354–358. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z. Stabilisation of Takagi–Sugeno fuzzy singular fractional-order systems subject to actuator saturation. Int. J. Syst. Sci. 2020, 51, 3225–3236. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Cao, J.; Zhou, Y.; Wang, H. Positivity and stability analysis for fractional-order delayed systems: A T-S fuzzy model approach. IEEE Trans. Fuzzy Syst. 2020, 29, 927–939. [Google Scholar] [CrossRef]
- Senan, S.; Ali, M.S.; Vadivel, R.; Arik, S. Decentralized event-triggered synchronization of uncertain Markovian jumping neutral-type neural networks with mixed delays. Neural Netw. 2017, 86, 32–41. [Google Scholar] [CrossRef]
- Vadivel, R.; Srinivasan, S.; Wu, Y.; Gunasekaran, N. Study on bifurcation analysis and Takagi–Sugeno fuzzy sampled-data stabilization of permanent magnet synchronous motor systems. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Vadivel, R.; Suresh, R.; Hammachukiattikul, P.; Unyong, B.; Gunasekaran, N. Event-Triggered Filtering for Network-Based Neutral Systems With Time-Varying Delays via TS Fuzzy Approach. IEEE Access 2021, 9, 145133–145147. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vadivel, R.; Hammachukiattikul, P.; Vinoth, S.; Chaisena, K.; Gunasekaran, N. An Extended Dissipative Analysis of Fractional-Order Fuzzy Networked Control Systems. Fractal Fract. 2022, 6, 591. https://doi.org/10.3390/fractalfract6100591
Vadivel R, Hammachukiattikul P, Vinoth S, Chaisena K, Gunasekaran N. An Extended Dissipative Analysis of Fractional-Order Fuzzy Networked Control Systems. Fractal and Fractional. 2022; 6(10):591. https://doi.org/10.3390/fractalfract6100591
Chicago/Turabian StyleVadivel, Rajarathinam, Porpattama Hammachukiattikul, Seralan Vinoth, Kantapon Chaisena, and Nallappan Gunasekaran. 2022. "An Extended Dissipative Analysis of Fractional-Order Fuzzy Networked Control Systems" Fractal and Fractional 6, no. 10: 591. https://doi.org/10.3390/fractalfract6100591





